Какие функции: Основные элементарные функции: их свойства и графики

Функции. Основные виды, графики, способы задания

Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».

Понятие «функция» человеческим языком

Понятие «функция» пронизывает все сферы математики и не только.

Мы все знаем, что функция записывается как  , но можешь ли ты ответить, что обозначает эта формула?

Если да, то ты большой молодец! А если нет – не страшно! Сейчас быстренько во всем разберемся!

Так вот, функция отражает зависимость величин друг от друга: то есть при изменении одного числа  , по некоторому закону   изменяется  .

Зависимость, или взаимосвязь — вот ключевые слова при определении понятия функции.

СОДЕРЖАНИЕ СТАТЬИ

---

Попробуй самостоятельно придумать несколько примеров из жизни, где четко проявляется зависимость одного от другого.

И?… Не можешь придумать ни один пример? Как так! Смотри:

Допустим автомобиль движется со средней скоростью   км/ч, как тогда выразить зависимость пути   от времени  ?

Правильно:

 

То есть чем больше времени автомобилист проведет за рулем, тем больше расстояние он преодолеет на своем автомобиле. Чем не зависимость?

Что в этом случае будет  , что  , и как будет выражено в итоге  ? Проведем параллели между физической формулой и привычной нам записью функции  :

•  , то есть путь, который проедет автомобилист;
•  , время, которое он проведет в пути;
•   — зависимость пути от времени, учитывая, что скорость на всем пути постоянна.

Разобрался что к чему? Теперь перейдем на математический язык.

Итак. Еще раз смотрим на нашу формулу:

 

Слева стоит   — это и есть функция. За этой буквой может быть все что угодно: температура, скорость, сила, путь – неважно!   — зависимая величина. Она может зависеть от множества критериев. Например, как в нашем случае, зависимость пути от времени, проведенном в дороге при движении с постоянной скоростью.

Справа у нас стоит  . Эта величина переменная, или, как говорят математики, «аргумент». Логично, что чем больше времени проведет автомобилист в дороге, тем большее расстояние он проедет (конечно, если скорость будет постоянна, и он не встрянет намертво в московских пробках).

Справа у нас также есть  , за этим скрываются все действия, совершаемые над  . В нашем случае мы говорим, что  , а так как  км/ч, то под   скрывается умножение на  , вот мы и получаем —  .

Теперь думаю тебе все понятно?

Подведем краткий итог:

1.   — это формула, обозначающая функцию, то есть зависимость одной переменной от другой;
2.   — переменная величина, или, аргумент;
3.   — зависимая величина – изменяется при изменении аргумента, то есть   согласно какой-либо определенной формуле  , отражающей зависимость одной величины от другой.

Теперь, когда ты понял суть понятия «функция», знаешь что такое переменная величина, а что постоянная, посмотрим на определение функции, каким его дают математики.

Определение функции, каким его дают математики.

Функцией называется правило  , по которому каждому элементу   множества   ставится в соответствие единственный элемент   множества  .

 

Вроде и   есть… и   есть, и даже правило   есть, но что это за множества такие? «О них мы ни слова не говорили!» — воскликнешь ты.

Не паникуй!:) Множества – это очень просто, сейчас все-все проясним!

Вернемся к нашему примеру

Автомобилист едет с постоянной скоростью и проезжает расстояние, которое зависит от того, сколько времени он провел в пути.

Все верно?

Разбираемся дальше. Мы говорили, что  , это как раз и есть время, проведенное в пути.

Каким оно может быть?

Ты сейчас можешь быть крайней удивлен  такой постановкой вопроса, но все же, каким может быть это время? 

Правильно, чисто теоретически от   до  .

Вот ты сам и определил для нашего конкретного случая множество  , а иначе говоря, допустимые значения аргумента или область определения функции  .

Запомнить очень легко: что определяет нашу функцию? От чего зависит игрек, и что мы меняем?

Функцию определяет икс! Соответственно, область определения – это возможные значения

 .

Теперь давай рассматривать, что такое множество  .

Думаю, ты сам ответишь, что путь не может быть отрицательным, так что   в нашей с тобой придуманной функции так же может принимать значения в промежутке от   до  .

Это называется областью значений функции  , то есть множество  , которые существуют для данной функции.

Итак, сделаем небольшой вывод по последнему:

Допустимые значения аргумента, или область определения функции   — это то, что связано с возможными  , при которых функция имеет смысл. Область значений функции  — это то, какие значения принимает  , при допустимых значениях  .

Легко? То-то же.

Давай потренируемся находить области определения функции и ее допустимые значения.

Как найти область определения функции и ее допустимые значения

 

 

Для начала попробуй найти область определения функции:

Справился? Сравним​ ответы:

А)  

Б)  

В)  

Г)  

Все верно? Молодец!

Теперь попробуем найти область значений функции:

Нашел? Сравниваем:

А)  

Б)  

В)  

Г)  

Сошлось? Молодец!

Еще раз поработаем с графиками, только теперь чуть-чуть посложнее – найти и область определения функции, и область значений функции.

Как найти и область определения и область значений функции (продвинутый вариант)

Вот что получилось:

А)  
 

Б)  
 

С графиками, я думаю, ты разобрался. Теперь попробуем в соответствии с формулами найти область определения функции (если ты не знаешь как это сделать, прочитай раздел про ОДЗ):

1.  
2.  
3.  
4.  

Справился? Сверим

ответы:

1.  , так как подкоренное выражение   должно быть больше или равно нулю.
2.  , так как на ноль делить нельзя и подкоренное выражение не может быть отрицательным.
3.  , так как  , соответственно   при всех  .
4.  , так как на ноль делить нельзя.

Однако, у нас остался еще один не разобранный момент…

Еще раз повторю определение и сделаю на нем акцент:

Функцией называется правило  , по которому каждому элементу   множества   ставится в соответствие единственный элемент   множества  .

 

Заметил? Слово «единственный» — это очень-очень важный элемент нашего определения. Постараюсь объяснить тебе на пальцах.

Допустим, у нас есть функция, заданная прямой.  . При  , мы подставляем данное значение в наше «правило» и получаем, что  . Одному значению   соответствует одно значение  . Мы даже можем составить таблицу различных значений и построить график данной функции, чтобы убедится в этом.

 

А вот и график с нашими отмеченными точками:

Как ты убедился – графиком является прямая, в которой одному значению   соответствует одно значение   (данный факт показан красными линиями).

Соответственно, данная зависимость подходит под определение функции.

А что ты скажешь о такой зависимости:  , то есть параболы? Является ли она функцией? Давай составим также табличку значений:

 

«Смотри! — скажешь ты, -«  » встречается два раза!» Так быть может парабола не является функцией? Нет, является!

То, что « » встречается два раза далеко не повод обвинять параболу в неоднозначности!

Дело в том, что, при расчёте для  , мы получили один игрек. И при расчёте с   мы получили один игрек. Так что все верно, парабола является функцией. Посмотри на график:

Разобрался? Если нет, вот тебе жизненный пример сооовсем далекий от математики!

Допустим, у нас есть группа абитуриентов, познакомившихся при подаче документов, каждый из которых в разговоре рассказал, где он живет:

Согласись, вполне реально, что несколько ребят живут в одном городе, но невозможно, чтобы один человек жил в нескольких городах одновременно. Это как бы логичное представление нашей «параболы» — нескольким разным икс соответствует один и тот же игрек.

Теперь придумаем пример, когда зависимость не будет функцией. Допустим, эти же ребята рассказывали, на какие специальности они подали документы:

Здесь у нас совершенно другая ситуация: один человек может спокойно подать документы как на одно, так и на несколько направлений. То есть одному элементу   множества   ставится в соответствие несколько элементов   множества  . Соответственно, это не функция.

Проверим твои знания на практике.

Определи по рисункам, что является функцией, а что нет:

Разобрался? А вот и ответы:

• Функцией является – В,Е.
• Функцией не является – А, Б, Г, Д.

Ты спросишь почему? Да вот почему:

На всех рисунках кроме В) и Е) на один   приходится несколько  !

Уверена, теперь, ты с легкостью отличишь функцию от не функции, скажешь, что такое аргумент и что такое зависимая переменная, а так же определишь область допустимых значений аргумента и область определения функции. Приступаем к следующему разделу – как задать функцию?

Способы задания функции

Как ты думаешь, что означают слова «задать функцию»? Правильно, это значит объяснить всем желающим, о какой функции в данном случае идет речь. Причем объяснить так, чтобы каждый понял тебя правильно и нарисованные людьми по твоему объяснению графики функций были одинаковы.

Как это можно сделать? Как задать функцию? Самый простой способ, который уже не раз применялся в этой статье – с помощью формулы. Мы пишем формулу, и, подставляя в нее значение  , высчитываем значение  . А как ты помнишь, формула – это закон, правило, по которому нам и другому человеку становится ясно, как икс превращается в игрек.

Обычно, именно так и делают – в заданиях мы видим уже готовые функции, заданные формулами, однако, существуют и другие способы задать функцию, про которые все забывают, в связи с чем вопрос «как еще можно задать функцию?» ставит в тупик. Разберемся во всем по порядку, а начнем с аналитического способа.

Аналитический способ задания функции

Аналитический способ это и есть задание функции с помощью формулы. Это самый универсальный и исчерпывающий и однозначный способ. Если у тебя есть формула, то ты знаешь о функции абсолютно все – ты можешь составить по ней табличку значений, можешь построить график, определить, где функция возрастает, а где убывает, в общем, исследовать ее по полной программе.

Рассмотрим функцию  . Чему равно  ?

«Что это значит?» – спросишь ты. Сейчас объясню.

Напомню, что в записи   выражение в скобках

Определение функции

Определение функции

Функцией y = f(x) называется закон (правило, отображение), согласно которому, каждому элементу x множества X ставится в соответствие один и только один элемент y множества Y.

Множество X называется областью определения функции.
Множество элементов y ∈ Y, которые имеют прообразы во множестве X, называется множеством значений функции (или областью значений).

Область определения функции иногда называют множеством определения или множеством задания функции.

Элемент x ∈ X называют аргументом функции или независимой переменной.
Элемент y ∈ Y называют значением функции или зависимой переменной.

Само отображение  f  называется характеристикой функции.

Характеристика  f  обладает тем свойством, что если два элемента и из множества определения имеют равные значения: , то .

Символ, обозначающий характеристику, может совпадать с символом элемента значения функции. То есть можно записать так: . При этом стоит помнить, что y – это элемент из множества значений функции, а – это правило, по которому для элемента x ставится в соответствие элемент y.

Сам процесс вычисления функции состоит из трех шагов. На первом шаге мы выбираем элемент x из множества X. Далее, с помощью правила , элементу x ставится в соответствие элемент множества Y. На третьем шаге этот элемент присваивается переменной y.

Частным значением функции называют значение функции при выбранном (частном) значении ее аргумента.

Графиком функции  f  называется множество пар .

Сложные функции

Определение
Пусть заданы функции и . Причем область определения функции f содержит множество значений функции g. Тогда каждому элементу t из области определения функции g соответствует элемент x, а этому x соответствует y. Такое соответствие называют сложной функцией:  .

Сложную функцию также называют композицией или суперпозицией функций и иногда обозначают так:  .

В математическом анализе принято считать, что если характеристика функции обозначена одной буквой или символом, то она задает одно и то же соответствие. Однако, в других дисциплинах, встречается и другой способ обозначений, согласно которому отображения с одной характеристикой, но разными аргументами, считаются различными. То есть отображения и считаются различными. Приведем пример из физики. Допустим мы рассматриваем зависимость импульса от координаты . И пусть мы имеем зависимость координаты от времени . Тогда зависимость импульса от времени является сложной функцией . Но ее, для краткости, обозначают так: . При таком подходе и – это различные функции. При одинаковых значениях аргументов они могут давать различные значения. В математике такое обозначение не принято. Если требуется сокращение, то следует ввести новую характеристику. Например . Тогда явно видно, что и – это разные функции.

Действительные функции

Область определения функции и множество ее значений могут быть любыми множествами.
Например, числовые последовательности – это функции, областью определения которых является множество натуральных чисел, а множеством значений – вещественные или комплексные числа.
Векторное произведение тоже функция, поскольку для двух векторов и имеется только одно значение вектора . Здесь областью определения является множество всех возможных пар векторов . Множеством значений является множество всех векторов.
Логическое выражение является функцией. Ее область определения – это множество действительных чисел (или любое множество, в котором определена операция сравнения с элементом “0”). Множество значений состоит из двух элементов – “истина” и “ложь”.

В математическом анализе большую роль играют числовые функции.

Числовая функция – это функция, значениями которой являются действительные или комплексные числа.

Действительная или вещественная функция – это функция, значениями которой являются действительные числа.

Максимум и минимум

Действительные числа имеют операцию сравнения. Поэтому множество значений действительной функции может быть ограниченным и иметь наибольшее и наименьшее значения.

Действительная функция называется ограниченной сверху (снизу), если существует такое число M, что для всех выполняется неравенство:
.

Числовая функция называется ограниченной, если существует такое число M, что для всех :
.

Максимумом M (минимумом m) функции f, на некотором множестве X называют значение функции при некотором значении ее аргумента , при котором для всех ,
.

Верхней гранью или точной верхней границей действительной, ограниченной сверху функции называют наименьшее из чисел, ограничивающее область ее значений сверху. То есть это такое число s, для которого для всех и для любого , найдется такой аргумент , значение функции от которого превосходит s′: .
Верхняя грань функции может обозначаться так:
.

Верхней гранью неограниченной сверху функции является бесконечно удаленная точка .

Нижней гранью или точной нижней границей действительной, ограниченной снизу функции называют наибольшее из чисел, ограничивающее область ее значений снизу. То есть это такое число i, для которого для всех и для любого , найдется такой аргумент , значение функции от которого меньше чем i′: .
Нижняя грань функции может обозначаться так:
.

Нижней гранью неограниченной снизу функции является бесконечно удаленная точка .

Таким образом, любая действительная функция, на не пустом множестве X, имеет верхнюю и нижнюю грани. Но не всякая функция имеет максимум и минимум.

В качестве примера рассмотрим функцию , заданную на открытом интервале .
Она ограничена, на этом интервале, сверху значением 1 и снизу – значением 0:
для всех .
Эта функция имеет верхнюю и нижнюю грани:
.
Но она не имеет максимума и минимума.

Если мы рассмотрим туже функцию на отрезке , то она на этом множестве ограничена сверху и снизу, имеет верхнюю и нижнюю грани и имеет максимум и минимум:
для всех ;
;
.

Монотонные функции

Определения возрастающей и убывающей функций
Пусть функция определена на некотором множестве действительных чисел X. Функция называется строго возрастающей (строго убывающей), если для всех таких что выполняется неравенство:
.
Функция называется неубывающей (невозрастающей), если для всех таких что выполняется неравенство:
.

Определение монотонной функции
Функция называется монотонной, если она неубывающая или невозрастающая.

Многозначные функции

Пример многозначной функции. Различными цветами обозначены ее ветви. Каждая ветвь является функцией.

Как следует из определения функции, каждому элементу x из области определения, ставится в соответствие только один элемент из множества значений. Но существуют такие отображения, в которых элемент x имеет несколько или бесконечное число образов.

В качестве примера рассмотрим функцию арксинус: . Она является обратной к функции синус и определяется из уравнения:
(1)   .
При заданном значении независимой переменной x, принадлежащему интервалу , этому уравнению удовлетворяет бесконечно много значений y (см. рисунок).

Наложим на решения уравнения (1) ограничение. Пусть
(2)   .
При таком условии, заданному значению , соответствует только одно решение уравнения (1). То есть соответствие, определяемое уравнением (1) при условии (2) является функцией.

Вместо условия (2) можно наложить любое другое условие вида:
(2.n)   ,
где n – целое. В результате, для каждого значения n, мы получим свою функцию, отличную от других. Множество подобных функций является многозначной функцией. А функция, определяемая из (1) при условии (2.n) является ветвью многозначной функции.

Многозначная функция – это совокупность функций, определенных на некотором множестве.

Ветвь многозначной функции – это одна из функций, входящих в многозначную функцию.

Однозначная функция – это функция.

Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Автор: Олег Одинцов.     Опубликовано: 10-04-2018   Изменено: 08-10-2018

Элементарные функции и их графики

Понятие функции — одно из ключевых в математике. О нём подробно рассказано в статье «Что такое функция».

И конечно, в задачах части 2 Профильного ЕГЭ по математике без них не обойтись. А если вы выбрали технический или экономический вуз — первая же лекция по матанализу будет посвящена именно элементарным функциями и их графикам.

Но это не всё. Математические функции, изучением которых мы занимаемся, — это не что-то такое выдуманное или существующее только в замкнутом пространстве учебника. Они являются отражением реальных взаимосвязей и процессов, происходящих в природе и обществе.

Существует всего пять типов элементарных функций:

1. Степенные
К этому типу относятся линейные, квадратичные, кубические, , , Все они содержат выражения вида x^α.

2. Показательные
Это функции вида y = a^x

3. Логарифмические
y = log_ax.

4. Тригонометрические
В их формулах присутствуют синусы, косинусы, тангенсы и котангенсы.

5. Обратные тригонометрические
Содержат arcsinx, arccosx, arctgx, arcctgx.

Элементарными они называются потому, что из них, как из элементов, получаются все остальные, встречающиеся в школьном курсе. Например, y = x² · e^x — произведение квадратичной и показательной функций; y = sin(a^x) — сложная функция, то есть комбинация двух функций — показательной и тригонометрической.

Графики и свойства основных элементарных функций следует знать наизусть.

 

Показательная функция y = a^x

a > 1
0 < a < 1

 

Логарифмическая функция y = log_ax

a > 1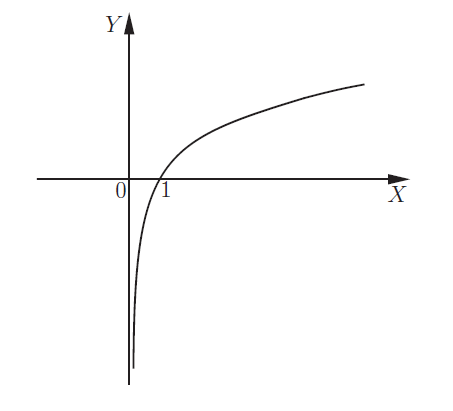
0 < a < 1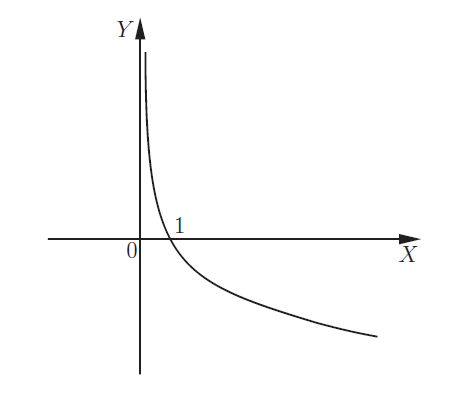

 

 

 

Выше приведены основные, «базовые» графики. А как будут выглядеть, например, графики функций y = sin(2x) или y = 4x² + 5? Об этом — статья «Преобразования графиков функций».

Обратите внимание: уравнения, которые вы решаете, обычно относятся к одному из этих пяти типов. Для каждого типа — свои способы решения. Это и понятно: они основаны на тех или иных свойствах функций.

Почему в уравнении 3^x = 3⁵ мы можем «отбросить» основания и записать, что x = 5? Да потому что показательная функция y = 3^x возрастает и каждое значение принимает только один раз.

Почему уравнение имеет бесконечно много решений, которые записываются в виде серии: , где n — целое? Потому что функция y = sinx — периодическая, то есть каждое свое значение принимает бесконечно много раз.

Зная графики элементарных функций, вы уже не запутаетесь с ОДЗ уравнений и неравенств. Вы сможете решать сложные задачи графически — а это часто во много раз легче и быстрее, чем аналитически.

Есть еще и такие уравнения, где слева и справа стоят функции разных типов. Для их решения есть графический способ, а также специальные приемы, о которых рассказывается в статье «Метод оценки».

« Основные свойства функции. » – Яндекс.Кью

К основным свойствам функции относятся:

1. Четность и нечетность функции

Функция называется четной, если
      – область определения функции симметрична относительно нуля
      – для любого х из области определения f(-x) = f(x)

!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image003.gif

График четной функции симметричен относительно оси 0y

Функция называется нечетной, если
      – область определения функции симметрична относительно нуля
      – для любого х из области определения f(-x) = –f(x)

!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image004.gif

График нечетной функции симметричен относительно начала координат.

2.Периодичность

Функция f(x) называется периодической с периодом !https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image005.gif, если для любого х из области определения f(x) = f(x+Т) = f(x-Т).

!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image006.gif

График периодической функции состоит из неограниченно повторяющихся одинаковых фрагментов.

3. Монотонность (возрастание, убывание)

Функция f(x) возрастает на множестве Р , если для любых x1 и x2 из этого множества, таких, что x1 < x2 выполнено неравенство f(x1)< f(x2).

!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image011.gif

Функция f(x) убывает на множестве Р , если для любых x1 и x2 из этого множества, таких, что x1 < x2 выполнено неравенство f(x1) > f(x2).

!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image013.gif

4. Экстремумы

Точка Хmax называется точкой максимума функции f(x) , если для всех х из некоторой окрестности Хmax , выполнено неравенство f(х)!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image014.gif f(Xmax).

Значение Ymax=f(Xmax) называется максимумом этой функции.

!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image015.gif

Хmax – точка максимума
Уmax – максимум

Точка Хmin называется точкой минимума функции f(x) , если для всех х из некоторой окрестности Хmin , выполнено неравенство f(х)!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image016.gif f(Xmin).

Значение Ymin=f(Xmin) называется минимумом этой функции.

!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image017.gif

Xmin – точка минимума
Ymin – минимум

Xmin, Хmax – точки экстремума
Ymin, Уmax – экстремумы.

5. Нули функции

Нулем функции y = f(x) называется такое значение аргумента х , при котором функция обращается в нуль: f(x) = 0.

!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image018.gif

Х1,Х2,Х3 – нули функции y = f(x).

Виды функций и их свойства. — Студопедия

1. Постоянная функция- функция, заданная формулой у=b,где b-некоторое число. Графиком постоянной функции у=b является прямая, параллельная оси абсцисс и проходящая через точку (0;b) на оси ординат

2. Прямая пропорциональность- функция, заданная формулой у=kx,где к0. Число k называется коэффициентом пропорциональности.

Cвойства функции y=kx:

1. Область определения функции- множество всех действительных чисел

2. y=kx — нечетная функция

3. При k>0 функция возрастает, а при k<0 убывает на всей числовой прямой

3)Линейная функция- функция, которая задана формулой y=kx+b, где kиb-действительные числа. Если в частности, k=0, то получаем постоянную функцию y=b; если b=0, то получаем прямую пропорциональность y=kx.

Свойства функции y=kx+b:

1. Область определения- множество всех действительных чисел

2. Функция y=kx+b общего вида, т.е. ни чётна, ни нечётна.

3. При k>0функция возрастает, а при k<0 убывает на всей числовой прямой

Графиком функции является прямая.

4)Обратная пропорциональность- функция, заданная формулой y=k/х,где k0 Число k называют коэффициентом обратной пропорциональности.

Свойства функции y=k/x:

1. Область определения- множество всех действительных чисел кроме нуля

2. y=k/x- нечетная функция

3. Если k>0, то функция убывает на промежутке (0;+) и на промежутке (-;0). Если k<0, то функция возрастает на промежутке (-;0) и на промежутке (0;+).

Графиком функции является гипербола.

5)Функция y=x²

Свойства функции y=x²:

1. Область определения- вся числовая прямая

2. y=x² —четная функция

3. На промежутке [0;+) функция возрастает

4. На промежутке (-;0] функция убывает

Графиком функции является парабола.

6)Функция y=x³

Свойства функции y=x³:

1. Область определения- вся числовая прямая

2. y=x³ —нечетная функция

3. Функция возрастает на всей числовой прямой

Графиком функции является кубическая парабола

7)Степенная функция с натуральным показателем- функция, заданная формулой y=xⁿ, где n— натуральное число. При n=1 получаем функцию y=x, ее свойства рассмотрены в п.2. При n=2;3 получаем функции y=x²; y=x³. Их свойства рассмотрены выше.

Пусть n- произвольное четное число, большее двух: 4,6,8… В этом случае функция y=xⁿ обладает теми же свойствами, что и функция y=x². График функции напоминает параболу y=x², только ветви графика при |х|>1 тем круче идут вверх, чем больше n, а при |х|<1 тем “теснее прижимаются” к оси Х, чем больше n.

Пусть n- произвольное нечетное число, большее трех: 5,7,9… В этом случае функция y=xⁿ обладает теми же свойствами, что и функция y=x³. График функции напоминает кубическую параболу.

Примеры

графиков степенных функций, соответствующих различным показателям

степени, приведены на рис

Графики простейших функций — линейная, параболы, гиперболы, экспоненты, показательные, степенные, логарифмическая, синус, косинус, тангенс, котангенс изучаемых в школе Справочная таблица. Примерно 7-9 класс (13-15 лет)

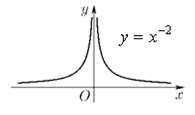
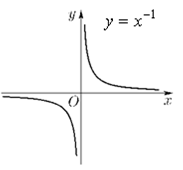
Название функции	Формула функции	График функции	Название графика	Комментарий
Линейная, прямая пропорциональность	y = kx		Прямая	Cамый простой частный случай линейной зависимости — прямая пропорциональность у = kx, где k ≠ 0 — коэффициент пропорциональности. На рисунке пример для k = 1, т.е. фактически приведенный график иллюстрирует функциональную зависимость, которая задаёт равенство значения функции значению аргумента.
Линейная, прямая пропорциональность со сдвигом	y = kx + b		Прямая	Общий случай линейной зависимости: коэффициенты k и b — любые действительные числа. Здесь k = 0.5, b = -1.
Квадратичная функция	y = x2		Парабола	Простейший случай квадратичной зависимости — симметричная парабола с вершиной в начале координат.
Квадратичная функция	y = ax2 + bx + c		Парабола	Общий случай квадратичной зависимости: коэффициент a — произвольное действительное число не равное нулю (a принадлежит R, a ≠ 0), b, c — любые действительные числа
Степенная функция	y = x3		Кубическая парабола	Самый простой случай для целой нечетной степени. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций».
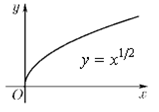
Степенная — корень квадратный	y = x1/2		График функции y = √x	Самый простой случай для дробной степени (x1/2 = √x). Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций».
Степенная — обратная пропорциональность	y = k/x		Гипербола	Самый простой случай для целой отрицательной степени (1/x = x-1) — обратно-пропорциональная зависимость. Здесь k = 1.
Показательная функция	y = ex		Экспонента	Экспоненциальной зависимостью называют показательную функцию для основания e — иррационального числа примерно равного 2,7182818284590…
Показательная функция	y = ax		График показательной функции а>1	Показательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = 2x (a = 2 > 1).
Показательная функция	y = ax		График показательной функции 0<a<1	Показательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = 0,5x (a = 1/2 < 1).
Логарифмическая функция	y = ln(x)		График логарифмической функции — натуральный логарифм	График логарифмической функции для основания e (натурального логарифма) иногда называют логарифмикой.
Логарифмическая функция	y = logax		График логарифмической функции — логарифм по основанию а>1	Логарифмы определены для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = log2x (a = 2 > 1).
Логарифмическая функция	y = logax		График логарифмической функции 0<a<1	Логарифмы определены для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = log0,5x (a = 1/2 < 1).
Синус	y = sinx		Синусоида	Тригонометрическая функция синус. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций».
Косинус	y = cosx		Косинусоида	Тригонометрическая функция косинус. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций».
Тангенс	y = tgx		Тангенсоида	Тригонометрическая функция тангенс. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций».
Котангенс	y = сtgx		Котангенсоида	Тригонометрическая функция котангенс. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций».

ФУНКЦИЯ — это… Что такое ФУНКЦИЯ?

ФУНКЦИЯ — (лат. functio – исполнение) обязанность, круг деятельности. «Функция – это существование, мыслимое нами в действии» (Гёте). Наука о функциях органов живых существ – физиология; специальная наука о функциях нервной системы – физиология органов… …   Философская энциклопедия

функция — Команда или группа людей, а также инструментарий или другие ресурсы, которые они используют для выполнения одного или нескольких процессов или деятельности. Например, служба поддержки пользователей. Этот термин также имеет другое значение:… …   Справочник технического переводчика

функция — См …   Словарь синонимов

ФУНКЦИЯ — (лат. functio). В физиологии: отправление каким либо органом ему одному свойственных действий, как напр., дыхание, пищеварение. 2) в математике: величина, зависящая от другой переменной величины. Словарь иностранных слов, вошедших в состав… …   Словарь иностранных слов русского языка

Функция — [function] 1. Зависимая переменная величина; 2. Соответствие y=f(x) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой величины x (аргумента или независимой переменной) соответствует определенное значение… …   Экономико-математический словарь

Функция — (от латинского functio исполнение, осуществление), 1) деятельность, обязанность, работа; внешнее проявление свойств какого–либо объекта в данной системе отношений (например, функция органов чувств, функция денег). 2) Функция в социологии роль,… …   Иллюстрированный энциклопедический словарь

ФУНКЦИЯ — (от лат. functio исполнение осуществление),..1) деятельность, обязанность, работа; внешнее проявление свойств какого либо объекта в данной системе отношений (напр., функция органов чувств, функция денег)2)] Функция в социологии роль, которую… …   Большой Энциклопедический словарь

ФУНКЦИЯ — ФУНКЦИЯ, в математике одно из основных понятий, выражение, определяющее регулярную зависимость между двумя множествами переменных величин, заключающуюся в том, что каждому элементу одного множества соответствует определенная, единственная… …   Научно-технический энциклопедический словарь

ФУНКЦИЯ — (function) Взаимосвязь между двумя и более переменными. Если у является функцией от х и записывается в виде y=f(x), то, если значение аргумента х известно, функция позволяет показывает, как найти значение у. Если у – однозначная функция от х, то… …   Экономический словарь

ФУНКЦИЯ —         (от лат. исполняю, совершаю)         центр, понятие в методологии функционального и структурно функционального анализа об в. Понятие “Ф.” стало активно использоваться в социальных науках со вт. пол. 19 в. в связи с проникновением сначала… …   Энциклопедия культурологии

Функция

| Определение, типы, примеры и факты

Функция , в математике выражение, правило или закон, определяющий связь между одной переменной (независимой переменной) и другой переменной (зависимой переменной). Функции повсеместно используются в математике и необходимы для формулирования физических соотношений в науках. Современное определение функции было впервые дано в 1837 году немецким математиком Петером Дирихле:

Подробнее по этой теме

Анализ

: Функции

Исчисление познакомило математиков со многими новыми функциями, предоставив новые способы их определения, например, с помощью бесконечных рядов и интегралов….

Если переменная y так связана с переменной x , что всякий раз, когда числовое значение присваивается x , существует правило, согласно которому определяется уникальное значение y , тогда y считается функцией независимой переменной x .

Это соотношение обычно обозначается как y = f ( x ). Помимо f ( x ), для представления функций независимой переменной x часто используются другие сокращенные символы, такие как g ( x ) и P ( x ), особенно когда природа функции неизвестна или не определена.

Общие функции

Многие широко используемые математические формулы являются выражениями известных функций. Например, формула для площади круга A = π r ² дает зависимую переменную A (площадь) как функцию независимой переменной r (радиус). Функции, включающие более двух переменных, также распространены в математике, что можно увидеть в формуле для площади треугольника: A = b h /2, которая определяет A как функцию от обоих b (основание) и h (высота).В этих примерах физические ограничения вынуждают независимые переменные быть положительными числами. Когда независимым переменным также разрешено принимать отрицательные значения — таким образом, любое действительное число — функции известны как функции с действительными значениями.

Britannica Premium: удовлетворение растущих потребностей искателей знаний. Получите 30% подписки сегодня. Подпишись сейчас

Формула площади круга является примером полиномиальной функции. Общий вид таких функций: P ( x ) = a ₀ + a ₁ x + a ₂ x ² + ⋯ + a _n х ^н , где указаны коэффициенты ( a ₀ , a ₁ , a ₂ ,…, a _n ), x может быть любым действительным числом, и все степени x — это счетные числа (1, 2, 3,…).(Когда степень x может быть любым действительным числом, результат известен как алгебраическая функция.) Полиномиальные функции изучались с давних времен из-за их универсальности — практически любые отношения, включающие действительные числа, можно точно аппроксимировать с помощью полиномиальная функция. Полиномиальные функции характеризуются наивысшей степенью независимой переменной. Для таких степеней от одного до пяти обычно используются специальные названия: линейная, квадратичная, кубическая, квартичная и квинтическая.

Полиномиальным функциям может быть дано геометрическое представление с помощью аналитической геометрии. Независимая переменная x нанесена на ось x (горизонтальная линия), а зависимая переменная y нанесена вдоль оси y (вертикальная линия). График функции состоит из точек с координатами ( x , y ), где y = f ( x ). Например, на рисунке показан график кубического уравнения f ( x ) = x ³ — 3 x + 2.

График кубического уравнения f ( x ) = x ³ — 3 x + 2. Точки на графике показывают, где происходят изменения кривизны. Encyclopædia Britannica, Inc.

Другой распространенный тип функций, который изучается с древних времен, — это тригонометрические функции, такие как sin x и cos x , где x — это мера угла ( см. Рисунок ). Из-за своей периодической природы тригонометрические функции часто используются для моделирования повторяющегося поведения или «циклов».Негебраические функции, такие как экспоненциальные и тригонометрические функции, также известны как трансцендентные функции.

графики некоторых тригонометрических функций Обратите внимание, что каждая из этих функций периодическая. Таким образом, функции синуса и косинуса повторяются каждые 2π, а функции тангенса и котангенса повторяются через каждые π. Encyclopædia Britannica, Inc.

Комплексные функции

Практическое применение функций, переменные которых являются комплексными числами, не так легко проиллюстрировать, но, тем не менее, они очень обширны.Они встречаются, например, в электротехнике и аэродинамике. Если комплексная переменная представлена ​​в виде z = x + i y , где i — мнимая единица (квадратный корень из -1), а x и y — действительные переменных ( см. рисунок ), можно разделить сложную функцию на действительную и мнимую части: f ( z ) = P ( x , y ) + i Q ( x , y ).

точка в комплексной плоскости Точка в комплексной плоскости. В отличие от действительных чисел, которые могут быть расположены одним числом со знаком (положительным или отрицательным) вдоль числовой прямой, для комплексных чисел требуется плоскость с двумя осями, одна ось для компонента действительного числа и одна ось для мнимого компонента. Хотя комплексная плоскость выглядит как обычная двумерная плоскость, где каждая точка определяется упорядоченной парой действительных чисел ( x , y ), точка x + i y является одной число. Encyclopædia Britannica, Inc.

Меняя ролями независимых и зависимых переменных в заданной функции, можно получить обратную функцию. Обратные функции делают то, что подразумевает их название: они отменяют действие функции, чтобы вернуть переменную в исходное состояние. Таким образом, если для данной функции f ( x ) существует функция g ( y ) такая, что g ( f ( x )) = x и f ( g ( y )) = y , тогда g называется обратной функцией для f и обозначается обозначением f ^-1 , где по соглашению переменные меняются местами.Например, функция f ( x ) = 2 x имеет обратную функцию: f ⁻¹ ( x ) = x /2.

Прочие функциональные выражения

Функция может быть определена с помощью степенного ряда. Например, бесконечный ряд можно использовать для определения этих функций для всех комплексных значений x . При необходимости можно использовать другие типы серий, а также бесконечное количество продуктов. Важным случаем является ряд Фурье, выражающий функцию через синусы и косинусы:

Такие представления имеют большое значение в физике, особенно при изучении волнового движения и других колебательных явлений.

Иногда функции удобнее всего определять с помощью дифференциальных уравнений. Например, y = sin x является решением дифференциального уравнения d ² y / d x ² + y = 0, где y = 0, d y / d x = 1, когда x = 0; y = cos x является решением того же уравнения, имеющего y = 1, d y / d x = 0, когда x = 0.

The Editors of Encyclopaedia Britannica Эта статья была недавно отредактирована и обновлена ​​Адамом Августином, управляющим редактором, справочное содержание.

Узнайте больше в этих связанных статьях Britannica:

.

внутренних функций Python — для чего они нужны? — Настоящий Python

Давайте рассмотрим три основных причины написания внутренних функций.

Примечание: В Python функции — это «граждане первого класса». Это означает, что они находятся на одном уровне с любым другим объектом (целыми числами, строками, списками, модулями и т. Д.). Вы можете динамически создавать или уничтожать их, передавать другим функциям, возвращать их как значения и так далее.

В этом руководстве используется Python версии 3.4.1.

Получите шпаргалку по Python (PDF) и изучите основы Python 3, такие как работа с типами данных, словарями, списками и функциями Python:

Инкапсуляция

Вы используете внутренние функции, чтобы защитить их от всего, что происходит вне функции, то есть они скрыты от глобальной области видимости.

Вот простой пример, подчеркивающий эту концепцию:

  def внешний (num1):
    def inner_increment (num1): # Скрыто от внешнего кода
        вернуть num1 + 1
    число2 = внутренний_инкремент (число1)
    печать (число1, число2)

внутренний_инкремент (10)
# внешний (10)
  

Попробуйте позвонить по номеру inner_increment () :

  Traceback (последний звонок последний):
  Файл "inner.py", строка 7, в 
    inner_increment ()
NameError: имя 'inner_increment' не определено
  

Теперь закомментируйте вызов inner_increment () и раскомментируйте вызов внешней функции, outer (10) , передав 10 в качестве аргумента:

Примечание: Имейте в виду, что это всего лишь пример.Хотя этот код действительно достигает желаемого результата, вероятно, лучше сделать inner_increment () «частной» функцией верхнего уровня, используя начальный символ подчеркивания: _inner_increment () .

Следующий рекурсивный пример — немного лучший вариант использования вложенной функции:

  деф-факториал (число):

    # Обработка ошибок
    если не isinstance (число, целое число):
        Raise TypeError ("К сожалению," число "должно быть целым числом.")
    если не число> = 0:
        поднять ValueError ("Извините.'number' должно быть нулем или положительным. ")

    def inner_factorial (число):
        если число <= 1:
            возврат 1
        номер возврата * inner_factorial (число-1)
    return inner_factorial (число)

# Вызов внешней функции.
печать (факториал (4))
  

Проверьте это тоже. Одним из основных преимуществ использования этого шаблона проектирования является то, что выполнение всех аргументов

.

c ++ - что означает объем функций?

Переполнение стека

1. Около
2. Товары
3. Для команд

1. Переполнение стека Общественные вопросы и ответы
2. Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
3. Вакансии Программирование и связанные с ним технические возможности карьерного роста
4. Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
5. Реклама Обратитесь к разработчикам и технологам со всего мира
6. О компании

Загрузка…

.