Калькулятор алгебра логика: Математическая логика · oнлайн с подробным объяснением

Содержание

Кафедры — Механико-математический факультет

НГУ
Механико-математический факультет
Кафедры
Кафедра дискретной математики и информатики

Задать вопрос

О кафедре

Подробнее

Одна из самых молодых кафедр механико-математического факультета, кафедра дискретной математики и информатики, была организована в 2003 году.
Заведующим кафедрой является академик РАН С.С. Гончаров. Коллектив кафедры в основном состоит из сотрудников Лаборатории логических систем и Лаборатории теории вычислимости и прикладной логики Института математики имени С.Л. Соболева СО РАН.

Сотрудниками кафедры являются такие известные специалисты по математической логике как А.С. Морозов, Н.Т. Когабаев, В.Л. Селиванов и др.
Кафедра сотрудничает с ведущими университетами России и мира. Студенты, специализирующиеся на кафедре, имеют возможность принимать участие в работе научных конференций самого высокого уровня и общаться с учеными, работающими на переднем крае современной науки.

Направления работы

теория вычислимости и ее приложения
теория вычислимых моделей
проблемы существования вычислимых и разрешимых моделей
проблемы характеризации моделей различных алгоритмических размерностей
вычислимые классы моделей
общая теория вычислимых нумераций для различных классов иерархий
проблемы формальных языков и их семантики
теория автоматных структур
проблемы построения гибридных систем на основе определимости
взаимоотношения различных типов вычислимости над абстрактными структурами
проблемы построения денотационных семантик
дискретные модели в генетике
проблемы обнаружения закономерностей

Состав кафедры

Заведующий кафедрой

Гончаров Сергей Савостьянович

д. ф.-м.н., профессор, академик РАН

Телефон: +7 (383) 333 2892

E-mail: [email protected]

Секретарь кафедры

Оспичев Сергей Сергеевич

к.ф.-м.н.

Телефон: +7 (383) 329 7684

E-mail: [email protected]

Преподаватели

Подробнее

Профессора

Бокуть Леонид Аркадьевич, д.ф.-м.н.
Витяев Евгений Евгеньевич, д.ф.-м.н.
Морозов Андрей Сергеевич, д.ф.-м.н
Пальчунов Дмитрий Евгеньевич, д.ф.-м.н.
Селиванов Виктор Львович, д.
ф.-м.н.

Доценты

Викентьев Александр Александрович, к.ф.-м.н.
Когабаев Нурлан Талгатович, к.ф.-м.н.
Кравченко Александр Владимирович, к.ф.-м.н.
Кудинов Олег Викторович, к.ф.-м.н.
Стукачев Алексей Ильич, к.ф.-м.н.
Хисамиев Асылхан Назифович, к.ф.-м.н.
Швидефски Марина Владимировна, д.ф.-м.н.

Старшие преподаватели

Власов Владимир Николаевич, к.ф.-м.н.
Орлов Юрий Львович, д.б.н., профессор РАН
Оспичев Сергей Сергеевич, к.ф.-м.н.

Ассистенты

Александрова Светлана Анатольевна
Баженов Николай Алексеевич, к.ф.-м.н.
Доржиева Марина Валериановна
Леонтьева Маргарита Николаевна
Марчук Маргарита Игоревна, к.ф.-м.н.

Сотрудники, готовые работать со студентами

Подробнее

Гончаров Сергей Савостьянович

Научные интересы:

Разрешимые модели и арифметические модели, в частности моделей теорий Эренфойхта (проблема Морли), теорий со счетным числом счетных моделей ( проблема Гончарова-Миллара).
Конструктивные модели, модели полиномиальной сложности и других сложностных классов ( проблемы существования, 10 проблема Гильберта, проблемы степеней автоустойчивости, степеней сложности представлений и т.д.).
Вычислимые нумерации (проблема Ершова о числе минимальных нумераций), вычислимые нумерации для классов иерархий арифметической, гиперарифметической, аналитической , иерархии Ершова, Иерархии Найт, вычислимых функционалов конечных типов.
Теория моделей, проблемы характеризации счетных моделей, в частности для Эренфойхтовых теорий.
Проблемы логического программирования на основе подхода Ершова-Гончарова-Свириденко и их применения к проблемам искусственного интеллекта, теории автоматической верификации и доказательства, онтологии и алгебраические абстрактные типы.

Ученики С.С.Гончарова, защитившие кандидатские и докторские диссертациию:
https://www.genealogy. math.ndsu.nodak.edu/id.php?id=59029

https://www.scopus.com/authid/detail.uri?authorId=56377536800#

Контакты: [email protected], +7 (383) 333 2892

Оспичев Сергей Сергеевич

Научные интересы: Математическая логика, теория вычислимости, теория нумераци, машинное обучение, семантическое программирование

Контакты: [email protected] ospichev.github.io

Марина Владимировна Швидефски

Научные интересы: Универсальная алгебра, теория решеток

Контакты: [email protected]

Орлов Юрий Львович

Научные интересы: Компьютерный анализ генетическихтекстов. Оценки сложности текста. Математические задачи биоинформатики

Контакты: [email protected]

Селиванов Виктор Львович

Научные интересы: Математическая логика,теория вычислений, теория автоматов, теория сложности и вычислимости в анализе и топологии, иерархии регулярных языков и сверхъязыков, теория областей Ершова-Скотта

Контакты: vseliv@ngs. ru

Спецкурсы и спецсеминары

Подробнее

2022–2023 учебный год

Спецкурсы

Биоинформатика, д.б.н. Ю.Л.Орлов, обращаться на почту [email protected]
Логика-2, к.ф.-м.н. А.Н.Ряскин, собрание по спецкурсу состоится 12 октября в 16:30, возле деканата ММФ, обращаться на почту [email protected]

Счетные и вычислимые булевы алгебры, академик С.С. Гончаров, по пятницам в 18:10, аудитория 4204, начало с 10 марта

Спецсеминары

Конструктивные модели , академик С.С. Гончаров, академик Ю.Л. Ершов, д.ф.-м.н. П.Е. Алаев, по понедельникам в 18:10, аудитория 417 ИМ СО РАН, для включения в рассылку обращаться на почту [email protected]
Теория вычислимости, академик С.С. Гончаров, д.ф.-м.н. А.С. Морозов, к.ф.-м.н. Н. А. Баженов, по вторникам в 18:10, фойе конференц-зала ИМ СО РАН, для включения в рассылку обращаться на почту [email protected]
Вычислимость и допустимые модели, д.ф.-м.н. А.С. Морозов([email protected]) и д.ф.-м.н. В.Г. Пузаренко([email protected]), по четвергам в НГУ в 18:10, аудитория 1133 (старт планируется на 02.03).

Топологические методы в универсальной алгебре, д.ф.-м.н. М.В. Швидефски, обращаться на почту [email protected]

Функции k-значной логики.

Аналогичным функциям алгебры двузначной логики, можно определить функции $k$-значной логики. Значения переменных и самих функций берутся из множества $\mathbb { E } _ { k } = \ { 0,1,\dots, k~—~1\ } , k \geq 3$. Множество всех таких функций обозначается через $\mathbb { P } _ { k } $. Как и булевы функции, каждую функцию $f(x_1,\dots, x_n)$ из $\mathbb { P } _ { k } $ можно задать таблицей.

$$ \begin{array} { | c c c || c | } \hline x_1 & \dots & x_n & f(x_1,\dots,x_n) \\ \hline 0 & \dots & 0 & f(x_1,\dots,x_n) \\ & \dots & & \dots \\ \sigma_1 & \dots & \sigma_n & f(\sigma_1,\dots,\sigma_n) \\ & \dots & & \dots \\ k~-~1 & \dots & k~-~1 & f(k~-~1,\dots,k~-~1) \\ \hline \end{array} $$

В таблице приведены значения некоторых элементарных функций при $k = 3$

$$ \begin{array} { | c | c | c | c | c | c | c | c | c | c | } \hline x & y & max(x,y) & min(x,y) & x+y(mod~3) & xy(mod~3)
& x\perp y & x\rightarrow y & x — y & V_3 { (x,y) } \\ \hline 0 & 0 & 0 & 0 & 0 & 0 & 0 & 2 & 0 & 1\\ \hline 0 & 1 & 1 & 0 & 1 & 0 & 0 & 2 & 2 & 2\\ \hline 0 & 2 & 2 & 0 & 2 & 0 & 0 & 2 & 1 & 0\\ \hline 1 & 0 & 1 & 0 & 1 & 0 & 1 & 1 & 1 & 2\\ \hline 1 & 1 & 1 & 1 & 2 & 1 & 0 & 2 & 0 & 2\\ \hline 1 & 2 & 2 & 1 & 0 & 2 & 0 & 2 & 2 & 0\\ \hline 2 & 0 & 2 & 0 & 2 & 0 & 2 & 0 & 2 & 0\\ \hline 2 & 1 & 2 & 1 & 0 & 2 & 1 & 1 & 1 & 1\\ \hline 2 & 2 & 2 & 2 & 1 & 1 & 0 & 2 & 0 & 2\\ \hline \end{array} $$

Пусть $p_k(n)$ — число всех функций $f(x_1,\dots, x_n)$ из $\mathbb { P } _ { k } $.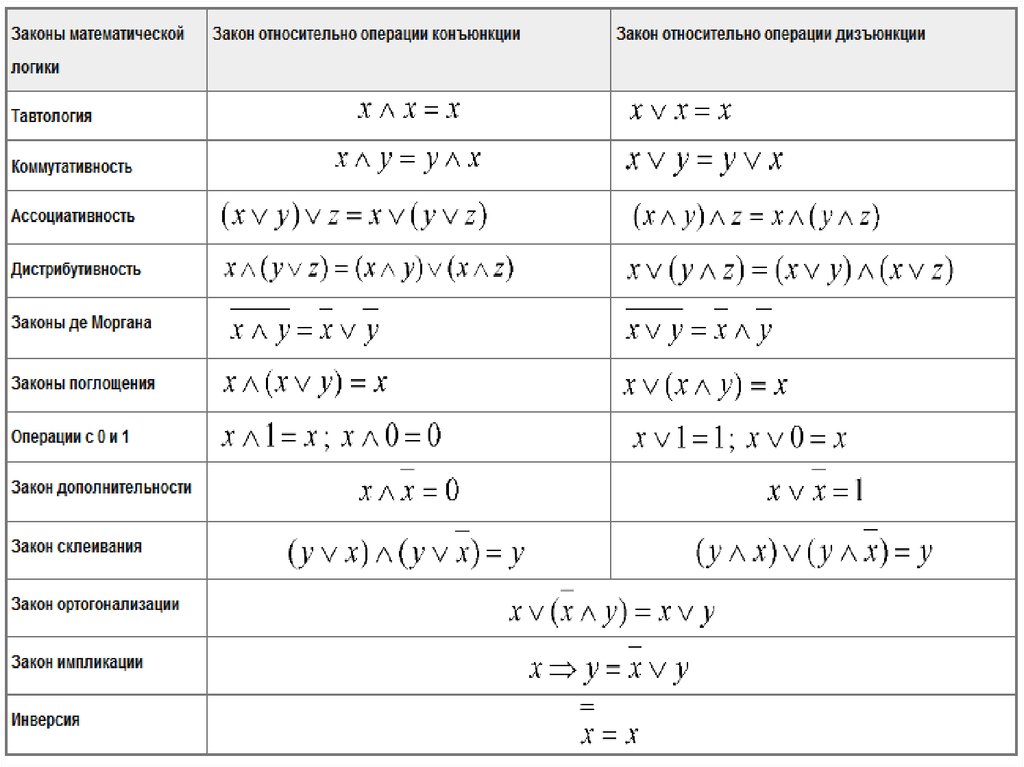 n } $. Это число очень быстро растет, например уже в $\mathbb { P } _ { 3 } $ число функций от переменных $x_1$ и $x_2$ равно $p_3(2) = 19683$. Все основные понятия, такие, как формула над множеством функций, значение формулы на наборе значений переменных, функция, реализуемая формулой, существенная и несущественная переменные и др., вводится точно так же, как и в двузначной логике { определения почти дословно повторяются } , и мы не будем их воспроизводить. Однако не следует забывать, что переменные и функции принимают уже не два значения, а больше. В частности, если известно значение $x$ из то нельзя определить значение $y$ из $\mathbb { E } _ { k } $ только на основе соотношения $y\neq x~( k \geq 3)$. Это приводит к принципиальным отличиям $\mathbb { P } _ { k } ,~k \geq 3$, от $\mathbb { P } _ { 2 } $ .

Известно, что при подстановке одной булевой функции в другую сохраняется существенная зависимость от переменных. Покажем, что для функций $k$-значной логики при $k \geq 3$ аналогичное утверждение неверно.

Рассмотрим функцию $\varphi(x_1, x_2)$, заданную табл.

$$ \begin{array} { | c | c c c | } \hline x_1 & 0 & 1 & 2 \\ \hline 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 2 & 0 & 0 & 1 \\ \hline \end{array} $$

Функция $\varphi$ принадлежит $\mathbb { P } _ { 3 } $ и принимает ненулевое значение только на наборе $(2,2)$. Поэтому функция $\varphi(x, \varphi(y,z))$ — константа 0, поскольку для любых $\beta$, $\gamma \in \mathbb { E } _ { 3 } $ выполняется неравенство $\varphi(\beta, \gamma)~\neq~2$

Рассмотрим следующие «элементарные» функции $k$-значной логики.

Константы $0,1,\dots, k~—~1$.
Тождественная функция $x$.
Отрицания: Функции $f (x) = \bar { x } = x + 1 (mod~k)$ — отрицание Поста или циклический сдвиг, $f (x) = \sim N(x) = k — 1 — x$ — отрицание Лукасевича; Эти функции являются обобщениями отрицания в $\mathbb { P } _ { 2 } $. Функция $N(x)$ является «зеркальным» отражением $x$. Она обозначается также $\sim x$
Характеристическая функция { 2-го рода } $I_i(x)$: $$I_i(x) = \begin{cases} k-1, & \text { если $x = i$ } \newline 0, & \text { если $x \neq i$ } \end{cases} $$
Характеристическая функция { 1-го рода } $j_i(x) = 0, 1, \dots ,k — 1$: $$j_i(x) = \begin{cases} 1, & \text { если $x = i$ } \newline 0, & \text { если $x \neq i$ } \end{cases} $$ Эти функции являются аналогами функции $x^\sigma$ в $\mathbb { P } _ { 2 } $;
Минимум: Функции $min(x_1,x_2)$ и $x_1x_2 (mod~k)$. Эти функции являются обобщением конъюнкции. Функция $min(x_1,x_2)$ обозначается также $x_1\wedge x_2$;
Максимум: Функция $max(x_1,x_2)$. Она является аналогом дизъюнкции в $\mathbb { P } _ { 2 } $ и обозначается также $x_1\vee x_2$;
Сложение по модулю $k$: $f(x, y) = x_1 + x_2~(mod~k)$;
Умножение по модулю $k$: $f (x, y) = xy~(mod~k)$;
Разность по модулю $k$: $$(x-y)mod~k = \begin{cases} k-(y-x), & \text { если $0 \leq x < y \leq k-1$ } \newline x-y, & \text { если $0 \leq y \leq x \leq k-1$ } \end{cases} $$
Усеченная разность $x\perp y$: $$x\perp y = \begin{cases} 0, & \text { если $0 \leq x < y \leq k-1$ } \newline x-y, & \text { если $0 \leq y \leq x \leq k-1$ } \end{cases} $$
Импликация $x\supset y$: $$x\supset y = \begin{cases} k-1, & \text { если $0 \leq x < y \leq k-1$ } \newline (k-1)-x+y, & \text { если $0 \leq y \leq x \leq k-1$ } \end{cases} $$
Функция Веба: $ \nu_k(x,y)=(max(x,y)+1)mod~k$:
Транспортизация чисел $i$ и $j: t_ { ij } (x),i,j\in \ { 0,1,\dots ,k-1\ } , i\neq j$ $$t_ { ij } (x) = \begin{cases} x, & \text { если $x\in\ { i,j\ } ,$ } \newline j, & \text { если $x = i$ } \newline i, & \text { если $x = j$ } \end{cases} $$

Теорема: Об аналоге правила де Моргана

$\sim (x_1\vee x_2) = (\sim x_1)\wedge (\sim x_2)$ $\sim (x_1\wedge x_2) = (\sim x_1)\vee (\sim x_2)$

Докажем $\sim (x_1\vee x_2) = (\sim x_1)\wedge (\sim x_2)$. 2 случая для $x_1, x_2\in E_k$

$x_1\geq x_2;~x_1\vee x_2=x_1$ $\sim (x_1\vee x_2) = k-1-x_1$ $\sim x_1 = k-1-x_1$ $\sim x_2 = k-1-x_2$ $(\sim x_1)\wedge (\sim x_2) = k-1-x_1$
$x_1 < x_2;~\sim (x_1\vee x_2) = k-1-x_2$ $(\sim x_1)\wedge (\sim x_2) = k-1-x_2$

Пример: Показать справедливость следующих утверждений;

$\sim min ( x,y ) = max ( \sim x, \sim y )$, но $\overline { min(x, y) } \neq max(\bar { x } ,\bar { y } )$.

Обозначим эти соотношения следующим образом: $f_1=f_2$ и $f_3 \neq f_4$. Тогда справедливость этих соотношений при $k=3$ видна из следующей таблицы.

$x$	$y$	$min(x,y)$	$f_1$	$\sim x$	$\sim y$	$f_2$	$f_3$	$\bar x$	$\bar y$	$f_4$
0	0	0	2	2	2	2	1	1	1	1
0	1	0	2	2	1	2	1	1	2	2
0	2	0	2	2	0	2	1	1	0	1
1	0	0	2	1	2	2	1	2	1	2
1	1	1	1	1	1	1	2	2	2	2
1	2	1	1	1	0	1	2	2	0	2
2	0	0	2	0	2	2	1	0	1	1
2	1	1	1	0	1	1	2	0	2	2
2	2	2	0	0	0	0	0	0	0	0

Поверхностный интеграл первого рода и его свойства

Скалярное поле, производная по направлению, градиент

Теорема о предполных классах

Поверхностный интеграл второго рода и его свойства

Формула Гаусса — Остроградского

Лемма о построении множества $[F]_{x1,x2}$

Полином Жегалкина. Теорема о представлении в виде полинома Жегалкина

Вычисление тройного интеграла. Теорема о переходе от тройного интеграла к повторному

Логические следствия

Инвариантное определение дивергенции

Линейный интеграл и циркуляция векторного поля

Функции 2-значной логики. Лемма о числе функций. Элементарные функции 1-ой и 2-х переменных

Логические операции над высказываниями

Формулы. Равенство функций и эквивалентность формул. Основные эквивалентности

Вычисление криволинейного интеграла первого рода. Плоский случай

Огравление $\Rightarrow $

04 сентября 2016, 23:36 проектирование км, кмд, кж Алгебра логики [Г.И. Просветов, Е.А. Фоминых, Ф.Г. Кораблёв] 0 15097 0

Изучите логику высказываний с помощью калькулятора

Учитесь на знаниях сообщества. Эксперты добавляют свои идеи в эту совместную статью на основе ИИ, и вы тоже можете.

Это новый тип статьи, которую мы начали с помощью ИИ, и эксперты продвигают ее вперед, делясь своими мыслями непосредственно в каждом разделе.

Если вы хотите внести свой вклад, запросите приглашение, поставив лайк или ответив на эту статью. Узнать больше

— Команда LinkedIn

Последнее обновление: 17 марта 2023 г.

Логика высказываний — это раздел математики, изучающий истинностные значения утверждений и то, как они сочетаются с логическими операторами. Это также полезный навык для аналитического мышления, поскольку он помогает вам оценивать аргументы, строить доказательства и решать проблемы. Но как вы можете научить или выучить логику высказываний, используя калькулятор в качестве инструмента или ресурса? В этой статье мы покажем вам несколько способов использования калькулятора для практики и применения концепций логики высказываний.

Основы логики высказываний

Логика высказываний использует символы для представления утверждений, которые могут быть как истинными, так и ложными, например p, q, r и т. д. Эти утверждения можно комбинировать с логическими операторами, такими как NOT ( ~), И (∧), ИЛИ (∨), ПОДРАЗУМЕВАЕТ (→) и ЭКВИВАЛЕНТ (↔), чтобы сформировать более сложные утверждения, такие как (p ∧ q) → r. Истинностное значение сложного утверждения зависит от истинностных значений простых утверждений и правил операторов. Таблица истинности — это таблица, которая показывает все возможные комбинации значений истинности для утверждений и сложного утверждения. Например, таблица истинности для (p ∧ q) → r:

р | д | р | (p ∧ q) → r

T | Т | Т | Т

Т | Т | Ф | Ф

Т | Ф | Т | Т

Т | Ф | Ф | Т

Ф | Т | Т | Т

Ф | Т | Ф | Т

Ф | Ф | Т | Т

Ф | Ф | Ф | T

Как использовать калькулятор для логики высказываний

Калькулятор может быть полезным инструментом для логики высказываний, поскольку он может выполнять вычисления с двоичными числами, которые соответствуют значениям истинности утверждений. Двоичные числа — это те, которые используют только две цифры, 0 и 1, для представления любого числа. Чтобы использовать калькулятор для логики высказываний, вам нужно преобразовать утверждения и операторы в двоичные числа и использовать функции калькулятора для вычисления истинностного значения сложного утверждения. Например, чтобы преобразовать утверждение в двоичное число, используйте 1 для истинности и 0 для ложно. Для операторов НЕ (~) эквивалентно функции дополнения (CPL), И (∧) эквивалентно логической функции И (И), ИЛИ (∨) эквивалентно логической функции ИЛИ (ИЛИ), ПРЕДПОЛАГАЕТ (→ ) эквивалентна логической функции НЕ-И (NAND), за которой следует функция дополнения (CPL), а ЭКВИВАЛЕНТ (↔) эквивалентен логической функции XOR (XOR), за которой следует функция дополнения (CPL). Чтобы вычислить истинность сложного утверждения, используйте функции калькулятора в порядке следования их логических операторов. Это может помочь вам проинформировать и успокоить заинтересованные стороны, а также предоставить ценную информацию для улучшения вашего состояния безопасности в облаке.

Как практиковать логику высказываний с помощью калькулятора

Использование калькулятора логики высказываний может помочь вам попрактиковаться и укрепить свое понимание понятий и правил. Вы можете создавать свои собственные утверждения и операторы, вычислять их значения истинности и проверять свои ответы с помощью таблицы истинности. Кроме того, вы можете найти примеры задач на логику высказываний в Интернете или в книгах и использовать калькулятор для их решения. Кроме того, вы можете использовать калькулятор для проверки обоснованности аргументов или доказательств, использующих логику высказываний. Для этого вам нужно преобразовать посылки и заключение в двоичные числа и использовать функции калькулятора для вычисления истинностного значения влияния посылок на заключение. Если результат всегда равен 1, то аргумент или доказательство верны; если он когда-либо равен 0, то он недействителен.

Как применять логику высказываний с помощью калькулятора

Логика высказываний является не только теоретическим предметом, но также имеет множество практических приложений в различных областях, таких как информатика, инженерия, философия и логические задачи. Вы можете использовать калькулятор, чтобы применить логику высказываний к этим полям и ситуациям. Например, его можно использовать для разработки и анализа цифровых схем, таких как вентили, триггеры и регистры. Его также можно использовать для кодирования и декодирования сообщений, таких как код Морзе или двоичный код. И его можно использовать для решения логических головоломок, таких как Судоку или Сапер. Калькулятор может представлять подсказки или правила в виде двоичных чисел и использовать свои функции для исключения возможных решений и поиска правильного.

Вот что еще нужно учитывать

Здесь можно поделиться примерами, историями или идеями, которые не вписываются ни в один из предыдущих разделов. Что бы вы еще хотели добавить?

Оцените эту статью

Мы создали эту статью с помощью ИИ. Что вы думаете об этом?

Спасибо за ваш отзыв

Ваш отзыв является частным. Поставьте лайк или отреагируйте, чтобы перенести разговор в свою сеть.

Решатель логических вентилей v1.2 | Архивы

Решатель логических вентилей v1.2

Все файлы
Программы TI-83 Plus/TI-84 Plus
Программы TI-83 Plus/TI-84 Plus BASIC
Образовательные программы TI-83 Plus/TI-84 Plus BASIC

Описание

Эта программа помогает решать различные логические элементы, в том числе элементы, которые не реализованы в калькуляторах z80. Работает с 83+/84+/SE. Прочтите файл Readme для получения дополнительной информации. Это обновление исправляет серьезную ошибку, которая ломает программу.

Скриншоты

Содержимое архива

Имя	Размер
Прочтите сейчас.txt	791 байт
БУЛЫLV.8xp	894 байта

Загрузить файл

Размер файла: 1,0 КБ
Короткая ссылка: http://ceme. tech/DL612

Метаданные

Автор: мобуту4
Загружено: 8 лет, 7 месяцев назад

Статистика

Рейтинг: 10/10 (1 голос)

Загрузки: 875
просмотров: 2231

Отзывы

Этот файл еще никто не просматривал.

Калькулятор алгебра логика: Математическая логика · oнлайн с подробным объяснением

Кафедры — Механико-математический факультет

Направления работы

Состав кафедры

Профессора

Доценты

Старшие преподаватели

Ассистенты

Гончаров Сергей Савостьянович

Оспичев Сергей Сергеевич

Марина Владимировна Швидефски

Орлов Юрий Львович

Селиванов Виктор Львович

2022–2023 учебный год

Функции k-значной логики.

Далее:

Изучите логику высказываний с помощью калькулятора

Основы логики высказываний

Как использовать калькулятор для логики высказываний

Как практиковать логику высказываний с помощью калькулятора

Как применять логику высказываний с помощью калькулятора

Вот что еще нужно учитывать

Оцените эту статью

Спасибо за ваш отзыв

Решатель логических вентилей v1.2 | Архивы

Описание

Скриншоты

Содержимое архива

Метаданные

Статистика

Отзывы

Добавить комментарий Отменить ответ