Инженерный калькулятор онлайн
Цель сайта Рассчитать Онлайн РУ — дать возможность пользователю произвести сложный или простой расчет удобно, быстро и бесплатно, находясь в любой точке мира с компьютера, телефона или планшета, главное, иметь доступ к интернету. Мы активно работает над внедрением любых калькуляторов, но если у Вас есть идея и Вы хотите что бы она появилась на нашем сайте, воспользуйтесь формой обратной связи, мы будем благодарны за любые идеи по улучшению и расширению сервиса. Цифры и операторы можно вводить прямо с клавиатуры, они сразу же отобразятся на дисплее. Для удаления истории и очистки найденного результата задачи, используйте клавишу калькулятора «С». Удачного использования!
Инструкция к вычислению, описание режимов калькулятора
Комплексные числа
Определение комплексных чисел
Комплексное число — это выражение вида a + bi, где a, b — действительные числа, а i — так называемая мнимая единица, символ, квадрат которого равен –1, то есть i2 = –1. a называется действительной частью, b — мнимой частью комплексного числа z = a + bi.
a называется действительной частью, b — мнимой частью комплексного числа z = a + bi.
Абсолютная величина
Синтаксис:
abs(a)
Входные аргументы:
a
Примеры использования:
abs(5.5)
abs(-5.5)
abs(5.5+6.6i)
abs(-5.5-6.6i)
Фаза (угол)
Синтаксис:
arg(a)
Входные аргументы:
a
Примеры использования:
arg(5.5)
arg(-5.5)
arg(5.5+6.6i)
arg(-5.5-6.6i)
Комплексные числа i
Примеры использования:
3+5i
Действительная часть
Синтаксис:
re(a)
Входные аргументы:
a
Примеры использования:
re(-5.5)
re(5.5+6.6i)
re(-5.5-6.6i)
Мнимая часть
Синтаксис:
im(a)
Входные аргументы:
a
Примеры использования:
im(5.5)
im(-5. 2+3x-3=9 )
2+3x-3=9 )
Линейная алгебра
Векторы
Синтаксис:
a + b
Входные аргументы:
a: Вектор
b: Вектор
Примеры использования:
(1, 2, 3)+(4, 5, 6)
Умножение векторов
Синтаксис:
a * b
Входные аргументы:
a: Вектор
b: Вектор
Примеры использования:
(1, 2, 3)*(4, 5, 6)
Векторное произведение векторов
Синтаксис:
a # b
Входные аргументы:
a: Вектор
b: Вектор
Примеры использования:
(1, 2, 3)#(4, 5, 6)
Умножение матриц
Синтаксис:
a * b
Входные аргументы:
a: матрица
b: матрица
Примеры использования:
[[1, 2, 3][4, -5, 6][7, 8, 9]]*[[9, 8, 7][6, -5, 4][3, 2, 1]]
Матрично-векторное произведение
Синтаксис:
a * b
Входные аргументы:
a: матрица
b: Вектор
Примеры использования:
[[1, 2, 3][4, -5, 6][7, 8, 9]]*(1, 2, 3)
Детерминант (определитель) матрицы
Синтаксис:
det(a)
Входные аргументы:
a: матрица
Примеры использования:
det([[1, 2, 3][4, -5, 6][7, 8, 9]])
Абсолютная величина
Синтаксис:
len(a)
Входные аргументы:
a: Вектор
Примеры использования:
len((1, 2, 3))
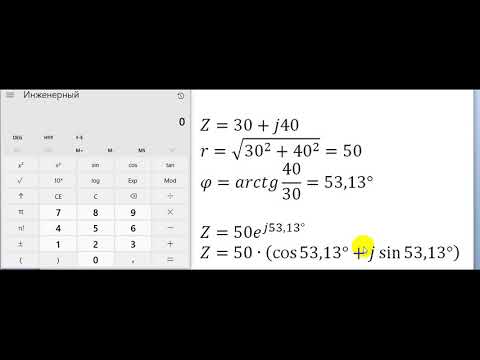
Действия с величинами (конвертирование, мат.
 5
5Целая часть (отбрасывает все цифры после запятой)
Синтаксис:
ceil(a)
Входные аргументы:
a
Примеры использования:
ceil(5)
ceil(5.2)
ceil(5.7)
Округление до целых (по правилам)
Синтаксис:
floor(a)
Входные аргументы:
a
Примеры использования:
floor(5)
floor(5.2)
floor(5.7)
Логарифм
Синтаксис:
log(a)
log10(a)
log(a, b)
Входные аргументы:
a и b
Примеры использования:
log(100)
log10(100)
log(8, 2)
Натуральный логарифм
Синтаксис:
ln(a)
Входные аргументы:
a
Примеры использования:
ln(100)
или
Синтаксис:
lg(a)
Входные аргументы:
a
Примеры использования:
lg(8)
Минимальное значение
Синтаксис:
min(a, b)
Входные аргументы:
a и b
Примеры использования:
min(8, 4)
Максимальное значение
Синтаксис:
max(a, b)
Входные аргументы:
a
b
Примеры использования:
max(8, 4)
Квадратный корень
Синтаксис:
sqr(a)
sqr2(a)
sqr3(a)
sqr(a, b)
Входные аргументы:
a и b Число
Примеры использования:
sqr(9)
sqr3(27)
sqr(27, 3)
Поддерживаемые функции:
Калькулятор поддерживает общепринятые функции, например, модуль x или |x|
acos(x) Функция — арккосинус от x, необходимо нажать на кнопку 2nd для активации
acosh(x) Арккосинус гиперболический от x, необходимо нажать на кнопку 2nd для активации
asin(x) Арксинус от x, необходимо нажать на кнопку 2nd для активации
asinh(x) Арксинус гиперболический от x, необходимо нажать на кнопку 2nd для активации
atgh(x) Арктангенс гиперболический от x, необходимо нажать на кнопку 2nd для активации
e Экспонента (примерно равна 2.
 2 Функция — Квадрат x
2 Функция — Квадрат xtan(x) Функция — Тангенс от x
tanh(x) Функция — Тангенс гиперболический от x
floor(x) Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
sign(x) Функция — Знак x
const справочник констант
Представлены основные функции. Подробное описание, представлено в разделе «Инструкция к вычислению».
Наши полезные калькуляторы:
Финансовые
НДС
Возвести комплексное число в степень онлайн калькулятор. Возведение комплексных чисел в степень
Начнем с любимого квадрата.
Пример 9
Возвести в квадрат комплексное число
Здесь можно пойти двумя путями, первый способ это переписать степень как произведение множителей и перемножить числа по правилу умножения многочленов.
Второй способ состоит в применение известной школьной формулы сокращенного умножения :
Для комплексного числа легко вывести свою формулу сокращенного умножения:
Аналогичную формулу можно вывести для
квадрата разности, а также для куба
сумма и куба разности. Но эти формулы
более актуальны длязадач
комплексного анализа. Что делать,
если комплексное число нужно возвести,
скажем, в 5-ую, 10-ую или 100-ую степень?
Ясно, что в алгебраической форме проделать
такой трюк практически невозможно,
действительно, подумайте, как вы будете
решать пример вроде?
Но эти формулы
более актуальны длязадач
комплексного анализа. Что делать,
если комплексное число нужно возвести,
скажем, в 5-ую, 10-ую или 100-ую степень?
Ясно, что в алгебраической форме проделать
такой трюк практически невозможно,
действительно, подумайте, как вы будете
решать пример вроде?
И здесь на помощь приходит тригонометрическая форма комплексного числа и, так называемая, формула Муавра : Если комплексное число представлено в тригонометрической форме , то при его возведении в натуральную степеньсправедлива формула:
Просто до безобразия.
Пример
10
Дано комплексное число , найти.
Что нужно сделать? Сначала нужно представить данное число в тригонометрической форме. Внимательные читатели заметили, что в Примере 8 мы это уже сделали:
Тогда, по формуле Муавра:
Упаси
боже, не нужно считать на калькуляторе
,
а вот угол в большинстве случае следует
упростить. Как упростить? Образно
говоря, нужно избавиться от лишних
оборотов. Один оборот составляетрадиан
или 360 градусов. Выясним сколько у нас
оборотов в аргументе.
Для удобства делаем дробь правильной:,
после чего становится хорошо видно, что
можно убавить один оборот:.
Надеюсь всем понятно, чтои–
это один и тот же угол.
Один оборот составляетрадиан
или 360 градусов. Выясним сколько у нас
оборотов в аргументе.
Для удобства делаем дробь правильной:,
после чего становится хорошо видно, что
можно убавить один оборот:.
Надеюсь всем понятно, чтои–
это один и тот же угол.
Таким образом, окончательный ответ запишется так:
Отдельная разновидность задачи возведения в степень – это возведение в степень чисто мнимых чисел.
Пример 12
Возвести в степень комплексные числа ,,
Здесь тоже всё просто, главное, помнить знаменитое равенство.
Если мнимая единица возводится в четную степень, то техника решения такова:
Если мнимая единица возводится в нечетную степень, то «отщипываем» одно «и», получая четную степень:
Если есть минус (или любой действительный коэффициент), то его необходимо предварительно отделить:
Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями
Рассмотрим пример:
Нельзя
извлечь корень? Если речь идет о
действительных числах, то действительно
нельзя. В комплексных числах извлечь
корень – можно! А точнее, два корня:
В комплексных числах извлечь
корень – можно! А точнее, два корня:
Действительно ли найденные корни являются решением уравнения ? Выполним проверку:
Что и требовалось проверить.
Часто используется сокращенная запись, оба корня записывают в одну строчку под «одной гребёнкой»: .
Такие корни также называют сопряженными комплексными корнями .
Как
извлекать квадратные корни из отрицательных
чисел, думаю, всем понятно:
,,,,и
т.д. Во всех случаях получается
Начнем с любимого квадрата.
Пример 9
Возвести в квадрат комплексное число
Здесь можно пойти двумя путями, первый способ это переписать степень как произведение множителей и перемножить числа по правилу умножения многочленов.
Второй способ состоит в применение известной школьной формулы сокращенного умножения :
Для комплексного числа легко вывести свою формулу сокращенного умножения:
Аналогичную формулу можно вывести для
квадрата разности, а также для куба
сумма и куба разности. Но эти формулы
более актуальны длязадач
комплексного анализа. Что делать,
если комплексное число нужно возвести,
скажем, в 5-ую, 10-ую или 100-ую степень?
Ясно, что в алгебраической форме проделать
такой трюк практически невозможно,
действительно, подумайте, как вы будете
решать пример вроде?
Но эти формулы
более актуальны длязадач
комплексного анализа. Что делать,
если комплексное число нужно возвести,
скажем, в 5-ую, 10-ую или 100-ую степень?
Ясно, что в алгебраической форме проделать
такой трюк практически невозможно,
действительно, подумайте, как вы будете
решать пример вроде?
И здесь на помощь приходит тригонометрическая форма комплексного числа и, так называемая, формула Муавра : Если комплексное число представлено в тригонометрической форме , то при его возведении в натуральную степеньсправедлива формула:
Просто до безобразия.
Пример 10
Дано комплексное число , найти.
Что нужно сделать? Сначала нужно представить данное число в тригонометрической форме. Внимательные читатели заметили, что в Примере 8 мы это уже сделали:
Тогда, по формуле Муавра:
Упаси
боже, не нужно считать на калькуляторе
,
а вот угол в большинстве случае следует
упростить. Как упростить? Образно
говоря, нужно избавиться от лишних
оборотов. Один оборот составляетрадиан
или 360 градусов. Выясним сколько у нас
оборотов в аргументе.
Для удобства делаем дробь правильной:,
после чего становится хорошо видно, что
можно убавить один оборот:.
Надеюсь всем понятно, чтои–
это один и тот же угол.
Один оборот составляетрадиан
или 360 градусов. Выясним сколько у нас
оборотов в аргументе.
Для удобства делаем дробь правильной:,
после чего становится хорошо видно, что
можно убавить один оборот:.
Надеюсь всем понятно, чтои–
это один и тот же угол.
Таким образом, окончательный ответ запишется так:
Отдельная разновидность задачи возведения в степень – это возведение в степень чисто мнимых чисел.
Пример 12
Возвести в степень комплексные числа ,,
Здесь тоже всё просто, главное, помнить знаменитое равенство.
Если мнимая единица возводится в четную степень, то техника решения такова:
Если мнимая единица возводится в нечетную степень, то «отщипываем» одно «и», получая четную степень:
Если есть минус (или любой действительный коэффициент), то его необходимо предварительно отделить:
Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями
Рассмотрим пример:
Нельзя
извлечь корень? Если речь идет о
действительных числах, то действительно
нельзя.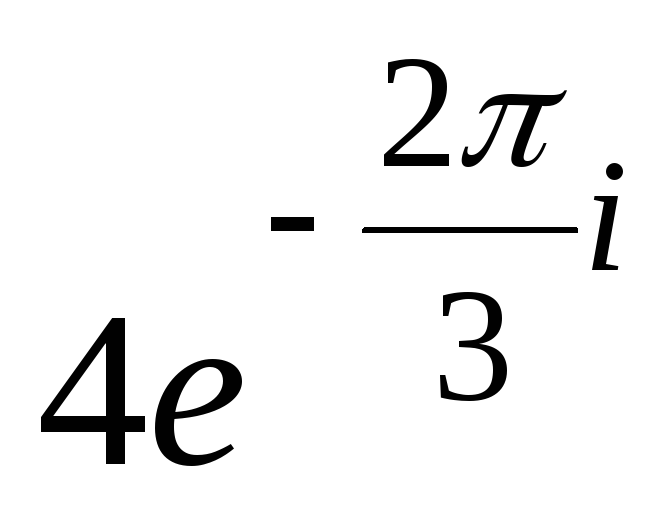 В комплексных числах извлечь
корень – можно! А точнее, два корня:
В комплексных числах извлечь
корень – можно! А точнее, два корня:
Действительно ли найденные корни являются решением уравнения ? Выполним проверку:
Что и требовалось проверить.
Часто используется сокращенная запись, оба корня записывают в одну строчку под «одной гребёнкой»: .
Такие корни также называют сопряженными комплексными корнями .
Как извлекать квадратные корни из отрицательных чисел, думаю, всем понятно: ,,,,и т.д. Во всех случаях получаетсядва сопряженных комплексных корня.
Пример 13
Решить квадратное уравнение
Вычислим дискриминант:
Дискриминант отрицателен, и в действительных числах уравнение решения не имеет. Но корень можно извлечь в комплексных числах!
По известным школьным формулам получаем два корня: – сопряженные комплексные корни
Таким образом, уравнение имеет два сопряженных комплексных корня:,
Теперь вы сможете решить любое квадратное уравнение!
И
вообще, любое уравнение с многочленом
«энной» степени
имеет
ровнокорней,
часть из которых может быть комплексными.
Простой пример для самостоятельного решения:
Пример 14
Найти корни уравнения и разложить квадратный двучлен на множители.
Разложение на множители осуществляется опять же по стандартной школьной формуле.
Онлайн расчеты. Математический калькулятор с расширенными возможностями.
ГлавнаяРазноеОнлайн расчеты
Онлайн калькуляторы и справочники
Данный сайт представляет собой каталог онлайн калькуляторов по различным тематикам. Каждый калькулятор снабжен пояснительным материалом, который поможет разобраться в тонкостях расчета для тех, кто хочет подробнее разобраться в теме.
Выполненный расчет можно распечатать или сохранить. В случае сохранения расчет будет доступен в личном кабинете. Это удобно, например, в таких случаях, когда необходимо «поиграть» с исходными значениями для получения различных результатов с целью их последующего сравнения.
На сайте представлены следующие калькуляторы:
Финансы
Авто
Бизнес
Математические
Здоровье
Перевод единиц
IT инструменты
Разное
Справочники
calcus. ru
ru
Онлайн расчеты :: SS20 Sport Club
Исходные данные
Диаметр обода Ширина колеса Обороты двигателя Главная пара
3.53.73.94.14.34.54.74.95.1 Первая передача
2.92 (5-й ряд)2.92 (6-й ряд) 2.92 (7-й ряд)3.42 (8-й ряд)3.42 (10-й ряд)3.63 (станд.)3.63 (11-й ряд)3.16 (12-й ряд)3.17 (15-й ряд)3.17 (18-й ряд)3.17 (20-й ряд)3.17 (102-й ряд)2.92 (103-й ряд)2.92 (104-й ряд)2.92 (200-й ряд)3.0 (026-й ряд)3.0 (711-й ряд)2.67 (745-й ряд)2.67 (74-й ряд)
Вторая передача
1.81 (5-й ряд)1.81 (6-й ряд)2.05 (7-й ряд)2.05 (8-й ряд)2.05 (10-й ряд)2.22 (11-й ряд)1.95 (станд.)1.95 (12-й ряд)1.81 (15-й ряд)2.11 (18-й ряд)1.9 (20-й ряд)1.95 (102-й ряд)1.95 (103-й ряд)1.95 (104-й ряд)2.22 (200-й ряд)2.53 (026-й ряд) 2.53 (711-й ряд) 1.93 (745-й ряд)1.93 (74-й ряд)
Третья передача
1. 28 (5-й ряд)1.28 (6-й ряд)1.56 (7-й ряд)1.36 (станд.)1.36 (8-й ряд)1.36 (10-й ряд)1.54 (11-й ряд)1.36 (12-й ряд)1.28 (15-й ряд)1.48 (18-й ряд)1.26 (20-й ряд)1.36 (102-й ряд)1.36 (103-й ряд)1.36 (104-й ряд)1.76 (200-й ряд)2.06 (026-й ряд)2.06 (711-й ряд)2.06 (45-й ряд)1.56 (74-й ряд)
28 (5-й ряд)1.28 (6-й ряд)1.56 (7-й ряд)1.36 (станд.)1.36 (8-й ряд)1.36 (10-й ряд)1.54 (11-й ряд)1.36 (12-й ряд)1.28 (15-й ряд)1.48 (18-й ряд)1.26 (20-й ряд)1.36 (102-й ряд)1.36 (103-й ряд)1.36 (104-й ряд)1.76 (200-й ряд)2.06 (026-й ряд)2.06 (711-й ряд)2.06 (45-й ряд)1.56 (74-й ряд)
Четвертая передача
0.94 (станд.)0.97 (5-й ряд)1.06 (6-й ряд)1.31 (7-й ряд)0.97 (8-й ряд)0.97 (10-й ряд)1.17 (11-й ряд)1.03 (12-й ряд)0.94 (15-й ряд)1.13 (18-й ряд)0.94 (20-й ряд)0.94 (102-й ряд)0.94 (103-й ряд)1.03 (104-й ряд)1.39 (200-й ряд)1.74 (026-й ряд)1.74 (711-й ряд)1.37 (745-й ряд)1.37 (74-й ряд)
Пятая передача
0.78 (станд.)0.78 (5-й ряд)0.94 (6-й ряд)1.13 (7-й ряд)0.78 (8-й ряд)0.78 (10-й ряд)0.89 (11-й ряд)0.78 (12-й ряд)0.73 (15-й ряд)0.89 (18-й ряд)0.73 (20-й ряд)0.73 (102-й ряд)0.69 (103-й ряд)0.73 (104-й ряд)1.17 (200-й ряд)1.48 (026-й ряд)1.48 (711-й ряд)1.2 (745-й ряд)0.79 (74-й ряд)
Шестая передача
нет0. 69 (станд.)0.94 (7-й ряд)0.78 (18-й ряд)0.94 (200-й ряд)
69 (станд.)0.94 (7-й ряд)0.78 (18-й ряд)0.94 (200-й ряд)
Рассчитать
ss20club.ru
Математический калькулятор онлайн | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Инженерный калькулятор позволяет использовать много разных математических функций: • решение гиперболических, тригонометрических и обратных тригонометрических функций: • возведение в степень и извлечение корней: • решение матриц и уравнений: • построение графиков и конвертертация величин: • вычисление логарифмов и экспоненты: • дифференцирование и интегрирование функций: • нахождение факториала, абсолютной величины числа, значения аргумента функции, биноминального коэффициента, наибольшего общего делителя, наименьшего общего кратного: • Использование мнимой единицы при расчётах комплексных чисел: • Выделение целой действительной части и исключение действительной части: • Разложение числа на простые множители. Инженерный калькулятор позволяет конвертировать физические величины разных систем измерений (масса, расстояние, время, компьютерные информационные единицы измерения и др. С возможностями нашего калькулятора вы сможете моментально перевести фунты в килограммы, мили в километры, секунды в часы и т. Для выполнения математических расчетов, просто введите последовательность математических выражений в соответствующее поле и для получения результата нажмите на кнопку со знаком равенства. Для построения графиков достаточно в поле ввода с помощью панели инструментов записать функцию и нажать на кнопку с изображением графика. Кнопка с надписью Unit предназначена для перехода в конвертер величин, для вычисления матриц нажмите на кнопку Matrix. В таблице указаны все клавиши (со значком * вызывается через дополнительную клавишу II) калькулятора и выполняемые ими операции.
Теперь, когда вам понадобится калькулятор, приходите на сайт и используйте бесплатный научный калькулятор. |
ncor.ru
| Нахождение обратного числа | Ввести число, для которого нужно найти обратное, нажать кнопку 1/x |
| Извлечение квадратного корня (корня 2-й степени) | Ввести число, из которого нужно извлечь квадратный корень, нажать кнопку √x |
| Извлечение кубического корня (корня 3-й степени) | Ввести число, из которого нужно извлечь кубический корень, нажать кнопку 3√x |
| Извлечение корня заданной степени | Ввести число, из которого нужно извлечь корень заданной степени, нажать кнопку y√x, ввести значение степени извлекаемого корня |
| Вычисление десятичного логарифма (логарифма по основанию 10) | Нажать кнопку log, ввести число, для которого нужно вычислить логарифм по основанию 10 |
| Операции с числом e | Если необходимо произвести математическую операцию с числом e или с использованием этой константы, то вместо введения значения этого числа нужно просто нажать кнопку e |
| Возведение числа 10 в степень | Нажать кнопку 10x, ввести значение степени, в которую нужно возвести число 10 |
| Возведение в квадрат (2-ю степень) | Ввести число, которое нужно возвести в квадрат, нажать кнопку x2 |
| Возведение в куб (3-ю степень) | Ввести число, которое нужно возвести в куб, нажать кнопку x3 |
| Возведение в заданную степень | Ввести число, которое нужно возвести в заданную степень, нажать кнопку xy, ввести значение степени |
| Операции с процентами | Для вычисления, чему равно определённое количество процентов от числа, нужно ввести это число, нажать кнопку x (т. е. умножить), ввести количество процентов и нажать %.Чтобы прибавить к числу (или вычесть) определённое количество процентов от него, нужно ввести это число, нажать кнопку + (или, соответственно, –), затем ввести количество процентов и нажать % е. умножить), ввести количество процентов и нажать %.Чтобы прибавить к числу (или вычесть) определённое количество процентов от него, нужно ввести это число, нажать кнопку + (или, соответственно, –), затем ввести количество процентов и нажать % |
| Операции с мнимой единицей (число i) | Для использования в вычислениях мнимой единицы (числа i), необходимо нажать кнопку i |
okcalc.com
Калькулятор онлайн. Бесплатный онлайн калькулятор с памятью.
Онлайн калькулятор: описание.
Перед вами лучший онлайн калькулятор, который можно использовать бесплатно и без регистрации. Данный онлайн калькулятор является одним из самых совершенных наших приложений. Он удобный, практичный и отличается высокой скоростью загрузки. Над разработкой этого приложения трудился целый коллектив. Калькулятор не требует установки и работает прямо в браузере.
Возможности онлайн калькулятора
Онлайн калькулятор выполняет стандартные математические действия: сложение/вычитание, умножение/деление, вычисление процентов, нахождение квадратного корня и возведение в степень. Также, доступна функция памяти, с помощью которой можно запоминать промежуточные результаты и выполнять многоступенчатые расчеты.
Также, доступна функция памяти, с помощью которой можно запоминать промежуточные результаты и выполнять многоступенчатые расчеты.
Калькулятор представляет собой браузерное приложение, которое можно использовать в режиме онлайн бесплатно и без регистрации. Он расчитан на широкий круг лиц и будет полезен всем, начиная от студентов и школьников, выполняющих простые арифметические вычисления, заканчивая бизнесменами, учеными и инженерами, которым приложение поможет осуществить сложные калькуляции.
Как пользоваться онлайн калькулятором?
Пользоваться калькулятором можно как с помощью клавиатуры, так и с помощью мыши. Если у вас не вводятся цифры с NumPad (группа цифр справа на клавиатуре), то, возможно, включен режим Num Lock. Отключите его нажатием на одноименную клавишу в левом верхнем углу NumPad. Дополнительно, можно регулировать размеры калькулятора с помощью кнопочек плюс и минус.
Расшифровка стандартных кнопок калькулятора:
«M+» — добавить число в память (либо прибавить к тому, которое уже в памяти). 4 = 10000).
4 = 10000).
normal-calc.ru
Очень продвинутый онлайн калькулятор
Как Вы, наши уважаемые читатели и читательницы, уже могли догадаться, речь пойдет об онлайн калькуляторах, если быть точнее — об одном из самых полезных и, частенько, незаменимых изобретений человека, которое не так давно перекочевало в интернет.
Мы долго выбирали роль самого классного, удобного и полезного онлайн калькулятора и выбор пал на молодой вебдванольный сервис — Web20calc.
Вы, наверное, уже успели возмутиться относительно важности этой темы? Честно говоря, это Вы зря — калькулятор Windows ему совсем не ровня, а ближайшие соперники — типа eCalc, может и превосходят его в функционале, но стоят от 45 евро за копию и при этом устанавливаются на ПК или нетбук или Iphone, что нам не так и нужно.Данный онлайн калькулятор может:
- Корректно выполнять стандартные математические функции, записанные одной строкой типа — 12*3-(7/2) и может обрабатывать числа больше, чемМы даже не знаем, как такое число назвать правильно (тут 34 знака и это совсем не предел).
 Выводится, к сожалению такое число в файл изображения (защита от автоматического использования скорее всего).
Выводится, к сожалению такое число в файл изображения (защита от автоматического использования скорее всего). - Кроме тангенса, косинуса, синуса и других стандартных функций — калькулятор поддерживает операции по расчёту арктангенса, арккотангенса и прочих.
- Доступны в арсенале логарифмы, факториалы и другие интересные функции
Но самое главное — данный онлайн калькулятор умеет строить графики!!! Если не верите, смотрим на скриншот:
Для построения графиков, сервис использует специальную кнопку (график серый нарисован) или буквенное представление этой функции (Plot).
Чтобы построить график в онлайн калькуляторе, достаточно записать функцию, например такую как у нас в скриншоте:
plot(tan(x)),x=-360..360
Мы взяли самый простой график для тангенса, и после запятой указали диапазон переменной X от -360 до 360.
Построить можно абсолютно любую функцию, с любым количеством переменных, например такую:
plot(cos(x)/3z, x=-180..360,z=4) или ещё более сложную, какую сможете придумать.
Обращаем внимание на поведение переменной X — указан промежуток от и до с помощью двух точек.Единственный минус (хотя трудно назвать это минусом) этого онлайн калькулятора это то, что он не умеет строить сферы и другие объёмные фигуры — только плоскость.
Для сравнения с калькулятором Майкрософта, приводим наглядный скриншот
Думаем игра «Найдите N отличий» Вам знакома. Теперь пора подвести некоторые итоги:
С помощью онлайн калькулятора мы можем:
- Серьезно облегчить себе жизнь в школе или институте.
- Получить профессиональный онлайн калькулятор в бесплатное пользование.
- Считать огромные числа на любом компьютере в любой точке планеты.
- Строить графики по сложным функциям прямо онлайн.
- Не захламлять свой ноутбук приложениями и, тем более, не тратить на них деньги.
Вполне добротный список преимуществ.Update 21.10.2011: Мы оформили более удобную страницу с примерами для эффективного использования калькулятором — посмотреть. Её можно открыть с любой точки нашего сайта.Update 02.12.2010: Теперь можно опробовать этот калькулятор в действии прямо у нас в журнале:
Её можно открыть с любой точки нашего сайта.Update 02.12.2010: Теперь можно опробовать этот калькулятор в действии прямо у нас в журнале:
UPDATE 09.04.2011: Функции арктангенса, арксинуса и т.д. запускаются кнопками:tan-1, sin-1 и т.д.Включить продвинутые функции для решения матриц, построения графиков, дифференциалов и другого можно с помощью специальных клавиш:
Для полной функциональности нужно использовать оригинал, но этот тоже сойдет для быстрых рассчетов.
Технический калькулятор | Онлайн калькулятор (⇒)
Сейчас другие читают
itpride.net
Калькуляторы для проведения онлайн расчетов
Калькулятор больничного пособия
Позволяет онлайн рассчитать пособие по временной нетрудоспособности:
- Укажите ваш доход за расчетный срок.
- Выберите подходящий страховой стаж.
- Укажите число больничных дней.
- Расчет проводится автоматически.
Калькулятор заработной платы по окладу
Позволяет онлайн рассчитать зарплату работника по его окладу за полный и неполный день:
- Укажите оклад и размер премии;
- Если положены вычеты, укажите их размер;
- Размер районного коэффициента, если установлен;
- Количество рабочих и отработанных дней.

Калькулятор компенсации за задержку зарплаты
Позволяет онлайн рассчитать денежную компенсацию за задержку заработной платы:
- Укажите сумму зарплаты, не выплаченную в срок;
- Внесите число дней задержки;
- Расчет проводится автоматически.
Калькулятор НДС
Позволяет онлайн выделить НДС из суммы или начислить его к сумме:
- Укажите сумму с налогом или без него, выберите ставку НДС.
- Калькулятор автоматически мгновенно онлайн проведет расчет.
Калькулятор пени по ставке рефинансирования
Позволяет рассчитать сумму пени по 1/300 ставки, исходя из:
- суммы долга;
- ставки рефинансирования;
- числа дней просрочки.
Калькулятор пени по страховым взносам
Позволяет рассчитать сумму пени по страховым взносам, исходя из:
- суммы недоимки;
- количества дней просрочки.
Калькулятор пособия по беременности и родам в 2017 году
Позволяет рассчитать онлайн размер декретного пособия, исходя из следующих параметров:
- Введите продолжительность декрета, количество исключаемых дней, размер доходов за расчетные года;
- Калькулятор автоматически онлайн рассчитает размер декретной выплаты.

Калькулятор пособия по беременности и родам в 2018 году
Позволяет провести расчет декретных в 2018 году.
Калькулятор пособия по уходу за ребенком до 1.5 лет в 2017 году
Позволяет рассчитать размер пособия на ребенка, исходя из:
- дохода для каждого расчетного года;
- исключаемых периодов.
- калькулятор считает размер ежемесячного пособия до 1.5 лет в онлайн режиме
Калькулятор пособия по уходу за ребенком в 2018 году
Позволяет рассчитать размер пособия до 1.5 лет в 2018 году.
Калькулятор расчета даты выхода в декрет.
Позволяет рассчитать дату начала отпуска по беременности и родам и дату его окончания:
- Введите длительность декретного отпуска и предполагаемую дату родов;
- Калькулятор рассчитает дату выхода в декрет и день его окончания.
Калькулятор расчета компенсации неиспользованного отпуска.
Позволяет рассчитать размер денежной компенсации за неиспользованный отпуск при увольнении:
- Введите зарплату;
- Общее число отработанных месяцев;
- Число уже использованных дней;
- Дату увольнения;
- Если есть неполностью отработанные месяцы — укажите это;
- нажмите рассчитать — калькулятор проведен онлайн расчет числа неиспользованных дней отпуска и положенной компенсации.

Калькулятор расчета отпускных.
Позволяет рассчитать размер отпускных при уходе в оплачиваемый отпуск:
- Введите ежемесячную зарплату;
- Укажите количество дней отпуска;
- Если есть неполные месяцы — укажите число отработанных дней.
- Калькулятор проведет расчет отпускных.
Калькулятор страховых взносов ИП за себя
Позволяет рассчитать размер страховых взносов ИП за себя:
- укажите доход за год;
- калькулятор рассчитает фиксированный и дополнительный взнос за себя.
buhland.ru
Калькулятор мнимых чисел онлайн.
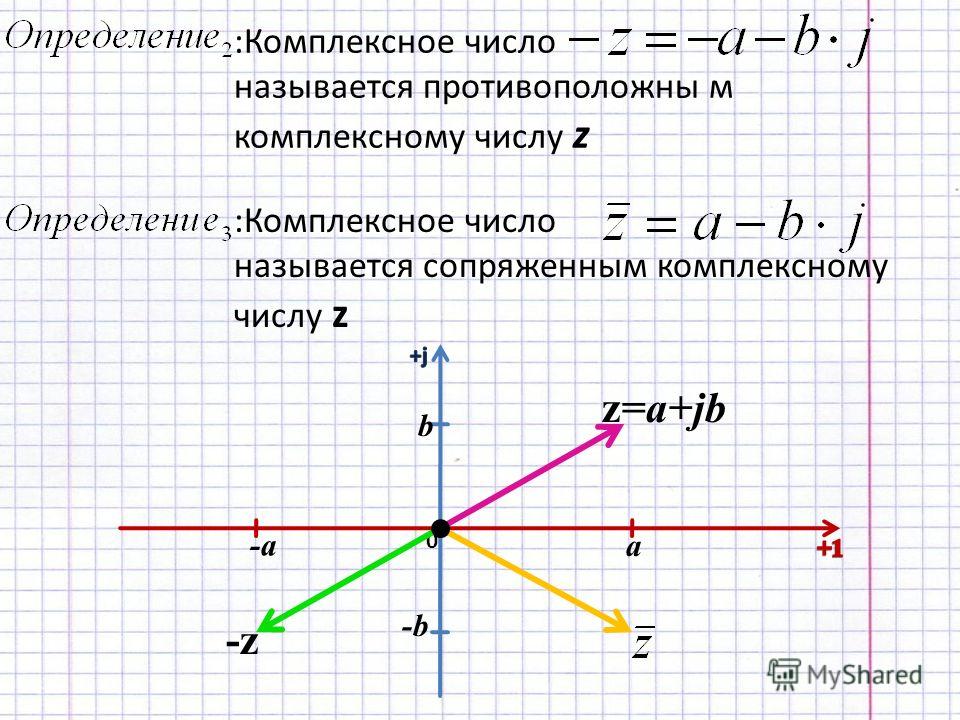 {i1{,}25\pi}}\]
{i1{,}25\pi}}\]В калькуляторе возможно использование констант, математических функций, дополнительных операций и более сложных выражений, ознакомиться с этими возможностями вы можете на странице общих правил использования калькуляторов на этом сайте.
Сайт находится в разработке, некоторые страницы могут быть недоступны.
Новости
07.07.2016
Добавлен калькулятор для решения систем нелинейных алгебраических уравнений: .
30.06.2016
На сайте реализован адаптивный дизайн, страницы адекватно отображаются как на больших мониторах, так и на мобильных устройствах.
Спонсор
РГРОнлайн.ru – мгновенное решение работ по электротехнике онлайн.
Начнем с любимого квадрата.
Пример 9
Возвести в квадрат комплексное число
Здесь можно пойти двумя путями, первый способ это переписать степень как произведение множителей и перемножить числа по правилу умножения многочленов.
Второй способ состоит в применение известной школьной формулы сокращенного умножения :
Для комплексного числа легко вывести свою формулу сокращенного умножения:
Аналогичную формулу можно вывести для
квадрата разности, а также для куба
сумма и куба разности. Но эти формулы
более актуальны длязадач
комплексного анализа. Что делать,
если комплексное число нужно возвести,
скажем, в 5-ую, 10-ую или 100-ую степень?
Ясно, что в алгебраической форме проделать
такой трюк практически невозможно,
действительно, подумайте, как вы будете
решать пример вроде?
Но эти формулы
более актуальны длязадач
комплексного анализа. Что делать,
если комплексное число нужно возвести,
скажем, в 5-ую, 10-ую или 100-ую степень?
Ясно, что в алгебраической форме проделать
такой трюк практически невозможно,
действительно, подумайте, как вы будете
решать пример вроде?
И здесь на помощь приходит тригонометрическая форма комплексного числа и, так называемая, формула Муавра : Если комплексное число представлено в тригонометрической форме , то при его возведении в натуральную степеньсправедлива формула:
Просто до безобразия.
Пример 10
Дано комплексное число , найти.
Что нужно сделать? Сначала нужно представить данное число в тригонометрической форме. Внимательные читатели заметили, что в Примере 8 мы это уже сделали:
Тогда, по формуле Муавра:
Упаси
боже, не нужно считать на калькуляторе
,
а вот угол в большинстве случае следует
упростить. Как упростить? Образно
говоря, нужно избавиться от лишних
оборотов. Один оборот составляетрадиан
или 360 градусов. Выясним сколько у нас
оборотов в аргументе.
Для удобства делаем дробь правильной:,
после чего становится хорошо видно, что
можно убавить один оборот:.
Надеюсь всем понятно, чтои–
это один и тот же угол.
Один оборот составляетрадиан
или 360 градусов. Выясним сколько у нас
оборотов в аргументе.
Для удобства делаем дробь правильной:,
после чего становится хорошо видно, что
можно убавить один оборот:.
Надеюсь всем понятно, чтои–
это один и тот же угол.
Таким образом, окончательный ответ запишется так:
Отдельная разновидность задачи возведения в степень – это возведение в степень чисто мнимых чисел.
Пример 12
Возвести в степень комплексные числа ,,
Здесь тоже всё просто, главное, помнить знаменитое равенство.
Если мнимая единица возводится в четную степень, то техника решения такова:
Если мнимая единица возводится в нечетную степень, то «отщипываем» одно «и», получая четную степень:
Если есть минус (или любой действительный коэффициент), то его необходимо предварительно отделить:
Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями
Рассмотрим пример:
Нельзя
извлечь корень? Если речь идет о
действительных числах, то действительно
нельзя. В комплексных числах извлечь
корень – можно! А точнее, два корня:
В комплексных числах извлечь
корень – можно! А точнее, два корня:
Действительно ли найденные корни являются решением уравнения ? Выполним проверку:
Что и требовалось проверить.
Часто используется сокращенная запись, оба корня записывают в одну строчку под «одной гребёнкой»: .
Такие корни также называют сопряженными комплексными корнями .
Как извлекать квадратные корни из отрицательных чисел, думаю, всем понятно: ,,,,и т.д. Во всех случаях получаетсядва сопряженных комплексных корня.
Начнем с любимого квадрата.
Пример 9
Возвести в квадрат комплексное число
Здесь можно пойти двумя путями, первый способ это переписать степень как произведение множителей и перемножить числа по правилу умножения многочленов.
Второй способ состоит в применение известной школьной формулы сокращенного умножения :
Для комплексного числа легко вывести свою формулу сокращенного умножения:
Аналогичную формулу можно вывести для
квадрата разности, а также для куба
сумма и куба разности. Но эти формулы
более актуальны длязадач
комплексного анализа. Что делать,
если комплексное число нужно возвести,
скажем, в 5-ую, 10-ую или 100-ую степень?
Ясно, что в алгебраической форме проделать
такой трюк практически невозможно,
действительно, подумайте, как вы будете
решать пример вроде?
Но эти формулы
более актуальны длязадач
комплексного анализа. Что делать,
если комплексное число нужно возвести,
скажем, в 5-ую, 10-ую или 100-ую степень?
Ясно, что в алгебраической форме проделать
такой трюк практически невозможно,
действительно, подумайте, как вы будете
решать пример вроде?
И здесь на помощь приходит тригонометрическая форма комплексного числа и, так называемая, формула Муавра : Если комплексное число представлено в тригонометрической форме , то при его возведении в натуральную степеньсправедлива формула:
Просто до безобразия.
Пример 10
Дано комплексное число , найти.
Что нужно сделать? Сначала нужно представить данное число в тригонометрической форме. Внимательные читатели заметили, что в Примере 8 мы это уже сделали:
Тогда, по формуле Муавра:
Упаси
боже, не нужно считать на калькуляторе
,
а вот угол в большинстве случае следует
упростить. Как упростить? Образно
говоря, нужно избавиться от лишних
оборотов. Один оборот составляетрадиан
или 360 градусов. Выясним сколько у нас
оборотов в аргументе.
Для удобства делаем дробь правильной:,
после чего становится хорошо видно, что
можно убавить один оборот:.
Надеюсь всем понятно, чтои–
это один и тот же угол.
Один оборот составляетрадиан
или 360 градусов. Выясним сколько у нас
оборотов в аргументе.
Для удобства делаем дробь правильной:,
после чего становится хорошо видно, что
можно убавить один оборот:.
Надеюсь всем понятно, чтои–
это один и тот же угол.
Таким образом, окончательный ответ запишется так:
Отдельная разновидность задачи возведения в степень – это возведение в степень чисто мнимых чисел.
Пример 12
Возвести в степень комплексные числа ,,
Здесь тоже всё просто, главное, помнить знаменитое равенство.
Если мнимая единица возводится в четную степень, то техника решения такова:
Если мнимая единица возводится в нечетную степень, то «отщипываем» одно «и», получая четную степень:
Если есть минус (или любой действительный коэффициент), то его необходимо предварительно отделить:
Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями
Рассмотрим пример:
Нельзя
извлечь корень? Если речь идет о
действительных числах, то действительно
нельзя. В комплексных числах извлечь
корень – можно! А точнее, два корня:
В комплексных числах извлечь
корень – можно! А точнее, два корня:
Действительно ли найденные корни являются решением уравнения ? Выполним проверку:
Что и требовалось проверить.
Часто используется сокращенная запись, оба корня записывают в одну строчку под «одной гребёнкой»: .
Такие корни также называют сопряженными комплексными корнями .
Как извлекать квадратные корни из отрицательных чисел, думаю, всем понятно: ,,,,и т.д. Во всех случаях получаетсядва сопряженных комплексных корня.
Пример 13
Решить квадратное уравнение
Вычислим дискриминант:
Дискриминант отрицателен, и в действительных числах уравнение решения не имеет. Но корень можно извлечь в комплексных числах!
По известным школьным формулам получаем два корня: – сопряженные комплексные корни
Таким образом, уравнение имеет два сопряженных комплексных корня:,
Теперь вы сможете решить любое квадратное уравнение!
И
вообще, любое уравнение с многочленом
«энной» степени
имеет
ровнокорней,
часть из которых может быть комплексными.
Простой пример для самостоятельного решения:
Пример 14
Найти корни уравнения и разложить квадратный двучлен на множители.
Разложение на множители осуществляется опять же по стандартной школьной формуле.
Лучшие калькуляторы для iPhone и iPad – Проект AppStudio
| Критерии сравнения | Calculator+ | CALC | Tydlig | Soulver | iRocks | PCalc | Calcbot 2 |
|---|---|---|---|---|---|---|---|
| Основная фишка | Графики | Для расчётов | Комбинированные вычисления | Математические функции | Внешний вид | ||
| Базовые функции | |||||||
| Возведение в квадрат и в куб | |||||||
| Возведение в любую степень | |||||||
| Извлечение квадратного корня | |||||||
| Извлечение корня любой степени | |||||||
| Тригонометрические функции | |||||||
| Обратные тригонометрические функции | |||||||
| Натуральные и десятичные логарифмы | |||||||
| Факториалы | |||||||
| Число пи | |||||||
| Обратные числа | |||||||
| Генератор случайных чисел | |||||||
| Экспонента | |||||||
| Степени 10 (EE) | |||||||
| Переключение «радианы-градусы» | |||||||
| Дополнительные возможности | |||||||
| Комплексные числа | |||||||
| Конвертер величин (валют) | |||||||
| Комбинаторика | |||||||
| Работа с функциями | |||||||
| Расчёт площади и объёма | |||||||
| Рисование графиков | |||||||
| Ведение расчётов | |||||||
| Регистр памяти | |||||||
| Несколько регистров памяти | |||||||
| Скобки | |||||||
| Учёт порядка действий | |||||||
| Сохранение истории вычислений | |||||||
| Отправка истории вычислений по почте | |||||||
| Использование результатов расчёта в других расчётах | |||||||
| Распечатка результатов | |||||||
| Комментарии к вычислениям | |||||||
| Финансовый формат чисел | |||||||
| Настраиваемая точность вычислений | |||||||
| Интерфейс | |||||||
| Клавиша Backspace | |||||||
| Стирание цифр swipe-жестом | |||||||
| Копирование из строки вычислений | |||||||
| Поддержка курсора в строке цифр | |||||||
| Поддержка нескольких рабочих пространств | |||||||
| Рукописный ввод цифр | |||||||
| Поддержка ландшафтного и портретного режима | |||||||
| Настраиваемый звук клавиш | |||||||
| Поддержка тем оформления | |||||||
| Установка любых картинок в качестве фона | |||||||
| Совместимость | |||||||
| Совместимость с iPhone / iPod touch | |||||||
| Адаптация под дисплеи с Face ID | |||||||
| Совместимость с iPad | |||||||
| Универсальное приложение (работает и на iPhone, и на iPad) | |||||||
| Поддержка Apple TV | |||||||
| Поддержка Apple Watch | |||||||
| Семейный доступ | |||||||
| Команды Siri | |||||||
| Виджет для Центра уведомлений | |||||||
| Тёмная тема интерфейса | |||||||
| Русификация | |||||||
| Версии для iPhone и iPod touch | |||||||
| Версия для iPhone / iPod touch | 2. 5.6 5.6 | 3.5.26 | 1.6 | 2.8.0 | 1.1.5 | 3.9.3 | 2.4.4 |
| Размер версии для iPhone / iPod touch (МБ) | 52,6 | 16,4 | 12,7 | 7,2 | 46,5 | 102,5 | 15,3 |
| Цена версии для iPhone / iPod touch в российском App Store | Бесплатно | 379 ₽ | 169 ₽ | 229 ₽ | Бесплатно | 749 ₽ | Бесплатно |
| Встроенные покупки в версии для iPhone | |||||||
| Минимально требуемая версия iOS для iPhone / iPod touch | 10.0 | 9.0 | 9.0 | 11.4 | 8.0 | 10.0 | 11.0 |
| Дата релиза последнего обновления версии для iPhone / iPod touch | 27. 11.19 11.19 | 25.09.19 | 29.11.17 | 21.09.19 | 22.11.18 | 20.11.19 | 23.09.19 |
| Версии для iPad | |||||||
| Версия для iPad | 2.5.6 | 3.5.26 | 1.6 | 2.8.0 | 1.1.5 | 3.9.3 | 2.4.4 |
| Размер версии для iPad (МБ) | 52,6 | 16,4 | 12,7 | 7,2 | 46,5 | 102,5 | 15,3 |
| Цена версии для iPad в российском App Store | FREE | 379Р | 169Р | 229Р | FREE | 749Р | FREE |
| Встроенные покупки в версии для iPad | |||||||
| Минимально требуемая версия iOS для iPad | 10.0 | 9.0 | 9.0 | 11.4 | 8. | 10.0 | 11.0 |
| Дата релиза последнего обновления версии для iPad | 27.11.19 | 25.09.19 | 29.11.17 | 21.09.19 | 22.11.18 | 20.11.19 | 23.09.19 |
| Lite-версии приложений | |||||||
| Наличие lite-версии для iPhone и iPod touch | |||||||
| Наличие lite-версии для iPad | |||||||
| Ограничения lite-версии | |||||||
| Скриншоты приложений | |||||||
| Скриншоты с iPhone / iPod touch | |||||||
| Скриншоты с iPad | |||||||
| Ссылки на App Store | |||||||
| Скачать / купить полную версию программы для iPhone / iPod touch | |||||||
| Скачать / купить полную версию программы для iPad | |||||||
| Рейтинги и отзывы | |||||||
| Средний рейтинг в App Store (и число оценок) | 561 | 770 | 1010 | 102 | 19016 | 68 | 710 |
| Выбор редакции AppStudio | |||||||
| Обзоры приложений на сайте AppStudio | |||||||
| Критерии сравнения | Calculator+ | CALC | Tydlig | Soulver | iRocks | PCalc | Calcbot 2 |
Дата прошлой перепроверки таблицы: 13 января 2020 года
Онлайн калькулятор: Комплексные числа
Учеба Математика Алгебра
Калькулятор отображает комплексное число и его сопряженное на комплексной плоскости, вычисляет абсолютное значение комплексного числа и главное значение аргумента. Он также демонстрирует элементарные операции над комплексными числами.
Он также демонстрирует элементарные операции над комплексными числами.
Начиная с 16-го века, математики столкнулись с необходимостью специальных чисел, также известных сегодня как комплексные числа. Комплексное число — это число вида a+bi, где a,b — действительные числа, а i — мнимая единица является решением уравнения: i 2 =-1.
Интересно проследить эволюцию взглядов математиков на проблемы комплексных чисел. Вот несколько цитат из древних сочинений на эту тему:
- 16 век : Так прогрессирует арифметическая тонкость, конец которой… столь же утончен, сколь и бесполезен. 1
- XVII век: Это чудо анализа, это чудо мира идей, почти амфибийный объект между Бытием и Небытием, который мы называем мнимым числом. 2
- 18 век : Квадратные корни из отрицательных чисел не равны нулю, они не меньше нуля, они не больше нуля. Квадратные корни отрицательных чисел не могут принадлежать действительным числам, поэтому они являются недействительными числами .
 Это обстоятельство заставляет использовать мысли о числах, которые по своей сути невозможны и обычно называются мнимыми, потому что их только в уме можно представить. 3
Это обстоятельство заставляет использовать мысли о числах, которые по своей сути невозможны и обычно называются мнимыми, потому что их только в уме можно представить. 3 - XIX век Никто не подвергает сомнению точность результатов, которые мы получаем с помощью исчисления мнимых величин, хотя они являются всего лишь алгебраическими формами и иероглифами недействительных величин. 4
Используется несколькими способами при определении комплексных чисел. Приведем три из них
Алгебраическая форма
,
где a и b — действительные числа, i — мнимая единица, так что i 2 =-1. а — соответствует действительной части, б — мнимой части.
Полярная форма
,
где r — абсолютное значение комплексного числа:
— расстояние между точкой 0 и комплексной точкой на комплексной плоскости, а φ — угол между положительной действительной осью и комплексным вектором (аргумент).
Экспоненциальная форма (форма Эйлера)
представляет собой упрощенную версию полярной формы, полученной из формулы Эйлера.
Complex number
Complex number
Calculation precision
Digits after the decimal point: 2
In polar form
In Euler form
Complex number
Absolute value
Argument основная стоимость (рад)
Главное значение аргумента (градусы)
Сопряжение
Комплексная плоскость
Файл очень большой. Во время загрузки и создания может происходить замедление работы браузера.
Аргумент комплексного числа является многозначной функцией для целого числа k. Главным значением аргумента является одно значение в открытом периоде (-π..π].
Главное значение может быть вычислено из алгебраической формы по следующей формуле:
Этот алгоритм реализован в функции javascript Math.atan2.
Все элементарные арифметические операции определены для комплексного числа:
Комплексный номер Элементарные операции
Номер 1 (Z1)
OperationAddsubtractmultiplyDivideexponentiateatak после запятой: 2
Результат (z)
Файл очень большой. Во время загрузки и создания может происходить замедление работы браузера.
Во время загрузки и создания может происходить замедление работы браузера.
Сложение комплексных чисел
Одно комплексное число может быть добавлено к другому так же, как многочлены:
Умножение комплексных чисел
Используя определение комплексного числа i*i=-1, мы можем легко объяснить формулу умножения комплексных чисел:
Деление комплексных чисел
Чтобы получить формулу деления комплексных чисел, умножаем числитель и знаменатель на сопряженное комплексное число (чтобы исключить мнимую единицу в знаменателе):
Сопряженное число определяется как:
Итак, окончательная формула деления:
Возведение комплексного числа в степень
Используя форму Эйлера, это просто:
Эта формула получена из формулы де Муавра:
Из формулы Де Муавра n корней n-й степени z (степень 1/n) задаются как:
,
имеется n корней, где k = 0..n-1 — целочисленный корневой индекс. Корни могут отображаться на комплексной плоскости как вершины правильного многоугольника.
Корни могут отображаться на комплексной плоскости как вершины правильного многоугольника.
Г. Кардано, Великое искусство или правила алгебры, (1539) ↩
Г. Лейбниц, (согласно Википедии) ↩
Л. Эйлер, Универсальная арифметика, (1768) § 142–143 ↩
Л. Карно, Размышления о метафизических принципах анализа бесконечно малых (1797) Тр. У. Р. Браунелл с. 104 ↩
URL скопирован в буфер обмена
Похожие калькуляторы
- • Complex polynomial value calculation
- • Two arguments arctangent
- • Complex fraction
- • The solution of a quadratic equation
- • Determinant by Gaussian elimination
- • Algebra section ( 108 calculators )
absolute value Algebra аргумент сложный аргумент комплексное число комплексная плоскость сопряжение главный аргумент математические операции с числами
PLANETCALC, комплексные числа
Anton 2021-12-05 21:45:58
Комплексный номер Калькулятор
Создан Wojciech SAS, кандидат PhD
. Просветано Bogna Szyk и Jack Bowater
Просветано Bogna Szyk и Jack Bowater
Последний
Содержание:- Что такое комплексное число? — Определение комплексных чисел
- Полярная форма комплексных чисел
- Основные операции с комплексными числами — сумма и разность
- Умножение и деление комплексных чисел
- Комплексная степень и комплексный логарифм
- Как использовать калькулятор комплексных чисел
- Свойства комплексных чисел
- Комплексные числа в реальной жизни
Наш калькулятор комплексных чисел (также известный как калькулятор мнимых чисел) является отличным инструментом для решение основных операций с комплексными числами. Читайте дальше, чтобы найти ответ на вопрос: «что такое комплексное число?», узнать об алгебраической и полярной форме комплексных чисел и освоить навыки умножения и деления комплексных чисел. В конце этого текста вы также можете найти информацию о свойствах комплексных чисел (большинство из которых основано на сопряженных или абсолютных значениях комплексных чисел) и даже о некоторых их практических применениях.
Что такое комплексное число? — Определение комплексного числа
Чтобы ответить на вопрос, что такое комплексное число, мы должны сначала спросить: «Что такое мнимое число?». Мнимое число — это квадратный корень из отрицательного числа . Основное мнимое число обозначается буквой i (иногда j , например, в электронике) и определяется как:
i = √(-1) .
Определение комплексного числа z представляет собой комбинацию действительных a и воображаемых b*i частей, так что:
z = a + bi .
Здесь и a , и b являются классически понимаемыми действительными числами. Когда b = 0,, число чисто действительное, а если , a = 0,, то число чисто мнимое. Вы можете использовать этот калькулятор комплексных чисел как калькулятор мнимых чисел — просто введите действительную составляющую, равную 0.
Другой способ записать две части комплексного числа — Re и Im , так что Re(z) = a и Im(z) = b . На самом деле есть числа с большим количеством мнимых частей: кватернионы. К счастью, здесь нам не о чем беспокоиться.
Сопряжение комплексного числа определяется как:
z = a - bi .
Как видим, сопряжение комплексного числа не влияет на действительную часть, а мнимая часть имеет знак, противоположный исходному.
Полярная форма комплексных чисел
Комплексные числа имеют много общего с декартовой системой координат, потому что они представляют собой пары чисел на декартовой комплексной плоскости . Полезно представлять комплексные числа как векторы на этой комплексной плоскости. Формулы, которые переводят комплексные числа из декартовой формы в полярную, точно такие же, как классические преобразования координат:
-
|z| = а² + б², -
tan(φ) = b / a,
, где |z| есть модуль/абсолютное значение комплексного числа , φ известно как аргумент или фаза (иногда мы используем обозначение arg(z) = φ ), а тангенс есть тангенс данный аргумент. Точно так же длина вектора в двумерной евклидовой плоскости — это расстояние между его концом и началом системы координат. Угол
Точно так же длина вектора в двумерной евклидовой плоскости — это расстояние между его концом и началом системы координат. Угол φ отсчитывается от оси X против часовой стрелки и может варьироваться от 0 до 2π или от -π до π (в зависимости от соглашения, поскольку оба эквивалентны).
Зная это, мы можем записать любое комплексное число, используя его полярные координаты на этой плоскости:
-
a = |z| * cosφ, -
б = |г| * sinφ.
Здесь sin и cos — основные тригонометрические функции. Эти формулы выводятся из соотношений в прямоугольном треугольнике на комплексной плоскости. Другими словами, комплексное число может быть записано как: г = | г | * (cosφ + i*sinφ) .
Существует также другой способ переписать это число, используя формулу Эйлера :
z = |z| * exp(i * φ) ,
где exp() — показательная функция, основанием которой является число e . Из-за свойства периодичности мы можем видеть, что:
Из-за свойства периодичности мы можем видеть, что:
exp(iφ) = exp(i(φ + 2kπ)) ,
, где k — любое целое число.
Полярная форма комплексных чисел очень полезна в различных вычислениях, включая умножение, деление и даже некоторые более сложные вычисления. Экспоненциальная форма особенно удобна, если вы недостаточно хорошо разбираетесь в тригонометрических законах или просто предпочитаете работать со степенями.
Основные операции с комплексными числами — сумма и разность
При выполнении простых операций с комплексными числами полезно думать о них как о векторах. Затем довольно просто добиться как сложения, так и вычитания комплексных чисел.
Обозначим первое число как F = a + bi , а второе как G = c + di . Тогда сумма двух комплексных чисел равна:
F + G = a + bi + c + di = (a + c) + (b + d)*i ,
, где Re(F + G) = a + c — действительная часть суммы, а Im(F + G) = b + d — мнимая.
Аналогично можно найти разность этих чисел:
F - G = a + bi - c + di = (a - c) + (b - d)*i ,
и теперь Re (F - G) = a - c и Im(F - G) = b - d .
Вы помните, как складывать или вычитать два 2D-вектора? Это точно так же, как мы делаем это в этом калькуляторе комплексных чисел — вам просто нужно сложить (или вычесть) каждую пару компонентов отдельно, и все!
Умножение и деление комплексных чисел
Теперь давайте перейдем к чему-то более сложному — мы хотим выяснить, как работает умножение комплексных чисел. Следуя обозначениям из предыдущего раздела, мы можем написать:
F * G = (a + bi) * (c + di) = a*c + a*d*i + b*c*i + b*d*i *i = (a*c - b*d) + (a*d + b*c)*i .
На этот раз действительную часть можно записать как Re(F * G) = a*c - b*d , а мнимую часть как Im(F * G) = a*d + b*c . Обратите внимание, что в действительной части стоит знак минус, так как в какой-то момент мы столкнулись с умножением двух мнимых чисел
Обратите внимание, что в действительной части стоит знак минус, так как в какой-то момент мы столкнулись с умножением двух мнимых чисел i*i , что равно -1 по определению.
Умножение комплексных чисел выглядит не так уж и страшно, не так ли? А как насчет деления комплексных чисел? Давайте посмотрим на вычисления с пошаговыми подсказками:
-
F / G = (a + bi) / (c + di) =, расширьте и числитель, и знаменатель на сопряжение комплексного числа последнего. -
= (a + bi) * (c - di) / ((c + di) * (c - di)) =, выполнить стандартное умножение. -
= (a*c - a*d*i + b*c*i - b*d*i*i) / (c² - (di)²) =, еще раз используйте тот факт, чтоi* я = -1. -
= (a*c + b*d + (b*c - a*d)*i) / (c² + d²).
Получаем следующие результаты: Re(F / G) = (a*c + b*d) / (c² + d²) , Im(F * G) = (b*c - a *d) / (c² + d²) . Конечно, деление возможно только при
Конечно, деление возможно только при г ≠ 0 .
Мы также можем рассмотреть вышеописанные операции в полярных обозначениях, скажем, F = |z₁|*exp(iφ₁) , G = |z₂|*exp(iφ₂) . Тогда умножение комплексных чисел задается следующим образом:
F * G = |z₁|*exp(iφ₁) * |z₂|*exp(iφ₂) = |z₁*z₂| * exp(i(φ₁+φ₂)) ,
и мы можем видеть, что: |F * G| = |z₁*z₂| и arg(F * G) = φ₁+φ₂ .
Деление комплексных чисел почти такое же с этой записью:
F / G = |z₁|*exp(iφ₁) / |z₂|*exp(iφ₂) = |z₁/z₂| * exp(i(φ₁-φ₂)) ,
переписывая результат как: |F / G| = |z₁/z₂| и arg(F / G) = φ₁-φ₂ . Используя эту форму, ясно видно, что результирующий модуль представляет собой просто отношение абсолютных значений обоих чисел. (Для получения дополнительной информации о соотношениях обратитесь к нашему калькулятору коэффициентов. )
)
Похоже, что вторая попытка намного проще, поэтому иногда стоит подумать об изменении формы наших выражений перед началом вычисления 9Г .
-
F G = (a + bi) (c + di) =, поскольку не очевидно, как расширить это выражение, мы можем записатьFв полярной форме комплексных чисел. -
= (|z₁|*exp(iφ₁)) (c + di) =, теперь произведение в любой степени суммы есть произведение каждого элемента на каждый компонент в отдельности. -
= |z₁|ᶜ * exp(iφ₁*c) * |z₁|ᵈⁱ * exp(-φ₁*d) =, мы можем использовать известное свойство экспоненты:x n = exp(n * ln(x)), гдеln— натуральный логарифм. -
= |z₁|ᶜ * exp(-φ₁*d) * exp(i(φ₁*c + d*ln|z₁|)).
Тогда абсолютное значение равно: |F G | = |z₁|ᶜ * exp(-φ₁* d) , а аргумент: arg(F G ) = φ₁c + d*ln|z₁| . Хотя мы смешиваем две разные нотации, это нормально. Мы также можем изменить их так, как вам нравится — это все на ваше усмотрение.
Хотя мы смешиваем две разные нотации, это нормально. Мы также можем изменить их так, как вам нравится — это все на ваше усмотрение.
Логарифм комплексного числа (также известное как комплексный логарифм ) можно вычислить следующим образом:
ln(F) = ln(|z₁|*exp(iφ₁)) = ln(|z₁|) + iφ₁ .
Одно важное замечание: поскольку фазы φ₁ и φ₁+2kπ эквивалентны, комплексный логарифм имеет бесконечное число решений, и общий результат дается как: ln(|z₁|) + i(φ₁ +2kπ) .
Как пользоваться калькулятором комплексных чисел
Этот инструмент очень прост в использовании. Все, что вам нужно сделать, это написать действительную и мнимую часть двух чисел. Если число чисто действительное или чисто мнимое, установите другой компонент равным 0. И все. В результате вы получите полярную форму комплексных чисел, сумму, разность, произведение, частное, а также первое число в степени второго и логарифм первого числа.
Свойства комплексных чисел
Есть несколько свойств комплексных чисел, в том числе сопряженные или абсолютные значения комплексных чисел, которые могут быть полезны при выполнении некоторых упражнений.
-
Re(z) = Re(z), -
Im(z) = -Im(z), -
z * z = |z|², -
|z₁ + z₂| ≤ |z₁| + |z₂|, -
|z₁ * z₂| = |z₁| * |z₂|, -
|z₁ / z₂| = |z₁| / |z₂|, - , если
z = 0, то обаa = 0иb = 0.
Комплексные числа в реальной жизни
Комплексные числа иногда очень полезны при алгебраических выражениях, особенно если они связаны с тригонометрическими функциями.
Многие физические задачи решаются с помощью комплексных чисел. Одной из основных областей использования комплексных чисел является мир волновых функций и гармонического движения. Множество задач из электроники можно значительно упростить с помощью комплексных чисел. Проверить, как это делается на практике, можно с помощью калькулятора делителя напряжения.
Проверить, как это делается на практике, можно с помощью калькулятора делителя напряжения.
Войцех Сас, кандидат наук
Первое число: z₁ = a + bi
Действительная часть (a)
Мнимая часть (b)
Величина |z₁|
Фаза (φ₁)
Второе число: z₂ = c + di
Действительная часть (c)
Мнимая часть (d)
Величина |z₂|
Фаза (φ₂)
Ознакомьтесь с 35 похожими калькуляторами алгебры 🔡
Уравнение абсолютного значенияАбсолютное неравенствоСложение и вычитание многочленов… 32 еще 9* $ и состоит из той же действительной части с противоположной мнимой частью.
Результаты
Сопряжение комплексных чисел — dCode
Теги: Геометрия
Поделиться
dCode и многое другое
dCode бесплатен, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и решении задач ежедневно!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !
Комплексно-сопряженный калькулятор
Комплексное число z См. также: Модуль/величина комплексного числа — Аргумент комплексного числа 9* $) и равен $\overline{z} = a-ib $, где $a = \Re(z)$ — действительная часть, а $b = \Im(z)$ — мнимая часть.
также: Модуль/величина комплексного числа — Аргумент комплексного числа 9* $) и равен $\overline{z} = a-ib $, где $a = \Re(z)$ — действительная часть, а $b = \Im(z)$ — мнимая часть.
Другими словами, сопряженным комплексу является число с той же действительной частью, но с противоположной мнимой частью.
На комплексной плоскости точки $z$ и $\overline{z}$ симметричны (симметрия относительно оси x).
Как вычислить сопряженное комплексное число?
Из алгебраической формы комплексного числа $ z = a+ib $ вычисляется сопряженное $ \overline{z} = a-ib $.
Пример: Определить сопряжение $ z = 1+i $ для вычисления $ \overline{z} = 1-i $
Другими словами, чтобы найти сопряжение комплексного числа, взять это же комплексное число число, но с противоположной (со знаком минус) его мнимой частью (содержащей $ i $).
Что такое комплексно-сопряженная пара?
Набор из 2-х элементов: комплексного числа $z$ и его сопряженного $\overline{z}$, образует пару сопряженных.
Каковы свойства конъюгатов?
Используя комплексные числа $ z, z_1, z_2 $, сопряжение имеет следующие свойства:
$$ \overline{z_1+z_2} = \overline{z_1} + \overline{z_2} $$
$$ \overline{z_1 \cdot z_2} = \overline{z_1} \times \overline{z_2} $$
$$ \overline{\left(\frac{z_1}{z_2}\right)} = \frac{\ overline{z_1}}{\overline{z_2}} \iff z_2 \neq 0 $$
Число без мнимой части равно своему сопряженному:
$$ \Im (z) = 0 \iff \overline{ г} = г $$
2 $$Это действительное число (без мнимой части $ i $) и строго положительное (сложение двух квадратов обязательно положительное)
Чему равно i?
Сопряженным числом $i$ является число $-i$
Как вычислить сопряжение действительного числа (без i)?
Сопряженным $ \overline{a} $ действительного числа $ a $ является само число $ a $: $ a=a+0i=a-0i=\overline{a} $
Пример: $ \overline{1 + 0 \times i} = 1 $
Исходный код
dCode сохраняет за собой право собственности на исходный код «Complex Number Conjugate». За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Сопряжение комплексных чисел», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Комплексное число Функции сопряжения» (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и загрузка всех данных, сценарий или доступ к API для «Complex Number Conjugate» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!
За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Сопряжение комплексных чисел», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Комплексное число Функции сопряжения» (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и загрузка всех данных, сценарий или доступ к API для «Complex Number Conjugate» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!
Напоминание: dCode можно использовать бесплатно.
Цитировать dCode
Копирование и вставка страницы «Комплексное числовое сопряжение» или любых его результатов разрешено, если вы цитируете dCode!
Цитировать как источник (библиографию):
Complex Number Conjugate на dCode. fr [онлайн-сайт], получено 27 сентября 2022 г., https://www.dcode.fr/complex-number-conjugate
fr [онлайн-сайт], получено 27 сентября 2022 г., https://www.dcode.fr/complex-number-conjugate
Сводка
- Калькулятор комплексных сопряжений
- Что такое сопряжение комплексного числа? (Определение)
- Как вычислить сопряженное комплексное число?
- Что такое комплексно-сопряженная пара?
- Каковы свойства конъюгатов?
- Что такое произведение комплексного числа и его сопряженного?
- Что является сопряженным i?
- Как вычислить сопряжение вещественного числа (без i)?
Аналогичные страницы
- Аргумент комплексного числа
- Комплексное число Модуль/величина
- Касательная кривой
- Изображение функции
- Предварительное представление о функции
- Неизвестные в треугольнике
- коэффициент склона
- DCODE List
70009
- DCODE
70009
- Pay -Pal Ключевые слова
сопряжение, комплекс, число, плоскость, симметрия, симметрия, вычислитель
Ссылки
▲
Калькулятор комплексных чисел — преобразование в полярные и мнимые числа
Онлайн-калькулятор комплексных чисел позволяет выполнять основные математические операции для упрощения заданных сложных выражений.
 Этот бесплатный калькулятор мнимых чисел быстро упростит любое сложное выражение с помощью пошаговых вычислений. Итак, продолжайте читать, чтобы понять, как упростить комплексные числа, такие как полярная форма, инверсия, сопряжение и модуль.
Этот бесплатный калькулятор мнимых чисел быстро упростит любое сложное выражение с помощью пошаговых вычислений. Итак, продолжайте читать, чтобы понять, как упростить комплексные числа, такие как полярная форма, инверсия, сопряжение и модуль.Что такое комплексное число?
В математике комплексное число определяется как комбинация действительных и мнимых чисел. Он выражается как x + yi. Здесь «i» — мнимое число, а «x» и «y» — действительные числа. Где «I» также известен как йота, и его значение равно \(\sqrt{-1}\). Калькулятор комплексных чисел может складывать, вычитать, умножать или делить мнимые числа. Короче говоря, мы можем использовать выражение как z = x + iy, где «x» — действительная часть, а «iy» — мнимая часть.
Основные операции с комплексными числами:
При выполнении простых операций с комплексными числами полезно думать о них как о векторах. Затем очень просто вычитать и складывать комплексные числа с помощью калькулятора комплексных решений.

Если первое число равно A = x + yi, а второе число равно B = m + ni, то сумма двух комплексных чисел равна:
$$ A + B = x + yi + m + ni = (x + m) + (y + n) * I $$
Где Re (A + B) = x + m — часть суммы действительных чисел, а Im(A + B) = y + n — часть суммы мнимого числа.
Если числа: A – B = x + yi – m + ni = (x – m) + (y – n) * I, то Re (A – B) = x – m и Im (A – B ) = у – п. Калькулятор комплексных чисел, сложите (или вычтите) каждую пару заданных компонентов отдельно!
Однако онлайн-калькулятор научной записи позволяет складывать, вычитать, умножать и делить числа в экспоненциальной записи.
Умножение и деление комплексных чисел:
Давайте посмотрим, как умножаются комплексные числа с помощью простого калькулятора комплексных чисел. Согласно обозначениям в предыдущем разделе:
- $$ A * B = (x + yi) * (m + ni) = x * m + x * n * i + y * m * i + y * n * i * i = (x * my * n) + (x * n + y * m) * i $$
- На этот раз действительную часть можно записать как Re(A * B) = x * m – y * n, а мнимую часть как Im(A * B) = x * n + y * m.

- Помните, что калькуляторы комплексных чисел используют отрицательный знак в действительной части, потому что в какой-то момент мы сталкиваемся с произведением двух чисел i * i, которое по определению равно -1.
- С помощью комплексного калькулятора умножение комплексных чисел не составляет труда. Давайте посмотрим на вычисление теоремы: A / B = (x + yi)/(m + ni) =, расширим числитель и знаменатель, объединив комплексные числа числителя и знаменателя. 9{nx} * exp (-φ_1 * d) = Мы можем использовать известное экспоненциальное свойство: xn = exp (n * ln (x)), где ln — натуральный логарифм.
- | z_1| Exp * exp(-φ_1 * d) * exp (i(φ_1 * m + n * ln |z_1|)).
- Таким образом, абсолютное значение равно: AB = | z_1| exp * exp (-φ_1 * d), а независимая переменная: arg(AB) = φ m + n * ln | z_1|
- Логарифм комплексного числа (также известный как комплексный логарифм) можно вычислить следующим образом: ln (F) = ln (|z_1| * exp (iφ_1)) = ln (|z_1|)+iφ_1.

Однако используйте онлайн-калькулятор составных функций, который вычисляет состав функций на основе введенных значений функций f(x) и g(x) в определенных точках.
Как работает калькулятор комплексных чисел?
Калькулятор мнимых чисел упрощает данное выражение с помощью следующих шагов:
Ввод:
- Сначала введите выражение с действительными и мнимыми числами.
- Нажмите кнопку расчета.
Выход:
- Калькулятор комплексных чисел обеспечивает обратную, сопряженную, модульную и полярную формы заданных выражений.
- Калькулятор отображает пошаговое решение умножения и других основных математических выражений.
Часто задаваемые вопросы:
Все ли числа сложные?
Каждое действительное число является комплексным числом, но не обязательно каждое комплексное число является действительным числом. Множество всех комплексных чисел представлено как Z ∈ C. Множество всех мнимых чисел выражается как Z ∈ C – R.

Где в реальной жизни используются комплексные числа?
Комплексные числа также используются для расчета напряжения, тока или сопротивления в цепи переменного тока (AC означает переменный ток).
Как работает комплексное число?
Комплексное число представляет собой сумму мнимого числа и действительного числа, выраженную как a + bi. Итак, точка пересечения действительной части находится на горизонтальной оси, а найденной мнимой части — на вертикальной оси.
Вывод:
Используйте этот онлайн-калькулятор комплексных чисел для выполнения основных операций, таких как умножение и деление с комплексными числами. Вы можете написать как мнимую, так и действительную часть двух чисел. Если число чисто мнимое или чисто действительное, то другую часть приравняйте к 0. После этого вы получите полярную форму данного сложного выражения.
Ссылка:Из источника Википедии: Обозначение, Визуализация, Декартова комплексная плоскость, Полярная комплексная плоскость, Модуль и аргумент, Сложные графы.

Из источника Brilliant: Комплексная плоскость, Воображаемая единица i, Арифметика комплексных чисел, Умножение комплексных чисел, Комплексно-сопряженные числа.
Из источника университетских наставников: комплексные числа, комплексная плоскость, чисто мнимая, мнимая единица, декартова плоскость.
калькулятор, операции, свойства и многое другое
Вам нужен калькулятор для преобразования полярной формы в биномиальную или из биномиальной в полярную? Здесь у вас есть инструмент, посвященный комплексным числам, а также гораздо больше информации, чтобы вы знали свойства, операции и многое другое.
Чтобы изменить число с полярного на биномиальное или наоборот , просто выберите изменение, которое вы хотите сделать, в нашем калькуляторе, напишите значения, которые соответствуют в каждом случае, и нажмите кнопку расчета, чтобы получить эквивалентность автоматически.
Разделы статей
- Что такое комплексное число?
- Преобразование полярной формы в биномиальную
- Преобразование биномиальной формы в полярную
- Операции
- Модуль комплексного числа
- Сопряжение комплексного числа
- Комплексные числа в Excel
Что такое комплексное число?
Комплексное число является расширением действительных чисел и состоит из действительной и мнимой частей.
 Комплексы могут быть представлены в биномиальной или полярной форме:
Комплексы могут быть представлены в биномиальной или полярной форме:- Биномиальная форма записываются в виде z = a + bi, где a — действительная часть, а b — мнимая часть.
- Полярная форма представлена как z= r α , где r — модуль, а α — аргумент.
А для чего нужны комплексные числа? Ответ длинный, но в качестве резюме мы можем сказать, что мы используем их для решения операций, которые не имеют реального решения (как квадратный корень из отрицательного числа).
Вот как мнимая единица, представленная буквой i y que equivale a la raíz cuadrada de — 1, es decir:
i = √-1
Переход от полярной формы к биномиальной
Для для преобразования комплексного числа из полярной формы в биномиальную Если мы не используем следующую математическую формулу, мы должны применить следующую математическую формулу:
z = r α = r (cos α + i sen α)
Например, если мы хотим, чтобы превратилось в бином, комплекс 3 240º Если мы не используем формулу, мы применим следующую формулу:
z = 3 240º = 3 (cos 240º + i sen 240º) = 3 (-0,5 — 0,866i) = -1,5 — 2,598i
Если вы найдете это полезным, здесь мы оставляем вам соответствующие калькуляторы для получения синуса: и косинуса.

Преобразование из биномиальной в полярную
Если мы хотим сделать обратное преобразование, т. е. передать комплексное число в декартову координату , то мы должны выполнить следующий процесс:
- Первое, что нужно сделать вычислить модуль комплексного числа (z = a + bi), для которого мы применяем эту формулу:
|г| = √(a 2 + b 2 )
- Теперь мы должны получить аргумент полярных координат , который получается по этой формуле:
α = arctg (b/a)
Мы оставляем вас с нашим калькулятором аркотангенса для немедленного решения вышеуказанной операции.
Мы предложим упражнение для решения , в котором мы собираемся поляризовать комплекс 1 + 2i.
|г| = √(1 2 + 2 2 ) = √(1 + 4) = √5
α = arctg (b/a) = arctg (2/1) = 63,43º.

Наконец, мы имеем, что наше комплексное число 1 + 2i в декартовых координатах выражается как √5 63,43º в полярных координатах
Операции
Здесь мы покажем вам, какие из них являются основными. операции, которые можно выполнить с комплексными числами .
Обратите внимание, что некоторые из этих операций только могут быть выполнены в биномиальной или полярной форме , поэтому вам нужно будет переключаться с одного формата на другой в зависимости от того, как выражается комплексное число, которое у вас есть.
Сложение и вычитание комплексных чиселСложение или вычитание комплексных чисел в биномиальной форме очень просто. Нам нужно только сложить действительные части и мнимые части, как вы можете видеть в следующем выражении:
(a+bi)+(c+di) = (a+c)+(b+d)i
( a+bi)-(c+di) = (a-c)+(b-d)iНапример:
(3 + 2i) + (1 + 5i) = (3 + 1) + (2 + 5)i = 4 + 7i
(4 + 3i) — (2 + 1i) = (4 — 2) + (3 — 1)i = 2 + 2iСвойства суммы
- Коммутативное свойство: z1 + z2 = z2 + z1
- Ассоциативное свойство (z1 + z2) + z3 = z1 + (z2 + z3)
- 0 — нейтральный элемент
Умножение комплексных чисел может выполняться как в полярной форме, так и в биномиальной форме .
 Давайте посмотрим, как это делается в каждом случае:
Давайте посмотрим, как это делается в каждом случае:Произведение комплексных чисел в биномиальной форме:
(a+bi)-(c+di) = (a-c — b-d)+(a-d+b-c)i
Упражнение решено:
(1 + 3i)·(2+1i) = 1·2 — 3i 2 + 1i + 6i = 2 — 3 + i + 6i = -1 + 7i
Помните, что i 2 равно -1
Произведение комплексных чисел в полярной форме:
m α ·m’ β =(m·m’) α+β
Пример решения:
2 30º — 5 35º = (2 — 5) 30º+35º. = 10 65º
Свойства умножения:
- Коммутативное свойство: z1 — z2 = z2 — z1
- Ассоциативное свойство: (z1 — z2) — z3 = z1 — (z2 — z3)
- Распределительное свойство: z1 — (z2 + z3) = z1 — z2 + z1 — z3
- 1 — нейтральный элемент (1 + 0i)
Деление — еще одна операция, которую позволяет нам работать как в биномиальной, так и в полярной форме.
 . Давайте посмотрим, как действовать в каждом из них:
. Давайте посмотрим, как действовать в каждом из них:Деление комплексных чисел в биномиальной форме
Если у нас есть два комплексных числа, выраженных в биномиальной форме, способ их деления выглядит следующим образом :
Если вы интересно узнать, как получается это выражение, вот демонстрация , в которой числитель и знаменатель умножаются на сопряженное знаменателю, так что мы получаем действительное число в той части дроби:
Деление комплексных чисел в полярной форме
Для разделить комплексные числа в полярной форме просто разделить модуль и вычесть аргументы, как показано в следующей формуле:
Степени комплексных чисел 9021 случае, когда мы должны вычислить степень комплексного числа В этом разделе мы объясним, как вычислить ее в каждом случае:Степень комплексного числа в биномиальной форме
Это формула , которую нужно разработать n раз для вычисления степени комплексного числа в биномиальной форме:
В зависимости от сложности вам может быть проще преобразовать комплексное число в полярную форму и вычислить power , как описано в следующем разделе.

Степени комплексного числа в полярной форме
На мой взгляд, вычисление степеней в полярной форме намного проще сделать , чем в биномиальной форме, поскольку нам нужно только применить следующую формулу:
(m α ) n = m n nα
Как видите, достаточно возвести модуль в степень n и умножить аргумент на значение n.
Модуль комплексного числа
Если вам нужна дополнительная информация о том, как модуль комплексного числаНажмите на ссылку, которую мы только что оставили вам.
Сопряжение комплексного числа
Сопряжение комплексного числа в биномиальной форме имеет ту же действительную часть и меняет знак мнимой части, так что если наш комплекс Z = a + bi, его сопряжение будет:
являются свойствами, которыми обладает комплексное число:
- Сопряженное действительное число есть само.
 Например, сопряженное 3+0i равно 3-0i, короче, оно равно 3 в обоих случаях.
Например, сопряженное 3+0i равно 3-0i, короче, оно равно 3 в обоих случаях. - Сопряжение мнимого числа является его противоположностью. Например: сопряженное число 5i равно -5i .
- Сопряжение сопряжения является исходным мнимым числом.
- Сумма комплексного числа плюс его сопряженное число равно удвоенной его действительной части:
- Вычитание комплекса минус его сопряженное равно удвоенной его мнимой части:
- Произведение комплекса его сопряженным равно квадрату действительной части плюс квадрат мнимой части:
- Для суммы и произведения нескольких сопряженных равен:
Комплексные числа в Excel
Excel имеет множество функций для работы с комплексными числами . Ниже приведена таблица, которая будет служить сводкой, чтобы увидеть, что они из себя представляют и что они делают.

Если вы не знаете, как его использовать или для чего он нужен, не стесняйтесь оставлять нам комментарии, и мы поможем вам во всем, что касается комплексных чисел.
Функция Описание КОМПЛЕКС Преобразование действительных и мнимых коэффициентов в комплексное число. IM.ABS Вычисляет модуль комплекса. ИМ.АНГУЛО Вычислить угол аргумента (в радианах) МНИМАЯ Дает нам коэффициент мнимой части ВМ.СОПРЯЖЕННЫЙ Вычисляет сопряжение комплекса IM.COS Это дает нам косинус комплексного числа. IM.DIV Мы будем использовать его для деления двух комплексных чисел IM.EXP Позволяет вычислить экспоненциальную форму комплекса IM.LN Возвращает неперовский логарифм комплексного числа. 
IM.LOG10 Логарифм по основанию 10 комплекса IM.LOG2 Эта функция вычисляет логарифм по основанию 2. IM.POT Помогает рассчитать мощность комплекса IM.PRODUCT Позволяет умножать до 29 комплексных чисел IM.ROOT2 Мы будем использовать его, чтобы получить квадратный корень из комплекса IM.REAL Дает нам действительную часть комплексного числа IM.SENO С помощью этой функции мы вычисляем синус комплексного числа IM.SUM Результатом будет сумма двух комплексных чисел IM.SUSTR Эта функция используется для вычитания двух комплексных чисел Nacho
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En Esta веб-те Ayudo hacer cálculos у преобразования sencillas дие кон-эль-Пасо-де-лос-Años се-нос-ха olvidado Cómo себе Hace.
 Si tienes dudas, déjame un commentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, напишите мне сообщение.
Si tienes dudas, déjame un commentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, напишите мне сообщение.Калькулятор комплексных чисел
Теория
Сложение двух комплексных чисел, представленных в алгебраической (прямоугольной) форме.
Сложение действительных и комплексных чисел, представленных в алгебраической (прямоугольной) форме.
Вычитание двух комплексных чисел, представленных в алгебраической (прямоугольной) форме.
Вычитание комплексного числа из действительного числа.
Вычитание вещественного числа из комплексного числа.
Умножение двух комплексных чисел, представленных в алгебраической (прямоугольной) форме..
Умножение действительного и комплексного числа, представленного в алгебраической (прямоугольной) форме.
Деление двух комплексных чисел, представленных в алгебраической (прямоугольной) форме.
Деление комплексного числа, представленного в алгебраической (прямоугольной) форме, действительным числом.
Деление действительного числа на комплексное число, представленное в алгебраической (прямоугольной) форме.
Сложение комплексных чисел, представленных в полярной форме.
Вычитание комплексных чисел, представленных в полярной форме.
Умножение комплексных чисел, представленных в полярной форме.
Деление комплексных чисел, представленных в полярной форме.
Сложение комплексных чисел, представленных в экспоненциальной форме.
Вычитание комплексных чисел, представленных в экспоненциальной форме.
Умножение комплексных чисел, представленных в экспоненциальной форме.
Деление комплексных чисел, представленных в экспоненциальной форме.
Модуль комплексного числа.
Аргумент (фаза) комплексного числа.
Представление комплексного числа в алгебраической (прямоугольной) форме в полярной форме.
Представление комплексного числа в алгебраической (прямоугольной) форме в экспоненциальной форме.
Представление комплексного числа в полярной форме в алгебраической (прямоугольной) форме.
Представление комплексного числа в полярной форме в экспоненциальной форме.
Представление комплексного числа в экспоненциальной форме в полярной форме.
Представление комплексного числа, записанного в экспоненциальной форме, в алгебраической (прямоугольной) форме.
Сопряжение комплексного числа, представленного в алгебраической (прямоугольной) форме.
Сопряжение комплексного числа, выраженное в полярной форме.
Сопряжение комплексного числа, выраженное в экспоненциальной форме.
Обратная величина комплексного числа, представленного в алгебраической (прямоугольной) форме.
Обратная величина комплексного числа, представленного в полярной форме.
Обратная величина комплексного числа, представленного в экспоненциальной форме.
Аддитивная инверсия комплексного числа.
Извлечение корня N комплексного числа, представленного в алгебраической (прямоугольной) форме.
Извлечение корня N из комплексного числа, представленного в полярной форме.
Извлечение корня N из комплексного числа, представленного в экспоненциальной форме.Сложение двух комплексных чисел, представленных в алгебраической (прямоугольной) форме
Чтобы сложить два комплексных числа, представленных в алгебраической (прямоугольной) форме, необходимо сложить их действительную и мнимую части:
(a + bi) + ( c + di) = (a + c) + (b + d)i
Приведем примеры:
Пример 1. Сложим два комплексных числа 2 + 3i и 1,6 + 7i
(2 + 3i) + (1,6 + 7i) = (2 + 1,6) + (3 + 7)i = 3,6 + 10i
Пример 2. Сложим два комплексных числа 3 + 4i и 8 − 6i
(3 + 4i) + (8 − 6i) = (3 + 8) + (4 − 6i) = 11 − 2i
Сложение действительных и комплексных чисел, представленных в алгебраической (прямоугольной) форме
Чтобы сложить комплексное число a + bi и действительное число c, вам нужно добавить действительное число к действительной части комплексного числа:
(a + bi) + c = (a + c) + bi
Приведем примеры:
Пример 1.
 Складываем комплексное число 2 + 3i и действительное число 10
Складываем комплексное число 2 + 3i и действительное число 10(2 + 3i) + 10 = (2 + 10) + 3i = 12 + 3i
Пример 2. Сложите комплексное число −6 + 3i и действительное число -23
(−6 + 3i) + ( −23) = (−6 + (−23)) + 3i = −29 + 3i
Вычитание двух комплексных чисел, представленных в алгебраической (прямоугольной) форме
Для вычитания двух комплексных чисел, представленных в алгебраической (прямоугольной) форме нужно вычесть их действительную и мнимую части:
(a + bi) − (c + di) = (a − c) + (b − d)i
Приведем примеры:
Пример 1. Вычтем два комплексных числа 3 + 9i и 5 + 6i
(3 + 9i) − (5 + 6i) = (3 − 5) + (9 − 6)i = − 2 + 3i
Пример 2. Вычесть два комплексных числа 6 + 23i и 57 + 68i
(6 + 23i) − (57 + 68i) = (6 − 57) + (23 − 68)i = −51 − 45i
Вычитание комплексного числа из действительного числа
Чтобы вычесть комплексное число c + di из действительного числа a, используйте следующую формулу:
a − (c + di) = (a − c) − di
Приведем примеры:
Пример 1.
 Вычесть из действительного числа 6 комплексное число 1 + 7i
Вычесть из действительного числа 6 комплексное число 1 + 7i6 − (1 + 7i) = (6 − 1) + 7i = 5 − 7i
Пример 2. Вычесть из действительного числа -15 комплексное число 1 + (−7)i
−15 − (1 + (−7)i) = (−15 − 1) − (−7)i = −16 + 7i
Вычитание действительного числа из комплексного числа
Чтобы вычесть действительное число c из комплексного числа a + bi, вам нужно вычесть действительное число из действительной части комплексного числа:
(a + bi) − c = (a − c) + bi
Приведем примеры:
Пример 1. Вычтем из комплексного числа 5 + 12i действительное число 8
(5 + 12i) − 8 = (5 − 8) + 12i = −3 + 12i
Пример 2. Вычесть из комплексного числа −1 + (−5)i действительное число −3
(−1 + (−5)i) − (− 3) = (−1 − (−3)) + (−5)i = 2 − 5i
Умножение двух комплексных чисел, представленных в алгебраической (прямоугольной) форме.
Чтобы умножить два комплексных числа, представленных в алгебраической (прямоугольной) форме, необходимо использовать следующую формулу:
(a + bi) × (c + di) = ac + adi + bci + bdi 2 = (ac + bdi 2 ) + (bc + ad)i = (ac − bd) + (bc + ad)i
Приведем примеры:
Пример 1.
 Перемножим два комплексных числа 2 + 5i и 3 + 7i
Перемножим два комплексных числа 2 + 5i и 3 + 7iРешение 1
(2 + 5i) × (3 + 7i) = ((2 × 3) − (5 × 7)) + ((5 × 3) + (2 × 7))i = (6 − 35) + (15 + 14)i = −29 + 29i
Решение 2
(2 + 5i) × (3 + 7i) = (2 × 3) + (2 × 7i) + (5i × 3) + (5i × 7i) = 6 + (14i) + (15i) + (35i 2 ) = 6 + (29i) + (35 × (−1)) = −29 + 29iПример 2. Перемножим два комплексных числа 0,4 + (−2)i и 3,023 + 0,25i
Решение 1
(0,4 + (-2)i) × (3,023 + 0,25i) = ((0,4 × 3,023) — (-2 × 0,25)) + (((-2) × 3,023) + (0,4 × 0,25))i = (1,2092 — (-0,5)) + (-6,046 + 0,1)i = 1,7092-5,946i
Решение 2
(0,4 + (-2)i) × (3,023 + 0,25i) = (0,4 × 3,023) + (0,4 × 0,25i) + ((–2)i × 3,023) + ((–2)i × 0,25i) = 1,2092 + (0,1i) + (-6,046i) + (-0,5i 2 ) = 1,2092 + (−5,946i) + ((−0,5 × (−1))) = 1,7092 − 5,946iУмножение действительного и комплексного числа, представленного в алгебраической (прямоугольной) форме
По порядку чтобы умножить действительное число a на комплексное число c + di, необходимо умножить действительную и мнимую части числа c + di на это число:
a × (c + di) = ac + adi
.
 приведите примеры:
приведите примеры:Пример 1. Умножьте комплексное число 3+4i и действительное число 1
1 × (3 + 4i) = (1 × 3) + (1 × 4)i = 3 + 4i
Пример 2. Умножьте комплексное число −5 + 4i и действительное число −74
−74 × (−5 + 4i) = (−74 × (−5)) + (−74 × 4)i = 370 − 296i
Деление двух комплексных чисел, представленных в алгебраической (прямоугольной) форме
Чтобы разделить два комплексных числа, представленных в алгебраической (прямоугольной) форме, необходимо использовать следующую формулу:
a + bi = C + DI (A + BI) × (C — DI) = (C + DI). ac + bd + c 2 + d 2 bc − ad c 2 + d 2 Приведем примеры:
Пример 1.
 Разделите комплекс № 4 + 3i на комплекс № 5 + 8I
Разделите комплекс № 4 + 3i на комплекс № 5 + 8I(4 + 3 I ) = (5 + 141415555915.)55555 ).).- 15915 55
(4 + 3 i ) × (5 − 8 i ) = (5 + 8 i ) × (5 − 8 i ) (4 × 5) + (3 × 8) + (5 2 + 8 2 ) (3 × 5) . 2 ) (20 + 24) + (25 + 64) 15 − 32 25 + 64 44 + 89 = 0.  49438202247191−0.1
49438202247191−0.1235955056 i
Example 2. Divide the complex number 6 + (− 2) I по комплексному числу −4 + 7i
(6 + (−2) I ) = (–4 + I ) (–4 + I ) (–4 + I )1335 (6 + (−2) i ) × (−4 − 7 i ) = (−4 + (−2) i i 917 ) (6 × (–4)) + (2 × 7) + (–4 (–4 47 (–4 7 (–4 7 (41643 + 7 (41643 + 7 (41643 + 7. .(−2 × (−4)) − (6 × 7) (−4 2 + 7 2 ) (−24 + (−14)) + (16 + 49) 8 − 42 16 + 49 −38 + 65 = −0.  584615384615385−0.523076
584615384615385−0.523076
6923 iДеление комплексного числа, представленного в алгебраической (прямоугольной) форме, на действительное число
Чтобы разделить комплексное число a + bi на действительное число c, необходимо разделить действительную часть комплексное число на действительное число и разделить мнимую часть комплексного числа на действительное число:
33a + bi = c Here’s an example:
Divide the complex number 3 + 6i by the real number 7
(3 + 6 i ) = 7 = 0,428571428571429 + 0,857142857142857 I Division по реальному номеру на A -AGELENGEMENTER
 используйте формулу ниже:
используйте формулу ниже:a = c + di a × (c − di) = (c + di) × (c − di ) ac − c 2 + d 2 ad c 2 + d 2 Here’s an example:
Divide the real number 5 by the complex number 2 + 9i
5 = (2 + 9 i ) 5 × (2 − 9 i ) = (2 + 9 i ) × (2 − 9 i ) 5 × − (2 2 + 9 2 ) 5 × (2 2 + 9 2 ) 10 − (4 + 81) 45 4 + 81 10 − 85 = 0.  117647058823529−0.529411764705882 i
117647058823529−0.529411764705882 i Addition of Complex Numbers Represented in Polar Form
To add two complex numbers in полярную форму, используйте следующую формулу:
z1 + z2 = (|z1| × (cos α + i sin α)) + (|z2| × (cos β + i sin β)) = ((|z1| × cos α) + (|z2| × cos β)) + i((|z1| × sin α) + (|z2| × sin β)), где
|z1| − модуль комплексного числа z1
α − аргумент комплексного числа z1
|z2| − модуль комплексного числа z2
β − аргумент комплексного числа z2Пример:
Сложим два комплексных числа √13 (cos 48° + i sin 48°) и √25 (cos 69° + i sin 69°)
√13 (cos 48° + i sin 48°) + √25 (cos 69° + i sin 69°) = ((√13 × cos(48°)) + (√25 × cos( 69°))) + i((√13 × sin(48°)) + (√25 × sin(69°)) = (2,41258471120918 + 1,77477265) + (2,67944677335447 + 4.667
2486) I = 4,20442445893568 + 7,347348047i
Вычитание комплексных чисел, представленных в полярной форме
по искуплению.
 α + i sin α)) − (|z2| × (cos β + i sin β)) = ((|z1| × cos α) − (|z2| × cos β)) + i((|z1| × sin α) − (|z2| × sin β)), где
α + i sin α)) − (|z2| × (cos β + i sin β)) = ((|z1| × cos α) − (|z2| × cos β)) + i((|z1| × sin α) − (|z2| × sin β)), где|z1| − модуль комплексного числа z1
α − аргумент комплексного числа z1
|z2| − модуль комплексного числа z2
β − аргумент комплексного числа z2Вот пример:
Вычесть из двух комплексных чисел 1/2 (cos π/2 + i sin π/2) число 1/3 (cos π/3 + i sin π/3)
1/2 (cos π/2 + i sin π/2) − 1/3 (cos π/3 + i sin π/3) = ((1/2 × cos((π/2 ))) − (1/3 × cos((π/3)))) + i((1/2 × sin((π/2))) – (1/3 × sin((π/3)) )) = (0 − 0,166666666666666) + (0,5 − 0,288675134594813)i = −0,166666666666666 + 0,211324865405187i
Умножение комплексных чисел, представленных в полярной форме
Чтобы умножить два комплексных числа в полярной форме, используйте следующую формулу:
z1 × z2 = (|z1| × |z2|) × (cos(α + β) + i × sin(α + β)), где
|z1| − модуль комплексного числа z1
α − аргумент комплексного числа z1
|z2| − модуль комплексного числа z2
β − аргумент комплексного числа z2Вот пример:
Умножьте два комплексных числа 2 (cos π/2 + i sin π/2) и 2 (cos π/3 + i sin π/3)
2 (cos π/2 + i sin π/2) × 2 (cos π/3 + i sin π/3) = (2 × 2) × (cos(π/2 + (π /3)) + я × sin(π/2 + (π/3))) =
16
× (cos(5π/6) + i × sin(5π/6)) =
16
× (cos(150°) + i × sin(150°))
Деление комплексных чисел, представленных в полярной форме
Чтобы разделить два комплексных числа, представленных в полярной форме, используйте следующую формулу:
z1 ÷ z2 = (|z1| ÷ |z2|) × (cos(α − β) + i × sin(α − β)), где
|z1| − модуль комплексного числа z1
α − аргумент комплексного числа z1
|z2| − модуль комплексного числа z2
β − аргумент комплексного числа z2Вот пример:
Разделить два комплексных числа 3 (cos 45° + i sin 45°) и 2 (cos 37° + i sin 37°)
3 (cos 45 ° + i sin 45°) ÷ 2 (cos 37° + i sin 37°) = (3 ÷ 2) × (cos(45° − 37°) + i × sin(45° − 37°)) =
2,25
× (cos(8°) + i × sin(8°))=
2,25
× (cos(2π/45) + i × sin(2π/45))
Сложение комплексных чисел, представленных в экспоненциальной форме
Чтобы сложить два комплексных числа в экспоненциальной форме, используйте следующую формулу:
|z1| e iα + |z2| e iβ = (|z1| × (cos α + i sin α)) + (|z2| × (cos β + i sin β)) = ((|z1| × cos α) + (|z2| × cos β)) + i((|z1| × sin α) + (|z2| × sin β)), где
|z1| − модуль комплексного числа z1
α − аргумент комплексного числа z1
|z2| − модуль комплексного числа z2
β − аргумент комплексного числа z2Вот пример:
Сложим два комплексных числа 3 × e (π/2)i и 2 × e (3π/2)i
3 × e (π/2)i + 2 × e (3π /2)i = ((3 × cos((π/2))) + (2 × cos((3π/2)))) + i((3 × sin((π/2))) + ( 2 × sin((3π/2)))) = (0 + 0) + (3 + (−2))i = 0 + 1i
Вычитание комплексных чисел, представленных в экспоненциальной форме
Вычитание двух комплексных чисел в экспоненциальной форме используйте следующую формулу:
|z1| e iα − |z2| е iβ = (|z1| × (cos α + i sin α)) − (|z2| × (cos β + i sin β)) = ((|z1| × cos α) − (|z2| × cos β)) + i((|z1| × sin α) − (|z2| × sin β)), где
|z1| − модуль комплексного числа z1
α − аргумент комплексного числа z1
|z2| − модуль комплексного числа z2
β − аргумент комплексного числа z2Вот пример:
Вычесть из числа 3 × e (π/2)i число 2 × e (3π/2) i
3 × e (π/2)i — 2 × e (3π/2)i = ((3 × cos((π/2))) – (2 × cos((3π/2)))) + i((3 × sin(( π/2))) − (2 × sin((3π/2)))) = (0 − 0) + (3 − (−2))i = 0 + 5i
Умножение комплексных чисел, представленных в экспоненциальном Форма
Чтобы умножить два комплексных числа в экспоненциальной форме, используйте следующую формулу:
|z1| e iα × |z2| e iβ = (|z1| × |z2|) × (cos(α + β) + i × sin(α + β)), где
|z1| − модуль комплексного числа z1
α − аргумент комплексного числа z1
|z2| − модуль комплексного числа z2
β − аргумент комплексного числа z2Пример:
Умножить два комплексных числа 3 × e (π/2)i и 2 × e (3π/2)i
(3 × e (π/2)i ) × (2 × e (3π/2)i ) = (3 × 2) × (cos(π/2 + (3π/2)) + i × sin(π/2 + (3π/2))) =
36
× (cos(360°) + i × sin(360°)) = 6 + 0i
Деление комплексных чисел, представленных в экспоненциальной форме
Чтобы разделить два комплексных числа, представленных в экспоненциальной форме, используйте следующую формулу:
|z1| e iα ÷ |z2| e iβ = (|z1| ÷ |z2|) × (cos(α − β) + i × sin(α − β)), где
|z1| − модуль комплексного числа z1
α − аргумент комплексного числа z1
|z2| − модуль комплексного числа z2
β − аргумент комплексного числа z2Вот пример:
Разделить два комплексных числа 3 × e (π/2)i и 2 × e (3π/2)i
(3 × e (π/2)i ) ÷ (2 × e (3π/2)i ) = (3 ÷ 2) × ( cos(π/2 − (3π/2)) + i × sin(π/2 − (3π/2))) =
2,25
× (cos(−180°) + i × sin(−180°) )) =
2,25
× (cos(−π) + i × sin(−π)) = −1,5 + 0i
Модуль комплексного числа
Модуль комплексного числа равен расстоянию от точки комплексной плоскости до начала координат и обозначается |z|.

Модуль комплексного числа z вычисляется по формуле:|z| =
a 2 + b 2
Вот пример:
Вычислить модуль комплексного числа 1 + 3i
|1 + 3i| =
1 2 + 3 2
=
1 + 9
=
10
= 3,160128768
Аргумент (фаза) комплексного числа
Аргументом ненулевого комплексного числа является угол φ между радиус-вектором соответствующей точки и положительной вещественной полуосью. Аргумент числа z обозначается Arg(z).
Аргумент комплексного числа z вычисляется по формуле:Arg(z) = arctg(b/a), a > 0
Arg(z) = arctg(b/a) + π, a < 0
Arg(z) = π/2, b > 0 и a = 0
Arg(z) = −π/2, b < 0 и a = 0
Главное значение аргумента должно быть таким, что — π < arctg(b/a) ⩽ π.
 Калькулятор вычисляет именно основное значение аргумента.
Калькулятор вычисляет именно основное значение аргумента.Вот пример:
Вычислить аргумент комплексного числа −4 + 7i
Arg(−4 + 7i) = arctg(7/(−4)) + π = 2,08994244104142 радиан
Arg(−4 + 7i) = 119,744881296942° градусовПредставление комплексного числа в алгебраической (прямоугольной) форме в полярной Форма
Для преобразования комплексного числа, представленного в алгебраической (прямоугольной) форме, в полярную форму, необходимо вычислить модуль и аргумент данного комплексного числа.
z = a + bi = |z| × (cos φ + i sin φ), где
|z| − модуль комплексного числа z
φ − аргумент комплексного числа zМодуль комплексного числа равен расстоянию от точки комплексной плоскости до начала координат и обозначается |z|.
Модуль комплексного числа z вычисляется по формуле:|z| =
a 2 + b 2
Вот пример:
Преобразование числа 2 + 3i в полярную форму
|2 + 3i| =
2 2 + 3 2
=
4 +
=
13
= 3,60555127546399
.
 точка и положительная действительная полуось. Аргумент числа z обозначается Arg(z).
точка и положительная действительная полуось. Аргумент числа z обозначается Arg(z).
Аргумент комплексного числа z вычисляется по формуле:Arg(z) = arctg(b/a), a > 0
Arg(z) = arctg(b/a) + π, a < 0
Arg(z) = π/2, b > 0 и a = 0
Arg(z) = −π/2, b < 0 и a = 0
Главное значение аргумента должно быть таким, что −π < arctg(b/a) ⩽ π. Калькулятор вычисляет именно основное значение аргумента.
Arg(2 + 3i) = arctg(3/2) = 0,982793723247329 радиан
Arg(2 + 3i) = arctg(3/2) = 56,30940202° градусов
Теперь мы можем записать комплексное число z в полярной форме:
z = 2 + 3i =
13
× (cos(arctg(3/2)) + sin(arctg(3/2))i) = 3,60555127546399 × (cos(56,309
40202°) + sin(56,309
40202°)i)
Представление комплексного числа, представленного в алгебраической (прямоугольной) форме, в экспоненциальной форме
Для преобразования комплексного числа, представленного в алгебраической (прямоугольной) форме, в показательную форму, необходимо вычислить модуль и аргумент данного комплекса количество.

z = a + bi = |z| × (cos φ + i sin φ), где
|з| − модуль комплексного числа z
φ − аргумент комплексного числа zМодуль комплексного числа равен расстоянию от точки комплексной плоскости до начала координат и обозначается |z|.
Модуль комплексного числа z вычисляется по формуле:|z| =
a 2 + b 2
Вот пример:
Представим число 2 + 2i в экспоненциальной форме
|2 + 2i| =
2 2 + 2 2
=
4 + 4
=
8
= 2,82842712474619
и положительная действительная полуось. Аргумент числа z обозначается Arg(z).
Аргумент комплексного числа z вычисляется по формуле:Arg(z) = arctg(b/a), a > 0
Arg(z) = arctg(b/a) + π, a < 0
Arg(z) = π/2, b > 0 и a = 0
Arg(z) = −π/2, b < 0 и a = 0
Главное значение аргумента должно быть таким, чтобы — π < arctg(b/a) ⩽ π.
 Калькулятор вычисляет именно основное значение аргумента.
Калькулятор вычисляет именно основное значение аргумента.Arg(2 + 2i) = arctg(2/2) = 0,785398163397448 радиан
Arg(2 + 2i) = arctg(2/2) = 45° градусовТеперь мы можем записать комплексное число z в экспоненциальной форме:
z = 2 + 2i =
8
× e 0,785398163397448i =
8
× E 45 ° I =
8
× E (π/4) I
Представление комплексного числа, представленного в поле Algebraic (Ryte Pryting 66666666666666.6666666666666666666 гг. Чтобы преобразовать комплексное число в полярной форме в алгебраическую (прямоугольную) форму z = a + bi, необходимо представить действительную часть a как cos φ, умноженную на модуль |z|, а мнимую часть b как sin φ умножить на модуль |z| комплексное число з.
|з| (cos φ + i sin φ) = (|z| × (cos φ)) + (|z| × (sin φ)i) = a + bi, где
a = |z| × cos φ
b = |z| × sin φВот пример:
Преобразование 2 × (cos(60°) + sin(60°)i) в алгебраическую (прямоугольную) форму
2 × (cos(60°) + sin(60°)i) = 2 × (0,5 + 0,86602540378444i) = (2 × 0,5) + (2 × 0,86602540378444i) = 1 + 1,73205080756888i
Представление комплексного числа в полярной форме в экспоненциальной форме
Чтобы преобразовать комплексное число из полярной формы в экспоненциальную, используйте следующую формулу:
|z| × (cos φ + i sin φ) = |z| e φi , где
|z| − модуль комплексного числа z
φ − аргумент комплексного числа zВот пример:
Представим число 2 × (cos(60°) + sin(60°)i) в экспоненциальной форме
2 × (cos(60°) + sin(60°)i) = 2 × e 60°i = 2 × e (π/3)i
Представление комплексного числа в экспоненциальной форме в полярных координатах Форма
Чтобы преобразовать комплексное число из экспоненциальной формы в полярную, используйте следующую формулу:
|z| e φi = |z| × (cos φ + i sin φ), где
|z| − модуль комплексного числа z
φ − аргумент комплексного числа zВот пример:
Преобразовать 2 × e (π/3)i в полярную форму
2 × e (π/3)i = 2 × (cos((π/3)) + sin((π/3))i)
Представление комплексного числа в экспоненциальной форме в алгебраической (прямоугольной) форме
Чтобы преобразовать комплексное число в экспоненциальной форме в алгебраическую (прямоугольную) форму, число должно быть сначала преобразовано в полярную форму.

|з| e φi = |z| × (cos φ + i sin φ), где
|z| − модуль комплексного числа z
φ − аргумент комплексного числа zЧтобы преобразовать комплексное число из полярной формы в алгебраическую (прямоугольную) форму z = a + bi, необходимо представить действительную часть a как cos φ, умноженное на модуль |z|, и мнимая часть b как sin φ, умноженная на модуль |z| комплексное число з.
|з| (cos φ + i sin φ) = (|z| × (cos φ)) + (|z| × (sin φ)i) = a + bi, где
a = |z| × cos φ
b = |z| × sin φВот пример:
Преобразуйте число 2 × e (π/3)i в алгебраическую (прямоугольную) форму
2 × e (π/3)i = 2 × (cos((π/3)) + sin((π/3))i) = 2 × (0,5 + 0,86602540378444i) = (2 × 0,5) + (2 × 0,86602540378444i) = 1 + 1,73205080756888i
Сопряжение комплексного числа, представленного в алгебраической (прямоугольной) форме
Два комплексно-сопряженных числа имеют одинаковые действительные части и противоположные мнимые части.

Сопряженное число z обозначается как z .
Для z = a + bi сопряженным является z = a − bi.Вот пример:
Вычислите сопряженное число для числа 2 + 3i
2 + 3i = 2 − 3i
Сопряжение комплексного числа, выраженное в полярной форме
Два комплексно-сопряженных числа имеют одинаковые действительные части и противоположные мнимые части.
Сопряженное число z обозначается как z .
Для z = |z| (cos φ + i sin φ) сопряженное число равно z = |z| (cos φ − i sin φ).Вот пример:
Вычислить сопряженное число для числа 2(cos((π/3)) + sin((π/3))i)
2(cos((π/3)) + sin((π/3))i) = 2(cos((π/3)) − sin((π/3))i)
Сопряжение комплексного числа, выраженное в экспоненциальной форме
Два комплексно-сопряженных числа имеют одинаковые действительные части и противоположные мнимые части.

Сопряженное число z обозначается как z .
Для z = |z| e iφ сопряженное z = |z| е − iφ .Вот пример:
Вычислите сопряженное число для числа 3)i
Обратная величина комплексного числа, представленного в алгебраической (прямоугольной) форме
Для каждого ненулевого комплексного числа существует обратная величина. Чтобы найти обратную величину числа а+би, нужно разделить единицу на это число. Поскольку единица выступает в роли делимого, формула деления упрощается и принимает вид:
1 = a + bi 1 × (a − bi) = (a + bi) × (a − bi ) a − a 2 + b 2 b a 2 + b 2 Here’s an example:
Calculate the reciprocal of the number 2 + 3i
1 = (2 + 3 i ) 2 − (2 2 + 3 2 ) 3 (2 2 + 3 2 ) 2 − (4 + 9) 3 4 + 9 2 − 13 = 0.  153846153846154−0.23076
153846153846154−0.23076
69231 iОбратная величина комплексного числа, выраженная в полярной форме
Чтобы вычислить обратную величину числа в полярной форме, используйте следующую формулу:
1/z = 1/|z| × (cos φ − i sin φ), где
|z| − модуль комплексного числа z
φ − аргумент комплексного числа zВот пример:
Вычислить обратную величину числа 2(cos((π/2)) + sin((π/2))i)
1/z = 1/2 × (cos (π/2) − i sin π/2) =
0,25
× (cos(π/2) − i × sin(π/2))
Обратная величина комплексного числа, представленного в экспоненциальной форме
Чтобы вычислить обратную величину числа в экспоненциальной форме, используйте следующую формулу:
1/z = (1/|z|)e −iφ , где
|з| − модуль комплексного числа z
φ − аргумент комплексного числа zВот пример:
Вычислить обратную величину числа 2 × e i(π/2)
1/z = 1/2 × e −i (π/2) =
0,25
× e −i (π/2)
Аддитивное обращение комплексного числа
Аддитивная инверсия комплексного числа Комплексное число — это число, которое при добавлении к исходному числу дает ноль.
 Аддитивное обратное комплексному числу — это число, в котором действительная и мнимая части умножаются на −1. Чтобы умножить число −1 на комплексное число a + bi. надо умножить действительную и комплексную части числа а+би на это число:
Аддитивное обратное комплексному числу — это число, в котором действительная и мнимая части умножаются на −1. Чтобы умножить число −1 на комплексное число a + bi. надо умножить действительную и комплексную части числа а+би на это число:−1 × (a + bi) = (−1 × a) + (−1 × bi)
Вот пример:
Вычислить обратную аддитивную величину для числа z = 2 + 3i
−z = (−1 × 2) + (−1 × 3) i = −2−3 i
Извлечение корня N из комплексного числа, представленного в алгебраической (прямоугольной) форме
Извлечение корня 3-й степени числа 3 + 2i
Чтобы извлечь корень n-й степени из ненулевого комплексного числа. во-первых, данное число должно быть преобразовано в полярную форму.
Для того чтобы комплексное число, записанное в алгебраической (прямоугольной) форме, представить в полярной форме, необходимо найти модуль и аргумент данного комплексного числа.

z = a + bi = |z| × (cos φ + i sin φ), где
|z| − модуль комплексного числа z
φ − аргумент комплексного числа zМодуль комплексного числа равен расстоянию от точки комплексной плоскости до начала координат и обозначается |z|.
Модуль комплексного числа z вычисляется по формуле:|з| =
a 2 + b 2
|3 + 2i| =
3 2 + 2 2
=
9 + 4
=
13
= 3,60555127546399
. точка и положительная действительная полуось. Аргумент числа z обозначается Arg(z).
Аргумент комплексного числа z вычисляется по формуле:Arg(z) = arctg(b/a), a > 0
Arg(z) = arctg(b/a) + π, a < 0
Arg(z) = π/2, b > 0 и a = 0
Arg(z) = −π/2, b < 0 и a = 0
Главное значение аргумента должно быть таким, чтобы −π < arctg(b/a) ⩽ π.
 Калькулятор вычисляет именно основное значение аргумента.
Калькулятор вычисляет именно основное значение аргумента.Arg(3 + 2i) = arctg(2/3) = 0,588002603547568 радиан
5259798° градусов
Arg(3 + 2i) = arctg(2/3) = 33,6Теперь мы можем записать комплексное число z в полярной форме:
z = 3 + 2i =
13
× (cos(arctg(2/3)) + sin(arctg(2/3))i) = 3,60555127546399 × (cos(33,6
5259798°) + sin(33,625°) )i)
Применим формулу де Муавра для извлечения корня n-й степени:
n √z = n √|z| × (cos (φ + 2πk)/n + i sin (φ + 2πk)/n)), где
|z| − модуль комплексного числа z
φ − аргумент комплексного числа z
n – степень корня (количество корней)
k – принимает значения 0, 1, 2, … n−1Z 1 = 3
3,60555127546399
× (COS ((33,6
5259798 ° + (2 × 180 × 0))/3) SIN (33,698 ° + (2 × 180 × 0)/3) + I SIN (33,657579. 1579.1979) (33,698 °. /3)) = 1.53340623701639 × (cos((33.65259798° + 0)/3) + i sin ((33.65259798° + 0)/3)) = (1.53340623701639 × (cos 11.2300225086599°)) + (1.53340623701639 × (sin 11.2300225086599 °))i = 1,50404648119798 + 0,298628314325244i
1579.1979) (33,698 °. /3)) = 1.53340623701639 × (cos((33.65259798° + 0)/3) + i sin ((33.65259798° + 0)/3)) = (1.53340623701639 × (cos 11.2300225086599°)) + (1.53340623701639 × (sin 11.2300225086599 °))i = 1,50404648119798 + 0,298628314325244iz 2 = 3
3,60555127546399
×00675259798° + (2 × 180 × 1))/3) + i sin ((33,65259798° + (2 × 180 × 1))/3)) = 1,53340623701639 × (cos((33,65259798° + 360)/3) + i sin ((33.65259798° + 360)/3)) = (1.53340623701639 × (cos 131.23002250866°)) + (1.53340623701639 × (sin 131.23002250866°))i = −1.01064294709398 + 1.15322830402742iz 3 = 3
3,60555127546399
× (cos((33,6
5259798° + (2 × 180 × 2))/3) + i sin ((33,65259798° + (2 × 180 × 2))/3)) = 1,53310639× (cos((33,65259798° + 720)/3) + i sin ((33,65259798° + 720)/3)) = (1,53340623701639 × (cos 251,23002250866°)) + (1,5334062°23701639 × 0,493403534104007 — 1,45185661835266iz 1 = 1.
 50404648119798 + 0.298628314325244i
50404648119798 + 0.298628314325244i
z 2 = −1.01064294709398 + 1.15322830402742i
z 3 = −0.493403534104007 − 1.45185661835266iz 1 = 1.53340623701639 × (cos(11.2300225086599°) + i грех(11.2300225086599 °))
Z 2 = 1,53340623701639 × (COS (131,23002250866 °) + I SIN (131,2300220866 °))
Z 3 = 1,53340623701666663.1163701666663.1163701666666666666666666666666666663.1163701666637016666666666666666666666666666666666666666666666666666666666666666666666666666663701637тели)).Извлечение корня N из комплексного числа, представленного в полярной форме
Вычисление корня 3-й степени из числа 3(cos((π/5)) + sin((π/5))i)
Применим формулу де Муавра для вычисления корня n-й степени:
n √z = n √|z| × (cos (φ + 2πk)/n + i sin (φ + 2πk)/n)), где
|z| − модуль комплексного числа z
φ − аргумент комплексного числа z
n – степень корня (количество корней)
k – принимает значения 0, 1, 2, … n−1z 1 = 3
3
× (cos((36° + (2 × 180 × 0))/3) + i sin ((36° + (2 × 180 × 0))/3)) = 1,44224957030741 × (cos( (36° + 0)/3) + i sin ((36° + 0)/3)) = (1,44224957030741 × (cos 12°)) + (1,44224957030741 × (SIN 12 °)) I = 1,41073295685556 + 0,299860546743801I
Z 2 = 3
3
× (Cos (Cos (36 ° + (2 ° + (2 ° + (2 ° + (2 ° + (2 ° + (2 ° + (2 ° + (2 ° + (2 ° + (2 ° + (2 ° + (2 ° + (2 ° + (2 ° + (2) (2) (2).
 sin ((36° + (2 × 180 × 1))/3)) = 1,44224957030741 × (cos((36° + 360)/3) + i sin ((36° + 360)/3)) = (1,44224957030741 × (cos 132°)) + (1.44224957030741 × (sin 132°))i = −0.965053329500603 + 1.07180030522094i
sin ((36° + (2 × 180 × 1))/3)) = 1,44224957030741 × (cos((36° + 360)/3) + i sin ((36° + 360)/3)) = (1,44224957030741 × (cos 132°)) + (1.44224957030741 × (sin 132°))i = −0.965053329500603 + 1.07180030522094iz 3 = 3
3
× (cos((36° + (2 × 180 × 2))/3) + i sin ((36° + (2 × 180 × 2))/3)) = 1,44224957030741 × (cos((36° + 720)/3) + i sin ((36° + 720)/3)) = (1,44224957030741 × (cos 252°)) + (1,44224957030741 × (sin 252°))i = −0,445679627354959 − 1,37166085196474i
z 1 = 1.41073295685556 + 0.299860546743801i
z 2 = −0.965053329500603 + 1.07180030522094i
z 3 = −0.445679627354959 − 1.37166085196474iz 1 = 1.44224957030741 × (cos(12°) + i sin(12°))
z 2 = 1,44224957030741 × (cos(132°) + i sin(132°))
z 3 = 1,44224957030741 × (cos(252°) + i sin(252°))Извлечение корня n-й степени из комплексного числа, представленного в экспоненциальной форме
Извлечение корня 3-й степени из числа 2 × e 45°i
Чтобы извлечь корень n-й степени из ненулевого комплексного числа.
 вы должны сначала представить это число в полярной форме,
вы должны сначала представить это число в полярной форме,Чтобы представить комплексное число в экспоненциальной форме в полярной форме, используйте следующую формулу:
|з| e φi = |z| × (cos φ + i sin φ), где
|z| − модуль комплексного числа z
φ − аргумент комплексного числа z2 × e 45°i = 2 × (cos(45°) + sin(45°)i)
Применим формулу де Муавра для извлечения n-й корень:
n √z = n √|z| × (cos (φ + 2πk)/n + i sin (φ + 2πk)/n)), где
|z| − модуль комплексного числа z
φ − аргумент комплексного числа z
n – степень корня (количество корней)
k – принимает значения 0, 1, 2, … n−1z 1 = 3
2
× (cos((45° + (2 × 180 × 0))/3) + i sin ((45° + (2 × 180 × 0))/3)) = 1,259
989487 × (cos((45° + 0)/3) + i sin ((45° + 0)/3)) = ( 1.


 д.
д.
 Выводится, к сожалению такое число в файл изображения (защита от автоматического использования скорее всего).
Выводится, к сожалению такое число в файл изображения (защита от автоматического использования скорее всего).


 0
0 Этот бесплатный калькулятор мнимых чисел быстро упростит любое сложное выражение с помощью пошаговых вычислений. Итак, продолжайте читать, чтобы понять, как упростить комплексные числа, такие как полярная форма, инверсия, сопряжение и модуль.
Этот бесплатный калькулятор мнимых чисел быстро упростит любое сложное выражение с помощью пошаговых вычислений. Итак, продолжайте читать, чтобы понять, как упростить комплексные числа, такие как полярная форма, инверсия, сопряжение и модуль.




 Комплексы могут быть представлены в биномиальной или полярной форме:
Комплексы могут быть представлены в биномиальной или полярной форме:

 Давайте посмотрим, как это делается в каждом случае:
Давайте посмотрим, как это делается в каждом случае: . Давайте посмотрим, как действовать в каждом из них:
. Давайте посмотрим, как действовать в каждом из них:
 Например, сопряженное 3+0i равно 3-0i, короче, оно равно 3 в обоих случаях.
Например, сопряженное 3+0i равно 3-0i, короче, оно равно 3 в обоих случаях.

 Si tienes dudas, déjame un commentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, напишите мне сообщение.
Si tienes dudas, déjame un commentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, напишите мне сообщение.
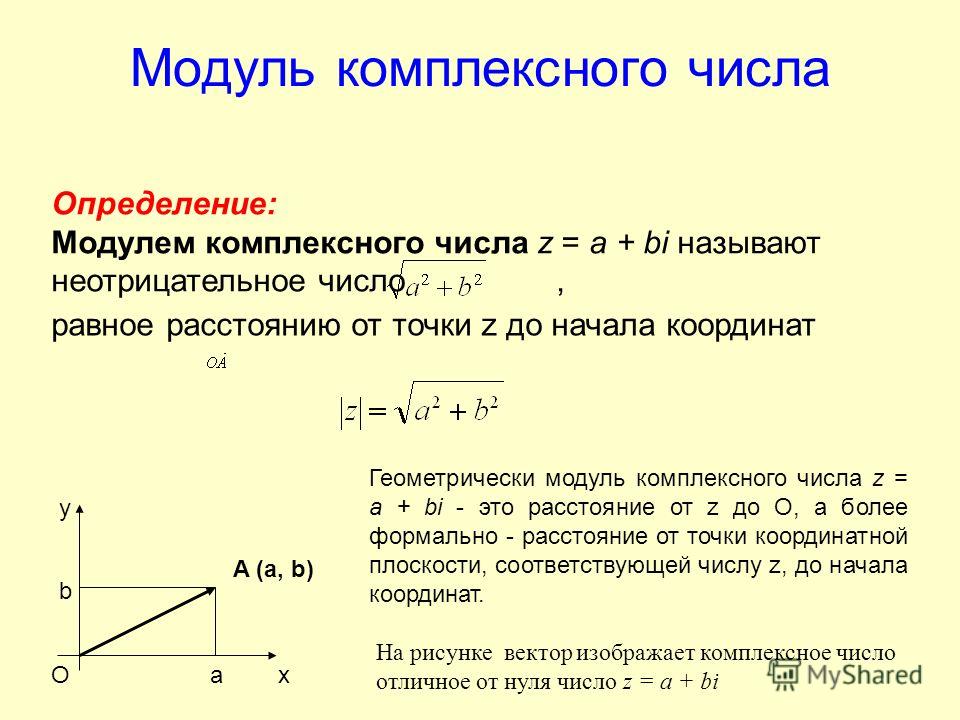

 Складываем комплексное число 2 + 3i и действительное число 10
Складываем комплексное число 2 + 3i и действительное число 10 Вычесть из действительного числа 6 комплексное число 1 + 7i
Вычесть из действительного числа 6 комплексное число 1 + 7i Перемножим два комплексных числа 2 + 5i и 3 + 7i
Перемножим два комплексных числа 2 + 5i и 3 + 7i приведите примеры:
приведите примеры: Разделите комплекс № 4 + 3i на комплекс № 5 + 8I
Разделите комплекс № 4 + 3i на комплекс № 5 + 8I 49438202247191−0.1
49438202247191−0.1 584615384615385−0.523076
584615384615385−0.523076 используйте формулу ниже:
используйте формулу ниже: 117647058823529−0.529411764705882 i
117647058823529−0.529411764705882 i  α + i sin α)) − (|z2| × (cos β + i sin β)) = ((|z1| × cos α) − (|z2| × cos β)) + i((|z1| × sin α) − (|z2| × sin β)), где
α + i sin α)) − (|z2| × (cos β + i sin β)) = ((|z1| × cos α) − (|z2| × cos β)) + i((|z1| × sin α) − (|z2| × sin β)), где
 Калькулятор вычисляет именно основное значение аргумента.
Калькулятор вычисляет именно основное значение аргумента. точка и положительная действительная полуось. Аргумент числа z обозначается Arg(z).
точка и положительная действительная полуось. Аргумент числа z обозначается Arg(z). 
 Калькулятор вычисляет именно основное значение аргумента.
Калькулятор вычисляет именно основное значение аргумента.


 153846153846154−0.23076
153846153846154−0.23076 Аддитивное обратное комплексному числу — это число, в котором действительная и мнимая части умножаются на −1. Чтобы умножить число −1 на комплексное число a + bi. надо умножить действительную и комплексную части числа а+би на это число:
Аддитивное обратное комплексному числу — это число, в котором действительная и мнимая части умножаются на −1. Чтобы умножить число −1 на комплексное число a + bi. надо умножить действительную и комплексную части числа а+би на это число:
 Калькулятор вычисляет именно основное значение аргумента.
Калькулятор вычисляет именно основное значение аргумента. 1579.1979) (33,698 °. /3)) = 1.53340623701639 × (cos((33.65259798° + 0)/3) + i sin ((33.65259798° + 0)/3)) = (1.53340623701639 × (cos 11.2300225086599°)) + (1.53340623701639 × (sin 11.2300225086599 °))i = 1,50404648119798 + 0,298628314325244i
1579.1979) (33,698 °. /3)) = 1.53340623701639 × (cos((33.65259798° + 0)/3) + i sin ((33.65259798° + 0)/3)) = (1.53340623701639 × (cos 11.2300225086599°)) + (1.53340623701639 × (sin 11.2300225086599 °))i = 1,50404648119798 + 0,298628314325244i 50404648119798 + 0.298628314325244i
50404648119798 + 0.298628314325244i  sin ((36° + (2 × 180 × 1))/3)) = 1,44224957030741 × (cos((36° + 360)/3) + i sin ((36° + 360)/3)) = (1,44224957030741 × (cos 132°)) + (1.44224957030741 × (sin 132°))i = −0.965053329500603 + 1.07180030522094i
sin ((36° + (2 × 180 × 1))/3)) = 1,44224957030741 × (cos((36° + 360)/3) + i sin ((36° + 360)/3)) = (1,44224957030741 × (cos 132°)) + (1.44224957030741 × (sin 132°))i = −0.965053329500603 + 1.07180030522094i вы должны сначала представить это число в полярной форме,
вы должны сначала представить это число в полярной форме,