калькулятор крамер
калькулятор крамерВы искали калькулятор крамер? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и калькулятор крамера, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «калькулятор крамер».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как калькулятор крамер,калькулятор крамера,калькулятор крамера матрицы онлайн,калькулятор крамера онлайн,калькулятор крамера с решением,калькулятор матриц крамера,калькулятор матриц метод крамера,калькулятор матриц метод крамера онлайн,калькулятор матриц методом крамера,калькулятор матриц онлайн метод крамера,калькулятор матриц онлайн методом крамера,калькулятор матриц онлайн с решением метод крамера,калькулятор матриц онлайн с решением методом крамера,калькулятор матриц с решением методом крамера онлайн,калькулятор матрица метод крамера,калькулятор матрицы крамера онлайн,калькулятор матрицы метод крамера,калькулятор матрицы метод крамера онлайн,калькулятор матрицы методом крамера,калькулятор матрицы онлайн метод крамера,калькулятор матрицы онлайн методом крамера,калькулятор матрицы онлайн с решением метод крамера,калькулятор матричный метод крамера,калькулятор метод крамера,калькулятор метод крамера онлайн с решением,калькулятор метода крамера,калькулятор методом крамера,калькулятор методом крамера онлайн,калькулятор онлайн для метода крамера,калькулятор онлайн матриц метод крамера,калькулятор онлайн матрицы метод крамера,калькулятор онлайн матрицы методом крамера,калькулятор онлайн методом крамера,калькулятор онлайн по формуле крамера онлайн калькулятор,калькулятор онлайн правило крамера,калькулятор онлайн решение матриц методом крамера,калькулятор онлайн решение систем методом крамера,калькулятор по методу крамера,калькулятор по формуле крамера,калькулятор решение методом крамера,калькулятор решение систем линейных уравнений методом крамера,калькулятор решение систем методом крамера,калькулятор решение уравнений методом крамера,калькулятор решения методом крамера,калькулятор системы уравнений онлайн методом крамера онлайн,калькулятор слау методом крамера,калькулятор формула крамера,калькулятор формула крамера онлайн,крамер калькулятор,крамер калькулятор онлайн,крамер онлайн,крамер онлайн калькулятор,крамера онлайн,крамера онлайн калькулятор,крамера решение онлайн,линейное уравнение методом крамера онлайн,матрица калькулятор метод крамера,матрица калькулятор онлайн метод крамера,матрица крамера онлайн,матрица метод крамера калькулятор,матрица метод крамера онлайн,матрица метод крамера онлайн калькулятор,матрица методом крамера онлайн,матрица онлайн калькулятор метод крамера,матрица онлайн крамера,матрица онлайн метод крамера,матрица онлайн методом крамера,матрицы калькулятор метод крамера,матрицы калькулятор методом крамера,матрицы калькулятор онлайн крамера,матрицы калькулятор онлайн метод крамера,матрицы метод крамера калькулятор,матрицы метод крамера онлайн,матрицы метод крамера онлайн калькулятор,матрицы метод крамера онлайн калькулятор с подробным решением,матрицы методом крамера калькулятор,матрицы онлайн калькулятор крамера,матрицы онлайн калькулятор метод крамера,матрицы онлайн калькулятор методом крамера,матрицы онлайн калькулятор с подробным решением метод крамера,матрицы онлайн калькулятор с решением метод крамера,матрицы онлайн метод крамера,матрицы онлайн методом крамера онлайн,матрицы онлайн решение методом крамера,матрицы онлайн решение методом крамера онлайн с,матрицы решение методом крамера онлайн,матрицы решение методом крамера онлайн с решением,матрицы решение онлайн методом крамера,матрицы решение онлайн методом крамера онлайн с,матричный калькулятор метод крамера,метод крамера калькулятор,метод крамера калькулятор онлайн,метод крамера калькулятор с подробным решением,метод крамера матриц онлайн калькулятор,метод крамера матрица онлайн,метод крамера матрицы калькулятор,метод крамера матрицы онлайн,метод крамера матрицы онлайн калькулятор,метод крамера матричный калькулятор,метод крамера онлайн,метод крамера онлайн калькулятор,метод крамера онлайн калькулятор матрицы,метод крамера онлайн калькулятор с подробным решением,метод крамера онлайн калькулятор с подробным решением и с проверкой,метод крамера онлайн калькулятор с подробным решением матрицы,метод крамера онлайн калькулятор с решением,метод крамера онлайн решение,метод крамера онлайн решение матриц,метод крамера онлайн с решением,метод крамера примеры с решением калькулятор,метод крамера примеры с решением онлайн,метод крамера решение матриц онлайн,метод крамера решение онлайн,метод крамера решения систем линейных уравнений онлайн,метод крамера с решением онлайн,метод решение матриц крамера онлайн,метода крамера калькулятор,методом крамера калькулятор,методом крамера онлайн,методом крамера онлайн калькулятор,методом крамера решить онлайн,методом крамера решить уравнение онлайн,онлайн калькулятор для метода крамера,онлайн калькулятор крамер,онлайн калькулятор крамера,онлайн калькулятор линейных уравнений методом крамера онлайн,онлайн калькулятор матриц метод крамера,онлайн калькулятор матриц метод крамера с решением,онлайн калькулятор матриц методом крамера,онлайн калькулятор матриц с решением метод крамера,онлайн калькулятор матрицы крамера,онлайн калькулятор матрицы метод крамера,онлайн калькулятор матрицы методом крамера,онлайн калькулятор метод крамера,онлайн калькулятор метод крамера матрицы,онлайн калькулятор метод крамера с решением,онлайн калькулятор методом крамера,онлайн калькулятор правило крамера,онлайн калькулятор решение линейных уравнений методом крамера,онлайн калькулятор решение матриц методом крамера,онлайн калькулятор решение методом крамера,онлайн калькулятор решение систем линейных уравнений методом крамера,онлайн калькулятор решение систем методом крамера,онлайн калькулятор решение систем уравнений методом крамера,онлайн калькулятор решение системы уравнений методом крамера,онлайн калькулятор решить систему методом крамера,онлайн калькулятор решить систему по правилу крамера,онлайн калькулятор систем линейных уравнений методом крамера онлайн,онлайн калькулятор систем методом крамера онлайн,онлайн калькулятор систем уравнений методом крамера онлайн,онлайн калькулятор система уравнений методом крамера онлайн,онлайн калькулятор системы уравнений методом крамера онлайн,онлайн калькулятор формула крамера,онлайн калькулятор формулы крамера,онлайн крамера,онлайн матрица крамера,онлайн матрица метод крамера,онлайн матрица методом крамера,онлайн матрицы метод крамера,онлайн методом крамера,онлайн правило крамера,онлайн решение крамера,онлайн решение крамера метод,онлайн решение линейных уравнений методом крамера,онлайн решение матриц крамера,онлайн решение матриц метод крамера,онлайн решение матрицы методом крамера,онлайн решение метод крамера,онлайн решение методом крамера,онлайн решение по крамеру,онлайн решение по формулам крамера онлайн,онлайн решение по формуле крамера,онлайн решение систем линейных уравнений методом крамера,онлайн решение систем линейных уравнений методом крамера онлайн,онлайн решение систем методом крамера,онлайн решение систем методом крамера онлайн с подробным решением,онлайн решение систем уравнений методом крамера,онлайн решение системы линейных уравнений методом крамера,онлайн решение системы линейных уравнений методом крамера онлайн,онлайн решение системы методом крамера,онлайн решение системы методом крамера онлайн калькулятор,онлайн решение системы уравнений методом крамера,онлайн решение слау методом крамера,онлайн решение уравнений крамера,онлайн решение уравнений методом крамера,онлайн решение уравнения методом крамера,онлайн решить систему линейных уравнений методом крамера,онлайн система крамера,онлайн система линейных уравнений методом крамера онлайн,онлайн система уравнений методом крамера,онлайн формула крамера,определитель онлайн методом крамера онлайн,по крамеру решение онлайн,по формулам крамера решить систему онлайн,по формуле крамера калькулятор,по формуле крамера решить систему уравнений онлайн,правило крамера калькулятор онлайн,правило крамера онлайн,правило крамера онлайн калькулятор,решение крамера онлайн,решение линейных систем уравнений методом крамера онлайн,решение линейных уравнений методом крамера калькулятор онлайн,решение линейных уравнений методом крамера онлайн,решение линейных уравнений методом крамера онлайн калькулятор,решение линейных уравнений онлайн методом крамера,решение матриц крамера онлайн,решение матриц метод крамера онлайн,решение матриц методом крамера онлайн,решение матриц методом крамера онлайн калькулятор,решение матриц методом крамера онлайн с подробным решением,решение матриц онлайн калькулятор методом крамера,решение матриц онлайн крамера,решение матриц онлайн метод крамера,решение матриц онлайн метод крамера онлайн,решение матриц онлайн методом крамера,решение матриц онлайн методом крамера онлайн,решение матриц онлайн методом крамера с подробным решением,решение матриц онлайн с подробным решением методом крамера,решение матрицы крамера онлайн,решение матрицы методом крамера онлайн,решение матрицы методом крамера онлайн с подробным решением,решение матрицы методом крамера онлайн с решением,решение матрицы онлайн крамера,решение матрицы онлайн методом крамера,решение матрицы онлайн методом крамера онлайн,решение матрицы онлайн методом крамера онлайн с,решение матрицы онлайн с подробным решением методом крамера,решение матричных уравнений методом крамера онлайн,решение матричных уравнений онлайн методом крамера,решение метод крамера онлайн,решение метод крамера решение онлайн,решение методом крамера калькулятор,решение методом крамера калькулятор онлайн,решение методом крамера матрицы онлайн,решение методом крамера матрицы онлайн калькулятор,решение методом крамера онлайн,решение методом крамера онлайн калькулятор,решение методом крамера онлайн с подробным решением,решение онлайн крамера,решение онлайн линейных уравнений методом крамера,решение онлайн матриц метод крамера,решение онлайн матрицы методом крамера,решение онлайн метод крамера,решение онлайн метод крамера онлайн,решение онлайн методом крамера,решение онлайн по крамеру,решение онлайн по формуле крамера,решение онлайн систем линейных уравнений методом крамера,решение онлайн систем линейных уравнений методом крамера онлайн,решение онлайн систем методом крамера,решение онлайн систем методом крамера онлайн с подробным решением,решение онлайн системы методом крамера онлайн калькулятор,решение онлайн слау методом крамера,решение по крамеру онлайн,решение по методу крамера онлайн,решение по формуле крамера онлайн,решение систем линейных уравнений методом крамера калькулятор,решение систем линейных уравнений методом крамера калькулятор онлайн,решение систем линейных уравнений методом крамера онлайн,решение систем линейных уравнений методом крамера онлайн калькулятор,решение систем линейных уравнений методом крамера онлайн с решением,решение систем линейных уравнений онлайн методом крамера,решение систем линейных уравнений онлайн методом крамера онлайн,решение систем линейных уравнений онлайн методом крамера онлайн с,решение систем методом крамера калькулятор,решение систем методом крамера калькулятор онлайн,решение систем методом крамера онлайн,решение систем методом крамера онлайн калькулятор,решение систем онлайн методом крамера,решение систем онлайн методом крамера онлайн с подробным решением,решение систем уравнений метод крамера онлайн,решение систем уравнений методом крамера онлайн,решение систем уравнений методом крамера онлайн калькулятор,решение систем уравнений методом крамера онлайн с подробным решением,решение систем уравнений онлайн метод крамера,решение систем уравнений онлайн методом крамера,решение систем уравнений онлайн методом крамера онлайн,решение систем уравнений онлайн с подробным решением методом крамера,решение системы линейных уравнений методом крамера онлайн,решение системы линейных уравнений методом крамера онлайн с решением,решение системы линейных уравнений онлайн методом крамера,решение системы линейных уравнений онлайн методом крамера онлайн,решение системы линейных уравнений онлайн методом крамера с решением,решение системы методом крамера онлайн,решение системы онлайн методом крамера,решение системы уравнений методом крамера онлайн,решение системы уравнений методом крамера онлайн калькулятор,решение системы уравнений методом крамера онлайн с решением,решение системы уравнений онлайн методом крамера,решение слау методом крамера онлайн,решение слау методом крамера онлайн с решением,решение слау онлайн методом крамера,решение уравнений крамера онлайн,решение уравнений методом крамера калькулятор,решение уравнений методом крамера онлайн,решение уравнений онлайн крамера,решение уравнений онлайн методом крамера,решение уравнений онлайн по формуле крамера онлайн,решение уравнения методом крамера онлайн,решение уравнения онлайн методом крамера,решить линейное уравнение методом крамера онлайн,решить линейное уравнение онлайн методом крамера,решить матрицу методом крамера онлайн,решить матрицу методом крамера онлайн калькулятор,решить матрицу методом крамера онлайн с подробным решением,решить матрицу онлайн калькулятор методом крамера,решить матрицу онлайн методом крамера,решить матрицу онлайн методом крамера онлайн,решить методом крамера онлайн,решить методом крамера систему линейных уравнений онлайн,решить онлайн матрицу методом крамера,решить онлайн систему линейных уравнений методом крамера,решить онлайн слау методом крамера,решить онлайн уравнение методом крамера,решить онлайн уравнение методом крамера с подробным решением,решить по формуле крамера онлайн,решить систему линейных уравнений методом крамера онлайн,решить систему линейных уравнений методом крамера онлайн с решением,решить систему линейных уравнений методом крамера решить онлайн,решить систему линейных уравнений онлайн методом крамера,решить систему линейных уравнений онлайн по формулам крамера,решить систему линейных уравнений по формулам крамера онлайн,решить систему методом крамера онлайн,решить систему методом крамера онлайн калькулятор,решить систему методом крамера онлайн с подробным решением,решить систему онлайн методом крамера,решить систему по правилу крамера онлайн,решить систему по правилу крамера онлайн калькулятор,решить систему по формулам крамера онлайн,решить систему по формулам крамера онлайн калькулятор,решить систему уравнений методом крамера онлайн,решить систему уравнений методом крамера онлайн с подробным решением,решить систему уравнений онлайн методом крамера,решить систему уравнений онлайн по формуле крамера,решить систему уравнений по формулам крамера онлайн с решением,решить систему уравнений по формуле крамера онлайн,решить слау методом крамера онлайн,решить слау онлайн методом крамера,решить уравнение методом крамера онлайн,решить уравнение методом крамера онлайн с подробным решением,решить уравнение онлайн методом крамера,система линейных уравнений методом крамера онлайн,система линейных уравнений методом крамера онлайн калькулятор,система линейных уравнений онлайн калькулятор методом крамера,система линейных уравнений онлайн методом крамера,система линейных уравнений онлайн методом крамера онлайн,система методом крамера онлайн,система уравнений методом крамера онлайн,система уравнений онлайн методом крамера,систему линейных уравнений решить по формулам крамера онлайн,слау методом крамера калькулятор,слау методом крамера онлайн,слау методом крамера онлайн решение,слау онлайн методом крамера онлайн,слау решение методом крамера онлайн,спецкласс ру онлайн калькулятор,формула крамера для решения системы линейных уравнений онлайн,формула крамера калькулятор,формула крамера онлайн,формула крамера онлайн калькулятор,формулы крамера онлайн калькулятор.
Решить задачу калькулятор крамер вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Решение системы по формулам Крамера
Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!
Рассмотрим систему уравнений
На
первом шаге вычислим определитель
,
его называют главным
определителем системы.
Если
,
то система имеет бесконечно много
решений или несовместна (не имеет
решений). В этом случае правило Крамера
не поможет, нужно использовать Метод
Гауса.
Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя: и
На практике вышеуказанные определители также могут обозначаться латинской буквой .
Корни уравнения находим по формулам: ,
Пример 7
Решить систему линейных уравнений
В подобных случаях и приходят на помощь формулы Крамера.
, значит, система имеет единственное решение.
;
;
Ответ: , .
Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
Пример
8 Решить
систему по формулам Крамера.
Ответ
представить в обыкновенных неправильных
дробях. Сделать проверку.
Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Находим главный определитель системы:
Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса.
Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя: , ,
И, наконец, ответ рассчитывается по формулам: , ,
Пример 9 Решить систему по формулам Крамера.
Решение: Решим систему по формулам Крамера. , значит, система имеет единственное решение.
Ответ: .
Элементарные
преобразования матрицы —
это такие преобразования матрицы,
в результате которых сохраняется
эквивалентность матриц. Таким образом,
элементарные преобразования не изменяют
множество решений системы
линейных алгебраических уравнений,
которую представляет эта матрица.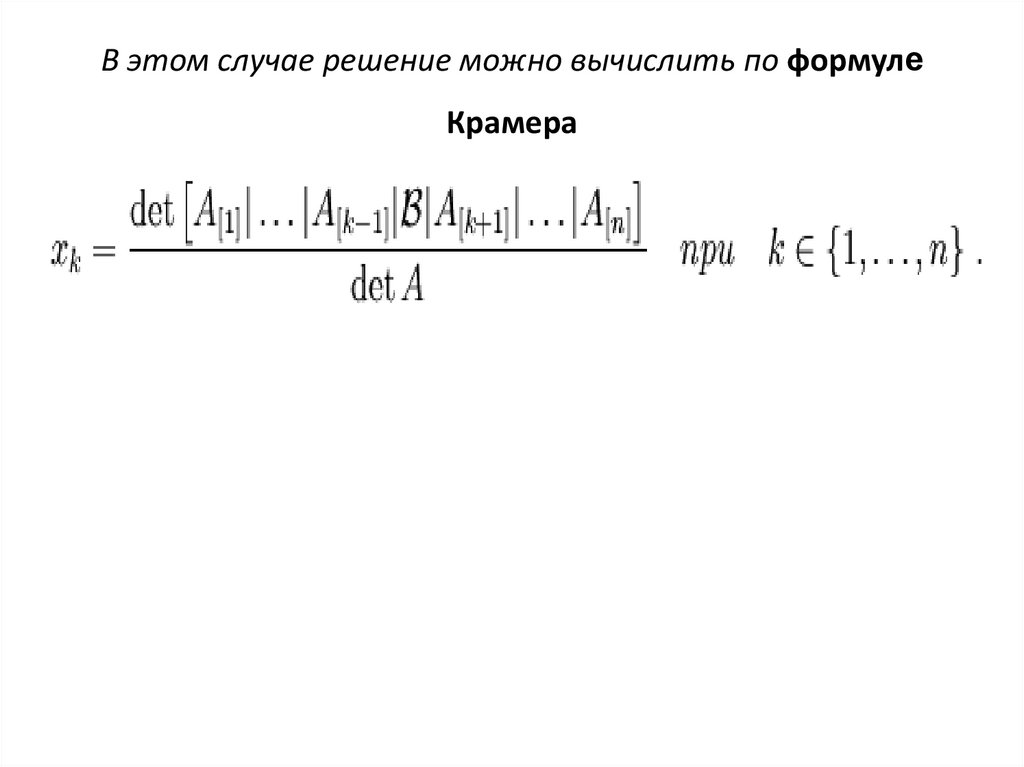
Элементарные преобразования используются в методе Гаусса для приведения матрицы к треугольному или ступенчатому виду.
Элементарными преобразованиями строк называют:
перестановка местами любых двух строк матрицы;
умножение любой строки матрицы на константу , ;
прибавление к любой строке матрицы другой строки, умноженной на константу , .
В некоторых курсах линейной алгебры перестановка местами двух строк матрицы не вносятся в определение элементарных преобразований так как перестановку местами любых двух строк матрицы можно получить используя умножение любой строки матрицы на константу , и прибавление к любой строке матрицы другой строки, умноженной на константу , .
Аналогично определяются элементарные преобразования столбцов.
Элементарные преобразования обратимы.
Обозначение
указывает
на то, что матрица
может
быть получена из
путём
элементарных преобразований (или
наоборот).
Ме́тод Га́усса[1] — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные[2].
Решить систему уравнений методом Гаусса:
x + y — 3z = 2,
3x — 2y + z = — 1,
2x + y — 2z = 0.
Решение. Выпишем расширенную матрицу данной системы
и произведем следующие элементарные преобразования над ее строками:
а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:
~ ;
б) третью строку умножим на (-5) и прибавим к ней вторую:
.
В результате всех этих преобразований данная система приводится к треугольному виду:
x + y — 3z = 2,
-5y + 10z = -7,
— 10z = 13.
Из последнего уравнения находим z = -1,3. Подставляя это значение во второе уравнение, имеем y = -1,2. Далее из первого уравнения получим x = — 0,7.
3.5 Детерминанты и правило Крамера – Алгебра колледжа для управленческих наук
[1]
Мы научились решать системы уравнений с двумя переменными и тремя переменными, а также несколькими методами: подстановкой, сложением, методом исключения Гаусса, использованием обратной матрицы и построением графика. Некоторые из этих методов легче применять, чем другие, и они более подходят в определенных ситуациях.
В этом разделе мы изучим еще две стратегии решения систем уравнений.
Вычисление определителя матрицы 2×2
Определитель — это действительное число, которое может быть очень полезно в математике, поскольку имеет множество применений, например, для вычисления площади, объема и других величин. Здесь мы будем использовать определители, чтобы определить, является ли матрица обратимой, используя элементы квадратной матрицы, чтобы определить, существует ли решение системы уравнений. Однако, возможно, одним из наиболее интересных приложений является их использование в криптографии. Защищенные сигналы или сообщения иногда отправляются закодированными в матрице. Данные можно расшифровать только с помощью обратимой матрицы и определителя. Для наших целей мы сосредоточимся на определителе как признаке обратимости матрицы. Вычисление определителя матрицы включает в себя следование определенным шаблонам, описанным в этом разделе.
Определитель матрицы 2 2, заданный
, определяется как:
det
Обратите внимание, что для определителей мы используем прямые вертикальные линии.
Другими словами, дет.
Выглядит знакомо? Должно. Помните, что это был знаменатель в скаляре, который мы умножаем на матрицу 2 2 с переключенными диагоналями и противоположными диагоналями, чтобы создать обратную. Таким образом, обратная матрица 2 2, как показано выше, будет:
.
Найдите определитель данной матрицы
det
Использование правила Крамера для решения системы двух уравнений с двумя переменными
Теперь мы представим последний метод решения систем уравнений, использующий определители. Этот метод, известный как правило Крамера, восходит к середине 18 века и назван в честь его новатора, швейцарского математика Габриэля Крамера (1704–1752), который представил его в 1750 году. системы с любым числом неизвестных при условии, что у нас есть такое же количество уравнений, что и неизвестных.
Правило Крамера даст нам единственное решение системы уравнений, если она существует. Однако, если система не имеет решения или имеет бесконечное число решений, на это будет указывать определитель .
Несогласованные решения имеют по крайней мере один определитель числителя, отличный от нуля. Зависимые решения имеют ноль в качестве определителя в обоих числителях. Для нахождения общего решения необходимо использовать другой метод.
Чтобы понять, как и почему работает правило Крамера, мы направим вас к исходному материалу в OpenStax College Algebra.
Короче говоря, правило Крамера начинается с системы уравнений, например:
и мы можем показать, что
Обратите внимание, что знаменатель для обоих и является определителем матрицы коэффициентов.
Мы можем использовать эти формулы для решения, но правило Крамера также вводит новое обозначение:
- : определитель матрицы коэффициентов
- : определитель матрицы, созданной матрицей коэффициентов с заменой -коэффициента константами
- : определитель матрицы, созданной матрицей коэффициентов с заменой -коэффициента константами
Обратите внимание, что ключом к правилу Крамера является замена интересующего столбца переменных столбцом констант и вычисление определителей.
Затем мы можем выразить и как:
Правило Крамера — это метод, использующий определители для решения систем уравнений, в которых число уравнений равно числу переменных.
Рассмотрим систему двух линейных уравнений с двумя переменными.
Решение с использованием правила Крамера дается как: Если мы ищем для , столбец заменяется постоянным столбцом.
Решите следующую систему, используя правило Крамера
Найти
Найти
Найти
Решение (2,-3).
Используйте правило Крамера, чтобы решить систему уравнений.
Вычисление определителя матрицы
Найти определитель матрицы несложно, но найти определитель матрицы сложнее. Один из методов состоит в том, чтобы дополнить матрицу повторением первых двух столбцов, получив матрицу. Затем мы вычисляем сумму произведений записей вниз по каждой из трех диагоналей (слева вверху справа внизу) и вычитаем произведения записей вверх по каждой из трех противоположных диагоналей (слева внизу справа вверху).
Это легче понять с визуальным и пример.
Найдите определитель матрицы.
Шаг 1: Дополнить первыми двумя столбцами:
Шаг 2: От верхнего левого угла к нижнему правому: Умножьте числа по первой диагонали. , затем начните с и умножьте слева направо по диагонали, а затем . Добавьте эти три продукта.
Шаг 3: Теперь сверху справа: умножьте записи по обратной диагонали. , затем начните с и умножьте справа налево по диагонали, а затем . Добавьте эти три продукта и вычтите это значение из значения на шаге 2.
Алгебра выглядит следующим образом:
Найдите определитель матрицы:
Дополните матрицу первыми двумя столбцами и следуйте формуле. Таким образом,
Детерминанты также можно найти с помощью технологий. После того, как матрица введена в ваш калькулятор. Переход к МАТРИЦА – МАТЕМАТИКА и det и вызов рассматриваемой матрицы предоставит определитель для матрицы.
В Excel =mdeterm также найдет определитель матрицы. Методы, упомянутые в этом разделе, работают только для указанного размера. Для больших матриц рекомендуется использовать калькулятор, Excel или другую программу.
Найдите определитель матрицы .
от
Использование правила Крамера для решения системы трех уравнений с тремя переменными
Теперь, когда мы можем найти определитель матрицы, мы можем применить правило Крамера для решения системы из трех уравнений и трех неизвестных. Правило Крамера для систем следует той же схеме, что и для систем. Однако требуются дополнительные расчеты.
Рассмотрим систему:
где:
Если мы записываем определитель, мы заменяем столбец постоянным столбцом. Если мы записываем определитель, мы заменяем столбец постоянным столбцом. Если мы записываем определитель, мы заменяем столбец постоянным столбцом. Всегда проверяйте ответ.
Решите следующую систему, используя правило Крамера.
Используйте правило Крамера.
Затем
Решение (1,3,-2).
Используйте правило Крамера для решения системы:
а. Решите систему уравнений (если возможно), используя правило Крамера.
Начнем с нахождения определителей:
Теперь мы знаем, что оно либо зависимо, либо несовместно. Давайте посмотрим на один из других определителей.
Поскольку -16 \neq 0, мы имеем противоречивое решение.
б. Решите следующую систему уравнений (если возможно, или дайте общее решение, если зависит).
Найдем D с помощью технологии, калькулятора или Excel.
Мы знаем, что это зависимая или противоречивая система. Мы могли бы найти все три других определителя, чтобы увидеть, является ли он зависимым, и если да, то нам пришлось бы использовать rref в калькуляторе, чтобы найти общее решение.
По этой причине сейчас быстрее просто использовать rref. Существует онлайн-версия от planetcalc.
Сокращенная эшелонная форма строки матрицы:
В виде уравнений это:
Таким образом, если любое действительное число, то:
Вот несколько свойств, которые могут упростить и ускорить поиск определителей.
- Если матрица имеет форму верхнего треугольника (в нижнем треугольнике под диагональю все нули), то определитель равен произведению элементов по главной диагонали.
- При перестановке двух строк определитель меняет знак.
- Если две строки или два столбца идентичны, определитель равен нулю.
- Если матрица содержит строку или столбец из нулей, определитель равен 0.
- Определитель обратной матрицы равен обратной величине определителя матрицы .
- Если какая-либо строка или столбец умножается на константу, определитель умножается на тот же коэффициент.
Media Attributions
clipartmax.com/max/m2i8d3Z5N4i8b1m2/»> takenote находится под лицензией Public Domain- др. по лицензии Creative Commons License 4.0 CC-BY ↵
7.8 Решение систем с помощью правила Крамера — Колледжская алгебра 2e
Цели обучения
В этом разделе вы:
- Оцените 2 × 2 определители.
- Используйте правило Крамера, чтобы решить систему уравнений с двумя переменными.
- Вычислите 3 × 3 определителей.
- Используйте правило Крамера, чтобы решить систему из трех уравнений с тремя переменными.
- Знать свойства определителей.
Мы научились решать системы уравнений с двумя переменными и тремя переменными, а также несколькими методами: подстановкой, сложением, методом исключения Гаусса, использованием обратной матрицы и построением графика. Некоторые из этих методов легче применять, чем другие, и они более подходят в определенных ситуациях.
В этом разделе мы изучим еще две стратегии решения систем уравнений.
Вычисление определителя матрицы 2×2
Определитель — это действительное число, которое может быть очень полезно в математике, поскольку имеет множество применений, например, для вычисления площади, объема и других величин. Здесь мы будем использовать определители, чтобы выяснить, является ли матрица обратимой, используя элементы квадратной матрицы, чтобы определить, существует ли решение системы уравнений. Однако, возможно, одним из наиболее интересных приложений является их использование в криптографии. Защищенные сигналы или сообщения иногда отправляются закодированными в матрице. Данные могут быть расшифрованы только с помощью обратимой матрицы и определителя. Для наших целей мы сосредоточимся на определителе как признаке обратимости матрицы. Вычисление определителя матрицы включает в себя следование определенным шаблонам, описанным в этом разделе.
Найдите определитель матрицы 2 × 2
Определитель матрицы 2×22×2, заданный
A=[abcd]A=[abcd]
определяется как
Обратите внимание на изменение обозначений.
Есть несколько способов указать определитель, включая det(A)det(A) и замену скобок в матрице прямыми линиями |A|.|A|.
Пример 1
Нахождение определителя матрицы 2 × 2
Нахождение определителя заданной матрицы.
А=[52-63]А=[52-63]
Решение
det(A)=|52−63|=5(3)−(−6)(2)=27det(A)=|52−63|=5(3)−(−6)(2)=27
Использование правила Крамера для решения системы двух уравнений с двумя переменными
Теперь мы представим последний метод решения систем уравнений, использующий определители. Этот метод, известный как правило Крамера, восходит к середине 18 века и назван в честь его новатора, швейцарского математика Габриэля Крамера (1704-1752), который представил его в 1750 году во Введении к анализу линий алгебры. Правило Крамера — жизнеспособный и эффективный метод поиска решений систем с произвольным числом неизвестных при условии, что у нас есть такое же количество уравнений, как и неизвестных.
Правило Крамера даст нам единственное решение системы уравнений, если она существует. Однако, если система не имеет решения или имеет бесконечное число решений, на это будет указывать нулевой определитель. Чтобы выяснить, является ли система противоречивой или зависимой, придется использовать другой метод, такой как исключение.
Чтобы понять правило Крамера, давайте внимательно посмотрим, как мы решаем системы линейных уравнений, используя основные операции со строками. Рассмотрим систему двух уравнений с двумя переменными.
a1x+b1y=c1(1)a2x+b2y=c2(2)a1x+b1y=c1(1)a2x+b2y=c2(2)
Мы исключаем одну переменную, используя операции со строками, и находим другую. Скажем, что мы хотим найти x.x. Если уравнение (2) умножить на коэффициент, противоположный коэффициенту yy в уравнении (1), уравнение (1) умножить на коэффициент yy в уравнении (2), и мы сложим два уравнения, переменная yy будет устранено.
b2a1x+b2b1y=b2c1Multiply R1by b2−b1a2x−b1b2y=−b1c2Multiply R2by−b1________________________________________________________ b2a1x−b1a2x=b2c1−b1c2b2a1x+b2b1y=b2c1Multiply R1by b2−b1a2x−b1b2y=−b1c2Multiply R2by−b1________________________________________________________ b2a1x−b1a2x=b2c1−b1c2
Теперь найдите х.
х.
B2A1X -B1A2X = B2C1 -B1C2X (B2A1 -B1A2) = B2C1-B1C2 X = B2C1 -B1C2B2A1-B1A2 = | C1B1C2B2 || A1B1A2B2 | B2A1X2 = | B2C1 -B2 -B2 -B2 -B2 -B2 -B2 -B2 -B2 -B2 -B2 -B2B1A2B2 −b1c2b2a1−b1a2=|c1b1c2b2||a1b1a2b2|
Аналогично, чтобы найти y,y, мы исключим x.x.
a2a1x+a2b1y=a2c1Multiply R1by a2−a1a2x−a1b2y=−a1c2Multiply R2by−a1________________________________________________________a2b1y−a1b2y=a2c1−a1c2a2a1x+a2b1y=a2c1Multiply R1by a2−a1a2x−a1b2y=−a1c2Multiply R2by−a1________________________________________________________a2b1y−a1b2y=a2c1−a1c2
Решение для YY дает
A2B1Y -A1B2Y = A2C1 -A1C2Y (A2B1 -A1B2) = A2C1 -A1C2 Y = A2C1 -A1C2A2B1 -A1B2 = A1C2 -A2C1A1B2-A2B1 = | A1B1 -A1B2 = A1C2 -A2C1A1B2-A2B1 = | A1B2 = A1C2 -A2C1A1B2B1A2B1A2 a1c2y(a2b1−a1b2)=a2c1−a1c2 y=a2c1−a1c2a2b1−a1b2=a1c2−a2c1a1b2−a2b1=|a1c1a2c2||a1b1a2b2|
Обратите внимание, что знаменатель для xx и yy является определителем матрицы коэффициентов.
Мы можем использовать эти формулы для решения xx и y,y, но правило Крамера также вводит новое обозначение:
- D:D: определитель матрицы коэффициентов
- Dx:Dx: определитель числителя в решении xx
x=DxDx=DxD
- Dy:Dy: определитель числителя в решении yy
y=DyDy=DyD
Ключом к правилу Крамера является замена интересующего столбца переменных столбцом констант и вычисление определителей.
Тогда мы можем выразить xx и yy как частное двух определителей.
Правило Крамера для систем 2×2
Правило Крамера — это метод, использующий определители для решения систем уравнений, в которых количество уравнений равно числу переменных.
Рассмотрим систему двух линейных уравнений с двумя переменными.
a1x+b1y=c1a2x+b2y=c2a1x+b1y=c1a2x+b2y=c2
Решение с использованием правила Крамера дается как
x=DxD=|c1b1c2b2||a1b1a2b2|,D≠0;y= DyD=|a1c1a2c2||a1b1a2b2|,D≠0.x=DxD=|c1b1c2b2||a1b1a2b2|,D≠0;y=DyD=|a1c1a2c2||a1b1a2b2|,D≠0.
Если мы находим x,x, столбец xx заменяется столбцом констант. Если мы ищем y, y, столбец yy заменяется столбцом констант.
Пример 2
Использование правила Крамера для решения системы 2 × 2
Решите следующую систему 2 × 22 × 2, используя правило Крамера.
12x+3y=15 2x−3y=1312x+3y=15 2x−3y=13
Решение
Решите для х.
х.
x=DxD=|15313−3||1232−3|=−45−39−36−6=−84−42=2x=DxD=|15313−3||1232−3|=−45−39 −36−6=−84−42=2
Решите для y.y.
y=DyD=|1215213||1232−3|=156−30−36−6=−12642=−3y=DyD=|1215213||1232−3|=156−30−36−6=−12642 =−3
Решение: (2,−3).(2,−3).
Попробуй #1
Используйте правило Крамера, чтобы решить систему уравнений 2 × 2.
х+2у=-11-2х+у=-13 х+2у=-11-2х+у=-13
Вычисление определителя матрицы 3 × 3
Найти определитель матрицы 2 × 2 несложно, но определить определитель матрицы 3 × 3 сложнее. Один из методов состоит в том, чтобы дополнить матрицу 3×3 повторением первых двух столбцов, получив матрицу 3×5. Затем вычисляем сумму произведений записей вниз по по каждой из трех диагоналей (слева вверху справа внизу) и вычесть произведения записей вверх по по каждой из трех диагоналей (слева внизу справа вверху).
Это легче понять с визуальным и пример.
Найдите определитель матрицы 3×3.
А=[a1b1c1a2b2c2a3b3c3]А=[a1b1c1a2b2c2a3b3c3]
- Дополните AA первыми двумя столбцами.
det(A)=|a1b1c1a2b2c2a3b3c3|a1a2a3b1b2b3|det(A)=|a1b1c1a2b2c2a3b3c3|a1a2a3b1b2b3|
- С левого верхнего угла в правый нижний: умножьте числа по первой диагонали. Прибавьте результат к произведению записей по второй диагонали. Добавьте этот результат к произведению записей вниз по третьей диагонали.
- Из нижнего левого угла в верхний правый: вычтите произведение записей вверх по первой диагонали. Из этого результата вычтите произведение вхождений вверх по второй диагонали. Из этого результата вычтите произведение вхождений вверх по третьей диагонали.
Алгебра выглядит следующим образом:
|A|=a1b2c3+b1c2a3+c1a2b3−a3b2c1−b3c2a1−c3a2b1|A|=a1b2c3+b1c2a3+c1a2b3−a3b2c1−b3c2a1−c3a2b1
Пример 3
Нахождение определителя матрицы 3 × 3
Нахождение определителя заданной матрицы 3 × 3
A=[0213−11401]A=[0213−11401]
Решение
Дополните матрицу первыми двумя столбцами, а затем следуйте формуле.
Таким образом,
|A|=|0213−11401|0342−10|=0(−1)(1)+2(1)(4)+1(3)(0)−4(−1)(1 )−0(1)(0)−1(3)(2)=0+8+0+4−0−6=6|A|=|0213−11401|0342−10|=0(−1) (1)+2(1)(4)+1(3)(0)−4(−1)(1)−0(1)(0)−1(3)(2)=0+8+0 +4−0−6=6
Попробуй #2
Найдите определитель матрицы 3 × 3.
det(A)=|1−371111−23|det(A)=|1−371111−23|
вопросы и ответы
Можем ли мы использовать тот же метод, чтобы найти определитель большей матрицы?
Нет, этот метод работает только для матриц 2×22×2 и 3×33×3. Для больших матриц лучше всего использовать графическую утилиту или компьютерное программное обеспечение.
Использование правила Крамера для решения системы трех уравнений с тремя переменными
Теперь, когда мы можем найти определитель матрицы 3 × 3, мы можем применить правило Крамера для решения системы трех уравнений с тремя переменными.
Правило Крамера является простым и следует шаблону, согласующемуся с правилом Крамера для матриц 2 × 2. Однако по мере увеличения порядка матрицы до 3 × 3 требуется гораздо больше вычислений.
Когда мы вычисляем, что определитель равен нулю, правило Крамера не указывает, имеет ли система решение или бесконечное число решений. Чтобы выяснить это, мы должны выполнить исключение в системе.
Рассмотрим систему уравнений 3 × 3.
х=DxD,y=DyD,z=DzD,D≠0x=DxD,y=DyD,z=DzD,D≠0
где
Если мы записываем определитель Dx,Dx, мы заменяем столбец xx столбцом констант. Если мы записываем определитель Dy,Dy, мы заменяем столбец yy столбцом констант. Если мы записываем определитель Dz,Dz, мы заменяем столбец zz столбцом констант. Всегда проверяйте ответ.
Пример 4
Решение системы 3 × 3 с использованием правила Крамера
Найдите решение данной системы 3 × 3, используя правило Крамера.
x+y-z=63x-2y+z=-5x+3y-2z=14x+y-z=63x-2y+z=-5x+3y-2z=14
Решение
Используйте правило Крамера.
D=|11−13−2113−2|,Dx=|61−1−5−21143−2|,Dy=|16−13−51114−2|,Dz=|1163−2−51314|D =|11−13−2113−2|,Dx=|61−1−5−21143−2|,Dy=|16−13−51114−2|,Dz=|1163−2−51314|
Тогда
x=DxD=-3-3=1y=DyD=-9-3=3z=DzD=6-3=-2x=DxD=-3-3=1y=DyD=-9-3 =3z=DzD=6−3=−2
Решение: (1,3,−2).(1,3,−2).
Попробуй #3
Используйте правило Крамера, чтобы решить матрицу 3 × 3.
x−3y+7z=13x+y+z=1x−2y+3z=4x−3y+7z=13x+y+z=1x−2y+3z=4
Пример 5
Использование правила Крамера для решения противоречивой системы
Решите систему уравнений, используя правило Крамера.
3x−2y=4 (1)6x−4y=0 (2)3x−2y=4 (1)6x−4y=0 (2)
Решение
Начнем с нахождения определителей D,Dx и Dy.D,Dx и Dy.
D=|3−26−4|=3(−4)−6(−2)=0D=|3−26−4|=3(−4)−6(−2)=0
Мы знаем, что определитель, равный нулю, означает, что система либо не имеет решений, либо имеет бесконечное число решений.
Чтобы увидеть, какой из них, мы используем процесс исключения. Наша цель — исключить одну из переменных.
- Умножить уравнение (1) на −2,−2.
- Добавьте результат к уравнению (2).(2).
−6x+4y=−86x−4y=0_______________0=−8−6x+4y=−86x−4y=0_______________0=−8
Получаем уравнение 0=−8,0=−8, которое неверно. Следовательно, система не имеет решения. График системы показывает две параллельные линии. См. рис. 1.
Рисунок 1
Пример 6
Использование правила Крамера для решения зависимой системы
Решите систему с бесконечным числом решений.
x−2y+3z=0(1)3x+y−2z=0(2)2x−4y+6z=0(3)x−2y+3z=0(1)3x+y−2z=0( 2)2x−4y+6z=0(3)
Решение
Сначала найдем определитель. Настройте матрицу, дополненную первыми двумя столбцами.
|1−2331−22−46 | 1−2312−4||1−2331−22−46 | 1−2312−4|
Тогда
1(1)(6)+(−2)(−2)(2)+3(3)(−4)−2(1)(3)−(−4)(−2 )(1)−6(3)(−2)=01(1)(6)+(−2)(−2)(2)+3(3)(−4)−2(1)(3) −(−4)(−2)(1)−6(3)(−2)=0
Поскольку определитель равен нулю, решения либо нет, либо существует бесконечное число решений.
Мы должны выполнить исключение, чтобы узнать.
- Умножьте уравнение (1) на −2−2 и добавьте результат к уравнению (3):
−2x+4y−6z=02x−4y+6z=00=0−2x+4y−6z=02x−4y+6z=00=0
- Получение ответа 0=0,0=0, утверждение, которое всегда верно, означает, что система имеет бесконечное число решений. Изобразив систему, мы видим, что две плоскости одинаковы и обе пересекают третью плоскость по прямой. См. рис. 2.
Рисунок 2
Понимание свойств определителей
Есть много свойств определителей. Здесь перечислены некоторые свойства, которые могут быть полезны при вычислении определителя матрицы.
Свойства определителей
- Если матрица имеет форму верхнего треугольника, определитель равен произведению элементов по главной диагонали.
- При перестановке двух строк определитель меняет знак.
- Если две строки или два столбца совпадают, определитель равен нулю.
- Если матрица содержит строку нулей или столбец нулей, определитель равен нулю.
- Определитель обратной матрицы A−1A−1 является обратной величиной определителя матрицы A.A.
- Если какая-либо строка или столбец умножается на константу, определитель умножается на тот же коэффициент.
Пример 7
Иллюстрация свойств определителей
Проиллюстрируйте каждое из свойств определителей.
Решение
Свойство 1 гласит, что если матрица имеет форму верхнего треугольника, определитель равен произведению элементов по главной диагонали.
A=[12302100−1]A=[12302100−1]
Дополнить AA первыми двумя столбцами.
A=[12302100−1|100220]A=[12302100−1|100220]
Затем
det(A)=1(2)(−1)+2(1)(0)+3(0 )(0)−0(2)(3)−0(1)(1)+1(0)(2)=−2det(A)=1(2)(−1)+2(1)(0 )+3(0)(0)−0(2)(3)−0(1)(1)+1(0)(2)=−2
Свойство 2 указывает, что при перестановке строк меняется знак.
Учитывая
A=[−154−3],det(A)=(−1)(−3)−(4)(5)=3−20=−17B=[4−3−15],det( B)=(4)(5)−(−1)(−3)=20−3=17A=[−154−3],det(A)=(−1)(−3)−(4)( 5)=3−20=−17B=[4−3−15],det(B)=(4)(5)−(−1)(−3)=20−3=17
Свойство 3 утверждает, что если две строки или два столбца совпадают, определитель равен нулю.
А=[122222−122 | 12−1 222]det(A)=1(2)(2)+2(2)(−1)+2(2)(2)+1(2)(2)−2(2)(1) −2(2)(2)=4−4+8+4−4−8=0A=[122222−122 | 12−1 222]det(A)=1(2)(2)+2(2)(−1)+2(2)(2)+1(2)(2)−2(2)(1) −2(2)(2)=4−4+8+4−4−8=0
Свойство 4 гласит, что если строка или столбец равны нулю, определитель равен нулю. Таким образом,
A=[1200],det(A)=1(0)−2(0)=0A=[1200],det(A)=1(0)−2(0)=0
Свойство 5 утверждает, что определитель обратной матрицы A-1A-1 является обратной величиной определителя A.A. Таким образом,
A=[1234],det(A)=1(4)−3(2)=−2A−1=[−2132−12],det(A−1)=−2(−12) −(32)(1)=−12A=[1234],det(A)=1(4)−3(2)=−2A−1=[−2132−12],det(A−1)=− 2(−12)−(32)(1)=−12
Свойство 6 гласит, что если любая строка или столбец матрицы умножается на константу, определитель умножается на тот же коэффициент.
Таким образом,
A=[1234],det(A)=1(4)−2(3)=−2B=[2(1)2(2)34],det(B)=2(4)−3( 4)=−4A=[1234],det(A)=1(4)−2(3)=−2B=[2(1)2(2)34],det(B)=2(4)− 3(4)=−4
Пример 8
Использование правила Крамера и свойств определителя для решения системы
Найдите решение данной системы 3 × 3.
2x+4y+4z=2(1)3x+7y+7z=−5(2) x+2y+2z=4(3)2x+4y+4z=2(1)3x+7y+7z=− 5(2) x+2y+2z=4(3)
Решение
Используя правило Крамера, мы имеем
D=|244377122|D=|244377122|
Обратите внимание, что второй и третий столбцы идентичны. Согласно свойству 3 определитель будет равен нулю, поэтому решения либо нет, либо решений бесконечное множество. Мы должны выполнить исключение, чтобы узнать.
- Умножьте уравнение (3) на –2 и добавьте результат к уравнению (1).
−2x−4y−4x=−8 2x+4y+4z=20=−6−2x−4y−4x=−8 2x+4y+4z=20=−6
Получение утверждения, являющегося противоречием, означает, что система не имеет решения.
7.8 Секционные упражнения
Устный
1.
Объясните, почему мы всегда можем вычислить определитель квадратной матрицы.
2.
Изучая правило Крамера, объясните, почему нет единственного решения системы, когда определитель вашей матрицы равен 0. Для простоты используйте матрицу 2×22×2.
3.
Объясните, что в терминах обратной матрицы означает наличие определителя, равного 0.
4.
Определитель матрицы 2×22×2 AA равен 3. Если вы поменяете строки и умножите первую строку на 6, а вторую строку на 2, объясните, как найти определитель, и дайте ответ.
Алгебраический
Для следующих упражнений найдите определитель.
5.
|1234||1234|
6.
|−123−4||−123−4|
7.
|2−5−16||2−5−16|
8.
|−84−15||−84−15|
9.
|103−4||103−4|
10.
|10200-10||10200-10|
11.
|100.250.1||100.250.1|
12.
|6−384||6−384|
13.
|−2−33,14 000||−2−33,14 000|
14.
|−1.10.67.2−0,5||−1.10.67.2−0,5|
15.
|−10001000−3||−10001000−3|
16.
|−14002300−3||−14002300−3|
17.
|101010100||101010100|
18.
|2-313-41-561||2-313-41-561|
19.
|−214−42−82−8−3||−214−42−82−8−3|
20.
|6-12-4-3519-1||6-12-4-3519−1|
21.
|51−12313−6−3||51−12313−6−3|
22.
|1,12−1−4004,1−0,42,5||1,12−1−4004,1−0,42,5|
23.
|2-1.63.11.13-8-9.302||2-1.63.11.13-8-9.302|
24.
|−12131415−16170018||−12131415−16170018|
Для следующих упражнений решите систему линейных уравнений, используя правило Крамера.
25.
2x−3y=−14x+5y=92x−3y=−14x+5y=9
26.
5x−4y=2−4x+7y=65x−4y=2−4x+7y=6
27.
6x−3y=2−8x+9y=−16x−3y=2−8x+9y=−1
28.
2x+6y=125x−2y=132x+6y=125x−2y=13
29.
4x+3y=232x-y=-14x+3y=232x-y=-1
30.
10x−6y=2−5x+8y=−110x−6y=2−5x+8y=−1
31.
4x−3y=−32x+6y=−44x−3y=−32x+6y=−4
32.
4x−5y=7−3x+9y=04x−5y=7−3x+9y=0
33.
4x+10y=180-3x-5y=-1054x+10y=180-3x-5y=-105
34.
8x−2y=−3−4x+6y=48x−2y=−3−4x+6y=4
Для следующих упражнений решите систему линейных уравнений, используя правило Крамера.
35.
x+2y-4z=-17x+3y+5z=26-2x-6y+7z=-6x+2y-4z=-17x+3y+5z=26-2x-6y+7z=-6
36.
−5x+2y−4z=−474x−3y−z=−943x−3y+2z=94−5x+2y−4z=−474x−3y−z=−943x−3y+2z=94
37.
4x+5y-z=-7-2x-9y+2z=85y+7z=214x+5y-z=-7-2x-9y+2z=85y+7z=21
38.
4x-3y+4z=105x-2z=-23x+2y-5z=-94x−3y+4z=105x−2z=−23x+2y−5z=−9
39.
4x-2y+3z=6-6x+y=-22x+7y+8z=244x-2y+3z=6-6x+y=-22x+7y+8z=24
40.
5x+2y-z=1-7x-8y+3z=1,56x-12y+z=75x+2y-z=1-7x-8y+3z=1,56x-12y+z=7
41.
13x-17y+16z=73-11x+15y+17z=6146x+10y-30z=-1813x-17y+16z=73-11x+15y+17z=6146x+10y-30z=-18
42.
−4x−3y−8z=−72x−9y+5z=0,55x−6y−5z=−2−4x−3y−8z=−72x−9y+5z=0,55x−6y−5z=−2
43.
4x-6y+8z=10-2x+3y-4z=-5x+y+z=14x-6y+8z=10-2x+3y-4z=-5x+y+z=1
44.
4x-6y+8z=10-2x+3y-4z=-512x+18y-24z=-304x-6y+8z=10-2x+3y-4z=-512x+18y-24z=-30
Технология
В следующих упражнениях используйте функцию определителя в графической утилите.
45.
|10810300243||10810300243|
46.
|10210-91330-2-1011-2||10210-91330-2-1011-2|
47.
|1217401210050022,0000002||1217401210050022,0000002|
48.
|1000230045607890||1000230045607890|
Реальные приложения
Для следующих упражнений создайте систему линейных уравнений для описания поведения. Затем вычислить определитель. Будет ли уникальное решение? Если да, то найти единственное решение.
49.
Два числа в сумме дают 56. Одно число на 20 меньше другого.
50.
Два числа в сумме дают 104. Если вы дважды сложите первое число и два раза второе число, получится 208
51.
Три числа в сумме дают 106. Первое число на 3 меньше второго числа. Третье число на 4 больше первого числа.
52.
Три числа в сумме дают 216. Сумма первых двух чисел равна 112. Третье число на 8 меньше, чем первые два вместе взятые.
Для следующих упражнений создайте систему линейных уравнений для описания поведения. Затем решите систему для всех решений, используя правило Крамера.
53.
Вы инвестируете 10 000 долларов на два счета, на которые начисляются 8% и 5% годовых. В конце года на ваших объединенных счетах было 10 710 долларов. Сколько было вложено в каждый счет?
54.
Вы инвестируете 80 000 долларов на два счета, 22 000 долларов на один счет и 58 000 долларов на другой счет. В конце года, при условии простых процентов, вы заработали 2470 долларов в виде процентов. Второй счет получает на полпроцента меньше, чем удвоенный процент по первому счету. Каковы процентные ставки для ваших счетов?
55.
Театру необходимо знать, сколько билетов для взрослых и детей было продано из 1200 билетов. Если детские билеты стоят 5,95 долл. США, билеты для взрослых — 11,15 долл.
США, а общая сумма выручки составила 12 756 долл. США, сколько было продано детских билетов и билетов для взрослых?
56.
Концертный зал продает одиночные билеты по 40 долларов США каждый и билеты для пар по 65 долларов США. Если общий доход составил 18 090 долларов США и был продан 321 билет, то сколько было продано одиночных билетов и сколько билетов для пар?
57.
Вы решили покрасить кухню в зеленый цвет. Вы создаете цвет краски, смешивая желтую и синюю краски. Вы не можете вспомнить, сколько галлонов каждого цвета вошло в вашу смесь, но вы знаете, что всего было 10 галлонов. Кроме того, вы сохранили квитанцию и знаете, что общая потраченная сумма составила 29,50 долларов США. Если каждый галлон желтого цвета стоит 2,59 доллара, а каждый галлон синего стоит 3,19 доллара, сколько галлонов каждого цвета входит в вашу зеленую смесь?
58.
Вы продали два вида шарфов на фермерском рынке и хотели бы знать, какой из них более популярен.
Всего было продано 56 шарфов, желтый шарф стоил 10 долларов, фиолетовый — 11 долларов. Если ваш общий доход составил 583 доллара, сколько желтых шарфов и сколько фиолетовых шарфов было продано?
59.
В вашем саду выращиваются помидоры двух видов: зеленые и красные. Красный весит 10 унций, а зеленый весит 4 унции. У вас есть 30 помидоров общим весом 13 фунтов 14 унций. Сколько у вас помидоров каждого вида?
60.
На рынке три самых популярных овоща составляют 53% продаж овощей. Продажи кукурузы на 4% выше, чем у брокколи, продажи которой на 5% выше, чем у лука. Какую долю рынка занимает каждый овощ?
61.
На том же рынке три самых популярных фрукта составляют 37% от общего количества продаваемых фруктов. Клубники продают вдвое больше, чем апельсинов, а киви продают на один процент больше, чем апельсинов. Для каждого фрукта найдите процент от общего количества проданных фруктов.
62.
Три артиста выступили на концертной площадке. Первый стоил 15 долларов за билет, второй артист — 45 долларов за билет, а последний — 22 доллара за билет. Было продано 510 билетов на общую сумму 12 700 долларов. Если у первой группы было на 40 зрителей больше, чем у второй группы, сколько билетов было продано на каждую группу?
63.
Кинотеатр продал билеты на три фильма. Билеты на первый фильм стоили 5 долларов, билеты на второй фильм — 11 долларов, а на третий фильм — 12 долларов. На первый фильм было продано 100 билетов. Общее количество проданных билетов составило 642, а общий доход составил 6 774 доллара. Сколько билетов на каждый фильм было продано?
Для следующих упражнений используйте этот сценарий: Компания, заботящаяся о своем здоровье, решает приготовить пищевую смесь из миндаля, сушеной клюквы и орехов кешью в шоколаде. Информация о пищевой ценности этих продуктов представлена в Таблице 1.
| Жир (г) | Белок (г) | Углеводы (г) | |
|---|---|---|---|
| Миндаль (10) | 6 | 2 | 3 |
| Клюква (10) | 0,02 | 0 | 8 |
| Кешью (10) | 7 | 3,5 | 5,5 |
Стол 1
64.
Для специальной «низкоуглеводной» трейловой смеси имеется 1000 штук смеси.