|
Random converter |
Калькулятор мощности трехфазного переменного токаЭтот калькулятор мощности трехфазного тока позволяет определить активную, полную и реактивную мощность по известным среднеквадратичным значениям напряжения, тока и коэффициенту мощности в системе с симметричным трехфазным напряжением и равномерной нагрузкой. Пример: Три равных индуктивных нагрузки с коэффициентом мощности 0,68 подключены звездой к сети с линейным напряжением 400 В 50 Гц. Ток каждой фазы 10 А. Рассчитать активную и реактивную нагрузку на каждой фазе, фазное напряжение, фазный ток, фазовый угол, линейный ток, активную, реактивную и полную мощность. Тип расчетов:Мощность и ток по напряжение и нагрузке Мощность и нагрузка по напряжению и току Входные данные Тип соединения Звезда (Y)Треугольник (Δ) Среднеквадратичное значение напряженияЛинейное напряжение UL rmsвольт (В)киловольт (кВ)мегавольт (МВ) Среднеквадратичное значение напряжения между линейными проводами (напряжение между фазами) в симметричной трехфазной системе. или Фазное напряжение Uph rmsвольт (В)киловольт (кВ)мегавольт (МВ) Среднеквадратичное значение напряжения на каждой фазе симметричной трехфазной системы относительно нейтрали. Импеданс нагрузки в каждой фазеАктивное сопротивление нагрузки в каждой фазе Rphмиллиом (мОм)ом (Ом)килоом (кОм)мегаом (МОм) Реактивное сопротивление нагрузки в каждой фазе Xph Ом Zph= Rph + jXph= R + jXОм ИЛИ Величина (модуль) импеданса нагрузки |Z|phмиллиом (мОм)ом (Ом)килоом (кОм)мегаом (МОм) Фазовый угол импеданса нагрузки φphградус (°)радиан (рад) Zph= |Z|ph ∠φph= |Z| ∠φ° Ом Вначале выберите тип расчёта. Поделиться Поделиться ссылкой на этот калькулятор, включая входные параметры Twitter Facebook Google+ VK Закрыть Выходные данные Полная мощность по всем трем фазам |S| ГВ·А Полная активная мощность P Вт Полная реактивная мощность Q Вар Полная комплексная мощность S ГВ·А Среднеквадратичное значение фазного тока Iph RMS А Среднеквадратичное значение линейного тока IL RMS А Фазовый сдвиг φ ° рад Коэффициент мощности PF Дано Найти Решение Однофазный и трехфазный ток Определения и формулы Генерация трехфазного тока Преимущества трехфазных систем Последовательность фаз Фазное напряжение и фазный ток Линейное напряжение и ток Симметричные и несимметричные системы и нагрузки Линейные и нелинейные нагрузки Соединение треугольником и звездой Напряжение и мощность в симметричной трехфазной нагрузке при соединении звездой Напряжение и мощность в симметричной трехфазной нагрузке при соединении треугольником Расчет симметричной нагрузки по известным напряжению, току и коэффициенту мощности Импеданс нагрузки Z Расчет тока и мощности по известным напряжению и нагрузке Фазный ток Преобразование из прямоугольных координат в полярные и наоборот Активное Rph и реактивное Xph сопротивление нагрузки Импеданс конденсатора и катушки индуктивности Параллельная нагрузка RLC Последовательная нагрузка RLC Примеры расчетов Пример 1. Пример 2. Расчет мощности и тока по заданным напряжению и нагрузке Пример 3. Расчет мощности и тока по заданным напряжению и нагрузке Пример 4. Расчет мощности и нагрузки по заданным напряжению и току Пример 5. Расчет мощности и тока по заданным напряжению и нагрузке Пример 6. Расчет мощности и тока по заданным напряжению и нагрузке Пример 7. Расчет мощности и нагрузки по заданным напряжению и току Однофазную сеть можно сравнить с проселочной дорогой — оно не позволяет получить большую мощность. Трехфазную сеть можно сравнить с автомагистралью — она обычно имеется в промышленных зданиях для питания оборудования большой мощности Установленный на столбе однофазный трансформатор, предназначенный для подачи электроэнергии в индивидуальные жилые дома (Канада) Термин «фаза» относится к распределению электрической энергии. Для далеких от физики людей однофазную и трехфазную сеть можно сравнить с иллюстрациями выше. В однофазной сети используются два или три провода. Всегда имеется один фазный провод и один провод, называемый нейтралью или нулевым проводом. Ток течет между этими двумя проводами. Если однофазная сеть содержит заземляющий провод, то используется трехпроводная сеть. Однофазная сеть хороша в тех случаях, когда типичными нагрузками являются чисто активные потребители, например, традиционные лампы накаливания и электрические обогреватели. Установленная на столбе группа из трех трансформаторов, обеспечивающая трехфазное питание небольшой промышленной установки В трехфазной сети используются три провода, называемые фазными или просто фазами. По этим проводам текут синусоидальные токи со сдвигом фаз относительно друг друга на 120°. В трехфазной системе может быть три или четыре провода. Если имеется четвертый провод, то трехфазную сеть можно использовать для подачи однофазного питания (три линии), например, в индивидуальные жилые дома. При этом от каждой фазы в нагрузку (дом) подается примерно одинаковая мощность. Нейтральный провод часто имеет меньшее сечение, потому что фазные токи взаимно гасятся и по нейтральному проводу обычно течет совсем небольшой ток. Трехфазная система обеспечивает постоянную передачу мощности в нагрузку, что позволяет подключить более высокую нагрузку. Определения и формулыГенерация трехфазного токаВ простейшем трехфазном генераторе имеется три идентичных обмотки, расположенных под углом 120° по отношению друг к другу. Здесь Up — пиковое значение (амплитуда) напряжения в вольтах, ω — угловая частота в радианах в секунду и t — время в секундах. Напряжение, наведенное в обмотке 2, отстает от напряжения в обмотке 1 на 120°, а напряжение, наведенное в обмотке 3, отстает от напряжения в обмотке 1 на 240°. Ниже на рисунке приведены векторные диаграммы и формы колебаний напряжений генератора: Если коэффициент мощности равен единице, то в каждой фазе трехфазной системы напряжение, ток и мощность сдвинуты относительно друг друга на 120°; последовательность фаз на этом рисунке U₁, U₂, U₃, потому что U₁ опережает U₂, U₂ опережает U₃, и U₃ опережает U₁. Преимущества трехфазных систем
Последовательность фазПоследовательность фаз определяется временем, при котором напряжения трех фаз достигают положительного максимума. Последовательность фаз называют также порядком фаз. На рисунке выше последовательность фаз 1-2-3, так как фаза 1 достигает положительного максимума раньше, чем фаза 2, а фаза 3 достигает положительного максимума позже фазы 2. Для определения порядка фаз на векторной диаграмме нужно знать, что векторы всегда вращаются против часовой стрелки. Например, на этих трех чертежах последовательность чередования фаз снова U₁, U₂, U₃: Фазное напряжение и фазный токФазным называется напряжение между каждым из трех фазных проводов и нейтралью. Его также называют напряжением между фазой и нейтралью. Ток, которые течет в нагрузке между фазным проводом и нейтралью, называется фазным током. Линейное напряжение и токЛинейным называется напряжение между любыми двумя фазами (линиями). Ток, протекающий в каждой из линий, называется линейным. Симметричные и несимметричные системы и нагрузкиВ сбалансированной (симметричной) трехфазной системе токи во всех трех фазах равны, а сумма всех токов равна нулю, поэтому ток по нейтрали не течет. То же можно сказать и о токах в симметричной системе: Если три нагрузки, присоединенные к трем линиям, имеют одинаковую величину и коэффициент мощности, она также называются сбалансированными или симметричными. Линейные и нелинейные нагрузкиВ линейных нагрузках в цепях переменного тока напряжения и токи имеют синусоидальную форму и в любое время ток в нагрузке прямо пропорционален напряжению на ней. Примерами линейных нагрузок являются нагреватели, лампы накаливания. конденсаторы и катушки индуктивности. Все линейные нагрузки подчиняются закону Ома. В линейных нагрузка коэффициент мощности равен cos φ. Подробнее о нелинейных нагрузках — в нашем Калькуляторе активной и реактивной мощности. В нелинейных нагрузках ток не пропорционален напряжению и содержит гармоники основной частоты 50 или 60 Гц. Соединение треугольником и звездойТри обмотки трехфазного генератора можно присоединить к нагрузке шестью проводами, по два на обмотку. Для уменьшения количества проводов обмотки присоединяются к нагрузке тремя или четырьмя проводами. Эти два способа подключения называются треугольником (Δ) и звездой (Y). В соединении треугольником начало каждой обмотки соединяется с концом следующей обмотки. Таким образом энергию можно передавать только по трем проводам. Соединение звездой (слева) и треугольником (справа) В симметричной соединении треугольником напряжения равны по амплитуде, отличаются по фазе на 120° и их сумма равна нулю: В симметричной четырехпроводной системе соединения звездой с тремя одинаковыми подключенными к каждой фазе нагрузками мгновенное значение тока, текущего по нейтрали, равно сумме трех фазных токов i₁, i₂, и i₃, которые имеют одинаковые амплитуды Ip и сдвинуты по фазе на 120°: Напряжение и мощность в симметричной трехфазной нагрузке при соединении звездойСоединение звездой; I₁, I₂, и I₃ — фазные токи, которые равны линейным токам Полная мощность в трехфазной системе является суммой мощностей, потребляемых нагрузками в каждой из трех фаз. Здесь φ — разность фаз между током и напряжением. Поскольку в трехфазном соединении звездой фазное Uph и линейное среднеквадратичное напряжение UL связаны как а среднеквадратичное значения линейного и фазного токов равны полная активная мощность определяется следующим уравнением: Полная реактивная мощность равна Комплексная мощность: И, наконец, полная мощность в трех фазах определяется формулой: Напряжение и мощность в симметричной трехфазной нагрузке при соединении треугольникомСоединение треугольником; I13, I23, и I32 — фазные токи, а I1, I2, и I3 — линейные токи; при этом IL = √3∙Iph При соединении треугольником нейтральный проводник отсутствует и конец одной обмотки генератора соединяется с началом следующей обмотки. При соединении треугольником фазные токи — это токи, текущие через фазные нагрузки. Мы рассматриваем симметричную систему, поэтому фазные среднеквадратичные значения токов Ip1, Ip2 и Ip3 по амплитуде равны (Ip) и отличаются по фазе на 120°: Как мы уже упоминали, общая мощность в трехфазной системе — это сумма мощностей, потребляемых в нагрузках трех фаз: где φ — сдвиг фаз между током и напряжением. Поскольку при соединении треугольником среднеквадратичные значения фазного Uph и линейного напряжений UL равны, а среднеквадратичные значения линейного и фазного токов связаны формулой активная мощность определяется следующим уравнением: Полная реактивная мощность равна Комплексная мощность: И полная мощность в трех фазах: Отметим, что приведенные выше уравнения для мощности при соединении звездой и треугольником одинаковые. То, что эти формулы мощности для звезды и треугольника одинаковые, иногда приводит к ошибочным выводам о том, что можно соединить обмотки одного и того же электродвигателя звездой или треугольником и потребляемая мощность (и ток!) не изменятся. Конечно, это неправильно. И если мы в калькуляторе соединение звездой изменим на треугольник, не изменяя нагрузку, мы увидим, что мощность и потребляемый ток изменятся. Рассмотрим пример. Трехфазный электродвигатель подключен по схеме треугольника и работает на полной номинальной мощности при линейном напряжении UL и линейном токе IL. Полная мощность в вольт-амперах (ВА) равна Затем обмотки того же двигателя соединили звездой. Линейное напряжение, приложенное к каждой обмотке, уменьшилось в 1/1,73 раза, при этом сетевое напряжение осталось прежним. Ток в каждой обмотке уменьшился в 1/1,73 раза по сравнению с током, потребляемым при соединении треугольником. Таким образом, полная мощность при соединении звездой равна одной трети мощности при соединении треугольником для нагрузки с тем же импедансом. Очевидно, что полный момент двигателя, обмотки которого соединены звездой, будет в три раза меньше момента того же двигателя при соединении обмоток треугольником. Иными словами, хотя новая мощность для соединения звездой рассчитывается по той же формуле, что и для треугольника, в расчет нужно вставить другие величины, а именно, напряжение и ток. уменьшенные в 1,73 раза (то есть в квадратный корень из 3). Расчет симметричной нагрузки по известным напряжению, току и коэффициенту мощностиДля расчета симметричной нагрузки (одинаковой в каждой фазе) по известным напряжению, току и коэффициенту мощности (опережающему или отстающему) используются следующие формулы: Импеданс нагрузкиZВ полярной форме: В комплексной форме: Расчет тока и мощности по известным напряжению и нагрузкеФазный токПо закону Ома, имеем: Преобразование из прямоугольных координат в полярные и наоборотДля преобразования из прямоугольных координат R, X в полярные координаты |Z|, φ, используйте следующие формулы: Треугольник импеданса В этих формулах R всегда положительно, а X положительно для индуктивной нагрузки (ток отстает от напряжения) и отрицательно для емкостной нагрузки (ток опережает напряжение). Преобразование из полярных координат r, φ в прямоугольные coordinates x, y, выполняется по формулам: АктивноеRph и реактивное Xph сопротивление нагрузкиИмпеданс конденсатора и катушки индуктивностиПараллельная нагрузка RLCПараллельное соединение RLC Для расчета используйте наш Калькулятор импеданса параллельной RLC-цепи. Последовательная нагрузка RLCПоследовательное соединение RLC Для расчета используйте наш Калькулятор импеданса последовательной RLC-цепи Более подробную информацию о нагрузки в форме RLC-цепи вы найдете в наших калькуляторах для расчета импеданса:
Примеры расчетовПример 1. Расчет мощности и тока по заданным напряжению и нагрузке Расчет мощности и тока по заданным напряжению и нагрузкеИндуктивная нагрузка из трех цепей с равными импедансами Zph = 5+j3 Ом подключена звездой к трехфазной сети с линейным напряжением 400 В 50 Гц. Рассчитать фазное напряжение Uph, фазовый угол φph, фазный ток Iph, линейный ток IL, активную P, реактивную Q, полную |S|, и комплексную S мощности. Пример 2. Расчет мощности и тока по заданным напряжению и нагрузкеИндуктивная нагрузка из трех цепей с равными импедансами Zph = 15 ∠60° Ом подключена звездой к трехфазной сети с фазным напряжением (между фазой и нейтралью) 110 В 50 Гц. Определить тип нагрузки (емкостная или индуктивная) фазное напряжение Uph, фазовый угол φph, фазный ток Iph, линейный ток IL, активную P, реактивную Q, полную |S|, и комплексную S мощности. Пример 3. Расчет мощности и тока по заданным напряжению и нагрузкеИндуктивная нагрузка из трех обмоток с равными импедансами и эквивалентной схемой в виде включенных последовательно сопротивления Rph = 20 Ом и индуктивности Lph = 440 мГн подключена звездой к трехфазной сети с фазным напряжением (между фазой и нейтралью) 230 В 50 Гц. Рассчитайте фазное напряжение Uph, фазовый угол φph, фазный ток Iph, линейный ток IL, активную P, реактивную Q, полную |S|, и комплексную S мощности. Найти линейный ток и потребляемую мощность для той же нагрузки, но соединенной треугольником. Совет: Для определения импеданса каждой обмотки воспользуйтесь Калькулятором последовательной RL-цепи. Пример 4. Расчет мощности и нагрузки по заданным напряжению и токуСимметричный трехфазный генератор подает фазное напряжение 230 В на включенную звездой нагрузку с отстающим (активно-индуктивным) коэффициентом мощности 0,75. Пример 5. Расчет мощности и тока по заданным напряжению и нагрузкеНагрузка, состоящая из трех одинаковых обмоток, имеющих сопротивление Rph = 10 Ом и индуктивность Lph = 310 мГн, подключена треугольником к трехфазной сети с напряжением между фазой и нейтралью 120 В, 60 Гц. Рассчитайте линейное напряжение UL, фазовый угол φph, фазный ток Iph, линейный ток IL, активную P, реактивную Q, полную |S|, и комплексную S мощности. Пример 6. Расчет мощности и тока по заданным напряжению и нагрузкеНагрузка из трех цепей с равными импедансами Zph = 7 – j5 Ом подключена треугольником к трехфазной сети с линейным напряжением (между двумя фазами) 208 В 60 Гц. Определить тип нагрузки (резистивно-емкостная или резистивно-индуктивная) фазное напряжение Uph, фазовый угол φph, фазный ток Iph, линейный ток IL, активную P, реактивную Q, полную |S|, и комплексную S мощности. Пример 7. Расчет мощности и нагрузки по заданным напряжению и токуСимметричная нагрузка подключена звездой к симметричному трехфазному генератору с линейным (между двумя фазами) напряжением 208 В 60 Гц. Автор статьи: Анатолий Золотков Вас могут заинтересовать и другие калькуляторы из группы «Электротехнические и радиотехнические калькуляторы»:Калькулятор резистивно-емкостной цепи Калькулятор параллельных сопротивлений Калькулятор параллельных индуктивностей Калькулятор емкости последовательного соединения конденсаторов Калькулятор импеданса конденсатора Калькулятор импеданса катушки индуктивности Калькулятор взаимной индукции Калькулятор взаимоиндукции параллельных индуктивностей Калькулятор взаимной индукции — последовательное соединение индуктивностей Калькулятор импеданса параллельной RC-цепи Калькулятор импеданса параллельной LC-цепи Калькулятор импеданса параллельной RL-цепи Калькулятор импеданса параллельной RLC-цепи Калькулятор импеданса последовательной RC-цепи Калькулятор импеданса последовательной LC-цепи Калькулятор импеданса последовательной RL-цепи Калькулятор импеданса последовательной RLC-цепи Калькулятор аккумуляторных батарей Калькулятор литий-полимерных аккумуляторов для дронов Калькулятор индуктивности однослойной катушки Калькулятор индуктивности плоской спиральной катушки для устройств радиочастотной идентификации (RFID) и ближней бесконтактной связи (NFC) Калькулятор расчета параметров коаксиальных кабелей Калькулятор светодиодов. Калькулятор цветовой маркировки резисторов Калькулятор максимальной дальности действия РЛС Калькулятор зависимости диапазона однозначного определения дальности РЛС от периода следования импульсов Калькулятор радиогоризонта и дальности прямой радиовидимости РЛС Калькулятор радиогоризонта Калькулятор эффективной площади антенны Симметричный вибратор Калькулятор частоты паразитных субгармоник (алиасинга) при дискретизации Калькулятор мощности постоянного тока Калькулятор мощности переменного тока Калькулятор пересчета ВА в ватты Калькулятор преобразования алгебраической формы комплексного числа в тригонометрическую Калькулятор коэффициента гармонических искажений Калькулятор законов Ома и Джоуля — Ленца Калькулятор времени передачи данных Калькулятор внутреннего сопротивления элемента питания батареи или аккумулятора Калькуляторы Электротехнические и радиотехнические калькуляторы |
Линейно зависимые (независимые) векторы: определение, пример
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel. ru Математика Геометрия Линейная зависимость векторов
ru Математика Геометрия Линейная зависимость векторов
В данной публикации мы рассмотрим, что такое линейная комбинация векторов, какие векторы являются линейно зависимыми и независимыми, а также разберем пример задачи по этой теме.
- Определение линейной зависимости векторов
- Пример задачи
Определение линейной зависимости векторов
Линейная комбинация векторов a1, …, an – это вектор, заданный выражением x1a1 + … + xnan, где x1, …, xn – коэффициенты.
Представленная комбинация может быть:
- Тривиальная – все коэффициенты x1, …, xn равняются нулю.
- Нетривиальная – хотя бы один из коэффициентов x1, …, xn не равен нулю.
Векторы a1, …, an линейно независимы, если только их тривиальная комбинация равна нулевому вектору. То есть:
То есть:
a1, …, an линейно независимы, если x1a1 + … + xnan = 0, исключительно когда x1 = 0, …, xn = 0.
Векторы a1, …, an линейно зависимы, если есть такая их нетривиальная комбинация, которая равняется нулевому вектору.
Свойства линейно зависимых векторов
- Линейно зависимые векторы в двух/трехмерном пространстве коллинеарны. Справедливо и обратное утверждение.
- В трехмерном пространстве три линейно зависимых вектора компланарны. Утверждение верно и в обратную сторону.
Пример задачи
Проверим, являются ли векторы a = {1; 2} и b = {2; 4} линейно зависимыми.
Решение:
Нам требуется найти значения коэффициентов, при которых линейная комбинация этих векторов равняется нулевому вектору.
xa + yb = 0
Полученное векторное уравнение можно представить в виде системы линейных уравнений:
Данная система имеет множество решений, при этом x = -2y.
То есть существует ненулевая комбинация коэффициентов x и y, при которых комбинация векторов a и b равняется нулевому вектору. Следовательно, заданные векторы линейно зависимы.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Линейная независимость
let A = { V 1 , V 2 ,…, V R } BE VECTOR .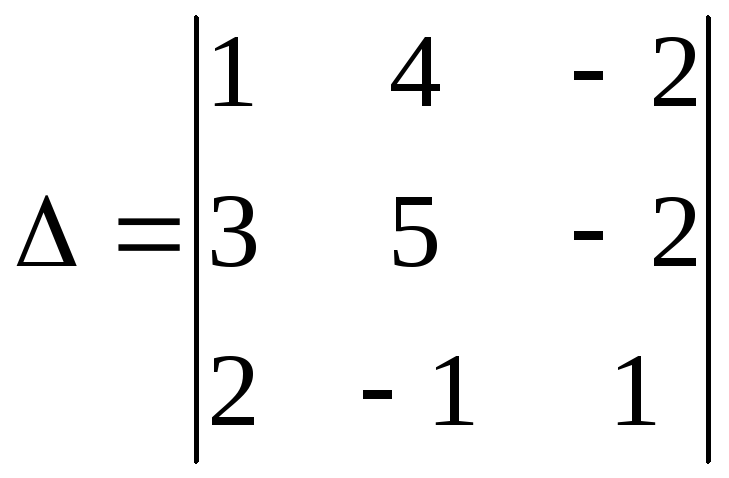 Если r > 2 и хотя бы один из векторов в A может быть записан как линейная комбинация других, то A называется линейно зависимым . Мотивация для этого описания проста: по крайней мере один из векторов зависит (линейно) от других. С другой стороны, если нет вектора в Говорят, что является линейно независимым набором . Также довольно часто говорят, что «векторы линейно зависимы (или независимы)», а не «множество, содержащее эти векторы, линейно зависимо (или независимо)».
Если r > 2 и хотя бы один из векторов в A может быть записан как линейная комбинация других, то A называется линейно зависимым . Мотивация для этого описания проста: по крайней мере один из векторов зависит (линейно) от других. С другой стороны, если нет вектора в Говорят, что является линейно независимым набором . Также довольно часто говорят, что «векторы линейно зависимы (или независимы)», а не «множество, содержащее эти векторы, линейно зависимо (или независимо)».
Пример 1 : Векторы v 1 = (2, 5, 3), v 2 = (1, 1, 1) и v 3 − = (4, 5, 2, 0) линейно независимы?
Если ни один из этих векторов не может быть выражен в виде линейной комбинации двух других, то векторы независимы; в противном случае они зависимы. Если, например, V 3 была линейной комбинацией V 1 и V 2 , затем существуют скаляры K 1 и K 2 Такие, что K . V 2 Такая, что K . V 2 Такая K . + к 2 v 2b = v 3 . Это уравнение выглядит как
V 2 Такая, что K . V 2 Такая K . + к 2 v 2b = v 3 . Это уравнение выглядит как
, что эквивалентно
.Однако это непоследовательная система. Например, вычитание первого уравнения из третьего дает k 1 = −4, и подстановка этого значения в первое или третье уравнение дает k 2 = 12. −4, 12) не удовлетворяет второму уравнению. Вывод состоит в том, что v 3 не является линейной комбинацией v 1 и v 2 . Аналогичный аргумент показал бы, что v 1 не является линейной комбинацией 9.0039 v 2 и v 3 и что v 2 не является линейной комбинацией v 1
 Таким образом, эти три вектора действительно линейно независимы.
Таким образом, эти три вектора действительно линейно независимы.Альтернативное — но полностью эквивалентное и часто более простое — определение линейной независимости звучит следующим образом. Набор векторов v 1 , v 2 , …, v R из R N линейно независимы, если единственные скарры, которые удовлетворяют K 1 = K 2 = ⃛ = K R 9008 9008 = 0. 0. 0. 0. 0. 0. 0. 0. 0,00007 2 = ⃛ = K R 9008 9008 =. называется тривиальной линейной комбинацией . Если, с другой стороны, существует нетривиальная линейная комбинация, которая дает нулевой вектор, то векторы зависимы.
Пример 2 : Используйте это второе определение, чтобы показать, что векторы из Примера 1— v 1 = (2, 5, 3), v 2 = (1, 1, 1), v 3 = (4, −2, 0) — линейно независимы .
Эти векторы линейно независимы, если единственные скаляры, удовлетворяющие
есть k 1 = k 2 = k 3 = 0. Но (*) эквивалентно однородной системе
Сокращение строки матрицы коэффициентов дает
Эта ступенчатая форма матрицы позволяет легко видеть, что k 3 = 0, откуда следует k 2 = 0 и k 1 = 0. Таким образом, уравнение (**) — а значит, (*) — удовлетворяет только k 1 = k 2 = k 3 = 0, что доказывает линейную независимость заданных векторов.
Пример 3 : Векторы v 1 = (4, 1, −2), v 2 = (−3, 0, 1) и v 3 (1, −2, 1) линейно независимы?
Уравнение K 1 V 1 + K 2 V 2 + K 3 V 3 . 9004 9004. 4.9004. система
9004 9004. 4.9004. система
Сокращение строки матрицы коэффициентов дает строку нулей:
Поскольку общее решение будет содержать свободную переменную, однородная система (*) имеет нетривиальные решения. Это показывает, что существует нетривиальная линейная комбинация векторов V 1 , V 2 и V 3 , которые дают нулевой вектор: V 1 , V 77777777777. V 1 , V 77777777777779. 1 , V. 2 и v 3 зависимы.
Пример 4 : Существует ровно одно значение c такие, что векторы
линейно зависимы. Найдите это значение c и определите нетривиальную линейную комбинацию этих векторов, которая равна нулевому вектору.
Как и прежде, рассмотрим однородную систему
и выполните следующие элементарные операции со строками над матрицей коэффициентов:
Для получения нетривиальных решений в этой ступенчатой форме матрицы должна быть хотя бы одна строка нулей.
нужен. Из операций со строками, выполненных выше, это уравнение эквивалентно
Последняя строка подразумевает, что k 4 можно взять в качестве свободной переменной; пусть k 4 = t . Затем в третьей строке указано
.Вторая строка подразумевает
и, наконец, первая строка дает
Таким образом, общее решение однородной системы (**) — и (*) — есть
на любой т на р . Выбор T = 1 , например, дает K 1 , K 2 , K 3 , K 4 SO
Выбор T = 1 , например, дает K 1 , K 2 , K 3 , K 4 SO
есть линейная комбинация векторов v 1 , v 2 , v 3 и v 4 , равная нулю. Чтобы убедиться, что
просто замените и упростите:
бесконечно многие другие нетривиальные линейные комбинации V 1 , V 2 , V 3
 v 4 .
v 4 .Если набор векторов из R n содержит более n векторов, то легко ответить на вопрос о его линейной независимости. Если С = { v 1 , v 2 , …, v m } is a collection of vectors from R n and m > n , then C должны быть линейно зависимы. Чтобы понять, почему это так, обратите внимание, что уравнение
эквивалентно матричному уравнению
Так как каждый вектор v j содержит n компонентов, это матричное уравнение описывает систему с m неизвестными и n уравнений. Любая однородная система с большим количеством неизвестных, чем уравнений, имеет нетривиальные решения, результат, который применим здесь, поскольку m > n . Поскольку уравнение (*) имеет нетривиальные решения, векторы в
Поскольку уравнение (*) имеет нетривиальные решения, векторы в
Пример 5 : Набор векторов {2 i − j , i + j , − i + 4j } from R 2 линейно зависимы, потому что любой набор из 3 (или более) векторов из R 2 должен быть зависим. Similarly, the collection { i + j − k , 2i − 3j + k , i − 4k , − 2j ,− 5i + j − 3k } векторов из R 3 не может быть независимым, потому что любой набор из 4 или более векторов из R 3 является зависимым.
Пример 6 : любая коллекция векторов от R N , который содержит нулевой вектор, автоматически зависит, для IF { V 1 , V 2 , V 77777. 7777777. 777777777777777 2 , V 77777. 77 700077 700077 700077. r−1 , 0 } такой набор, то для любых k ≠ 0,
— нетривиальная линейная комбинация, дающая нулевой вектор.
Линейная независимость
Цели
- Понять концепцию линейной независимости.
- Изучите два критерия линейной независимости.
- Понимание взаимосвязи между линейной независимостью и сводными столбцами/свободными переменными.
- Рецепт: проверить, является ли набор векторов линейно независимым / найти уравнение линейной зависимости.
- Изображение: является ли набор векторов в R2 или R3 линейно независимым или нет.

- Словарь: отношение линейной зависимости / уравнение линейной зависимости .
- Основные словарные слова: линейно независимые , линейно зависимые .
Иногда диапазон набора векторов «меньше», чем вы ожидаете от количества векторов, как на рисунке ниже. Это означает, что (по крайней мере) один из векторов является избыточным: его можно удалить, не затрагивая диапазон. В настоящем разделе мы формализуем эту идею в понятии линейная независимость .
Span{v,w}vwSpan{u,v,w}vwuFigure1Изображения наборов линейно зависимых векторов. Обратите внимание, что в каждом случае один вектор находится в диапазоне других, поэтому диапазон не увеличивается.Определение
Набор векторов {v1,v2,…,vk} является линейно независимым , если векторное уравнение
x1v1+x2v2+···+xkvk=0
имеет только тривиальное решение x1=x2=···=xk=0. Множество {v1,v2,…,vk} линейно зависимо иначе.
Другими словами, {v1,v2,…,vk} линейно зависима, если существуют числа x1,x2,…,xk, не все равные нулю, такие, что
x1v1+x2v2+···+xkvk=0.
Это называется отношением линейной зависимости или уравнением линейной зависимости .
Обратите внимание, что понятия линейной зависимости и линейной независимости относятся к набору векторов . Нет смысла говорить что-то вроде «этот вектор линейно зависит от этих других векторов» или «эта матрица линейно независима».
Пример(Проверка линейной зависимости)
Пример (Проверка линейной независимости)
Пример (Векторная параметрическая форма)
Приведенные выше примеры приводят к следующему рецепту.
Рецепт: Проверка линейной независимости
Набор векторов {v1,v2,…,vk} линейно независим тогда и только тогда, когда векторное уравнение
x1v1+x2v2+···+xkvk=0
имеет только тривиальное решение тогда и только тогда, когда матричное уравнение Ax=0 имеет только тривиальное решение, где A — матрица со столбцами v1,v2,. ..,vk:
..,vk:
А=Е|||v1v2···vk|||F.
Это верно тогда и только тогда, когда A имеет точку поворота в каждом столбце.
Решение матричного уравнения Ax=0 либо проверяет, что столбцы v1,v2,…,vk линейно независимы, либо создает отношение линейной зависимости, заменяя любые ненулевые значения для свободных переменных.
(Напомним, что Ax=0 имеет нетривиальное решение тогда и только тогда, когда A имеет столбец без опорной точки: см. это наблюдение в разделе 2.4.)
Предположим, что A имеет больше столбцов, чем строк. Тогда A не может иметь опорную точку в каждом столбце (она имеет не более одной опорной точки на строку), поэтому ее столбцы автоматически линейно зависимы.
Широкая матрица (матрица с большим количеством столбцов, чем строк) имеет линейно зависимые столбцы.
Например, четыре вектора в R3 автоматически линейно зависимы. Обратите внимание, что длинная матрица может иметь или не иметь линейно независимых столбцов.
Факты о линейной независимости
- Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны, т.
 е. один из них скалярно кратен другому.
е. один из них скалярно кратен другому. - Любой набор, содержащий нулевой вектор, линейно зависим.
- Если подмножество {v1,v2,…,vk} линейно зависимо, то {v1,v2,…,vk} также линейно зависимо.
Что касается первого факта, обратите внимание, что нулевой вектор кратен любому вектору, поэтому он коллинеарен любому другому вектору. Следовательно, факты 1 и 2 согласуются друг с другом.
В этом подразделе мы даем два критерия линейной независимости набора векторов. Имейте в виду, однако, что фактическое определение приведено выше.
Теорема
Набор векторов {v1,v2,…,vk} линейно зависим тогда и только тогда, когда один из векторов находится в промежутке других.
Любой такой вектор может быть удален без изменения диапазона.
Доказательство
Предположим, например, что v3 находится в Span{v1,v2,v4}, поэтому у нас есть уравнение вида
v3=2v1−12v2+6v4.Мы можем вычесть v3 из обеих частей уравнения, чтобы получить
0=2v1−12v2−v3+6v4.
Это отношение линейной зависимости.
В этом случае любая линейная комбинация v1,v2,v3,v4 уже является линейной комбинацией v1,v2,v4:
x1v1+x2v2+x3v3+x4v4=x1v1+x2v2+x3G2v1-12v2+6v4H+x4v4=(x1+2×3)v1+Gx2-12x3Hv2+(x4+6)v4.Следовательно, Span{v1,v2,v3,v4} содержится в Span{v1,v2,v4}. Любая линейная комбинация v1,v2,v4 также является линейной комбинацией v1,v2,v3,v4 (с коэффициентом v3, равным нулю), поэтому Span{v1,v2,v4} также содержится в Span{v1, v2,v3,v4}, а значит, они равны.
В другом направлении, если у нас отношение линейной зависимости типа
0=2v1−12v2+v3−6v4,, то мы можем переместить любой ненулевой член в левую часть уравнения и разделить на его коэффициент:
v1=12G12v2−v3+6v4H.Это показывает, что v1 находится в Span{v2,v3,v4}.
Мы предоставляем читателю возможность обобщить это доказательство для любого набора векторов.
Предупреждение
В линейно зависимом множестве {v1,v2,…,vk} вообще неверно, что любой вектор vj находится в промежутке других, а только то, что хотя бы один из из них.
Например, множество CA10B,A20B,A01BD линейно зависимо, но A01B не находится в промежутке двух других векторов. Также см. этот рисунок ниже.
Предыдущая теорема уточняет, в каком смысле множество линейно зависимых векторов является избыточным.
Теорема (критерий увеличения диапазона)
Набор векторов {v1,v2,…,vk} линейно независим тогда и только тогда, когда для каждого j вектор vj не лежит в Span{v1,v2,…,vj−1}.
Доказательство
Это эквивалентно тому, чтобы показать, что {v1,v2,…,vk} линейно зависимы тогда и только тогда, когда vj находится в Span{v1,v2,…,vj−1} для некоторого j. Импликация «если» является непосредственным следствием предыдущей теоремы. Предположим тогда, что {v1,v2,…,vk} линейно зависимы. Это означает, что некоторые vj находятся в промежутке других. Выберите наибольшее такое j. Мы утверждаем, что этот vj находится в Span{v1,v2,…,vj−1}. Если нет, то
vj=x1v1+x2v2+···+xj−1vj−1+xj+1vj+1+···+xkvk
, где не все xj+1,. ..,xk равны нулю. Предположим для простоты, что xkA=0. Затем мы можем переставить:
..,xk равны нулю. Предположим для простоты, что xkA=0. Затем мы можем переставить:
Это говорит о том, что vk находится в промежутке {v1,v2,…,vp−1}, что противоречит нашему предположению, что vj является последним вектором в промежутке других.
Мы можем перефразировать это следующим образом:
Если вы создаете набор векторов, добавляя по одному вектору за раз, и если диапазон увеличивается каждый раз, когда вы добавляете вектор, то ваш набор является линейно независимым.
Набор, содержащий один вектор {v}, линейно независим, когда vA=0, поскольку xv=0 подразумевает x=0.
Span{v}vНабор из двух неколлинеарных векторов {v,w} линейно независим:
- Ни один из них не находится в промежутке другого, поэтому мы можем применить первый критерий.
- Диапазон стал больше, когда мы добавили w, поэтому мы можем применить критерий увеличения диапазона.
Набор из трех векторов {v,w,u} ниже линейно зависим:
- u находится в Span{v,w}, поэтому мы можем применить первый критерий.

- Диапазон не увеличился, когда мы добавили u, поэтому мы можем применить критерий увеличения диапазона.
На рисунке ниже обратите внимание, что v находится в Span{u,w}, а w находится в Span{u,v}, поэтому мы можем удалить любой из трех векторов, не уменьшая диапазон.
Span{v}Span{w}Span{v,w}vwuДва коллинеарных вектора всегда линейно зависимы:
- w находится в Span{v}, поэтому мы можем применить первый критерий.
- Диапазон не увеличился, когда мы добавили w, поэтому мы можем применить критерий увеличения диапазона.
Эти три вектора {v,w,u} линейно зависимы: действительно, {v,w} уже линейно зависимы, поэтому мы можем использовать третий факт.
Span{v}vwuInteractive: Линейная независимость двух векторов в R2
Interactive: Линейная зависимость трех векторов в R2
Два приведенных ниже вектора {v,w} линейно независимы, поскольку они не лежат на одной прямой.
vwSpan{v}Span{w} Три приведенных ниже вектора {v,w,u} линейно независимы: диапазон стал больше, когда мы добавили w, затем еще раз, когда мы добавили u, поэтому мы можем применить критерий увеличения диапазона.
Три компланарных вектора {v,w,u} ниже линейно зависимы:
- u находится в Span{v,w}, поэтому мы можем применить первый критерий.
- Диапазон не увеличился, когда мы добавили u, поэтому мы можем применить критерий увеличения диапазона.
Обратите внимание, что три вектора линейно зависимы тогда и только тогда, когда они компланарны . В самом деле, {v,w,u} линейно зависимы тогда и только тогда, когда один вектор находится в промежутке двух других, который является плоскостью (или линией) (или {0}).
Четыре приведенных ниже вектора {v,w,u,x} линейно зависимы: они являются столбцами широкой матрицы. Обратите внимание, однако, что u не содержится в Span{v,w,x}. См. это предупреждение.
vwuxSpan{v}Span{w}Span{v,w}Рисунок 20. Векторы {v,w,u,x} линейно зависимы, но u не содержится в Span{v,w,x}.Interactive: Линейная независимость двух векторов в R3
Interactive: Линейная независимость трех векторов в R3
В свете этого важного замечания и этого критерия естественно задаться вопросом, какие столбцы матрицы являются избыточными, т. е. какие столбцы мы можем удалить, не затрагивая диапазон столбцов.
е. какие столбцы мы можем удалить, не затрагивая диапазон столбцов.
Теорема
Пусть v1,v2,…,vk — векторы в Rn, и рассмотрим матрицу
А=Е|||v1v2···vk|||F.
Затем мы можем удалить столбцы A без поворотов (столбцы, соответствующие свободным переменным), без изменения Span{v1,v2,…,vk}.
Сводные столбцы линейно независимы, поэтому мы не можем удалить другие столбцы без изменения диапазона.
Доказательство
Если матрица представлена в виде редуцированного эшелона строк:
А=Е102001300001Ф
, то столбец без опоры будет виден в диапазоне опорных столбцов:
Э230Ф=2Э100Ф+3Э010Ф+0Э001Ф,
, а опорные столбцы линейно независимы:
E000F=x1E100F+x2E010F+x4E001F=Ex1x2x4F=⇒x1=x2=x4=0.
Если матрица не в сокращенной ступенчатой форме строк, то мы уменьшаем строки:
A=E1723324160-1-2-84FRREF—→E102001300001F.
Следующие два векторных уравнения имеют один и тот же набор решений, поскольку они получены из эквивалентных строк матриц:
x1E12-1F+x2E74-2F+x3E2316-8F+x4E304F=0x1E100F+x2E010F+x3E230F+x4E001F=0.
Делаем вывод, что
E2316-8F=2E12-1F+3E74-2F+0E304F
и что
x1E12-1F+x2E74-2F+x4E304F=0
имеет только тривиальное решение.
Обратите внимание, что необходимо уменьшить строку A, чтобы определить, какие столбцы являются ее основными столбцами. Однако диапазон столбцов сокращенной матрицы строк обычно равен , а не и равен диапазону столбцов матрицы A: необходимо использовать сводные столбцы исходной матрицы из . См. теорему в Разделе 2.7 для переформулировки вышеуказанной теоремы.
Пример
Сводные столбцы и измерение
Пусть d будет количеством опорных столбцов в матрице
А=Е|||v1v2···vk|||F.
- Если d=1, то Span{v1,v2,…,vk} является линией.
- Если d=2, то Span{v1,v2,…,vk} является плоскостью.
- Если d=3, то Span{v1,v2,…,vk} является 3-мерным пространством.
- и так далее.
Число d называется размерностью. Мы обсуждали это понятие в этом важном примечании в разделе 2.

 Обратите внимание также на примеры в конце описания калькулятора.
Обратите внимание также на примеры в конце описания калькулятора. Для расчёта мощности и нагрузки по известным напряжению и току выберите тип соединения (звезда или треугольник) и введите напряжение (линейное ИЛИ фазное), ток (линейный ИЛИ фазный) и коэффициент мощности. Нажмите на кнопку Рассчитать. Мощность и параметры нагрузки будут рассчитаны автоматически. Также можно, рассчитать мощность и ток по известным напряжению и нагрузке. Для этого выберите тип соединения (звезда ИЛИ треугольник) и введите напряжение (линейное ИЛИ фазное) и импеданс нагрузки в каждой фазе в комплексной ИЛИ полярной форме. Нажмите на кнопку Рассчитать. Калькулятор автоматически рассчитает мощность и ток.
Для расчёта мощности и нагрузки по известным напряжению и току выберите тип соединения (звезда или треугольник) и введите напряжение (линейное ИЛИ фазное), ток (линейный ИЛИ фазный) и коэффициент мощности. Нажмите на кнопку Рассчитать. Мощность и параметры нагрузки будут рассчитаны автоматически. Также можно, рассчитать мощность и ток по известным напряжению и нагрузке. Для этого выберите тип соединения (звезда ИЛИ треугольник) и введите напряжение (линейное ИЛИ фазное) и импеданс нагрузки в каждой фазе в комплексной ИЛИ полярной форме. Нажмите на кнопку Рассчитать. Калькулятор автоматически рассчитает мощность и ток. Расчет мощности и тока по заданным напряжению и нагрузке
Расчет мощности и тока по заданным напряжению и нагрузке Однофазная сеть — как проселочная дорога, ее возможности по мощности невысоки и используется она в основном в жилых домах и квартирах. Однофазная сеть проста и экономична. Однако однофазную сеть нельзя использовать для питания эффективных трехфазных электродвигателей. С другой стороны, трехфазная сеть — как автомагистраль, она позволяет использовать мощные нагрузки и обычно применяется в промышленных зданиях и намного реже в индивидуальных жилых домах и квартирах. Все мощные потребители энергии, такие как водонагреватели, большие электродвигатели и системы кондиционирования воздуха обычно подключаются к трехфазной сети.
Однофазная сеть — как проселочная дорога, ее возможности по мощности невысоки и используется она в основном в жилых домах и квартирах. Однофазная сеть проста и экономична. Однако однофазную сеть нельзя использовать для питания эффективных трехфазных электродвигателей. С другой стороны, трехфазная сеть — как автомагистраль, она позволяет использовать мощные нагрузки и обычно применяется в промышленных зданиях и намного реже в индивидуальных жилых домах и квартирах. Все мощные потребители энергии, такие как водонагреватели, большие электродвигатели и системы кондиционирования воздуха обычно подключаются к трехфазной сети. Однофазная система не годится для питания мощных электродвигателей.
Однофазная система не годится для питания мощных электродвигателей.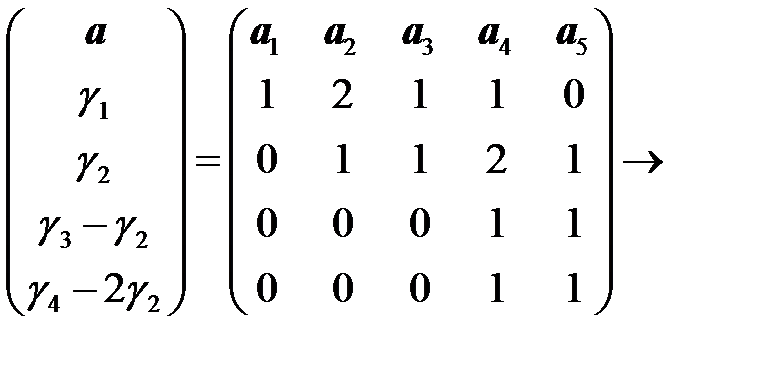 В результате с обмоток снимаются напряжения (фазы) со сдвигом по фазе 120°. Эти три напряжения не зависят друг от друга и их мгновенные значения определяются формулами:
В результате с обмоток снимаются напряжения (фазы) со сдвигом по фазе 120°. Эти три напряжения не зависят друг от друга и их мгновенные значения определяются формулами:
 Отметим, что нам безразлично направление вращения ротора генератора, потому вращающийся по часовой стрелке ротор можно обойти и мы будем наблюдать вращение против часовой стрелки. Нам интересен только порядок чередования фаз напряжений, вырабатываемых генератором.
Отметим, что нам безразлично направление вращения ротора генератора, потому вращающийся по часовой стрелке ротор можно обойти и мы будем наблюдать вращение против часовой стрелки. Нам интересен только порядок чередования фаз напряжений, вырабатываемых генератором.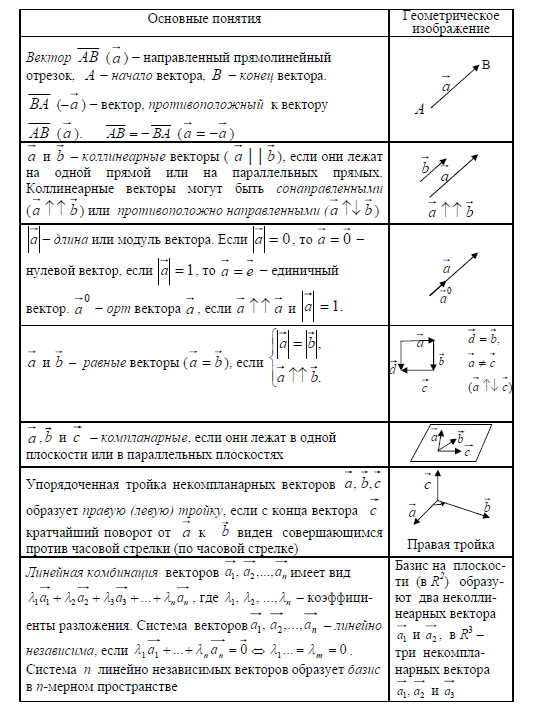 Амплитуды и частоты напряжений и токов одинаковые. Отличаются они только сдвигом фаз: напряжение в каждой фазе отстает от предыдущей на 2π/3, или на 1/3 цикла, или на 120°. Векторная сумма трех напряжений равна нулю:
Амплитуды и частоты напряжений и токов одинаковые. Отличаются они только сдвигом фаз: напряжение в каждой фазе отстает от предыдущей на 2π/3, или на 1/3 цикла, или на 120°. Векторная сумма трех напряжений равна нулю: Примерами нелинейных нагрузок являются блоки питания компьютеров, лазерные принтеры, светодиодные и компактные люминесцентные лампы, электронные регуляторы оборотов электродвигателей и многие другие потребители электроэнергии. Искажение формы гармонических колебаний тока приводит к искажению формы напряжения. К нелинейным нагрузкам неприменим закон Ома. В таких нагрузках коэффициент мощности не равен cos φ.
Примерами нелинейных нагрузок являются блоки питания компьютеров, лазерные принтеры, светодиодные и компактные люминесцентные лампы, электронные регуляторы оборотов электродвигателей и многие другие потребители электроэнергии. Искажение формы гармонических колебаний тока приводит к искажению формы напряжения. К нелинейным нагрузкам неприменим закон Ома. В таких нагрузках коэффициент мощности не равен cos φ. В связи с тем, что нагрузки симметричные, в каждой фазе потребляется одинаковая мощность и полная активная мощность во всех трех фазах равна
В связи с тем, что нагрузки симметричные, в каждой фазе потребляется одинаковая мощность и полная активная мощность во всех трех фазах равна Фазное напряжение — это напряжение на каждой обмотке. Линейное напряжение — это напряжение между двумя фазами, то есть также на каждой из обмоток. Таким образом, среднеквадратичные напряжения на обмотках и между фазами одинаковые, то есть для соединения треугольником можно написать
Фазное напряжение — это напряжение на каждой обмотке. Линейное напряжение — это напряжение между двумя фазами, то есть также на каждой из обмоток. Таким образом, среднеквадратичные напряжения на обмотках и между фазами одинаковые, то есть для соединения треугольником можно написать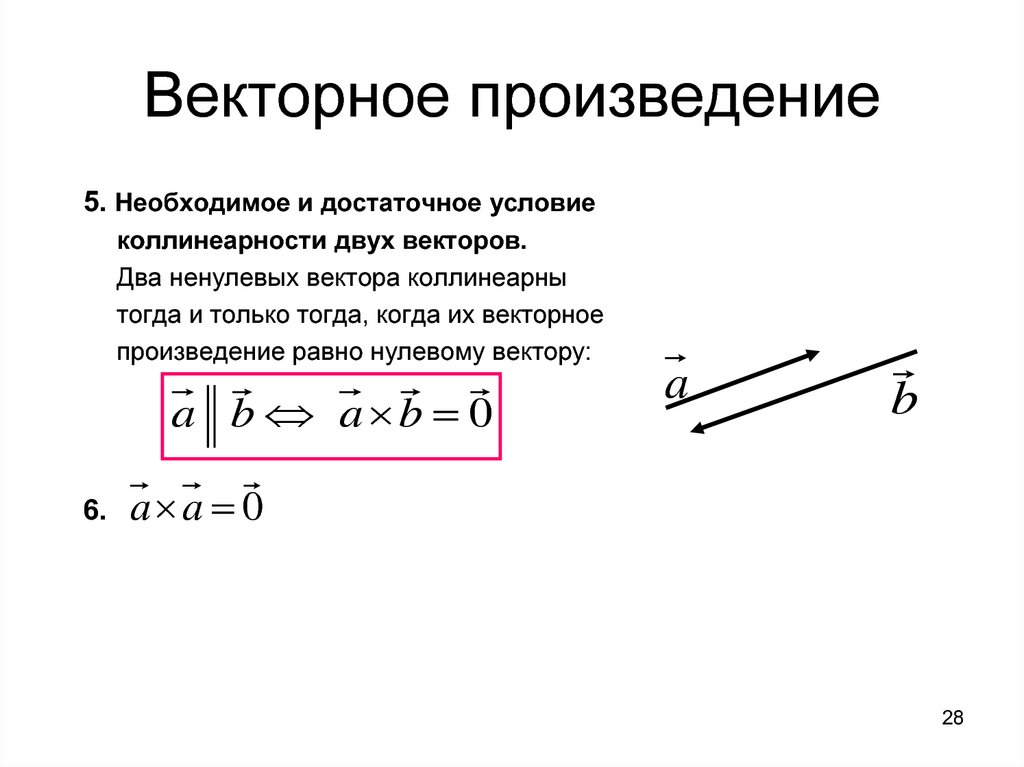 Мы используем их в этом калькуляторе.
Мы используем их в этом калькуляторе.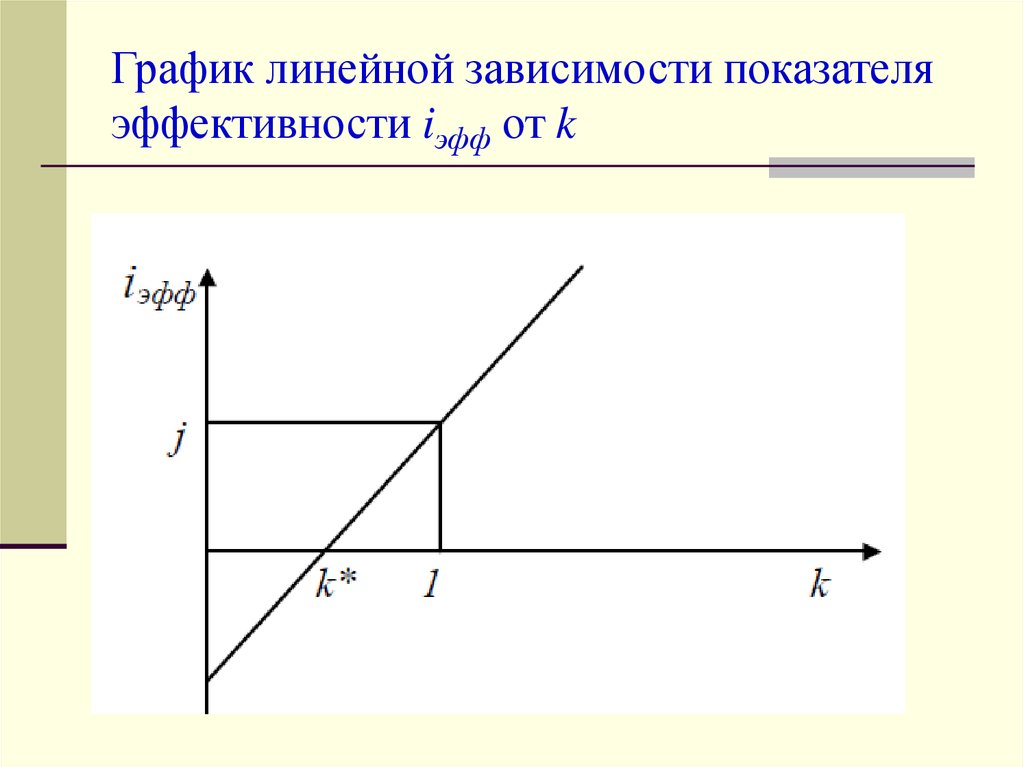 Полная мощность также уменьшилась:
Полная мощность также уменьшилась:

 Ток в каждой фазе равен 28,5 А. Рассчитать импеданс нагрузки, активное и реактивное сопротивление в каждой фазе. Также рассчитать полную, активную и реактивную мощности. Описать что произойдет, если для той же нагрузки изменить соединение со звезды на треугольник. Совет: используйте режим определения мощности и нагрузки по заданным току и напряжению, а затем для ответа на последний вопрос воспользуйтесь этим же калькулятором в режиме определения мощности и тока по заданным напряжению и нагрузке.
Ток в каждой фазе равен 28,5 А. Рассчитать импеданс нагрузки, активное и реактивное сопротивление в каждой фазе. Также рассчитать полную, активную и реактивную мощности. Описать что произойдет, если для той же нагрузки изменить соединение со звезды на треугольник. Совет: используйте режим определения мощности и нагрузки по заданным току и напряжению, а затем для ответа на последний вопрос воспользуйтесь этим же калькулятором в режиме определения мощности и тока по заданным напряжению и нагрузке. Как изменятся ток и мощность, если эту же нагрузку подключить звездой? Совет: воспользуйтесь нашим Калькулятором импеданса последовательной RL-цепи для определения импеданса каждой катушки, а затем введите данные в этот калькулятор.
Как изменятся ток и мощность, если эту же нагрузку подключить звездой? Совет: воспользуйтесь нашим Калькулятором импеданса последовательной RL-цепи для определения импеданса каждой катушки, а затем введите данные в этот калькулятор. В каждом фазном проводе протекает ток Iph = 20 А с запаздыванием относительно напряжения на 15°. Определите фазное напряжение, импеданс нагрузки в каждой фазе в полярной и комплексной форме, активную и реактивную мощности.
В каждом фазном проводе протекает ток Iph = 20 А с запаздыванием относительно напряжения на 15°. Определите фазное напряжение, импеданс нагрузки в каждой фазе в полярной и комплексной форме, активную и реактивную мощности. Расчет ограничительных резисторов для одиночных светодиодов и светодиодных массивов
Расчет ограничительных резисторов для одиночных светодиодов и светодиодных массивов
 е. один из них скалярно кратен другому.
е. один из них скалярно кратен другому.