Калькулятор онлайн обычных дробей: Калькулятор дробей онлайн

Калькулятор онлайн — Сложение, сокращение, умножение, деление, вычитание неправильных числовых дробей (с подробным решением)

С помощью данного калькулятора онлайн вы можете умножить, вычесть, поделить, сложить и сократить числовые дроби с разными знаменателями.

Программа работает с правильными, неправильными и смешанными числовыми дробями.

Данная программа (калькулятор онлайн) умеет:
— выполнять сложение смешанных дробей с разными знаменателями
— выполнять вычетание смешанных дробей с разными знаменателями
— выполнять деление смешанных дробей с разными знаменателями
— выполнять умножение смешанных дробей с разными знаменателями
— приводить дроби к общему знаменателю
— преобразовывать смешанные дроби в неправильные
— сокращать дроби

Также можно ввести не выражение с дробями, а одну единственную дробь.
В этом случае дробь будет сокращена и из результата выделена целая часть.

Калькулятор онлайн для вычисления выражений с числовыми дробями не просто даёт ответ задачи, он приводит подробное решение с пояснениями, т.е. отображает процесс нахождения решения.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Если вы не знакомы с правилами ввода выражений с числовыми дробями, рекомендуем с ними ознакомиться.

Правила ввода выражений с числовыми дробями

В качестве числителя, знаменателя и целой части дроби может выступать только целое число.

Знаменатель не может быть отрицательным.

При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3 + 7/5
Результат: \( -\frac{2}{3} + \frac{7}{5} \)

Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&2/3 * 5&8/3
Результат: \( -1\frac{2}{3} \cdot 5\frac{8}{3} \)

Деление дробей вводится знаком двоеточие: :
Ввод: -9&37/12 : -3&5/14
Результат: \( -9\frac{37}{12} : \left( -3\frac{5}{14} \right) \)
Помните, что на ноль делить нельзя!

При вводе выражений с числовыми дробями можно использовать скобки.
Ввод: -2/3 * (6&1/2-5/9) : 2&1/4 + 1/3
Результат: \( -\frac{2}{3} \cdot \left( 6 \frac{1}{2} — \frac{5}{9} \right) : 2\frac{1}{4} + \frac{1}{3} \)

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.

Сообщение отправлено. Спасибо.

Обыкновенные дроби. Деление с остатком

Если нам нужно разделить 497 на 4, то при делении мы увидим, что 497 не делится на 4 нацело, т.е. остаётся остаток от деления. В таких случаях говорят, что выполнено деление с остатком, и решение записывают в таком виде:
497 : 4 = 124 (1 остаток).

Компоненты деления в левой части равенства называют так же, как при делении без остатка: 497 — делимое, 4 — делитель. Результат деления при делении с остатком называют неполным частным. В нашем случае это число 124. И, наконец, последний компонент, которого нет в обычном делении, — остаток. В тех случаях, когда остатка нет, говорят, что одно число разделилось на другое без остатка, или нацело. Считают, что при таком делении остаток равен нулю. В нашем случае остаток равен 1.

Остаток всегда меньше делителя.

Проверку при делении можно сделать умножением. Если, например, имеется равенство 64 : 32 = 2, то проверку можно сделать так: 64 = 32 * 2.

Часто в случаях, когда выполняется деление с остатком, удобно использовать равенство
а = b * n + r ,
где а — делимое, b — делитель, n — неполное частное, r — остаток.

Частное от деления натуральных чисел можно записать в виде дроби.

Числитель дроби — это делимое, а знаменатель — делитель.

Поскольку числитель дроби — это делимое, а знаменатель — делитель, считают, что черта дроби означает действие деление. Иногда бывает удобно записывать деление в виде дроби, не используя знак «:».

Частное от деления натуральных чисел m и n можно записать в виде дроби \( \frac{m}{n} \), где числитель m — делимое, а знаменатель п — делитель:
\( m:n = \frac{m}{n} \)

Верны следующие правила:

Чтобы получить дробь \( \frac{m}{n} \), надо единицу разделить на n равных частей (долей) и взять m таких частей.

Чтобы получить дробь \( \frac{m}{n} \), надо число m разделить на число n.

Чтобы найти часть от целого, надо число, соответствующее целому, разделить на знаменатель и результат умножить на числитель дроби, которая выражает эту часть.

Чтобы найти целое по его части, надо число, соответствующее этой части, разделить на числитель и результат умножить на знаменатель дроби, которая выражает эту часть.

Если и числитель, и знаменатель дроби умножить на одно и то же число (кроме нуля), величина дроби не изменится:
\( \large \frac{a}{b} = \frac{a \cdot n}{b \cdot n} \)

Если и числитель, и знаменатель дроби разделить на одно и то же число (кроме нуля), величина дроби не изменится:
\( \large \frac{a}{b} = \frac{a : m}{b : m} \)
Это свойство называют основным свойством дроби.

Два последних преобразования называют сокращением дроби.

Если дроби нужно представить в виде дробей с одним и тем же знаменателем, то такое действие называют приведением дробей к общему знаменателю.

Правильные и неправильные дроби. Смешанные числа

Вы уже знаете, что дробь можно получить, если разделить целое на равные части и взять несколько таких частей. Например, дробь \( \frac{3}{4} \) означает три четвёртых доли единицы. Во многих задачах предыдущего параграфа обыкновенные дроби использовались для обозначения части целого. Здравый смысл подсказывает, что часть всегда должна быть меньше целого, но как тогда быть с такими дробями, как, например, \( \frac{5}{5} \) или \( \frac{8}{5} \)? Ясно, что это уже не часть единицы. Наверное, поэтому такие дроби, у которых числитель больше знаменателя или равен ему, называют неправильными дробями. Остальные дроби, т. е. дроби, у которых числитель меньше знаменателя, называют правильными дробями.

Как вы знаете, любую обыкновенную дробь, и правильную, и неправильную, можно рассматривать как результат деления числителя на знаменатель. Поэтому в математике, в отличие от обычного языка, термин «неправильная дробь» означает не то, что мы что-то сделали неправильно, а только то, что у этой дроби числитель больше знаменателя или равен ему.

Если число состоит из целой части и дроби, то такие дроби называются смешанными.

Например:
\( 5:3 = 1\frac{2}{3} \) : 1 — целая часть, а \( \frac{2}{3} \) — дробная часть.

Если числитель дроби \( \frac{a}{b} \) делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её числитель разделить на это число:
\( \large \frac{a}{b} : n = \frac{a:n}{b} \)

Если числитель дроби \( \frac{a}{b} \) не делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её знаменатель умножить на это число:
\( \large \frac{a}{b} : n = \frac{a}{bn} \)

Заметим, что второе правило справедливо и в том случае, когда числитель делится на n. Поэтому мы можем его применять тогда, когда трудно с первого взгляда определить, делится числитель дроби на n или нет.

Действия с дробями. Сложение дробей.

С дробными числами, как и с натуральными числами, можно выполнять арифметические действия. Рассмотрим сначала сложение дробей. Легко сложить дроби с одинаковыми знаменателями. Найдем, например, сумму \( \frac{2}{7} \) и \( \frac{3}{7} \). Легко понять, что \( \frac{2}{7} + \frac{2}{7} = \frac{5}{7} \)

Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.

Используя буквы, правило сложения дробей с одинаковыми знаменателями можно записать так:
\( \large \frac{a}{c} + \frac{b}{c} = \frac{a+b}{c} \)

Если требуется сложить дроби с разными знаменателями, то их предварительно следует привести к общему знаменателю. Например:
\( \large \frac{2}{3}+\frac{4}{5} = \frac{2\cdot 5}{3\cdot 5}+\frac{4\cdot 3}{5\cdot 3} = \frac{10}{15}+\frac{12}{15} = \frac{10+12}{15} = \frac{22}{15} \)

Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства сложения.

Сложение смешанных дробей

Такие записи, как \( 2\frac{2}{3} \), называют смешанными дробями. При этом число 2 называют целой частью смешанной дроби, а число \( \frac{2}{3} \) — ее дробной частью. Запись \( 2\frac{2}{3} \) читают так: «две и две трети».

При делении числа 8 на число 3 можно получить два ответа: \( \frac{8}{3} \) и \( 2\frac{2}{3} \). Они выражают одно и то же дробное число, т.е \( \frac{8}{3} = 2 \frac{2}{3} \)

Таким образом, неправильная дробь \( \frac{8}{3} \) представлена в виде смешанной дроби \( 2\frac{2}{3} \). В таких случаях говорят, что из неправильной дроби выделили целую часть.

Вычитание дробей (дробных чисел)

Вычитание дробных чисел, как и натуральных, определяется на основе действия сложения: вычесть из одного числа другое — это значит найти такое число, которое при сложении со вторым дает первое. Например:
\( \frac{8}{9}-\frac{1}{9} = \frac{7}{9} \) так как \( \frac{7}{9}+\frac{1}{9} = \frac{8}{9} \)

Правило вычитания дробей с одинаковыми знаменателями похоже на правило сложения таких дробей:
чтобы найти разность дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель оставить прежним.

С помощью букв это правило записывается так:
\( \large \frac{a}{c}-\frac{b}{c} = \frac{a-b}{c} \)

Умножение дробей

Чтобы умножить дробь на дробь, нужно перемножить их числители и знаменатели и первое произведение записать числителем, а второе — знаменателем.

С помощью букв правило умножения дробей можно записать так:
\( \large \frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d} \)

Пользуясь сформулированным правилом, молено умножать дробь на натуральное число, на смешанную дробь, а также перемножать смешанные дроби. Для этого нужно натуральное число записать в виде дроби со знаменателем 1, смешанную дробь — в виде неправильной дроби.

Результат умножения надо упрощать (если это возможно), сокращая дробь и выделяя целую часть неправильной дроби.

Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства умножения, а также распределительное свойство умножения относительно сложения.

Деление дробей

Возьмем дробь \( \frac{2}{3} \) и «перевернем» ее, поменяв местами числитель и знаменатель. Получим дробь \( \frac{3}{2} \). Эту дробь называют обратной дроби \( \frac{2}{3} \).

Если мы теперь «перевернем» дробь \( \frac{3}{2} \), то получим исходную дробь \( \frac{2}{3} \). Поэтому такие дроби, как \( \frac{2}{3} \) и \( \frac{3}{2} \) называют взаимно обратными.

Взаимно обратными являются, например, дроби \( \frac{6}{5} \) и \( \frac{5}{6} \), \( \frac{7}{18} \) и \( \frac{18}{7} \).

С помощью букв взаимно обратные дроби можно записать так: \( \frac{a}{b} \) и \( \frac{b}{a} \)

Понятно, что произведение взаимно обратных дробей равно 1. Например: \( \frac{2}{3} \cdot \frac{3}{2} =1 \)

Используя взаимно обратные дроби, можно деление дробей свести к умножению.

Правило деления дроби на дробь:
чтобы разделить одну дробь на другую, нужно делимое умножить на дробь, обратную делителю.

Используя буквы, правило деления дробей можно записать так:
\( \large \frac{a}{b} : \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} \)

Если делимое или делитель является натуральным числом или смешанной дробью, то, для того чтобы воспользоваться правилом деления дробей, его надо предварительно представить в виде неправильной дроби.

Онлайн калькулятор: Непрерывная дробь

Этот калькулятор отображает входную дробь в виде непрерывной (цепной дроби). Также списком отображаются элементы цепной дроби. Чуть больше информации по непрерывным дробям можно найти сразу за калькулятором.

Перевод дроби к виду непрерывной дроби

Непрерывная дробь

 

Коэффициенты

 

save Сохранить extension Виджет

Обратное преобразование из коэффициентов цепной дроби в рациональное число.

Из непрерывной дроби к простой дроби

Точность вычисления

Знаков после запятой: 5

Непрерывная дробь

 

save Сохранить extension Виджет

Непрерывные (цепные) дроби

Непрерывной или цепной дробью называется представление числа в виде суммы целой части и дроби дробной части. Числитель дробной части всегда единица, знаменатель также сумма целой и дробной части. Знаменатель дробной части в свою очередь может снова содержать сумму целой части и дробь и так далее:

a₀,a₁,a₂…a_n — элементы непрерывной дроби.
Для вычисления элементов дроби мы используем следующий алгоритм:

// n - числитель (целое число)
// d - знаменатель (целое число)
loop while d ≠ 0
        r ⟵  n mod d;
        output ⟵ (n-r)/d;
        n ⟵ d;
        d ⟵ r;
 end loop  

Алгоритм обратного преобразования:

// f[] - массив коэффициентов цепной дроби с индексами 0...k-1
// k - количество коэффициентов
n ⟵ f[k-1];
d ⟵ 1;
loop while k greater than 1 
        r ⟵  d;
        d ⟵ n;
        k ⟵ k-1;
        n ⟵ f[k-1]*n+r;
end loop  
output ⟵ n/d;

Калькулятор дробей онлайн | umath.ru

Дробь — форма представления числа в математике. Дробная черта обозначает операцию деления. Числителем дроби называется делимое, а знаменателем — делитель. Например, в дроби 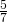числителем является число 5, а знаменателем — 7.

Сложение. Чтобы сложить две дроби, нужно

1. Привести дроби к общему знаменателю
2. Сложить новые числители обеих дробей, а знаменатель оставить без изменений

Пример:

   

Вычитание. Чтобы вычесть одну дробь из другой, нужно

1. Привести дроби к общему знаменателю
2. Вычесть из числителя первой дроби числитель второй, а знаменатель оставить без изменений

Пример:

   

Умножение. Чтобы умножить одну дробь на другую, следует перемножить их числители и знаменатели:

   

Деление. Чтобы разделить одну дробь на другую, следует числитель первой дроби умножить на знаменатель второй, а знаменатель первой дроби умножить на числитель второй:

   

Онлайн калькулятор дробей с решением

Данный калькулятор помогает вычислить сумму, разность, произведение и частное двух дробей. При этом выводится не только конечный ответ, но и решение с подробными пояснениями.

90000 Fraction Calculator 90001 90002 Below are multiple fraction calculators capable of addition, subtraction, multiplication, division, simplification, and conversion between fractions and decimals. Fields above the solid black line represent the numerator, while fields below represent the denominator. 90003 90004 90005 Simplify Fractions Calculator 90006 90004 90005 Decimal to Fraction Calculator 90006 90004 90005 Fraction to Decimal Calculator 90006 90002 90014 90003 90002 In mathematics, a fraction is a number that represents a part of a whole.It consists of a numerator and a denominator. The numerator represents the number of equal parts of a whole, while the denominator is the total number of parts that make up said whole. For example, in the fraction 90003, the numerator is 3, and the denominator is 5. A more illustrative example could involve a pie with 8 slices. 1 of those 8 slices would constitute the numerator of a fraction, while the total of 8 slices that comprises the whole pie would be the denominator. If a person were to eat 3 slices, the remaining fraction of the pie would therefore be as shown in the image to the right.Note that the denominator of a fraction can not be 0, as it would make the fraction undefined. Fractions can undergo many different operations, some of which are mentioned below. 90018 Addition: 90019 90002 Unlike adding and subtracting integers such as 2 and 8, fractions require a common denominator to undergo these operations. The equations provided below account for this by multiplying the numerators and denominators of all of the fractions involved in the addition by the denominators of each fraction (excluding multiplying itself by its own denominator).Multiplying all of the denominators ensures that the new denominator is certain to be a multiple of each individual denominator. Multiplying the numerator of each fraction by the same factors is necessary, since fractions are ratios of values ​​and a changed denominator requires that the numerator be changed by the same factor in order for the value of the fraction to remain the same. This is arguably the simplest way to ensure that the fractions have a common denominator. Note that in most cases, the solutions to these equations will not appear in simplified form (though the provided calculator computes the simplification automatically).An alternative to using this equation in cases where the fractions are uncomplicated would be to find a least common multiple and then add or subtract the numerators as one would an integer. Depending on the complexity of the fractions, finding the least common multiple for the denominator can be more efficient than using the equations. Refer to the equations below for clarification. 90003 90018 Subtraction: 90019 90002 Fraction subtraction is essentially the same as fraction addition. A common denominator is required for the operation to occur.Refer to the addition section as well as the equations below for clarification. 90003 90026 90027 90028 90029 — 90030 90028 90029 = (90030 90028 90029 × 90030 90028 90029) — (90030 90028 90029 × 90030 90028 90029) = 90030 90028 90047 90048 90018 Multiplication: 90019 90002 Multiplying fractions is fairly straightforward. Unlike adding and subtracting, it is not necessary to compute a common denominator in order to multiply fractions.Simply, the numerators and denominators of each fraction are multiplied, and the result forms a new numerator and denominator. If possible, the solution should be simplified. Refer to the equations below for clarification. 90003 90018 Division: 90019 90002 The process for dividing fractions is similar to that for multiplying fractions. In order to divide fractions, the fraction in the numerator is multiplied by the reciprocal of the fraction in the denominator. The reciprocal of a number 90056 a 90057 is simply 90003.When a is a fraction, this essentially involves exchanging the position of the numerator and the denominator. The reciprocal of the fraction would therefore be. Refer to the equations below for clarification. 90018 Simplification: 90019 90002 It is often easier to work with simplified fractions. As such, fraction solutions are commonly expressed in their simplified forms. 90003 for example, is more cumbersome than. The calculator provided returns fraction inputs in both improper fraction form, as well as mixed number form.In both cases, fractions are presented in their lowest forms by dividing both numerator and denominator by their greatest common factor. 90018 Converting between fractions and decimals: 90019 90002 Converting from decimals to fractions is straightforward. It does however require the understanding that each decimal place to the right of the decimal point represents a power of 10; the first decimal place being 10 90066 1 90067, the second 10 90066 2 90067, the third 10 90066 3 90067, and so on.Simply determine what power of 10 the decimal extends to, use that power of 10 as the denominator, enter each number to the right of the decimal point as the numerator, and simplify. For example, looking at the number 0.1234, the number 4 is in the fourth decimal place which constitutes 10 90066 4 90067, or 10,000. This would make the fraction 90003, which simplifies to, since the greatest common factor between the numerator and denominator is 2. 90002 Similarly, fractions with denominators that are powers of 10 (or can be converted to powers of 10) can be translated to decimal form using the same principles.Take the fraction 90003 for example. To convert this fraction into a decimal, first convert it into the fraction. Knowing that the first decimal place represents 10 90066 1 90067, can be converted to 0.5. If the fraction were instead, the decimal would then be 0.05, and so on. Beyond this, converting fractions into decimals requires the operation of long division. 90018 Common Engineering Fraction to Decimal Conversions 90019 90002 In engineering, fractions are widely used to describe the size of components such as pipes and bolts.The most common fractional and decimal equivalents are listed below. 90003 90083 90084 90029 64 90066 th 90067 90030 90029 32 90066 nd 90067 90030 90029 16 90066 th 90067 90030 90029 8 90066 th 90067 90030 90029 4 90066 th 90067 90030 90029 2 90066 nd 90067 90030 90029 Decimal 90030 90029 Decimal 90004 (inch to mm) 90030 90047 90084 90029 1/64 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.015625 90030 90029 0.396875 90030 90047 90084 90029 2/64 90030 90029 1/32 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.03125 90030 90029 0.79375 90030 90047 90084 90029 3/64 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.046875 90030 90029 1.190625 90030 90047 90084 90029 4/64 90030 90029 2/32 90030 90029 1/16 90030 90029 90030 90029 90030 90029 90030 90029 0.0625 90030 90029 1.5875 90030 90047 90084 90029 5/64 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.078125 90030 90029 1.984375 90030 90047 90084 90029 6/64 90030 90029 3/32 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.09375 90030 90029 2.38125 90030 90047 90084 90029 7/64 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.109375 90030 90029 2.778125 90030 90047 90084 90029 8/64 90030 90029 4/32 90030 90029 2/16 90030 90029 1/8 90030 90029 90030 90029 90030 90029 0.125 90030 90029 3.175 90030 90047 90084 90029 9/64 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.140625 90030 90029 3.571875 90030 90047 90084 90029 10/64 90030 90029 5/32 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.15625 90030 90029 3.96875 90030 90047 90084 90029 11/64 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.171875 90030 90029 4.365625 90030 90047 90084 90029 12/64 90030 90029 6/32 90030 90029 3/16 90030 90029 90030 90029 90030 90029 90030 90029 0.1875 90030 90029 4.7625 90030 90047 90084 90029 13/64 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.203125 90030 90029 5.159375 90030 90047 90084 90029 14/64 90030 90029 7/32 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.21875 90030 90029 5.55625 90030 90047 90084 90029 15/64 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.234375 90030 90029 5.953125 90030 90047 90084 90029 16/64 90030 90029 8/32 90030 90029 4/16 90030 90029 2/8 90030 90029 1/4 90030 90029 90030 90029 0.25 90030 90029 6.35 90030 90047 90084 90029 17/64 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.265625 90030 90029 6.746875 90030 90047 90084 90029 18/64 90030 90029 9/32 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.28125 90030 90029 7.14375 90030 90047 90084 90029 19/64 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.296875 90030 90029 7.540625 90030 90047 90084 90029 20/64 90030 90029 10/32 90030 90029 5/16 90030 90029 90030 90029 90030 90029 90030 90029 0.3125 90030 90029 7.9375 90030 90047 90084 90029 21/64 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.328125 90030 90029 8.334375 90030 90047 90084 90029 22/64 90030 90029 11/32 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.34375 90030 90029 8.73125 90030 90047 90084 90029 23/64 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.359375 90030 90029 9.128125 90030 90047 90084 90029 24/64 90030 90029 12/32 90030 90029 6/16 90030 90029 3/8 90030 90029 90030 90029 90030 90029 0.375 90030 90029 9.525 90030 90047 90084 90029 25/64 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.390625 90030 90029 9.921875 90030 90047 90084 90029 26/64 90030 90029 13/32 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.40625 90030 90029 10.31875 90030 90047 90084 90029 27/64 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.421875 90030 90029 10.715625 90030 90047 90084 90029 28/64 90030 90029 14/32 90030 90029 7/16 90030 90029 90030 90029 90030 90029 90030 90029 0.4375 90030 90029 11.1125 90030 90047 90084 90029 29/64 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.453125 90030 90029 11.509375 90030 90047 90084 90029 30/64 90030 90029 15/32 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.46875 90030 90029 11.90625 90030 90047 90084 90029 31/64 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.484375 90030 90029 12.303125 90030 90047 90084 90029 32/64 90030 90029 16/32 90030 90029 8/16 90030 90029 4/8 90030 90029 2/4 90030 90029 1/2 90030 90029 0.5 90030 90029 12.7 90030 90047 90084 90029 33/64 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.515625 90030 90029 13.096875 90030 90047 90084 90029 34/64 90030 90029 17/32 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.53125 90030 90029 13.49375 90030 90047 90084 90029 35/64 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.546875 90030 90029 13.890625 90030 90047 90084 90029 36/64 90030 90029 18/32 90030 90029 9/16 90030 90029 90030 90029 90030 90029 90030 90029 0.5625 90030 90029 14.2875 90030 90047 90084 90029 37/64 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.578125 90030 90029 14.684375 90030 90047 90084 90029 38/64 90030 90029 19/32 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.59375 90030 90029 15.08125 90030 90047 90084 90029 39/64 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.609375 90030 90029 15.478125 90030 90047 90084 90029 40/64 90030 90029 20/32 90030 90029 10/16 90030 90029 5/8 90030 90029 90030 90029 90030 90029 0.625 90030 90029 15.875 90030 90047 90084 90029 41/64 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.640625 90030 90029 16.271875 90030 90047 90084 90029 42/64 90030 90029 21/32 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.65625 90030 90029 16.66875 90030 90047 90084 90029 43/64 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.671875 90030 90029 17.065625 90030 90047 90084 90029 44/64 90030 90029 22/32 90030 90029 11/16 90030 90029 90030 90029 90030 90029 90030 90029 0.6875 90030 90029 17.4625 90030 90047 90084 90029 45/64 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.703125 90030 90029 17.859375 90030 90047 90084 90029 46/64 90030 90029 23/32 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.71875 90030 90029 18.25625 90030 90047 90084 90029 47/64 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.734375 90030 90029 18.653125 90030 90047 90084 90029 48/64 90030 90029 24/32 90030 90029 12/16 90030 90029 6/8 90030 90029 3/4 90030 90029 90030 90029 0.75 90030 90029 19.05 90030 90047 90084 90029 49/64 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.765625 90030 90029 19.446875 90030 90047 90084 90029 50/64 90030 90029 25/32 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.78125 90030 90029 19.84375 90030 90047 90084 90029 51/64 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.796875 90030 90029 20.240625 90030 90047 90084 90029 52/64 90030 90029 26/32 90030 90029 13/16 90030 90029 90030 90029 90030 90029 90030 90029 0.8125 90030 90029 20.6375 90030 90047 90084 90029 53/64 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.828125 90030 90029 21.034375 90030 90047 90084 90029 54/64 90030 90029 27/32 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.84375 90030 90029 21.43125 90030 90047 90084 90029 55/64 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.859375 90030 90029 21.828125 90030 90047 90084 90029 56/64 90030 90029 28/32 90030 90029 14/16 90030 90029 7/8 90030 90029 90030 90029 90030 90029 0.875 90030 90029 22.225 90030 90047 90084 90029 57/64 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.890625 90030 90029 22.621875 90030 90047 90084 90029 58/64 90030 90029 29/32 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.90625 90030 90029 23.01875 90030 90047 90084 90029 59/64 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 90030 90029 0.921875 90030 90028 90047 90048.90000 Fractions Calculator 90001 90002 Calculator Use 90003 90004 Use this fraction calculator for adding, subtracting, multiplying and dividing fractions. Answers are fractions in lowest terms or mixed numbers in reduced form. 90005 90004 Input proper or improper fractions, select the math sign and click Calculate. This is a fraction calculator with steps shown in the solution. 90005 90004 If you have negative fractions insert a minus sign before the numerator.So if one of your fractions is -6/7, insert -6 in the numerator and 7 in the denominator. 90005 90004 Sometimes math problems include the word «of,» as in 90011 What is 1/3 of 3/8? 90012 Of means you should multiply so you need to solve 1/3 × 3/8. 90005 90004 To do math with mixed numbers (whole numbers and fractions) use the Mixed Numbers Calculator. 90005 90016 Math on Fractions with Unlike Denominators 90003 90004 There are 2 cases where you need to know if your fractions have different denominators: 90005 90020 90021 if you are adding fractions 90022 90021 if you are subtracting fractions 90022 90025 90016 How to Add or Subtract Fractions 90003 90028 90021 Find the least common denominator 90022 90021 You can use the LCD Calculator to find the least common denominator for a set of fractions 90022 90021 For your first fraction, find what number you need to multiply the denominator by to result in the least common denominator 90022 90021 Multiply the numerator and denominator of your first fraction by that number 90022 90021 Repeat Steps 3 and 4 for each fraction 90022 90021 For addition equations, add the fraction numerators 90022 90021 For subtraction equations, subtract the fraction numerators 90022 90021 Convert improper fractions to mixed numbers 90022 90021 Reduce the fraction to lowest terms 90022 90047 90016 How to Multiply Fractions 90003 90028 90021 Multiply all numerators together 90022 90021 Multiply all denominators together 90022 90021 Reduce the result to lowest terms 90022 90047 90016 How to Divide Fractions 90003 90028 90021 Rewrite the equation as in «Keep, Change, Flip» 90022 90021 90011 Keep 90012 the first fraction 90022 90021 90011 Change 90012 the division sign to multiplication 90022 90021 90011 Flip 90012 the second fraction by switching the top and bottom numbers 90022 90021 Multiply all numerators together 90022 90021 Multiply all denominators together 90022 90021 Reduce the result to lowest terms 90022 90047 90016 Fraction Formulas 90003 90004 There is a way to add or subtract fractions without finding the least common denominator (LCD).This method involves cross multiplication of the fractions. See the formulas below. 90005 90004 You may find that it is easier to use these formulas than to do the math to find the least common denominator. 90005 90004 The formulas for multiplying and dividing fractions follow the same process as described above. 90005 90004 The formula for adding fractions is: 90005 90004 \ (\ dfrac {a} {b} + \ dfrac {c} {d} = \ dfrac {ad + bc} {bd} \) 90005 90004 Example steps: 90005 90004 \ (\ dfrac {2} {6} + \ dfrac {1} {4} = \ dfrac {(2 \ times4) + (6 \ times1)} {6 \ times4} \) 90005 90004 \ (= \ dfrac {14} {24} = \ dfrac {7} {12} \) 90005 90004 The formula for subtracting fractions is: 90005 90004 \ (\ dfrac {a} {b} — \ dfrac {c} {d} = \ dfrac {ad — bc} {bd} \) 90005 90004 Example steps: 90005 90004 \ (\ dfrac {2} {6} — \ dfrac {1} {4} = \ dfrac {(2 \ times4) — (6 \ times1)} {6 \ times4} \) 90005 90004 \ (= \ dfrac {2} {24} = \ dfrac {1} {12} \) 90005 90004 The formula for multiplying fractions is: 90005 90004 \ (\ dfrac {a} {b} \ times \ dfrac {c} {d} = \ dfrac {ac} {bd} \) 90005 90004 Example steps: 90005 90004 \ (\ dfrac {2} {6} \ times \ dfrac {1} {4} = \ dfrac {2 \ times1} {6 \ times4} \) 90005 90004 \ (= \ dfrac {2} {24} = \ dfrac {1} {12} \) 90005 90004 The formula for dividing fractions is: 90005 90004 \ (\ dfrac {a} {b} \ div \ dfrac {c} {d} = \ dfrac {ad} {bc} \) 90005 90004 Example steps: 90005 90004 \ (\ dfrac {2} {6} \ div \ dfrac {1} {4} = \ dfrac {2 \ times4} {6 \ times1} \) 90005 90004 \ (= \ dfrac {8} {6} = \ dfrac {4} {3} = 1 \ dfrac {1} {3} \) 90005 90130 Related Calculators 90131 90004 To perform math operations on mixed number fractions use our Mixed Numbers Calculator.This calculator can also simplify improper fractions into mixed numbers and shows the work involved. 90005 90004 If you want to simplify an individual fraction into lowest terms use our Simplify Fractions Calculator. 90005 90004 For an explanation of how to factor numbers to find the greatest common factor (GCF) see the Greatest Common Factor Calculator. 90005 90004 If you are simplifying large fractions by hand you can use the Long Division with Remainders Calculator to find whole number and remainder values.90005 90130 Notes 90131 90004 This calculator performs the reducing calculation faster than other calculators you might find. The primary reason is that it utilizes Euclid’s Algorithm for reducing fractions which can be found on The Math Forum. 90005 .90000 Mixed Numbers Calculator 90001 90002 Calculator Use 90003 90004 Do math calculations with mixed numbers (mixed fractions) performing operations on fractions, whole numbers, integers, mixed numbers, mixed fractions and improper fractions. The Mixed Numbers Calculator can add, subtract, multiply and divide mixed numbers and fractions. 90005 90006 Mixed Numbers Calculator (also referred to as Mixed Fractions): 90007 90004 This online calculator handles simple operations on whole numbers, integers, mixed numbers, fractions and improper fractions by adding, subtracting, dividing or multiplying.The answer is provided in a reduced fraction and a mixed number if it exists. 90005 90004 Enter mixed numbers, whole numbers or fractions in the following formats: 90005 90012 90013 Mixed numbers: Enter as 1 1/2 which is one and one half or 25 3/32 which is twenty five and three thirty seconds. Keep exactly one space between the whole number and fraction and use a forward slash to input fractions. You can enter up to 3 digits in length for each whole number, numerator or denominator (123 456/789).90014 90013 Whole numbers: Up to 3 digits in length. 90014 90013 Fractions: Enter as 3/4 which is three fourths or 3/100 which is three one hundredths. You can enter up to 3 digits in length for each the numerators and denominators (e.g., 456/789). 90014 90019 90020 Adding Mixed Numbers using the Adding Fractions Formula 90003 90022 90013 Convert the mixed numbers to improper fractions 90014 90013 Use the algebraic formula for addition of fractions: 90026 a / b + c / d = (ad + bc) / bd 90014 90013 Reduce fractions and simplify if possible 90014 90030 90006 Adding Fractions Formula 90007 90004 \ (\ dfrac {a} {b} + \ dfrac {c} {d} = \ dfrac {(a \ times d) + (b \ times c)} {b \ times d} \) 90005 90006 Example 90007 90004 Add 1 2/6 and 2 1/4 90005 90004 \ (1 \ dfrac {2} {6} + 2 \ dfrac {1} {4} = \ dfrac {8} {6} + \ dfrac {9} {4} \) 90005 90004 \ (= \ dfrac {(8 \ times 4) + (9 \ times 6)} {6 \ times 4} \) 90005 90004 \ (= \ dfrac {32 + 54} {24} = \ dfrac {86} {24} = \ dfrac {43} {12} \) 90005 90004 \ (= 3 \ dfrac {7} {12} \) 90005 90004 1 2/6 + 2 1/4 = 8/6 + 9/4 = (8 * 4 + 9 * 6) / 6 * 4 = 86/24 90005 90004 So we get 86/24 and simplify to 3 7/12 90005 90020 Subtracting Mixed Numbers using the Subtracting Fractions Formula 90003 90022 90013 Convert the mixed numbers to improper fractions 90014 90013 Use the algebraic formula for subtraction of fractions: a / bc / d = (ad — bc) / bd 90014 90013 Reduce fractions and simplify if possible 90014 90030 90006 Subtracting Fractions Formula 90007 90004 \ (\ dfrac {a} {b} — \ dfrac {c} {d} = \ dfrac {(a \ times d) — (b \ times c)} {b \ times d} \) 90005 90006 Example 90007 90004 Subtract 2 1/4 from 1 2/6 90005 90004 1 2/6 — 2 1/4 = 8/6 — 9/4 = (8 * 4 — 9 * 6) / 6 * 4 = -22 / 24 90005 90004 Reduce the fraction to get -11/12 90005 90020 Multiplying Mixed Numbers using the Multiplying Fractions Formula 90003 90022 90013 Convert the mixed numbers to improper fractions 90014 90013 Use the algebraic formula for multiplying of fractions: a / b * c / d = ac / bd 90014 90013 Reduce fractions and simplify if possible 90014 90030 90006 Multiplying Fractions Formula 90007 90004 \ (\ dfrac {a} {b} \ times \ dfrac {c} {d} = \ dfrac {a \ times c} {b \ times d} \) 90005 90006 Example 90007 90004 multiply 1 2/6 by 2 1/4 90005 90004 1 2/6 * 2 1/4 = 8/6 * 9/4 = 8 * 9/6 * 4 = 72/24 90005 90004 Reduce the fraction to get 3/1 and simplify to 3 90005 90020 Dividing Mixed Numbers using the Dividing Fractions Formula 90003 90022 90013 Convert the mixed numbers to improper fractions 90014 90013 Use the algebraic formula for division of fractions: a / b ÷ c / d = ad / bc 90014 90013 Reduce fractions and simplify if possible 90014 90030 90006 Dividing Fractions Formula 90007 90004 \ (\ dfrac {a} {b} \ div \ dfrac {c} {d} = \ dfrac {a \ times d} {b \ times c} \) 90005 90006 Example 90007 90004 divide 1 2/6 by 2 1/4 90005 90004 1 2/6 ÷ 2 1/4 = 8/6 ÷ 9/4 = 8 * 4/9 * 6 = 32/54 90005 90004 Reduce the fraction to get 16/27 90005 90006 Related Calculators 90007 90004 To perform math operations on simple proper or improper fractions use our Fractions Calculator.This calculator simplifies improper fraction answers into mixed numbers. 90005 90004 If you want to simplify an individual fraction into lowest terms use our Simplify Fractions Calculator. 90005 90004 For an explanation of how to factor numbers to find the greatest common factor (GCF) see the Greatest Common Factor Calculator. 90005 90004 If you are simplifying large fractions by hand you can use the Long Division with Remainders Calculator to find whole number and remainder values.90005 90004 Note: 90005 90004 This calculator performs the reducing calculation faster than others you might find. The primary reason is that the code utilizes Euclid’s Theorem for reducing fractions which can be found at The Math Forum: LCD, LCM. 90005 .90000 Decimal to Fraction Calculator 90001 90002 Calculator Use 90003 90004 This calculator converts a decimal number to a fraction or a decimal number to a mixed number. For repeating decimals enter how many decimal places in your decimal number repeat. 90005 90004 90007 Entering Repeating Decimals 90008 90005 90010 90011 For a repeating decimal such as 0.66666 … where the 6 repeats forever, enter 0.6 and since the 6 is the only one trailing decimal place that repeats, enter 1 for decimal places to repeat. The answer is 2/3 90012 90011 For a repeating decimal such as 0.363636 … where the 36 repeats forever, enter 0.36 and since the 36 are the only two trailing decimal places that repeat, enter 2 for decimal places to repeat. The answer is 4/11 90012 90011 For a repeating decimal such as 1.8333 … where the 3 repeats forever, enter 1.83 and since the 3 is the only one trailing decimal place that repeats, enter 1 for decimal places to repeat. The answer is 1 5/6 90012 90011 For the repeating decimal 0.857142857142857142 ….. where the 857142 repeats forever, enter 0.857142 and since the 857142 are the 6 trailing decimal places that repeat, enter 6 for decimal places to repeat. The answer is 6/7 90012 90019 90020 How to Convert a Negative Decimal to a Fraction 90003 90022 90011 Remove the negative sign from the decimal number 90012 90011 Perform the conversion on the positive value 90012 90011 Apply the negative sign to the fraction answer 90012 90029 90004 If a = b then it is true that -a = -b.90005 90020 How to Convert a Decimal to a Fraction 90003 90022 90011 Step 1: Make a fraction with the decimal number as the numerator (top number) and a 1 as the denominator (bottom number). 90012 90011 Step 2: Remove the decimal places by multiplication. First, count how many places are to the right of the decimal. Next, given that you have x decimal places, multiply numerator and denominator by 10 90038 x 90039. 90012 90011 Step 3: Reduce the fraction.Find the Greatest Common Factor (GCF) of the numerator and denominator and divide both numerator and denominator by the GCF. 90012 90011 Step 4: Simplify the remaining fraction to a mixed number fraction if possible. 90012 90029 90046 Example: Convert 2.625 to a fraction 90047 90004 1. Rewrite the decimal number number as a fraction (over 1) 90005 90004 \ (2.625 = \ dfrac {2.625} {1} \) 90005 90004 2.Multiply numerator and denominator by by 10 90038 3 90039 = 1000 to eliminate 3 decimal places 90005 90004 \ (\ dfrac {2.625} {1} \ times \ dfrac {1000} {1000} = \ dfrac {2625} {1000} \) 90005 90004 3. Find the Greatest Common Factor (GCF) of 2625 and 1000 and reduce the fraction, dividing both numerator and denominator by GCF = 125 90005 90004 \ (\ dfrac {2625 \ div 125} {1000 \ div 125} = \ dfrac {21} {8} \) 90005 90004 4.Simplify the improper fraction 90005 90004 \ (= 2 \ dfrac {5} {8} \) 90005 90004 Therefore, 90005 90004 \ (2.625 = 2 \ dfrac {5} {8} \) 90005 90070 Decimal to Fraction 90071 90010 90011 For another example, convert 0.625 to a fraction. 90012 90011 Multiply 0.625 / 1 by 1000/1000 to get 625/1000. 90012 90011 Reducing we get 5/8.90012 90019 90020 Convert a Repeating Decimal to a Fraction 90003 90022 90011 Create an equation such that x equals the decimal number. 90012 90011 Count the number of decimal places, y. Create a second equation multiplying both sides of the first equation by 10 90038 y 90039. 90012 90011 Subtract the second equation from the first equation. 90012 90011 Solve for x 90012 90011 Reduce the fraction.90012 90029 90046 Example: Convert repeating decimal 2.666 to a fraction 90047 90004 1. Create an equation such that x equals the decimal number 90099 Equation 1: 90005 90004 \ (x = 2. \ overline {666} \ tag {1} \) 90005 90004 2. Count the number of decimal places, y. There are 3 digits in the repeating decimal group, so y = 3. Ceate a second equation by multiplying both sides of the first equation by 10 90038 3 90039 = 1000 90099 Equation 2: 90005 90004 \ (1000 x = 2666.\ Overline {666} \ tag {2} \) 90005 90004 3. Subtract equation (1) from equation (2) 90005 90004 \ (\ eqalign {1000 x & = & \ hfill2666.666 … \ cr x & = & \ hfill2.666 … \ cr \ hline 999x & = & 2664 \ cr} \) 90005 90004 We get 90005 90004 \ (999 x = 2664 \) 90005 90004 4. Solve for x 90005 90004 \ (x = \ dfrac {2664} {999} \) 90005 90004 5. Reduce the fraction. Find the Greatest Common Factor (GCF) of 2664 and 999 and reduce the fraction, dividing both numerator and denominator by GCF = 333 90005 90004 \ (\ dfrac {2664 \ div 333} {999 \ div 333} = \ dfrac {8} {3} \) 90005 90004 Simplify the improper fraction 90005 90004 \ (= 2 \ dfrac {2} {3} \) 90005 90004 Therefore, 90005 90004 \ (2.\ Overline {666} = 2 \ dfrac {2} {3} \) 90005 90070 Repeating Decimal to Fraction 90071 90010 90011 For another example, convert repeating decimal 0.333 to a fraction. 90012 90011 Create the first equation with x equal to the repeating decimal number: 90099 x = 0.333 90012 90011 There are 3 repeating decimals. Create the second equation by multiplying both sides of (1) by 10 90038 3 90039 = 1000: 90099 1000X = 333.333 (2) 90012 90011 Subtract equation (1) from (2) to get 999x = 333 and solve for x 90012 90011 x = 333/999 90012 90011 Reducing the fraction we get x = 1/3 90012 90011 Answer: x = 0.333 = 1/3 90012 90019 90020 Related Calculators 90003 90004 To convert a fraction to a decimal see the Fraction to Decimal Calculator.90005 90070 References 90071 90004 Wikipedia contributors. «Repeating Decimal,» Wikipedia, The Free Encyclopedia. Last visited 18 July, 2016. 90005 .