Калькулятор с одной дробью: Сложение и вычитание дробей

Сложение и вычитание дробей

Навигация по странице:

• Сложение дробей
  • Сложение дробей с одинаковыми знаменателями
  • Сложение обыкновенных дробей
  • Сложение смешаных чисел
• Вычитание дробей
  • Вычитание дробей с одинаковыми знаменателями
  • Вычитание обыкновенных дробей
  • Вычитание смешаных чисел

Сложение дробей

Сложение дробей с одинаковыми знаменателями.

Определение.

Чтобы сложить две дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменений:

a	+	b	=	a + b
c		c		c

Примеры сложения дробей с одинаковыми знаменателями

Пример 1.

Найти сумму двух дробей с одинаковыми знаменателями:

1	+	2	=	1 + 2	=	3
5		5		5		5

Пример 2.

Найти сумму двух дробей с одинаковыми знаменателями:

3	+	2	=	3 + 2	=	5
7		7		7		7

Онлайн калькулятор дробей

Упражнения на тему сложение и вычитание дробей с равными знаменателями

Сложение обыкновенных дробей.

Примеры сложения обыкновенных дробей

Пример 3.

Найти сумму двух дробей:

1	+	1	=	1·2	+	1	=	2	+	1	=	2 + 1	=	3	=	3	=	1
3		6		3·2		6		6		6		6		6		3·2		2

Пример 4.

Найти сумму двух дробей:

29	+	44	=	29·3	+	44·2	=	87	+	88	=	87 + 88	=
30		45		30·3		45·2		90		90		90

=	175	=	35·5	=	35	=	18 + 17	= 1	17
	90		18·5		18		18		18

Онлайн калькулятор дробей

Упражнения на тему сложение и вычитание двух обыкновенных дробей

Сложение смешанных чисел

Примеры сложения смешанных чисел

Пример 5.

Найти сумму двух смешанных чисел:

2	+	1	1	=	2·2	+	1	1·3	=	4	+	1	3	=	1 +	4 + 3	=
3			2		3·2			2·3		6			6			6

=	1 +	7	=	1 +	6 + 1	=	1 + 1	1	= 2	1
		6			6			6		6

Пример 6.

Найти сумму двух смешанных чисел:

1	5	+	2	3	=	1	5·4	+	2	3·3	=	1	20	+	2	9	=	3 +	20 + 9	=
	6			8			6·4			8·3			24			24			24

=	3 +	29	=	3 +	24 + 5	=	3 + 1	5	= 4	5
		24			24			24		24

Онлайн калькулятор дробей

Упражнения на тему сложение и вычитание двух смешанных чисел

Вычитание дробей

Вычитание дробей с одинаковыми знаменателями.

Определение.

Чтобы найти разницу двух дробей с одинаковыми знаменателями, нужно вычесть из числителя первой дроби числитель второй, а знаменатель оставить без изменений:

a	—	b	=	a — b
c		c		c

Примеры вычитания дробей с одинаковыми знаменателями

Пример 7.

Найти разность двух дробей с одинаковыми знаменателями:

3	—	1	=	3 — 1	=	2
5		5		5		5

Пример 8.

Найти разность двух дробей с одинаковыми знаменателями:

8	—	5	=	8 — 5	=	3
41		41		41		41

Онлайн калькулятор дробей

Упражнения на тему сложение и вычитание дробей с равными знаменателями

Вычитание обыкновенных дробей.

Примеры вычитания обыкновенных дробей

Пример 9.

Найти разность двух дробей:

5	—	1	=	5	—	1·3	=	5	—	3	=	5 — 3	=	2	=	2	=	1
6		2		6		2·3		6		6		6		6		2·3		3

Пример 10.

Найти разность двух дробей:

3	—	1	=	3·3	—	1·5	=	9	—	5	=	9 — 5	=	4	=	2·2	=	2
10		6		10·3		6·5		30		30		30		30		15·2		15

Онлайн калькулятор дробей

Упражнения на тему сложение и вычитание двух обыкновенных дробей

Вычитание смешанных чисел.

Примеры вычитания смешанных чисел

Пример 11.

Найти разность двух смешанных чисел:

2	1	—	1	1	=	2	1·3	—	1	1·2	=	(2 — 1)	+	3	—	2	=
	2			3			2·3			3·2				6		6

=	1	+	3 -2	=	1	+	1	=	1	1
			6				6			6

Пример 12.

Найти разность двух смешанных чисел:

3	1	—	1	3	=	3	1·4	—	1	3·3	=	3	4	—	1	9	=
	6			8			6·4			8·3			24			24

=	2	24 + 4	—	1	9	=	1 +	28 — 9	=	1 +	19	= 1	19
		24			24			24			24		24

Пример 13.

Найти разность двух смешанных чисел:

1	1	—	3	2	=	1	1	—	3	2·2	=	1	1	—	3	4	=	(1-3)	+	1 — 4	=
	6			3			6			3·2			6			6				6

= -2	—	3	=	-2	—	3	=	-2	—	1	=	-2	1
		6				2·3				2			2

Онлайн калькулятор дробей

Упражнения на тему сложение и вычитание двух смешанных чисел

Дроби Виды дробей (обыкновенная правильная, неправильная, смешанная, десятичная) Основное свойство дроби Сокращение дроби Приведение дробей к общему знаменателю Преобразование неправильной дроби в смешанное число Преобразование смешанного числа в неправильную дробь Сложение и вычитание дробей Умножение дробей Деление дробей Сравнение дробей Преобразование десятичной дроби в обыкновенную дробь

Онлайн калькуляторы дробей

Онлайн упражнения с дробями

Дробь 2 9/2 в виде десятичной дроби

Калькулятор «Конвертер обыкновенных дробей в десятичные»

Как записать 2 целых 9/2 в виде десятичной дроби?

Ответ: Дробь 2 9/2 в десятичном виде это 6,5

Объяснение конвертации дроби 2 9/2 в десятичную

Для того, чтобы перевести дробь 2 9/2 в десятичный формат необходимо разделить числитель 9 на знаменатель 2.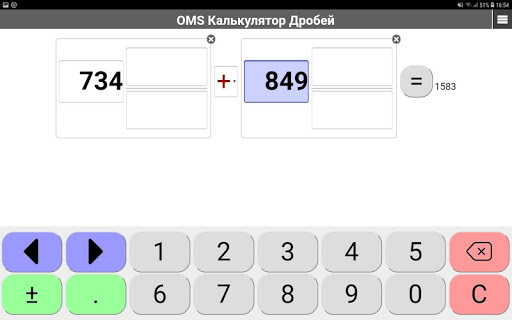 Результат деления:

9 ÷ 2 = 6,5

и прибавить целую часть (2):

4.5 + 2 = 6,5

---

Другой способ перевод дроби 2 целых 9/2 в десятичный формат заключается в том, чтобы перевести эту смешанную дробь в неправильную дробь. Для этого необходимо сперва умножить целую часть (2) на знаменатель (2):

2 × 2 = 4

после чего прибавить результат к числителю (9):

4 + 9 = 13

и в конце разделить результат на числитель (2):

= 13 ÷ 2 =6,5

Поделитесь текущим расчетом

Печать

https://calculat.io/ru/number/fraction-as-a-decimal/2—9—2

<a href=»https://calculat.io/ru/number/fraction-as-a-decimal/2—9—2″>Дробь 2 9/2 в виде десятичной дроби — Calculatio</a>

О калькуляторе «Конвертер обыкновенных дробей в десятичные»

Данный онлайн-конвертер обыкновенных дробей в десятичные является полезным инструментом, предназначенным для легкого преобразовывания любой дроби в ее эквивалентную десятичную форму. Например, он может помочь узнать как записать 2 целых 9/2 в виде десятичной дроби? Независимо от того, являетесь ли вы учеником, студентом или профессионалом, этот конвертер может сэкономить ваше время и усилия при выполнении ручных вычислений.

Чтобы использовать этот конвертер, просто введите дробь, которую вы хотите преобразовать, в соответствующие поля. Вам необходимо ввести целую часть (если есть), числитель и знаменатель дроби. Например, если вы хотите преобразовать 2 9/2 в его десятичный эквивалент, вы введете ‘2’ как целую часть, ‘9’ как числитель и ‘2’ как знаменатель.

После того, как вы ввели дробь, нажмите кнопку ‘Конвертировать’, чтобы получить результаты. Конвертер отобразит десятичный эквивалент дроби, который в нашем случае равен 6,5. Кроме того, он предоставит пошаговое объяснение процесса преобразования, чтобы вы могли понять, как был получен десятичный эквивалент дроби. Если результат является периодической десятичной дробью, конвертер отобразит повторяющийся шаблон, используя скобки для обозначения повторяющихся цифр.

Одной из ключевых особенностей этого конвертера является его способность выводить периодические десятичные дроби. В математике периодическая десятичная дробь — это десятичная дробь, в которой есть повторяющийся шаблон цифр, например, 0,33333… или 0,142857142857… Это отличает такие дроби от непериодических десятичных дробей, которые заканчиваются после определенного числа цифр, например, 0,5 или 0,75.

Использование этого онлайн-конвертера дробей в десятичные является быстрым и простым способом преобразования любой дроби в ее десятичный эквивалент. Он может быть особенно полезен тем, кто испытывает трудности с ручными вычислениями или кто часто выполняет преобразования.

Калькулятор «Конвертер обыкновенных дробей в десятичные»

Таблица конвертации обыкновенных дробей в десятичные

Дробь	Десятичная
2 9/1	11
2 9/2	6,5
2 9/3	5
2 9/4	4,25
2 9/5	3,8
2 9/6	3,5
2 9/7	3,(285714)
2 9/8	3,125
2 9/9	3
2 9/10	2,9
2 9/11	2,(81)
2 9/12	2,75
2 9/13	2,(692307)
2 9/14	2,6(428571)
2 9/15	2,6
2 9/16	2,5625
2 9/17	2,(5294117647058823)
2 9/18	2,5
2 9/19	2,(473684210526315789)
2 9/20	2,45
2 9/21	2,(428571)
2 9/22	2,4(09)
2 9/23	2,(3913043478260869565217)
2 9/24	2,375
2 9/25	2,36
2 9/26	2,3(461538)
2 9/27	2,(3)
2 9/28	2,32(142857)
2 9/29	2,(3103448275862068965517241379)
2 9/30	2,3

Расчет промилле, калькулятор промилле, промилле, калькулятор промилле

Завершите предложение, описывающее вашу проблему.

Введите значения и нажмите Вычислить .

• Express 6027
  Express снижение на 8 процентов на миллион.
• Опрыскивание от насекомых
  В 600 мл опрыскивания находится 5 мл действующего вещества. Сколько это за милю?
• Рассчитайте 72994
  Рассчитайте 50 промилле от 340.
• Синдром Дауна
  Синдром Дауна — одно из серьезных заболеваний, вызванных генной мутацией. Синдром Дауна встречается примерно у каждого 550 родившегося ребенка. Выразите заболеваемость синдромом Дауна у новорожденных в промилле.
• Золотая монета
  Золотая монета содержит 900 промилле чистого золота. Вес монеты 950 грамм. Сколько промилле золота? Сколько грамм золота?
• Десятичный 26301
  Запишите промилле в виде десятичного числа 2 ‰ 50 ‰ 2,5 ‰ 0,6 ‰
• Promile
  Рассчитайте 4,6 ‰ от 199.
• Штраф ежедневно
  Джон должен был заплатить 1500 чешских крон. Если он не заплатит вовремя, с него будет начислен штраф в размере 0,5 промилле причитающейся суммы за каждый день просрочки. Он вспомнит через 30 дней. Сколько стоит штраф?
• Амфитеатр
  Амфитеатр имеет форму полукруга, зрители сидят по периметру полукруга, а сцена образует диаметр полукруга. Кто из зрителей, P, Q, R, S, T, видит сцену под наибольшим углом обзора?
• Неизвестно 73244
  75 промилле неизвестного числа равно 60. Что такое неизвестное число?
• Дивиденды
  Трое друзей разделили выигрыш на вложенные деньги. Карлос получил три восьмых, Джон 320 пермиль, а остальные достались Мартину. Кто получил больше, а кто меньше?
• Золотая монета
  Золотая монета содержит чистое золото 962 промилле, что составляет 7,5 г. Каков вес монеты в граммах?
• Пермилл
  Сколько на мельницы будет 978 из 84370?
• Автомобильная авария
  После дорожно-транспортного происшествия полиция измерила 1,16 промилле алкоголя в крови водителя. В организме человека циркулирует около 5 кг крови. Какое количество алкоголя было у водителя в крови?
• Железная дорога
  Железнодорожная линия имеет уклон 12 промилле. На сколько метров он поднимется на расстояние 4 км по горизонтали?
• AMSL и катание на лыжах
  Томас идет на лыжах из точки A (3200 м над уровнем моря в точку B. Гора имеет уклон 20%. Горизонтальное расстояние между стартом и финишем 2,5 км. На какой высоте находится точка B?
• Километры 81387
  Рассчитайте уклон железнодорожной линии, высота которой составляет 22,5 метра на участке длиной 1,5 километра. Для железных дорог результат дается в ч (промилле).

другие математические задачи »

Часто искомые расчеты промилле

• десятичные дроби
• дроби
• треугольник ΔABC
• проценты %
• промилле ‰
• простые множители
• комплексные числа
• LCM
• НОД
• LCD
• комбинаторика
• уравнения
• статистика
• … все математические калькуляторы

Калькулятор дробей: сложение и вычитание дробей

Как использовать калькулятор дробей: Введите значения числителя и знаменателя, выберите арифметический оператор, а калькулятор сделает все остальное.

Основное определение дроби

Дробь — это числовая величина, представляющая часть целого числа. В математических терминах дробь выражается делением одного целого числа (числителя) на другое целое число (знаменатель), например 1/3, 1/5, 2/7 и т. д.

На повседневном языке мы можем просто сказать, что дробь — это количество частей определенного размера, например одна восемь пятых.

Простые методы вычисления дробей

Простое сложение дробей

Ключевой момент для правильного сложения дробей — всегда помнить о самой важной части дроби, то есть о числе под чертой, известном как знаменатель. Если у нас есть ситуация, когда знаменатели в дробях, участвующих в процессе сложения, одинаковы, то мы просто складываем числа, которые находятся над разделительной чертой, или, как сказал бы математик, «складываем только числители». Мы можем посмотреть на пример сложения двух дробей, таких как 3/7 и 4/7. Выражение будет выглядеть так: 3/7 + 4/7 = 7/7. В случае, когда числитель равен знаменателю, как в предыдущем примере, его также можно приравнять к 1.

Однако это был один из самых простых примеров сложения дробей. Процесс может немного усложниться, если мы столкнемся с ситуацией, когда знаменатели дробей, участвующих в расчете, различны. Тем не менее, существует правило, которое позволяет нам эффективно выполнять этот тип расчета. Запомните первое: при сложении дробей знаменатели всегда должны быть одинаковыми, или, выражаясь языком математиков, у дробей должен быть общий знаменатель. Для этого нам нужно посмотреть на знаменатель, который у нас есть. Вот пример: 2⁄3 + 3⁄5. Так что общего знаменателя у нас пока нет. Поэтому воспользуемся таблицей умножения, чтобы найти число, которое является произведением 5 на 3. Это 15. Значит, общим знаменателем для этой дроби будет 15. Однако это еще не конец. Если мы разделим 15 на 3, то получим 5. Итак, теперь нам нужно умножить числитель первой дроби на 5, что даст нам 10 (2 х 5). Кроме того, мы умножаем числитель второй дроби на 3, потому что 15/5 = 3. Получаем 9(3 х 3 = 9). Теперь мы можем ввести все эти числа в выражение: 10/15 + 9/15 = 19/15.

Примечание. Если числитель больше знаменателя, мы делим его на последний.

Простое вычитание дробей

Для правильного вычитания дробей важно всегда помнить, что самой важной частью дроби является число под чертой, известное как знаменатель. Если у нас есть ситуация, когда знаменатели в дробях, участвующих в процессе вычитания, одинаковы, то мы просто вычитаем числа, которые находятся над разделительной линией или, как сказал бы математик: «вычитание только числителей». Мы можем посмотреть на пример вычитания двух дробей, таких как 3/7 и 4/7. Выражение будет выглядеть так: 4/7 — 3/7 = 1/7.

Однако это был один из самых простых примеров вычитания дробей. Процесс может немного усложниться, если мы столкнемся с ситуацией, когда знаменатели дробей, участвующих в расчете, различны. Тем не менее, существует правило, которое позволяет нам эффективно выполнять этот тип расчета. Запомните первое: при вычитании дробей знаменатели всегда должны быть одинаковыми, или, выражаясь языком математиков, у дробей должен быть общий знаменатель.