Калькулятор угол между векторами: Онлайн калькулятор. Вычисление угла между векторами

Угол между векторами калькулятор

Укажите размерность пространства 23
Укажите форму представления первого вектора Координаты точек начала и конца первого вектораКоординаты первого вектора
Укажите форму представления второго вектора Координаты точек начала и конца второго вектораКоординаты второго вектора

Задайте координаты первого вектора
a̅ = { ; }

Задайте координаты вектора b
b̅ = { ; }

Как найти угол между векторами

Чтобы вычислить угол между векторами a и b, где a = {a_x; a_y} и b = {b_x; b_y} необходимо:

1.Вычислить скалярное произведение векторов a и b.

2. Вычислить длину вектора a.

3. Вычислить длину вектора b.

4. Вычислить произведение длин векторов a и b.

5. Вычислить косинус α. Разделить скалярное произведение векторов на произведение длин векторов.

6. Вычислить арккосинус α.

---

Формулы вычисления угла между векторами

Если векторы a и b заданы координатами, где a = {a_x; a_y} и b = {b_x; b_y}, то косинус угла α вычисляется по формуле:

Формула вычисления косинуса угла α между векторами a и b, где
a = {a_x; a_y}
b = {b_x; b_y}

Если векторы a и b заданы координатами, где a = {a_x; a_y} и b = {b_x; b_y}, то угол в радианах вычисляется по формуле:

Формула вычисления угла между векторами a и b в радианах, где
a = {a_x; a_y}
b = {b_x

; b_y}

Если векторы a и b заданы координатами, где a = {a_x; a_y; a_z} и b = {b_x; b_y; b_z}, то косинус угла α вычисляется по формуле:

Формула вычисления косинуса угла α между векторами a и b, где
a = {a_x; a_y; a_z}
b = {b_x; b_y; b_z}

Если векторы a и b заданы координатами, где a = {a_x; a_y; a_z} и b = {b_x; b_y; b_z}, то угол в радианах вычисляется по формуле:

Формула вычисления угла между векторами a и b в радианах, где
a = {a_x; a_y; a_z}
b = {b_x; b_y; b_z}

Если координаты обоих векторов заданы точками – вектора a задан точками A(x, y) и B(x, y), вектор

b задан точками C(x, y) и D(x, y), то косинус угла α вычисляется по формуле:

Формула вычисления косинуса угла α между векторами a и b, где
A = (A_x; A_y)
B = (B_x; B_y)
C = (C_x; C_y)
D = (D_x; D_y)

Если координаты обоих векторов заданы точками – вектора a задан точками A(x, y) и B(x, y), вектор b задан точками C(x, y) и D(x, y), то угол α в радианах вычисляется по формуле:

Формула вычисления угла α в радианах между векторами a и b, где
A = (A_x; A_y)
B = (B_x; B_y)
C = (C_x; C_y)
D = (D_x; D_y)

Если координаты обоих векторов заданы точками – вектора

a задан точками A(x, y, z) и B(x, y, z), вектор b задан точками C(x, y, z) и D(x, y, z), то косинус угла α вычисляется по формуле:

Формула вычисления косинуса угла α между векторами a и b, где
A = (A_x; A_y; A_z)
B = (B_x; B_y; B_z)
C = (C_x; C_y; C_z)
D = (D_x; D_y; D_z)

Если координаты обоих векторов заданы точками – вектора a задан точками A(x, y, z) и B(x, y, z), вектор b задан точками C(x, y, z) и D(x, y, z), то угол α в радианах вычисляется по формуле:

Формула вычисления угла α в радианах между векторами a и b, где
A = (A_x; A_y; A_z)
B = (B_x; B_y; B_z)
C = (C _x; C_y; C_z)
D = (D_x; D_y; D_z)

Если необходимо вычислить значение угла в градусах, то необходимо значение угла между векторами умножить на 180 и получившееся значение разделить на π

Перевод значения угла в радианах в градусы

---

Примеры вычисления угла между векторами

Пример 1. Найдем угол между векторами плоскости. Координаты обоих векторов заданны точками.

Координаты точки А вектора AB: (5 ; 9)
Координаты точки B вектора AB: (-2 ; 11)
Координаты точки C вектора CD: (0 ; 12)
Координаты точки D вектора CD: (-3 ; 1)

cos α =	AB ⋅ CD
	|AB| ⋅ | CD|

Решение:

1) Вычислим модуль (длину) первого и второго векторов:

|AB| =

(B_x — A_x)² + (B_y — A_y)²

=

(-2 — 5)² + (11 — 9)²

=

(-7)² + 2²

=

49 + 4

=

53

= 7. 28010988928052
|CD| =

(D_x — C_x)² + (D_y — C_y)²

=

(-3 — 0)² + (1 — 12)²

=

(-3)² + (-11)

2

=

9 + 121

=

130

= 11.4017542509914

2) Вычислим произведение модулей векторов:

|AB| ⋅ |CD| =

53

⋅

130

=

6890

3) Вычислим координаты первого вектора по двум точкам A и B:

AB = {B_x — A_x  ; B_y — A_y} = {-2 — 5 ; 11 — 9} = {-7 ; 2}

4) Вычислим координаты второго вектора по двум точкам C и D:

CD = {D_x — C_x  ; D_y — C_y} = {-3 — 0 ; 1 — 12} = {-3 ; -11}

5) Найдем скалярное произведение векторов: AB и CD

AB ⋅ CD = AB_xCD_x + AB_yCD_y = -7 ⋅ (-3) + 2 ⋅ (-11) = 21 + (-22) = -1

6) Вычислим косинус угла между векторами:

cos α =	AB ⋅ CD	=
	|AB| ⋅ |CD|

-1 / 6890 = -0. 0120473184147734

7) Вычислим значение угла ∠α между векторами:

∠α = 1.58284393664908 Radians
∠α = 90.6902771978651° Degrees

---

Пример 2. Найдем угол между векторами плоскости.

Координаты вектора a: (5 ; 9)
Координаты вектора b: (-1 ; 7)

cos α =	a ⋅ b
	|a | ⋅ |b|

Решение:

1) Вычислим модуль (длину) первого и второго векторов:

|a| =

a_x² + a_y²

=

5² + 9²

=

25 + 81

=

106

= 10.295630140987
|b| =

b_x² + b_y²

=

(-1)² + 7²

=

1 + 49

=

50

= 5

2

= 7. 07106781186548

2) Вычислим произведение модулей векторов:

|a| ⋅ |b| =

106

⋅

50

=

5300

3) Найдем скалярное произведение векторов: a и b

a ⋅ b = a_xb_x + a_yb_y = 5 ⋅ (-1) + 9 ⋅ 7 = -5 + 63 = 58

4) Вычислим косинус угла между векторами:

cos α =	a ⋅ b	=
	|a| ⋅ |b|

58 / 5300 = 0.796691270902396

5) Вычислим значение угла ∠α между векторами:

∠α = 0.648995558996501 Radians
∠α = 37.1847064532332° Degrees

---

Пример 3. Найдем угол между векторами пространства.

Координаты обоих векторов заданны точками.

Координаты точки А вектора AB: (7; 0.2 ; 69)
Координаты точки B вектора AB: (-1 ; 0 ; 2/8)
Координаты точки C вектора CD: (-4 ; -6 ; 2)
Координаты точки D вектора CD: (3 ; 0 ; 9)

cos α =	AB ⋅ CD
	|AB| ⋅ |CD|

Решение:

1) Вычислим модуль (длину) первого и второго векторов:

|AB| =

(B_x — A_x)² + (B_y — A_y)² + (B_z — A_z)²

=

(-1 — 7)² + (0 — 0.2)² + (2/8 — 69)²

=

(-8)² + (-0.2)² + (-275/4)²

=

64 + 0. 04 + (75625/16)

=

	1916241
	400

69.2141784607749

|CD| =

(D_x — C_x)² + (D_y — C_y)² + (D_z — C_z)²

=

(3 — (-4))² + (0 — (-6))² + (9 — 2)²

=

7² + 6² + 7²

=

49 + 36 + 49

=

134

= 11.5758369027902

2) Вычислим произведение модулей векторов:

|AB| ⋅ |CD| =

1916241/400

⋅

134

=

641940. 735

3) Вычислим координаты первого вектора по двум точкам A и B:

AB = {B_x — A_x  ; B_y — A_y; B_z — A_z} = {-1 — 7 ; 0 — 0.2 ; 2/8 — 69} = {-8 ; -1/5 ; -275/4}

4) Вычислим координаты второго вектора по двум точкам C и D:

CD = {D_x — C_x  ; D_y — C_y; D_z — C_z} = {3 — (-4) ; 0 — (-6) ; 9 — 2} = {7 ; 6 ; 7}

5) Найдем скалярное произведение векторов: AB и CD

AB ⋅ CD = AB_xCD_x + AB_yCD_y + AB_zCD_z = -8 ⋅ 7 + (-1/5) ⋅ 6 + (-275/4) ⋅ 7 = -56 + (-6/5) + (-1925/4) = -10769/20 = -538.45

6) Вычислим косинус угла между векторами:

cos α =	AB ⋅ CD	=
	|AB| ⋅ |CD|

-538.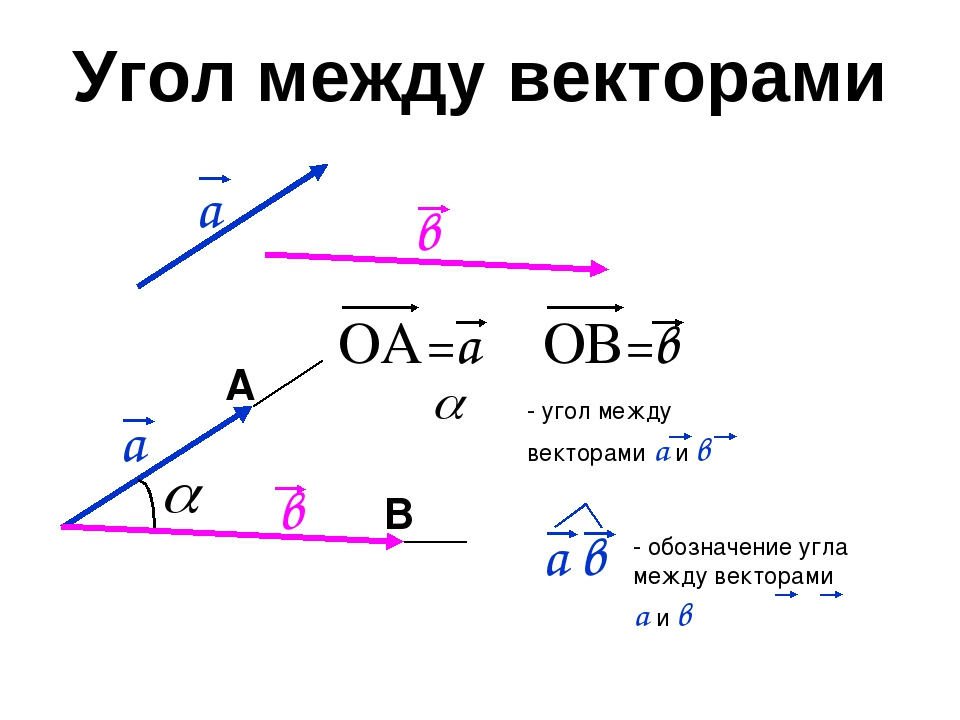 45 / 641940.735 = -0.672044318228661

7) Вычислим значение угла ∠α между векторами:

∠α = 2.30776235411475 Radians
∠α = 132.225043009951° Degrees

---

Пример 4. Найдем угол между векторами пространства.

Координаты вектора a: (5 ; 1 ; 7)
Координаты вектора b: (2 ; 4 ; 6)

cos α =	a ⋅ b
	|a| ⋅ |b|

Решение:

1) Вычислим модуль (длину) первого и второго векторов:

|a| =

a_x² + a_y² + a_z²

=

5² + 1² + 7²

=

25 + 1 + 49

=

75

= 5

3

= 8. 66025403784439
|b| =

b_x² + b_y² + b_z²

=

2² + 4² + 6²

=

4 + 16 + 36

=

56

= 2

14

= 7.48331477354788

2) Вычислим произведение модулей векторов:

|a| ⋅ |b| =

75

⋅

56

=

4200

3) Найдем скалярное произведение векторов: a и b

a ⋅ b = a_xb_x + a_yb_y + a_zb_z = 5 ⋅ 2 + 1 ⋅ 4 + 7 ⋅ 6 = 10 + 4 + 42 = 56

4) Вычислим косинус угла между векторами:

cos α =	a ⋅ b	=
	|a| ⋅ |b|

56 / 4200 = 0. 864098759787715

5) Вычислим значение угла ∠α между векторами:

∠α = 0.527439299499548 Radians
∠α = 30.2200458106607° Degrees

XYZ — Скалярное произведение векторов. Он-лайн калькуляторы скалярного произведения и угла между векторами по координатам.

Скалярное произведение векторов. Он-лайн калькуляторы скалярного произведения и угла между векторами по координатам. Скалярное произведение векторов — это операция над двумя векторами, результатом которой является число (не вектор). Определяется скалярное произведение, как правило, следующим образом: Иными словами, скалярное произведение векторов равно произведению длин этих векторов на косинус угла между ними . Необходимо заметить, что угол между двумя векторами — это угол, который они образуют, если отложить их от одной точки, то есть начала векторов должны совпадать. Непосредственно из определения следуют следующие простейшие свойства: 1. Скалярное произведение произвольного вектора а на себя же (скалярный квадрат вектора а) всегда неотрицательно, и равно квадрату длины этого вектора. Причем скалярный квадрат вектора равен нулю тогда и только тогда, когда данный вектор — нулевой. 2.Скалярное произведение любых перпендикулярных векторов a и b равно нулю. 3. Скалярное произведение двух векторов равно нулю тогда и только тогда, когда они перепендикулярны или хотя бы один из них — нулевой. 4. Скалярное произведение двух векторов a и b положительно тогда и только тогда, когда между ними острый угол. 5.Скалярное произведение двух векторов a и b отрицательно тогда и только тогда, когда между ними тупой угол. Альтернативное определение скалярного произведения, или вычисление скалярного произведения двух векторов, заданных своими координатами. (Вычислить координаты вектора, если заданы координаты его начала и его конца очень просто — Пусть есть вектор AB, А — начало вектора, В — конец, и координаты этих точек А=(a1,a2,a3),        В=(b1,b2,b3) Тогда координаты вектора АВ: АВ={b1-a1, b2-a2, b3-a3}. Аналогично в двухмерном пространстве — просто отсутствуют третьи координаты) Итак, пусть даны два вектора, заданные набором своих координат: а) В двухмерном пространстве(на плоскости). Тогда их скалярное произведение можно вычислить по формуле: б) В трехмерном пространстве Аналогично двухмерному случаю, их скалярное произведение вычисляется по формуле: Вычисление угла между векторами с помощью скалярного произведения. Самое распространенное математическое приложение скалярного произведения двух векторов — это вычисление угла между векторами, заданными своими координатами. Для примера возьмем трехмерный случай. (Если вектора заданы на плоскости, то есть двумя координатами, во всех формулах просто отсутствуют третьи координаты.) Итак, пусть у нас есть два вектора: И нам нужно найти угол между ними. С помощью их координат найдем их длины, а затем просто приравняем две формулы для скалярного произведения. Таким образом мы получим косинус искомого угла. Длина вектора а вычисляется как корень из скалярного квадрата вектора а, который мы вычислим по формуле для скалярного произведения векторов, заданных координатами: Аналогично вычисляется длина вектора b. Итак, Значит, Искомый угол найден. Он-лайн калькулятор скалярного произведения двух векторов. Чтобы найти скалярное произведение двух векторов с помощью данного калькулятора, нужно ввести в первую строку по порядку координаты первого вектора, во вторую- второго. Координаты векторов могут быть вычислены по координатам их начала и конца (см. выше Альтернативное определение скалярного произведения, или вычисление скалярного произведения двух векторов, заданных своими координатами. ) Если вектора заданы двумя координатами, то на месте третьей координаты каждого вектора нужно поставить ноль. Координаты первого вектора: { ,    ,    } Координаты второго вектора: { ,    ,    } Ответ:  Он-лайн калькулятор угла между векторами. Аналогично предыдущему калькулятору, необходимо ввести координаты обоих векторов по порядку, и если вектора заданы двумя координатами — на месте третьих координат следует поставить ноль. Координаты первого вектора: { ,    ,    } Координаты второго вектора: { ,    ,    } Ответ:  o

Калькулятор угла между двумя векторами

Онлайн-калькулятор угла между двумя векторами позволяет найти угол, величину и скалярное произведение между двумя векторами. Неважно, являются ли векторные данные 2D или 3D, наш калькулятор хорошо работает во всех аспектах. Итак, продолжайте читать, чтобы узнать, как использовать формулы и несколько примеров, чтобы найти угол между двумя векторами.

Что такое угол между двумя векторами?

В математике угол между двумя векторами определяется как кратчайший угол, на который один из векторов поворачивается в положение, соответствующее другому вектору. Помните, что векторные величины имеют как величину, так и направление. 2)}}]$$ 92)}]}$$

Вы можете определить один угол по координатам, а другой по конечной точке с калькулятором угла между двумя векторами.

Как найти угол между двумя векторами

Скалярное произведение выражается как произведение размеров или величин векторов на cos угла между ними (здесь обозначается θ): 92)})]$$

Эти формулы используются калькулятором угла между векторами для величины двумерных и трехмерных векторов.

Тем не менее, используйте бесплатный онлайн-калькулятор косинуса, который поможет вам рассчитать значение косинуса заданного угла в градусах и радианах.

Пример: найти угол между двумя трехмерными векторами

A = {4, 6, 8}

B = {3, 2, 5}

Теперь начнем с скалярного произведения A и B, A.B

$$A ⋅B =Ax . Вх+Ау. По + Аз . Бз$$ 92}$$

$$|A|=\sqrt{(4)2+(6)2+(8)2}$$

$$|A|=\sqrt{16+36+64}$ $

$$|A|=10,77033$$

Величина вектора B:

$$|B|=\sqrt{Bx2+By2+Bz2}$$

$$|B|=\sqrt {(3)2+(2)2+(5)2}$$

$$|B|=\sqrt{9+4+25}$$

$$|B|=6,16441$$

Угол между векторами A и B:

$$cosθ=(A, B)/(|A||B|)$$

$$cosθ=(64)/(10,77033∗6,16441)$$

$$cosθ=(64)/(66,39277)$$

$$cosθ=0,9639604$$

$$θ=15. 42911 град$$

Однако вы можете получить точные значения, подставив одинаковые значения в калькулятор угла между векторами.

Как работает калькулятор угла между двумя векторами?

Калькулятор угла между векторами Найдите угол θ, разделяющий два вектора A и B в двухмерном и трехмерном пространстве, с помощью следующих шагов:

Ввод:

• Сначала выберите двумерное или трехмерное измерение векторов.
• Теперь выберите векторное представление (по координатам или конечным точкам) из раскрывающегося списка.
• Затем вставляет все заданные значения в соответствующие поля.
• Чтобы увидеть результаты, нажмите кнопку «Рассчитать».

Вывод:

• Калькулятор угла между двумя векторами обеспечивает пошаговые вычисления скалярного произведения, величины и угла между векторами.
• Вы можете многократно находить 2D- и 3D-векторы в соответствии с требованиями, нажав кнопку пересчета.

Часто задаваемые вопросы:

Определить угол между двумя антипараллельными векторами?

Антипараллельные векторы — это параллельные векторы в противоположных направлениях. Угол между этими двумя векторами равен 180°.

Какова величина единичного вектора?

Поскольку единичный вектор равен 1 по определению, если вы хотите использовать единичный вектор в направлении A, вы должны разделить на эту величину.

Является ли угол векторной величиной?

На самом деле угол представляет собой безразмерный вектор. У него есть направление и величина. Мы можем измерять углы по часовой стрелке и против часовой стрелки, основываясь на их поведении при вращении. Следовательно, этот угол действительно является «векторной величиной».

Вывод:

Используйте этот калькулятор угла между двумя векторами, чтобы определить угол между компонентами вектора. Понятие угла вектора используется для описания угловой разницы физической величины, приписываемой величине и направлению. Угол вектора рассчитывается от первой конечной точки. Этот бесплатный онлайн-калькулятор быстро рассчитывает скалярное произведение и величину со 100% точностью.

Ссылка:

Из источника Википедии: Алгебраическое определение, Геометрическое определение, Скалярная проекция и первые свойства, Эквивалентность определений, Применение к закону косинусов, Отношения векторной алгебры, Величины.

Из источника Wiki Как: найти угол между двумя векторами, определить формулу угла, написать закон косинусов для этого треугольника.

Из источника Кристы Кинг Математика: Угол между двумя векторами, Формула для угла между векторами, Как вычислить угол, Нахождение угла между двумя векторами в трех измерениях.

 

Калькулятор угла между двумя векторами

Калькулятор угла между двумя векторами

Требуемая единица ответа:

Радианы, градусы

Как использовать этот калькулятор

Решение

Вернуться к калькулятору

Заполните поля ввода для вычисления решения.

Хотите неограниченный доступ к калькуляторам, ответам и шагам решения?

Присоединяйтесь сейчас

100% без риска. Отменить в любое время.

Угол между двумя векторами Урок

Обзор угла между двумя векторами

Вектор — это величина, которая имеет как величину, так и направление. Это часто изображается стрелкой заданной длины (величины), указывающей в определенном направлении в двухмерном или трехмерном пространстве. Кратчайший угол, на который одна из стрелок (векторов) поворачивается, чтобы соответствовать направлению другой стрелки (вектора), известен как угол между двумя векторами.

Рис. 1 — Угол θ Между векторами u и v

Почему мы узнаем об угле между двумя векторами?

Скалярные произведения векторов и углов между ними могут быть полезными строительными блоками не только для понимания теоретических отношений между векторами, но и для понимания того, как эти отношения коррелируют с нашей жизнью практическим или материальным образом.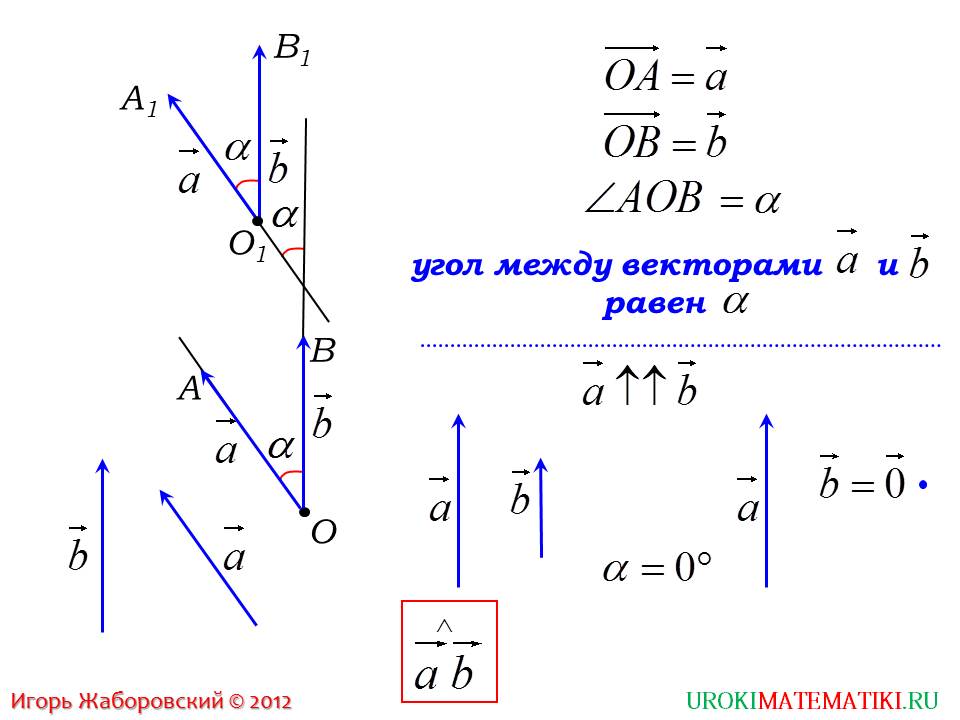

А что может быть более осязаемым, чем сесть в автомобиль для катания на американских горках и рухнуть вниз с крутого обрыва?

Автомобиль для катания на американских горках

Допустим, мы проектируем новые американские горки и хотим получить общее представление о некоторых характеристиках аттракциона, основанных на профиле трассы и весе транспортного средства. В этом случае мы хотим получить оценку работы, выполняемой транспортным средством под действием силы тяжести, когда оно ускоряется вниз по линейному склону.

Рисунок 2. Американские горки, ускоряющиеся вниз по трассе

Зная вес транспортного средства, пройденное линейное расстояние и угол трассы, мы можем использовать концепцию скалярных произведений и угол между векторами для оценки работы, проделанной над транспортным средством. к тому времени, когда он достигнет дна капли. Это полезная информация, потому что мы можем предсказать, сколько энергии потребуется тормозной системе, чтобы остановить транспортное средство в конце падения.

Теперь давайте посмотрим на уравнение работы и сравним его с уравнением, используемым для связи угла между двумя векторами с скалярным произведением двух векторов:

$$\begin{align} & \text{Work } = F \cdot d = |F| |д| \: cos \: \theta \\ \\ & cos \: \theta = \frac{\textbf{u} \cdot \textbf{v}}{\left| \textbf{и} \право| \влево| \textbf{v} \right|} \end{align}$$

Как видите, второе уравнение представляет собой измененную версию первого. Теперь, если мы применим уравнение работы к нашему примеру, мы получим следующее:

$$\begin{align} & \text{Work } = W \cdot d = |W| |д| \: cos \: \theta \end{align}$$

Это помогает нам понять потребности в энергии для нашей тормозной системы, чтобы транспортное средство можно было безопасно остановить в конце падения.

Как вычислить угол между двумя векторами

Мы можем вычислить угол между двумя векторами, используя следующее уравнение:

$$\begin{align} & cos \: \theta = \frac{\textbf{u} \ cdot \textbf{v}}{\left| \textbf{и} \право| \влево| \textbf{v} \right|} \hspace{10ex} \textbf{ (1) } \end{align}$$

Где u · v — скалярное произведение векторов u и v , | и | величина вектора u , | против | — величина вектора v , а θ — угол между векторами u и v .

Шаги для определения угла между двумя векторами следующие:

1. Вычислить скалярное произведение u · v .
2. Найти | и | (величина вектора u ).
3. Найти | против | (величина вектора v ).
4. Заглушка u · v , | и |, и | против | в уравнение для нахождения угла между двумя векторами (уравнение 1) и решить для θ .
5. (Необязательно) При необходимости конвертируйте ответ в градусы из радианов.

Угол между двумя векторами Пример задачи

$$\begin{align} & \text{Дано:} \\ \\ & \textbf{u} = \langle 1, 2, 3\rangle \text{ и } \textbf {v} = \langle 4, 5, 6\rangle \\ \\ & \text{Найти угол между векторами } \textbf{u} \text{ и } \textbf{v} \text{.}\\ \ \ & \text{1.) Уравнение для нахождения угла } \theta \text{ между двумя векторами имеет вид:} \\ \\ & \hspace{3ex} cos \: \theta = \frac{\textbf{ u} \cdot \textbf{v}}{\left| \textbf{и} \право| \влево| \textbf{v} \right|} \\ \\ & \hspace{3ex} \text{Где: } \\ & \hspace{3ex} \textbf{u} \cdot \textbf{v} \text{ скалярное произведение векторов } \textbf{u} \text{ и } \textbf{v} \text{, } \left| \textbf{и} \право| \text{ является величиной } \\ & \hspace{3ex} \text{vector} \textbf{u} \text{, } \left| \textbf{v} \право| \text{ — величина вектора } \textbf{v} \text{, а } \theta \text{ — угол между} \\ & \hspace{3ex} \text{vectors} \textbf{u} \text { и } \textbf{v} \text{. }\\ \\ & \text{2.) Начнем с поиска } \textbf{u} \cdot \textbf{v} \: \text{:}\\ \\ & \hspace{4ex} \text{2.1) } \textbf{u} \cdot \textbf{v} = \langle1, 2, 3\rangle \cdot \langle 4, 5, 6\rangle = (1) (4) + (2)(5) + (3)(6) \\ \\ & \hspace{8ex} \Longrightarrow (4) + (10) + (18) = 32\\ \\ & \hspace{ 8ex} \Longrightarrow \textbf{u} \cdot \textbf{v} = 32\\ \\ & \text{3.) Далее найдем} \left| \textbf{и} \право| \text{ и} \left| \textbf{v} \право| \: \text{:}\\ \\ & \hspace{4ex} \text{3.1) } \left| \textbf{и} \право| = \ sqrt {\ textbf {u} \ cdot \ textbf {u}} = \ sqrt {\ langle1, 2, 3 \ rangle \ cdot \ langle1, 2, 3 \ rangle} = \ sqrt {(1) (1) + (2)(2) + (3)(3)} \\ \\ & \hspace{8ex} \Longrightarrow \sqrt{(1) + (4) + (9)} = \sqrt{(14)} = 3.74166\\ \\ & \hspace{8ex} \Longrightarrow \left| \textbf{и} \право| = 3.74166\\ \\ & \hspace{4ex} \text{3.2) } \left| \textbf{v} \право| = \ sqrt {\ textbf {v} \ cdot \ textbf {v}} = \ sqrt {\ langle4, 5, 6 \ rangle \ cdot \ langle4, 5, 6 \ rangle} = \ sqrt {(4) (4) + (5)(5) + (6)(6)} \\ \\ & \hspace{8ex} \Longrightarrow \sqrt{(16) + (25) + (36)} = \sqrt{(77)} = 8.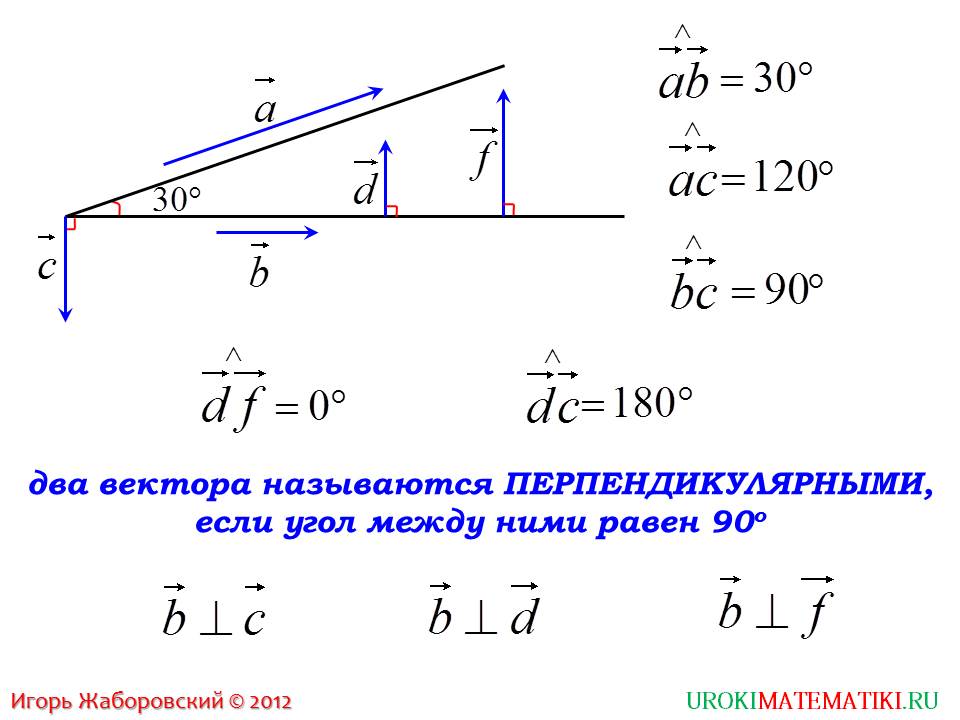 77496\\ \\ & \hspace{8ex} \Longrightarrow \left| \textbf{v} \право| = 8.77496\\ \\ & \text{4.) Теперь давайте подставим значения для } \textbf{u} \cdot \textbf{v} \text{, } \left| \textbf{и} \право| \text{, и} \left| \textbf{v} \право| \text{ в данное уравнение} \\ & \hspace{3ex} \text{из шага 1 и решить для } \theta \: \text{:}\\ \\ & \hspace{4ex} \text{4.1) } потому что \: \ theta = \ frac {\ textbf {u} \ cdot \ textbf {v}} {\ left | \textbf{и} \право| \влево| \textbf{v} \right|} \Longrightarrow cos \: \theta = \frac{(32)}{(3,74166)(8,7749{\circ} \text{.}\end{align}$$

Калькулятор угла между двумя векторами состоит из нескольких языков программирования. Эти языки включают HTML (язык гипертекстовой разметки), CSS (каскадные таблицы стилей) и JS (JavaScript).

HTML используется для создания базовой структуры полей калькулятора и решения. Этим полям присваиваются специальные идентификаторы, на которые ссылаются при стилизации элементов калькулятора, при выполнении специальных операций во время расчета и при использовании выпадающего меню для выбора единицы ответа.