Калькулятор упрощение выражений: Упрощение выражений · Калькулятор Онлайн

Упрощение Выражений — Mathcracker.Com

Инструкции: Используйте этот калькулятор упрощения выражений для сокращения любого действительного алгебраического выражения, которое вы предоставите, показывая все шаги. Пожалуйста, введите выражение, которое вы хотите упростить, используя правила PEMDAS.

Подробнее о калькулятор для упрощения выражений

Калькулятор упрощения с шагами позволяет упростить любое действительное выражение, включающее основные операции, в том числе сложение, вычитание, умножение, деление, дроби, радикалы и т.д.

Все, что вам нужно предоставить, это правильное выражение, включающее основные операции.

3+5+1/6)».

После того как вы введете правильное выражение, вам нужно нажать на кнопку «Рассчитать», и вам будут показаны все этапы упрощения вычислений.

Калькулятор сделает все возможное, чтобы показать значимые шаги для вычислений, и он, безусловно, достигает этого для большинства простых выражений.

Как упростить выражения с помощью умножения

Этот вопрос связан с другим вопросом — как упрощать выражения с суммами, а еще интереснее, как упростить выражения, в которых смешаны суммы и умножения? Ответ прост: PEMDAS

PEMDAS обеспечивает четкое правило того, какие операции имеют приоритет для выполнения в первую очередь. Следуйте этим правилам PEMDAS:

• Первый: «P» (что соответствует «круглым скобкам»). В алгебраическом выражении круглые скобки имеют приоритет всегда.
• Следующий: «E» (экспоненты). После круглых скобок приоритет отдается экспонентам
• Следующий: «М» (умножение). После экспоненты приоритет отдается умножению
• Следующий: «D» (деление). После умножения приоритет отдается делению
• Следующий: «А» (дополнение). После делений приоритет отдается дополнениям
• Наконец: «S» (вычитание). После сложения приоритет отдается вычитанию

Эти правила позволят вам однозначно оценить составное выражение. Этот калькулятор покажет вам этапы упрощения, следуя правилам приоритета PEMDAS

Каковы шаги упрощения выражения

• Шаг 1: Оцените, хорошо ли определено выражение. Это может быть не прямое или простое определение, в зависимости от сложности передаваемого выражения
• Шаг 2: Если он недействителен, остановитесь, процесс завершается. Если он действителен, то вы используете PEMDAS для руководства процессом упрощения
• Шаг 3: Перейдите к упрощению по приоритетам, при необходимости сделайте много шагов, следя поочередно за приоритетами PEMDAS, пока выражение не будет невозможно упростить дальше

Как упростить выражения с дробями?

В целом, это легко упрощать дроби , потому что стратегию невозможно пропустить: нужно найти общие знаменатели. Например, в простейшем случае с 2 дробями, вы получите:

\[\displaystyle \frac{a}{b} \times \frac{c}{d} = \displaystyle \frac{ac}{bd} \]

К сожалению, существуют выражения, которые намного сложнее простых дроби . {1/2}\), что означает, что квадратный корень из 3 равен возведению 3 в степень 1/2 (поэтому 1/2 — это экспонента).

Теперь этот калькулятор будет упрощать выражения, содержащие другие операции, чем просто a уменьшение количества радикалов . Таким образом, этот калькулятор хорош при упрощении алгебраических выражений в целом

Это калькулятор для упрощения экспоненты?

Да. Все элементарные операции, включенные в PEMDAS, поддерживаются этим калькулятором упрощения, включая экспоненты («E» в PEMDAS).

Теперь, когда у вас есть экспоненты, смешанные с выражениями, в которых нет экспонент, получаются сложные выражения, но это нормально. В худшем случае выражение не будет иметь дальнейших упрощений.

Пример: вычисление упрощения выражения

Вычислите следующее: \( \displaystyle \frac{1}{3} + \frac{5}{4} — \frac{5}{6} \times \sqrt{8} \)

Отвечать: Нам нужно вычислить и упростить следующее выражение: \(\displaystyle \frac{1}{3}+\frac{5}{4}-\frac{5}{6}\cdot\sqrt{8}\).

Получается следующий расчет:

\( \displaystyle \frac{1}{3}+\frac{5}{4}-\frac{5}{6}\sqrt{8}\)

By simplifying the radical: \(\displaystyle \sqrt{8} = \sqrt{ 2^2 \cdot 2} = 2\sqrt{ 2}\)

\( = \,\,\)

\(\displaystyle \frac{1}{3}+\frac{5}{4}-\frac{5}{6}\cdot 2\sqrt{2}\)

Canceling 2 from the denominator of \(\displaystyle -\frac{ 5}{ 6} \)

\( = \,\,\)

\(\displaystyle \frac{1}{3}+\frac{5}{4}-\frac{5}{3}\sqrt{2}\)

Amplifying in order to get the common denominator 12

\( = \,\,\)

\(\displaystyle \frac{1}{3}\cdot\frac{4}{4}+\frac{5}{4}\cdot\frac{3}{3}-\frac{5}{3}\sqrt{2}\)

We need to use the common denominator: 12

\( = \,\,\)

\(\displaystyle \frac{1\cdot 4+5\cdot 3}{12}-\frac{5}{3}\sqrt{2}\)

Expanding each term: \(4+5 \times 3 = 4+15\)

\( = \,\,\)

\(\displaystyle \frac{4+15}{12}-\frac{5}{3}\sqrt{2}\)

Adding up each term in the numerator

\( = \,\,\)

\(\displaystyle \frac{19}{12}-\frac{5}{3}\sqrt{2}\)

чем завершается расчет.

Пример: упрощение выражения

Вычислите следующее: \(\displaystyle \left(\frac{1}{3} + \frac{5}{4} — \frac{5}{6}\right)/(2+3 \times \sqrt{8}) \)

Отвечать: Нам нужно вычислить и упростить следующее выражение: \(\displaystyle \frac{\frac{1}{3}+\frac{5}{4}-\frac{5}{6}}{2+3\sqrt{8}}\).

Получается следующий расчет:

\( \displaystyle \frac{\frac{1}{3}+\frac{5}{4}-\frac{5}{6}}{2+3\sqrt{8}}\)

By simplifying the radical: \(\displaystyle \sqrt{8} = \sqrt{ 2^2 \cdot 2} = 2\sqrt{ 2}\)

\( = \,\,\)

\(\displaystyle \frac{\frac{1}{3}+\frac{5}{4}-\frac{5}{6}}{2+3\cdot 2\sqrt{2}}\)

Reducing the integers that can be multiplied together: \(\displaystyle 3\times2 = 6\)

\( = \,\,\)

\(\displaystyle \frac{\frac{1}{3}+\frac{5}{4}-\frac{5}{6}}{2+6\sqrt{2}}\)

Amplifying in order to get the common denominator 12

\( = \,\,\)

\(\displaystyle \frac{\frac{1}{3}\cdot \frac{4}{4}+\frac{5}{4}\cdot \frac{3}{3}-\frac{5}{6}\cdot \frac{2}{2}}{2+6\sqrt{2}}\)

Finding a common denominator: 12

\( = \,\,\)

\(\displaystyle \frac{\frac{1\cdot 4+5\cdot 3-5\cdot 2}{12}}{2+6\sqrt{2}}\)

Expanding each term in the numerator: \(4+5 \times 3-5 \times 2 = 4+15-10\)

\( = \,\,\)

\(\displaystyle \frac{\frac{4+15-10}{12}}{2+6\sqrt{2}}\)

Adding each term

\( = \,\,\)

\(\displaystyle \frac{\frac{9}{12}}{2+6\sqrt{2}}\)

We can factor out 3 for both the numerator and denominator.

\( = \,\,\)

\(\displaystyle \frac{\frac{3\cdot 3}{3\cdot 4}}{2+6\sqrt{2}}\)

Now we cancel 3 out from the numerator and denominator.

\( = \,\,\)

\(\displaystyle \frac{\frac{3}{4}}{2+6\sqrt{2}}\)

и на этом расчеты завершены.

Пример: еще одно упрощение выражения

Рассчитайте \( \displaystyle \frac{1}{\left(\frac{2}{3} \times \frac{6}{5} \right)} + \frac{2}{5} \).

Отвечать: Нам нужно вычислить и упростить следующее выражение: \(\displaystyle \frac{1}{\frac{2}{3}\cdot\frac{6}{5}}+\frac{2}{5}\).

Получается следующий расчет:

\( \displaystyle \frac{1}{\frac{2}{3}\cdot\frac{6}{5}}+\frac{2}{5}\)

We can multiply the terms in the top and bottom, and we get \(\displaystyle\frac{ 2}{ 3} \times \frac{ 6}{ 5}= \frac{ 2 \times 6}{ 3 \times 5} \)

\( = \,\,\)

\(\displaystyle \frac{1}{\frac{2\cdot 6}{3\cdot 5}}+\frac{2}{5}\)

Factoring out the term \(\displaystyle 3\) in the numerator and denominator of \(\displaystyle \frac{ 2 \times 6}{ 3 \times 5}\)

\( = \,\,\)

\(\displaystyle \frac{1}{\frac{2\cdot 2}{5}}+\frac{2}{5}\)

After simplifying the common factors in the numerator and denominator

\( = \,\,\)

\(\displaystyle \frac{1}{\frac{4}{5}}+\frac{2}{5}\)

Multiplying by 1 preserves the value: \(\displaystyle 1 \times \frac{ 5}{ 4} = \frac{ 5}{ 4}\)

\( = \,\,\)

\(\displaystyle \frac{5}{4}+\frac{2}{5}\)

Amplifying in order to get the common denominator 20

\( = \,\,\)

\(\displaystyle \frac{5}{4}\cdot\frac{5}{5}+\frac{2}{5}\cdot\frac{4}{4}\)

Finding a common denominator: 20

\( = \,\,\)

\(\displaystyle \frac{5\cdot 5+2\cdot 4}{20}\)

Expanding each term: \(5 \times 5+2 \times 4 = 25+8\)

\( = \,\,\)

\(\displaystyle \frac{25+8}{20}\)

Operating the terms in the numerator

\( = \,\,\)

\(\displaystyle \frac{33}{20}\)

что завершает расчет.

Другие полезные калькуляторы по алгебре

Естественно, для упрощение дроби когда никакие другие операции не требуют более легкого подхода. Вы также можете использовать калькулятор выражений для получения числового значения выражения, что может пригодиться.

Что касается операций с дробями, вы также можете использовать следующее калькулятор смешанных дробей , который представляет собой простой калькулятор, не всегда доступный в других калькуляторах.

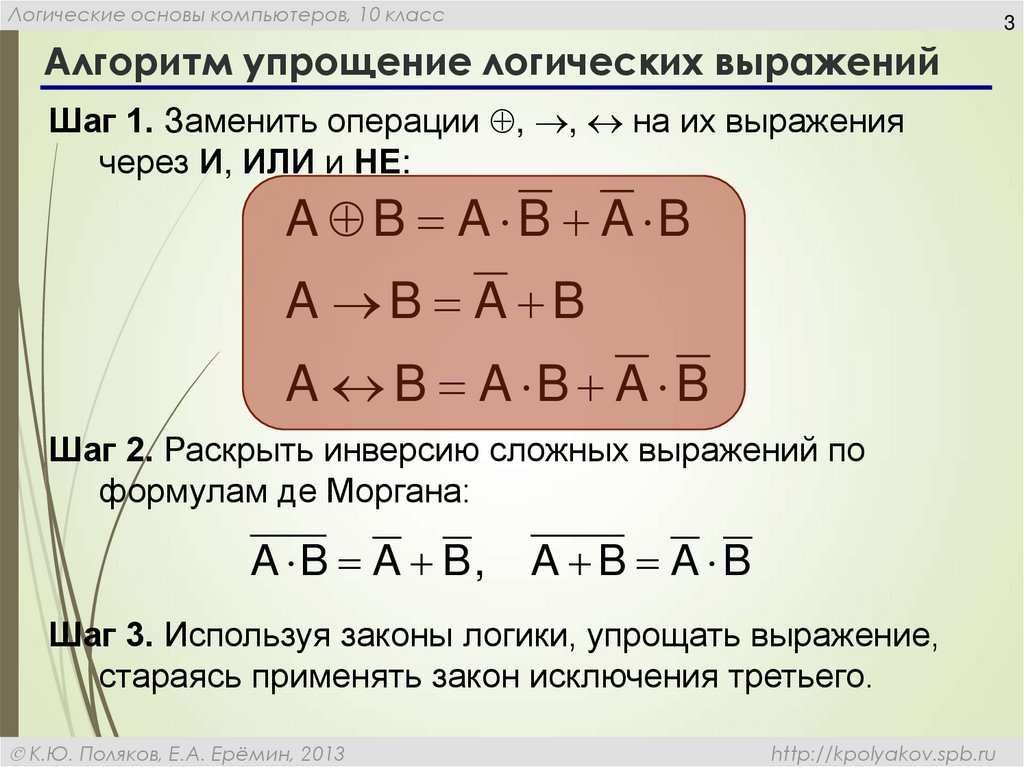
1.2. Упрощение выражений (Simplify)

Упрощение выражений – наиболее часто применяемая операция. Символический процессор MathCAD стремится так преобразовать выражения, чтобы они приобрели более простую форму. При этом используются различные арифметические формулы, приведение подобных слагаемых, тригонометрические тождества, пересчет обратных функций и др.

Задание 2. Упростить выражение .

Порядок выполнения задания.

1. Введите текстовую область Задание 2.

2. Используя палитру Calculator (Калькулятор ), введите упрощаемое выражение.

3. Выделите выражение целиком и подайте команду Symbolics, Simplify (Символика, Упростить). Компьютер выдаст результат: .

4. Сохраните изменения в документе.

5. Повторите процедуру упрощения выражения, используя команду simplify палитры Symbolic (Символика).

Сохраните изменения в документе Алгебра.

1.3. Разложение на множители (Factor)

Разложение выражений на простые множители производится при помощи команды Symbolics, Factor (Символика, Фактор (Разложить на множители)) либо с использованием вместе с оператором символьного вывода ключевого слова factor. Это операция позволяет разложить полиномы на произведение боле простых полиномов, а целые числа – на простые сомножители. Применяя команду меню, не забывайте выделить все выражение или его часть, которую планируете разложить на множители.

Задание 3. Разложите на множители выражение: x⁴-16

1. Введите текстовую область Задание 3.

2. Введите выражение, выделите его и получите результат, используя команду меню Symbolics, Factor (Символика, Фактор). На экране появится выражение: (x-2)·(x+2)·(x²+4).

3. Повторите операцию разложение на множители, используя команду factor палитры Symbolic (Символика).

Задание 4. Самостоятельно разложите на множители число 28 и алгебраическое выражение: .

1.4. Приведение подобных слагаемых

Задание 5. Привести подобные слагаемые полинома с помощью меню, выполнив следующие операции:

1. Введите текстовую область Задание 5.

2. Введите выражение .

3. Выделите в выражении имя переменной, относительно которой надо привести подобные слагаемые (например, по y).

4. Выберите команду Symbolics, Collect (Символика, Собрать). На экране появится выражение: .

5. Самостоятельно приведите подобные относительно переменной x.

6. Повторно введите исходное выражение и приведите подобные, используя оператор collect палитры Symbolic (Символика).

В местозаполнитель этого оператора нужно вставить имя переменной, относительно которой производится приведение подобных, например, x. Должен получиться следующий результат: .

7. Сохраните изменения в текущем документе.

1.5. Определение коэффициентов полинома (Polynomial Coefficients)

Если выражение является некоторым полиномом относительно переменной x, заданным не в обычном виде , а как произведение других, более простых полиномов, то коэффициенты легко определяются символьным процессором MathCAD. Коэффициенты сами могут быть функциями других переменных.

Задание 6. Вычислить полиномиальные коэффициенты в выражении: .

Порядок выполнения задания:

1. Введите текстовую область Задание 6.

2. Введите выражение и выделите в нем переменную z.

3. Выполните команду Symbolic, Polynomial Coefficients (Символика, Полиномиальные коэффициенты). Результат будет выдан в виде вектора

.

Первый элемент вектора является свободным членом а₀, второй – а₁, и т.д.

4. Повторно введите исходное выражение и вычислите коэффициенты полинома относительно переменной x с использованием оператора символьного вывода coeffs палитры Символика. Процесс должен выглядеть так:

.

5. Сохраните изменения в текущем документе.

MathCAD дает возможность определения коэффициентов не только для отдельных переменных, но и для сложных выражений, входящих в формулу в качестве составной части. Например:

Введите эти выражение и получите результаты самостоятельно.

Калькулятор упрощенных выражений — Онлайн-калькулятор упрощенных выражений

Выражение представляет собой комбинацию терминов или чисел, которые объединяются с помощью математических операций сложения, вычитания, умножения и деления.

Что такое калькулятор упрощенных выражений?

‘ Калькулятор упрощения выражений ‘ — это онлайн-инструмент, который помогает упростить заданное выражение. Онлайн-калькулятор упрощения выражений поможет вам упростить заданное выражение за несколько секунд.

Калькулятор упрощения выражений

ПРИМЕЧАНИЕ. Введите выражение только с точки зрения x и y.

Как пользоваться калькулятором упрощенных выражений?

Чтобы упростить выражение, выполните следующие действия:

• Шаг 1: Введите выражение в указанное поле ввода.
• Шаг 2:  Нажмите кнопку  «Упростить» , чтобы упростить данное выражение.
• Шаг 3:  Нажмите на «Сброс» кнопка для очистки полей и ввода нового выражения.

Как найти калькулятор упрощения выражений?

Чтобы упростить выражение, мы просто объединяем похожие термины. Следовательно, подобные переменные будут объединены вместе. Теперь из одинаковых переменных будут складываться одинаковые мощности.

Давайте рассмотрим пример, чтобы кратко понять.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Книга A Бесплатный пробный класс

Решенные примеры для упрощенного калькулятора выражений

Пример 1:

Упростить заданное выражение 6x ³ + x ² + 4x ³ + 2x – 40061 2 2 + 4x ³ + 2X — 40061 2 2 + 4x ³ + 2x — 40061 2 + 4x ³ + 2x — 40061 2 + 4x ³ + 2x — 40061 2 + 1 + 3x

Решение:

= 6x ³ + x ² + 4x ³ + 2x — 4x ² + 1 + 3x

= (6x ^{3 9006 + 4x}

= (6x ^{3 9006 + 4x}

= (6x ^{3 9006 + 4x}

= (6x ^{3 9006 + 4x}

= (6x ^{3 9006 + 4x}

= (6x ^{3 9006 + 4x}

= (6x ^{3 9006 + 4. 3} ) + (х ²  — 4x ² ) + (2x + 3x) + 1

= 10x ³ — 3x ² + 5x + 1

Пример 2:

Упростить заданное выражение 5x ³ + x. ² + 3x ³  + 2x + 4x ²  — 5 + 4x

Solution:

= 5x ³  + x ² + 3x ³  + 2x + 4x ²  — 5 + 4x

= (5x ³ + 3x ³ ) + (x ²  + 4x ² ) + (2x + 4x) — 5

= 8x ³ + 5x ² + 6x — 5

Пример 3:

Упростить заданное выражение 8x ⁴ — 40061111111111119. 2 + 4x ³ + 2x — 4x ² + 7 — 3x

Решение:

= 8x ⁴ — 4x ² + 4x ³ + 2x -40066 2 + 4x ³ + 2 — 4x ² + 4x ³ + 2 — 4x ² + 4x ³ + 2 — 4x ² + 4x ³ + 2 — 4x ² + 4x ³ + 2 — 4x ^{2 + 4x 3 + 2 2 . + 7 — 3x}

= 8x ⁴  + 4x ³  — (4x ²  + 4x ² ) + (2x — 3x) + 7

= 8x ⁴  + 4x ³ — 8x ²  — x + 7

, вы можете попробовать упростить выражения для калькулятора. следующие:

• 5cos ² x + 6sin ² x + 5sin ² x + 6cos ² x
• 8x ⁴  + 3x ²  — 2x + 6x ²  — 10x ³  — 4x ⁴  + 10

☛ Статьи по теме:

• Упрощенные выражения
• Алгебраические выражения

☛ Математические калькуляторы:

Упростить выражения — MathCracker.com

Инструкции: Используйте этот калькулятор упрощения выражений, чтобы уменьшить любое допустимое алгебраическое выражение, которое вы вводите, показывая все шаги. Введите выражение, которое вы хотите упростить с помощью правил PEMDAS.

Подробнее о калькуляторе для упрощения выражений

Этот калькулятор упрощения с пошаговыми инструкциями позволяет упростить любое допустимое выражение, включающее основные операции, включая суммы, вычитание, умножение, деление, дроби, радикалы и т. 3+5+1/6)».

После того, как вы укажете действительное выражение, вам нужно нажать на кнопку «Рассчитать», и вы все шаги упрощения расчеты будут показаны вам.

Калькулятор сделает все возможное, чтобы показать значимые шаги для вычислений, и он, безусловно, достигает этого для большинства простых выражений.

Как упростить выражения с умножением

Этот вопрос связан с другим вопросом как упростить выражения с суммами, а еще интереснее, как упростить выражения, которые смешивают суммы и умножения? Ответ прост: PEMDAS

PEMDAS предоставляет четкое правило, определяющее, какие операции имеют приоритет для выполнения в первую очередь. Следуйте этим правилам PEMDAS:

• Сначала: «P» (что соответствует «круглым скобкам»). В алгебраическом выражении скобки всегда имеют приоритет.
• Далее: «E» (показатели). После скобок приоритет отдается показателям
.
• Далее: «М» (умножение). После показателей степени приоритет отдается умножениям
.
• Далее: «D» (деление). После умножения приоритет идет к делениям
• Далее: «А» (дополнение). После делений приоритет отдается дополнениям
.
• Наконец: «S» (вычитание). После сложений приоритет отдается вычитаниям

Эти правила позволят однозначно оценить составное выражение. Этот калькулятор покажет вам шаги упрощения, следующие за Правила приоритета PEMDAS

Какие шаги упрощают выражение

• Шаг 1: Оцените, правильно ли определено выражение. Это может быть не прямым или простым, в зависимости от сложности переданного выражения
• Шаг 2: Если это неверно, остановитесь, процесс завершится. Если это действительно так, вы используете PEMDAS для управления процессом упрощения
.
• Шаг 3. Упрощайте по приоритету и при необходимости выполняйте много шагов, следуя приоритету PEMDAS один за другим, пока выражение не может быть дополнительно упрощено

Как упростить выражения с дробями?

Упрощать дроби вообще легко, потому что стратегию невозможно пропустить: нужно найти общие знаменатели. {1/2}\), что означает, что квадратный корень из 3 — это то же самое, что возведение 3 в степень 1/2 (поэтому 1/2 — показатель степени).

Теперь этот калькулятор упростит выражения, которые содержат другие операции, кроме простого сокращения радикалов. Так этот калькулятор хорош для упрощения алгебраических выражений в целом

Это калькулятор для упрощения показателей?

Да. Все элементарные операции, включенные в PEMDAS, поддерживаются этим калькулятором упрощения, включая показатели степени («E» в PEMDAS).

Теперь, когда у вас есть экспоненты, смешанные с выражениями, которые не имеют экспонент, будут давать сложные выражения, но это нормально. Наихудший сценарий что выражение не будет иметь дальнейших упрощений..

Пример: Расчет упрощения выражения

Вычислите следующее: \( \displaystyle \frac{1}{3} + \frac{5}{4} — \frac{5}{6} \times \sqrt{8} \)

Решение: Нам нужно вычислить и упростить следующее выражение: \(\displaystyle \frac{1}{3}+\frac{5}{4}-\frac{5}{6 }\cdot\sqrt{8}\).

Получается следующий расчет:

\( \displaystyle \frac{1}{3}+\frac{5}{4}-\frac{5}{6}\sqrt{8}\) 92 \cdot 2} = 2\sqrt{ 2}\)

знак равно

\(\displaystyle \frac{1}{3}+\frac{5}{4}-\frac{5}{6}\cdot 2\sqrt{2}\)

Вычеркивание 2 из знаменателя \(\displaystyle -\frac{ 5}{ 6} \)

знак равно

\(\displaystyle \frac{1}{3}+\frac{5}{4}-\frac{5}{3}\sqrt{2}\)

Усиление для получения общего знаменателя 12

знак равно

\(\displaystyle \frac{1}{3}\cdot\frac{4}{4}+\frac{5}{4}\cdot\frac{3}{3}-\frac{5}{3} \sqrt{2}\)

Нам нужно использовать общий знаменатель: 12

знак равно

\(\displaystyle \frac{1\cdot 4+5\cdot 3}{12}-\frac{5}{3}\sqrt{2}\)

Расширение каждого члена: \(4+5 \times 3 = 4+15\)

знак равно

\(\displaystyle \frac{4+15}{12}-\frac{5}{3}\sqrt{2}\)

Сложение каждого члена в числителе

знак равно

\(\displaystyle \frac{19}{12}-\frac{5}{3}\sqrt{2}\)

, что завершает расчет.

Пример: упрощение выражения

Вычислите следующее: \(\displaystyle \left(\frac{1}{3} + \frac{5}{4} — \frac{5}{6}\right)/ (2+3 \times \sqrt{8}) \)

Решение: Нам нужно вычислить и упростить следующее выражение: \(\displaystyle \frac{\frac{1}{3}+\frac{5}{ 4}-\frac{5}{6}}{2+3\sqrt{8}}\).

Получается следующий расчет: 92 \cdot 2} = 2\sqrt{ 2}\)

знак равно

\(\displaystyle \frac{\frac{1}{3}+\frac{5}{4}-\frac{5}{6}}{2+3\cdot 2\sqrt{2}}\)

Сокращение целых чисел, которые можно перемножить: \(\displaystyle 3\times2 = 6\)

знак равно

\(\displaystyle \frac{\frac{1}{3}+\frac{5}{4}-\frac{5}{6}}{2+6\sqrt{2}}\)

Усиление для получения общего знаменателя 12

знак равно

\(\ displaystyle \ frac {\ frac {1} {3} \ cdot \ frac {4} {4} + \ frac {5} {4} \ cdot \ frac {3} {3} — \ frac {5} {6}\cdot \frac{2}{2}}{2+6\sqrt{2}}\)

Нахождение общего знаменателя: 12

знак равно

\(\displaystyle \frac{\frac{1\cdot 4+5\cdot 3-5\cdot 2}{12}}{2+6\sqrt{2}}\)

Расширение каждого члена в числителе: \(4+5 \умножить на 3-5 \умножить на 2 = 4+15-10\)

знак равно

\(\displaystyle \frac{\frac{4+15-10}{12}}{2+6\sqrt{2}}\)

Добавление каждого термина

знак равно

\(\displaystyle \frac{\frac{9}{12}}{2+6\sqrt{2}}\)

Мы можем вынести 3 как из числителя, так и из знаменателя.

знак равно

\(\ displaystyle \ frac {\ frac {3 \ cdot 3} {3 \ cdot 4}} {2 + 6 \ sqrt {2}} \)

Теперь мы сокращаем 3 из числителя и знаменателя.

знак равно

\(\displaystyle \frac{\frac{3}{4}}{2+6\sqrt{2}}\)

и на этом расчет окончен.

Пример: другое упрощение выражения

Вычислить \( \displaystyle \frac{1}{\left(\frac{2}{3} \times \frac{6}{5} \right)} + \frac {2}{5} \).

Решение. Нам нужно вычислить и упростить следующее выражение: \(\displaystyle \frac{1}{\frac{2}{3}\cdot\frac{6}{5}}+\frac{2}{ 5}\).

Получается следующий расчет:

\( \displaystyle \frac{1}{\frac{2}{3}\cdot\frac{6}{5}}+\frac{2}{5}\)

Мы можем перемножить члены сверху и снизу, и мы получим \(\displaystyle\frac{ 2}{ 3} \times \frac{ 6}{ 5}= \frac{ 2 \times 6}{ 3 \times 5 } \)

знак равно

\(\displaystyle \frac{1}{\frac{2\cdot 6}{3\cdot 5}}+\frac{2}{5}\)

Выносим член \(\displaystyle 3\) в числителе и знаменателе \(\displaystyle \frac{ 2 \times 6}{ 3 \times 5}\)

знак равно

\(\displaystyle \frac{1}{\frac{2\cdot 2}{5}}+\frac{2}{5}\)

После упрощения общих множителей в числителе и знаменателе

знак равно

\(\displaystyle \frac{1}{\frac{4}{5}}+\frac{2}{5}\)

Умножение на 1 сохраняет значение: \(\displaystyle 1 \times \frac{ 5}{ 4} = \frac{ 5}{ 4}\)

знак равно

\(\displaystyle \frac{5}{4}+\frac{2}{5}\)

Усиление для получения общего знаменателя 20

знак равно

\(\displaystyle \frac{5}{4}\cdot\frac{5}{5}+\frac{2}{5}\cdot\frac{4}{4}\)

Нахождение общего знаменателя: 20

знак равно

\(\displaystyle \frac{5\cdot 5+2\cdot 4}{20}\)

Расширение каждого члена: \(5 \times 5+2 \times 4 = 25+8\)

знак равно

\(\displaystyle \frac{25+8}{20}\)

Работа с членами в числителе

знак равно

\(\displaystyle \frac{33}{20}\)

, который завершает расчет.