Катер прошел расстояние между пристанями по течению реки за 4 часа, а против течения- за 6 часов. Найдите собственную скорость катера, если течение реки 1,5 км/ч.
Любая задача состоит из трёх частей: условие, объект, требование (вопрос) задачи.
3. Приступая к решению какой-либо задачи, надо её внимательно изучить, установить, в чем состоят её требования, каковы условия, исходя из которых надо её решать. Всё это называется анализом задачи.
Весь процесс решения задачи можно разделить на восемь этапов:
1- анализ;
2- схематическая запись;
3- поиск способа решения;
4- осуществление решения:
5- проверка решения;
6- исследование задачи;
7- формулировка ответа;
8- анализ решения.
Стандартная схема решения таких задач включает в себя:
1.Выбор и обозначение неизвестных.
2.Составление уравнений (возможно неравенств) с использованием неизвестных и всех условий задачи.
3.
Решение полученных уравнений (неравенств).
4.Отбор решений по смыслу задачи.
Задачи на движение
В задачах на движение используются обычно формулы, выражающие законы равномерного движения:S=V·t , где S— пройденное расстояние, V— скорость равномерного движения,t— время движения.
При составлении уравнений в таких задачах часто бывает удобно прибегнуть к геометрической иллюстрации процесса движения: путь изображается в виде отрезка прямой, место встречи движущихся с разных сторон объектов точкой на отрезке и т.д.
Часто для усложнения задачи её условие формулируется в различных единицах измерения(метры, километры, часы, минуты и т.д.). В этом случае при выписывании уравнений необходимо пересчитывать все данные задачи в одинаковых единицах измерения:
1. Если расстояние между двумя движущимися навстречу друг другу телами равно S, а их скорости V1 и V2, то время t через которое они встретятся, находиться по формуле t= S\ V1+V2 .
2. Если движение вдогонку, то есть первое тело следует за вторым, то время t , через которое первое тело догонит второе, находится по формуле t=S\V1-V2 .
3. В задачах на движение по воде скорость течения считается неизменной. При движении по течению скорость течения прибавляется к скорости плывущего тела, при движении против течения – вычитается из скорости тела . Скорость плота считается равной скорости течения.
4. Средняя скорость вычисляется по формуле V=S\t , где S- путь, пройденный телом, а t- время, за которое этот путь пройден. Если путь состоит из нескольких участков, то следует вычислить всю длину пути и всё время движения.
Рассмотреть решение данных задач, разобраться в их решениях.
Задача 1. Велосипедист ехал 2 часа по лесной дороге и 1 час по шоссе, всего он проехал 40 км. Скорость его по шоссе была на 4 км/ч больше, чем скорость на лесной дороге. С какой скоростью велосипедист ехал по лесной дороге, и с какой по шоссе?
Решение:
Пусть x
Тогда его скорость на шоссе будет (x+4)км/ч. За 2 часа по лесной дороге велосипедист проехал 2·x км., а за час по шоссе (x+4) км. Весь путь по условию равен 40км. Составляем уравнение:2x+(x+4) = 40;
2x+x = 40 — 4;
3x = 36;
x = 36:3;
x=12.
Значит скорость на лесной дороге 12 км/ч, а на шоссе 12+4=16 (км/ч).
Ответ: 12 км/ч ; 16 км/ч.
Задача 2. От пристани против течения реки отправилась моторная лодка, собственная скорость которой 10 км/ч. Через 45 минут после выхода у лодки испортился мотор, и лодку течением реки через 3 часа принесло обратно к пристани. Какова скорость течения реки?
Решение:
Пусть x км/ч скорость течения реки. Моторная лодка против течения реки шла со скоростью (10-x) км/ч. В пути была 45 минут.
часа.
Путь против течения равен Далее лодка с испорченным двигателем плыла по течению со скоростью xкм/ч 3 часа обратно к пристани.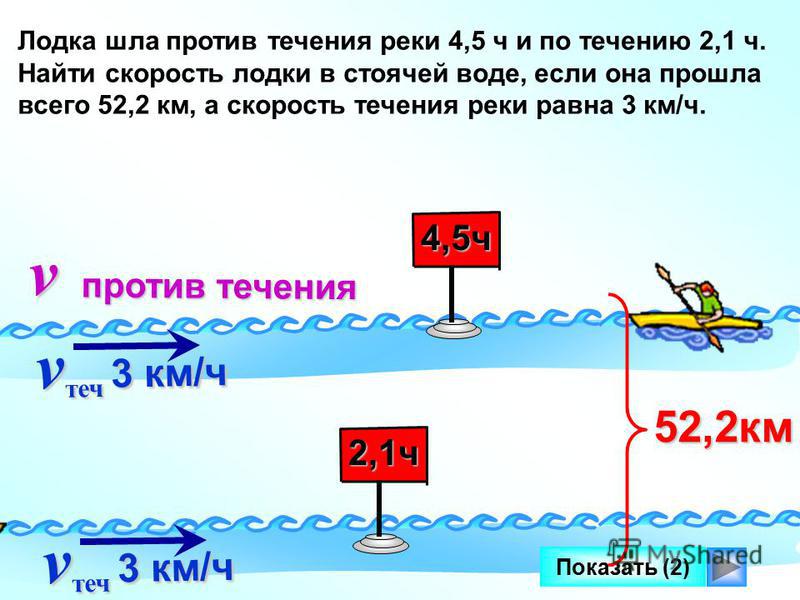
Весь этот путь равен3∙x км. Но расстояния туда и обратно равны:
Ответ: 2 км/ч.
Задача 3. Из двух городов, расстояние между которыми 200 км, одновременно навстречу друг другу выехали легковой автомобиль и грузовик и встретились через 2 часа. Скорость легкового автомобиля 60 км/ч. Найти скорость грузовика.
Решение:
Пусть скорость грузовика равна xкм/ч. Поскольку машины выехали одновременно навстречу друг другу, то скорость сближения (сумма скоростей) равна(x+60) км/ч. Каждый из них до встречи находится в пути 2 часа.
Поэтому:
2(x+60) = 200
x+60 = 100
x = 100-60
x = 40
Скорость грузовика 40 км/ч.
Ответ: 40 км/ч.
Задача 4. Из пунктов А и В, расстояние между которыми 94км, отправились одновременно навстречу друг другу пешеход и велосипедист. Скорость пешехода на 16 км/ч меньше скорости велосипедиста. Найти скорость каждого, если известно, что встретились они через 4ч и пешеход сделал в пути получасовую остановку.
Решение:
Пусть скорость пешехода равнах км/час, тогда скорость велосипедиста (х+16) км/ч. Отправляются навстречу друг другу одновременно. Встречаются через 4 часа. Пешеход делал в пути получасовую остановку. Значит шел до встречи 4-0,5=3,5 часа, велосипедист до встречи ехал 4 час.
Итак, путь пешехода3,5х км, а путь велосипедиста4(х+16)км. Сумма по условию 94. Составляем уравнение:
4(x+16)+3,5x=94;
4x+64+3,5x=94;
7,5x=30;
x=30:7,5;
x=300:75
x=4.
Скорость пешехода 4км/ч, велосипедиста 16+4=20км/час
Ответ: 4км/ч; 20км/ч.
Задача 5. Пароход прошел 4 км против течения реки, а затем прошел еще 33 км по течению, затратив на весь путь один час. Найдите собственную скорость парохода, если скорость течения реки равна 6,5 км/ч.
Решение. Пусть х км/ч – собственная скорость парохода. Тогда (х + 6,5)км/ч – скорость парохода по течению, а (х – 6,5) км/ч – скорость парохода против течения.
Так как против течения пароход прошел4 кмсо скоростью (х – 6,5)км/ч, то 4 / (х — 6,5 ) – время движения парохода против течения.
А так как по течению пароход прошел 33 км со скоростью (х+6,5) км/ч, то 33 / (х + 6,5 ) – время движения парохода по течению.
По условию 4 / (х — 6,5) = 33 / (х + 6,5) = 1.
Решая это уравнение, получим
Осуществим отбор полученных решений. Через х мы обозначили собственную скорость парохода, при этом скорость течения реки6,5 км/ч, поэтому х1=4,5 км/ч не подходит по смыслу задачи(при такой скорости пароход не выплыл бы против течения). Поэтому, собственная скорость парохода равна 32,5 км/ч. Ответ: v=32,5 км/ч.
ДОМА: решить задачи.
1. Расстояние от пристани А до пристани В катер проплыл за 6 часов, а от пристани В до пристани А за 7,5 ч. Скорость течения реки 2 км/ч.
Найдите собственную скорость катера.
Два поезда движутся в противоположных направлениях от станции А. От станции А первый поезд находится на расстоянии 70,5 км, а второй- на расстоянии 56,75 км. Первый поезд едет со скоростью 57 км/ч, а второй – со скоростью 62,5 км/ч. Через сколько часов оба поезда будут находиться на одинаковом расстоянии от станции А?
Катер прошел расстояние между пристанями по течению реки за 4 часа, а против течения- за 6 часов. Найдите собственную скорость катера, если течение реки 1,5 км/ч.
Задачи можно решать, составляя таблицу:
| Расстояние (км) | Скорость (км/ч) | Время (ч) | |
| По течению | |||
| Против течения |
73, 74, 75.
Задачи на движение по воде73, 74, 75. Задачи на движение по воде
Это надо знать
В задачах на движение по воде скорость реки считается постоянной и неизменной.
При движении по течению скорость реки прибавляется к собственной скорости плывущего тела
При движении против течения от собственной скорости вычитается скорость реки, так как в этом случае скорость реки мешает движущемуся телу.
Скорость плота считается равной скорости реки.
Пример:
Пусть скорость движения лодки 5 км/ч, а скорость течения — 2 км/ч.
1) 5 + 2= 7 (км/ч) — скорость лодки по течению
2) 5 — 2 = 3 (км/ч) — скорость лодки против течения
Пусть наша лодка проплыла 2 часа по течению реки и 3 часа против течения реки. Найдем расстояние, которое проплывет лодка.
3) 7 ∙ 2 = 14 (км) — плыла лодка по течению
4) 3 ∙ 3 = 9 (км) — плыла лодка против течения
5) 14 + 9 = 23 (км) — все расстояние
Ответ: 23 км.
Видеоурок
Домашнее задание
К уроку 73 (на 16.12)
П. 4.11
№ 1
Скорость катера в стоячей воде (собственная скорость) 12 км/ч, а скорость течения реки 3 км/ч. Определите:
1) скорость катера по течению и против течения реки;
2) путь катера по течению реки за 3 ч;
3) путь катера против течения реки за 5 ч.
№ 2
Скорость катера против течения равна 23 км/ч, а скорость течения 4 км/ч. Найдите скорость катера по течению.
№ 3
Скорость моторной лодки по течению реки равна 14 км/ч/ а скорость течения 3 км/ч. Найдите скорость лодки против течения
К уроку 74 (на 17.12)
П. 4.11
№ 5.302
Расстояние между пристанями прогулочный теплоход проплывает по течению за 3 ч со скоростью 24 км/ч, а за 4 ч возвращается обратно.
№ 5.303
Путешественник спустился вниз по течению реки за 2 сут. на плоту, а обратно вернулся теплоходом за 2 ч. Найдите собственную скорость теплохода, если скорость течения реки равна 2 км/ч.
№ 5.304
Наша Таня громко плачет, уронила в речку мячик. Но проплакав 2 мин, Таня поплыла за мячиком и через 2 мин догнала его. С какой скоростью плыла Таня, если скорость течения реки равна 35 м/мин?
К уроку 75 (на 18.12)
П. 4.11
№ 5.306
Вниз по течению реки плывет моторная лодка, а навстречу ей катер. Через какое время после начала движения лодка и катер встретятся, если их собственные скорости равны 12 км/ч и 15 км/ч соответственно, скорость течения реки равна 2 км/ч; лодка и катер начали движение одновременно, находясь на расстоянии 54 км друг от друга?
№ 5.297
Из поселка Веселково одновременно в противоположных направлениях отправились два рейсовых автобуса.
Скорость одного автобуса равна 56 км/ч, другого — на 8 км/ч больше. Через сколько часов расстояние между автобусами будет равно 480 км?
Главная страница
Подписаться на: Сообщения (Atom)
Патрульному катеру потребовалось 5 часов, чтобы пройти 60 км вверх по реке против течения, и 3 часа обратно по течению. Найдите скорость катера в стоячей воде и spe
. РЕШЕНИЕ: Патрульному катеру потребовалось 5 часов, чтобы пройти 60 км вверх по реке против течения, и 3 часа, чтобы вернуться по течению. Найдите скорость лодки в стоячей воде и скоростьАлгебра -> Системы координат и линейные уравнения -> Линейные уравнения и системные словесные задачи -> РЕШЕНИЕ: Патрульному катеру потребовалось 5 часов, чтобы пройти 60 км вверх по реке против течения, и 3 часа, чтобы вернуться по течению. Найдите скорость лодки в стоячей воде и скорость Войти
|
Сложные задачи 
Найдите скорость лодки в стоячей воде и скорость течения. Моторная лодка идет 5 часов.
..Алгебра преалгебры
Кристен Н.
спросил 15/11/20Моторная лодка проходит 150 миль вверх по течению за 5 часов. Обратный путь вниз по течению занимает 3 часа. Какова скорость лодки в стоячей воде и какова скорость течения?
Скорость лодки в стоячей воде:
Скорость течения:
Подписаться І 3
Подробнее
Отчет
2 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: ЛучшиеНовыеСамыеСтарые
Том В. ответил 15.11.20
Репетитор
5,0 (220)
Высококвалифицированный опытный сертифицированный преподаватель математики преалгебры
См. таких репетиторов
Смотрите таких репетиторов
Привет, Кристен,
Предположим, что течение течет с постоянной скоростью и скорость лодки в стоячей воде постоянна.
Тогда пусть x = скорость тока.
Скорость против течения составляет 30 миль в час (150/5).
Скорость движения по течению составляет 50 миль в час (150 / 3)
Два уравнения теперь могут представлять скорость лодки в стоячей воде (против течения) 30 + x (по течению) 50 — x
Приравняйте два уравнения друг к другу. 30 + х = 50 — х;
Объедините одинаковые члены и найдите x. 2х = 20; x = 10 (скорость течения)
Подставьте скорость течения (10) в каждое исходное уравнение для скорости лодки в стоячей воде.
30 + 10 = 40 миль в час. 50 — 10 = 40 миль в час
Итак,
Скорость лодки в стоячей воде = 40 миль в час
Скорость течения = 10 миль в час.
Береги себя,
Том
Голосовать за 1 Понизить голос
Подробнее
Отчет
Марк М.
ответил 15.11.20
Репетитор
5,0 (263)
Учитель математики – высококвалифицированный специалист NCLB
Об этом репетиторе ›
Об этом репетиторе ›
d = r * t
150 выше по течению = (b — c)5
150 ниже по течению = (b + c)3
30 = b — c
9 90 = b4 + c 90 = b4 + c 2b
40 = b
Можете ли вы определить скорость тока и ответ?
Голосовать за 0 Понизить голос
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.
Задайте вопрос бесплатно
Получите бесплатный ответ на быстрый вопрос.