Коллинеарность векторов: условия, правила и примеры
Поможем понять и полюбить математику
Начать учиться
С 7‑го класса вы знакомы с такими физическими величинами, как сила, скорость, ускорение, перемещение, импульс. А что отличает их от другой группы величин, таких как длина, время, масса, объем, температура и плотность? Первая группа величин — векторные, то есть они характеризуются не только числовым значением, но и направлением. Нам важно знать не только скорость, но и ее направление; не только силу, с которой толкают груз, но и в каком направлении его толкают.
Ученики 9-го класса, помимо понятия вектора, должны знать, что такое коллинеарные векторы, а также условия коллинеарности векторов.
Вектор — это направленный отрезок. Вектор обозначается двумя заглавными латинскими буквами со стрелочкой над ними или одной маленькой со стрелочкой над ней .
Нулевой вектор — вектор, начало которого совпадает с концом. То есть в геометрической интерпретации это просто точка.
Теперь, когда мы вспомнили базовые понятия, можно переходить к определению коллинеарных векторов.
Что значит «коллинеарные векторы»
Коллинеарные векторы — это ненулевые векторы, лежащие на одной прямой или на параллельных прямых. Причем считается, что нулевой вектор коллинеарен каждому другому вектору. То есть, попросту говоря, коллинеарность — это параллельность векторов. Если векторы и коллинеарны, то это записывают так: .
Коллинеарные векторы можно разделить по направлению на две группы: сонаправленные и противоположно направленные.
Векторы и лежат на параллельных прямых, а также имеют одно направление, поэтому и — сонаправленные векторы: .
Векторы и лежат на параллельных прямых, но имеют разное направление, поэтому и — противоположно направленные векторы: .
Задача № 1
Найдите сонаправленные и противоположно направленные векторы.
Благодаря клетчатому фону мы можем определить, что все векторы на рисунке коллинеарны, то есть лежат на параллельных прямых. Осталось посмотреть на направление векторов и сделать выводы:
,
,
,
.
Но не забываем о нулевом векторе — он будет сонаправлен с каждым вектором.
Но согласитесь, что визуальная оценка параллельности не самая точная вещь на планете, а математика славится своей точностью и четкостью. Поэтому возникает вопрос: как проверить коллинеарность векторов алгебраическими способами? Для этого существуют признаки коллинеарности векторов.
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Признаки коллинеарности векторов
Первый критерий коллинеарности векторов: векторы и коллинеарны, если .
Второй критерий коллинеарности векторов: два вектора коллинеарны, если отношения их координат равны.
Но здесь важно понимать, что это условие параллельности векторов работает только для всех ненулевых координат. Значит, если хотя бы один компонент вектора равен нулю, то правило неприменимо.
Третий критерий коллинеарности векторов, который могут применять одиннадцатиклассники, взрослые и все, кто увлечен математикой: два ненулевых вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.

Применим условия коллинеарности векторов при решении задач.
Задача № 2
Докажите, что векторы и коллинеарны.
У нас с вами есть два способа определить или доказать коллинеарность векторов, однако в координатах каждого вектора есть нули — значит, подходит только первый критерий, который еще называется свойством коллинеарных векторов: если , то .
Для начала определим . А теперь проверим, выполняется ли условие :
, значит, . Что и требовалось доказать.
Задача № 3
Какие из векторов , и коллинеарны?
А здесь очень удобно использовать второй критерий коллинеарности векторов, который звучит так: отношения соответствующих координат коллинеарных векторов равны.
Проверим коллинеарность векторов и : должно выполняться условие , т. е. — верно, значит, .

Проверим коллинеарность векторов и : должно выполняться условие , т. е. — неверно, значит, и неколлинеарны.
Проверим коллинеарность векторов и : должно выполняться условие , т. е. — неверно, значит, и неколлинеарны.
Задача № 4
Определите, при каком значении k векторы и коллинеарны.
Так как по условию векторы должны быть коллинеарны, а в их координатах не содержится нуля, то можно использовать второй критерий коллинеарности, а именно — должно выполняться условие , то есть .
По свойству пропорции выразим k:
;
k = 27.
Значит, при k = 27 векторы и коллинеарны.Если же вам нужно проверить коллинеарность векторов в пространстве, а не на плоскости, то все эти условия продолжают работать, но помните, что к проверке присоединяется третья координата векторов. Рассмотрим пару примеров.
Рассмотрим пару примеров.
Задача № 5
Докажите, что векторы и коллинеарны.
Поступим аналогично решению в задаче 2 — применим первый критерий, который еще называется свойством коллинеарных векторов, т. е. если , то .
Для начала определим . А теперь проверим, выполняется ли условие :
, значит, . Что и требовалось доказать.
Задача № 6
Определите, при каких значениях k и f векторы и коллинеарны.
Аналогично задаче 4: так как по условию векторы должны быть коллинеарны и в их координатах не содержится нуля, то можно использовать второй критерий коллинеарности. А именно — должно выполняться условие , то есть .
Рассмотрим первую и вторую дроби, по свойству пропорции выразим k:
;
k = 27.
Рассмотрим первую и третью дроби, по свойству пропорции выразим f:
;
f = 2.
Значит, при k = 27 и f = 2 векторы и коллинеарны.
Векторы — удивительная тема, с помощью которой можно решить многие физические задачи, легко и просто доказать самые сложные геометрические теоремы. Сегодня вы узнали, какие векторы называются коллинеарными, но это лишь один аспект большой главы о векторах. Чтобы узнать остальные действия с векторами, познакомиться с интересными задачами и способами решений, приходите на онлайн-курсы математики для детей в Skysmart.
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Кристина Тоскина
К предыдущей статье
Как подготовиться к ОГЭ по математике в 2023 году
К следующей статье
Уравнение касательной к графику функции
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Коллинеарность векторов.
 Онлайн калькулятор.
Онлайн калькулятор.Коллинеарность векторов — это отношение параллельности векторов, так два ненулевых вектора являются коллинеарными (параллельными), если они лежат на параллельных прямых или на одной прямой.
Укажите размерность пространства 23
Укажите форму представления первого вектора Координаты точек начала и конца первого вектораКоординаты первого вектора
Укажите форму представления второго вектора Координаты точек начала и конца второго вектораКоординаты второго вектора
Задайте координаты первого вектора
a̅ =
{
;
}
Задайте координаты второго вектора
b̅ =
{
;
}
Как проверить являются ли два вектора коллинеарными (параллельными)
Если два ненулевых вектора a и b лежат на одной прямой или на параллельных прямых, то такие векторы называются – коллинеарными.
Сонаправленные векторы – одинаково направленные коллинеарные векторы.
Антиколлинеарные векторы – противоположено направленные коллинеарные векторы.
Коллинеарные векторы обозначаются как: a||b.
Определить что векторы a = {ax; ay; az} и b = {bx; by; bz} являются коллинеарными можно если вычислить их векторное произведение. Если векторное произведение векторов равно нулю, то векторы коллинеарны.
Например, найдем векторное произведение векторов a и b
a = {2; 2; 10} b = {1; 1; 5}
Решение
N̅ = [a × b] =
= i̅i̅ j̅ k̅ ax ay az bx by bz
— j̅ay az by bz
+ k̅ax az bx bz
= i̅ ayax ay bx by
i̅ (aybz — byaz) — j̅ (axbz — bxaz) + k̅ (axby — bxay)
ax = 2
ay = 2
az = 10
bx = 1
by = 1
bz = 5
N̅ = [a × b] = i̅ (2 ⋅ 5 — 1 ⋅ 10) — j̅ (2 ⋅ 5 — 1 ⋅ 10) + k̅ (2 ⋅ 1 — 1 ⋅ 2) = i̅ (10 — 10) — j̅ (10 — 10) + k̅ (2 — 2) = 0i̅ +0j̅ +0k̅
N̅ = [a × b] = 0i̅ +0j̅ +0k̅
N̅ = {0 ; 0 ; 0}
Векторное произведение векторов равно нулю, следовательно, векторы a и b коллинеарны.
Так как векторное произведение векторов находится при помощи определителя квадратной матрицы, то для векторов a = {ax; ay} и b = {bx; by} определить являются ли векторы коллинеарными можно если координаты векторов связаны отношением:
Условие коллинеарности векторовa = {ax; ay}
b = {bx; by}
q – коэффициент пропорциональности Условие коллинеарности векторов
a = {ax; ay; az}
b = {bx; by; bz}
q – коэффициент пропорциональности
Если коэффициент пропорциональности q > 0, то векторы a и b сонаправленны.
Если коэффициент пропорциональности q a и b антиколлинеарные, т. е. противоположно направлены.
е. противоположно направлены.
Чтобы проверить выполняется ли равенство необходимо составить систему уравнений и вычислить коэффициент пропорциональности q в каждом уравнении:
a = {ax; ay;}b = {bx; by;}
q – коэффициент пропорциональности
Если в первом и во втором уравнении коэффициенты пропорциональности q равны, то координаты векторов пропорциональны и векторы коллинеарны.
a = {ax; ay; az}b = {bx; by; bz}
q – коэффициент пропорциональности
Если в первом, втором и в третьем уравнении коэффициенты пропорциональности q равны, то координаты векторов пропорциональны и векторы коллинеарны.
Пример 1.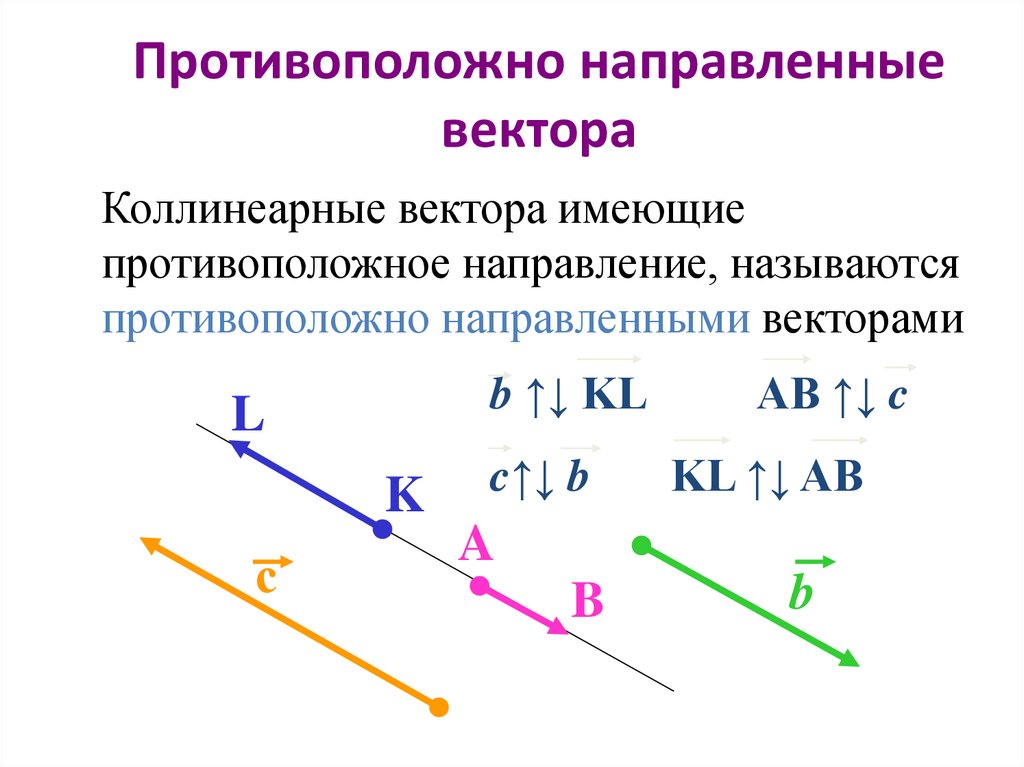 Определим, являются ли два вектора плоскости коллинеарными (параллельными). Координаты обоих векторов заданны точками.
Определим, являются ли два вектора плоскости коллинеарными (параллельными). Координаты обоих векторов заданны точками.
Координаты точки А вектора AB: (5 ; 9)
Координаты точки B вектора AB: (-2 ; 11)
Координаты точки C вектора CD: (0 ; 12)
Координаты точки D вектора CD: (-3 ; 1)
Вычислим координаты первого вектора по двум точкам A и B:
AB = {Bx — Ax ; By — Ay} = {-2 — 5 ; 11 — 9} = {-7 ; 2}
Вычислим координаты второго вектора по двум точкам C и D:
CD = {Dx — Cx ; Dy — Cy} = {-3 — 0 ; 1 — 12} = {-3 ; -11}
Проверим, есть ли для векторов AB и CD коэффициент пропорциональности q (имеющий одинаковое значение для всех уравнений в системе), для этого составим систему и проверим выполняется ли равенство:
ABx = q ⋅ CDx
ABy = q ⋅ CDy
| -7 = q ⋅ (-3) тогда, q = — | 7 |
| -3 |
| 2 = q ⋅ (-11) тогда, q = | 2 |
| -11 |
| = — | 2 |
| 11 |
| ≠ — | 2 |
| 11 |
| В первом уравнении коэффициент пропорциональности равен | 7 |
| 3 |
| , во втором — | 2 |
| 11 |
Следовательно, система несовместима и не имеет решений. Координаты векторов AB и CD не пропорциональны, значит векторы AB и CD не коллинеарны. Координаты векторов AB и CD не пропорциональны, значит векторы AB и CD не коллинеарны. |
Пример 2. Определим, являются ли два вектора плоскости коллинеарными (параллельными).
Координаты вектора a: (2 ; 6)
Координаты вектора b: (7 ; 21)
Проверим, есть ли для векторов a и b коэффициент пропорциональности q (имеющий одинаковое значение для всех уравнений в системе), для этого составим систему и проверим выполняется ли равенство:
ax = q ⋅ bx
ay = q ⋅ by
| 2 = q ⋅ 7 тогда, q = | 2 |
| 7 |
| 6 = q ⋅ 21 тогда, q = | 6 |
| 21 |
| В первом уравнении коэффициент пропорциональности равен | 2 |
| 7 |
| , во втором | 2 |
| 7 |
Коэффициент пропорциональности в каждом уравнении имеет одно и тоже значение, следовательно координаты векторов a и b пропорциональны и следовательно векторы коллинеарны. Значение коэффициента пропорциональности больше нуля, значит векторы a и b сонаправлены. Значение коэффициента пропорциональности больше нуля, значит векторы a и b сонаправлены. |
Пример 3. Определим, являются ли два вектора пространства коллинеарными (параллельными). Координаты обоих векторов заданны точками.
Координаты точки А вектора AB: (7; 0.2 ; 69)
Координаты точки B вектора AB: (-1 ; 0 ; 2/8)
Координаты точки C вектора CD: (-4 ; -6 ; 2)
Координаты точки D вектора CD: (3 ; 0 ; 9)
Вычислим координаты первого вектора по двум точкам A и B:
AB = {Bx — Ax ; By — Ay; Bz — Az} = {-1 — 7 ; 0 — 0.2 ; 2/8 — 69} = {-8 ; 1/5 ; -275/4}
Вычислим координаты второго вектора по двум точкам C и D:
CD = {Dx — Cx ; Dy — Cy; Dz — Cz} = {3 — (-4) ; 0 — (-6) ; 9 — 2} = {7 ; 6 ; 7}
Проверим, есть ли для векторов AB и CD коэффициент пропорциональности q (имеющий одинаковое значение для всех уравнений в системе), для этого составим систему и проверим выполняется ли равенство:
ABx = q ⋅ CDx
ABy = q ⋅ CDy
ABz = q ⋅ CDz
| -8 = q ⋅ 7 тогда, q = — | 8 |
| 7 |
| 1/5 = q ⋅ 6 тогда, q = | 1/5 |
| 6 |
| -275/4 = q ⋅ 7 тогда, q = — | 275/4 |
| 7 |
| = — | 275 |
| 28 |
| ≠ — | 275 |
| 28 |
| В первом уравнении коэффициент пропорциональности равен — | 8 |
| 7 |
| , во втором | 1 |
| 30 |
| и в третьем — | 275 |
| 28 |
Следовательно, система несовместима и не имеет решений. Координаты векторов AB и CD не пропорциональны, значит векторы AB и CD не коллинеарны. Координаты векторов AB и CD не пропорциональны, значит векторы AB и CD не коллинеарны. |
Пример 4. Определим, являются ли два вектора пространства коллинеарными (параллельными).
Координаты вектора a: (0 ; 1 ; 7)
Координаты вектора b: (2 ; 0 ; 6)
Проверим, есть ли для векторов a и b коэффициент пропорциональности q (имеющий одинаковое значение для всех уравнений в системе), для этого составим систему и проверим выполняется ли равенство:
ax = q ⋅ bx
ay = q ⋅ by
az = q ⋅ bz
| 0 = q ⋅ 2 тогда, q = | 0 |
| 2 |
| 1 = q ⋅ 0 | |
| 7 = q ⋅ 0 | |
| Сделаем проверку, подставим значение коэффициента в уравнения | ||
Следовательно, система несовместима и не имеет решений. Координаты векторов a и b не пропорциональны, значит векторы a и b не коллинеарны. Координаты векторов a и b не пропорциональны, значит векторы a и b не коллинеарны. |
Коллинеарные векторы
Навигация по странице:
- Коллинеарные векторы — определение
- Условие коллинеарности векторов
- Примеры задач
- плоские задачи
- пространственных задач
Онлайн-калькулятор для проверки коллинеарности векторов.
Онлайн упражнение. Коллинеарные векторы на плоскости.
Онлайн упражнение. Коллинеарные векторы в пространстве.
Определение.
Векторы, параллельные одной прямой или лежащие на одной прямой, называются коллинеарными векторами (рис. 1).
| Рис. 1 |
Условие коллинеарности векто
a = n · b
Условие коллинеарности векторов 2. Два вектора коллинеарны , если отношения их координат равны.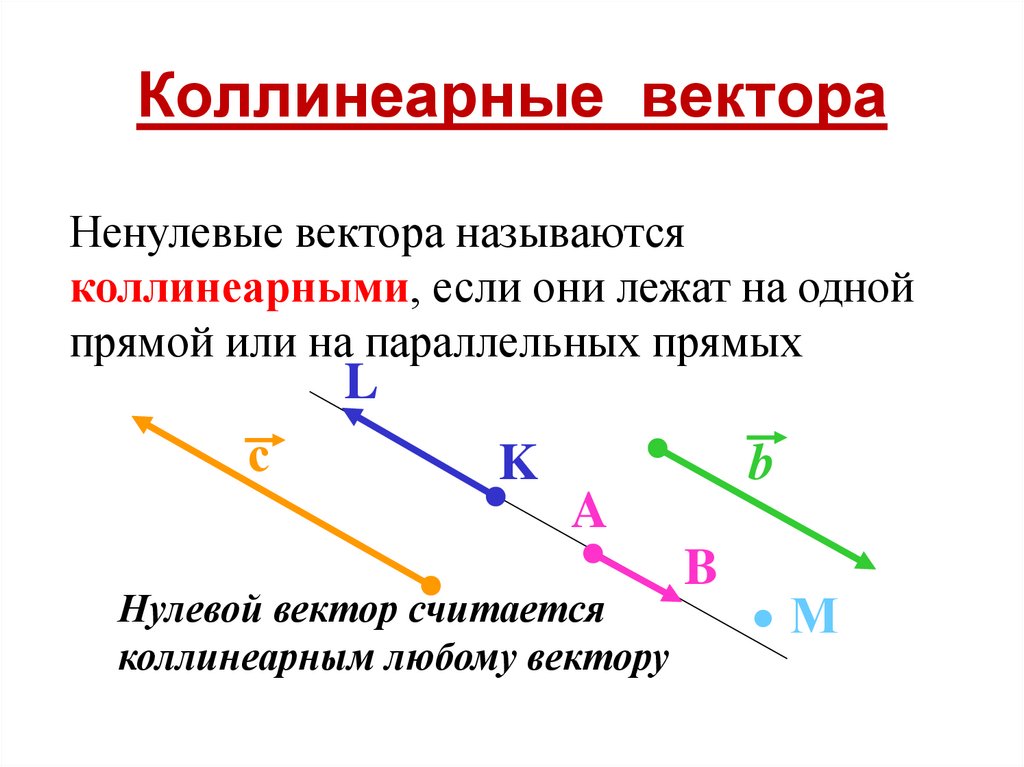
N.B. Условие 2 неверно, если один из компонентов вектора равен нулю.
Условие коллинеарности векторов 3. Два вектора коллинеарны , если их векторное произведение равно нулевому вектору.
N.B. Условие 3 применимо только к трехмерным (пространственным) задачам.
Доказательство условия коллинеарности 3
Пусть имеются два коллинеарных вектора a = {a x ; а и ; a z } и b = {na x ; нет и ; na z }. Находим их векторное произведение
| a × b = | и | к | к | = i (a y b z — a z b y ) — j (a x b z 7 — 007 x z 9 2 ) + k (a x b y — a y b x ) = |
| а x | z | |||
| б х | б у | б z |
= i (a y na z — a z na y ) — j (a x 9007a 2 z 9 0072 na
Примеры задач
Примеры задач плоскости
Пример 1. Какой из векторов a = {1; 2}, б = {4; 8}, с = {5; 9} коллинеарны?
Какой из векторов a = {1; 2}, б = {4; 8}, с = {5; 9} коллинеарны?
Решение: Так как вектора не содержат компоненты a равные нулю, то используем условие коллинеарности 2, что в случае плоской задачи для векторов a и b будет иметь вид:
| a x | = | . | |
| б х | б г |
Означает:
| Векторы a и b коллинеарны, потому что | 1 | = | 2 | . |
| 4 | 8 |
| Векторы а и с не коллинеарны, так как | 1 | ≠ | 2 | . |
| 5 | 9 |
| Векторы с и b не коллинеарны, так как | 5 | ≠ | 9 | .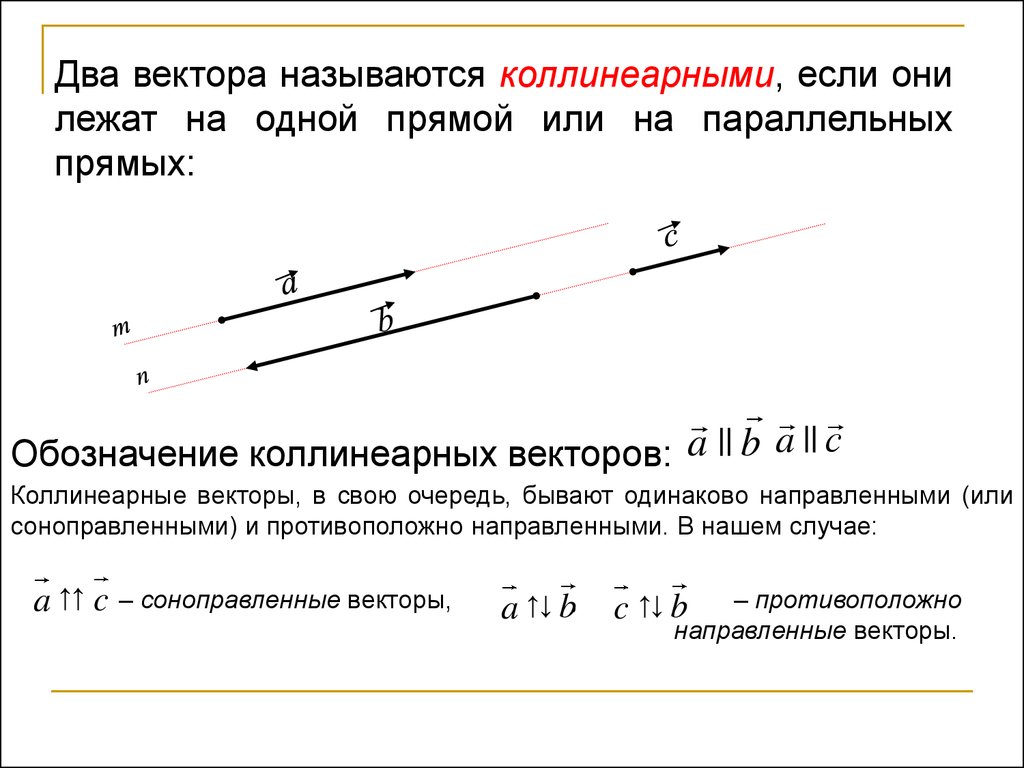 |
| 4 | 8 |
Пример 2. Докажите, что вектор a = {0; 3} и б = {0; 6} коллинеарны.
Решение: Поскольку компоненты вектора содержат ноль, то воспользовавшись условием коллинеарности 1, находим число n, для которого:
б = нет данных.
Для этого находим ненулевую компоненту вектора a в данном случае это a y . Если векторы коллинеарны, то
| n = | б г | = | 6 | = 2 |
| а у | 3 |
Рассчитать значение na:
па = {2 · 0; 2 · 3} = {0; 6}
Поскольку b = 2a, векторы a и b коллинеарны.
Пример 3. Найти значение n, при котором векторы a = {3; 2} и б = {9; n} коллинеарны.
Решение: Так как вектор не содержит компонентов равных нулю, то используем условие коллинеарности 2
| a x | = | . | |
| б х | б г |
Средства:
| 3 | = | 2 | . |
| 9 | п |
Решите это уравнение:
| n = | 2 · 9 | = 6 |
| 3 |
Ответ: векторов a и b коллинеарны при n = 6,
Примеры пространственных задач
Пример 4. Какой из векторов a = {1; 2; 3}, б = {4; 8; 12}, с = {5; 10; 12} коллинеарны?
Решение: Так как вектора не содержат компоненты a равные нулю, то используем условие коллинеарности 2, что в случае плоской задачи для векторов a и b будет иметь вид:
| a x | = | = | а г | .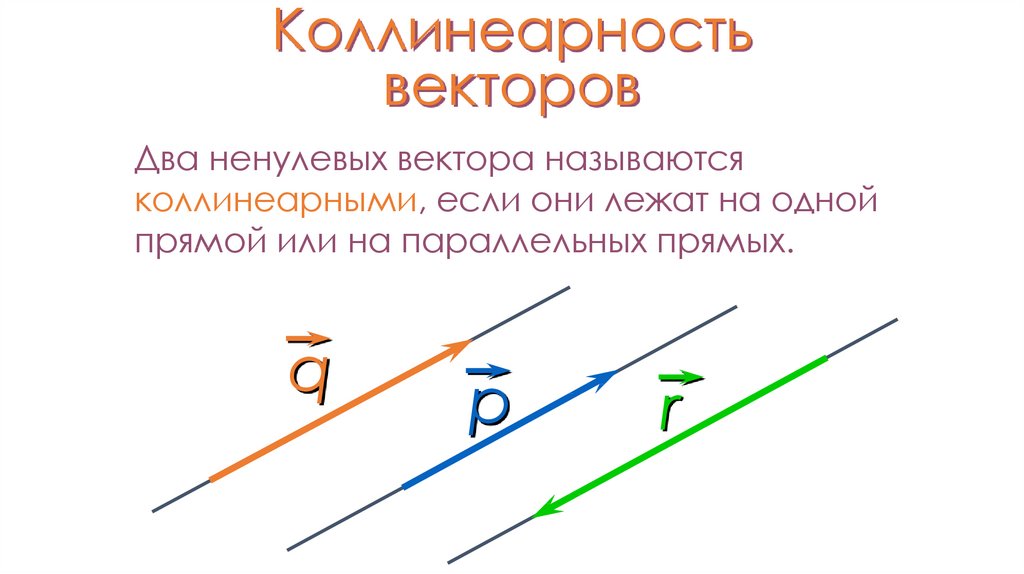 | |
| б х | б г | б г |
Средние значения:
| Векторы a и b коллинеарны, потому что | 1 | = | 2 | = | 3 | . |
| 4 | 8 | 12 |
| Векторы а и с не коллинеарны, так как | 1 | = | 2 | ≠ | 3 | . |
| 5 | 10 | 12 |
| Векторы с и b не коллинеарны, так как | 5 | = | 10 | ≠ | 12 | . |
| 4 | 8 | 12 |
Пример 5. Докажите, что вектор a = {0; 3; 1} и б = {0; 6; 2} коллинеарны.
Докажите, что вектор a = {0; 3; 1} и б = {0; 6; 2} коллинеарны.
Решение: Так как компоненты вектора содержат ноль, то воспользовавшись условием коллинеарности 1, находим число n, для которого:
b = na.
Для этого находим ненулевую компоненту вектора а в данном случае это и . Если векторы коллинеарны, то
| n = | б г | = | 6 | = 2 |
| а у | 3 |
Рассчитать значение na:
па = {2 · 0; 2 · 3; 2 · 1} = {0; 6; 2}
Поскольку b = 2a, векторы a и b коллинеарны.
Пример 6. Найти значения n и m, при которых векторы a = {3; 2; m} и b = {9; н; 12} коллинеарны.
Решение: Так как вектор не содержит компонентов равных нулю, то используем условие коллинеарности 2
| a x | = | = | а г | . | |
| б х | б г | б г |
Средства:
| 3 | = | 2 | = | м |
| 9 | п | 12 |
Из этих соотношений получаем два уравнения:
| 3 | = | 2 |
| 9 | п |
| 3 | = | м |
| 9 | 12 |
Решите следующие уравнения:
| n = | 2 · 9 | = 6 |
| 3 |
| м = | 3 · 12 | = 4 |
| 9 |
Ответ: векторов a и b коллинеарны, когда n = 6 и m = 4.
Векторы Определение векторов. Основная информация Компонентная форма вектора с начальной и конечной точками Длина вектора Направленные косинусы вектора Равные векторы Ортогональные векторы Коллинеарные векторы Компланарные векторы Угол между двумя векторами Векторная проекция Сложение и вычитание векторов Скалярно-векторное умножение Скалярное произведение двух векторов Перекрестное произведение двух векторов (векторное произведение) Скалярное тройное произведение (смешанный продукт) Линейно зависимые и линейно независимые векторы Разложение вектора по базису
Онлайн калькуляторы с векторами
Задания и упражнения с вектором 2D
Задания и упражнения с вектором 3D
Коллинеарные векторы — определения, условия, примеры
Коллинеарные векторы считаются одним из важных понятий в векторной алгебре. Когда два или более заданных вектора лежат вдоль одной и той же заданной прямой, то их можно рассматривать как коллинеарные векторы. Мы можем рассматривать два параллельных вектора как коллинеарные векторы, поскольку эти два вектора указывают точно в одном и том же направлении или в противоположном направлении.
Мы можем рассматривать два параллельных вектора как коллинеарные векторы, поскольку эти два вектора указывают точно в одном и том же направлении или в противоположном направлении.
В этой статье давайте узнаем о коллинеарных векторах, их определении, условиях коллинеарности векторов на решенных примерах.
| 1. | Что такое коллинеарные векторы? |
| 2. | Условия коллинеарных векторов |
| 3. | Часто задаваемые вопросы о коллинеарных векторах |
Что такое коллинеарные векторы?
Любые два заданных вектора можно рассматривать как коллинеарные векторы, если эти векторы параллельны одной и той же заданной прямой. Таким образом, мы можем рассматривать любые два вектора как коллинеарные векторы тогда и только тогда, когда эти два вектора либо лежат на одной прямой, либо эти векторы параллельны друг другу. Чтобы любые два вектора были параллельны друг другу, условие состоит в том, что один из векторов должен быть скалярно кратным другому вектору.
Чтобы любые два вектора были параллельны друг другу, условие состоит в том, что один из векторов должен быть скалярно кратным другому вектору.
На приведенной выше диаграмме векторы, параллельные одной прямой, коллинеарны друг другу, а пересекающиеся векторы неколлинеарны.
Условия коллинеарных векторов
Для того чтобы любые два вектора были коллинеарными, они должны удовлетворять определенным условиям. Вот важные условия коллинеарности векторов:
- Условие 1: Два вектора \(\overrightarrow{p}\) и \(\overrightarrow{q}\) считаются коллинеарными векторами, если существует скаляр ‘n’ такое, что \(\overrightarrow{p}\) = n · \(\overrightarrow{q}\)
- Условие 2: два вектора \(\overrightarrow{p}\) и \(\overrightarrow{q}\) считаются коллинеарными тогда и только тогда, когда отношения их соответствующих координат равны. Это условие не выполняется, если одна из компонент данного вектора равна нулю.
- Условие 3. Два вектора \(\overrightarrow{p}\) и \(\overrightarrow{q}\) считаются коллинеарными векторами, если их векторное произведение равно нулевому вектору.
 Это условие применимо только к трехмерным или пространственным задачам.
Это условие применимо только к трехмерным или пространственным задачам.
Доказательство условия 3:
Рассмотрим два коллинеарных вектора \(\overrightarrow{a}\) = {\(a_{x}\),\(a_{y}\),\(a_{z}\ )} и \(\overrightarrow{b}\) = {n\(a_{x}\),n\(a_{y}\),n\(a_{z}\)}. Мы можем найти векторное произведение между ними как:
\(\overrightarrow{a}\) × \(\overrightarrow{b}\) = \(\left|\begin{array}{ccc}
\boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k} \\
а_{х} и а_{у} и а_{г} \\
b_{x} и b_{y} и b_{z}
\end{массив}\right|\)
= i (\(a_{y}\)\(b_{z}\) — \(a_{z}\)\(b_{y}\)) — j (\(a_{x}\)\(b_{z}\) — \(a_{z}\)\(b_{x}\)) + k (\(a_{x}\)\(b_ {y}\) — \(a_{y}\)\(b_{x}\))
= i (\(a_{y}\)n\(a_{z}\) — \(a_{ z}\)n\(a_{y}\)) — j (\(a_{x}\)n\(a_{z}\) — \(a_{z}\)n\(a_{x} \)) + k (\(a_{x}\)n\(a_{y}\) — \(a_{y}\)n\(a_{x}\))
= 0i + 0j + 0k = \(\overrightarrow{0}\) [Поскольку разные компоненты одного и того же вектора перпендикулярны друг другу и, следовательно, их произведение равно 0. ]
]
Похожие статьи о коллинеарных векторах
Ознакомьтесь со следующими страницами, посвященными коллинеарному вектору
- Добавление калькулятора векторов
- Калькулятор угла между двумя векторами
- Обработка векторов, указанных в форме i-j
- Неравенство треугольников в векторах
- Вычитание двух векторов
Важные примечания о коллинеарных векторах
Вот несколько точек, которые следует помнить при изучении коллинеарных векторов
- Любые два данных вектора можно рассматривать как коллинеарные векторы, если эти векторы параллельны одной и той же заданной прямой .
- Таким образом, мы можем считать любые два вектора коллинеарными тогда и только тогда, когда эти два вектора либо лежат на одной прямой, либо эти векторы параллельны друг другу.
Примеры коллинеарных векторов
Пример 1: Определите, являются ли заданные векторы коллинеарными векторами.
 \(\overrightarrow{P}\) = (3,4,5), \(\overrightarrow{Q}\) = (6,8,10).
\(\overrightarrow{P}\) = (3,4,5), \(\overrightarrow{Q}\) = (6,8,10).Решение: Два вектора считаются коллинеарными, если отношения их соответствующих координат равны.
P 1 /Q 1 = 3/6 = 1/2
P 2 /Q 2 = 4/8 = 1/2
P 3 /Q 3 = 5/10 = 1/2
Поскольку P 1 /Q 1 = P 2 /Q 9007 90 9 0072 2 2 072/Q 3 , векторы \(\overrightarrow{P}\) и \(\overrightarrow{Q}\) можно рассматривать как коллинеарные векторы.
Пример 2: Определите, являются ли заданные векторы коллинеарными векторами. \(\overrightarrow{P}\) = i + j + k, \(\overrightarrow{Q}\) = — i — j — k
Решение: Два вектора считаются коллинеарными векторами, если один вектор является скалярным кратным другого вектора.
Вектор Q = — i — j — k = — (i + j + k) = — (Вектор P)
⇒ Вектор Q является скалярным множителем вектора P.

Кроме того, поскольку P 1 /Q 1 = P 2 /Q 2 = P 3 /Q 3 = -1, векторы \(\overrightarrow{P}\) и \(\overrightarrow{Q}\) могут быть рассматриваются как коллинеарные векторы.
перейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами.
Часто задаваемые вопросы о коллинеарных векторах
Что такое коллинеарные векторы?
Любые два заданных вектора можно рассматривать как коллинеарные векторы, если эти векторы параллельны одной и той же заданной прямой. Таким образом, мы можем считать любые два вектора коллинеарными тогда и только тогда, когда эти два вектора либо лежат на одной прямой, либо эти векторы параллельны друг другу. Чтобы любые два вектора были параллельны друг другу, условие состоит в том, что один из векторов должен быть скалярно кратным другому вектору.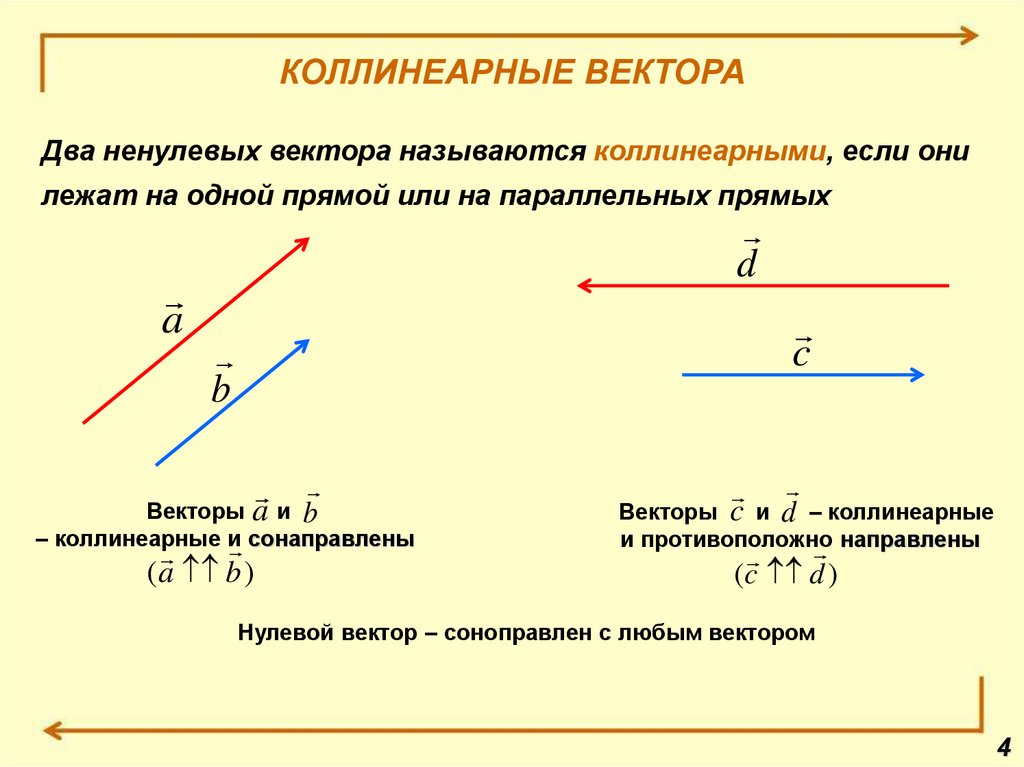
Как узнать, является ли вектор коллинеарным?
Для того, чтобы любые два вектора были коллинеарными, они должны удовлетворять определенным условиям. Вот важные условия коллинеарности векторов:
- Условие 1: Два вектора \(\overrightarrow{p}\) и \(\overrightarrow{q}\) считаются коллинеарными векторами, если существует число ‘n’ такое, что \(\overrightarrow{p}\) = n · \(\overrightarrow{q}\)
- Условие 2: два вектора \(\overrightarrow{p}\) и \(\overrightarrow{q}\) считаются коллинеарными тогда и только тогда, когда отношения их соответствующих координат равны. Это условие не выполняется, если одна из компонент данного вектора равна нулю.
- Условие 3. Два вектора \(\overrightarrow{p}\) и \(\overrightarrow{q}\) считаются коллинеарными векторами, если их векторное произведение равно нулевому вектору. Это условие применимо только к трехмерным или пространственным задачам.
Параллельные и коллинеарные векторы — одно и то же?
Да, параллельные и коллинеарные векторы — это одно и то же. Два вектора называются коллинеарными, если они имеют одинаковое направление, параллельны или антипараллельны. Два вектора параллельны, если они имеют одинаковое или противоположное направление.
Два вектора называются коллинеарными, если они имеют одинаковое направление, параллельны или антипараллельны. Два вектора параллельны, если они имеют одинаковое или противоположное направление.
Как доказать коллинеарность трех позиционных векторов?
Рассмотрим три отрезка PQ, QR и PR. Если PQ + QR = PR, то мы можем считать эти три точки коллинеарными. Три заданных сегмента линии могут быть переведены в соответствующие векторы PQ, QR и PR. Величины этих трех векторов равны длине трех отрезков, упомянутых здесь.
Приведите пример коллинеарных векторов
Рассмотрим два вектора \(\overrightarrow{P}\) = (3,4,5), \(\overrightarrow{Q}\) = (6,8,10). Два вектора считаются коллинеарными, если отношения их координат равны.
P 1 /Q 1 = 3/6 = 1/2
P 2 /Q 2 = 4/8 = 1/2
, так как P 1 /Q 1 = P 2 /Q 2 = P 3 /Q 3 , Vectors \ (Vectors \ (\ (Vectors \ (\ (Vectors \ (Vectors \ (Vectors \ (Vectors \ (Vectors \ (Vectors \ (Vectors \ (Vectors \ (Vectors \ (Vectors \ (Vectors \ (Vector \overrightarrow{P}\) и \(\overrightarrow{Q}\) можно рассматривать как коллинеарные векторы.



 Это условие применимо только к трехмерным или пространственным задачам.
Это условие применимо только к трехмерным или пространственным задачам.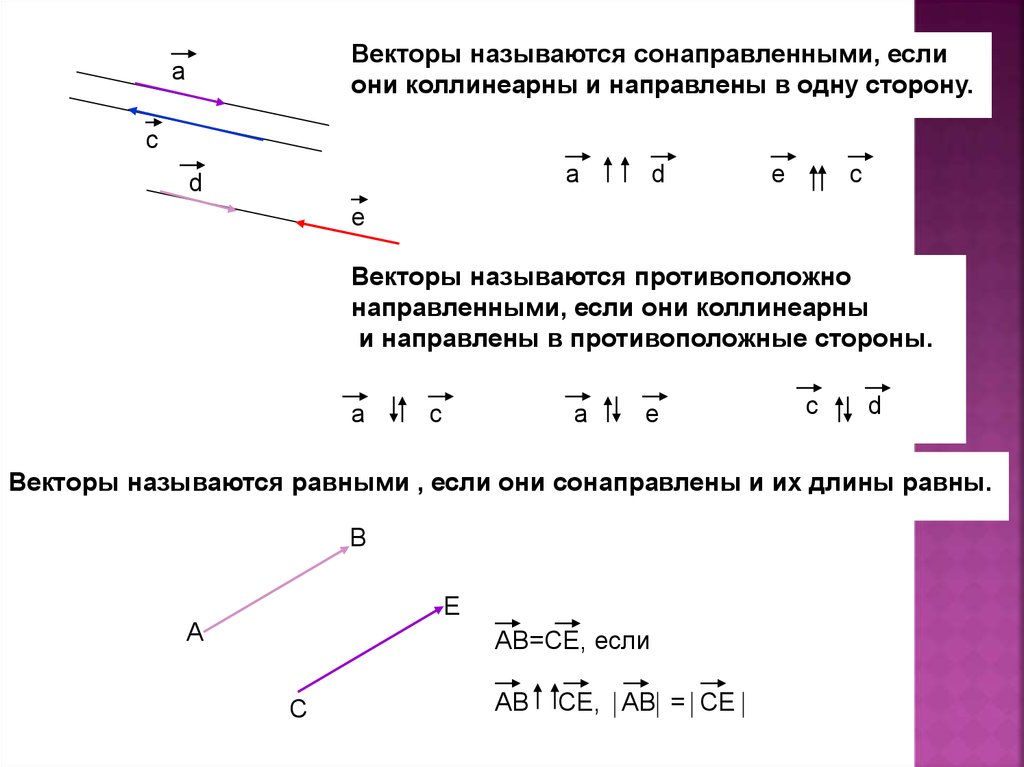 \(\overrightarrow{P}\) = (3,4,5), \(\overrightarrow{Q}\) = (6,8,10).
\(\overrightarrow{P}\) = (3,4,5), \(\overrightarrow{Q}\) = (6,8,10).