|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 2 из 5Следующая ⇒ Цель занятия: уметь применять основные формулы комбинаторики и знать условия применения этих формул; знать свойства биномиальных коэффициентов и уметь определять разложение бинома при конкретных значениях n. План занятия: 1. Число размещений. 2. Число перестановок. 3. Число сочетаний. 4. Повторения. 5. Бином Ньютона. Треугольник Паскаля. Методические указания по изучению темы Во многих практических случаях возникает необходимость подсчитать количество возможных комбинаций объектов, удовлетворяющих определенным условиям. Такие задачи называются комбинаторными. Разнообразие комбинаторных задач не поддается исчерпывающему описанию, но среди них есть целый ряд особенно часто встречающихся, для которых известны способы подсчета.
Комбинаторика Пусть есть некоторое множество из n элементов: x1, x2, x3, …, xn. Из этого множества можно образовать различные подмножества, то есть выборки, каждая из которых содержит m элементов (0 ≤ m ≤ n). Различают упорядоченные выборки (размещения), перестановки и неупорядоченные выборки (сочетания). Размещения Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком. Число размещений из n элементов по m элементов обозначают (А – первая буква французского слова arrangement, что означает размещение, приведение в порядок) и вычисляют по формуле: Понятие факториала Произведение n натуральных чисел от 1 до n обозначается символом n! (n факториал), то есть Например, 2!= 3!= 5!= Заметим, что удобно рассчитывать 0!, полагая по определению, 0!=1. Примеры: Из последних двух формул следует, что
Пример. В однокруговом турнире по футболу участвуют 8 команд. Сколько существует вариантов призовой тройки? Решение: Так как порядок команд в призовой тройке важен, то мы имеем дело с размещениями. Тогда (вариантов).
Пример. Сколькими способами можно выбрать три лица на три различные должности из десяти кандидатов? Решение: (способов).
Пример. Сколько можно составить телефонных номеров из 5 цифр так, чтобы в каждом отдельно взятом номере все цифры были различными? Решение: (телефонных номеров).
Перестановки Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок из n элементов обозначают Pn (P – первая буква французского слова permutation, что означает перестановка) и вычисляют по формуле: Пример. В финальном забеге на 100 метров участвуют 8 спортсменов. Сколько существует вариантов протокола забега? Решение: В данном случае речь идёт обо всех перестановках из 8 элементов. Тогда (вариантов)
Пример. Сколькими различными способами могут разместиться на скамейке10 человек? Решение: (способов)
Пример. Сколькими способами можно разместить 7 лиц за столом, на котором поставлено 7 столовых приборов? Решение: (способов).
Сочетания Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом. Число сочетаний вычисляют по формуле: (С — первая буква французского слова combinasion). Пример. Сколькими способами можно выбрать три лица на три одинаковые должности из десяти кандидатов? Решение: (способов).
Пример. Сколькими способами можно выбрать три детали из ящика, содержащего 15 деталей? Решение: (способов).
Другой вид формул числа размещений и числа сочетаний ; , то есть . Свойства числа сочетаний: 1) 2) 3) 4) 5) При решении задач комбинаторики используют следующие правила: Правило суммы.Если некоторый объект А может быть выбран из совокупности объектов n способами, а другой объект В – k способами, то объект «либо А, либо В» можно выбрать n+k способами.
Правило произведения.Если некоторый объект А может быть выбран из совокупности объектов n способами и после каждого такого выбора другой объект В – k способами, то пара объектов (А, В) в указанном порядке может быть выбрана n×k способами.
Если некоторые элементы повторяются, то в этом случае комбинации с повторениями вычисляют по другим формулам. Размещения с повторениями Число размещений по m элементов с повторениями из n различных элементов равно nm ,то есть Пример. Из цифр 1,2,3,4,5 можно составить 53 =125 трехзначных чисел, если в одном и том же числе могут попадаться и одинаковые цифры. Перестановки с повторениями Если среди n элементов есть n1 элементов одного вида, n2 элементов другого вида и т.д., то число перестановок с повторениями где Пример. Сколько различных перестановок букв можно сделать в слове «математика»? Решение:
Сочетания с повторениями Число сочетаний с повторениями из n различных элементов по m элементов равно числу сочетаний без повторений из (n+m-1) различных элементов по m элементов: Пример. Найти число сочетаний с повторениями из четырех элементов Решение: Искомое число будет Бином Ньютона Для произвольного положительного целого числа n справедлива следующая формула: . Это бином Ньютона. Коэффициенты называются биномиальными коэффициентами. При n = 2 получим формулу ; При n = 3 получим формулу . Пример. Определить разложение при n=4. Решение:
.
Биномиальные коэффициенты обладают рядом свойств: 1. ; 2. ; 3. ; 4. . Рассмотрим следующий треугольник: …………………………. Строка под номером n содержит биномиальные коэффициенты разложения . Воспользовавшись свойством , можно заметить, что каждый внутренний элемент треугольника равен сумме двух элементов, расположенных над ним, а боковые элементы треугольника – единицы: 1 1 1 2 1 1 3 3 1 1 4 6 4 1 ………………………. Это треугольник Паскаля. Он позволяет быстро найти значения биномиальных коэффициентов. Решение примеров рекомендуется выполнять в среде табличного процессора MS Excel. При этом надо учитывать некоторую терминологическую путаницу. В русскоязычной литературе перестановки, составленные из n различных элементов выбором по m элементов, которые отличаются либо составом элементов, либо их порядком, обычно называют размещениями, а под перестановками понимают всю совокупность комбинаций, состоящих из одних и тех же n различных элементов и отличающихся только порядком их расположения. В этом смысле число всех возможных перестановок для множества из n различных элементов считается по формуле факториала Pn = n! или в Excel «=ФАКТР(N)» (см. рис. № 1)
Рис. 1
В Excel считать «перестановки», т.е. размещения, очень удобно, не нужно даже вычислять факториалы (см. рис. №2 и №3): «=ПЕРЕСТ(N;K)». Вместо N и K задаются целые положительные числа, N≥K.
Рис. 2
Рис. 3
Например, если ввести «=ПЕРЕСТ(3;2)», получим 6. Это 6 комбинации: (1,2), (2,1), (1,3), (3,1), (2,3), (3,2). А вот встроенная функция «=ЧИСЛКОМБ(N;K)» выдает комбинаторную формулу, называемую у нас «Число сочетаний». В русскоязычной литературе так именуют перестановки, составленные из n различных элементов выбором по m элементов, которые отличаются только составом элементов, а порядок их выбора безразличен (см. рис, №4)
Рис. 4
При использовании встроенных функций пользуйтесь «Справкой по этой функции». Например:
Задачи для самостоятельного решения 1. Вычислить: 2. Вычислить: 3. Вычислить: 4. Найти n, если 5Сn3 = 5. Найти n, если
6. Найти n, если
7. Найти n, если
8. Найти n, если , k n
9. Решить уравнение
10. Решить систему 11. Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2?
12.
13. Сколько можно составить телефонных номеров из 6 цифр так, чтобы в каждом отдельно взятом номере все цифры были различны?
14. В классе 10 учебных предметов и 5 разных уроков в день. Сколькими способами могут быть распределены уроки в один день?
15. Сколько можно записать четырёхзначных чисел, используя без повторения все 10 цифр?
16. Фирма производит выбор из девяти кандидатов на три различные должности. Сколько существует способов такого выбора?
17. В восьмом классе изучается 15 предметов. Сколькими способами можно составить расписание на среду, если известно, что в этот день должно быть 6 уроков?
18. В высшей лиге чемпионата страны по футболу 16 команд. Борьба идет за золотые, серебряные и бронзовые медали. Сколькими способами медали могут быть распределены между командами?
19. Сколькими способами можно разместить 9 лиц за столом, на котором поставлено 9 приборов?
20.
21. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только один раз?
22. Сколькими различными способами можно расставить 10 различных книг на полке, чтобы определённые 4 книги стояли рядом?
23. В однокруговом турнире по футболу участвуют 8 команд. Сколько всего матчей будет сыграно?
24. Из 25 студентов нужно выбрать трех делегатов на конференцию. Сколькими способами это можно сделать?
25. Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей?
26. В колоде 36 карт, из них 4 туза. Сколькими способами можно извлечь 6 карт так, чтобы среди них было 2 туза?
27. Комплексная бригада состоит из двух маляров, трёх штукатуров и одного столяра. Сколько различных бригад можно создать из рабочего коллектива, в котором 15 маляров, 10 штукатуров и 5 столяров?
28.
29. Из 12 человек выбирают четверых для назначения на 4 одинаковые должности. Сколькими способами можно сделать такой выбор?
30. Сколькими различными способами можно составить разведывательную группу из 3-х солдат и одного командира, если имеется 12 солдат и 3 командира?
31. На плоскости дано n точек, из которых никакие три не лежат на одной прямой. Найти число прямых, которые можно получить, соединяя точки попарно.
32. Буквы азбуки Морзе образуются как последовательность точек и тире. Сколько различных букв можно образовать, если использовать 5 символов?
33. Сколько существует различных семизначных телефонных номеров?
34. Пусть буквы некоторой азбуки образуются как последовательность точек, тире и пробелов. Сколько различных букв можно образовать, если использовать 5 символов?
35.
36. В почтовом отделении продаются открытки пяти видов. Определить число способов покупки семи открыток.
37. Два коллекционера обмениваются марками. Найти число способов обмена, если первый коллекционер обменивает 3 марки, а второй – 6 марок. ( Обмен происходит по одной марке ).
38. У одного студента 6 книг по математике, а у другого – 5. Сколькими способами они могут обменять 2 книги одного на 2 книги другого?
39. Сколько различных перестановок букв можно сделать в словах: «замок», «ротор», «обороноспособность», «колокол», «семинар»?
40. Сколькими различными способами можно разместить в 9 клетках следующие 9 букв: а, а, а, б, б, б, в, в, в?
41. В автомашине 6 мест. Сколькими способами 6 человек могут сесть в эту машину, если занять место водителя могут только двое из них?
42.
43. Определить разложение при n=5. 44. Определить разложение при n=8. 45. Найти член разложения , не содержащий x (то есть содержащий x в нулевой степени). 46. Найти шестой член разложения , если биномиальный коэффициент третьего от конца члена равен 45.
47. В разложении коэффициент третьего члена на 44 больше коэффициента второго члена. Найти свободный член, то есть член разложения, не зависящий от x (членом, не зависящим от x, будет тот, который содержит x в нулевой степени).
48. В разложении бинома найти члены, не содержащие иррациональности. 49. Найти номер того члена разложения , который содержит a и b в одинаковых степенях.
Практическое занятие №2 (интерактивное занятие в малых группах) Булевы функции Цель занятия: уметь строить различные булевы функции, проверять эквивалентность булевых формул (используя таблицу истинности), определять существенные и фиктивные переменные. План занятия: 1. Основные операции 2. Булевы функции от n переменных 3. Основные эквивалентности 4. Формулы
⇐ Предыдущая12345Следующая ⇒ Читайте также: Формы дистанционного обучения Передача мяча двумя руками снизу Значение правильной осанки для жизнедеятельности человека Основные ошибки при выполнении передач мяча на месте |
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 4118; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. |
Формулы комбинаторики
Практические задачи с решениями можно найти на странице http://mathprofi.ru/zadachi_po_kombinatorike_primery_reshenij.html
Основные формулы комбинаторики
1) Факториал (произведение всех натуральных чисел от 1 до n включительно)
1! 1 2! 1 2 2
3! 1 2 3 6 4! 1 2 3 4 24
5! 1 2 3 4 5 120 6! 1 2 3 4 5 6 720
7! 1 2 3 4 5 6 7 5040
…
(n 1)! 1 2 3 4 5 … (n 2)(n 1) n! 1 2 3 4 5 … (n 2)(n 1)n
(n 1)! 1 2 3 4 5 … (n 2)(n 1)n(n 1)
…
Кроме того: 0! 1
2) Перестановки, сочетания и размещения без повторений
Участники действий: множество, состоящее из n различных объектов (либо объектов,
считающихся в контексте той или иной задачи различными)
Формула количества перестановок: Pn n!
Типичная смысловая нагрузка: «Сколькими способами можно переставить n объектов?»
Формула количества сочетаний: Сnm | n! | |
(n m)! m! | ||
|
Типичная смысловая нагрузка: «Сколькими способами можно выбрать m объектов из n ?». Поскольку выборка проводится из множества, состоящего из n объектов, то справедливо неравенство 0 m n
Поскольку выборка проводится из множества, состоящего из n объектов, то справедливо неравенство 0 m n
Формула количества размещений: Anm (n m 1) … (n 1)n
Типичная смысловая нагрузка: «сколькими способами можно выбрать m объектов (из n объектов) и в каждой выборке переставить их местами (либо распределить между ними какие-нибудь уникальные атрибуты)»
Исходя из вышесказанного, справедлива следующая формула:
Сnm Pm Anm
И в самом деле:
С m P | n! | m! | n! |
| 1 2 3 … | (n m)(n m 1) … | (n 1)n | (n m 1) … | (n 1)n Am | |
|
|
|
|
|
| |||||
n m | (n m)! m! |
| (n m)! |
|
| 1 2 3 (n m) |
|
| n | |
|
|
|
|
|
|
| ||||
© http://mathprofi. ru, Емелин А., Высшая математика – просто и доступно!
ru, Емелин А., Высшая математика – просто и доступно!
Практические задачи с решениями можно найти на странице http://mathprofi.ru/zadachi_po_kombinatorike_primery_reshenij.html
3) Бином Ньютона и треугольник Паскаля
Под биномом Ньютона чаще всего подразумевают формулу возведения двучлена (a b) в целую неотрицательную степень n :
(a b)0 1
(a b)1 C10a C11b a b
(a b)2 C20a2 C21a1b1 C22b2 a2 2ab b2
(a b)3 C30a3 C31a2b1 C32a1b2 C33b3 a3 3a2b 3ab2 b3
(a b)4 C40a4 C41a3b1 C42a2b2 C43a1b3 C44b4 a4 4a3b 6a2b2 4ab3 b4
(a b)5 C50a5 C51a4b1 C52a3b2 C53a2b3 C54a1b4 C55b5 a5 5a4b 10a3b2 10a2b3 5ab4 b5
…
(a b)n Cn0an Cn1an 1b1 Cn2an 2b2 Cn3an 3b3 … Cnn 2a2bn 2 Cnn 1a1bn 1 Cnnbn
…
Биномиальные коэффициенты Cnm можно рассчитать по стандартной формуле (см. пункт 2), но
удобнее воспользоваться так называемым треугольником Паскаля, который представляет собой бесконечную таблицу биномиальных коэффициентов. По бокам этого треугольника расположены единицы, а каждое внутреннее число равно сумме двух ближайших верхних чисел (красные метки):
Так, например, для возведения двучлена в 6-ю степень следует руководствоваться общей формулой бинома, после чего сразу записать числа из строки № 6 треугольника Паскаля:
(a b)6 C60a6 C61a5b1 C62a4b2 C63a3b3 C64a2b4 C65a1b5 C66b6
a6 6a5b 15a4b2 20a3b3 15a2b4 6ab5 b6
Кроме того, данная таблица позволяет быстро находить отдельно взятые биномиальные
коэффициенты (например, в целях проверки вычислений по формуле Сnm | n! |
| ): |
|
| ||
(n m)! m! |
|
| |||||
|
|
|
|
|
| ||
C 2 | – находим строку № 6 | и (внимание!) 2 + 1 = 3-й элемент слева (зелёный кружок): | C | 2 | 15 ; | ||
6 |
|
|
|
| 6 |
| |
C5 | – находим строку № 9 | и выбираем 5 + 1 = 6-й элемент слева (малиновый кружок): | C5 126 ; | ||||
9 |
|
|
|
|
| 9 |
|
C 3 | – находим строку № 10 и выбираем 3 + 1 = 4-й элемент слева (коричневый кружок): |
| C3 120 . | ||||
10 |
|
|
|
|
|
| 10 |
© http://mathprofi.ru, Емелин А., Высшая математика – просто и доступно!
Практические задачи с решениями можно найти на странице http://mathprofi.ru/zadachi_po_kombinatorike_primery_reshenij.html
4) Комбинаторное правило суммы и комбинаторное правило произведения
Если объект A можно выбрать из некоторого множества объектов m способами, а другой объект B – n способами, то выбор объекта A или объекта B (без разницы какого) возможен m n способами.
Если объект A можно выбрать из некоторого множества объектов m способами и после каждого такого выбора объект B можно выбрать n способами, то упорядоченная пара объектов ( A; B)
может быть выбрана mn способами.
Данные принципы справедливы и для бОльшего количества объектов.
Важная содержательная часть правил состоит в том, знак «плюс» понимается и читается как союз ИЛИ, а знак «умножить» – как союз И.
5) Перестановки, сочетания и размещения с повторениями
Участники действий: множество, состоящее из объектов, среди которых есть одинаковые
(либо считающиеся таковыми по смыслу задачи)
Формула количества перестановок с повторениями: | Pn (пов т) | n! |
| , | |
|
| ||||
n1! n2! n3! … nk | ! | ||||
|
|
| |||
где n1 n2 n3 … nk n |
|
|
|
| |
Типичная смысловая нагрузка: «Количество способов, которыми можно переставить | |||||
n объектов, среди которых 1-й объект повторяется n1 | раз, 2-й объект повторяется n2 раз, | ||||
3-й объект – n3 раз,…, k -й объект – nk раз» |
|
|
|
| |
Следует отметить, что в подавляющем большинстве задач в совокупности есть и уникальные (не повторяющиеся) объекты, в этом случае соответствующие значения ni равны единице,
и в практических расчётах их можно не записывать в знаменатель.
Формула количества сочетаний с повторениями: С m С m (n m 1)! n (пов т) n m 1 (n 1)! m!
Типичная смысловая нагрузка: «Для выбора предложено n множеств, каждое из которых состоит из одинаковых объектов. Сколькими способами можно выбрать m объектов?»
То есть, здесь в выборке могут оказаться одинаковые объекты, и если m n , то совпадения точно будут. По умолчанию предполагается, что исходная совокупность содержит не менее m объектов каждого вида, и поэтому выборка может полностью состоять из одинаковых объектов.
Формула количества размещений с повторениями: Anm(повт) nm
Типичная смысловая нагрузка: «Дано множество, состоящее из n объектов, при этом любой объект можно выбирать неоднократно. Сколькими способами можно выбрать m объектов,
если важен порядок их расположения в выборке? »
Для бОльшей ясности здесь удобно представить, что объекты извлекаются последовательно (хотя это вовсе не обязательное условие). В частности, возможен случай, когда из n имеющихся объектов m раз будет выбран какой-то один объект.
© http://mathprofi.ru, Емелин А., Высшая математика – просто и доступно!
Перестановка/комбинация — SAT Math
Все математические ресурсы SAT
16 диагностических тестов 660 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 Следующая →
SAT Math Help » Арифметика » Целые числа » Permutation/Combination
У Марка в шкафу 5 штанов и 7 рубашек. Он хочет носить новую комбинацию брюк и рубашки каждый день, не покупая новую одежду, как можно дольше. Сколько недель он может это делать?
Возможные ответы:
Правильный ответ:
5
Объяснение:
Фундаментальный принцип подсчета гласит, что если вы хотите определить количество способов, которыми могут произойти два независимых события, умножьте количество способов, которыми каждое событие может произойти вместе. В этом случае есть 5 * 7 или 35 уникальных комбинаций брюк и рубашек, которые может носить Марк. Если он носит одну комбинацию каждый день, он может продержаться 35 дней или 5 недель, не покупая новую одежду.
В этом случае есть 5 * 7 или 35 уникальных комбинаций брюк и рубашек, которые может носить Марк. Если он носит одну комбинацию каждый день, он может продержаться 35 дней или 5 недель, не покупая новую одежду.
Сообщить об ошибке
Двадцать учеников участвуют в школьном конкурсе. Конкурс предлагает первый, второй и третий приз. Сколько различных комбинаций 1-го, 2-х -х, -х и 3-х мест может быть?
Возможные ответы:
400
4620
8000
20
6840
Правильный ответ:
6840
Объяснение:
Это задача на перестановку, потому что мы ищем количество групп победителей. Рассмотрите три позиции и количество вариантов для каждой позиции: есть 20 вариантов для 1-го места, 19за 2 место и 18 за 3 место.
20, 19, 18
Умножьте, чтобы получить 6840.
Сообщить об ошибке
У пекаря есть четыре разных вида глазури, три разных вида посыпки и 8 разных формочек для печенья. Сколько различных комбинаций печенья может создать пекарь, если каждое печенье имеет один тип глазури и один тип посыпки?
Возможные ответы:
15
48
24
96
Правильный ответ:
96
Объяснение:
Так как это проблема комбинирования, и мы хотим знать, сколько различных способов могут быть созданы файлы cookie, мы можем решить ее, используя фундаментальный принцип подсчета. 4 x 3 x 8 = 96
Перемножение всех возможных вариантов.
Сообщить об ошибке
Если необходимо изготовить серию номерных знаков, каждая из которых имеет одинаковую схему из трех букв, за которыми следуют три цифры, сколько примерно буквенно-цифровых комбинаций возможно?
Возможные ответы:
180 млн.
11 млн.
1 тысяча
18 млн.
18 тысяча
Правильный ответ:
миллионов
. Объяснение:
Общее количество возможных комбинаций ряда элементов равно произведению общей возможности для каждого из элементов. Таким образом, для букв есть 26 возможностей для каждого из 3-х слотов, а для чисел есть 10 возможностей для каждого из 3-х слотов. Тогда общее количество комбинаций равно: 26 х 26 х 26 х 10 х 10 х 10 = 17 576 000 ≈ 18 миллионов.
Сообщить об ошибке
Если на плоскости 8 точек, и никакие 3 из них не лежат на одной прямой, сколько уникальных линий можно провести между парами этих 8 точек?
Возможные ответы:
29
27
30
28
Правильный ответ:
28
Объяснение:
Формула для количества прямых, определяемых n точками, никакие три из которых не лежат на одной прямой (коллинеарными), равна n(n-1)/2. Чтобы найти количество линий, определяемое 8 точками, мы используем 8 в формуле, чтобы найти 8(8-1)/2=8(7)/2=56/2=28. (Формула получена из двух фактов: того факта, что каждая точка образует прямую с каждой другой точкой, следовательно, n(n-1), и того факта, что это отношение симметрично (т. е. если a образует прямую с b, то b образует линию с a), следовательно, деление на 2.)
Чтобы найти количество линий, определяемое 8 точками, мы используем 8 в формуле, чтобы найти 8(8-1)/2=8(7)/2=56/2=28. (Формула получена из двух фактов: того факта, что каждая точка образует прямую с каждой другой точкой, следовательно, n(n-1), и того факта, что это отношение симметрично (т. е. если a образует прямую с b, то b образует линию с a), следовательно, деление на 2.)
Сообщить об ошибке
8 человек, запертых в комнате, по очереди берутся за руки с каждым человеком только один раз. Сколько захватов рук происходит?
Возможные ответы:
15
21
28
24
Правильный ответ: 4 50
28904 Пояснение:Первый человек держит 7 рук. Второй держит шестерых в силу уже имеющейся помощи руки первого человека. Так продолжается до тех пор, пока не пройдут все 8 человек. 7+6+5+4+3+2+1=28.
Сообщить об ошибке
В магазине мороженого есть 5 вкусов мороженого: клубничное, ванильное, шоколадное, мятное и банановое. Сколько разных рожков для мороженого с тремя вкусами можно сделать?
Сколько разных рожков для мороженого с тремя вкусами можно сделать?
Возможные ответы:
5
20
60
30
10
Правильный ответ:
10
Объяснение:
Есть 5x4x3 способов расположить 5 вкусов 3 способами. Однако в этом случае порядок вкусов не имеет значения (например, рожок с клубникой, мятой и бананом такой же, как рожок с мятой, бананом и клубникой). Итак, мы должны разделить 5x4x3 на количество способов, которыми мы можем расположить 3 разных вещи, то есть 3x2x1. Итак, (5x4x3)/(3x2x1) равно 10,
Можно также использовать формулу комбинации для этой задачи: n C r = n! / (н-р)! р!
Следовательно: 5 C 3 = 5! / 3! 2!
= 10
(Примечание. Примером задачи подсчета, в которой порядок имеет значение, является ситуация с замком или кодом доступа. Перестановка 3-5-7 для трехзначного замка или кода доступа отличается от 5- 7-3, поэтому оба должны быть учтены.)
Перестановка 3-5-7 для трехзначного замка или кода доступа отличается от 5- 7-3, поэтому оба должны быть учтены.)
Сообщить об ошибке
В гастрономе вы можете выбрать итальянский хлеб, цельнозерновой хлеб или хлеб на закваске. Вы можете выбрать индейку или ростбиф в качестве мяса и проволоне или моцареллу в качестве сыра. Если вам нужно выбрать хлеб, мясо и сыр, сколько возможных комбинаций бутербродов у вас может быть?
Возможные ответы:
10
14
7
12
8
Правильный ответ:
12
Пояснение:
У вас есть 3 возможных вида хлеба, 2 возможных вида мяса и 2 возможных вида сыра. Умножая их, вы получаете 3*2*2, что дает вам 12 возможных комбинаций.
Сообщить об ошибке
Шеннон решила пойти пообедать в соседнее кафе. Она может приготовить бутерброд на пшеничном или белом хлебе. Кафе предлагает выбор сыра чеддер, швейцарский и американский. Из мяса Шеннон может выбрать ветчину, индейку, колбасу, ростбиф или салями. Сколько вариантов сэндвичей с сыром и мясом есть на выбор у Шеннон?
Кафе предлагает выбор сыра чеддер, швейцарский и американский. Из мяса Шеннон может выбрать ветчину, индейку, колбасу, ростбиф или салями. Сколько вариантов сэндвичей с сыром и мясом есть на выбор у Шеннон?
Возможные ответы:
35
25
10
30
20
Правильный ответ:
30
Объяснение:
2 варианта хлеба * 3 варианта сыра * 5 вариантов мяса = 30 вариантов сэндвичей
Сообщить об ошибке
Кафе-мороженое предлагает 36 вкусов мороженого. Вы можете заказать любой вкус в маленьком, среднем или большом размере и выбрать между вафельным рожком и чашкой. Сколько возможных комбинаций вы могли бы заказать?
Возможные ответы:
144
72
172
216
108
Правильный ответ:
216
Пояснение:
36 возможных вкусов * 3 возможных размера * 2 возможных конуса = 216 возможных комбинаций.
Сообщить об ошибке
← Назад 1 2 3 Далее →
Уведомление об авторских правах
Все математические ресурсы SAT
16 Диагностические тесты 660 практических тестов Вопрос дня Карточки Учитесь по концепции
Объяснение урока: Свойства комбинаций
В этом объяснении мы узнаем, как использовать свойства комбинаций для упрощения выражений и решения уравнений.
Комбинация — это набор 𝑟 предметов, выбранных без
повторение из сборника
𝑛 предметы, в которых
порядок не имеет значения. Ключевое различие между комбинацией и перестановкой
заключается в том, что порядок не имеет значения. Для перестановки,
порядок имеет значение. Попробуйте подсчитать количество способов, которыми мы можем назначить роль
президента и вице-президента в
группа из 5 человек: Мона, Амер, Самар, Бассем,
и Далия. Если мы выберем
Мона, потом Далия, это будет не то же самое, что Далия,
то мона так как первый выбор
будет президентом, а второй — вице-президентом. Однако,
если бы мы просто хотели комитет из двух человек,
не важно, выберем ли мы Мону, затем Далию или Далию,
затем Мона. Следовательно, считая
с перестановками приводит к тому, что мы пересчитываем количество возможных вариантов, если
порядок не имеет значения. Фактически,
мы пересчитываем ровно в 𝑟 раз. Таким образом, мы можем определить число
𝑟 комбинаций из 𝑛 как число
из 𝑟
перестановки 𝑛 разделить на 𝑟.
Однако,
если бы мы просто хотели комитет из двух человек,
не важно, выберем ли мы Мону, затем Далию или Далию,
затем Мона. Следовательно, считая
с перестановками приводит к тому, что мы пересчитываем количество возможных вариантов, если
порядок не имеет значения. Фактически,
мы пересчитываем ровно в 𝑟 раз. Таким образом, мы можем определить число
𝑟 комбинаций из 𝑛 как число
из 𝑟
перестановки 𝑛 разделить на 𝑟.
Определение: Количество комбинаций заданного размера
Количество комбинаций размера 𝑟, взятых из коллекция предметов 𝑛 предоставлена 𝐶=𝑃𝑟=𝑛𝑟𝑛−𝑟.
Обозначение 𝐶 можно прочитать как
𝑛-𝐶-𝑟 или как
𝑛 выберите 𝑟 и также называется биномиальным
коэффициент. Еще одно чрезвычайно распространенное обозначение 𝐶:
𝑛𝑟; однако существуют также различные другие формы обозначений
обычно используется, например, 𝐶,
𝐶,
𝐶, и
𝐶(𝑛,𝑟).
Этот объяснитель сосредоточится на ключевых свойствах 𝐶 и как мы можем применить их для упрощения выражений и решения уравнений. Мы начинаем с рассмотрим пример, в котором мы используем формулу для вычисления выражения, включающего комбинации.
Пример 1. Оценка комбинаций
Определите значение 𝐶𝐶 без использования калькулятора.
Ответить
Напомнить, что 𝐶=𝑛𝑟𝑛−𝑟.
Подставляя 𝑛=23 и 𝑟=8, получаем 𝐶=23823−8=238×15.
Аналогично, подставляя 𝑛=23 и 𝑟=6, получаем 𝐶=236×17.
Подставляя их в данное выражение, получаем ××𝐶𝐶=2381523617.
Используя правила дробей, мы можем переписать это как 𝐶𝐶=238×156×1723.
Отменив общий множитель 23, мы получим 𝐶𝐶=6×178×15.
Поскольку 𝑛=𝑛(𝑛−1)×⋯×2×1, мы можем упростить это, чтобы получить 17×168×7=347.
Чтобы решить предыдущий пример, мы могли бы просто использовать комбинации
на нашем калькуляторе, чтобы вычислить выражение. Тем не менее, рост
умение оперировать формулами перестановок и комбинаций
даст нам необходимые навыки, необходимые для решения более сложных задач.
Тем не менее, рост
умение оперировать формулами перестановок и комбинаций
даст нам необходимые навыки, необходимые для решения более сложных задач.
Давайте рассмотрим пример, где мы находим неизвестное из уравнения, которое включает перестановку и комбинацию.
Пример 2: Равенство комбинаций и перестановок
Если 𝐶=𝑃, найдите значение (я) числа 𝑟.
Ответ
Напомним, что из определения комбинаций мы имеем 𝐶=𝑃𝑟.
Подставив это в данное уравнение, получим 𝑃=𝐶=𝑃𝑟.
Перекрестное умножение на 𝑟 и деление на 𝑃, мы можем переписать это как 𝑟=1.
У нас может возникнуть соблазн сразу же сделать вывод, что 𝑟=1. Однако это будет лишь частичным ответом, поскольку, вспоминая определение факториала, мы также имеем, что 0=1.
Обратите внимание, что когда 𝑟=0, мы имеем
𝐶=𝑃=1
и когда 𝑟=1, мы имеем
𝐶=𝑃=𝑛.
Следовательно, два возможных значения 𝑟 равны 1 и 0.
В следующем примере мы найдем выражение, включающее перестановки, которое равно заданному выражению, включающему комбинации.
Пример 3: Связь между комбинациями и перестановками
Что из следующего равно 𝐶×𝐶𝐶?
- 𝑃𝑃
- 𝑃𝑃
- 𝑃𝑃
- 𝑃𝑃
Ответ
Начнем с того, что заметим, что 𝐶=𝑛. Следовательно, мы можем переписать выражение: 𝐶×𝐶𝐶=𝑛𝐶𝐶.
Поскольку все, что мы пытаемся найти, это выражение, включающее перестановки, мы должны попытаться выразить комбинации в терминах перестановок. Для этого можно использовать определение, что 𝐶=𝑃𝑟 переписать наше выражение как 𝐶×𝐶𝐶=𝑛67.
Отмена 6, имеем
𝐶×𝐶𝐶=7𝑛𝑃𝑃,
который мы также можем записать как
𝐶×𝐶𝐶=𝑃.
Вспоминая свойство перестановок, что 𝑛𝑃=𝑃, мы можем переписать 𝑃7𝑛=𝑃.
Следовательно, 𝐶×𝐶𝐶=𝑃𝑃.
Следовательно, правильный ответ C.
До сих пор мы просто использовали определение и формулу для 𝐶 для решения проблем. Много проблем с участием комбинаций можно решить таким образом. Однако часто мы можем решать проблемы более простым и понятным способом, будучи знакомым со свойствами комбинаций. Одно из таких свойств связано с симметрией комбинаций.
Уведомление из определения 𝐶=𝑛𝑟𝑛−𝑟 что существует симметрия относительно знаменателя. Если мы заменим 𝑛−𝑟 вместо 𝑟 в формуле мы находим, что мы получаем одно и то же выражение: 𝐶=𝑛𝑛−𝑟𝑛−(𝑛−𝑟)=𝑛𝑟𝑛−𝑟.
Это приводит к общей идентичности комбинаций.
Тождество: симметрия комбинаций
Для заданных натуральных чисел 𝑟 и 𝑛, удовлетворяющих 𝑟𝑛, имеем
𝐶=𝐶.
Это имеет некоторые интересные последствия для решения уравнений, включающих 𝐶 с неизвестными в 𝑟. Следующий пример продемонстрирует одно из таких следствий.
Пример 4: Симметрия комбинаций
Найдите возможные значения 𝑟, которые удовлетворяют уравнению 𝐶=𝐶.
Ответ
Используя правило 𝐶=𝐶, мы получаем это 𝐶=𝐶=𝐶.
Таким образом, 𝑟=15 или 𝑟=6.
Последний пример показал, что если 𝐶=𝐶 тогда 𝑎=𝑏 или 𝑎=𝑛−𝑏.
Рассмотрим другой пример, требующий симметрии комбинаций.
Пример 5: Использование симметрии комбинаций
Если 𝐶+𝐶=2𝐶, найти 𝑛.
Ответ
Используя свойство 𝐶=𝐶, мы можем переписать 𝐶=𝐶. Замена это в данное уравнение, мы находим 2𝐶=2𝐶.
Отсюда следует, что 𝑛−42=43 или 𝑛−42=𝑛−43. Поскольку последний из них несовместим, мы имеем, что единственный
решение 𝑛=85.
В следующем примере мы определим неизвестную константу в комбинациях, когда нам известно, что выражения, включающие комбинации, образуют арифметическую последовательность.
Пример 6. Решение задач на комбинации
Учитывая, что 3×𝐶,4×𝐶,6×𝐶, — арифметическая прогрессия, найдите все возможные значения 𝑛.
Ответ
В арифметической прогрессии существует постоянная разница между последовательными условия. Следовательно, разница между двумя первыми и двумя последними членами будет равны, и мы можем написать 6×𝐶−4×𝐶=4×𝐶−3×𝐶.
Переставляя, получаем 8×𝐶=6×𝐶+3×𝐶.
Использование определения 𝐶=𝑛𝑟𝑛−𝑟, мы можем переписать это как 8𝑛11𝑛−11=6𝑛12𝑛−12+3𝑛10𝑛−10.
Разделив на общий делитель числа 𝑛, получим 811𝑛−11=612𝑛−12+310𝑛−10.
Теперь мы можем умножить на
12𝑛−10, чтобы получить
8×12𝑛−1011𝑛−11=6×12𝑛−1012𝑛−12+3×12𝑛−1010𝑛−10.
Используя свойство факториала, которое 𝑛=𝑛𝑛−1, мы можем переписать это как 8×12×1111×(𝑛−10)𝑛−11𝑛−11=6×1212×(𝑛−10)(𝑛−11)𝑛−12𝑛−12+3×12×11×1010×𝑛−10𝑛−10 .
Сокращая общие множители в числителях и знаменателях, имеем 8×12(𝑛−10)=6(𝑛−10)(𝑛−11)+3×12×11.
Теперь мы можем разделить на 6, чтобы получить 8×2(𝑛−10)=(𝑛−10)(𝑛−11)+3×2×11.
Раскрывая скобки, получаем 16𝑛−160=𝑛−21𝑛+110+66.
Собирая подобные члены, мы приходим к квадратичному 0=𝑛−37𝑛+336.
Решая это с помощью факторизации или квадратичной формулы, получаем 𝑛=21 и 𝑛=16.
Одним из других ключевых свойств комбинаций является рекурсивная связь:
Формула: Рекурсивная связь в комбинациях
𝐶+𝐶=𝐶 где 0𝑟𝑛.
Чтобы вывести эту формулу, мы можем использовать определение 𝐶 писать левую часть как 𝐶+𝐶=𝑛−1𝑟𝑛−𝑟−1+𝑛−1𝑟−1𝑛−𝑟.
Мы хотели бы выразить это как одну дробь над общим знаменателем
𝑟𝑛−𝑟. Мы можем сделать это, умножив первый член на 𝑛−𝑟𝑛−𝑟
а второй член через 𝑟𝑟 следующим образом:
𝐶+𝐶=(𝑛−𝑟)𝑛−1𝑟(𝑛−𝑟)𝑛−𝑟−1+𝑟𝑛−1𝑟𝑟−1𝑛−𝑟.
Мы можем сделать это, умножив первый член на 𝑛−𝑟𝑛−𝑟
а второй член через 𝑟𝑟 следующим образом:
𝐶+𝐶=(𝑛−𝑟)𝑛−1𝑟(𝑛−𝑟)𝑛−𝑟−1+𝑟𝑛−1𝑟𝑟−1𝑛−𝑟.
Используя свойства факториалов, которые 𝑛=𝑛𝑛−1, мы можем переписать это как 𝐶+𝐶=(𝑛−𝑟)𝑛−1𝑟𝑛−𝑟+𝑟𝑛−1𝑟𝑛−𝑟.
Выразив это в виде одной дроби и раскрыв скобки, мы имеем 𝐶+𝐶=𝑛𝑛−1−𝑟𝑛−1+𝑟𝑛−1𝑟𝑛−𝑟.
Упрощая и используя то же правило факториалов, мы имеем 𝐶+𝐶=𝑛𝑟𝑛−𝑟=𝐶 как требуется.
Сейчас мы обратим внимание на один пример, где мы применяем это свойство упростить уравнение.
Пример 7: Попарные суммы комбинаций
Определите значение 𝐶+𝐶.
Ответ
Похоже, это выражение будет чрезвычайно трудоемко вычислить или вычислить.
трудно упростить. Тем не менее, первое понимание, которое мы получаем, замечая
что когда 𝑟=15 в сумме, мы имеем термин
𝐶=𝐶. Убрав это слагаемое из суммирования, имеем
Убрав это слагаемое из суммирования, имеем
В этот момент мы можем применить рекурсивное отношение, 𝐶+𝐶=𝐶, и упростить это до 𝐶+𝐶=𝐶+𝐶.
Теперь мы видим, что если мы проделаем то же самое еще раз и возьмем последний член из суммирования, мы имеем
Следовательно, 𝐶+𝐶=𝐶+𝐶.
Продолжая тот же метод, мы в конце концов придем к последнему члену в сумме, 𝐶, и имеют выражение
Таким образом, все выражение упрощается до 𝐶+𝐶=𝐶.
Для последней пары примеров мы будем рассматривать суммы всех комбинаций 𝐶 для данного 𝑛.
Пример 8: суммы комбинаций
Найдите значение 𝐶+𝐶+𝐶+⋯+𝐶.
Ответ
Использование определения
𝐶=𝑛𝑟𝑛−𝑟,
мы можем переписать это выражение как
𝐶+𝐶+𝐶+⋯+𝐶=50×5+51×4+52×3+⋯+55×0.
Оценивая каждое слагаемое, имеем 𝐶+𝐶+𝐶+⋯+𝐶=1+5+10+10+5+1=32.
В последнем примере мы обнаружили, что сумма всех комбинаций 𝐶 для 𝑛=5 есть 32; не случайно это равно 2. На самом деле общее правило состоит в том, что сумма всех 𝐶 для любого заданного 𝑛 равно 2. Мы можем записать это как 𝐶+𝐶+𝐶+⋯+𝐶+𝐶=2, или более кратко, мы имеем следующее тождество.
Идентичность: сумма комбинаций
Для любого положительного целого числа 𝑛 имеем 𝐶=2.
Возможно, это правило не так уж удивительно, если учесть рекурсивное отношение для каждого термина: 𝐶+𝐶=𝐶.
Поскольку это не относится к 𝑟=0 или 𝑟=𝑛, мы можем переписать сумму как 𝐶 = 𝐶+ 𝐶+𝐶+𝐶+𝐶+𝐶+𝐶+⋯+𝐶+𝐶+𝐶.
Поскольку 𝐶=1=𝐶 и
𝐶=1=𝐶,
мы можем переписать это выражение как
𝐶=𝐶+𝐶+𝐶+𝐶+𝐶+𝐶+𝐶+⋯+𝐶+𝐶+𝐶.
Перегруппировав термины, мы имеем 𝐶=𝐶+𝐶+𝐶+𝐶+𝐶+𝐶+⋯+𝐶+𝐶=2𝐶+𝐶 𝐶.
Следовательно, сумма 𝐶 вдвое больше суммы 𝐶. Более того, поскольку 𝐶=1, мы видим, что сумма 𝐶 для данного 𝑛 будет сила двух; в частности, это будет 2.
Наконец, рассмотрим переменную сумму комбинаций.
Пример 9: Переменные суммы комбинаций
Найдите значение 𝐶−𝐶+𝐶−𝐶+𝐶.
Ответ
Напомним, что 𝐶=𝑛𝑟𝑛−𝑟. Используя это, мы видим, что 𝐶−𝐶+𝐶−𝐶+𝐶=40×4−41×3+42×2−43×1+44×0.
Оценка каждого термина дает нам 𝐶−𝐶+𝐶−𝐶+𝐶=1−4+6−4+1=0.
Опять же, общее правило состоит в том, что чередующиеся суммы 𝐶 равны нулю: 𝐶−𝐶+𝐶−⋯+(−1)𝐶+(−1)𝐶=0 или, более кратко,
Идентичность: чередующаяся сумма комбинаций
Для любого натурального числа 𝑛 имеем
(−1)𝐶=0.









 Сколькими способами можно выбрать четыре лица на четыре различные должности из девяти кандидатов?
Сколькими способами можно выбрать четыре лица на четыре различные должности из девяти кандидатов? На собрании выступят 6 ораторов. Сколькими способами их фамилии можно расположить в списке?
На собрании выступят 6 ораторов. Сколькими способами их фамилии можно расположить в списке? В отборочном турнире за 3 путёвки на чемпионат мира участвуют 10 команд. Сколько существует вариантов «счастливой тройки»?
В отборочном турнире за 3 путёвки на чемпионат мира участвуют 10 команд. Сколько существует вариантов «счастливой тройки»? При игре в бридж между четырьмя игроками распределяется колода карт в 52 листа по 13 карт каждому игроку. Сколько существует различных способов раздать карты?
При игре в бридж между четырьмя игроками распределяется колода карт в 52 листа по 13 карт каждому игроку. Сколько существует различных способов раздать карты?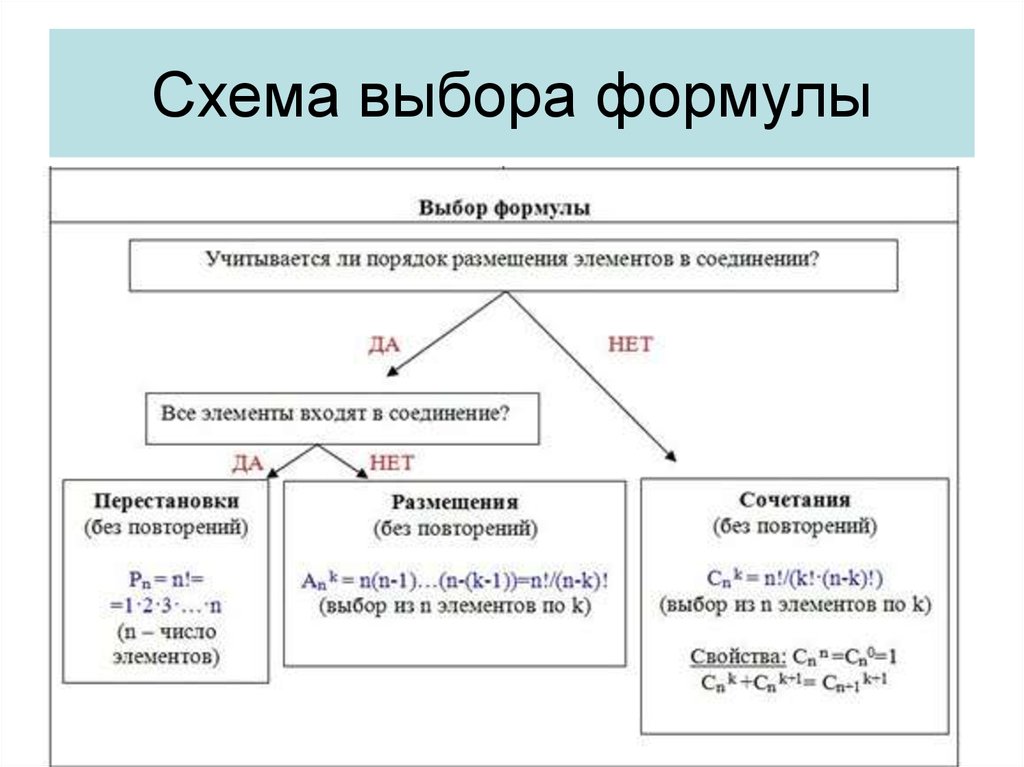 Сколькими способами из колоды в 52 карты можно извлечь 6 карт, содержащих туза и короля одной масти?
Сколькими способами из колоды в 52 карты можно извлечь 6 карт, содержащих туза и короля одной масти?
 Обратная связь — 161.97.168.212 (0.004 с.)
Обратная связь — 161.97.168.212 (0.004 с.)