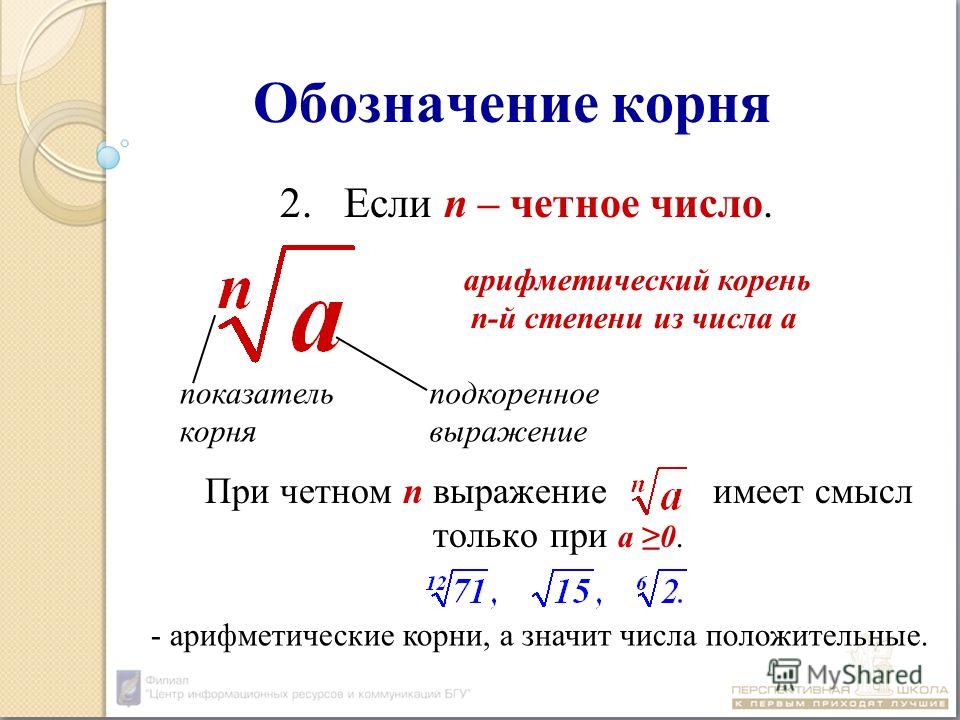
Чему равен квадратный корень из −1? (Математика, Оксфорд) . Вопрос на засыпку. Как заставить мозги шевелиться
Это, пожалуй, самый трудный вопрос в математике, над которым на протяжении тысячелетий бились практически все великие ученые. Впрочем, проблема заключается в поиске корня не только из –1, но и из любого отрицательного числа. Квадратный корень числа – это значение, которое при возведении в квадрат дает оригинальное число. Так, квадратный корень из 9 равен 3 (3 ? 3 = 9), квадратный корень из 4 равен 2 (2 ? 2 = 4), а квадратный корень из 1 равен 1 (1 ? 1 = 1). Но это неприменимо к отрицательным числам, поскольку два отрицательных числа при умножении дают положительное: так, ?2 ? ?2 = (+)4, а ?1 ? ?1 = (+)1.
И как же тогда найти корень из отрицательного числа, например из –1? Дело в том, что никак, и математики называют такие значения мнимыми числами. С тем же успехом их можно было бы назвать нереальными, абсурдными или просто дурацкими числами, поскольку они, по-видимому, не существуют.
Однако сейчас мы едва ли можем представить нашу жизнь без них. Они необходимы для передовой квантовой физики, они важны для проектирования подвесных мостов и крыльев самолетов. Они мнимые, поскольку не обозначают какое-либо существующее число, но они реальны, поскольку являются частью реального мира. Поэтому, как ни парадоксально, они одновременно воображаемые и настоящие, невозможные и возможные.
Данное противоречие обнаружили еще древние египтяне, а также один из величайших математиков Античности Герон Александрийский, который столкнулся с отрицательными числами около 2000 лет назад, когда пытался вычислить объем усеченной пирамиды. В расчетах ему понадобилось найти квадратный корень из 81–144 (то есть ??63). Поскольку получить корень из отрицательного числа не представлялось возможным, Герон просто поменял его на положительное и извлек корень из 63. Разумеется, античный ученый просто подогнал ответ под желаемый, но что ему оставалось делать? В те времена даже к отрицательным числам относились с крайней осторожностью, что там говорить о квадратных корнях из них!
Средневековые математики порой сталкивались с данной проблемой при решении кубических уравнений, но они просто рассматривали корни из отрицательных чисел как невозможные.
Первым нарушил устоявшийся подход пользовавшийся (по-видимому) сомнительной репутацией у современников итальянский астролог Джероламо Кардано, и, пожалуй, именно такой человек идеально подходил для решения казавшихся невозможными задач. В конце жизни Кардано работал астрологом в Ватикане, но до этого, в 1545 году, он исследовал в своем трактате «Великое искусство» проблему корня из ?1. Он утверждал, что подобное число возможно, хотя и счел его абсолютно бесполезным.
Рафаэль Бомбелли в своем изданном в 1572 году труде «Алгебра» отнесся более положительно к отрицательным числам. Бомбелли доказал, что произведение двух отрицательных чисел дает действительное число. Поначалу он счел свои выводы несколько сомнительными. «Данная проблема относится скорее к области софистики, – писал он. – Но я изучал ее очень долго, и мне удалось доказать, что мои результаты верны».
На протяжении двух последующих столетий различные ученые высказывали свое мнение относительно корней из отрицательных чисел, признавая или отвергая их существование.
В итоге проблему удалось решить гениальному швейцарскому математику Леонарду Эйлеру (1707–1783) в поздние годы жизни. Он ввел «мнимую единицу», символ i. Символ i обозначает мнимое число, квадрат которого равен ?1. Таким образом, i можно представить как ??1. Идея Эйлера предполагает, что квадратный корень любого отрицательного числа может использоваться в уравнении как число i, помноженное на квадратный корень числа. Он утверждал, что корни любых отрицательных чисел – ??1, ??2, ??3 и т. д. – являются мнимыми, но не бессмысленными: это просто их математическое наименование.
Символ i представлял собой простое, но гениальное решение, позволившее математикам наконец-то использовать ??1 и квадратные корни из других отрицательных чисел в уравнениях, выражая их с использованием i. Это означает, что математикам больше не приходилось рассматривать природу мнимых чисел: они могли просто использовать их в практических целях.
Однако парадокс так и не был решен. Эйлер, несмотря на то что его изобретение сделало мнимые числа реальными, сам признавал их нереальность, говоря: «Мы можем считать, что они не больше, чем ничто, и не меньше, чем ничто, что неизбежно делает их мнимыми или невозможными».
Множество скептических отзывов не смущало Эйлера. По его мнению, если мнимые числа применимы в математике, они реальны, как действительные числа.
Идеи Эйлера дали понять, что нам не обязательно находить ответы на все вопросы для исследования тех или иных областей бытия. Мнимые числа могут быть окутаны тайной, равно как и квадратный корень из ?1, но это не означает, что мы не имеем права их использовать. С такой же смелостью Ньютон разработал теорию гравитации исключительно как математическую модель, даже не пытаясь представить, как она впишется в рамки дальнодействия и короткодействия. Мы до сих пор не представляем, как работает гравитация, но теория Ньютона остается одной из важнейших вех в истории науки. Аналогичным образом мнимые числа подтвердили свою практическую пользу и широко применяются передовыми математиками, хоть и по-прежнему остаются загадкой. Это доказывает, что воображение и математическая логика не противоречат друг другу.
| 1 | Найти объем | сфера (5) | |
| 2 | Найти площадь | окружность (5) | |
| 3 | Найти площадь поверхности | сфера (5) | |
| 4 | Найти площадь | окружность (7) | |
| 5 | Найти площадь | окружность (2) | |
| 6 | Найти площадь | окружность (4) | |
| 7 | Найти площадь | окружность (6) | |
| 8 | Найти объем | сфера (4) | |
| 9 | Найти площадь | окружность (3) | |
| 10 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 11 | Разложить на простые множители | 741 | |
| 12 | Найти объем | сфера (3) | |
| 13 | Вычислить | 3 квадратный корень из 8*3 квадратный корень из 10 | |
| 14 | Найти площадь | окружность (10) | |
| 15 | Найти площадь | окружность (8) | |
| 16 | Найти площадь поверхности | сфера (6) | |
| 17 | Разложить на простые множители | 1162 | |
| 18 | Найти площадь | окружность (1) | |
| 19 | Найти длину окружности | окружность (5) | |
| 20 | Найти объем | сфера (2) | |
| 21 | Найти объем | сфера (6) | |
| 22 | Найти площадь поверхности | сфера (4) | |
| 23 | Найти объем | сфера (7) | |
| 24 | Вычислить | квадратный корень из -121 | |
| 25 | Разложить на простые множители | 513 | |
| 26 | Вычислить | квадратный корень из 3/16* квадратный корень из 3/9 | |
| 27 | Найти объем | прямоугольный параллелепипед (2)(2)(2) | |
| 28 | Найти длину окружности | окружность (6) | |
| 29 | Найти длину окружности | окружность (3) | |
| 30 | Найти площадь поверхности | сфера (2) | |
| 31 | Вычислить | 2 1/2÷22000000 | |
| 32 | Найти объем | прямоугольный параллелепипед (5)(5)(5) | |
| 33 | Найти объем | прямоугольный параллелепипед (10)(10)(10) | |
| 34 | Найти длину окружности | окружность (4) | |
| 35 | Перевести в процентное соотношение | 1. 2-4*-1+2 | |
| 45 | Разложить на простые множители | 228 | |
| 46 | Вычислить | 0+0 | |
| 47 | Найти площадь | окружность (9) | |
| 48 | Найти длину окружности | окружность (8) | |
| 49 | Найти длину окружности | окружность (7) | |
| 50 | Найти объем | сфера (10) | |
| 51 | Найти площадь поверхности | сфера (10) | |
| 52 | Найти площадь поверхности | сфера (7) | |
| 53 | Определить, простое число или составное | 5 | |
| 54 | Перевести в процентное соотношение | 3/9 | |
| 55 | Найти возможные множители | 8 | |
| 56 | Вычислить | (-2)^3*(-2)^9 | |
| 57 | Вычислить | 35÷0. 2 | |
| 60 | Преобразовать в упрощенную дробь | 2 1/4 | |
| 61 | Найти площадь поверхности | сфера (12) | |
| 62 | Найти объем | сфера (1) | |
| 63 | Найти длину окружности | окружность (2) | |
| 64 | Найти объем | прямоугольный параллелепипед (12)(12)(12) | |
| 65 | Сложение | 2+2= | |
| 66 | Найти площадь поверхности | прямоугольный параллелепипед (3)(3)(3) | |
| 67 | Вычислить | корень пятой степени из 6* корень шестой степени из 7 | |
| 68 | Вычислить | 7/40+17/50 | |
| 69 | Разложить на простые множители | 1617 | |
| 70 | Вычислить | 27-( квадратный корень из 89)/32 | |
| 71 | Вычислить | 9÷4 | |
| 72 | Вычислить | 2+ квадратный корень из 21 | |
| 73 | Вычислить | -2^2-9^2 | |
| 74 | Вычислить | 1-(1-15/16) | |
| 75 | Преобразовать в упрощенную дробь | 8 | |
| 76 | Оценка | 656-521 | |
| 77 | Вычислить | 3 1/2 | |
| 78 | Вычислить | -5^-2 | |
| 79 | Вычислить | 4-(6)/-5 | |
| 80 | Вычислить | 3-3*6+2 | |
| 81 | Найти площадь поверхности | прямоугольный параллелепипед (5)(5)(5) | |
| 82 | Найти площадь поверхности | сфера (8) | |
| 83 | Найти площадь | окружность (14) | |
| 84 | Преобразовать в десятичную форму | 11/5 | |
| 85 | Вычислить | 3 квадратный корень из 12*3 квадратный корень из 6 | |
| 86 | Вычислить | (11/-7)^4 | |
| 87 | Вычислить | (4/3)^-2 | |
| 88 | Вычислить | 1/2*3*9 | |
| 89 | Вычислить | 12/4-17/-4 | |
| 90 | Вычислить | 2/11+17/19 | |
| 91 | Вычислить | 3/5+3/10 | |
| 92 | Вычислить | 4/5*3/8 | |
| 93 | Вычислить | 6/(2(2+1)) | |
| 94 | Упростить | квадратный корень из 144 | |
| 95 | Преобразовать в упрощенную дробь | 725% | |
| 96 | Преобразовать в упрощенную дробь | 6 1/4 | |
| 97 | Вычислить | 7/10-2/5 | |
| 98 | Вычислить | 6÷3 | |
| 99 | Вычислить | 5+4 | |
| 100 | Вычислить | квадратный корень из 12- квадратный корень из 192 |
Квадратный корень из числа
Прежде чем понять, что такое квадратный корень из числа, важно понять значение корня из числа.
Корень числа — это равный делитель числа. Например, вот как найти корень из 16.
Во-первых, нам нужно разложить 16. Ниже показаны различные способы разложения 16.
16 = 1 × 16
16 = 2 × 8
16 = 4 × 4
Корень из 16 равен 4, потому что 4 является равным множителем для 16. Мы называем 4 квадратный корень из 16, и мы пишем √16 = 4.
4 называется квадратным корнем, потому что мы должны возвести 4 в квадрат или возвести 4 в степень 2, чтобы получить 16.
Другие примеры, показывающие, как найти квадрат корень числа.
Найдите квадратный корень из 4. Вы можете разложить 4 двумя способами.
4 = 1 × 4
4 = 2 × 2
Коэффициент равенства равен 2, поэтому 2 — это квадратный корень из 4, и мы пишем √4 = 2.
Найдите квадратный корень из 64.
64 = 1 × 64
64 = 2 × 32
64 = 4 × 16
68 = 8 × 8
Коэффициент равенства равен 8, поэтому квадрат 64 равен 8, и мы пишем √64 = 8.
Может ли квадратный корень числа быть отрицательным?
Да, конечно! Если умножить положительное число само на себя, получится положительное произведение. Если вы умножите отрицательное число само на себя, вы также получите положительное произведение.
Например, поскольку -8 × -8 = 64, -8 также является квадратным корнем из 64. Однако, если не указано иное, знак квадратного корня ( √ ) относится к положительному корню числа, также называемому главным квадратом корень.
Может ли квадратный корень числа быть действительным числом?
Для приведенных выше чисел квадратный корень был равен целому числу.
не всегда возможно получить квадратный корень в виде целого числа.
Иногда вы можете получить действительное число при извлечении квадратного корня.
Например, используйте приведенный ниже калькулятор квадратного корня, чтобы найти квадратный корень из 5.
Результат включает много чисел после запятой.
Готовы к большим испытаниям? Так же, как деление в длину, научитесь вычислять квадратный корень без калькулятора для любого числа, не являющегося полным квадратом. Обещаю, вы не будете слишком потеть!
Учителя! Вам нужна готовая таблица квадратных корней, к которой учащиеся могут быстро обращаться при решении своих основных математических задач? Получите таблицу квадратных корней.
Рациональные числа — определение и примеры
15, 23 марта 07:45
Чтобы узнать о рациональных числах, напишите их десятичное представление и распознайте рациональные числа, которые повторяют десятичные дроби и завершают десятичные дроби.
Подробнее
Площадь трапеции — определение, формула и примеры
13, 23 марта 07:52
Узнайте, как получить площадь трапеции, используя прямоугольник и треугольник, формулу, а также когда высота трапеции отсутствует.
Подробнее
Как найти квадратный корень числа
Опубликовано от Maths With Mum
Как найти квадратный корень числаПримерВидеоВопросыУрок
Поделиться в Google Classroom
ExampleVideoQuestionsLesson
Поделиться в Google Classroom
- Чтобы найти квадратный корень из числа, подумайте: «Какое число, умноженное само на себя, дает нам это число?»
- Квадратный корень из числа, умноженный сам на себя, дает это число.
- Квадратный корень из целого числа меньше исходного числа.
- Математический символ √ означает нахождение квадратного корня из следующего за ним числа.
- Квадратный корень из 1 равен 1, потому что 1 × 1 = 1.
- Квадратный корень из 4 равен 2, потому что 2 × 2 = 4.
- Квадратный корень из 9 равен 3, потому что 3 × 3 = 9.
- Квадратный корень из 16 равен 4, потому что 4 × 4 = 16.
- Квадратный корень из 25 равен 5, потому что 5 × 5 = 25.
равным этому заданному числу.
Список квадратных корней
- Чтобы найти квадратный корень из числа, найдите число, которое можно умножить само на себя, чтобы получить его.
- 5 × 5 = 25 и, следовательно, квадратный корень из 25 равен 5.
- √25 означает найти квадратный корень из 25.
- Мы можем написать √25 = 5.
- 5 см в длину. Его площадь 25 см 2 .
- Длина стороны квадрата равна квадратному корню из площади этого квадрата.
Калькулятор квадратного корня
Введите число, чтобы вычислить его квадратный корень:
Поиск квадратных корней: интерактивные вопросы
Поиск квадратных корней: интерактивные вопросы
Нахождение квадратного корня. Рабочие листы и ответы
Что такое квадратный корень?
Квадратный корень числа — это другое число, которое при умножении само на себя равно этому числу.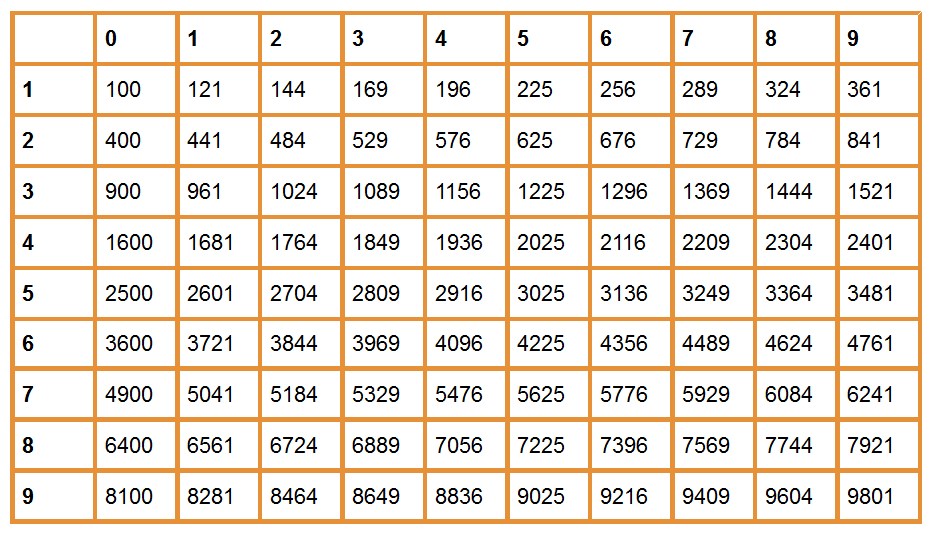
Например, квадратный корень из 25 равен 5, потому что 5 × 5 = 25.
Вместо того, чтобы писать «найдите квадратный корень из» перед каждым числом, быстрее использовать знак квадратного корня.
Математический символ для нахождения квадратного корня — √. Оно пишется непосредственно перед числом, из которого нужно извлечь квадратный корень. Например, √36 означает найти квадратный корень из 36. Это означает найти число, которое при умножении само на себя равно 36. √36 = 6, потому что 6 × 6 = 36.
Вот список квадратных корней:
| Номер | Квадратный корень |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 36 | 6 |
| 49 | 7 |
| 64 | 8 |
| 81 | 9 |
| 100 | 10 |
| 121 | 11 |
| 144 | 12 |
Вот загружаемый, пригодный для печати плакат, показывающий первые 12 квадратных корней целых чисел.
Скачать PDF
Квадратные корни называются квадратными корнями, потому что любой квадрат имеет длину стороны, равную квадратному корню из площади. Отношение между числом и его квадратным корнем можно показать с помощью квадрата. Корень слова просто означает решение уравнения.
Например, вот квадрат площадью 25.
Площадь квадрата – это произведение длины одной из сторон на себя.
Длина каждой стороны квадрата равна 5. Площадь квадрата 5 × 5 = 25.
Когда число умножается само на себя, мы говорим, что число возведено в квадрат.
Мы говорим, что 5 в квадрате равно 25.
Извлечение квадратного корня противоположно возведению числа в квадрат. Это обратные функции. Возведение в квадрат означает умножение числа само на себя. Найти квадратный корень означает найти число, которое можно умножить само на себя, чтобы получить это число.
Поскольку мы знаем, что 5 × 5 = 25, мы знаем, что 5 — это квадратный корень из 25.
Квадратный корень из заданного числа можно рассматривать как длину стороны квадрата, площадь которого равна данному числу.
Как найти квадратный корень из числа
Чтобы найти квадратный корень из заданного числа, найдите число, которое можно умножить само на себя, чтобы получить данное число. Знание таблицы умножения помогает быстрее находить квадратные корни.
Полный квадратный корень — это квадратный корень из целого числа.
Вот список идеальных квадратных корней:
- √1 = 1.
- √4 = 2.
- √9 = 3.
- √16 = 4.
- √25 = 5.
- √36 = 6.
- √49 = 7,
- √64 = 8.
- √81 = 9,
- √100 = 10.
- √121 = 11.
- √144 = 12.
Совершенные квадратные корни — это квадратные корни из квадратных чисел. Это всегда целые числа.
Представляя идею квадратных корней, лучше всего начать с нахождения квадратных корней из полных квадратов.
Вы можете найти квадратный корень из всех чисел, кроме отрицательных. Отрицательные числа не имеют квадратного корня. Это потому, что когда число умножается само на себя, ответ всегда положительный. Даже отрицательное число, умноженное само на себя, дает положительный ответ, потому что два отрицательных числа, умноженные вместе, сокращаются.
Квадратный корень из 0 равен 0, потому что 0 × 0 = 0.
Чтобы найти квадратные корни неполных квадратов, самый простой и распространенный способ — использовать калькулятор. Просто нажмите клавишу √, введите число и нажмите клавишу =.
На этой странице есть калькулятор квадратного корня, который можно использовать для нахождения квадратных корней неполных квадратов.
Квадратные корни неполных квадратов будут находиться между квадратными корнями полных квадратов по обе стороны от числа.