Арккосинус
Прежде всего, мы должны понять, что такое арккосинус и как их записать в математике. Тригонометрические функции можно найти для четко определенных интервалов, даже если они не являются взаимно однозначными функциями. Некоторыми из наиболее важных обратных тригонометрических функций являются обратный загар, обратный синус и обратный косинус. Давайте рассмотрим арккосинус в этой статье.
Определение и представление арккосинуса
Предположим, нам дано, что cos(a) = x. Отсюда следует, что cos-1 (x)=a. (Это читается как косинус, обратный х). То есть обратный косинусу числа х есть а; где а — угол, для которого косинус дал число х. Чтобы было понятнее, возьмем пример. Что такое cos-1 (0,5)?
Мы знаем, cos (π/3) = 0,5. То есть cos-1 (0,5) = π/3.
Как было сказано ранее, чтобы иметь обратные функции, функции должны иметь четко определенный интервал. В случае обратного косинуса x, x должен лежать между -1 и 1, а угол a должен лежать между 0 и π.
Следовательно, мы можем сказать следующее:
Основная область определения арккосинуса [-1,1]
Область, соответствующая основной области значений, равна [0,π]
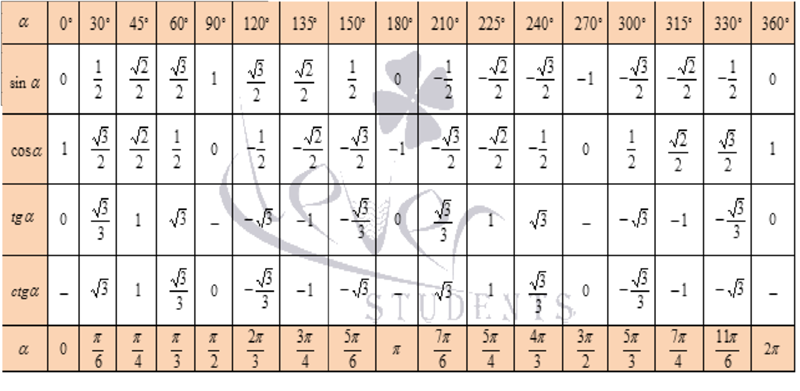
Используя эту информацию, мы можем найти значения некоторых арккосинусов. Они равны
Cos-1 (-1)=π
Cos-1 (0)=π/2
Cos-1 (1)=0
[Изображение будет загружено в ближайшее время]
Теперь давайте посмотрим на график обратной тригонометрической функции, включая арккосинус.
Некоторые важные свойства арккосинуса
Как и тригонометрические функции, обратные тригонометрические функции обладают важными свойствами и формулами, необходимыми для полного понимания этих функций.
Давайте рассмотрим некоторые свойства на нескольких примерах.
Пример 1:
Предположим, нам дали вопрос, чтобы найти ответ на сек -1 (2). Можем ли мы сделать это, используя формулы, которые мы уже изучили?
Мы знаем, что cos(θ) = 1/сек(θ).
Аналогично,
Следовательно, мы можем легко найти ответ на наш вопрос.
Так как sec-1 (2) = cos-1(1/2), что равно cos-1(0,5)
= π/3, мы можем написать sec-1(2) = π/3.
Пример 2:
Предположим, нам нужно найти значение cos-1 (-1/2). Как мы решаем эту проблему?
Мы знаем значение cos-1(1/2) как π/3. Мы также знаем, что это означает, что cos(π/3) =1/2.
Если мы умножим обе части на -1,
получим –cos(π/3) = -1/2.
Следовательно, мы можем написать
cos-1 (-1/2) = -π/3.
Но наш диапазон от 0 до π, а –π/3 находится за пределами нашего диапазона.
Однако из тригонометрии мы знаем –π/3 = π-π/3 = 2π/3.
То есть мы нашли ответ на cos-1(-1/2) = π-cos-1(1/2) = 2π/3.
Мы можем обобщить это в правило следующим образом:
Пример 3:
Теперь давайте рассмотрим два очень важных свойства.
1)Cos-1 (cos(θ)) = θ, если θ∈[0,π]
2)Cos(cos-1(x)) = x, если x ∈ [-1,1]
Эти важные свойства очень легко понять. Рассмотрим первое свойство.
Предположим, что cos(θ) = x. Это означает, что cos-1(x) = θ.
Следовательно, мы можем написать Cos-1 (cos(θ)) = θ, если θ∈[0,π]. Точно так же мы можем объяснить и второе свойство.
Попробуем решить некоторые задачи, применяя эти свойства. Найдите значение тангенса (cos-1 (3/5)).
Пример 4: Предположим, что cos-1(3/5) = θ; Это означает, что cos(θ)=3/5.
{2 }}\] , если x,y>0 и x2+y2≤1.9{2}}\], если x,y>0 и x2+y2≤1
Таким образом, ответ на нашу задачу равен cos-1(1/2-\[\sqrt{1/2}\]\ [\sqrt{1/2}\] = cos-1(½-½) = cos-1(0) ; То есть ответ π/2.
Теперь аналогично cos(2θ) и cos(3θ ), мы имеем тождества для 2cos-1(x) и 3cos-1(x):
2cos-1(x)=cos-1(2×2-1), если x ∈ [-1,1]
3cos-1(x)=cos-1(4×3-3x),если x ∈ [1/2,1]
Самое главное обратить внимание на домен и диапазон, в котором указанные свойства и формулы работают. Как видно из статьи, свойства, тождества и формулы могут меняться при изменении домена и диапазона. Важно научиться адаптировать наши формулы в соответствии с доменом и диапазоном.
алгебраическое предварительное исчисление — Почему $\cos(-2\pi/3) = -1/2$?
спросил
Изменено 4 года, 4 месяца назад
Просмотрено 101 раз
$\begingroup$
Я знаю, что функция косинуса четная, но не понимаю, почему она так работает.
{th}$ четверти единичной окружности? Поскольку $\cos(\theta)$ равно $\frac{\text{напротив}}{\text{гипотенуза}}$ или $\frac{x}{R}$, а $R$ на единичной окружности равно всегда равен $1$, почему ответ не положительный?
- алгебра-предварительное исчисление
- тригонометрия
$\endgroup$
4
$\begingroup$
Обратите внимание, что $-2\pi/3 $ находится в третьем квадранте, потому что вы должны начать с $0$ и двигаться по часовой стрелке, $120$ градусов, и вы окажетесь в третьем квадранте.
Таким образом, косинус отрицательный.
Другой способ взглянуть на это состоит в том, что функция косинуса четна и $\cos ( -2\pi /3) = \cos ( 2\pi /3)= -1/2.$
$\endgroup$
$\begingroup$
Соглашение Меня учили, что квадранты начинаются с «северо-восток» как 1, «северо-запад» как 2, «юго-запад» как 3 и «юго-восток» как 4.