Конспект урока алгебры «Синус и косинус двойного угла»
Муниципальное бюджетное общеобразовательное учреждение «Сеяхинская школа – интернат» 10 класс Разработчик: Спирякова Екатерина Алексеевна с. Сеяха |
Класс: 10
Предмет: алгебра и начала анализа.
Тема урока: синус и косинус двойного угла.
Тип урока: изучение нового материала.
Педагогические задачи: рассмотреть нахождение синуса и косинуса двойного угла.
Планируемые результаты образования:
Предметные: систематизировать знания о синусе и косинусе двойного угла и уметь применять при решении различных задач.
Метапредметные (критерии сформированности/оценки компонентов универсальных учебных действий – УУД):
Регулятивные: под руководством учителя формулируют учебную задачу урока, определяют последовательность действий, осуществляют контроль собственной деятельности и деятельности партнера, при необходимости корректируют свою деятельность, способны к мобилизации волевых усилий.
Познавательные: формируют познавательную активность и мотивацию изучения математики; умения сравнивать, обобщать изучаемые факты; выделяют и формулируют познавательную цель, структурируют знания, самостоятельно создают алгоритм деятельности, развивают у учащихся самостоятельность в мышлении и учебной деятельности;
Коммуникативные: развивают эмоции учащихся путем привлечения наглядности; развивают умение грамотно излагать свои мысли, обосновывать свои действия, умеют слушать, слышать и понимать партнера, правильно выражать свои мысли в речи.
Личностные: формируют информационную культуру, работают по инструкции, демонстрируют самостоятельность, ответственность, умение сотрудничать, формируют адекватность оценки собственной деятельности, чувство гордости за свои успехи и успехи товарищей, развивают аккуратность в работе.
Методы и формы обучения: частично-поисковый, практический; индивидуальная, групповая.
Материалы и оборудование: компьютер, проектор, интерактивная доска, музыка для оргмомента
Наглядно-демонстрационный материал: презентация (Приложение 1).
Основные понятия и термины: синус, косинус, формулы.
Время: 40 минут
Структура урока
Организационный момент (1 мин.)
Актуализация знаний (5 мин.)
а) Ребус (2мин)
б) Историческая справка ( 1 мин)
в) Проверка домашнего задания ( 2 мин)
г) Подготовка к изучению нового материала (3 мин)
3.
Изучение нового материала (15 мин.)
4. Физминутка (2 мин.)
Проверка усвоения знаний (Самостоятельная работа 10 мин).
Домашнее задание (1 мин.)
Рефлексия (1 мин.)
Подведение итогов урока (2 мин.)
Ход урока.
Организационная часть:
Отметить отсутствующих, привести в порядок класс.
Повторение.
1. Актуализация знаний
Слайд 2: Устно: 1.Мы продолжаем изучение главы, чтобы вспомнить отгадаем ребус.
(тригонометрия)
2. Историческая справка.
Зарождение тригонометрии относится к глубокой древности. Еще задолго до новой эры вавилонские учёные умели предсказывать солнечные и лунные затмения. Это позволяет делать вывод о том, что им были известны некоторые простейшие сведения из тригонометрии.
Постепенно в геометрии и астрономии установили понятия синус, косинус и тангенс угла.
Одним из основоположников тригонометрии считается древнегреческий астроном Гиппарх, живший во 2 веке до нашей эры. Гиппарх является автором первых тригонометрических таблиц.
Важный вклад в развитие тригонометрии был внесён индийской математикой в период 5-7 вв. н.э. Индийским математикам были известны соотношения sin2 α + cos2 α = 1,
cos α = sin (900 — α ).
Современный вид тригонометрия получила в трудах великого ученого, члена Российской академии наук
Л.Эйлера.(1707-1783). Ему принадлежит принятая, в наши дни символика.
3. Домашнее задание: Ответы на слайдах № 339(1,2)
Слайд 3: Ответы:1) cosα = — √ 1 – 3/9 = — √6/3.
2) sin α = — √ 1 – 5/9 = — 2/3, tg α = 2√5/5.
Применили при решении заданий основное тригонометрическое тождество sin2 α + cos2 α = 1.
4. Подготовка к изучению нового материала и актуализация опорных знаний
Сегодня ещё раз повторим значения синуса и косинуса наиболее чаще встречающихся углов.
На доске (карточка у каждого ученика)
2.Найдите соответствие между значениями.
1 вариант | ||
1. | sin 450 | |
2. | cos 300 | 0 |
3. | sin 300 | |
4. | cos 00 | |
5. | sin 1800 | 1 |
2.Найдите соответствие между значениями
2 вариант | ||
1. | cos 600 | |
2. | sin 600 | 1 |
3. | cos 450 | |
4. | sin 900 | 0 |
5. | cos 2700 | |
Изучение нового материала.
Мы, сегодня познакомимся ещё с одной формулой тригонометрии синус и косинус двойного угла.
Научимся применять формулу при выполнении преобразований тригонометрических выражений.
На доске один ученик выводит формулу синуса двойного угла из формулы синуса суммы двух углов α,
sin (α + α) = sin α cosα + cos α sin α = 2 sin α cosα
На доске один ученик выводит формулу косинуса двойного угла из формулы косинуса суммы двух углов α,
cos (α + α) = cos α cosα — sinα sinα = cos2 α – sin2 α
Слайд 4:Вывод: 1.
Sin 2α =2 sin α cosα.
cos 2α = cos2 α – sin2 α.
Слайд 5: Частные случаи:
1. sin 2α =2 sin α cosα = 2 sin α sin ().
2. cos 2α = cos2 α – sin2 α = 2 cos2 α – 1= 1 –2 sin2 α.
5. Рассмотреть по учебнику страница 123.
Задача 1, Задача 2.
6. Первичное закрепление нового материала.
№ 310(2).
Дано:
сosα = -, π .
Вычислить: sin 2 α.
Решение.
sin 2α =2 sin α cosα; π , 3 четверть, sinα sin2 α + cos2 α = 1 следует, что sin2 α = 1- cos2 α,
sin α =, sin α = — .
sin 2α =2 sin α cosα = 2.Sin 2α= .
Ответ: sin 2α= .
№ 311(2)
Дано: sin α = — .
Вычислите: сos 2α.
Решение.
cos 2α = cos2 α – sin2 α, из основного тригонометрического тождества sin2 α + cos2 α = 1 следует, что
cos2 α = 1-sin2 α = 1 — .
cos 2α = cos2 α – sin2 α =
cos 2α =.
Ответ: cos 2α =.
№308 (2, 4)
2) cos2 150 – sin2 150 = cos 2. 150 = cos 300= .
4) (cos 150 + sin 150)2 = cos2 150 +2 sin 150 cos150 + sin2 150=
= 1 + 2 sin 150 cos150 =1 + sin 300=1 + = .
7. Вторичное закрепление. Проверка усвоения темы.
Самостоятельная работа.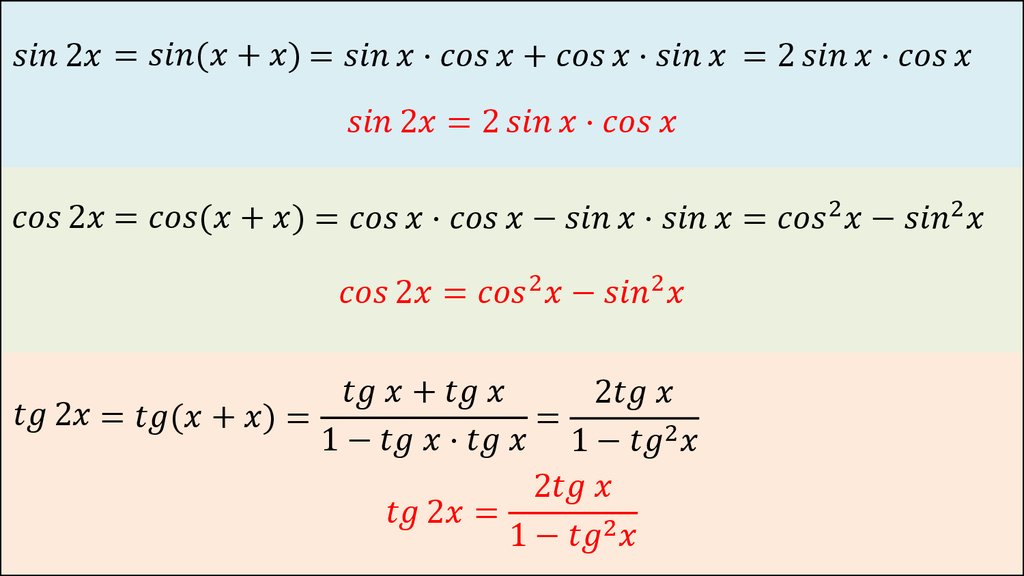
Слайд 6: Вариант 1.
Вычислите:
а) 2sin π/8 cos π/8; б) (cos π/12 — sin π/12) (cos π/12 + sin π/12)
Вычислите cos 2α, sin 2α, если sin α = 0,6,
Слайд 7:
Вариант 2.
Вычислите:
а) 2sin π/12 cos π/12; б) (cos π/8 — sin π/8) (cos π/8 + sin π/8)
Вычислите sin 2α, cos 2α, если cos α = 0,8 и 3π/2 π.
Слайд 8:
Ответы: 1 вариант:1) а) ; б) . 2) 0,28, -0,96.
Ответы: 2 вариант: 1) а) ; б) . 2)-0,96, 0,28.
8. Итоги. Рефлексия:
Что я узнал нового…
Я познакомился ….
Д/з п. 25, №308(1,3), 310(1), 311(1).
Оценки. «5»- «4» — «3» —
Формулы двойного угла — Без Сменки
26 мая, 2022
1 мин
Мтмт 📈
Сегодня будет максимально информативный блок на запоминание формул!
Представляю тебе формулы, которые чаще всего помогают выполнить числовые преобразования.
Синус двойного угла:
sin2α = 2sinα⋅cosα
Косинус двойного угла:
cos2α = cos2α − sin2α = 2cos2α − 1 = 1 − 2sin2α
Тангенс двойного угла:
tg2α = 2tgα/(1 − tg2α)
Аналогично для тройного угла!
👉🏻 Распознать, что требуются именно эти, а не какие-нибудь другие формулы очень просто: если ты видишь выражения сильно похожие на косинус, синус, тангенс двойных углов, то смело можно свернуть выражение в одну из этих формул в первую очередь ✨
Математика — обязательный для сдачи на ЕГЭ предмет, без которого не получишь аттестат.
Это также один из самых сложных экзаменов для выпускников. Рассказываем, как сдать ЕГЭ по математике на 80+ баллов и делимся лучшими ресурсами для подготовки.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
Редакция Без Сменки
Честно. Понятно. С душой.
44 подписчиков
+ Подписаться
Редакция Без Сменки
02 июня, 2022
1 мин
Ист 🤴
«Из варяг в греки» 🚣
Ты слышал/а это словосочетание из уст учительницы, но не особо помнишь, что это? 🤔 Время.
..
Редакция Без Сменки
15 июня, 2022
1 мин
Инф 💻
Проверка на делимость
Задание: 🔎 Рассматривается множество целых чисел, принадлежащих отрезку , произведение цифр…
Редакция Без Сменки
01 июля, 2022
1 мин
Лит 📚
Анафора и эпифора
Из пункта А в пункт Э выехали художественные средства, основанные на повторе. Это были Анафора…
Редакция Без Сменки
01 июля, 2022
1 мин
Хим 🧪
Химические свойства фенола
Фенол обладает слабыми кислотными свойствами!
1️⃣ Взаимодействие с щелочными металлами
2С₆H₅OH.
..
Идентичности половинного угла, двойного угла и триггера продукта (видео)
Привет! Добро пожаловать в это видео, посвященное некоторым распространенным тригонометрическим тождествам. В этом видео мы рассмотрим тождества половинного угла, тождества двойного угла и свойства продукта.
Давайте сразу же найдем синус 15 градусов, используя тождества половинного угла. Вот полуугловая идентичность для синуса:
\(\sin{(\frac{\theta}{2})}=\pm \sqrt{\frac{1-\cos{\theta}}{2} }\)
Используется для нахождения синуса половины известного угла. Для нашей задачи мы можем использовать его, чтобы найти половину от 30 градусов, что равно 15 градусам. Мы также могли бы использовать его, чтобы найти половину от 45 градусов, что составляет 22,5 градуса.
Чтобы найти синус 15 градусов, мы будем использовать 30 градусов как \(\theta\), так как половина этого даст нам 15.
Как всегда, мы начинаем со сбора необходимой информации и определения \ (\тета\).
\(\тета=30°\)
\((\frac{\sqrt{3}}{2},\frac{1}{2})\)
Затем мы просто подставляем все соответствующие значения в формулу.
\(\sin{(\frac{\theta}{2})}= \sqrt{\frac{1-\cos{(\theta)}}{2}}\)
\(\sin {(\frac{30°}{2})}=\sqrt{\frac{1-\frac{\sqrt{3}}{2}}{2}}\)
Наконец, мы упрощаем .
\(\sin{(15°)}=\sqrt{\frac{1-\frac{\sqrt{3}}{2}}{\sqrt{2}}}\)
На этот раз у нас есть радикал в нашем знаменателе, поэтому нам нужно рационализировать его. Однако процесс для этого немного отличается, поскольку радикал является мономом. Мы умножаем верх и низ нашего ответа на знаменатель, чтобы наш новый знаменатель стал целым числом.
\(\frac{\sqrt{1-\frac{\sqrt{3}}{2}}}{\sqrt{2}}\cdot \frac{\sqrt{2}}{\sqrt{2 }} = \ frac {\ sqrt {2} \ sqrt {1- \ frac {\ sqrt {3}} {2}}} {2} = \ frac {\ sqrt {2- \ sqrt {3}}} { 2}\)
Вот так мы получили ответ.
Как оказалось, у нас есть тождества полууглов также для косинуса и тангенса. На самом деле, тангенс имеет два!
\(\cos{(\frac{\theta}{2})}=\pm \sqrt{\frac{1+\cos{\theta}}{2}}\) \(\tan{( \frac{\theta}{2})}=\frac{\sin{\theta}}{1+\cos{\theta}}\)
\(\tan{(\frac{\theta}{2})}=\frac{1-\cos{\theta}}{\sin{\theta}}\)
Давайте продолжим и используйте одно из тождеств касательной половины угла, чтобы найти тангенс 22,5 градусов. Поскольку 22,5 составляет половину от 45, мы можем использовать 45 для \(\theta\). Неважно, какое из тождеств касательных половин угла мы выберем; мы получим тот же ответ в любом случае. Пойдем с первым.
И снова наш процесс тот же. Запишите информацию, которая нам понадобится, а затем вставьте эту информацию в нашу формулу.
\(\theta=45°\)
\((\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})\)
\(\ tan{(\frac{\theta}{2})}=\frac{\sin{\theta}}{1+\cos{\theta}}\)
\(\tan{(\frac{45°) }{2})}=\frac{\frac{\sqrt{2}}{2}}{1+\frac{\sqrt{2}}{2}}\)
Немного сложно, так как у нас есть дроби внутри дробей, но записать это как дробное деление делает это проще.
Для этого нам нужно записать знаменатель в виде одной дроби, что мы делаем, превращая единицу в дробь \((\frac{2}{2})\), а затем переписывая весь знаменатель.
\(\ frac {\ frac {\ sqrt {2}} {2}} {1+ \ frac {\ sqrt {2}} {2}} = \ frac {\ frac {\ sqrt {2}} {2}}{\frac{2+\sqrt{2}}{2}}=\frac{\sqrt{2}}{2}\div \frac{2+\sqrt{2}}{2}= \ frac {\ sqrt {2}} {2} \ cdot \ frac {2} {2+ \ sqrt {2}} = \ frac {\ sqrt {2}} {2+ \ sqrt {2}} \)
Наконец, мы должны рационализировать наши знаменатели, умножив верхнюю и нижнюю часть наших ответов на сопряженное число знаменателя, которое выглядит точно так же, как знаменатель, но имеет противоположный знак между двумя членами.
9{2}{\theta}}\)
Тождества двойных углов не так полезны при работе с углами единичной окружности, поскольку мы уже знаем значения двойных углов, заданных для него. Но их определенно можно использовать для задачи, где задан другой угол (скажем, 10 градусов) и нам нужно найти косинус 20 градусов.
Или, если мы хотим убедиться, что ответ, полученный нами при использовании формулы половинного угла, верен, формула двойного угла «отменит» то, что мы сделали с формулой половинного угла. 9{2}\)
В формуле косинуса двойного угла наши подставляемые значения возводятся в квадрат, что очень хорошо удаляет наши радикалы.
\(\frac{1}{4}-\frac{3}{4}\)
Наконец, мы вычитаем наши дроби и получаем ответ \(-\frac{1}{2) }\).
Проверяя единичный круг, мы видим, что косинус 120 градусов равен \(-\frac{1}{2}\), так что мы правы! На самом деле это один из тех случаев, когда калькулятор тоже выдаст нам точное значение, так как это рациональный ответ. Также обратите внимание, что косинус 120 градусов отрицательный. Это потому, что 120 градусов находятся в квадранте II, где косинус всегда отрицательный.
Наши последние тождества, которые мы рассмотрим, это формулы для нахождения произведения синусов или косинусов двух углов.
Например, что, если мы хотим узнать точное значение синуса 45 градусов, умноженного на косинус 15 градусов? Мы могли бы сделать это, найдя косинус 15 градусов, используя тождество косинуса половины угла, а затем умножив на синус 45 градусов единичную окружность. Но есть и другой способ, используя формулы продуктов, которые выглядят так:
Обратите внимание, что каждая формула относится к разным продуктам. Первый — это когда мы находим произведение двух косинусов. Второй, когда мы находим произведение двух синусов. Третье, когда произведение синуса и косинуса, и последнее, когда произведение косинуса и синуса.
Наша задача ищет \(\sin{(45°)}\cos{(15°)}\), поэтому мы хотим использовать третий.
Начнем с того, что установим \(\alpha\) равным 45 градусам и \(\beta\) равным 15 градусам.
\(\alpha=45°\)
\(\beta=15°\)
Затем записываем нашу формулу, убедившись, что все знаки указаны правильно.
\(\sin{(\alpha)}\cos{(\beta)}=\frac{1}{2}[\sin{(\alpha + \beta)}+ \sin{(\alpha – \beta)}]\)
Затем мы подставляем наши значения для \(\alpha\) и \(\beta\).
\(\sin{(45°)}\cos{(15°)}=\frac{1}{2}[\sin{(45°+15°)}+\sin{(45°- 15°)}]\)
Затем мы добавляем и вычитаем наши углы в скобках, чтобы найти то, что нам нужно.
\(\sin{(45°)}\cos{(15°)}=\frac{1}{2}[\sin{(60°)}+\sin{(30°)}]\ )
Нам потребуется знать синус 60 градусов и синус 30 градусов. Возвращаясь к единичному кругу, мы находим эти два значения и подставляем их в нашу формулу.
\(\sin{(45°)}\cos{(15°)}=\frac{1}{2}[\frac{\sqrt{3}}{2}+\frac{1}{ 2}]\)
Наконец, упростим.
\(\frac{1}{2}[\frac{\sqrt{3}+1}{2}]=\frac{\sqrt{3}+1}{4}\)
Мы можем проверить наш ответ на калькуляторе, оценив наш ответ, а затем найдя приблизительное значение \(\sin{(45°)}\cos{(15°)}\). В обоих случаях получаем:
\(\frac{\sqrt{3}+1}{4}=0,683012701892\)
\(\sin{(45°)}\cos{(15°) }=0,683012701892\)
Эти формулы также можно использовать для преобразования произведений в суммы или сумм в произведения, особенно когда углы заданы как переменные.
Надеюсь, этот обзор был вам полезен, и вы уже на пути к освоению этих триггерных формул. Спасибо за просмотр и удачной учебы!
Двуугольные и полуугольные удостоверения
Горячая математикаДвухугольные тождества
Двухугольные тождества (на самом деле это всего лишь частные случаи Формулы Бхаскарачарьи , когда ты знак равно в )
грех ( 2 ты ) знак равно 2 грех ( ты ) потому что ( ты ) потому что ( 2 ты ) знак равно потому что 2 ( ты ) − грех 2 ( ты ) потому что ( 2 ты ) знак равно 2 потому что 2 ( ты ) − 1 потому что ( 2 ты ) знак равно 1 − 2 грех 2 ( ты ) загар ( 2 ты ) знак равно 2 загар ( ты ) 1 − загар 2 ( ты )
Пример 1:
Перепишем в более простой форме, используя тригонометрическое тождество:
2 грех ( 5 п ) потому что ( 5 п )
Используйте формулу двойного угла для синуса, где
ты знак равно 5 п
Примените формулу.
2 грех ( 5 п ) потому что ( 5 п ) знак равно грех ( 2 ⋅ 5 п ) знак равно грех ( 10 п )
Идентичности, уменьшающие власть
Их можно получить из приведенных выше тождеств, решив для
грех
2
(
ты
)
,
потому что
2
(
ты
)
, или же
загар
2
(
ты
)
.
грех 2 ( ты ) знак равно 1 − потому что ( 2 ты ) 2 потому что 2 ( ты ) знак равно 1 + потому что ( 2 ты ) 2 загар 2 ( ты ) знак равно 1 − потому что ( 2 ты ) 1 + потому что ( 2 ты )
Полуугольные тождества
Это то же самое, что и тождества выше, но с извлечением квадратного корня из обеих сторон и
θ
заменен на
2
ты
.
грех ( θ 2 ) знак равно ± 1 − потому что ( θ ) 2 загар ( θ 2 ) знак равно ± 1 − потому что ( θ ) 1 + потому что ( θ ) потому что ( θ 2 ) знак равно ± 1 + потому что ( θ ) 2 загар ( θ 2 ) знак равно 1 − потому что ( θ ) грех ( θ ) загар ( θ 2 ) знак равно грех ( θ ) 1 + потому что ( θ )
Пример 2:
Определить точное значение
потому что
(
15
°
)
.