Косинус какого угла равен 2 3: Таблица синусов и косинусов

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значение
sin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67
Найти точное значение		cos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )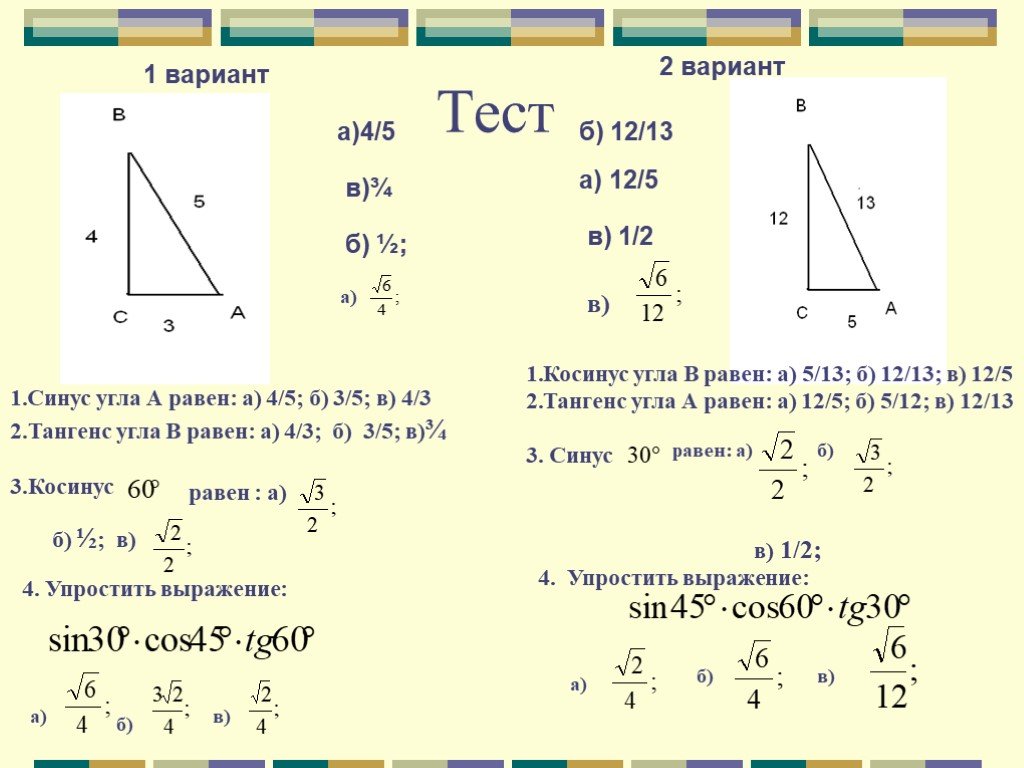
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значениеsin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

Урок по теме «Теорема косинусов»

Тип урока: Урок изучения нового материала.

Цели:

  • Повторить теоретический материал необходимый для изучения нового материала.
  • Сформировать и доказать теорему косинусов.
  • Отработать запись в виде равенства теоремы косинусов применительно к данному треугольнику.

Структура урока:

  1. Организационный момент.
  2. Анализ контрольной работы.
  3. Подготовка к изучению нового материала.
  4. Ознакомление с новым материалом.
  5. Первичное осмысление и применение изученного материала.
  6. Тест.
  7. Итог урока.

Оборудование: кодоскоп.

Раздаточный материал: тест.

ХОД УРОКА

I. Организационный момент.

II. Анализ контрольной работы.

Объявляются оценки за контрольную работу, разбираются основные ошибки, допущенные в работе. При помощи кодоскопа проектируются чертежи.

III. Подготовка к изучению нового материала через повторение и актуализацию опорных знаний.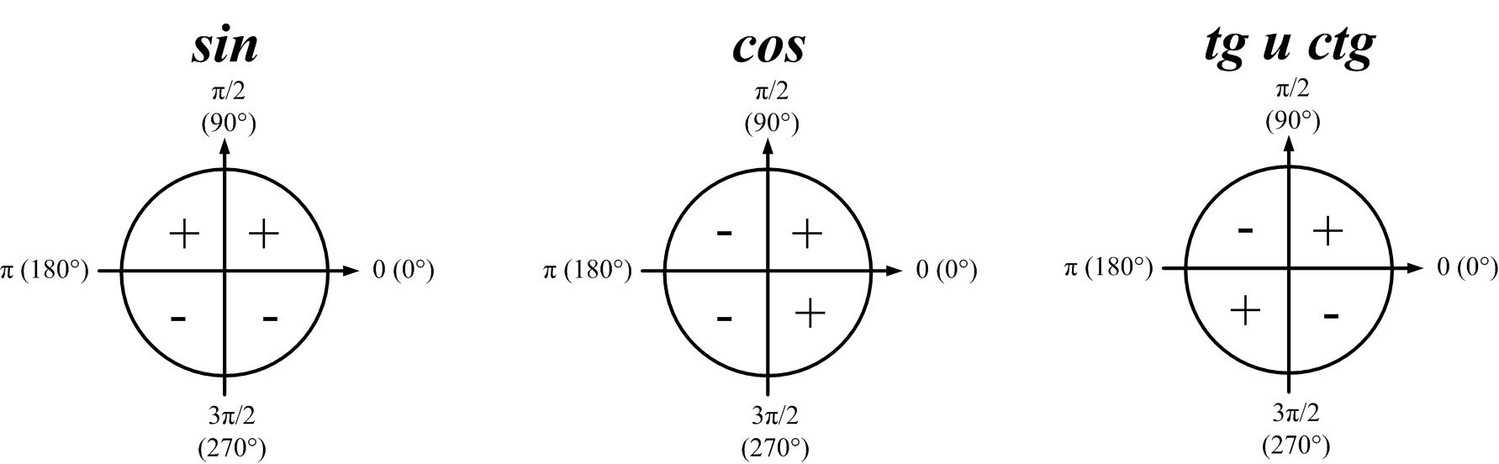 Объявляется тема урока через разгадывание кроссворда, который проектируется при помощи кодоскопа.

Кроссворд

  1. Разность между делимым и произведение делителя на неполное частное.
  2. Часть прямой, которая состоит из всех точек прямой, лежащих между двумя данными.
  3. Основные утверждения геометрических фигур.
  4. Вторая координата точки на плоскости.
  5. Линия, соединяющая середины двух боковых сторон треугольника и трапеции.
  6. Параллелограмм, у которого все углы прямые.
  7. Утверждение, не требующее доказательства.
  8. Координатная прямая.
  9. Древнегреческий учёный-математик.

Вопрос: Что такое вектор?

Ответ: Вектором называется направленный отрезок. Направление вектора определяется указанием его начала и конца.

Задача 1 (на доске начерчен треугольник).

Дан треугольник АВС. Найдите:

а) сумму векторов и

б) разность векторов и

Ответ:

а) + = ;

б) – = .

Задача 2

В том же треугольнике выразите сторону ВС через векторы

а) и ;

б) и .

Ответ:

а) = + ;

б) = – .

Вопрос: Что такое абсолютная величина вектора?

Ответ: Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор.

Задача 3

Абсолютные величины векторов и равны 2 и 3 соответственно, угол между этими векторами 60°. Найдите скалярное произведение векторов и .

Ответ:

IV. Ознакомление с новым материалом.

Историческая справка: Впервые теорема косинусов была доказана учёным –математиком аль-Бируни (973-1048 г.г.). С помощью данной теоремы и теоремы синусов которая будет доказана на последующих уроках, можно будет полностью решить поставленную в теме “Решение треугольников” задачу, т.е. вопрос о том, как зная одни из основных элементов треугольника (их 6: 3 угла и 3 стороны), найти другие.

Теорема: Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.

Дано:

Треугольник АВС.

Доказать:

1. ;

2. ;

3. .

(Первое равенство проговаривает и записывает учитель, а второе и третье кто-нибудь из учащихся.)

Доказательство:

Докажем первое равенство, два других доказываются аналогично.

(Доказательство проводит кто-нибудь из учащихся по желанию при помощи учителя)

Запишем теорему косинусов в общем виде:

;

;

.

(Первое равенство проговаривает и записывает учитель, а второе и третье кто-нибудь из учащихся.)

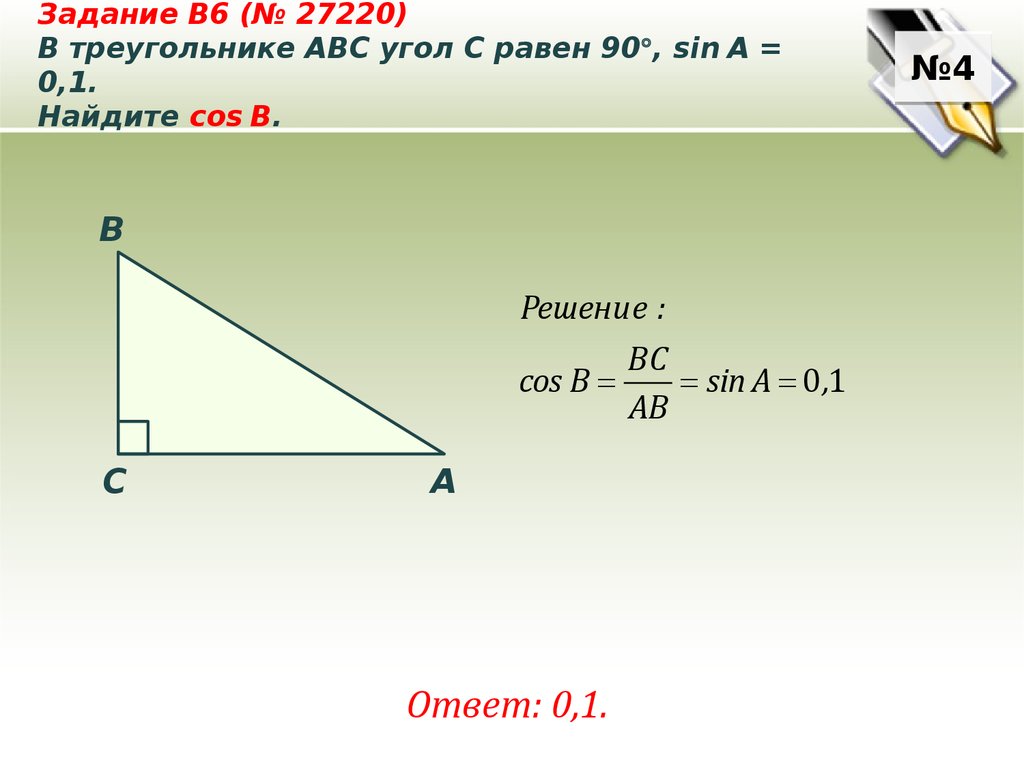
Иногда теорему косинусов называют обобщённой теоремой Пифагора. Такое название объясняется тем, что в теореме косинусов содержится как частный случай, теорема Пифагора. В самом деле, если в треугольнике АВС угол А прямой, то соs А = соs 90° = 0 и по формуле получаем , то есть квадрат гипотенузы равен сумме квадратов катетов.

V. Первичное осмысление и применение изученного материала.

Задачи по готовым чертежам. Чертежи проектируются при помощи кодоскопа. При решении задач учащиеся каждый раз проговаривают формулировку теоремы.

Задача 1

Ответ: .

Задача 2

Ответ: 4.

Задача 3

Ответ: 60°.

Ещё раз повторить, как звучит теорема косинусов.

VI. Тест.

I  вариант.

1. Закончи предложение. Квадрат любой стороны треугольника равен …

а) сумме квадратов двух других сторон, минус произведение этих сторон на косинус угла между ними;

б) сумме квадратов двух других его сторон;

в) сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.

2. Заполни пропуски. В треугольнике KHT .

а) KH;

б) HT;

в) TK.

3. В треугольнике CDO известны стороны CD и CO. Величину, какого угла необходимо знать, чтобы найти длину стороны DO?

а) C;

б) D;

в) O.

4. Дан треугольник DEF. Выберите верное равенство:

а) ;

б) ;

в) .

5. В треугольнике CKE найдите сторону CE, если CK = 6, KE = 8, ? K = 60°.

а) 52;

б) 4;

в) .

II вариант.

1. Выберите верное утверждение.

а) Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон.

б) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.

в) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон, минус произведение этих сторон на косинус угла между ними.

2. Заполни пропуски. В треугольнике ESR

.

а) SE;

б) SR;

в) ER.

3. В треугольнике АВС известны: длина стороны ВС и величина угла С. Чтобы вычислить сторону АВ, нужно знать:

а) АС;

б) В;

в) С.

4. Выберите верное равенство:

а) ;

б) ;

в) .

5. В треугольнике KHN найдите сторону KN, если KH = , HN = 5, H = 45°.

а) 53;

б) 13;

в) .

Ответы:

  • I вариант: в, в, а, б, в.
  • II вариант: б, б, а, б, в.

(После проведения теста с помощью кодоскопа учащимся, выполнившим верно 4-5 заданий, выставляются положительные оценки в журнал).

VII. Итоги урока.

1. Выставляются оценки за урок.

2. Домашнее задание:

  • § 12, п. 109, стр. 191-192;
  • вопросы 1, 2 ( самостоятельно доказать теорему для тупоугольного треугольника) стр. 197;
  • № 1, 2, 3 стр. 198.

Список используемой литературы.

  1. Программно методические материалы. Математика. 5-11 классы. Тематическое планирование. Издательство “Дрофа” 1998 год.
  2. С.Г. Манвелов. Конструирование современного урока математики. Москва “Просвещение” 2002 год.
  3. Л.С. Карнацевич. Изучение геометрии в 8-м классе. Москва “Просвещение” 1984 год.
  4. А.В. Погорелов. Геометрия. Учебник для 7-11-х классов общеобразовательных учреждений. Москва “Просвещение” 1995 год.
3 6 Решить для ? cos(x)=1/2 7 Найти x sin(x)=-1/2 8 Преобразование градусов в радианы 225 9 Решить для ? cos(x)=(квадратный корень из 2)/2 10 Найти x cos(x)=(квадратный корень из 3)/2 11 Найти x sin(x)=(квадратный корень из 3)/2 92=9 14 Преобразование градусов в радианы 120 градусов 15 Преобразование градусов в радианы 180 16 Найти точное значение желтовато-коричневый(195) 92-4 38 Найти точное значение грех(255) 39 Оценить лог база 27 из 36 40 Преобразовать из радианов в градусы 2 шт. 92-3sin(x)+1=0 43 Найти x tan(x)+ квадратный корень из 3=0 44 Найти x sin(2x)+cos(x)=0 45 Упростить (1-cos(x))(1+cos(x)) 92=25 59 График f(x)=- натуральный логарифм x-1+3 60 Найдите значение с помощью единичного круга угловой синус(-1/2) 61 Найти домен квадратный корень из 36-4x^2 92=0 66 Найти x cos(2x)=(квадратный корень из 2)/2 67 График у=3 68 График f(x)=- логарифмическая база 3 x-1+3 92 71 Найти x квадратный корень из x+4+ квадратный корень из x-1=5 72 Решить для ? cos(2x)=-1/2 73 Найти x логарифмическая база x из 16=4 9х 75 Упростить (cos(x))/(1-sin(x))+(1-sin(x))/(cos(x)) 76 Упростить сек(х)sin(х) 77 Упростить кубический корень из 24 кубический корень из 18 92=0 96 Найти x 3x+2=(5x-11)/(8г) 97 Решить для ? sin(2x)=-1/2 98 Найти x (2x-1)/(x+2)=4/5 93 6 Решить для ? cos(x)=1/2 7 Найти x sin(x)=-1/2 8 Преобразование градусов в радианы 225 9 Решить для ? cos(x)=(квадратный корень из 2)/2 10 Найти x cos(x)=(квадратный корень из 3)/2 11 Найти x sin(x)=(квадратный корень из 3)/2 92=9 14 Преобразование градусов в радианы 120 градусов 15 Преобразование градусов в радианы 180 16 Найти точное значение желтовато-коричневый(195) 92-4 38 Найти точное значение грех(255) 39 Оценить лог база 27 из 36 40 Преобразовать из радианов в градусы 2 шт.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *