Косинус ряд тейлора: Разложение косинуса в ряд Тейлора

{i\pi} + 1 = 0

5 мая, 2020

© 2007-2023 Психичная чашка ползла

ряд Тейлора . Магия математики [Как найти x и зачем это нужно]

Доказывая в конце прошлой главы уравнение Эйлера, мы воспользовались тремя загадочными формулами:

Перед тем как разбираться, как мы пришли к этому, давайте немного поиграем. Интересно, что получится, если взять отдельно каждый член ряда e^x и продифференцировать? Правило дифференцирования степенной функции говорит нам, что производной функции x⁴/4! будет (4x³)/4! = x³/3! то есть предшествующий член ряда! Другими словами, продифференцировав ряд e^x, мы вновь получим ряд e^x, что полностью соответствует тому, что мы знаем о показательной функции e^x!

Последовательно дифференцируя x – x³/3! + x⁵/5! – x⁷/7! +…, получаем 1 – x²/2! + x⁴/4! – x⁶

/6! +…, что соотносится с тем, что производная синуса – это косинус. Справедливо и обратное: производная косинуса – это синус со знаком минус. А еще этот ряд лишний раз доказывает, что cos 0 = 1, и поскольку каждая степень в нем выражена четным числом, значение cos (–x) будет равно cos x. Впрочем, нам это уже известно (например, (–x)⁴/4! = x⁴/4!). Следуя той же логике, мы можем прийти к sin 0 = 0, а поскольку каждая степень выражена нечетным числом, sin (–x) = –sin x, как мы и предполагали.

Теперь давайте попытаемся понять, откуда, собственно говоря, берутся эти формулы. Мы знаем, как найти производные наиболее популярных функций. Но бывают такие ситуации, когда одну и ту же функцию нужно продифференцировать несколько раз, разыскав ее вторую (f»(x)), третью (f»’(x)) и т. д. производную. f»(x) выражает крутизну наклона функции (то есть ее

вогнутость) в точке (x, f(x)), f»’(x) делает то же для второй производной и т.  д.

Для этого имеются специальные формулы. Они называются рядами Тейлора, потому что первым, кто ввел их в оборот, был английский математик Брук Тейлор (1685–1731). Для функции f(x) с производными f’(x), f»(x), f»’(x) и т. д. мы имеем

при любом значении x, «достаточно близком» к 0. Что значит «достаточно близком»? В некоторых функциях – например, ex, sin x или cos x – x может быть практически любой величиной. Но есть и такие функции (мы встретимся с ними чуть позже), которые имеют смысл только при очень маленьких значениях x.

Проследим, как меняется формула для f(x) = e^x

. Так как e^x равна своей собственной первой (равно как и второй, и третьей и т. д.) производной, следовательно

f(0) = f’(0) = f»(0) = f»’(0) =… = e⁰ = 1

то есть ряд Тейлора для ex превращается в 1 + x + x²/2! + x³/3! + x⁴/4! +…, как и предполагалось.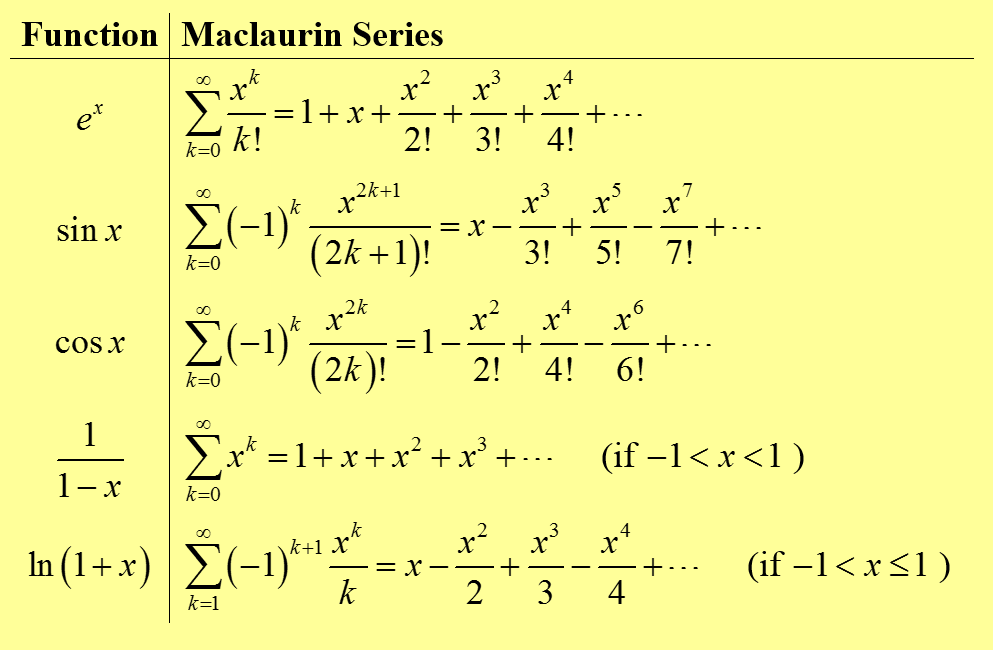 При небольшом значении x нам достаточно посчитать лишь несколько членов ряда, чтобы получить точную аппроксимацию верного ответа.

Посчитаем с его помощью проценты. Как мы выяснили в прошлой главе, если положить на счет $1000 под 5 %, то, при условии непрерывных начислений, к концу года мы будем иметь $1000

e^0,05 = $1051,27. И мы знаем, как это подсчитать. Но к тому же ответу можно прийти и с помощью формул сначала второго –

$1000(1 + 0,05 + (0,05)?/2!) = $1051,25

а потом и третьего порядка аппроксимации: $1051,27.

Аппроксимации Тейлора могут быть представлены в виде графика, на котором вместе с первыми тремя многочленами Тейлора изображена показательная (экспоненциальная) функция y = e^x.

Постепенно увеличивая степень многочлена, мы достигаем все большей точности аппроксимации, особенно если x близок к 0. Но что же такого особенного в многочленах Тейлора, что делает их настолько эффективными? Аппроксимация первого порядка (называемая линейной) утверждает, что при x, близком к 0,

f(x) ? f

(0) + f’(0)x

На графике получается прямая линия, проходящая через точку (0, f(0)) с наклоном f’(0). Значит, многочлен Тейлора степени n будет проходить через ту же точку (0, f(0)) и иметь такие же первую, вторую, третью и т. д., вплоть до n-ной, производные, что и начальная функция f(x).

Отступление

Кстати, многочлены и ряды Тейлора отлично показывают себя при работе и с другими величинами (не только 0), к которым стремится х. Так, ряд Тейлора для f(x) с начальной точкой a равен

При a = 0 он будет равен f(x) для всех действительных или комплексных значений x, близких к a.

Возьмем ряд Тейлора для f(x) = sin x

. Посмотрите: f’(x) = cos x, f»(x) = –sin x, f»’(x) = –cos x, а f»»(x) = sin x = f(x). При сопоставлении с 0, начав с f(0), мы придем к циклу 0, 1, 0, –1, 0, 1, 0, –1…. , в котором каждое четное значение x попросту исчезает из ряда. Следовательно, получается, что при любом x, выраженном в радианах,

Аналогично, для f(x) = cos x имеем

Ну и напоследок давайте возьмем пример, в котором ряд Тейлора равен функции при некоторых – но не всех – значениях x. Пусть это будет Здесь f(0) = 1, и, согласно цепному правилу, первые несколько производных выглядят как

Следуя и дальше этой закономерности (или воспользовавшись методом индукции), мы неизбежно придем к заключению, что n-ная производная (1 –

x)^–1 будет равна n!(1 – x)^{?(n + 1)} (а при x = 0 – просто n!). Следовательно, ряд Тейлора трансформируется в

что будет верно только при таком значении x, которое находится в диапазоне от –1 до 1. Если же x, например, будет больше 1, то складываемые величины будут становиться все больше и больше, пока сумму станет вовсе невозможно определить.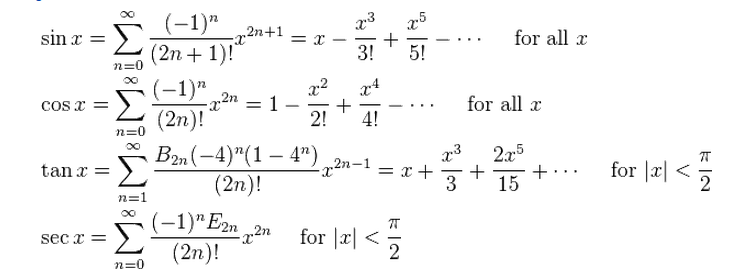 {N+1}. $$ 9{-3}$? Что, если интервал вместо $[1,3/2]$? (отвечать)

Пример 13.11.3 Найдите первые три ненулевых члена ряда Тейлора для $\tan x$ на $[-\pi/4,\pi/4]$, и вычислить гарантированный член ошибки, как указано Теорема Тейлора. (Вы можете использовать Мудрец или аналогичная помощь.) (отвечать)

Пример 13.11.4 Покажите, что $\cos x$ равно своему ряду Тейлора для всех $x$ показав, что предел члена ошибки равен нулю, когда $N$ приближается бесконечность.

92}{2!} + …$. Теперь мы проверим ряд Маклорена для синусоидальной функции $f(x) = \sin x$.

Сначала взгляните на следующую таблицу, содержащую производные от $f$ и производные от $f$, вычисленные при $x = 0$:

9n} \biggr \rvert = \lim_{n \to \infty} \frac{(2n+1)!}{(2n+3)!} = \lim_{n \to \infty} \frac{1}{ (2n+2)(2n+3)} = 0 \end{align}

Следовательно, радиус сходимости равен $R = \infty$, поэтому этот ряд сходится для всех $x \in \mathbb{R}$.

$f(x) = \sin x$	$f(0) = \sin (0) = 0$
$f'(x) = \cos x$	$f'(0) = \cos (0) = 1$
$f»(x) = -\sin x$	$f»(0) = -\sin (0) = 0$