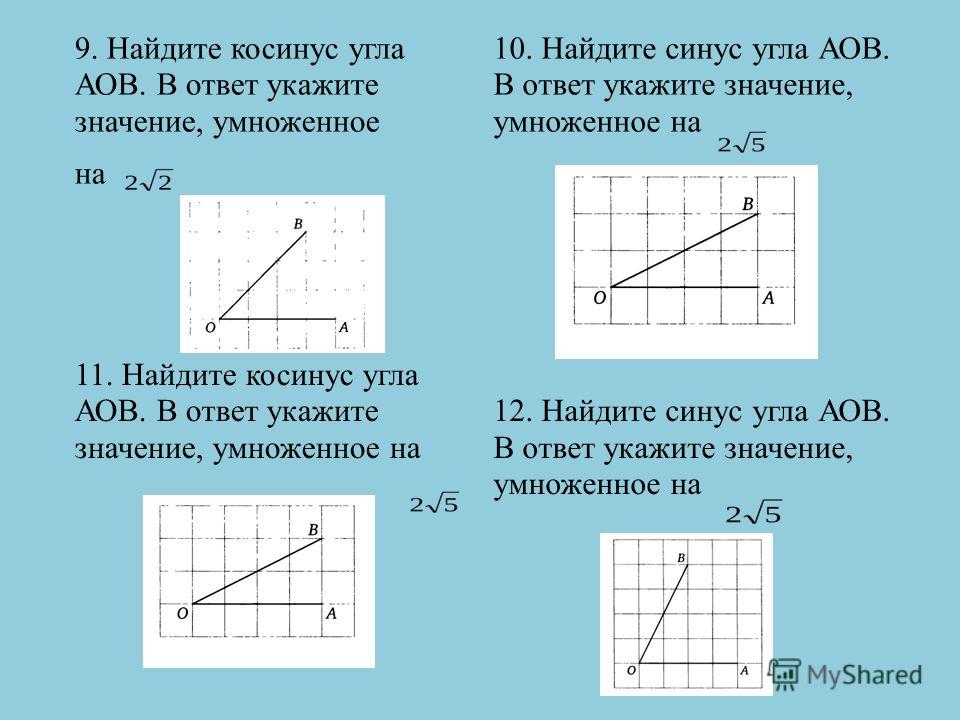
Косинус угла онлайн. Таблица косинусов. Формула косинуса угла.
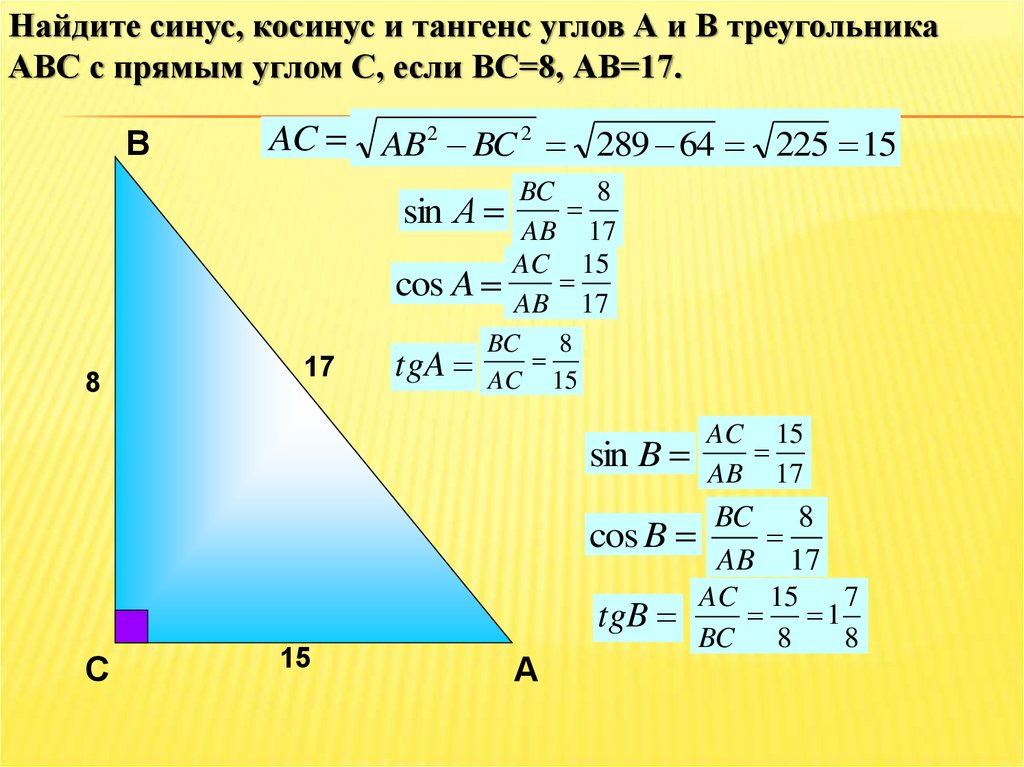
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
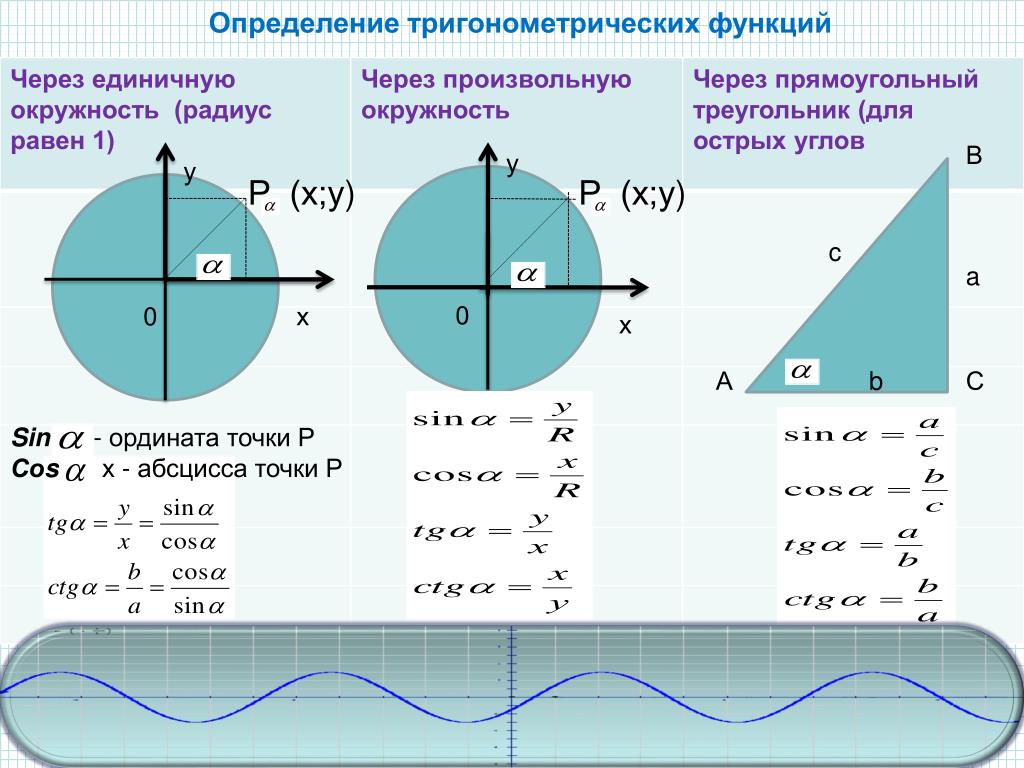
Косинусом угла α называется абсцисса точки B единичной окружности, полученной при повороте точки P(1;0) на угол α.
cos(0°) = 1cos(π/12) = cos(15°) = 0.9659258263cos(π/6) = cos(30°) = 0.8660254038cos(π/4) = cos(45°) = 0.7071067812cos(π/3) = cos(60°) = 0.5cos(5π/12) = cos(75°) = 0.2588190451cos(π/2) = cos(90°) = 0cos(7π/12) = cos(105°) = -0.2588190451cos(2π/3) = cos(120°) = -0.5cos(3π/4) = cos(135°) = -0.7071067812cos(5π/6) = cos(150°) = -0.8660254038cos(11π/12) = cos(165°) = -0.9659258263cos(π) = cos(180°) = -1cos(13π/12) = cos(195°) = -0.9659258263cos(7π/6) = cos(210°) = -0.8660254038cos(5π/4) = cos(225°) = -0.7071067812cos(4π/3) = cos(240°) = -0.5cos(17π/12) = cos(255°) = -0.2588190451cos(3π/2) = cos(270°) = 0cos(19π/12) = cos(285°) = 0.2588190451cos(5π/3) = cos(300°) = 0.5cos(7π/4) = cos(315°) = 0. 7071067812cos(11π/6) = cos(330°) = 0.8660254038cos(23π/12) = cos(345°) = 0.9659258263
7071067812cos(11π/6) = cos(330°) = 0.8660254038cos(23π/12) = cos(345°) = 0.9659258263
| cos(0) = 1 | cos(120) = -0.5 | cos(240) = -0.5 |
| cos(1) = 0.9998476952 | cos(121) = -0.5150380749 | cos(241) = -0.4848096202 |
| cos(2) = 0.999390827 | cos(122) = -0.5299192642 | cos(242) = -0.4694715628 |
| cos(3) = 0.9986295348 | cos(123) = -0.544639035 | cos(243) = -0.4539904997 |
| cos(4) = 0.9975640503 | cos(124) = -0.5591929035 | cos(244) = -0.4383711468 |
| cos(5) = 0.9961946981 | cos(125) = -0.5735764364 | cos(245) = -0.4226182617 |
| cos(6) = 0.9945218954 | cos(126) = -0.5877852523 | cos(246) = -0.4067366431 |
| cos(7) = 0.9925461516 | cos(127) = -0.6018150232 | cos(247) = -0.3907311285 |
| cos(8) = 0.9902680687 | cos(128) = -0.6156614753 | cos(248) = -0.3746065934 |
cos(9) = 0.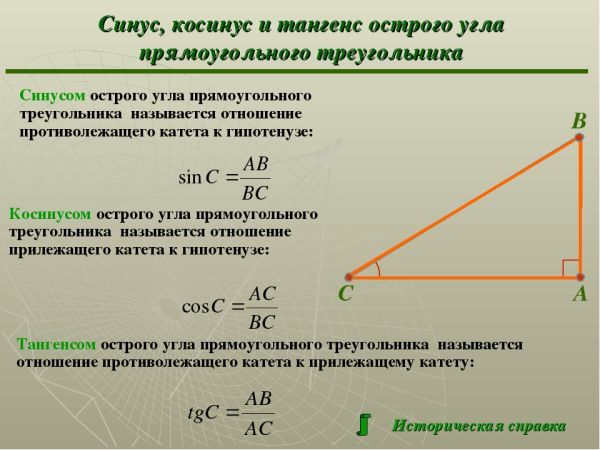 9876883406 9876883406 | cos(129) = -0.629320391 | cos(249) = -0.3583679495 |
| cos(10) = 0.984807753 | cos(130) = -0.6427876097 | cos(250) = -0.3420201433 |
| cos(11) = 0.9816271834 | cos(131) = -0.656059029 | cos(251) = -0.3255681545 |
| cos(12) = 0.9781476007 | cos(132) = -0.6691306064 | cos(252) = -0.3090169944 |
| cos(13) = 0.9743700648 | cos(133) = -0.6819983601 | cos(253) = -0.2923717047 |
| cos(14) = 0.9702957263 | cos(134) = -0.6946583705 | cos(254) = -0.2756373558 |
| cos(15) = 0.9659258263 | cos(135) = -0.7071067812 | cos(255) = -0.2588190451 |
| cos(16) = 0.9612616959 | cos(136) = -0.7193398003 | cos(256) = -0.2419218956 |
| cos(17) = 0.956304756 | cos(137) = -0.7313537016 | cos(257) = -0.2249510543 |
| cos(18) = 0.9510565163 | cos(138) = -0.7431448255 | cos(258) = -0. 2079116908 2079116908 |
| cos(19) = 0.9455185756 | cos(139) = -0.7547095802 | cos(259) = -0.1908089954 |
| cos(20) = 0.9396926208 | cos(140) = -0.7660444431 | cos(260) = -0.1736481777 |
| cos(21) = 0.9335804265 | cos(141) = -0.7771459615 | cos(261) = -0.156434465 |
| cos(22) = 0.9271838546 | cos(142) = -0.7880107536 | cos(262) = -0.139173101 |
| cos(23) = 0.9205048535 | cos(143) = -0.79863551 | cos(263) = -0.1218693434 |
| cos(24) = 0.9135454576 | cos(144) = -0.8090169944 | cos(264) = -0.1045284633 |
| cos(25) = 0.906307787 | cos(145) = -0.8191520443 | cos(265) = -0.08715574275 |
| cos(26) = 0.8987940463 | cos(146) = -0.8290375726 | cos(266) = -0.06975647374 |
| cos(27) = 0.8910065242 | cos(147) = -0.8386705679 | cos(267) = -0.05233595624 |
| cos(28) = 0.8829475929 | cos(148) = -0.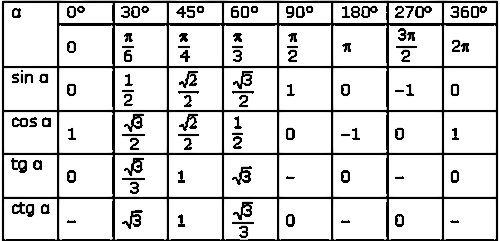 8480480962 8480480962 | cos(268) = -0.0348994967 |
| cos(29) = 0.8746197071 | cos(149) = -0.8571673007 | cos(269) = -0.01745240644 |
| cos(30) = 0.8660254038 | cos(150) = -0.8660254038 | cos(270) = 0 |
| cos(31) = 0.8571673007 | cos(151) = -0.8746197071 | cos(271) = 0.01745240644 |
| cos(32) = 0.8480480962 | cos(152) = -0.8829475929 | cos(272) = 0.0348994967 |
| cos(33) = 0.8386705679 | cos(153) = -0.8910065242 | cos(273) = 0.05233595624 |
| cos(34) = 0.8290375726 | cos(154) = -0.8987940463 | cos(274) = 0.06975647374 |
| cos(35) = 0.8191520443 | cos(155) = -0.906307787 | cos(275) = 0.08715574275 |
| cos(36) = 0.8090169944 | cos(156) = -0.9135454576 | cos(276) = 0.1045284633 |
| cos(37) = 0.79863551 | cos(157) = -0.9205048535 | cos(277) = 0.1218693434 |
cos(38) = 0.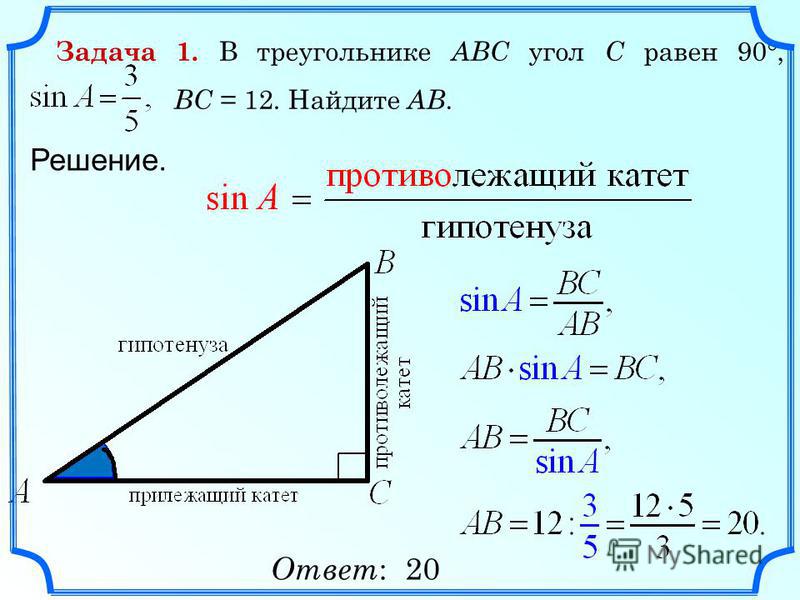 7880107536 7880107536 | cos(158) = -0.9271838546 | cos(278) = 0.139173101 |
| cos(39) = 0.7771459615 | cos(159) = -0.9335804265 | cos(279) = 0.156434465 |
| cos(40) = 0.7660444431 | cos(160) = -0.9396926208 | cos(280) = 0.1736481777 |
| cos(41) = 0.7547095802 | cos(161) = -0.9455185756 | cos(281) = 0.1908089954 |
| cos(42) = 0.7431448255 | cos(162) = -0.9510565163 | cos(282) = 0.2079116908 |
| cos(43) = 0.7313537016 | cos(163) = -0.956304756 | cos(283) = 0.2249510543 |
| cos(44) = 0.7193398003 | cos(164) = -0.9612616959 | cos(284) = 0.2419218956 |
| cos(45) = 0.7071067812 | cos(165) = -0.9659258263 | cos(285) = 0.2588190451 |
| cos(46) = 0.6946583705 | cos(166) = -0.9702957263 | cos(286) = 0.2756373558 |
| cos(47) = 0.6819983601 | cos(167) = -0.9743700648 | cos(287) = 0.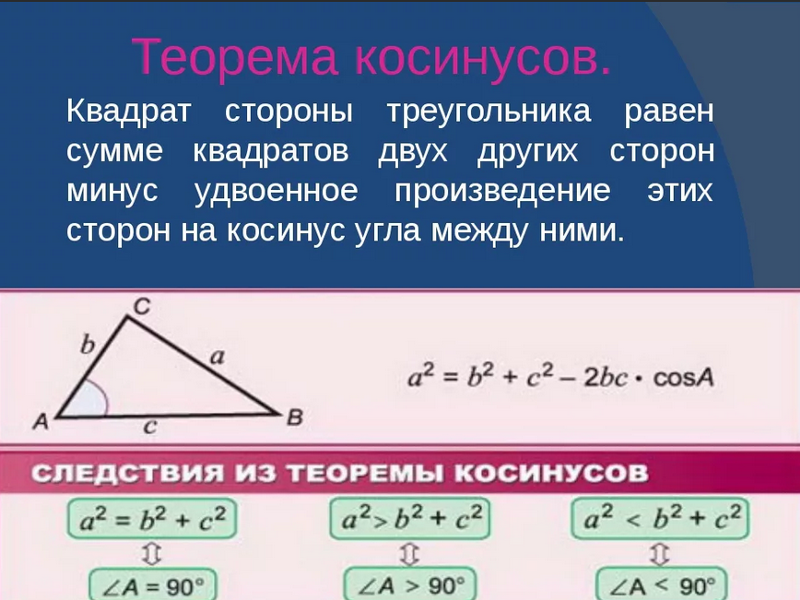 2923717047 2923717047 |
| cos(48) = 0.6691306064 | cos(168) = -0.9781476007 | cos(288) = 0.3090169944 |
| cos(49) = 0.656059029 | cos(169) = -0.9816271834 | cos(289) = 0.3255681545 |
| cos(50) = 0.6427876097 | cos(170) = -0.984807753 | cos(290) = 0.3420201433 |
| cos(51) = 0.629320391 | cos(171) = -0.9876883406 | cos(291) = 0.3583679495 |
| cos(52) = 0.6156614753 | cos(172) = -0.9902680687 | cos(292) = 0.3746065934 |
| cos(53) = 0.6018150232 | cos(173) = -0.9925461516 | cos(293) = 0.3907311285 |
| cos(54) = 0.5877852523 | cos(174) = -0.9945218954 | cos(294) = 0.4067366431 |
| cos(55) = 0.5735764364 | cos(175) = -0.9961946981 | cos(295) = 0.4226182617 |
| cos(56) = 0.5591929035 | cos(176) = -0.9975640503 | cos(296) = 0.4383711468 |
| cos(57) = 0.544639035 | cos(177) = -0.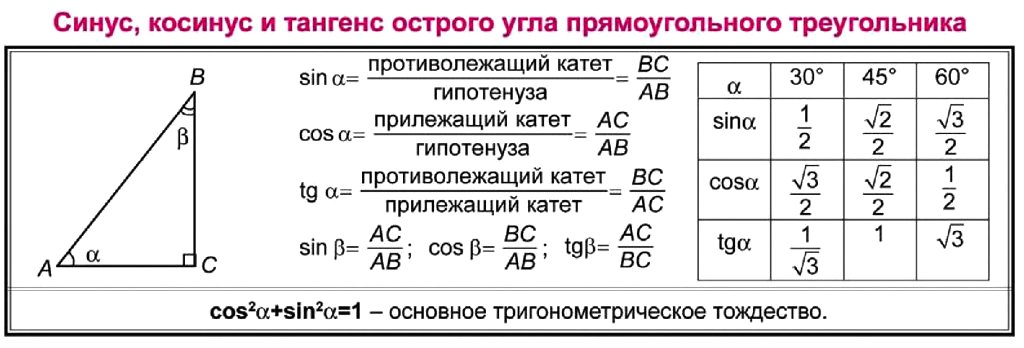 9986295348 9986295348 | cos(297) = 0.4539904997 |
| cos(58) = 0.5299192642 | cos(178) = -0.999390827 | cos(298) = 0.4694715628 |
| cos(59) = 0.5150380749 | cos(179) = -0.9998476952 | cos(299) = 0.4848096202 |
| cos(60) = 0.5 | cos(180) = -1 | cos(300) = 0.5 |
| cos(61) = 0.4848096202 | cos(181) = -0.9998476952 | cos(301) = 0.5150380749 |
| cos(62) = 0.4694715628 | cos(182) = -0.999390827 | cos(302) = 0.5299192642 |
| cos(63) = 0.4539904997 | cos(183) = -0.9986295348 | cos(303) = 0.544639035 |
| cos(64) = 0.4383711468 | cos(184) = -0.9975640503 | cos(304) = 0.5591929035 |
| cos(65) = 0.4226182617 | cos(185) = -0.9961946981 | cos(305) = 0.5735764364 |
| cos(66) = 0.4067366431 | cos(186) = -0.9945218954 | cos(306) = 0.5877852523 |
| cos(67) = 0.3907311285 | cos(187) = -0. 9925461516 9925461516 | cos(307) = 0.6018150232 |
| cos(68) = 0.3746065934 | cos(188) = -0.9902680687 | cos(308) = 0.6156614753 |
| cos(69) = 0.3583679495 | cos(189) = -0.9876883406 | cos(309) = 0.629320391 |
| cos(70) = 0.3420201433 | cos(190) = -0.984807753 | cos(310) = 0.6427876097 |
| cos(71) = 0.3255681545 | cos(191) = -0.9816271834 | cos(311) = 0.656059029 |
| cos(72) = 0.3090169944 | cos(192) = -0.9781476007 | cos(312) = 0.6691306064 |
| cos(73) = 0.2923717047 | cos(193) = -0.9743700648 | cos(313) = 0.6819983601 |
| cos(74) = 0.2756373558 | cos(194) = -0.9702957263 | cos(314) = 0.6946583705 |
| cos(75) = 0.2588190451 | cos(195) = -0.9659258263 | cos(315) = 0.7071067812 |
| cos(76) = 0.2419218956 | cos(196) = -0.9612616959 | cos(316) = 0.7193398003 |
cos(77) = 0. 2249510543 2249510543 | cos(197) = -0.956304756 | cos(317) = 0.7313537016 |
| cos(78) = 0.2079116908 | cos(198) = -0.9510565163 | cos(318) = 0.7431448255 |
| cos(79) = 0.1908089954 | cos(199) = -0.9455185756 | cos(319) = 0.7547095802 |
| cos(80) = 0.1736481777 | cos(200) = -0.9396926208 | cos(320) = 0.7660444431 |
| cos(81) = 0.156434465 | cos(201) = -0.9335804265 | cos(321) = 0.7771459615 |
| cos(82) = 0.139173101 | cos(202) = -0.9271838546 | cos(322) = 0.7880107536 |
| cos(83) = 0.1218693434 | cos(203) = -0.9205048535 | cos(323) = 0.79863551 |
| cos(84) = 0.1045284633 | cos(204) = -0.9135454576 | cos(324) = 0.8090169944 |
| cos(85) = 0.08715574275 | cos(205) = -0.906307787 | cos(325) = 0.8191520443 |
| cos(86) = 0.06975647374 | cos(206) = -0.8987940463 | cos(326) = 0. 8290375726 8290375726 |
| cos(87) = 0.05233595624 | cos(207) = -0.8910065242 | cos(327) = 0.8386705679 |
| cos(88) = 0.0348994967 | cos(208) = -0.8829475929 | cos(328) = 0.8480480962 |
| cos(89) = 0.01745240644 | cos(209) = -0.8746197071 | cos(329) = 0.8571673007 |
| cos(90) = 0 | cos(210) = -0.8660254038 | cos(330) = 0.8660254038 |
| cos(91) = -0.01745240644 | cos(211) = -0.8571673007 | cos(331) = 0.8746197071 |
| cos(92) = -0.0348994967 | cos(212) = -0.8480480962 | cos(332) = 0.8829475929 |
| cos(93) = -0.05233595624 | cos(213) = -0.8386705679 | cos(333) = 0.8910065242 |
| cos(94) = -0.06975647374 | cos(214) = -0.8290375726 | cos(334) = 0.8987940463 |
| cos(95) = -0.08715574275 | cos(215) = -0.8191520443 | cos(335) = 0.906307787 |
| cos(96) = -0.1045284633 | cos(216) = -0. 8090169944 8090169944 | cos(336) = 0.9135454576 |
| cos(97) = -0.1218693434 | cos(217) = -0.79863551 | cos(337) = 0.9205048535 |
| cos(98) = -0.139173101 | cos(218) = -0.7880107536 | cos(338) = 0.9271838546 |
| cos(99) = -0.156434465 | cos(219) = -0.7771459615 | cos(339) = 0.9335804265 |
| cos(100) = -0.1736481777 | cos(220) = -0.7660444431 | cos(340) = 0.9396926208 |
| cos(101) = -0.1908089954 | cos(221) = -0.7547095802 | cos(341) = 0.9455185756 |
| cos(102) = -0.2079116908 | cos(222) = -0.7431448255 | cos(342) = 0.9510565163 |
| cos(103) = -0.2249510543 | cos(223) = -0.7313537016 | cos(343) = 0.956304756 |
| cos(104) = -0.2419218956 | cos(224) = -0.7193398003 | cos(344) = 0.9612616959 |
| cos(105) = -0.2588190451 | cos(225) = -0.7071067812 | cos(345) = 0.9659258263 |
cos(106) = -0. 2756373558 2756373558 | cos(226) = -0.6946583705 | cos(346) = 0.9702957263 |
| cos(107) = -0.2923717047 | cos(227) = -0.6819983601 | cos(347) = 0.9743700648 |
| cos(108) = -0.3090169944 | cos(228) = -0.6691306064 | cos(348) = 0.9781476007 |
| cos(109) = -0.3255681545 | cos(229) = -0.656059029 | cos(349) = 0.9816271834 |
| cos(110) = -0.3420201433 | cos(230) = -0.6427876097 | cos(350) = 0.984807753 |
| cos(111) = -0.3583679495 | cos(231) = -0.629320391 | cos(351) = 0.9876883406 |
| cos(112) = -0.3746065934 | cos(232) = -0.6156614753 | cos(352) = 0.9902680687 |
| cos(113) = -0.3907311285 | cos(233) = -0.6018150232 | cos(353) = 0.9925461516 |
| cos(114) = -0.4067366431 | cos(234) = -0.5877852523 | cos(354) = 0.9945218954 |
| cos(115) = -0.4226182617 | cos(235) = -0.5735764364 | cos(355) = 0. 9961946981 9961946981 |
| cos(116) = -0.4383711468 | cos(236) = -0.5591929035 | cos(356) = 0.9975640503 |
| cos(117) = -0.4539904997 | cos(237) = -0.544639035 | cos(357) = 0.9986295348 |
| cos(118) = -0.4694715628 | cos(238) = -0.5299192642 | cos(358) = 0.999390827 |
| cos(119) = -0.4848096202 | cos(239) = -0.5150380749 | cos(359) = 0.9998476952 |
Косинус онлайн калькулятор
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Данный калькулятор вычислит синус, косинус, тангенс, котангенс, секанс, косеканс угла как в градусной, так и в радианной мере.

Введите число
Что такое косинус угла
Пусть задан прямоугольный треугольник ABC с острым углом α, тогда косинусом угла α будет отношение прилежащего катета к гипотенузе cos α = AB/AC.
Так же для определения косинуса угла можно воспользоваться окружностью, построенной в декартовой системе координат, радиуса R и центром в начале координат O.
На окружности отметим точку P с координатами (1;0), теперь повернем луч OP на некоторый угол α. Направление против часовой стрелки считается положительным, по часовой стрелки – отрицательным.
Косинусом угла α будет отношение абсциссы точки XP к радиусу окружности.
cos α = XP/R, в случае, если окружность единичная (радиус окружности = 1), формула примет вид cos α = XP.
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор уравнений |
| Калькулятор суммы |
| Калькулятор пределов функций |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Калькулятор делителей числа |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
соз(х) | функция косинуса
cos(x), функция косинуса.
- Определение косинуса
- График косинуса
- Правила косинуса
- Функция арккосинуса
- Таблица косинусов
- Калькулятор косинуса
Определение косинуса
В прямоугольном треугольнике ABC синус α, sin(α) равен определяется как отношение между стороной, примыкающей к углу α, и сторона, противоположная прямому углу (гипотенуза):
cos α = b / c
Пример
b = 3 дюйма
c = 5 дюймов
9002 cos
α 24 / с = 3 / 5 = 0,6
График косинуса
TBD
Правила косинуса
| Название правила | Правило |
|---|---|
| Симметрия | cos(- θ ) = cos θ |
| Симметрия | cos(90°- θ ) = грех θ |
| Пифагорейское тождество | грех 2 (α) + cos 2 (α) = 1 |
| cos θ = sin θ / тангенс θ | |
| cos θ = 1/сек θ | |
| Двойной уголок | cos 2 θ = cos 2 θ — sin 2 θ |
| Сумма углов | cos( α+β ) = cos α cos β — грех α грех β |
| Разница углов | cos( α-β ) = cos α cos β + sin α грех β |
| Сумма к продукту | cos α + cos β = 2 cos [( α+β )/2] cos [( α-β )/2] |
| Отличие от продукта | cos α — cos β = — 2 sin [( α+β )/2] грех [( α-β )/2] |
| Закон косинусов | |
| Производная | cos’ x = — sin x |
| Интеграл | ∫ cos x d x = sin x + C |
| Формула Эйлера | , потому что х = ( e ix + e — ix ) / 2 |
Функция арккосинуса
Арккосинус x определяется как функция арккосинуса x, когда -1≤x≤1.
Когда косинус y равен x:
cos y = x
Тогда арккосинус x равен функции арккосинуса x, которая равна y:
arccos5 x = cos -1 х = у
Пример
arccos 1 = cos -1 1 = 0 рад = 0 °
См.: Функция Arccos
Косинус Таблица
| x (°) | 70054||
|---|---|---|
| x (°) | 7 x (рад) | соз х |
| 180° | № | -1 |
| 150° | 5π/6 | -√3/2 |
| 135° | 3π/4 | -√2/2 |
| 120° | 2π/3 | -1/2 |
| 90° | №/2 | 0 |
| 60° | №/3 | 1/2 |
| 45° | №/4 | √2/2 |
| 30° | №/6 | √3/2 |
| 0° | 0 | 1 |
См.
 также
также- Калькулятор Cos
- Функция Arccos
- Синусоидальная функция
- Перевод градусов в радианы
Калькулятор закона косинусов
Создано Bogna Szyk и Hanna Pamula, PhD
Отзыв от Jack Bowater
Последнее обновление: 10 февраля 2023 г.
Содержание:- Что такое закон косинусов 9005 косинусы?
- Применение закона косинусов
- Закон косинусов доказательство
- Как пользоваться калькулятором закона косинусов
- Закон косинусов – SSS пример
- Часто задаваемые вопросы
Калькулятор закона косинусов может помочь вам решить огромное количество треугольных задач. Вы узнаете, что такое закон косинусов (также известный как правило косинусов), формулу закона косинусов и ее приложения. Прокрутите вниз, чтобы узнать, когда и как использовать закон косинусов, и ознакомьтесь с доказательствами этого закона. Благодаря этому калькулятору треугольников вы сможете быстро найти свойства любого произвольного треугольника.
Но если вам почему-то интересно, что такое косинус, лучше взгляните на наш калькулятор косинуса.
Формула закона косинусов
Закон косинусов гласит, что для треугольника со сторонами и углами, обозначенными символами, как показано выше, a² + c² — 2ac × cos(β)
c² = a² + b² - 2ab × cos(γ)
Для прямоугольного треугольника угол гамма, который является углом между катетами a и b , равно 90°. Косинус угла 90° = 0, поэтому в этом частном случае формула закона косинусов сводится к известному уравнению теоремы Пифагора:
a² = b² + c² - 2bc × cos(90°)
a² = b² + c²
Что такое закон косинусов?
Закон косинусов (альтернативно формула косинуса или правило косинуса) описывает отношение между длинами сторон треугольника и косинусом его углов. Его можно применять ко всем треугольникам, а не только к прямоугольным. Этот закон обобщает теорему Пифагора, так как позволяет вычислить длину одной из сторон, зная длину обеих сторон и угол между ними.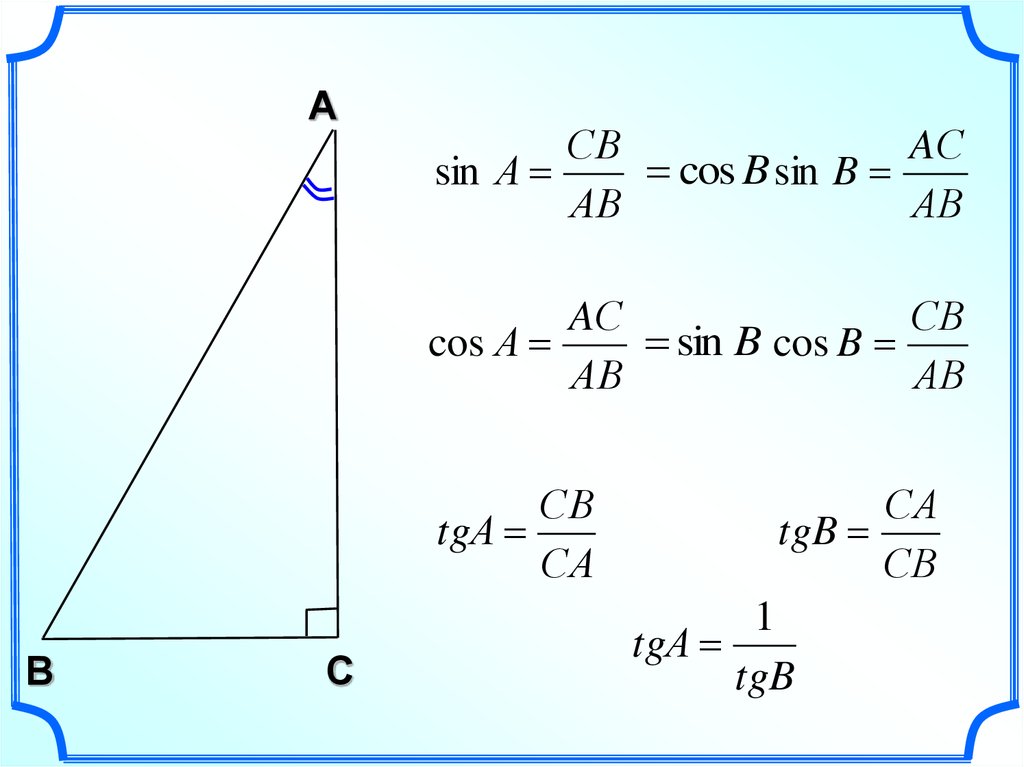
Закон появился в Элементе Евклида, математическом трактате, содержащем определения, постулаты и геометрические теоремы. Евклид не сформулировал его так, как мы изучаем его сегодня, поскольку понятие косинуса еще не было разработано.
AB² = CA² + CB² - 2 × CA × CH (для острых углов, «+» для тупых)
Однако мы можем легко переформулировать теорему Евклида в текущей форме формулы косинуса:
CH = CB × cos(γ) , поэтому AB² = CA² + CB² - 2 × CA × (CB × cos(γ))
Меняя обозначения, получаем знакомое выражение:
c² = a² + b² - 2ab × cos(γ) первое явное уравнение косинуса было представлено персидским математиком д'Аль-Каши в 15 веке. В 16 веке закон был популяризирован известным французским математиком Виете, прежде чем он получил свою окончательную форму в 19 веке.
Применение закона косинусов
Вы можете преобразовать эти формулы закона косинусов для решения некоторых задач триангуляции (решение треугольника).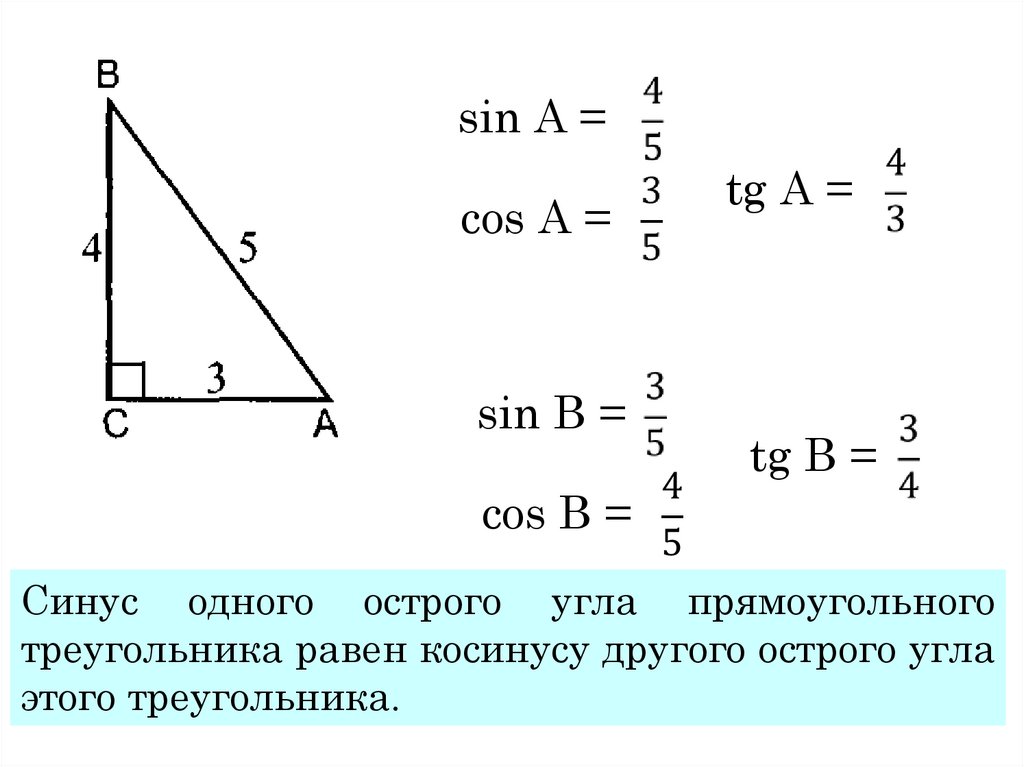 Вы можете использовать их, чтобы найти:
Вы можете использовать их, чтобы найти:
Третья сторона треугольника , зная две стороны и угол между ними (SAS):
а = √[b² + c² - 2bc × cos(α)]b = √[a² + c² - 2ac × cos(β)]с = √[a² + b² - 2ab × cos(γ)]
Углы треугольника , зная все три стороны (SSS):
α = arccos [(b² + c² - a²)/(2bc)]β = arccos [(a² + c² - b²)/(2ac)]γ = arccos [(a² + b² - c²)/(2ab)]
Третья сторона треугольника , зная две стороны и угол, противолежащий одной из них (SSA):
a = b × cos(γ) ± √[c² - b² × sin²(γ)]b = c × cos(α) ± √[a² - c² × sin²(α)]c = a × cos(β) ± √[b² - a² × sin²(β)]
Просто помните, что зная две стороны и прилежащий угол, можно получить два различных возможных треугольника (или одно или ноль положительных решений, в зависимости от заданных данных).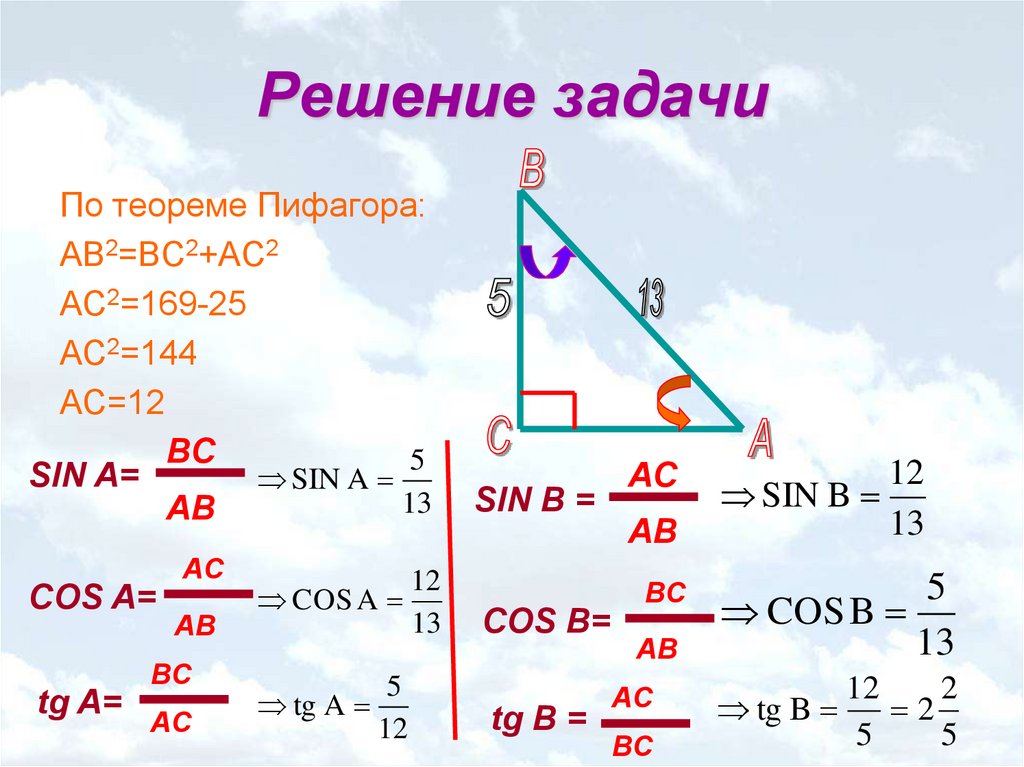 Вот почему мы решили реализовать в этом инструменте SAS и SSS, но не SSA.
Вот почему мы решили реализовать в этом инструменте SAS и SSS, но не SSA.
Закон косинусов — один из основных законов, широко используемый во многих геометрических задачах. Мы также используем этот закон во многих Omnitools, если упомянуть лишь некоторые из них:
- Калькулятор угла треугольника
- Калькулятор площади треугольника
- Калькулятор периметра треугольника
- Калькулятор с треугольной призмой
Также калькулятор закона косинусов можно совмещать с законом синусов для решения других задач, например, нахождения стороны треугольника по двум углам и одной стороне (AAS и ASA).
Доказательство закона косинусов
Есть много способов доказать уравнение уравнения косинусов. Вы уже читали об одном из них — он исходит непосредственно из формулировки закона Евклидом и применения теоремы Пифагора. Вы можете написать другие доказательства закона косинусов, используя:
1. Тригонометрия
Проведите линию для высоты треугольника и разделите перпендикулярную к ней сторону на две части:
b = b₁ + b₂
Из определений синуса и косинуса можно выразить b₁ как a × cos (γ) и b₂ = c × cos (α) . Отсюда:
Отсюда:
b = a × cos(γ) + c × cos(α) и, умножая на b , получаем:
b² = ab × cos(γ) + bc × cos(α ) (1)
Аналогичные уравнения можно вывести для двух других сторон:
a² = ac × cos(β) + ab × cos(γ) (2)
c² = bc × cos(α) + ac × cos( β) (3)
Чтобы закончить доказательство закона косинусов, нужно сложить уравнения (1) и (2) и вычесть (3):
a² + b² - c² = ac × cos(β) + ab × cos(γ) + bc × cos(α) + ab × cos(γ) - bc × cos(α) - ac × cos(β)
Сокращение и упрощение уравнения дают одну из форм правило косинусов:
a² + b² - c² = 2ab × cos(γ)
c² = a² + b² - 2ab × cos(γ)
Изменяя порядок их сложения и вычитания, можно вывести формулу другого закона косинуса.
2. Формула расстояния
Пусть C = (0,0) , A = (b,0) , как на рисунке.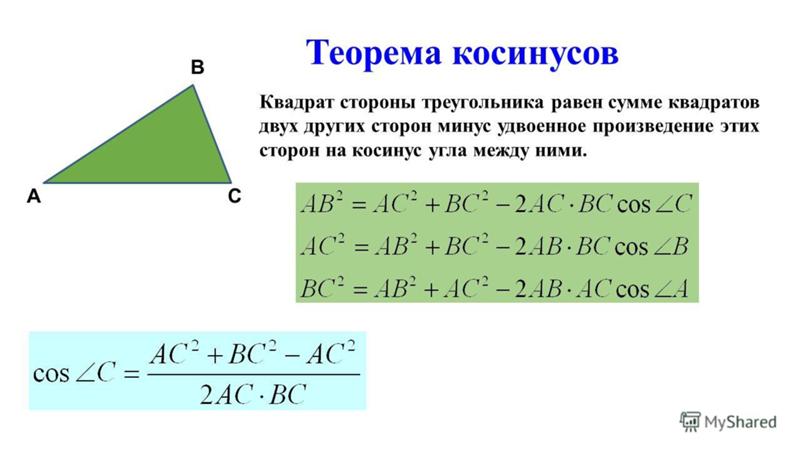
Чтобы найти координаты B, мы можем использовать определение синуса и косинуса:
B = (a × cos(γ), a × sin(γ))
Из формулы расстояния мы можем найти, что:
c = √[(x₂ - x₁)² + (y₂ - y₁)²] = √[(a × cos(γ) - b)² + ( a × sin(γ) - 0)²]
Таким образом:
c² = a² × cos(γ)² - 2ab × cos(γ) + b² + a² × sin(γ)²
c² = b² + a²(sin(γ)² + cos(γ)²) - 2ab × cos(γ)
Поскольку сумма квадратов синуса и косинуса равна 1, получаем окончательную формулу:
c² = a² + b² - 2ab × cos(γ)
3. Теорема Птолемея
Доказательство другого закона косинусов, которое относительно легко понять, использует теорему Птолемея:
Предположим, у нас есть треугольник ABC, нарисованный по описанной окружности, как показано на рисунке.
Постройте конгруэнтный треугольник ADC, где AD = BC и DC = BA
Высоты из точек B и D делят основание AC на E и F соответственно.
 CE равно FA.
CE равно FA.Из определения косинуса мы можем выразить CE как а × cos(γ) .
Таким образом, мы можем написать, что BD = EF = AC - 2 × CE = b - 2 × a × cos(γ) .
Тогда для нашего четырехугольника ADBC мы можем использовать теорему Птолемея , которая объясняет связь между четырьмя сторонами и двумя диагоналями. Теорема утверждает, что для вписанных четырехугольников сумма произведений противоположных сторон равна произведению двух диагоналей:
ВС × DA + CA × BD = AB × CD
, в нашем случае:
.a² + b × (b - 2 × a × cos(γ)) + a² = c²
После сокращения получаем окончательную формулу:
c² = a² + b² - 2ab × cos(γ))
Большим преимуществом этих трех доказательств является их универсальность — они работают для остроугольных, прямоугольных и тупоугольных треугольников.
- Использование закона синусов
- Использование определения скалярного произведения
- Сравнение площадей
- Геометрия круга
Последние два доказательства требуют различия между различными случаями треугольника. Доказательство, основанное на определении скалярного произведения, показано в другой статье, а доказательство с использованием закона синусов довольно сложное, поэтому мы решили не воспроизводить его здесь. Если вам интересно узнать об этих доказательствах закона косинусов, ознакомьтесь с объяснением в Википедии.
Как пользоваться калькулятором закона косинусов
Начните с формулирования проблемы. Например, вы можете знать две стороны треугольника и угол между ними и искать оставшуюся сторону.
Введите известные значения в соответствующие поля этого калькулятора треугольников.
 Не забудьте еще раз свериться с рисунком выше, правильно ли вы обозначили стороны и углы правильными символами.
Не забудьте еще раз свериться с рисунком выше, правильно ли вы обозначили стороны и углы правильными символами.Посмотрите, как наш калькулятор закона косинусов выполнит все расчеты за вас!
Закон косинусов – пример SSS
Если ваша задача состоит в том, чтобы найти углы треугольника по всем трем сторонам, все, что вам нужно сделать, это использовать преобразованные формулы правила косинуса:
α = arccos [(b² + c² - a²)/(2bc)]
β = arccos [(a² + c² - b²)/(2ac)]
γ = arccos [(a² + b² - c²)/(2ab)]
Вычислим один из углов. Предположим, у нас есть a = 4 дюйма, b = 5 дюймов и c = 6 дюймов. Мы будем использовать первое уравнение, чтобы найти α:
α = arccos [(b² + c² - a²)/(2bc)]
= arccos [(5² + 6² - 4²)/(2 × 5 × 6)]
= arccos [( 25 + 36 - 16)/60]
= arccos [(45/60)] = arccos [0,75]
α = 41,41°
Второй угол можно вычислить из второго уравнения аналогично, а третий угол можно найти, зная, что сумма углов треугольника равна 180° (π/2).
Если вы хотите сэкономить время, введите длины сторон в наш калькулятор закона синусов - наш инструмент - беспроигрышный вариант! Просто следуйте этим простым шагам:
Выберите вариант в зависимости от заданных значений . Нам нужно выбрать второй вариант — SSS (3 стороны) .
Введите известные значения . Введите стороны: a = 4 дюйма, b = 5 дюймов и c = 6 дюймов.
Калькулятор показывает результат! В нашем случае углы равны α = 41,41°, β = 55,77° и γ = 82,82°.
После такого объяснения мы уверены, что вы поняли, что такое закон косинуса и когда его использовать. Попробуйте этот инструмент, выполните несколько упражнений и помните, что практика делает его постоянным!
Часто задаваемые вопросы
Когда следует использовать закон косинусов?
Используйте закон косинусов, если вам нужно вычислить:
- Сторона треугольника, равная двум другим сторонам и углу между ними.

- Три угла треугольника при данных его сторонах.
- Сторона треугольника, если даны две другие стороны и угол, противолежащий одной из этих сторон.
Когда следует использовать закон косинусов против теоремы Пифагора?
Закон косинусов является обобщением теоремы Пифагора, поэтому всякий раз, когда работает последняя, можно применять и первую. Но не наоборот!
Закон косинусов справедлив только для прямоугольных треугольников?
Нет , закон косинусов справедлив для всех треугольников. На самом деле, применяя закон косинусов к прямоугольному треугольнику, вы придёте к старой доброй теореме Пифагора.
Чему равна третья сторона треугольника со сторонами 5 и 6?
Кроме двух сторон нужно знать один из внутренних углов треугольника. Допустим, это угол γ = 30° между сторонами 5 и 6 . Тогда:
- Вспомним формулу закона косинусов c² = a² + b² - 2ab × cos(γ)
- Подставьте значения a = 5 , b = 6 , γ = 30° .


 CE равно FA.
CE равно FA. Не забудьте еще раз свериться с рисунком выше, правильно ли вы обозначили стороны и углы правильными символами.
Не забудьте еще раз свериться с рисунком выше, правильно ли вы обозначили стороны и углы правильными символами.