Квадратичная функция, ее график.
1º. Функция, заданная формулой , гдеx, y– переменные,a, b, c– действительные числа, причема ≠ 0, называетсяквадратичной.
2º. Графиком функции является парабола – кривая, симметричная относительно прямой, проходящей через вершину параболы.
Координаты вершины параболы определяются по формулам:
.
Если квадратичную функцию путем выделения полного квадрата привести к виду, то точка (x0;y0) – вершина параболы.
График квадратичной функции получается из графика функциис помощью параллельного переноса.
3º. Если коэффициент a > 0, ветви параболы направлены вверх, еслиa < 0– вниз.
При
парабола пересекает ось абсцисс в двух
точках, приD=0– в одной (т.
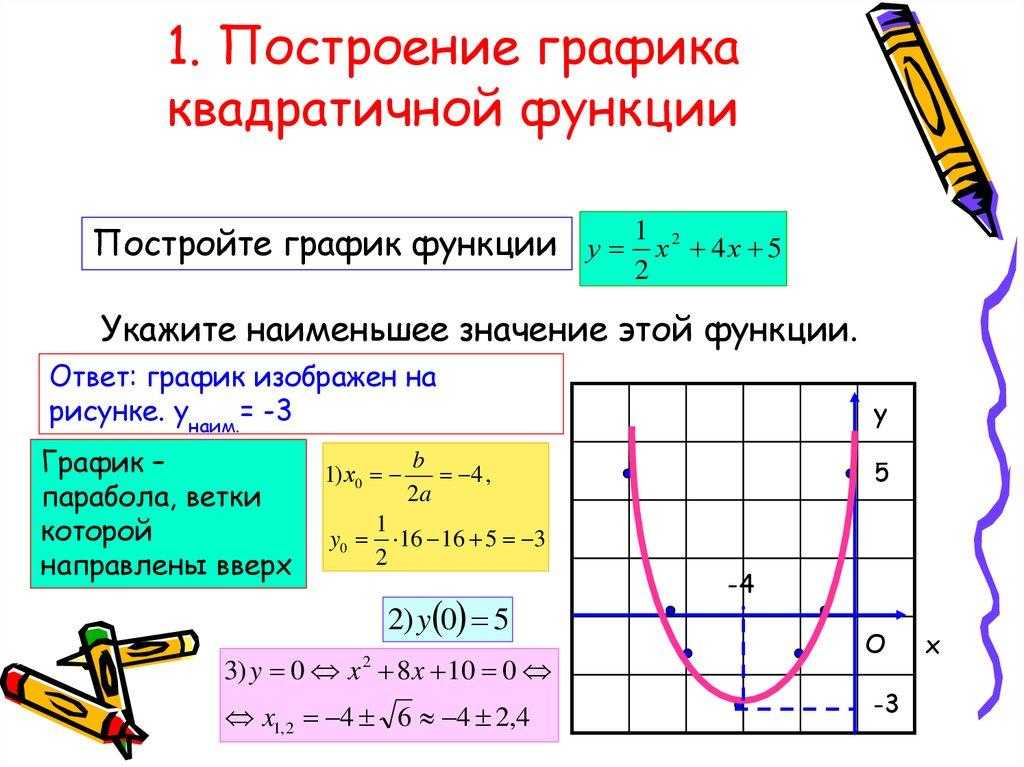
Пример 3. Построим график функции .
Выполним следующие преобразования (называемые «выделением полного квадрата»):
График функции получается из графика функциипараллельным переносом на 2 единицы влево и на две единицы вниз.
Уравнения, содержащие переменную под знаком модуля.
1º. Модуль (абсолютная величина)числааопределяется следующим образом:
.
Геометрический смысл модуля: |a| есть расстояние от точки числовой оси, изображающей данное числоа, до начала отсчета — точки О, а |x—a| есть расстояние между точками числовой оси, соответствующими числамхиа.
2º. Уравнения вида можно решать геометрически.
Рассмотрим аналитические способы решения уравнений, содержащих переменную под знаком модуля, на примерах.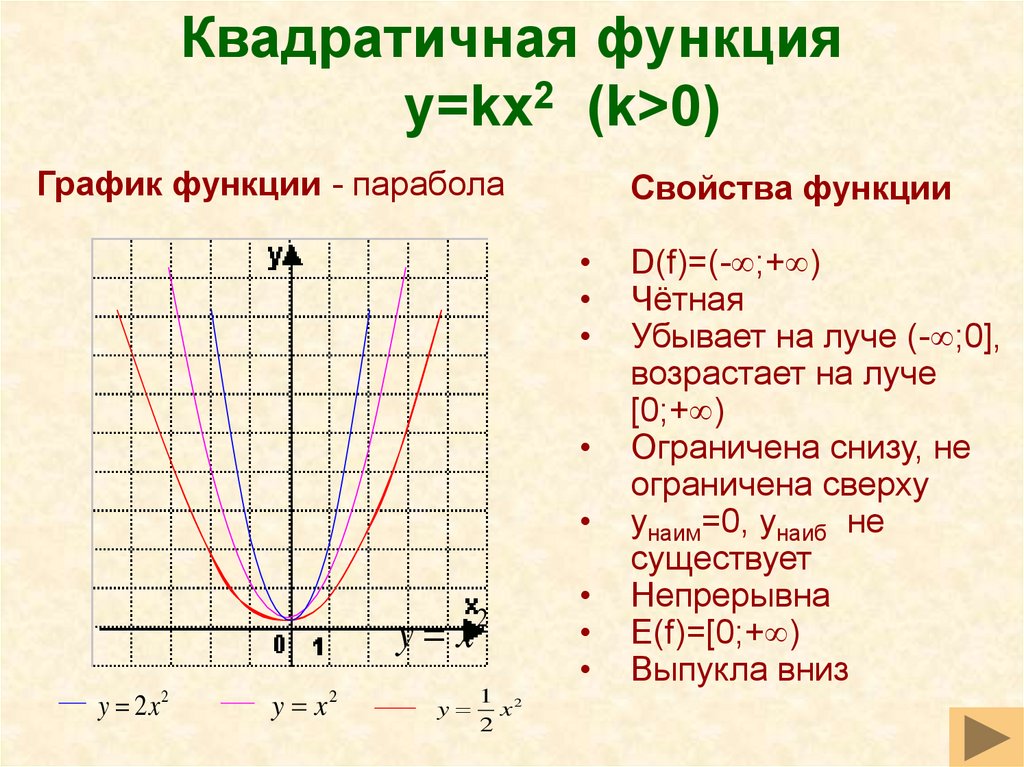
При решении уравнений важно уметь в соответствии с определением модуля освободиться от вертикальных скобок.
Например, , еслиa≥ 5;
, еслиa< 5.
Пример 4. Решим уравнение , используя определение модуля числа.
Решение: Уравнение имеет решение, если x+1≥0, т.е.x≥-1.
.
Условие x≥-1 выполняется в обоих случаях.
Ответ: 4; 2/3.
Пример 5. Решим уравнение , используя свойство модулей («модули противоположных чисел равны»).
Решение:
.
|2
|2x+1|-3=-4 => |2x+1|=-1 – нет решений.
Ответ: 3; -4.
Пример 6. Решим уравнение
,
рассматривая решения на интервалах.
Решим уравнение
,
рассматривая решения на интервалах.
Решение: Найдем нули модулей, т.е. такие значения x, при которыхи: .
Рассмотрим уравнение на интервалах (-∞; -2), [-2; -1), [-1; +∞).
а) Для уравнение примет вид:
-(x+1)-(x+2)=2; —x-1-x-2=2; -2x=5; x=-2,5;=>x=-2,5– корень уравнения.
б) Для уравнение примет вид:
-(x+1)+(x+2)=2; —x-1+x+2=2; 0·x=1- нет корней.
в) Для уравнение примет вид:
x+1+x+2=2; 2 x=-1; x=-0,5;=>x=-0,5– корень уравнения.
Ответ: -2,5; -0,5.
Дидактический материал.
Решите уравнения, сводящиеся к линейным:
1. ; 2.; 3.;
4. ; 5.;
6. ; 7.;
8. ; 9.;
10. ; 11..
Решите квадратные уравнения:
12. ; 13.;
14. ; 15.;
16. .
Разложите на линейные множители:
17. ; 18.; 19.;
; 18.; 19.;
20. ; 21..
Сократите дроби:
22. ; 23.; 24.;
25. ; 26.; 27..
Упростите выражение:
28. ; 29..
Найдите среднее арифметическое всех действительных корней уравнения:
30. ; 31.;
32. ; 33.;
34. ; 35.;
36. .
Найдите расстояние от вершины параболы до точки М:
37. ; 38.;
39. ; 39..
Постройте график функции:
40. ; 41.; 42.;
43. ; 44.; 45.;
46. ; 47.; 48.;
49. ; 50.; 51..
52. По графику квадратичной функции определить знаки ее коэффициентов и их суммы:
Найдите рациональные корни уравнения:
53. ; 54.; 55.;
56. ; 57.; 58.;
59. ; 60.; 61..
Решите уравнения:
62. ; 63.; 64.;
65. ; 66.; 67.;
68. ; 69.;
70. ; 71.; 72..
Квадратичная функция определение, свойства, формулы, уравнения и знаки корней, алгоритм построения графиков по заданным параметрам, примеры парабол
Раздел «Квадратичная функция», ее свойства и график проходят в средней школе в 8 — 9 классах. Но не все учителя объясняют доступно. А вышедшим из ученического возраста может понадобиться обновить познания.
Но не все учителя объясняют доступно. А вышедшим из ученического возраста может понадобиться обновить познания.
Поэтому рассмотрим простые примеры построения графиков квадратичной функции.
Содержание
- Определение и формула квадратичной функции
- Примеры построения парабол
- График функции при а = 1, b = c = 0
- График функции, когда b = c = 0, а > 1 и а < 1
- График функции при b = 0, с ≠0
- Общий случай a ≠0, b ≠0, c ≠0
- Пересечения с осью абсцисс (y = 0)
- Вершина
- Ось симметрии
- Приблизительный вид
- Пример построения графика
- Свойства параболы
- Заключение
Определение и формула квадратичной функции
Квадратичной называют функцию канонического вида:
Формально конструкция именуется «квадратный трехчлен». Сразу заметно, что область определения не ограничена, а четность не выявлена.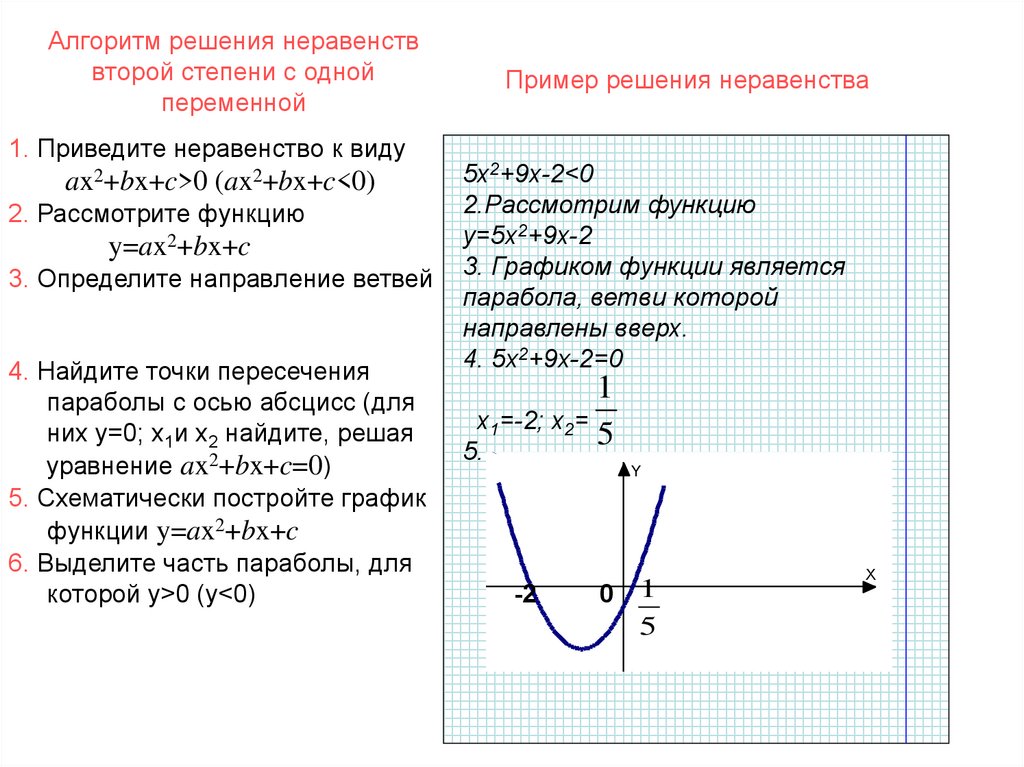
Примеры построения парабол
Займемся упрощенными случаями и подметим закономерности.
График функции при а = 1, b = c = 0
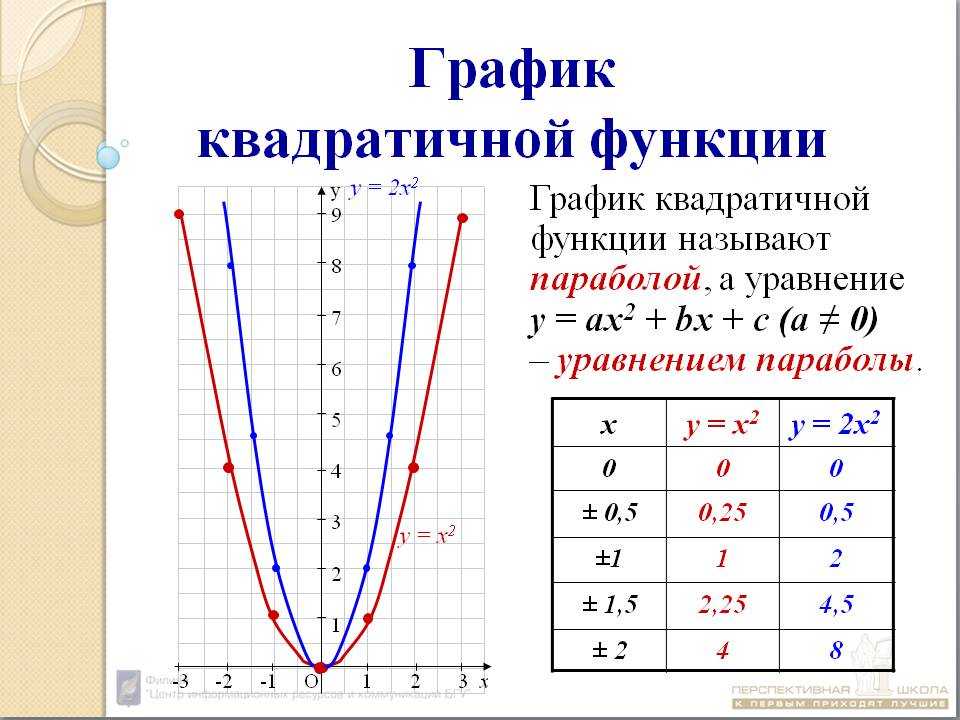
Наиболее тривиальная, но наглядная и информативная разновидность с формулой:
y = x2
Функция четная, возрастающая. Построим по точкам.
Получившаяся кривая называется «парабола». Характерна для уравнений с «квадратом».
Нижнюю точку с координатами (0; 0) называют «вершиной». Единственное место, где одной функции соответствует один аргумент. В данном случае – это минимум функции.
Уходящие вверх части кривой – «ветви». На всех участках кроме вершины к одному (y) относятся сразу (±x).
Вывод: ветви данной параболы имеют ось симметрии — вертикальную прямую ординат Y.
График функции, когда b = c = 0, а > 1 и а < 1
Кривая задается, например, так:
y = 2x2
Ветви «сожмутся» относительно оси симметрии.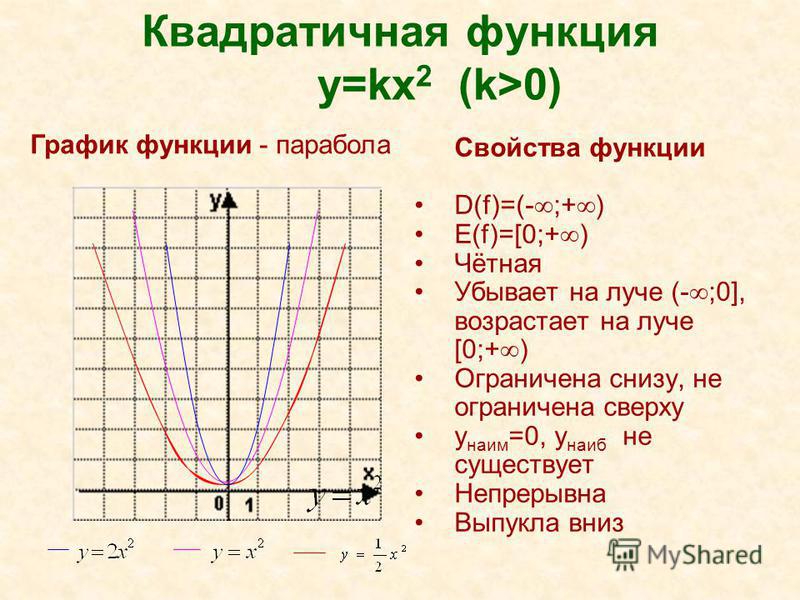
Построим другой график.
y = 0,5x2
Ветви «разойдутся».
Куда интереснее переместить коэффициент a в отрицательную область.
y = -x2
Парабола «повернется» на 180°. И вершина станет максимумом.
График функции при b = 0, с ≠0
Рассмотрим такой вариант:
y = x2 + 1
Вершина сдвинется на величину c по оси Y.
А если параметр c отрицателен? Уравнение выглядит так:
y = x2 — 1
Смещение произойдет ниже точки (0; 0).
Общий случай a ≠0, b ≠0, c ≠0
Попробуем найти характерные точки.
Пересечения с осью абсцисс (y = 0)
Иными словами, следует решить уравнение:
ax2 + bx + c = 0
Корнями уравнения будут:
Подкоренное выражение называется «дискриминант» и обозначается «D».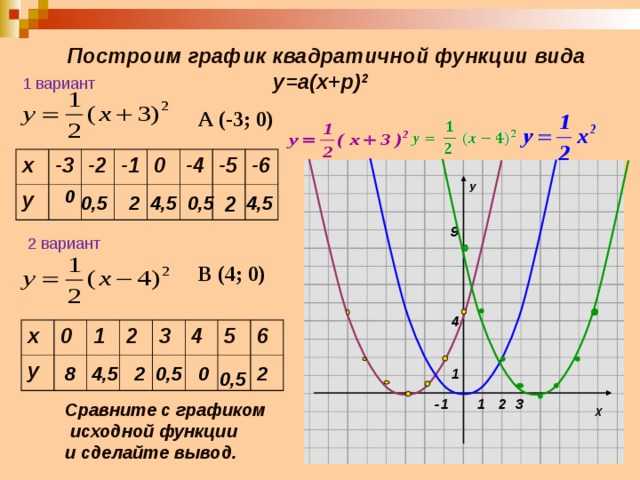
D отрицателен, D > 0. В таком случае действительные корни не существуют. Парабола не пересекает ось Х.
D положителен, D > 0. Существуют оба корня. Кривая пересекает X в двух известных местах.
D = 0. Корень один – -b/2a. Пересечение единственно. А такое возможно в одном случае: найденное означает абсциссу вершины.
Вершина
Горизонтальная координата вычисляется по формуле:
Вертикальная:
Касательная в вершине параболы совпадает с осью X или параллельна ей. Значит тангенс её относительного наклона равен 0. А это производная функции:
Нашли x0, а y0 находится подстановкой в уравнение найденного.
Ось симметрии
Параллельная оси ординат прямая x = x0.
Приблизительный вид
По уравнению можно прикинуть общую картину:
положительное значение коэффициента a говорит о направленности ветвей вверх и наоборот;
по дискриминанту определим расположение относительно X;
находим пересечения (если есть).

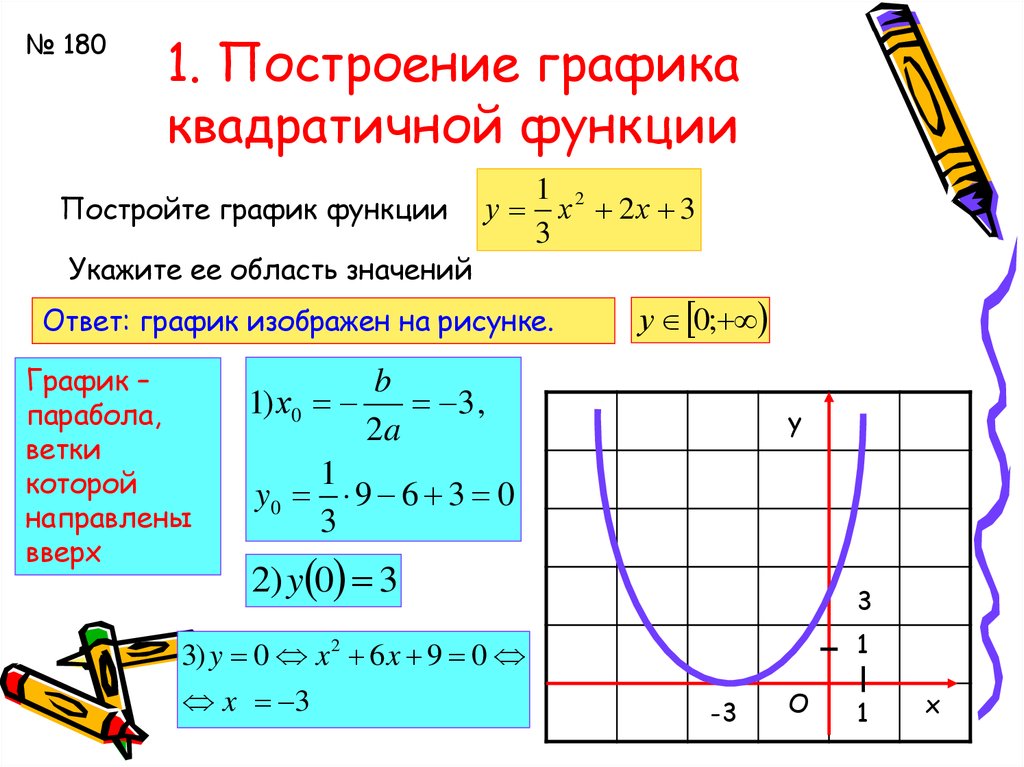
Пример построения графика
Дано:
y = x2 + 2x — 3
Проанализируем:
Алгоритм построения графика квадратичной функции:
1. Находим вершину:
2. Определяем точки пересечения с осью X:
3. Посчитав еще 2 — 3 точки правее и левее оси симметрии x = -1, получим достоверный график.
Свойства параболы
Основные свойства следующие:
Область определения – все действительные числа.
Вершина является минимумом при положительном коэффициенте x2, максимумом – при отрицательном.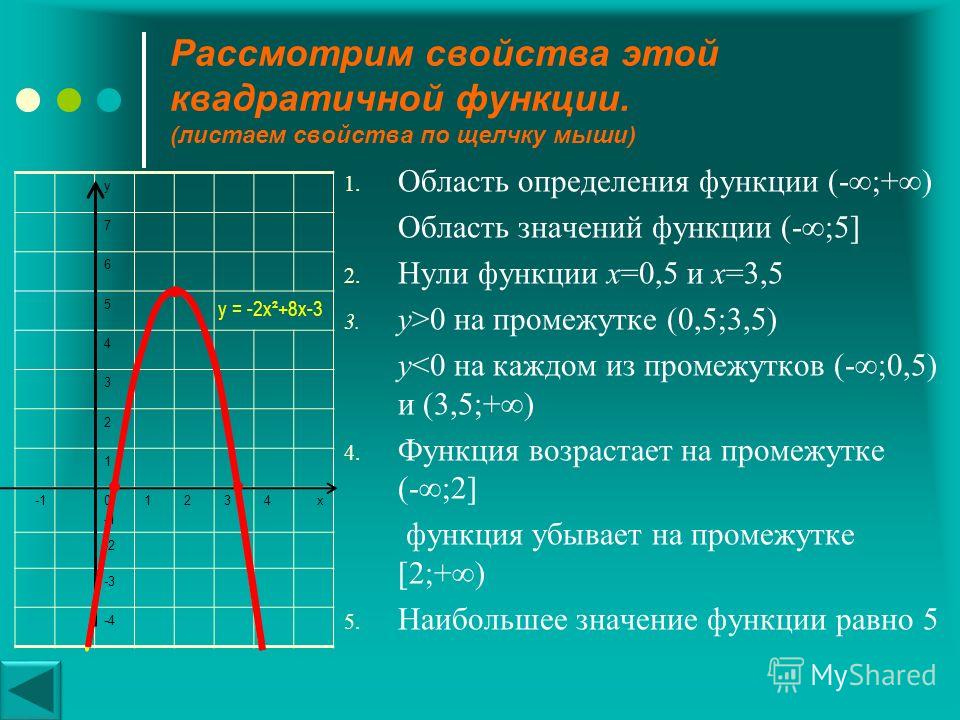
Координаты вершины зависят только от коэффициентов.
Ось симметрии проходит через вершину и параллельна оси ординат.
Заключение
В интернете существует масса онлайн-калькуляторов для облегчения работы с кривой. Приведенные же приемы и перечисленные свойства позволяют лучше понять сущность квадратичного выражения.
Параболические отражатели позволяют получать параллельный пучок света от точечного источника. Антенна такого типа позволяет концентрировать и усиливать радиосигнал. Не абстрактная линия на бумаге.
Предыдущая
АлгебраГипербола определение, свойства и виды, каноническое уравнение, формула нахождения фокуса, алгоритмы и примеры построения графика функции
Следующая
АлгебраУгол между прямыми определение, формула нахождения между скрещивающимися прямыми, методы и примеры решения задач
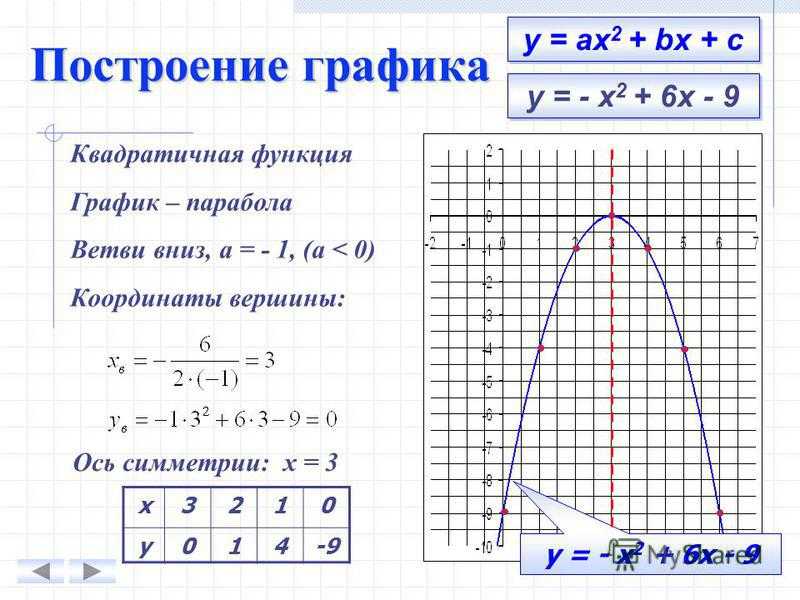
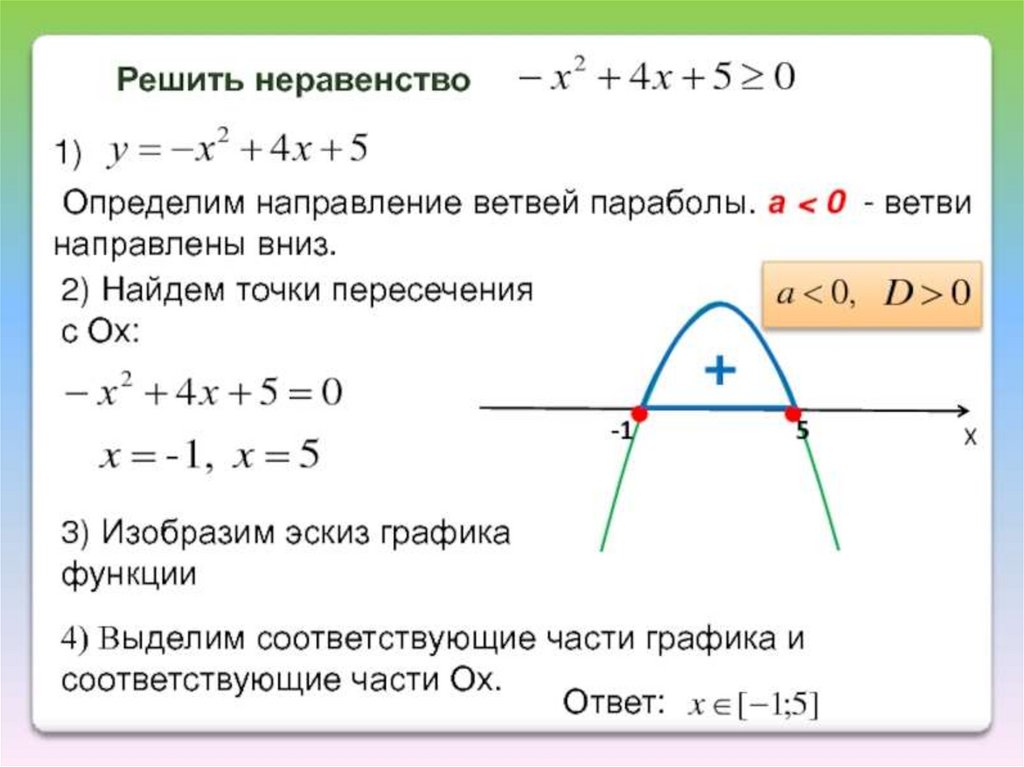
Квадратичная функция, ее график.
1º. Функция, заданная формулой , где x, y – переменные, a, b, c – действительные числа, причем а ≠ 0, называется квадратичной.
2º. Графиком функции является парабола – кривая, симметричная относительно прямой , проходящей через вершину параболы.
Координаты вершины параболы определяются по формулам:
.
Если квадратичную функцию путем выделения полного квадрата привести к виду , то точка (x0; y0) – вершина параболы.
График квадратичной функции получается из графика функции с помощью параллельного переноса.
3º. Если коэффициент a > 0, ветви параболы направлены вверх, если a < 0 – вниз.
При парабола пересекает ось абсцисс в двух точках, при D=0 – в одной (т.е. касается оси Ох), при D<0 — парабола не пересекает ось абсцисс.
Пример 3. Построим график функции .
Выполним следующие преобразования (называемые «выделением полного квадрата»):
График функции получается из графика функции параллельным переносом на 2 единицы влево и на две единицы вниз.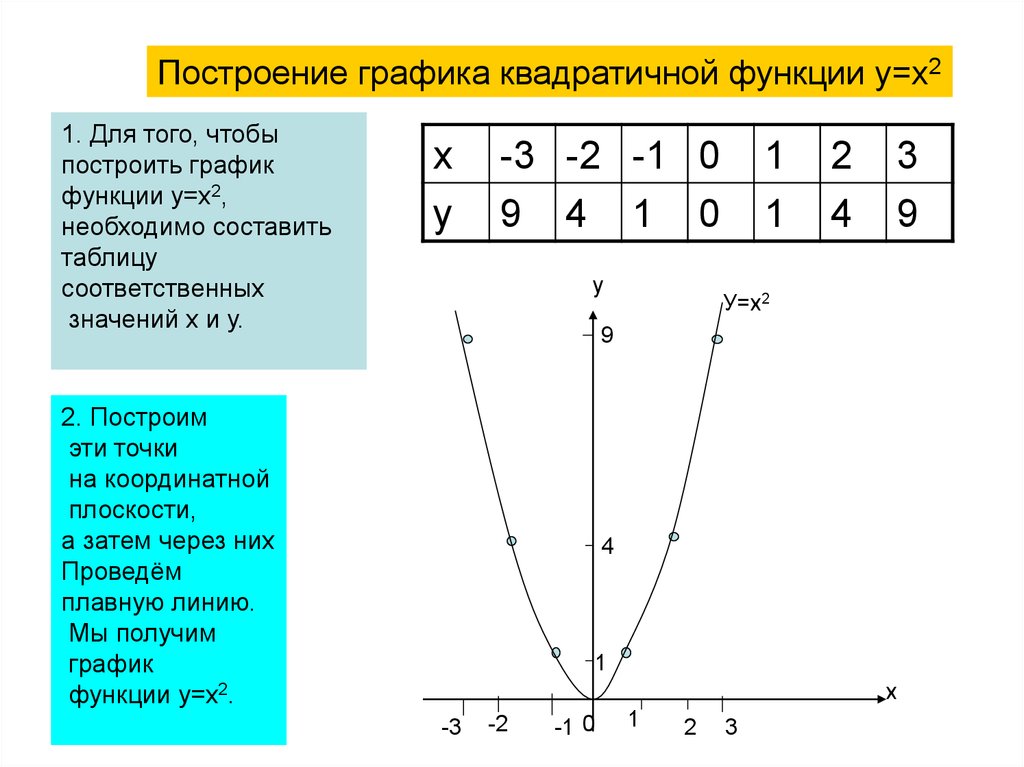
Уравнения, содержащие переменную под знаком модуля.
1º. Модуль (абсолютная величина) числа а определяется следующим образом:
.
Геометрический смысл модуля: |a| есть расстояние от точки числовой оси, изображающей данное число а, до начала отсчета — точки О, а |x-a| есть расстояние между точками числовой оси, соответствующими числам х и а.
2º. Уравнения вида можно решать геометрически.
Рассмотрим аналитические способы решения уравнений, содержащих переменную под знаком модуля, на примерах.
При решении уравнений важно уметь в соответствии с определением модуля освободиться от вертикальных скобок.
Например, , если a ≥ 5;
, если a < 5.
Пример 4. Решим уравнение , используя определение модуля числа.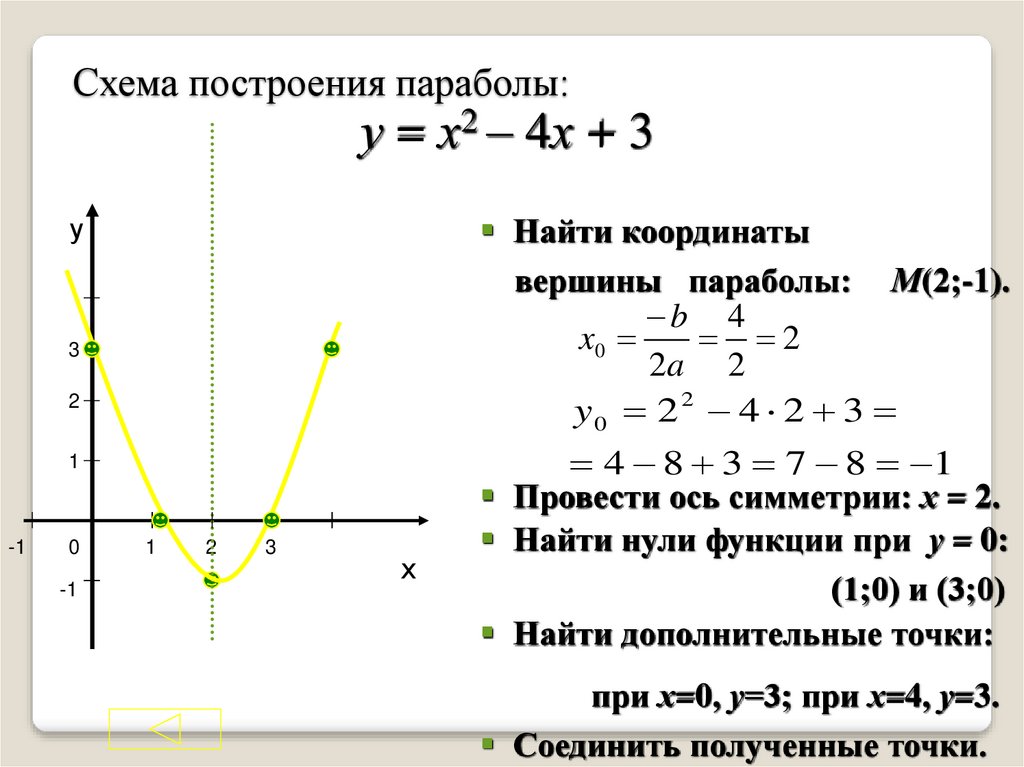
Решение: Уравнение имеет решение, если x+1≥0, т.е. x≥-1.
.
Условие x≥-1 выполняется в обоих случаях.
Ответ: 4; 2/3.
Пример 5. Решим уравнение , используя свойство модулей («модули противоположных чисел равны»).
Решение:
.
1) |2x+1|=7 => 2x+1=7 или 2x+1=-7 => x=3 или x=-4
2) |2x+1|-3=-4 => |2x+1|=-1 – нет решений.
Ответ: 3; -4.
Пример 6. Решим уравнение , рассматривая решения на интервалах.
Решение: Найдем нули модулей, т.е. такие значения x, при которых и : .
Рассмотрим уравнение на интервалах (-∞; -2), [-2; -1), [-1; +∞).
а) Для уравнение примет вид:
-(x+1)-(x+2)=2; —x-1-x-2=2; -2x=5; x=-2,5; => x=-2,5 – корень уравнения.
б) Для уравнение примет вид:
-(x+1)+(x+2)=2; —x-1+x+2=2; 0·x=1- нет корней.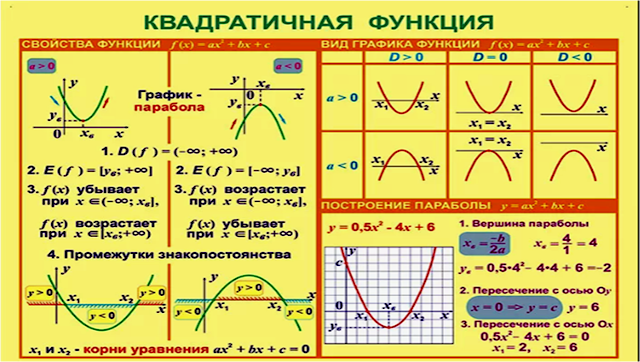
в) Для уравнение примет вид:
x+1+x+2=2; 2x=-1; x=-0,5; => x=-0,5 – корень уравнения.
Ответ: -2,5; -0,5.
Дидактический материал.
Решите уравнения, сводящиеся к линейным:
1. ; 2. ; 3. ;
4. ; 5. ;
6. ; 7. ;
8. ; 9. ;
10. ; 11. .
Решите квадратные уравнения:
12. ; 13. ;
14. ; 15. ;
16. .
Разложите на линейные множители:
17. ; 18. ; 19. ;
20. ; 21. .
Сократите дроби:
22. ; 23. ; 24. ;
25. ; 26. ; 27. .
Упростите выражение:
28. ; 29. .
Найдите среднее арифметическое всех действительных корней уравнения:
30. ; 31. ;
32. ; 33. ;
34. ; 35.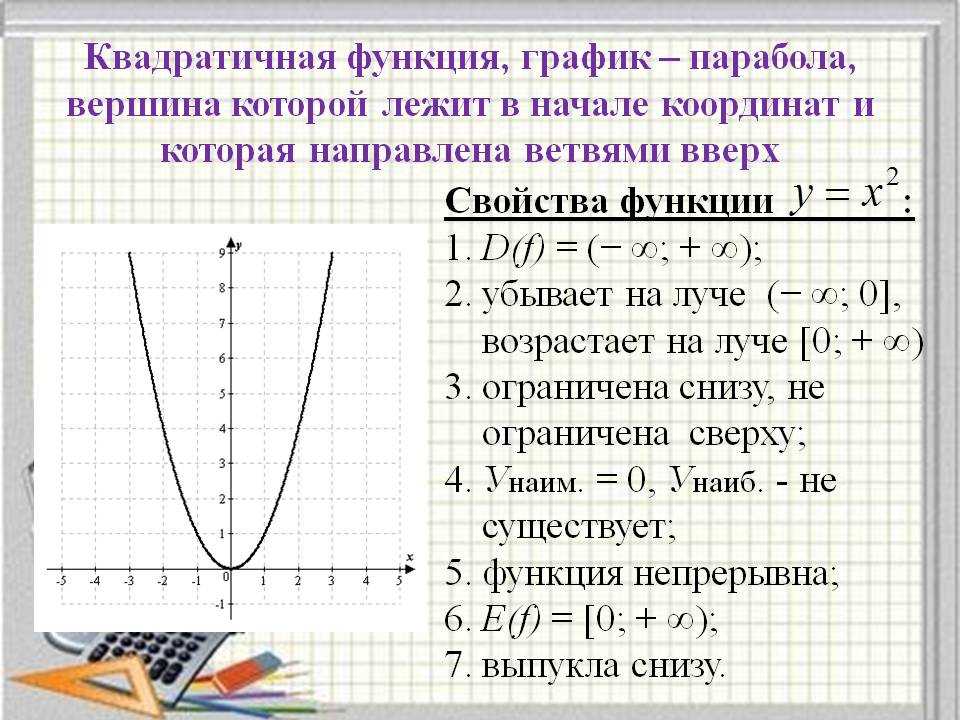 ;
;
36. .
Найдите расстояние от вершины параболы до точки М:
37. ; 38. ;
39. ; 39. .
Постройте график функции:
40. ; 41. ; 42. ;
43. ; 44. ; 45. ;
46. ; 47. ; 48. ;
49. ; 50. ; 51. .
52. По графику квадратичной функции определить знаки ее коэффициентов и их суммы:
Найдите рациональные корни уравнения:
53. ; 54. ; 55. ;
56. ; 57. ; 58. ;
59. ; 60. ; 61. .
Решите уравнения:
62. ; 63. ; 64. ;
65. ; 66. ; 67. ;
68. ; 69. ;
70. ; 71. ; 72. .
Тема №3.
Степени и корни.
Степень с целым показателем.
1º. Степенью числа а ( ) с целым показателем n называется число , определяемое следующим образом:
1) если n = 0, а ≠ 0: ;
2) если : ;
3) если а ≠ 0: .
При этом число а называется основанием степени, а число n – показателем степени. 2º. Степень с целым показателем удовлетворяет следующим свойствам:
Арифметический корень. Степень с рациональным показателем.
1º. Арифметическим корнем k-ой степени ( ) из числа а ≥ 0 называется неотрицательное число b, k-ая степень которого равна а:
2º. Замечание. Для любого действительного числа а, любого натурального числа n действуют правила:
в частности .
3º. Свойства арифметических корней. Пусть . Тогда:
1) ; 2) ; 3) ;
4) ; 5) ; 6) ;
7) .
4º. Степенью числа a с рациональным показателем определяется равенством:
Степень с рациональным показателем обладает теми же свойствами, что и степень с целым показателем.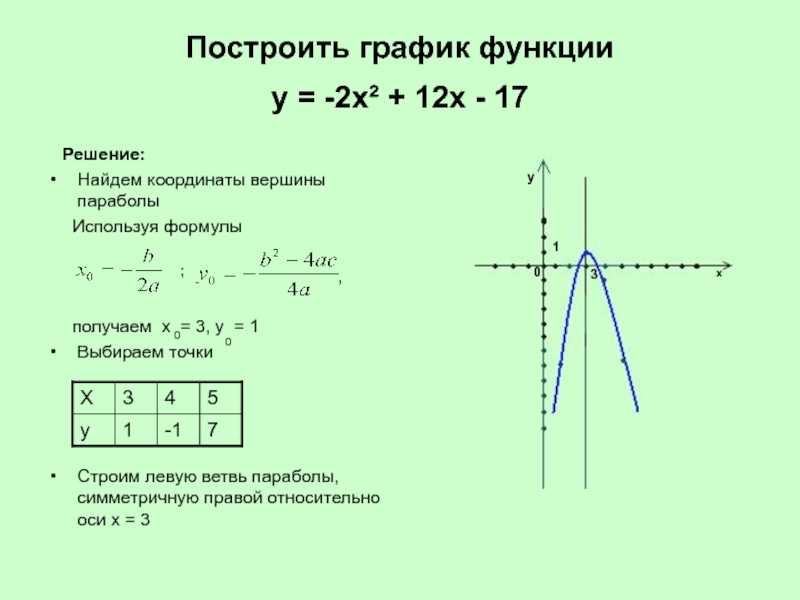
Пример 7. Упростить выражение: .
Решение. Используя определение степени и ее свойства, получим:
Формулы сокращенного умножения.
1º. Во всякого рода алгебраических преобразованиях используются формулы сокращенного умножения:
; ;
; ;
;
; .
Так, если а ≥ 0, b ≥ 0, то .
Или .
Пример 8. Вычислить .
Решение:
Ответ: 4.
Дидактический материал.
Вычислите:
1. ; 2. ; 3. ;
4. ; 5. ; 6. ;
7. ; 8. ;
9. ; 10. ;
11. ; 12. ;
13. ; 14. ; 15. .
Внесите множители под знак общего корня:
16. ; 17. ; 18. .
Упростите выражения:
19. ; 20. ; 21. ;
22. ; 23. ;
;
24. ; 25. ;
26. ;
27. .
Ответы: 19. ; 20. x + 4; 21. 0,5; 22. -1; 23. ; 24. 1; 25. 3; 26. x – y;
27. .
Тема №4.
Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычислить, когда этот…
Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам…
ЧТО ПРОИСХОДИТ ВО ВЗРОСЛОЙ ЖИЗНИ? Если вы все еще «неправильно» связаны с матерью, вы избегаете отделения и независимого взрослого существования…
Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.)…
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Квадратичная функция — стандартная форма, формула, примеры
Квадратичные функции используются в различных областях техники и науки для получения значений различных параметров.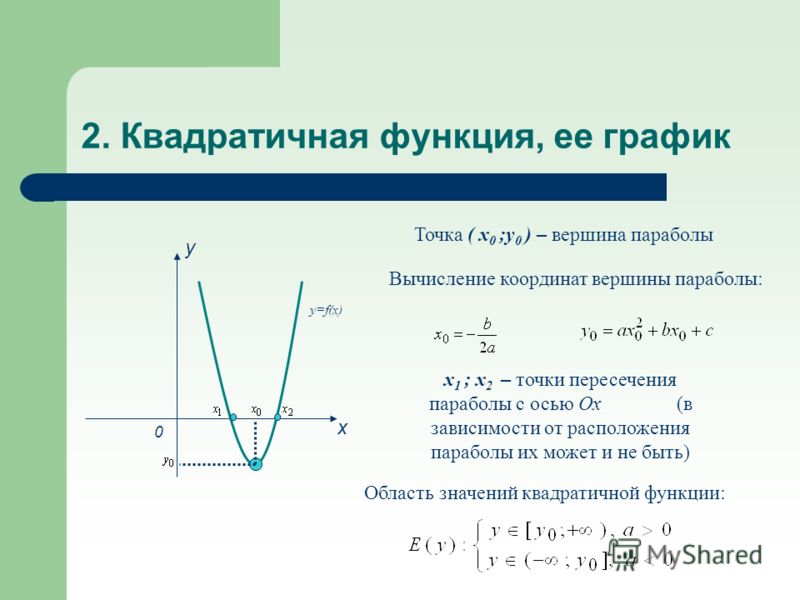 Графически они изображаются параболой. В зависимости от коэффициента высшей степени решается направление кривой. Слово «Квадрат» происходит от слова «Квадрат», что означает квадрат. Другими словами, квадратичная функция — это «полиномиальная функция степени 2». Существует множество сценариев, в которых используются квадратичные функции. Знаете ли вы, что при запуске ракеты ее траектория описывается квадратичной функцией?
Графически они изображаются параболой. В зависимости от коэффициента высшей степени решается направление кривой. Слово «Квадрат» происходит от слова «Квадрат», что означает квадрат. Другими словами, квадратичная функция — это «полиномиальная функция степени 2». Существует множество сценариев, в которых используются квадратичные функции. Знаете ли вы, что при запуске ракеты ее траектория описывается квадратичной функцией?
В этой статье мы исследуем мир квадратичных функций в математике. Вы узнаете о графиках квадратичных функций, формулах квадратичных функций и других интересных фактах по теме. Мы также будем решать примеры на основе концепции для лучшего понимания.
| 1. | Что такое квадратичная функция? |
| 2. | Стандартная форма квадратичной функции |
| 3. | Формула квадратичных функций |
| 4. | Различные формы квадратичной функции |
5. | Область и диапазон квадратичной функции |
| 6. | График квадратичной функции |
| 7. | Максимумы и минимумы квадратичной функции |
| 8. | Часто задаваемые вопросы о квадратичной функции |
Что такое квадратичная функция?
Квадратичная функция — это полиномиальная функция с одной или несколькими переменными, в которой старший показатель переменной равен двум. Поскольку высший член квадратичной функции имеет вторую степень, поэтому его также называют многочленом степени 2. Квадратичная функция имеет минимум одного члена второй степени. Это алгебраическая функция.
Родительская квадратичная функция имеет вид f(x) = x 2 и соединяет точки, координаты которых имеют вид (число, число 2 ). К этой функции можно применить преобразования, на которых она обычно имеет вид f(x) = a (x — h) 2 + k, а далее ее можно преобразовать в вид f(x) = ax 2 + бх + в.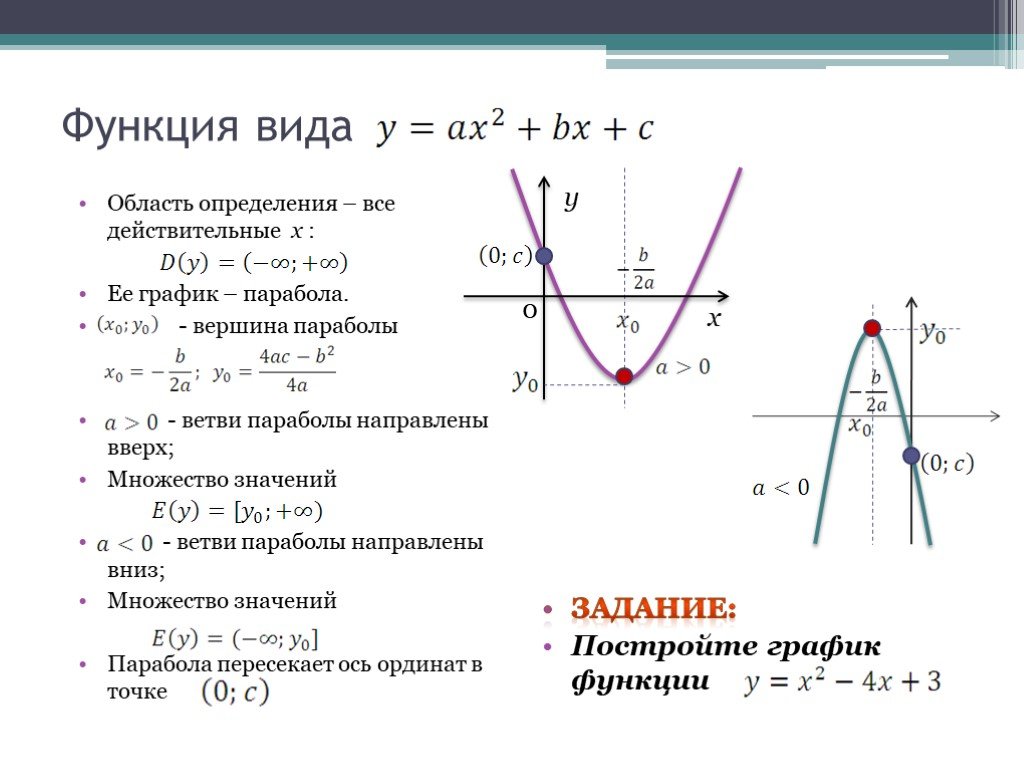 Давайте подробно изучим каждый из них в следующих разделах.
Давайте подробно изучим каждый из них в следующих разделах.
Стандартная форма квадратичной функции
Стандартная форма квадратичной функции имеет вид f(x) = ax 2 + bx + c, где a, b и c — действительные числа с a ≠ 0.
Примеры квадратичных функций
Уравнение квадратичной функции имеет вид f(x) = ax 2 + bx + c, где a ≠ 0. Рассмотрим несколько примеров квадратичных функций:
- f(x) = 2x 2 + 4x — 5; Здесь а = 2, б = 4, с = -5
- f(x) = 3x 2 — 9; Здесь а = 3, б = 0, с = -9
- f(x) = x 2 — x; Здесь а = 1, Ь = -1, с = 0
Теперь рассмотрим f(x) = 4x-11; Здесь a = 0, поэтому f(x) НЕ является квадратичной функцией.
Вершина квадратичной функции
Вершина квадратичной функции (в форме буквы U) находится там, где функция имеет максимальное или минимальное значение. Ось симметрии квадратичной функции пересекает функцию (параболу) в вершине.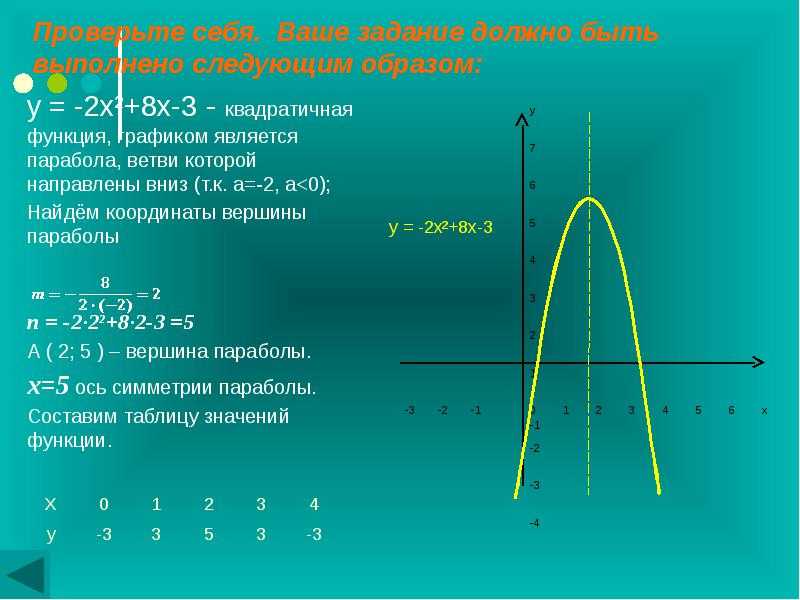
Формула квадратичных функций
Квадратичную функцию всегда можно разложить на множители, но процесс факторизации может быть затруднен, если нули выражения являются нецелыми действительными числами или недействительными числами. В таких случаях мы можем использовать квадратную формулу для определения нулей выражения. Общая форма квадратичной функции задается следующим образом: f(x) = ax 2 + bx + c, где a, b и c — действительные числа с a ≠ 0. Корни квадратичной функции f(x) можно рассчитать по формуле квадратичной функции:
- х = [-b ± √(b 2 — 4ac)] / 2a
Различные формы квадратичной функции
Квадратичная функция может иметь различные формы: стандартную форму, форму вершины и форму пересечения. Вот общие формы каждого из них:
- Стандартная форма: f(x) = ax 2 + bx + c, где a ≠ 0,
- Форма вершины: f(x) = a(x — h) 2 + k, где a ≠ 0, а (h, k) — вершина параболы, представляющая квадратичную функцию.

- Форма точки пересечения: f(x) = a(x — p)(x — q), где a ≠ 0, а (p, 0) и (q, 0) — точки пересечения по оси x параболы, представляющей квадратичную функцию.
Парабола открывается вверх или вниз в зависимости от значения ‘a’ меняется:
- Если a > 0, то парабола открывается вверх.
- Если a < 0, то парабола направлена вниз.
Мы всегда можем преобразовать одну форму в другую. Мы можем легко преобразовать форму вершины или форму перехвата в стандартную форму, просто упростив алгебраические выражения. Давайте посмотрим, как преобразовать стандартную форму в форму каждой вершины и форму пересечения.
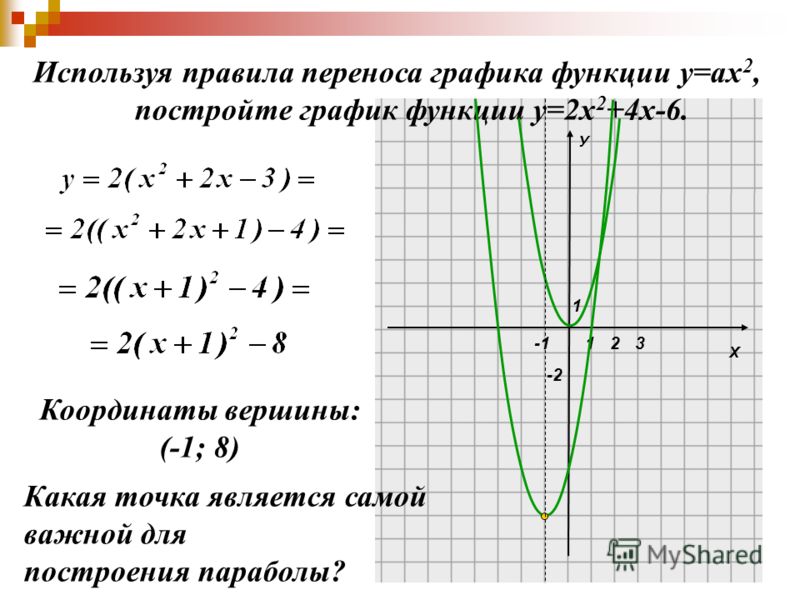
Преобразование стандартной формы квадратичной функции в вершинную форму
Квадратичная функция f(x) = ax 2 + bx + c может быть легко преобразована в вершинную форму f(x) = a (x — h) 2 + k, используя значения h = -b/2a и k = f(-b/2a). Вот пример.
Пример: Преобразовать квадратичную функцию f(x) = 2x 2 — 8x + 3 в вершинную форму.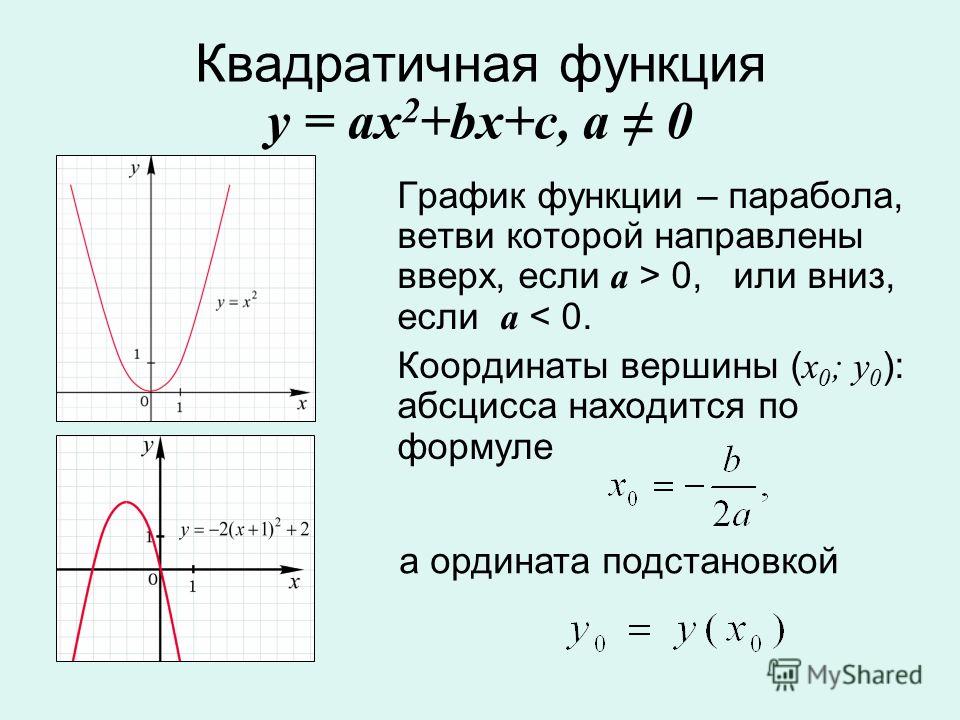
- Шаг — 1: Сравнивая данную функцию с f(x) = ax 2 + bx + c, получаем a = 2, b = -8 и c = 3.
- Шаг — 2: Найдите ‘h’ по формуле: h = -b/2a = -(-8)/2(2) = 2.
- Шаг — 3: Найдите ‘k’ по формуле: k = f(-b/2a) = f(2) = 2(2) 2 — 8(2) + 3 = 8 — 16 + 3 = -5.
- Шаг — 4: Подставляем значения в форму вершины: f(x) = 2 (x — 2) 2 — 5.
Преобразование стандартной формы квадратичной функции в форму точки пересечения
Квадратичная функция f(x) = ax 2 + bx + c может быть легко преобразована в вершинную форму f(x) = a (x — p)(x — q), используя значения p и q (x-отрезки) путем решения квадратного уравнения ax 2 + bx + c = 0.
Пример: Преобразуйте квадратичную функцию f(x) = x 2 — 5x + 6 в форму пересечения.
- Шаг — 1: Сравнивая данную функцию с f(x) = ax 2 + bx + c, получаем a = 1,
- Шаг — 2: Решите квадратное уравнение: x 2 — 5x + 6 = 0
Разложив на множители левую часть, получим
. (х — 3) (х — 2) = 0
(х — 3) (х — 2) = 0
х = 3, х = 2 - Шаг – 3: Подставьте значения в форму вычленения: f(x) = 1 (x – 3)(x – 2).
Домен и диапазон квадратичной функции
Область определения квадратичной функции — это набор всех значений x, определяющих функцию, а диапазон квадратичной функции — это набор всех значений y, которые функция получает путем замены различных значений x.
Область квадратичной функции
Квадратичная функция — это полиномиальная функция, определенная для всех действительных значений x. Итак, область определения квадратичной функции — это множество действительных чисел, то есть R. В интервальной записи областью определения любой квадратичной функции является (-∞, ∞).
Диапазон квадратичной функции
Диапазон квадратичной функции зависит от открытой стороны и вершины графика. Итак, найдите самое нижнее и самое верхнее значения f(x) на графике функции, чтобы определить диапазон квадратичной функции. Область значений любой квадратичной функции с вершиной (h, k) и уравнением f(x) = a(x — h) 2 + k равно:
Область значений любой квадратичной функции с вершиной (h, k) и уравнением f(x) = a(x — h) 2 + k равно:
- y ≥ k (или) [k, ∞), когда a > 0 (поскольку парабола раскрывается, когда a > 0).
- y ≤ k (или) (-∞, k], когда a < 0 (поскольку парабола раскрывается вниз, когда a < 0).
График квадратичной функции
График квадратичной функции представляет собой параболу. т. е. открывается вверх или вниз в форме буквы U. Вот шаги для построения графика квадратичной функции.
- Шаг — 1: Найдите вершину.
- Шаг — 2: Вычислить таблицу квадратичных функций с двумя столбцами x и y с 5 строками (мы можем взять и больше строк) с вершиной в одной из точек и взять два случайных значения по обе стороны от нее.
- Шаг — 3: Найдите соответствующие значения y, подставив каждое значение x в заданную квадратичную функцию.
- Шаг — 4: Теперь у нас есть две точки по обе стороны от вершины, поэтому, нанеся их на координатную плоскость и соединив их кривой, мы можем получить идеальную форму.
 Кроме того, расширьте график с обеих сторон. Вот график квадратичной функции.
Кроме того, расширьте график с обеих сторон. Вот график квадратичной функции.
Пример: Постройте график квадратичной функции f(x) = 2x 2 — 8x + 3.
Решение:
Сравнивая это с f(x) = ax + 2 x , b получаем a = 2, b = -8 и c = 3.
- Шаг — 1: Найдем вершину.
x-координата вершины = -b/2a = 8/4 = 2
y-координата вершины = f(-b/2a) = 2(2) 2 — 8(2) + 3 = 8 — 16 + 3 = -5.
Следовательно, вершина = (2, -5). - Шаг — 2: Создайте таблицу с вершиной, записанной в средней строке.
х и 2 -5 - Шаг — 3: Заполните первый столбец двумя случайными числами по обе стороны от 2.

х и 0 1 2 -5 3 4 - Шаг — 4: Найдите y, подставив каждое значение x в заданную квадратичную функцию. Например, когда x = 0, y = 2(0) 2 — 8(0) + 3 = 3.
х и 0 3 1 -3 2 -5 3 -3 4 3 - Шаг — 5: Просто нанесите указанные выше точки и соедините их плавной кривой.

Примечание: Мы можем построить точки пересечения по осям x и y квадратичной функции, чтобы получить более аккуратную форму графика.
График квадратичных функций также можно получить с помощью калькулятора квадратичных функций.
Максимумы и минимумы квадратичной функции
Максимумы или минимумы квадратичных функций находятся в его вершине. Его также можно найти с помощью дифференцирования. Чтобы лучше понять концепцию, давайте рассмотрим пример и решим его. Возьмем пример квадратичной функции f(x) = 3x 2 + 4x + 7.
Дифференцируя функцию,
⇒f'(x) = 6x + 4
Приравнивая к нулю,
⇒6x + 4 = 0
⇒ x = -2/3 x) = 6 > 0
Поскольку двойная производная функции больше нуля, у нас будут минимумы при x = -2/3 (по тесту второй производной), а парабола направлена вверх.
Аналогично, если двойная производная в стационарной точке меньше нуля, то функция будет иметь максимумы.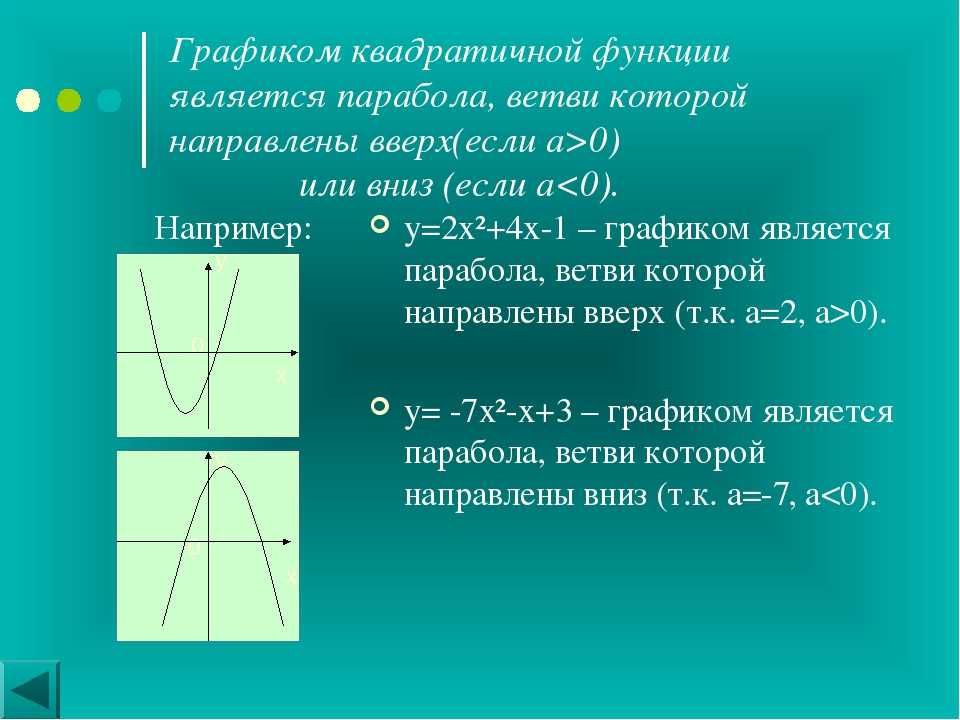 Следовательно, используя дифференцирование, мы можем найти минимум или максимум квадратичной функции.
Следовательно, используя дифференцирование, мы можем найти минимум или максимум квадратичной функции.
☛ Статьи по теме
- Калькулятор квадратных уравнений
- Калькулятор корней квадратного уравнения
Важные замечания по квадратичной функции:
- Стандартная форма квадратичной функции: f(x) = ax 2 +bx+c, где a ≠ 0,
- График квадратичной функции имеет форму параболы.
- Квадратная формула используется для решения квадратного уравнения ax 2 + bx + c = 0 и определяется как x = [-b ± √(b 2 — 4ac)] / 2a.
- Дискриминант квадратного уравнения ax 2 + bx + c = 0 равен b 2 -4ac. Это используется для определения характера нулей квадратичной функции.
Примеры квадратичной функции
Пример 1: Определить вершину квадратичной функции f(x) = 2(x+3) 2 — 2,
Решение: Имеем f(x) = 2(x+3) 2 — 2, что можно записать как f(x) = 2(x-(-3)) 2 + (-2 )
Сравнивая данную квадратичную функцию с вершинной формой квадратичной функции f(x) = a(x-h) 2 + k, где (h,k) вершина параболы, имеем
h = — 3, k = -2
Следовательно, вершина f(x) равна (-3,-2)
Ответ: Вершина = (-3,-2)
Пример 2: Найдите нули квадратичной функции f(x) = x 2 + 3x — 4, используя формулу квадратичной функции.

Решение: Квадратичная функция f(x) = x 2 + 3x — 4. Сравнивая f(x) с общей формой ax 2 + bx + c, получаем a = 1, b = 3, c = -4
Нули квадратичной функции получаются путем решения f(x) = 0.
Для этого воспользуемся квадратичной формулой: x = [ -b ± √(b 2 — 4ac) ] / 2а
х = [ -3 ± √{3 2 — 4(1)(-4)}] / 2(1) = [ -3 ± √(9 + 16) ] / 2 = [ -3 ± √25 ] / 2,
х = [ — 3 + 5 ] / 2, [ -3 — 5 ] / 2
= 1, -4
Ответ: Корни f(x) = x 2 + 3x — 4 равны 1 и -4
Пример 3: Запишите квадратичную функцию f(x) = (x-12)(x+3) в общем виде ax 2 + bx + c.
Решение: У нас есть квадратичная функция f(x) = (x-12)(x+3). Мы просто расширим (умножим биномы) его, чтобы записать в общем виде.
f(x) = (x-12)(x+3)
= x(x+3) — 12(x+3)
= x 2 + 3x — 12x — 36
= x 2 — 9x — 36
Ответ: x 2 — 9x — 36
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.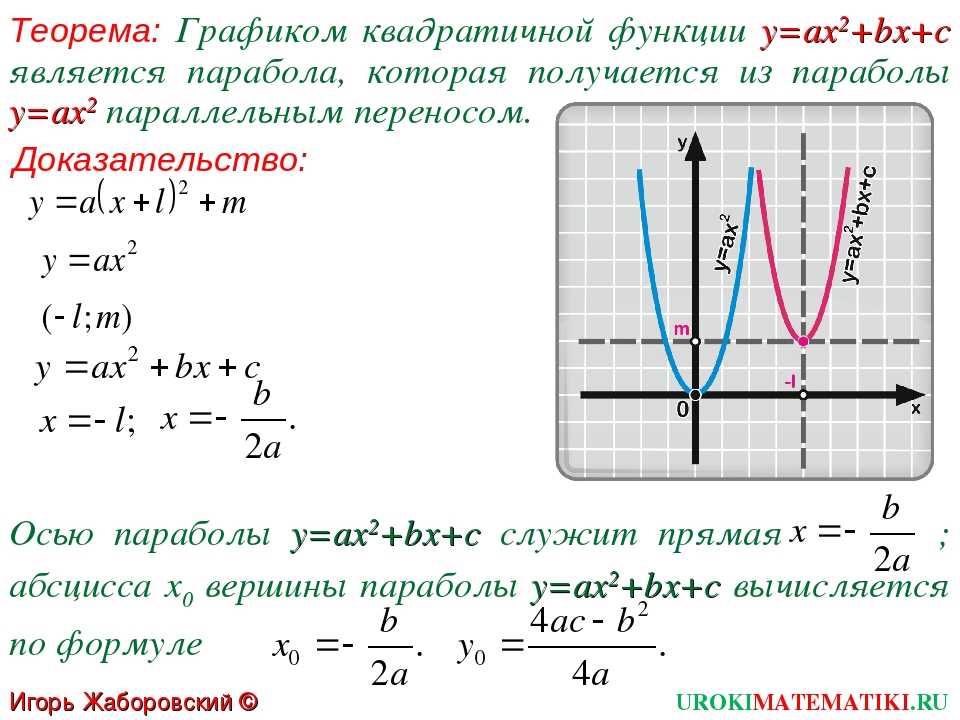
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Забронировать бесплатный пробный урок
Практические вопросы по квадратичной функции
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о квадратичной функции
Что такое квадратичная функция в математике?
Квадратичная функция — это полиномиальная функция с одной или несколькими переменными, в которой старший показатель переменной равен двум. Другими словами, квадратичная функция — это «полиномиальная функция степени 2».
Почему название квадратичной функции?
Значение «quad» означает «квадрат». Следовательно, полиномиальная функция степени 2 называется квадратичной функцией.
Что такое квадратичное функциональное уравнение?
Квадратичная функция является многочленом степени 2, поэтому уравнение квадратичной функции имеет вид f(x) = ax 2 + bx + c, где «a» — ненулевое число; a, b и c — действительные числа.
Что такое вершина квадратичной функции?
Вершина квадратичной функции — это точка, в которой парабола меняет направление и пересекает ось симметрии. Это точка, в которой парабола меняется с возрастающей на убывающую или с убывающей на возрастающую. В этой точке производная квадратичной функции равна 0,
Что такое нули квадратичной функции?
Нули квадратичной функции — это точки, в которых график функции пересекает ось x. В нулях функции координата y равна 0, а координата x представляет собой нули квадратичной полиномиальной функции. Нули квадратичной функции также называют корнями функции.
Что такое таблица квадратичных функций?
Таблица квадратичных функций — это таблица, в которой мы определяем значения координат y, соответствующие каждой координате x, и наоборот. Таблица состоит из координат графика квадратичных функций. Мы обычно записываем вершину квадратичной функции в квадратичной функции в одной из строк таблицы.
Как рисовать квадратичный график?
График квадратичной функции представляет собой параболу. Его можно нарисовать, нанеся координаты на график. Мы подставляем значения x и получаем соответствующие значения y, таким образом получая координаты графика. После нанесения координат на график, свободной рукой соединяем точки, чтобы получить график квадратичных функций. Нахождение вершины помогает в построении квадратичного графа.
Его можно нарисовать, нанеся координаты на график. Мы подставляем значения x и получаем соответствующие значения y, таким образом получая координаты графика. После нанесения координат на график, свободной рукой соединяем точки, чтобы получить график квадратичных функций. Нахождение вершины помогает в построении квадратичного графа.
Как найти точку пересечения по оси x квадратичной функции?
X-пересечение квадратичной функции можно найти, рассматривая квадратичную функцию f(x) = 0 и затем определяя значение x. Другими словами, точка пересечения с осью x есть не что иное, как нуль квадратного уравнения.
Является ли парабола квадратичной функцией?
Парабола — это график квадратичной функции. Квадратичная функция имеет вид f(x) = ax 2 + bx + c, где a не равно 0. Парабола представляет собой U-образный или перевернутый U-образный график квадратичной функции.
Как найти обратную квадратичную функцию?
Обратную квадратичную функцию f(x) можно найти, заменив f(x) на y.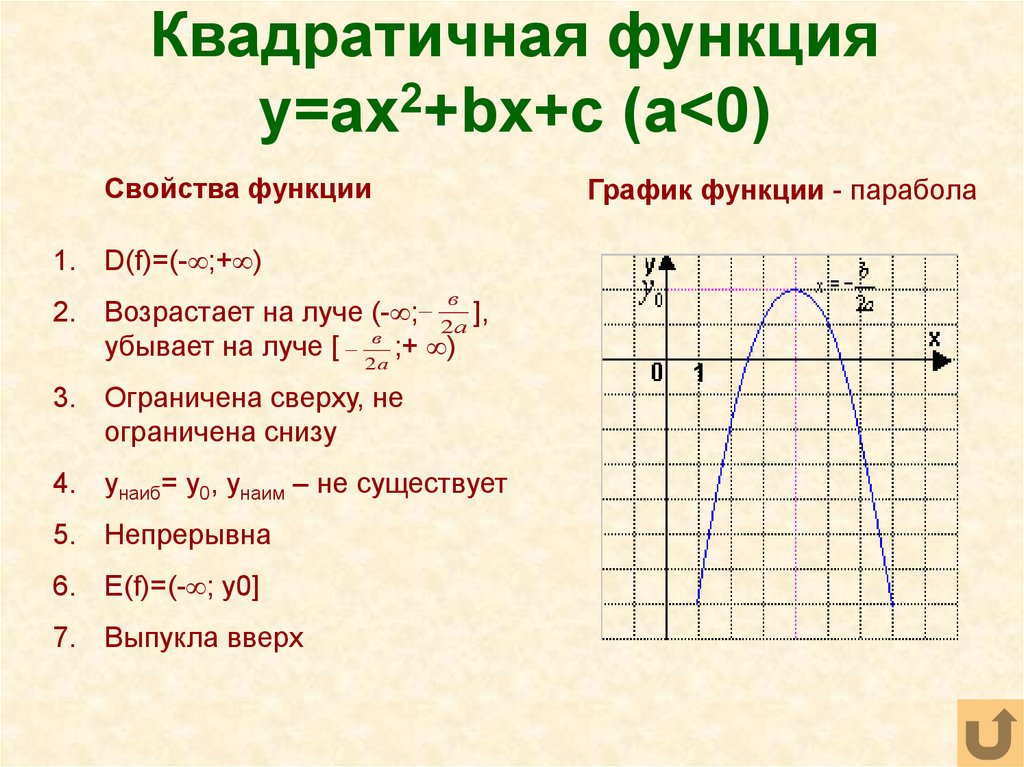 Затем мы меняем роли x и y, то есть заменяем x на y, а y на x. После этого мы решаем y относительно x, а затем заменяем y на f -1 (x), чтобы получить обратную квадратичную функцию f(x).
Затем мы меняем роли x и y, то есть заменяем x на y, а y на x. После этого мы решаем y относительно x, а затем заменяем y на f -1 (x), чтобы получить обратную квадратичную функцию f(x).
Какие формы квадратичной функции?
Квадратичная функция может иметь различные формы: стандартную форму, форму вершины и форму пересечения. Вот общие формы каждого из них:
- Стандартная форма: f(x) = ax 2 + bx + c, где a ≠ 0,
- Форма вершины: f(x) = a(x — h) 2 + k, где a ≠ 0, а (h, k) — вершина параболы, представляющая квадратичную функцию.
- Форма точки пересечения: f(x) = a(x — p)(x — q), где a ≠ 0, а (p, 0) и (q, 0) — точки пересечения по оси x параболы, представляющей квадратичную функцию.
Мы можем преобразовать одну из этих форм в другие формы. Нажмите сюда, для получения дополнительной информации.
В чем разница между квадратичной функцией и квадратным уравнением?
Квадратичная функция имеет вид f(x) = ax 2 + bx + c, где a ≠ 0.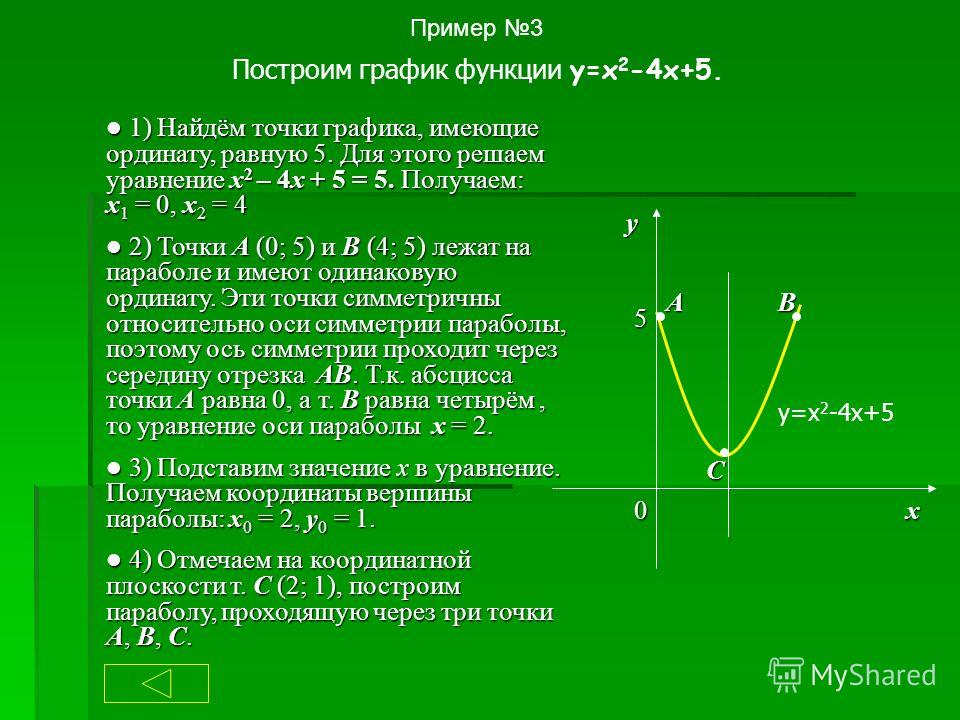 Каждая точка на ее графике имеет вид (x, ax 2 + bx + c). Это для графической цели. С другой стороны, квадратное уравнение имеет форму ax 2 + bx + c = 0, где a ≠ 0. Это нужно для нахождения решения, и оно дает определенные значения x в качестве решения.
Каждая точка на ее графике имеет вид (x, ax 2 + bx + c). Это для графической цели. С другой стороны, квадратное уравнение имеет форму ax 2 + bx + c = 0, где a ≠ 0. Это нужно для нахождения решения, и оно дает определенные значения x в качестве решения.
10.3 – Применение квадратичных функций
Цели обучения
- (10.3.1) – Решение прикладных задач с квадратичными функциями
- Объекты в свободном падении
- Определение ширины границы
- Нахождение максимального и минимального значения квадратичной функции
Квадратные уравнения широко используются в науке, бизнесе и технике. Квадратные уравнения обычно используются в ситуациях, когда две вещи перемножаются, и обе они зависят от одной и той же переменной. Например, при работе с площадью, если оба измерения записываются в терминах одной и той же переменной, вы используете квадратное уравнение. Поскольку количество проданного продукта часто зависит от цены, иногда вы используете квадратное уравнение, чтобы представить доход как произведение цены и проданного количества.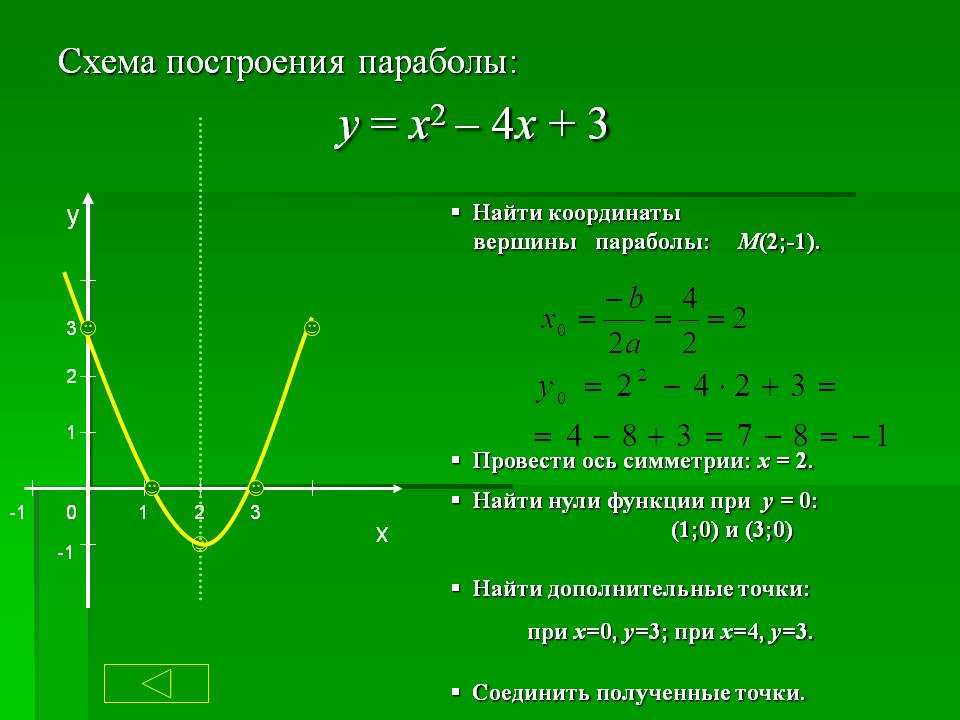 Квадратные уравнения также используются, когда задействована сила тяжести, например, траектория движения мяча или форма тросов подвесного моста.
Квадратные уравнения также используются, когда задействована сила тяжести, например, траектория движения мяча или форма тросов подвесного моста.
Объекты в свободном падении
Очень распространенное и простое для понимания приложение — высота мяча, брошенного на землю со здания. Поскольку гравитация будет увеличивать скорость мяча при падении, можно использовать квадратное уравнение для оценки его высоты в любое время до того, как он упадет на землю. Примечание. Уравнение не совсем точное, поскольку трение о воздух немного замедляет мяч. Для наших целей это достаточно близко.
В следующем видео мы покажем еще один пример того, как можно использовать квадратное уравнение для определения времени, которое требуется объекту в свободном падении, чтобы удариться о землю. 9{2}+96t+112[/латекс].
а. Когда камень достигает максимальной высоты?
б. Какова максимальная высота скалы?
в. Когда камень падает в океан?
Решение
Применение квадратичных функций: определение ширины границы
Приведенная ниже задача площади не выглядит так, как будто она включает в себя квадратичную формулу любого типа, и кажется, что эту задачу вы уже много раз решали простым умножением. Но для того, чтобы решить ее, вам нужно будет использовать квадратное уравнение.
Но для того, чтобы решить ее, вам нужно будет использовать квадратное уравнение.
Вот видео, в котором показан еще один пример использования квадратичной формулы для решения геометрической задачи, включающей границу вокруг стеганого одеяла.
Нахождение максимального и минимального значения квадратичной функции
Существует множество реальных сценариев, в которых требуется найти максимальное или минимальное значение квадратичной функции, например приложения, связанные с площадью и доходом.
ПРИМЕР
Найдите два числа [латекс]х[/латекс] и [латекс]у[/латекс], разность которых равна 100 и произведение которых является минимальным.
Показать ответ
Пример: нахождение максимального значения квадратичной функции
Фермер хочет выделить прямоугольное пространство для нового сада на своем огороженном заднем дворе. Она купила 80 футов проволочного ограждения, чтобы огородить три стороны, и она будет использовать часть забора заднего двора в качестве четвертой стороны.
Она купила 80 футов проволочного ограждения, чтобы огородить три стороны, и она будет использовать часть забора заднего двора в качестве четвертой стороны.
- Найдите формулу площади ограждения, если стороны ограждения, перпендикулярные существующему ограждению, имеют длину [латекс]L[/латекс].
- Каких размеров она должна сделать свой сад, чтобы увеличить огороженную площадь?
Решение
Как сделать: Учитывая приложение, связанное с доходом, используйте квадратное уравнение, чтобы найти максимум.
- Напишите квадратное уравнение для дохода.
- Найдите вершину квадратного уравнения.
- Определите значение [latex]y[/latex] вершины.
Пример: Определение максимального дохода
Цена за единицу товара влияет на его спрос и предложение. То есть, если цена за единицу растет, спрос на товар обычно снижается. Например, местная газета в настоящее время имеет 84 000 подписчиков при ежеквартальной оплате в размере 30 долларов.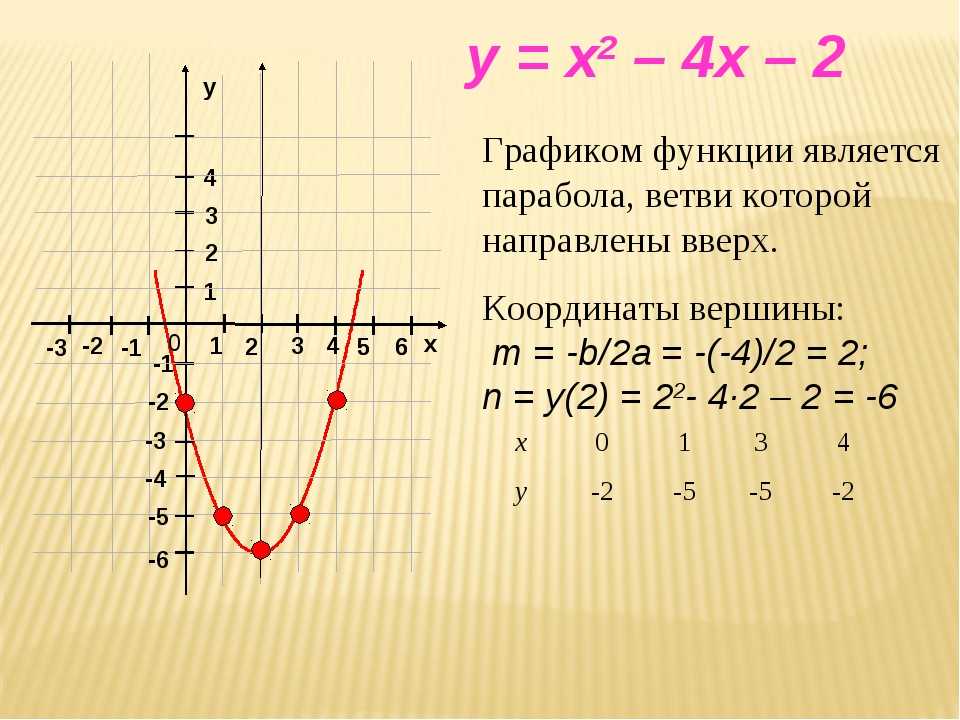 Исследование рынка показало, что если владельцы поднимут цену до 32 долларов, они потеряют 5000 подписчиков. Предполагая, что подписка линейно связана с ценой, какую цену должна взимать газета за ежеквартальную подписку, чтобы максимизировать свой доход?
Исследование рынка показало, что если владельцы поднимут цену до 32 долларов, они потеряют 5000 подписчиков. Предполагая, что подписка линейно связана с ценой, какую цену должна взимать газета за ежеквартальную подписку, чтобы максимизировать свой доход?
Решение
Попробуйте
Координатная сетка наложена на квадратичную траекторию баскетбольного мяча на рисунке ниже. Найдите уравнение траектории мяча. Стрелок попадает в корзину?
(кредит: модификация работы Дэна Мейера)
Решение
Когда квадратное уравнение имеет одно решение? (3 способа сказать) – JDM Educational
При работе с квадратными уравнениями мы часто видим либо два действительных решения, либо два сложных решения. Однако также возможно, что квадратное уравнение будет иметь ровно одно решение.
Итак, когда квадратное число имеет одно решение? Квадратное уравнение имеет одно решение, когда дискриминант равен нулю.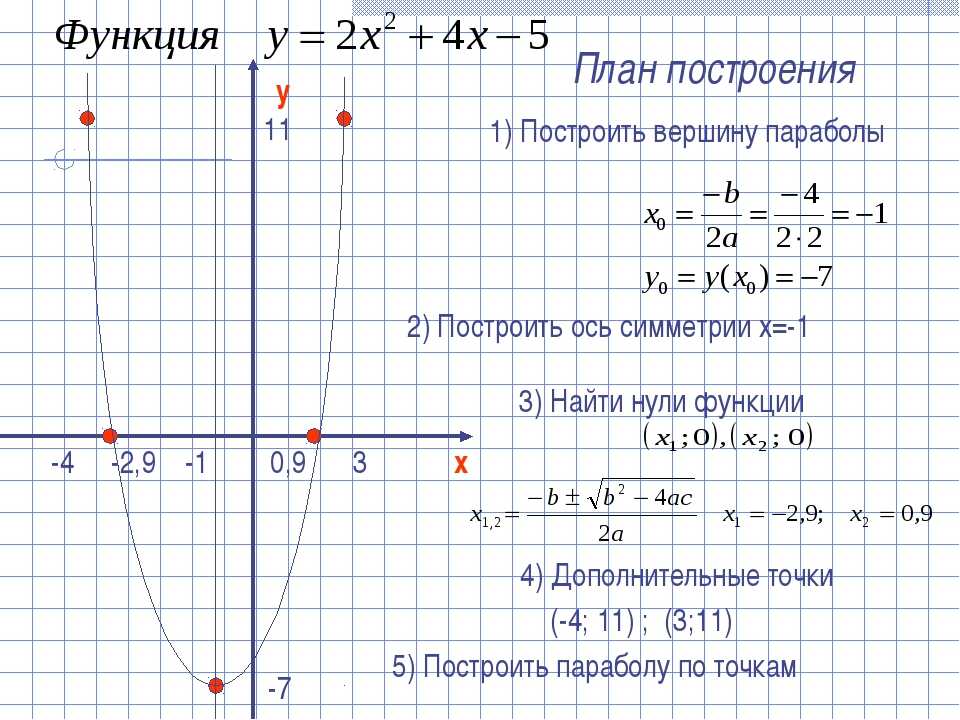 С точки зрения алгебры это означает b 2 = 4ac. Визуально это означает, что граф квадратичного уравнения (параболы) будет иметь вершину, покоящуюся на оси x.
С точки зрения алгебры это означает b 2 = 4ac. Визуально это означает, что граф квадратичного уравнения (параболы) будет иметь вершину, покоящуюся на оси x.
Конечно, мы также можем посмотреть на коэффициенты в квадратном уравнении, чтобы определить, имеет ли оно одно решение.
В этой статье мы поговорим о том, как определить, что квадратное число имеет одно решение. Мы также рассмотрим несколько примеров, а также то, как написать квадратное уравнение, если оно имеет только одно решение.
Начнем.
Когда квадратное уравнение имеет одно решение?
Есть несколько способов определить, имеет ли квадратное уравнение одно решение:
- Посмотрите на дискриминант — если он равен нулю, у квадратного уравнения есть только одно решение.
- Посмотрите на график – если вершина параболы опирается на ось абсцисс, есть только одно решение квадратного уравнения.
- Посмотрите на коэффициенты — есть специальный шаблон, который подскажет, когда есть только одно решение квадратного уравнения (подробнее об этом далее в статье!)
Начнем с метода, использующего дискриминант.
Посмотрите на дискриминант
Первый способ узнать, имеет ли квадратное уравнение одно решение, это посмотреть на дискриминант. Если дискриминант равен нулю, то квадратное уравнение имеет только одно действительное решение.
Дискриминантом является выражение b 2 – 4ac под радикалом в квадратичной формуле. Его знак может сказать нам о характере решений соответствующего квадратного уравнения.Помните, что для квадратного уравнения
- ax 2 + bx + c = 0
дискриминант есть выражение b 2 94070 – 0 . Дискриминант – это выражение под знаком радикала в квадратичной формуле:
Дискриминант – это выражение под знаком радикала в квадратичной формуле.Чтобы получить дискриминант нуля, нам нужно установить b 2 – 4ac равным нулю. Это дает нам:
- B 2 — 4AC = 0
- B 2 = 4AC
Вот один пример квадратичного уравнения только с одним решением:
- x 9009 2 7070707070 2 .
 9
9
В этом случае a = 1, b = -6 и c = 9. Это дает нам:
- b 2 = (-6) 2 = 364
- 98 90 = 4(1)(9) = 36
Итак, b 2 = 4ac, и, таким образом, дискриминант равен нулю. Это означает, что квадратное уравнение имеет только одно решение: x = 3,9.0005
Это решение можно найти с помощью квадратичной формулы. Вы также можете найти его, разложив квадратное число на множители:
- x 2 – 6x + 9 = (x – 3)(x – 3)
Посмотрите на график
имеет одно решение — посмотреть на график квадратичного уравнения. Для любого квадратного уравнения его графиком будет парабола .
Помните, что ключевой особенностью параболы является ее вершина. Вершина параболы похожа на «вершину горы» (для отрицательных значений а) или «дно долины» (для положительных значений а).
Как видите, квадратичная функция f(x) = x 2 – 4x + 4 имеет вершину (дно долины) на оси x в точке x = 2. Это означает, что квадратное уравнение имеет одно действительное решение.
Это означает, что квадратное уравнение имеет одно действительное решение.Как вы можете видеть на графике выше, вершина (дно впадины) этой параболы лежит на оси x. Это означает, что квадратное уравнение x 2 – 4x + 4 имеет одно действительное решение (при x = 2).
Будьте осторожны: чтобы квадратное уравнение имело только одно действительное решение (двойной корень), его график должен касаться оси x ровно один раз .
Если график дважды касается оси x, то он имеет два различных действительных решения.
Если график вообще не касается оси x, то он имеет два комплексных решения (и никаких действительных решений).
Посмотрите на коэффициенты
Вы также можете посмотреть на коэффициенты квадратного уравнения в стандартной форме, чтобы определить, имеет ли оно единственное действительное решение. Помните, что стандартная форма квадратного уравнения имеет ноль с одной стороны и члены в порядке убывания с другой:
- ax 2 + bx + c = 0
Здесь можно иметь дело с двумя возможными случаями: либо a = 1, либо a не равно 1.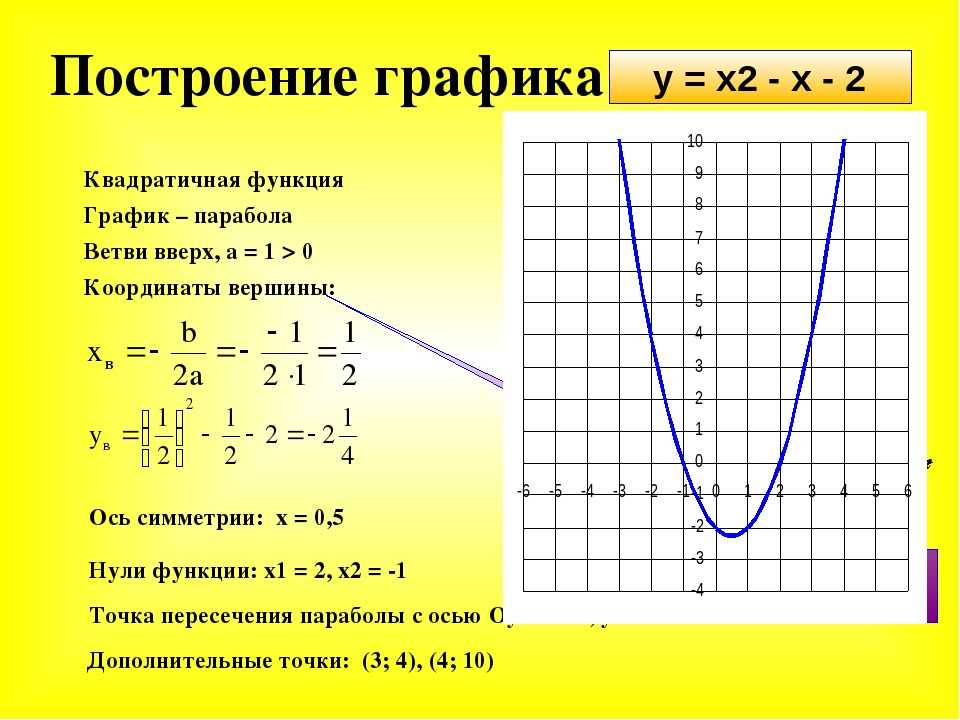
Когда коэффициент x
2 равно 1 (a = 1)В этом случае мы ищем c = b 2 / 4. Если это так, то квадратное уравнение имеет одно решение: x = -b / 2.
Например, квадратное уравнение x 2 + 8x + 16 имеет одно решение. В этом случае a = 1, b = 8 и c = 16. Тогда имеем:
- B 2 /4
- = 8 2 /4
- = 64 /4
- = 16
, как это значение. Одно решение: P
- x = -b / 2
- x = -8/2
- x = -4
Мы также можем найти это квадратичное решение, разложив его на множители:
- х 2 + 8х + 16 = (х + 4)(х + 4)
, что дает нам решение x = -4 (действительный повторяющийся корень). Мы также можем использовать квадратичную формулу с a = 1, b = 8 и c = 16, чтобы получить тот же результат x = -4.
Когда коэффициент x
2 не равен 1 (a не равно 1)В этом случае разделите все квадратное уравнение на a. Тогда вы находитесь в первом случае, когда коэффициент при х 2 равен 1.
Например, рассмотрим уравнение:
- 2x 2 + 12x + 18 = 0
Поскольку a = 2, мы разделим обе части на 2. 0
Для этого нового квадратного уравнения мы имеем a = 1, b = 6 и c = 9.
Тогда мы имеем:
- b 2 / 4 5 = 6 9209035 / 4
- = 36 / 4
- = 9
- x 2 + 6x + 9 = (x + 3)(x + 3)
- The quadratic coefficient (x 2 coefficient) means a
- The linear coefficient (x coefficient) means b
- The constant coefficient means c
- x 2 + 2x + 1 = 0 (решение: x = -1)
- x 2 + 4x + 4 = 0 (решение: x = -2) 2 + 6x + 9 = 0 (решение: x = -3)
- x 2 + 8x + 16 = 0 (решение: x = -4)
- x + 2 + 5 = 0 (решение: x = -5)
- 2, 4, 6, 8 и 10
- 1, 4, 9, 16 и 25
- Сначала выберите целое число n. Помните, что целое число не имеет дробей или десятичных знаков. Для этого примера я выбираю n = 7.
- Затем вычислите 2n. Это будет значение b. Для этого примера b = 2n = 2*7 = 14.
- Затем вычислите n 2 . Это будет значение c. Для этого примера c = n 2 = 7 2 = 49.
- Наконец, ваше квадратное число с одним решением имеет a = 1, b = 2n и c = n 2 .
 Таким образом, квадратное число будет выглядеть как x 2 + 2n + n 2 . Решение будет –n (отрицательное целое число n, которое вы выбрали в начале).
Таким образом, квадратное число будет выглядеть как x 2 + 2n + n 2 . Решение будет –n (отрицательное целое число n, которое вы выбрали в начале). - x 2 — 2x + 1 = 0 (решение: x = 1)
- x 2 — 4x + 4 = 0 (решение: x = 2)
- x 2 – 6x + 9 = 0 (решение: x = 3)
- x 2 – 8x + 16 = 0 (решение: x = 4)
- x 2 – 10×0 (решение = 25 : x = 5)
- (x – n)(x – n) = 0
- (x — 3) (x — 3) = 0
- x 2 — 6x + 9 = 0
- 2x 2 – 12x + 18 = 0 (умножить на 2)
- 3x 2 — 18x + 27 = 0 (умноженное на 3)
- 4x 2 — 24x + 36 = 0 (умноженное на 4)
- 5x 2 — 30x + 45 = 0 (Умнозировано 5)
- Если дискриминант положительный, существует ровно 2 действительных решения (они различны, то есть мы получаем два разных действительных числа в качестве решений).
- Если дискриминант равен нулю, существует ровно одно действительное решение (повторяющийся корень: одно и то же действительное число появляется в качестве решения дважды).

- Если дискриминант отрицательный, то комплексных решений ровно 2 (они различны и являются комплексно-сопряженными).
, что совпадает со значением c. Единственное решение: x = -b / 2 = -6 / 2 = -3.
Мы также можем найти это решение, разложив квадратное выражение на множители:
, что дает нам решение x = — 3 (действительный кратный корень). Мы также можем использовать квадратичную формулу с a = 1, b = 6 и c = 9, чтобы получить тот же результат x = -3.
Мы также можем использовать квадратичную формулу с a = 1, b = 6 и c = 9, чтобы получить тот же результат x = -3.
Помните, что вы всегда можете воспользоваться калькулятором, чтобы проверить решения квадратного уравнения. Вы также можете использовать решатель квадратных уравнений, такой как этот от WolframAlpha.
For WolframAlpha’s calculator, remember that:
Примеры квадратных уравнений с одним решением
Вот несколько примеров квадратных уравнений с одним решением. Посмотрите на них, чтобы увидеть, заметили ли вы шаблон , прежде чем читать дальше.
Вы можете заметить, что все коэффициенты x (значения b) являются четными числами:
Они получаются путем удвоения чисел 1, 2, 3, 4 и 5.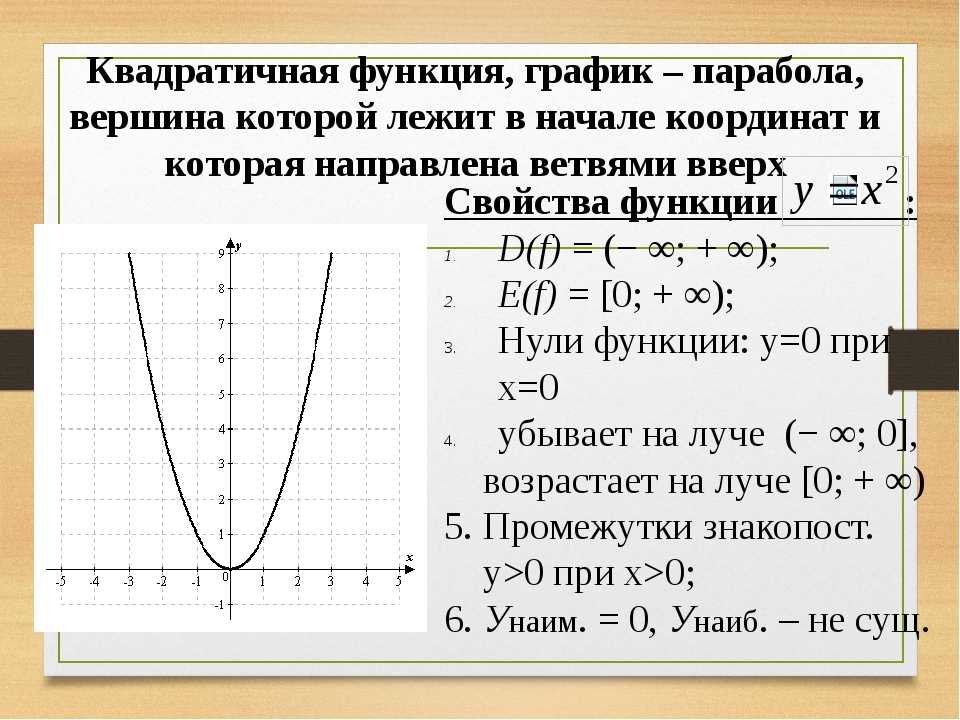
Вы также можете заметить, что постоянные члены (значения c) все являются полными квадратами:
Они получаются путем возведения в квадрат чисел 1, 2, 3, 4 и 5. решения представляют собой отрицания чисел 1, 2, 3, 4 и 5.
После того, как мы заметили закономерность, мы видим ее красоту: вы можете выбрать любое целое число n и составить квадратное уравнение с единственным решением (решение равно n).
Вот как это сделать.
В этом примере наш квадратичный показатель с одним решением равен x 2 + 14x + 49. Решение равно x = -7.
Мы также можем изменить знак всех значений b, чтобы получить совершенно новый набор квадратных уравнений только с одним решением:
Наконец, мы можем взять любое заданное квадратное уравнение с одним решением и умножить его на любое число (кроме нуля), чтобы получить новое квадратное уравнение с тем же решением.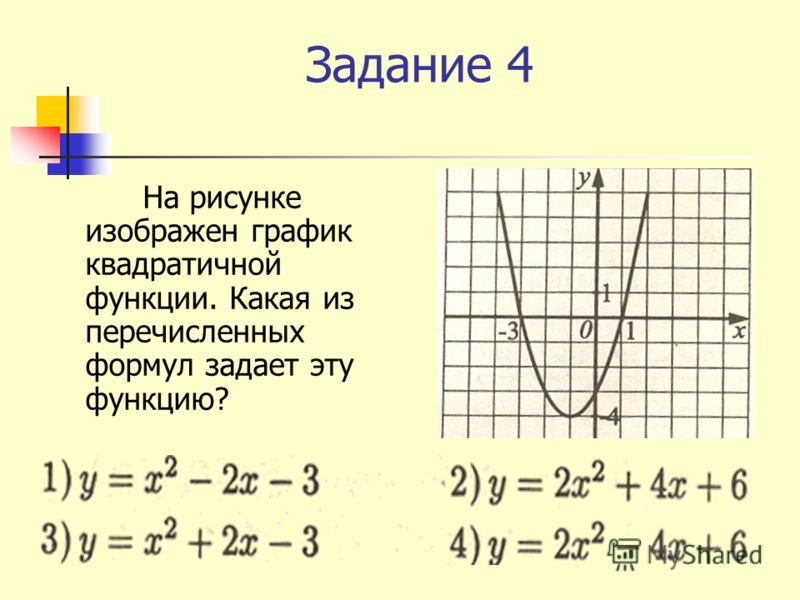
Как написать квадратное уравнение с одним решением?
Теперь пришло время подумать о работе в обратном направлении. Это означает, что нужно взять одно число и написать квадратное уравнение, единственным решением которого является это число.
Это легко сделать. Более того, существует бесконечно много таких уравнений для данного решения.
Допустим, мы хотим написать квадратное уравнение, имеющее только одно решение. Предположим также, что мы хотим, чтобы решением было число n.
Для этого мы просто напишем уравнение:
После использования фольги в скобках мы получим уравнение
Это уравнение имеет ровно одно решение: x = n (это двойной действительный корень).
Пример: Написание квадратного уравнения с одним действительным решением
Например, допустим, мне нужно квадратное уравнение с решением n = 3.
Тогда уравнение будет
После использования фольги мы получим уравнение
ровно одно решение, которое является значением x = 3. Мы также можем сгенерировать столько уравнений, сколько захотим, просто умножив обе части на 2, 3, 4, 5 и т. д.:
Мы также можем сгенерировать столько уравнений, сколько захотим, просто умножив обе части на 2, 3, 4, 5 и т. д.:
Всегда ли квадратное уравнение имеет два решения?
С точки зрения действительных решений, всегда существует 0, 1 или 2 действительных решения квадратного уравнения, в зависимости от знака дискриминанта.
Однако всегда есть хотя бы 1 решение, если считать и вещественные, и комплексные числа.
(Более подробно о том, что представляют собой решения квадратной формулы, вы можете узнать из моей статьи здесь.)
Помните, что два комплексно-сопряженных числа имеют форму a + bi и a – bi. Другими словами, они имеют одинаковую действительную часть, но противоположные мнимые части.
Например, 2 + 3i и 2 – 3i являются комплексно-сопряженными.
Заключение
Теперь вы знаете, когда квадратное уравнение имеет ровно одно решение. Вы также знаете, на что обращать внимание с точки зрения дискриминанта, графика и коэффициентов.
Надеюсь, эта статья оказалась вам полезной. Если это так, пожалуйста, поделитесь ею с теми, кто может использовать эту информацию.
Вы можете узнать больше о других методах решения квадратичных уравнений в этом ресурсе Университета Ламара.
Вы можете узнать больше о квадратичных уравнениях в других моих статьях о квадратичных уравнениях без действительных решений и квадратичных уравнениях с действительными решениями.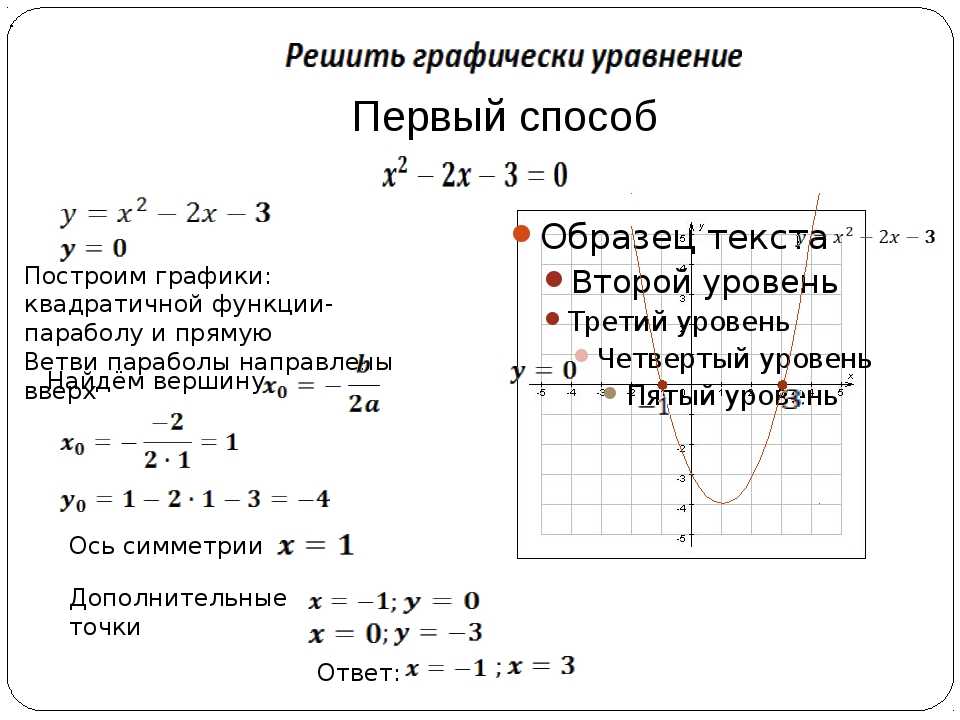


 (х — 3) (х — 2) = 0
(х — 3) (х — 2) = 0 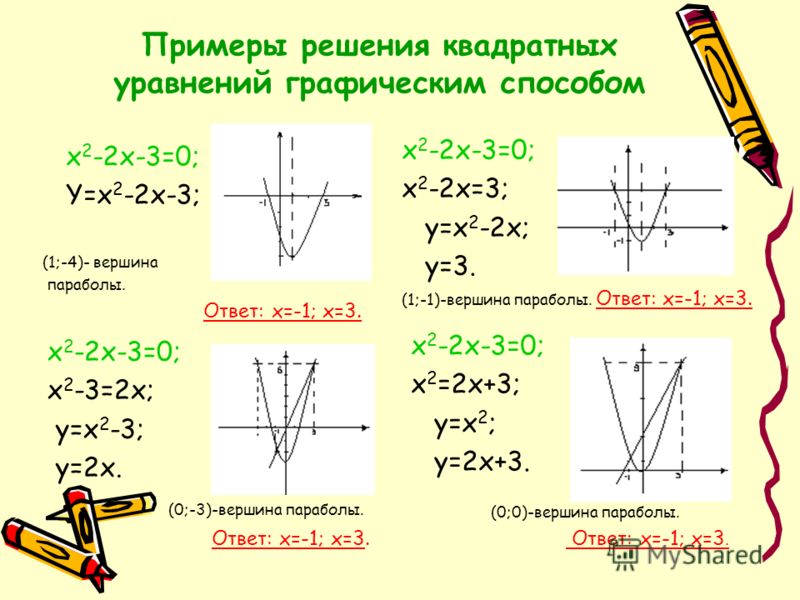 Кроме того, расширьте график с обеих сторон. Вот график квадратичной функции.
Кроме того, расширьте график с обеих сторон. Вот график квадратичной функции.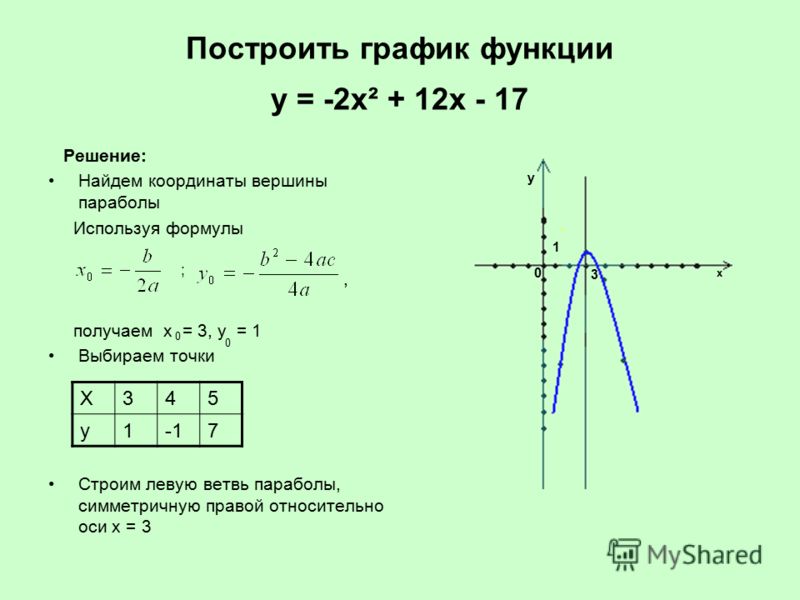

 9
9  Таким образом, квадратное число будет выглядеть как x 2 + 2n + n 2 . Решение будет –n (отрицательное целое число n, которое вы выбрали в начале).
Таким образом, квадратное число будет выглядеть как x 2 + 2n + n 2 . Решение будет –n (отрицательное целое число n, которое вы выбрали в начале).