Квадратные уравнения и их решения: Квадратные уравнения — урок. Алгебра, 8 класс.

Содержание

Квадратные уравнения (способы решения)

Першина Елена Петровна

Разделы: Математика

Необходимость решать уравнения не только первой, но и второй степени ещё в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики.

Квадратные уравнения умели решать около 2000 лет до нашей эры в Вавилоне. Применяя современную алгебраическую запись, можно сказать, что в их книгописных текстах встречаются, кроме неполных, и такие, как полные квадратные уравнения.

Определение

Уравнение вида ax²+ bx + c = 0, где a, b, c — действительные числа, причем

a ≠ 0, называют квадратным уравнением.

Если a = 1 , то квадратное уравнение называют приведенным; если a ≠ 1, то неприведенным .
Числа a, b, c носят следующие названия: a — первый коэффициент, b — второй коэффициент, c — свободный член.

Корни уравнения ax² + bx + c = 0 находят по формуле

Выражение D = b²— 4ac называют дискриминантом квадратного уравнения.

если D < 0, то уравнение не имеет действительных корней;
если D = 0, то уравнение имеет один действительный корень;
если D > 0, то уравнение имеет два действительных корня.

В случае, когда D = 0, иногда говорят, что квадратное уравнение имеет два одинаковых корня.

Формулы

Полное квадратное уравнение

Неполные квадратные уравнения

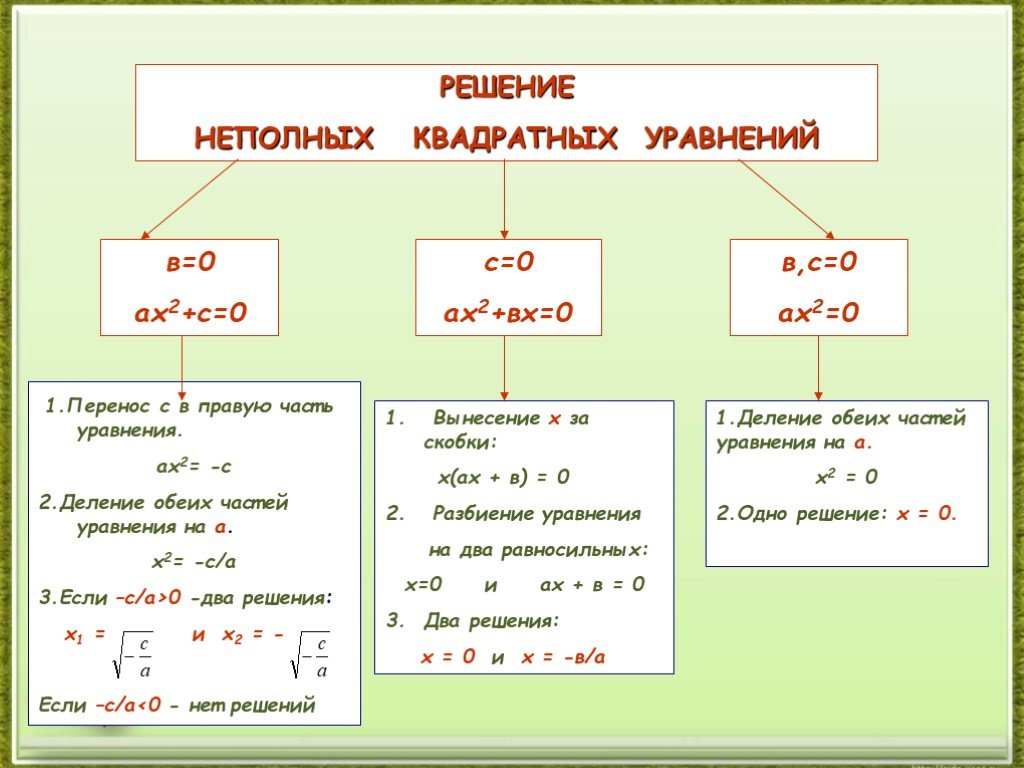
Если в квадратном уравнении ax² + bx + c = 0 второй коэффициент b или свободный член c равен нулю, то квадратное уравнение называется неполным.

Неполные уравнения выделяют потому, что для отыскания их корней можно не пользоваться формулой корней квадратного уравнения — проще решить уравнение методом разложения его левой части на множители.

Способы решения неполных квадратных уравнений:

c = 0, то уравнение примет вид
ax² + bx = 0.
x(ax + b) = 0 ,
x = 0 или ax + b = 0, x = —b : a .
b = 0, то уравнение примет вид
ax² + c = 0,
x² = —c / a,
x_{1, 2} = ±√(-c / a).
b = 0 и c = 0 , то уравнение примет вид
ax² = 0,
x = 0

Решение неполного квадратного уравнения

Квадратные уравнения с комплексными переменными

Сначала рассмотрим простейшее квадратное уравнение z² = a, где a-заданное число, а z-неизвестное. На множестве действительных чисел это уравнение:

имеет один корень z = 0, если а = 0;
имеет два действительных корня z_{1, 2} = ±√a
Не имеет действительных корней, если
a < 0

Решение квадратных уравнений с помощью графиков

Не используя формул квадратное уравнение можно решить графическим способом. Например x² + x + 1 = 0.
Решим уравнение. Для этого построим два графика y = x²; y = x + 1.

y = x², квадратичная функция, график парабола.
y = x + 1, линейная функция, график прямая.

Графики пересекаются в двух точках, уравнение имеет два корня.
Ответ: x ≈ -0,6; x ≈ 2,6.

Решение задач с помощью квадратных уравнений

Процессы	Скорость км/ч	Время ч.	Расстояние км.
Вверх по реке	10 — x	35 / (10 — x)	35
Вверх по протоку	10 — x + 1	18 / (10 — x + 1)	18
V течения	x
V притока	x + 1

Зная, что скорость в стоячей воде равна 10 км/ч, составим уравнение.

ОДЗ: ∀ x ≠ 9, 10.

Практикум

т.к. D₁ < 0, то корней нет.
Ответ: корней нет.

Ответ: x = 2,5.

Заключение

Ещё в древности люди пользовались ими не зная, что это – квадратные уравнения.

В наше время невозможно представить себе решение как простейших, так и сложных задач не только в математике, но и в других точных науках, без применения решения квадратных уравнений.

Надеюсь и вы открыли для себя что-нибудь новое

Презентация

20.06.2009

Квадратные уравнения. Их решение по формуле

1. Материал к урокам алгебры в 8 классе по теме:

Квадратные уравнения.
Их решение по формуле.
Кувакина Наталия Александровна

2. Вступление.

Данная работа может быть использована
на обобщающем уроке по теме «Решение
квадратных уравнений»с целью
повторения и обобщения изученного
материала
Отдельные части работы могут быть
использованы и на обучающих уроках или
во внеклассной работе с целью
ознакомления с дополнительными
сведениями.

3. Содержание:

Теоретический материал
Примеры решения квадратных уравнений по
формуле
Проверим знания (тест)
Кроссворд
Это интересно (дополнительные сведения о
решении квадратных уравнений)
Из истории решения квадратных уравнений
Проверь себя (решение квадратного уравнения
при помощи языка программирования)
Использованная литература

4.

Теоретические сведенияОпределение квадратного уравнения
Примеры квадратных уравнений.
Алгоритм решения квадратного уравнения
по формуле

5. Определение квадратного уравнения.

Квадратным уравнением называется уравнение
вида ах²+вх+с=0, где х – переменная, а,в,с –
некоторые числа, причем а≠0.
Числа а, в, с – коэффициенты квадратного
уравнения. Число а – первый коэффициент, в –
второй коэффициент, с – свободный член.
Если в квадратном уравнении ах²+вх+с=0 хотя бы
один из коэффициентов в или с равен нулю, то
такое уравнение называется неполным
квадратным уравнением.
Квадратное уравнение, в котором коэффициент
а=1 называется приведенным квадратным
уравнением.

6. Примеры квадратных уравнений:

Например: а) –х²+6х+1,2=0, где а=-1, в=6,
с=1,2;
б) 5х²-2=0 – неполное квадратное
уравнение, где а=5, в=0, с=-2;
в) -3х²+7х=0 — неполное квадратное
уравнение, где а=-3, в=7, с=0;
г) 7х²=0 — неполное квадратное уравнение,
где а=7, в=0, с=0;
д) х²+4х-12=0 – приведенное квадратное
уравнение, где а=1, в=4, с=-12.

7. Алгоритм решения квадратного уравнения:

ах²+вх+с=0
Определить
коэффициенты а,в,с
Вычислить дискриминант
D=в²-4ас
Если D<0, то
Уравнение не
имеет корней
Если D=0, то
1 корень
х
х
в
2а
в
2а
Если D>0, то
2 корня
х1, 2
х1, 2
вв D
D
2а
2а

8. Примеры решения квадратных уравнений по формуле

Пример1: 3х²+11х+6=0 а=3; в=11;с=6.
D=11²-4*3*6=121-72=49>0 – уравнение
имеет 2 корня
11 49 11 7
х1, 2
2*3
6
11 7
х1
3;
6
11 7
2
х2
6
3

9. Примеры решения квадратных уравнений по формуле:

Пример2. 9х²-6х+1=0
а=9; в=-11;с=1.
D=(-6)²-4*9*1=36-36=0=0 –
уравнение имеет 1 корень.
Х=
( 6) 6 1
2 * 9 18 3

10. Примеры решения квадратных уравнений по формуле:

Пример 3: -2х²+3х-5=0
а=-2; в=3;с=-5.
D=3²-4*(-2)*5=9-40=-31<0 –
уравнение не имеет корней.
Тест 1. Установить, истинны или ложны
утверждения.

Тест 2. Установить верный ответ из числа
предложенных.

12. Тест 1. Установите, истинны или ложны следующие утверждения :

Ответы давать : да или нет. Время для
выполнения – 10 минут.
Указание: не выполнять задания 8 и 9.
Текст теста:

13. Тест 2. Выбрать правильный ответ из предложенных вариантов:

Время для выполнения – 15 минут.
Указание: не выполнять задания 6 и 7.
Текст теста:

14. Кроссворд

1
2
3
4
5
6
7
8
9
1
0
1
1
1
2
1. Уравнение вида ах²+вх+с=о
2.Квадратные уравнения, у которых первый
коэффициент равен 1.
3. Уравнения с одной переменной, имеющие
одни и те же корни.
4. Числа а,в и с в квадратном уравнении.
5. Значение переменной, при котором
уравнение обращается в верное равенство.
6. Равенство, содержащее неизвестное.
7. Неотрицательное значение квадратного
корня.
8. Древнегреческий математик, который
нашел приемы решения квадратных
уравнений без обращения к геометрии.

9. Квадратное уравнение, в котором хотя бы
один из коэффициентов в или с равен 0.
10. «Дискриминант» — по-латыни.
11. Коэффициент с квадратного уравнения.
12. Французский математик, который вывел
формулы, выражающие зависимость корней
уравнения от его коэффициентов.
Если вы разгадаете этот кроссворд верно, то
сможете в выделенном вертикальном
столбце прочитать термин, относящийся к
теме.

15. Это интересно (дополнительные сведения о нахождении корней квадратного уравнения в особых случаях):

1 случай. Если a+b+c=0, то х1=1; х2= с/а
2 случай. Если a-b+c=0, то х1=-1; х2= -с/а
Нахождение корней приведенного
квадратного уравнения: х²+px+q=0. здесь
полезно воспользоваться формулой:
х1,2 р / 2 ( р / 2) q
2
Формула запоминается надолго, если
выучить ее в стихотворной форме:

16. Стихотворение для запоминания формулы

Стихотворение для запоминания
2
х
р
/
2
(
р
/
2
)
q
формулы 1,2
«Пэ», со знаком взяв обратным,
На два мы его разделим.

И от корня аккуратно
Знаком минут-плюс отделим.
А под корнем, очень кстати,
Половина «пэ» в квадрате,
Минус «ку». И вот решенье
Небольшого уравненья.

17. Из истории решения квадратных уравнений.

Уравнения 2-ой степени умели решать еще
в Древнем Вавилоне во II тысячелетии до
н.э. Математики Древней Греции решали
квадратные уравнения геометрически;
например, Евклид – при помощи деления
отрезка в среднем и крайнем отношениях.
Задачи, приводящие к квадратным
уравнениям, рассматриваются во многих
древних математических рукописях и
трактатах. Например.

18. Из истории решения квадратных уравнений.

Формула корней квадратного уравнения
«переоткрывалась» неоднократно. Один из
первых дошедших до наших дней выводов этой
формулы принадлежит индийскому математику
Брахмагупте (около 598 г.).
Среднеазиатский ученый ал-Хорезми (IX в.) в
трактате «Китаб аль-джебр валь -мукабала»
получил эту формулу методом выделения полного
квадрата с помощью геометрической
интерпретации.

См.подробнее.

19. Вывод формулы корней квадратного уравнения ал-Хорезми:

Суть его рассуждений видна из
рисунка (рассматривается
решение уравнения х²+10х=39.
Площадь большого квадрата
равна (х+5)². Она складывается
из площади х²+10х фигуры,
закрашенной голубым цветом,
равной левой части
рассматриваемого уравнения,
и площади четырех квадратов
со стороной 5/2, равной 25.
Таким образом, (х+5)²=39+25;
х1=3; х2=-13.
5х/2
х²
5х/2

20. Задача из китайского трактата «Математика в девяти книгах»(примерно II в.до н.э.)

«Имеется город с границей в виде квадрата со
стороной неизвестного размера, в центре каждой
стороны находятся ворота. На расстоянии 20 бу(1
бу=1,6 м) от северных ворот (вне города) стоит
столб. Если пройти от южных ворот прямо 14 бу,
затем повернуть на запад и пройти еще 1775 бу,
то можно увидеть столб. Спрашивается: какова
сторона границы города?»
Решение смотри здесь:

21.

Решение задачи о границах города:Обозначим сторону квадрата
через х. Из подобия
треугольников BED и ABC
(см.рис.) получим:
k/0.5x=(k+x+l)/d.
Поэтому, чтобы определить
неизвестную сторону квадрата,
получаем квадратное уравнение
х2+(k+l)-2kd=0.
В данном случае уравнение
имеет вид х2+34х-71000=0, откуда
х=25000 бу.
Отрицательных корней (в данном
случае х=-284) китайские
математики не рассматривали,
хотя в этом же трактате
содержатся операции с
отрицательными числами.
В
Д
Е
х
l
С
d
А

22. Проверь себя ( решение задачи при помощи языка программирования):

Программа, позволяющая решать
квадратные уравнения (язык Turbo Pascal)

23. Использованная литература:

Алтынов П.А. Тесты. Алгебра.7-9 – Москва,
«Дрофа», 2002 год
Макарычев Ю.Н. Алгебра, 8 класс – Москва,
«Просвещение», 2000 год
Ткачева М.В. Домашняя математика, 8 классМосква, «Просвещение», 1996 год
Худадатова С.

С. Математика в ребусах,
кроссвордах – Москва, «Школьная Пресса», 2003
год
Энциклопедический словарь юного математика –
Москва, «Педагогика», 1985 год
Энциклопедия «Я познаю мир. Математика» Москва, АСТ, 1996 год.

24. Брахмагупт(около 598-660 г.г.)

Индийский математик и астроном. Основное
сочинение «Усовершенствованное учение
Брахмы» («Брахмаспхутасиддханта», 628 г.),
значительная часть которого посвящена
арифметике и алгебре. Брахмагупта , изложил
общее правило решения квадратных уравнений,
приведенных к единой канонической
форме:
ax2 + bх = с, а> 0. (1)
В уравнении (1) коэффициенты, кроме а, могут
быть и отрицательными.
Правило
Брахмагупты по существу совпадает с нашим.

25. Диофант Александрийский (около 3 в.).

Древнегреческий математик. В основном
труде «Арифметика» (сохранились 6 книг
из 13), дал решение задач, приводящихся
к т.н. диофантовым уравнениям, и впервые
ввел буквенную символику в алгебру.

26. Евклид (3 в. До н.э.)

Древнегреческий математик,
работал в Александрии. Лавный
труд «Начала»(15 книг),
содержит основы античной
математики, элементарной
геометрии, теории чисел, общей
теории отношений и метода
определения площадей и
объемов, включавшего
элементы теории пределов,
оказал огромное влияние на
развитие математики.

27. Аль-Хорезми.

Наибольших успехов в математике достиг согдиец Мухаммед ибн Муса аль-Хорезми (то есть, родом
из Хорезма — с берегов Сыр-Дарьи). Он работал в первой половине 9 века и был любимцем
ученейшего из халифов — Маамуна (сына знаменитого Гаруна ар-Рашида). Главная книга Хорезми
названа скромно: «Учение о переносах и сокращениях», то есть техника решения алгебраических
уравнений. По-арабски это звучит «Ильм аль-джебр ва»ль-мукабала»; отсюда произошло наше слово
«алгебра».
Другое известное слово — «алгоритм», то есть четкое правило решения задач определенного типа произошло от прозвания «аль-Хорезми».

Третий известный термин, введенный в математику
знаменитым согдийцем — это «синус», хотя в этом деле не обошлось без курьеза.
В алгебраическом трактате ал-Хорезми дается классификация линейных и квадратных уравнений.
Автор насчитывает 6 видов уравнений, выражая их следующим образом:
«Квадраты равны корням», т. е. ах2 = bх.
«Квадраты равны числу», т. е. ах2 = с.
«Корни равны числу», т. е. ах = с.
«Квадраты и числа равны корням», т. е. ах2 + с = bх.
«Квадраты и корни равны числу», т. е. ах2 + bх =с.
«Корни и числа равны квадратам», т. е. bх + с == ах2.
Для ал-Хорезми, избегавшего употребления отрицательных чисел, члены
каждого из этих
уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у
которых нет положительных решений. Автор
излагает способы решения указанных уравнений,
пользуясь приемами ал-джабр и ал-мукабала. Его решение, конечно,не совпадает полностью с
нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при
решении неполного квадратного уравнения первого вида ал-Хорезми, как и все математики до XVII
в.

, не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не
имеет значения. При
решении полных квадратных уравнений ал-Хорезми на частных числовых
примерах излагает правила решения, а затем их геометрические доказательства.

28. Ответы к кроссворду:

1. Квадратное.
2. Приведенное.
3. Равносильное.
4. Коэффициент.
5. Корень.
6. Уравнение.
7. Арифметический.
8. Диофант.
9. Неполное.
10. Различитель.
11. Свободный.
12. Виет.
В выделенном столбце : ДИСКРИМИНАНТ

29. Ответы к тесту 1.

Вариант 1. 1,2,3,4,10-да; 5,6,7 – нет.
Вариант 2. 1,3,4,10 – да; 2,5,6,7 — нет

30. Ответ к тесту 2.

Вариант 1. 1 -г , 2-г , 3 — г, 4 -б , 5 -г .
Вариант 2. 1 — в, 2- б , 3 — в, 4 — б, 5 — б .

Что представляют собой решения квадратного уравнения? – JDM Educational

Вы проведете много времени на уроках алгебры, пытаясь найти решения квадратных уравнений. Однако знать, как найти эти решения, не то же самое, что знать, что они означают.

Итак, что представляют собой решения квадратного уравнения? Решения квадратного уравнения представляют собой значения x, при которых уравнение истинно. Мы можем факторизовать квадратное уравнение в стандартной форме с этими решениями. Визуально решения квадратного уравнения представляют собой точки, в которых парабола пересекает ось x (то есть, где y = 0).

Конечно, для квадратного уравнения в стандартной форме решения говорят нам, когда левая часть равна нулю. Для квадратичной функции f(x) решения квадратного уравнения говорят нам, когда f(x) = 0.

В этой статье мы поговорим о решениях квадратного уравнения и о том, что они представляют. Мы также более подробно рассмотрим некоторые случаи для решений и когда они возникают.

Начнем.

Что представляют собой решения квадратного уравнения?

Решения квадратного уравнения представляют значения x, которые делают уравнение верным. Для квадратного уравнения в стандартной форме эти значения x сделают левую часть уравнения равной нулю.

Для квадратичной функции f(x) решениями являются значения x, которые делают y равным нулю. Эти значения x также называются корнями квадратного уравнения.

То есть, если x = a является решением квадратичной функции f(x), то f(a) = 0.

Каково ожидаемое значение Dic…

Пожалуйста, включите JavaScript

Каково ожидаемое значение броска костей?

Например, рассмотрим квадратичную функцию f(x) = x ² – 1 с решениями x = 1 и x = -1. Мы можем увидеть это, если разложим это как разность квадратов:

f(x) = x ² – 1
f(x) = (x + 1)(x – 1) [ фактор как разность квадратов]

Мы можем проверить эти два решения, подставив их вместо x в квадратичной функции:

f(1) = 1 ² – 1 = 1 – 1 = 0
f(-1) = (-1) ² – 1 = 1 – 1 = 0

Решения квадратного уравнения также представляют собой способ факторизации. Учитывая квадратичную функцию f(x) = ax ² + bx + c, решения x = r и x = s дают нам полную факторизацию:
f(x) = a(x – r)(x – s)
Например, рассмотрим квадратичную функцию f(x) = 5x ² -15x + 10. Если мы знаем, что корни равны x = 1 и x = 2, то мы можем полностью разложить на множители с a = 5, r = 1 и s = 2:
f(x) = a(x – r)(x – s)
f(x) = 5(x – 1)(x – 2)
Мы можем использовать FOIL и Distributive Property, чтобы проверить это:
f(x) = 5(x – 1)(x – 2)
f(x) = 5(x ² – 2x – x + 2)
f(x) = 5 (х ² – 3х + 2)
f(x) = 5x ² – 15x + 10
Конечно, решения квадратного уравнения имеют и наглядную интерпретацию. Они представляют собой очень специфические точки на графике параболы.
Что представляют решения квадратного уравнения на графике?
Решения квадратного уравнения представляют собой точки на графике, где парабола пересекает ось x. То есть, когда y = 0 или когда f(x) = 0.
Помните, что мы можем построить график квадратичной функции f(x) = ax ² + bx + c в виде параболы (показана ниже).
Квадратное уравнение изображено в виде параболы. Решения квадратного уравнения представляют собой точки, в которых парабола пересекает ось x.
В зависимости от решений парабола может пересекать ось абсцисс дважды, один раз или не пересекать ее вовсе. Количество пересечений определяется типом решения: два различных действительных корня, один повторяющийся действительный корень или два комплексно-сопряженных корня.
Помните, что парабола — это функция, но она не является взаимно однозначной функцией. Таким образом, она может пересекать ось x (прямую y = 0) более одного раза.
Чтобы определить точные решения квадратного уравнения, мы можем использовать формулу квадратного уравнения (показана ниже).
Квадратичная формула. Выражение под радикалом b ² – 4ac называется дискриминантом и помогает определить характер решений квадратного уравнения.
Приведя квадратное уравнение к стандартной форме, ax ² + bx + c = 0, мы можем найти a, b и c для использования в квадратной формуле.
Чтобы найти характер решений квадратного уравнения (какие у нас есть решения), мы можем использовать одну часть формулы: дискриминант.
Дискриминантом квадратного уравнения является выражение под подкоренным знаком в квадратной формуле: b ² – 4ac.
Возможны три случая знака дискриминанта, соответствующие типу решений квадратного уравнения:
Положительный дискриминант : когда b ² – 4ac > 0, мы имеем два различных действительных решения уравнения Квадратное уравнение.
Нулевой дискриминант : когда b ² – 4ac = 0, у нас есть одно повторяющееся действительное решение квадратного уравнения.
Отрицательный дискриминант : когда b ² – 4ac < 0, мы имеем два комплексно-сопряженных решения квадратного уравнения.
В таблице и на графике ниже показаны различные случаи решения квадратного уравнения и то, что будет иметь соответствующий график для пересечений оси X.
Знак
Дискриминант
b ² – 4ac Природа
Решения График
Интерпретация
Positive
(b ² > 4ac) 2 Real
Solutions Crosses
x-axis
twice
Zero
(b ² = 4ac) 1 Real
Repeated
Solution Vertex
rests on
x-axis
Negative
(b ² < 4ac) 2 Complex
Conjugate
Solutions Never
touches
x-axis
В этой таблице показаны различные случаи для решений
квадратного уравнения и то, что
соответствующий график имел бы
для пересечений оси x.
Дискриминантом является выражение b ² – 4ac под радикалом в квадратичной формуле. Его знак может сказать нам о характере решений соответствующего квадратного уравнения.
Что важно в решениях квадратного уравнения?
Решения квадратного уравнения важны, потому что они позволяют нам разложить квадратное уравнение на множители в стандартной форме (пока мы знаем значение a, коэффициент x ² в уравнении).
Решения квадратного уравнения в стандартной форме также говорят нам, где соответствующая парабола будет пересекать ось x (если вообще будет), когда мы начертим функцию. Это упрощает построение графика, так как мы можем использовать решения, чтобы помочь нам.
Какое наибольшее число решений может иметь квадратное уравнение?
Наибольшее число действительных решений, которое может иметь квадратное уравнение, равно двум. На самом деле квадратное уравнение имеет ровно два комплексных решения , хотя они не всегда могут быть действительными числами.
Как мы узнали ранее, квадратное уравнение может иметь два различных действительных решения, одно повторяющееся действительное решение или два комплексно-сопряженных решения.
Предел двух решений квадратного уравнения гарантируется Основной теоремой алгебры, которая утверждает, что:
Многочлен степени n от одной переменной с комплексными коэффициентами имеет n комплексных корней.
Поскольку квадратное уравнение имеет степень n = 2, мы знаем, что оно имеет ровно два решения. Повторяющийся действительный корень (когда дискриминант равен нулю) считается за два решения из-за кратности.
Вершина этой параболы опирается на ось x, что означает, что она представляет собой квадратное уравнение с одним вещественным кратным корнем (здесь двойной корень из x = 0).
Зная, как выглядит парабола (всегда одна и та же вогнутость и одна точка поворота), легко увидеть, что квадратное уравнение может иметь не более двух действительных решений. Эти решения представляют собой точки (если есть), где парабола пересекает ось x (y = 0).
Сколько действительных решений может иметь квадратное уравнение?
Квадратное уравнение может иметь 0, 1 или 2 действительных решения. Это полностью зависит от знака дискриминанта, b ² – 4ac (выражение под радикалом в квадратной формуле):
Положительный дискриминант : когда b ² – 4ac > 0, квадратное уравнение имеет два действительных решения.
Нулевой дискриминант : когда b ² – 4ac = 0, квадратное уравнение имеет одно действительное решение (двойной корень).
Отрицательный дискриминант : когда b ² – 4ac > 0, квадратное уравнение не имеет не действительных решений (вместо этого оно имеет два комплексно-сопряженных решения).
Обратите внимание, что случаи, когда дискриминант отличен от нуля (положительный или отрицательный), — это случаи, когда у нас есть квадратное уравнение с двумя решениями.
В таблице ниже показаны различные случаи действительных решений квадратного уравнения в зависимости от знака дискриминанта.
Sign Of
Discri-
minant
b ² – 4ac Number
Of Real
Solutions
Positive
(b ² > 4ac) 2 (real &
distinct
Zero
(B ² = 4AC) 1 (Реальный
)
Отрицательный0225
Эта таблица иллюстрирует различные случаи
для действительных решений квадратного уравнения
в зависимости от знака
дискриминанта.
Как квадратное уравнение может не иметь решения?
Квадратное уравнение всегда имеет решения, но они не всегда могут быть реальными. Чтобы у квадратного уравнения не было действительного решения, у нас должно быть два комплексно-сопряженных решения.
Это происходит, когда дискриминант отрицателен (b ² – 4ac < 0).
Когда мы рисуем такое квадратное уравнение, результирующая парабола вообще не будет пересекать ось x. То есть значение y никогда не будет равно нулю, как вы можете видеть ниже:
Эта парабола представляет собой график квадратного уравнения без действительных решений (имеет два комплексно-сопряженных решения). Обратите внимание, что она никогда не пересекает ось x.
Парабола будет либо:
Всегда будет выше оси x (y > 0 для всех x), что может произойти, когда a > 0 и c > 0.
Всегда находиться ниже оси x (y < 0 для всех x), что может произойти, когда a < 0 и c < 0.
Обратите внимание, что мы можем получить комплексные решения только с ненулевой мнимой частью для квадратное уравнение, когда а и с имеют одинаковые знаки (оба положительные или оба отрицательные).
Заключение
Теперь вы точно знаете, что представляют собой решения квадратного уравнения, как алгебраически, так и графически.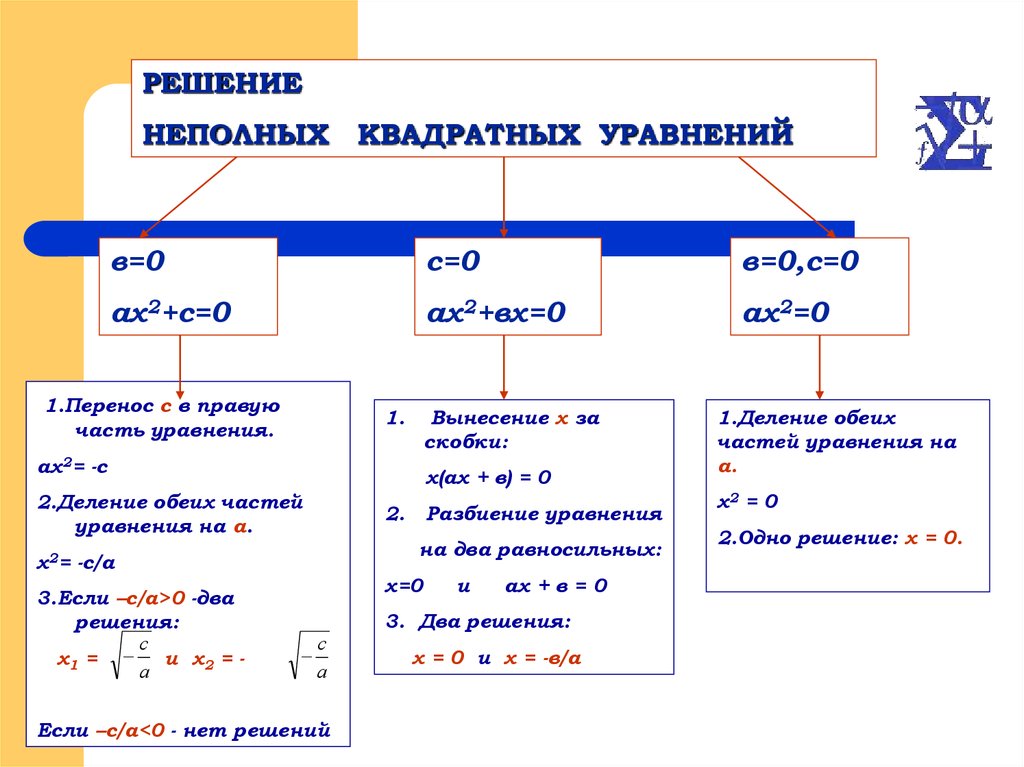 Вы также знаете, когда возникают различные случаи (два действительных, одно действительное или два комплексно-сопряженных решения).
Подробнее о корнях и коэффициентах квадратного уравнения можно узнать из моей статьи здесь.
Вы также можете прочитать мою статью, в которой я отвечаю на некоторые распространенные вопросы о квадратичных функциях.
Надеюсь, эта статья оказалась вам полезной. Если это так, пожалуйста, поделитесь ею с теми, кто может использовать эту информацию.
Не забудьте подписаться на мой канал YouTube и получать обновления о новых математических видео!
Подпишитесь на наш канал на YouTube!
~ Джонатон
Решения квадратного уравнения на графике (Видео)
Привет и добро пожаловать в это видео о решениях квадратного уравнения на графике ! Сегодня мы научимся находить решения квадратичной функции, глядя на ее график. Мы также поговорим о том, как построить график квадратного уравнения и проанализировать график, чтобы найти решения.
Прежде чем мы начнем, давайте рассмотрим несколько вещей. Во-первых, квадратичная функция

является полиномиальной функцией, и ее член наивысшей степени имеет вторую степень. График квадратичной функции представляет собой двумерную кривую, называемую 9{2}\), вершина — это точка в нижней части U-образной параболы, показанная здесь в точке (0,0).
Обратите внимание, что эта парабола симметрична относительно оси Y, которая является осью симметрии на этом графике. Вершина — это точка в нижней части U-образной формы.
Если график квадратичной функции пересекает ось x в двух точках, то уравнение имеет два действительных рациональных решения. Эти решения также называются x- пересечений или корней 9{2}+x-6=0\). Обратите внимание, что \(y\) заменено на \(0\). Замена \(y\) на \(0\) указывает на то, что мы находим \(x\) путем идентификации пересечений x.
Глядя на график, мы видим, что эта квадратичная функция имеет два решения.
{2}+4=0\). 9{2}+1=0\).
Глядя на этот график, мы видим, что он вообще не проходит через ось \(x\), а значит, нет пересечений по оси x. Другими словами, у этого уравнения нет реальных решений.
Квадратичные функции встречаются во многих реальных ситуациях. Многие вопросы о времени, скорости и расстоянии требуют решения квадратных уравнений. Примером этого является подбрасывание мяча в воздух. Как только мяч брошен, он замедляется и в конце концов падает обратно. При броске мяч движется по перевернутой U-образной траектории или параболе. Квадратное уравнение можно использовать, чтобы найти положение мяча за время, в течение которого он находится в воздухе.
Другой пример — лодка, плывущая против течения реки. Если лодка пройдет 10 миль вверх по течению и развернется, чтобы вернуться в исходную точку, ее путь будет представлять собой U-образную параболу. С помощью квадратного уравнения можно найти скорость лодки и длину пути.

Есть много других примеров решения задач, в которых полезны квадратные уравнения. Их понимание помогает нам применять математические концепции в реальном мире. Давайте взглянем на сюжетную задачу, которую мы можем решить, построив график квадратичной функции. 9{2}\). Найдите размеры поля.

Сначала начнем с формулы площади прямоугольника, которая равна \(A=\text{длина}\times \text{ширина}\). В словесной задаче длина поля не указана, поэтому используйте переменную \(x\) для представления длины. Поскольку ширина на 2 метра меньше длины, используйте выражение \(x-2\) для представления ширины.
Затем подставьте значения в формулу площади. Итак, мы сказали:
\(\text{A}=\text{lw}\) 9{2}-2x-48=0\). Квадратные уравнения могут быть факторизованы как \((x-p)(x-q)=0\), где \(p\) и \(q\) являются решениями уравнения.

Чтобы разложить уравнение на множители, определите два числа с суммой -2 (\(b\)) и произведением -48 (\(c\)). Два числа с суммой -2 и произведением -48 равны -8 и 6. Следовательно, мы можем разложить это квадратное уравнение на множители, записав его как \((x-8)(x+6)=0\). Теперь заметьте, что раньше мы говорили, что это \((x-p)(x-q)\), но здесь у нас есть знак плюс. Ну, это действительно то же самое, что и \((x-(-6))\), которое затем упрощается до \((x+6)\) из-за вычитания отрицательного значения.
Затем подставьте вместо \(x\) значения, которые сделают каждое уравнение верным. Поскольку \(8-8=0\), \(x=8\). Поскольку \(-6+6=0\), \(x=-6\). Решения для \(x\) равны 8 и -6. Таким образом, координаты этих \(x\)-отрезков равны (8,0) и (-6,0). Итак, функция проходит через эти две точки.
Теперь, когда мы определили координаты \(x\)-отрезков, мы можем найти координаты вершины. Начните с нахождения \(x\)-координаты вершины. Поскольку вершина является средней точкой двух пересечений по оси x, координата \(x\) вершины представляет собой сумму двух пересечений \(x\), деленную на 2. Итак, давайте сделаем это. У нас есть две точки пересечения, 8 и -6, и чтобы найти среднее значение этих двух точек, мы сложим их вместе и разделим на 2.9{2}-2(1)-48\)

\(y=1-2-48\)

\(y=-1-48\)

\(y=-49\)
Итак, наша координата y равна -49. Следовательно, вершина находится в точке (1,-49).
Теперь, когда мы определили точки пересечения \(x\) и вершину, мы можем использовать эти точки для построения графа. Нанесите точки и соедините их плавной кривой, как показано на рисунке.
Теперь, когда мы построили график функции, давайте еще раз рассмотрим контекст задачи со словами. Напомним, что мы пытаемся определить размеры прямоугольного поля. Поскольку метры не могут быть измерены отрицательными числами, единственное разумное решение для x здесь равно 8. Напомним, что x представляет собой длину поля, которая составляет 8 метров. Напомним, что ширина на 2 метра меньше длины. Поскольку \(8-2=6\), ширина поля равна 6 метрам. Длина поля 8 метров, ширина 6 метров. 9{2}-6x-16=0\). Для этого нам нужно идентифицировать два числа, которые имеют сумму -6 (\(b\)) и произведение -16 (\(c\)). Затем мы запишем эти числа в факторизованное уравнение \((x\text{})(x\text{})=0\). Правильные числа -8 и 2, потому что \(-8\умножить на 2=-16\) и \(-8+2=-6\). {2}-6x-16\): 9{2}-6(3)-16\)

\(y=9-18-16\)

\(y=-9-16\)

\(y=-25\)
Следовательно, вершина находится в точке (3,-25).
Теперь, когда мы определили точки пересечения \(x\) и вершину, мы можем использовать точки (8,0), (-2,0) и (3,-25) для построения графа. Нанесите точки и соедините их плавной кривой.
Отличная работа!
Надеюсь, это видео о решениях квадратного уравнения на графе было полезным. Спасибо за просмотр и удачной учебы! 92+3x-28=0\), используя график, показанный ниже:
\(x=-28\)
\(x=-4 \text{ и }x=7\)
\( x=-7 \text{ и }x=4\)
Нет действительного решения
Показать ответ
Ответ:
Глядя на график, мы видим, что квадратичная функция пересекает \(x\)- оси в двух точках. Это означает, что существует два действительных решения этого уравнения. График пересекает ось \(x\) в точках \((-7,0)\) и \((4,0)\), поэтому решения для \(x\) равны –7 и 4,92+10x+25=0\), используя приведенный ниже график:
\(x=5\)
\(x=-5\)
\(x=5\text{ or }x =-5\)
Нет реального решения
Показать ответ
Ответ:
Глядя на график, мы видим, что квадратичная функция касается оси \(х\) ровно в одной точке. Это означает, что существует одно действительное решение этого уравнения. Вершина касается оси \(x\) в точке \((-5,0)\), поэтому решение для \(x\) равно –5.
Скрыть ответ 92+x+4=0\), используя приведенный ниже график:
\(x=-0,5\text{ или }x=4\)
\(x=-4\text{ или }x =0.5\)
\(x=4\)
Нет действительных решений
Показать ответ
Ответ:
Глядя на график, мы видим, что квадратичная функция не проходит через \(x\ )-ось вообще. Это означает, что реальных решений этого уравнения нет.
Скрыть ответ
Вопрос №4:

Длина прямоугольного флага на 4 фута больше его ширины. Площадь 96 квадратных метров. Найдите размеры флага, написав квадратное уравнение и изобразив его на координатной плоскости.
Ширина -12 футов, длина -8 футов.
Ширина 8 футов, длина 12 футов.
Ширина -2 фута, длина -100 футов.
Ширина 2 фута, длина 100 футов.
Показать ответ
Ответ:
Для начала вспомните формулу площади прямоугольника, которая равна длине, умноженной на ширину. Подставьте значения из слова задача в эту формулу. Поскольку ширина неизвестна, используйте w для представления ширины. Поскольку длина флага на 4 фута больше его ширины, используйте \(w+4\) для представления длины.
\(A=lw\)
\(96=w\left(w+4\right)\)
Далее упростим уравнение, распределив \(w\). Запишите квадратное уравнение в стандартной форме.
\(92+4w-96=0\)
Затем определите координаты \(x\)-отрезков. Умножьте уравнение, найдя два числа, которые дают в сумме 4 и произведение -96. Это числа 12 и -8.
\(\left(w+12\right)\left(w-8\right)=0\)
Отсюда приравняйте каждый двучлен к 0 и найдите \(w\). Решения равны -12 или 8. Координаты этих \(x\)-отрезков равны \((-12,0)\) и \((8,0)\). График функции проходит через ось \(х\) в точках -12 и 8.
92+4\влево(-2\вправо)-96\)
\(k=4-8-96\)
\(k=-100\)
Вершина этой функции есть \((-2, -100)\). Нанесите вершину и точки пересечения \(x\) на координатную плоскость и соедините точки плавной кривой.
Поскольку эта задача касается площади флага, отрицательное решение -12 к этому сценарию неприменимо. Следовательно, ширина флага составляет 8 футов. Поскольку длина флага на 4 фута больше его ширины, длина флага составляет 12 футов. 92=0\). Нарисуйте график этой квадратичной функции, чтобы выяснить, где мяч падает на землю относительно того, где стоит Николь.
Мяч Николь падает на землю в 2 футах от того места, где она стоит.
Мяч Николь упал на землю в 4 футах от того места, где она стоит.
Мяч Николь упал на землю в -2 футах от того места, где она стоит.
Мяч Николь упал на землю в -4 футах от того места, где она стоит.
No related posts.