valuate lim (1-sinx COS X 2 ?
Scholr
| Share this question |
1 Answers
Chinmayi GopalGrade 8 |
As this limit is in 0 power 1 form,
lim is so limit is just 0.
| 0 | Share this answer |
Similar Questions
|
6 2x = 2 sinx cos x = рди … |
(i) J(sinx + cos x) dx . .. .. |
V/cos(2x)+V(I + si n 2x)== 2V(sinx+cos x), if (A) 57. sinx + cosx=0 … |
cos2xdx 16 (sinx + cosx) sinX COS X (b) log isinx + cosx| + c (c) log I sinx- cosxl + C . .. .. |
2 tan x Example 22 Find the derivative of x cos x sinx 5 … |
1. {\pi / 2} \frac{\sin x}{\sin x+\cos x}properties.
sinx +cosx
… {\pi / 2} \frac{\sin x}{\sin x+\cos x}properties.
sinx +cosx
… |
sinx QoS X using properties — गुणधमां का । DIE la sinx sin x + cos x … |
Scholr is India’s Largest Knowledge Sharing Platform. Send Your Questions to
Experts.
Send Your Questions to
Experts.
Ask
Copyright Scholr 2018 ©
मन में है सवाल?
घर
पूछें
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
реальный анализ — Найти $\lim_{x\to 0} \frac{1+\sin x-\cos x}{1+\sin(px)-\cos(px)}$
спросил
Изменено 1 год, 8 месяцев назад
Просмотрено 379 раз
$\begingroup$
Найдите предел $$\lim_{x\to 0} \frac{1+\sin x-\cos x}{1+\sin(px)-\cos(px)}$$ без l’Hospital .
Я попытался расширить $1-\cos(x)$, чтобы получить что-то вроде $$\lim_{x\to 0}\frac{\sin x}{x}$$, но не смог решить эту задачу. Ответ: $1/p$.
- реальный анализ
- исчисление
- пределы
- анализ
- пределы без капитала
$\endgroup$
3
$\begingroup$
Немного тригонометрии делает свое дело: $$\begin{выравнивание} \lim_{x\to 0} \frac{1+\sin x-\cos x}{1+\sin(px)-\cos(px)} &= \lim_{x\to 0}\frac{1 +\sqrt 2\sin(x-\pi/4)}{1+\sqrt 2 \sin(px-\pi/4)} \\[1мм] &= \lim_{x\to 0}\frac{\frac{1}{\sqrt 2} + \sin(x-\pi/4)}{\frac{1}{\sqrt 2} + \sin( px — \pi/4)} \\[1мм] &= \lim_{x\to 0}\frac{\sin(\pi/4) + \sin(x-\pi/4)}{\sin(\pi/4) + \sin(px — \pi /4)} \\[1мм] &= \lim_{x\to0} \frac{\sin(x/2)\cos(\pi/2)}{\sin(px/2)\cos(\pi/2)} \\[1 мм] &= \lim_{x\to0} \underbrace{\frac{\sin(x/2)}{\color{red}{x/2}}}_{\to 1}\underbrace{\frac{\color {синий} p \ цвет {красный} {x / 2}} {\ sin (px / 2)}} _ {\ to 1} \ frac {1} {\ color {синий} p} \\ [1 мм] &= \frac 1p\end{align}$$
См.
обсуждение MSE о $\lim_{x\to0}\frac{\sin x}{x}=1$
$\endgroup$
3
$\begingroup$
Пусть $f(x) = \sin{x} — \cos{x}$. Тогда $$1 = f'(0) = \lim_{h \to 0} \frac{f(h)-f(0)}{h} = \lim_{h \to 0} \frac{\sin{ h} — \cos{h} + 1}{h}$$ Сделайте замену $h\mapsto ph$, и этот предел станет $$1 = f'(0) = \lim_{h \to 0} \frac{\ sin{ph} — \cos{ph} + 1}{ph}$$ Наконец, обратите внимание, что: $$ 1 = \frac{1}{1} = \frac{f'(0)}{f'(0 )} = \lim_{h \to 0} \left ( \frac{\frac{\sin{h} — \cos{h} + 1}{h}}{\frac{\sin{ph} — \cos {ph} + 1}{ph}} \right )$$ Итак, $$\lim_{h\to 0} \frac{1+\sin h-\cos h}{1+\sin{ph}-\ cos{ph}} = \frac{1}{p}$$ 92 x/2}{\lim_{x\to 0}\sin(px)+\lim_{x\to 0}2\sin px/2} = \lim_{x\to 0}\frac{\sin x }{\sin пикс.}.$$
Алгебраические манипуляции:
$$\lim_{x\to 0}\frac{x\sin x}{x\sin px}=\lim_{x\to 0}\frac{\sin x}{x}\lim_{x\to 0 }\frac{x}{\sin px}=1\cdot\lim_{x\to 0/p}\frac{x/p}{\sin x}=\frac{1}{p}.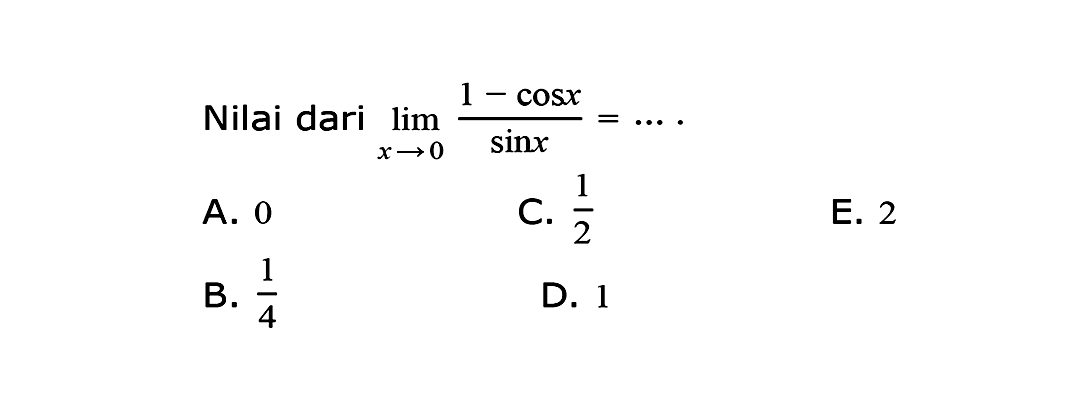

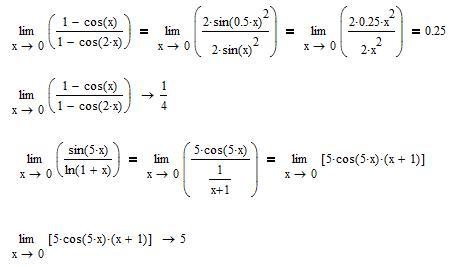 ..
.. обсуждение MSE о $\lim_{x\to0}\frac{\sin x}{x}=1$
обсуждение MSE о $\lim_{x\to0}\frac{\sin x}{x}=1$