Линейное программирование применяется для: НОУ ИНТУИТ | Лекция | Математическое программирование. Линейное программирование. Виды задач линейного программирования. Постановка задач линейного программирования и исследование их структуры. Решение задач линейного программирования симплекс-методом

Содержание

2.Линейное программирование и его применение для решения экономических задач.

Линейное программирование — математическая дисциплина, посвящённая теории и методам решения экстремальных задач на множествах n-мерного векторного пространства, задаваемых системами линейных уравнений и неравенств. В 1939 году Леонид Витальевич Канторович опубликовал работу «Математические методы организации и планирования производства», в которой сформулировал новый класс экстремальных задач с ограничениями и разработал эффективный метод их решения, таким образом были заложены основы линейного программирования. Джордж Данциг разработал симплекс-метод и считается «отцом линейного программирования» на западе.

Линейное программирование является частным случаем выпуклого программирования, которое в свою очередь является частным случаем математического программирования. Одновременно оно — основа нескольких методов решения задач целочисленного и нелинейного программирования. .

Термин «программирование» нужно понимать в смысле «планирования». Он был предложен в середине 1940-х годов Джорджем Данцигом, одним из основателей линейного программирования, ещё до того, как компьютеры были использованы для решения линейных задач оптимизации.

Математическая формулировка задачи линейного программирования

Нужно определить максимум линейной целевой функции (линейной формы)

при условиях

при .

Иногда на x_i также накладывается некоторый набор ограничений в виде равенств, но от них можно избавиться, последовательно выражая одну переменную через другие и подставляя её во всех остальных равенствах и неравенствах (а также в функции f).

Такую задачу называют «основной» или «стандартной» в линейном программировании.

Транспортная задача

Имеется некий однородный груз, который нужно перевести с n складов на m заводов.

Для каждого склада i известно, сколько в нём находится груза a_i, а для каждого завода известна его потребность b_j в грузе. Стоимость перевозки пропорциональна расстоянию от склада до завода (все расстояния c_ij от i-го склада до j-го завода известны). Требуется составить наиболее дешёвый план перевозки.

Решающими переменными в данном случае являются x_ij — количества груза, перевезённого из i-го склада на j-й завод. Они удовлетворяют ограничениям:

Целевая функция имеет вид: , которую надо минимизировать.

Наиболее известным и широко применяемым на практике для решения общей задачи линейного программирования (ЛП) является симплекс-метод. Несмотря на то, что симплекс-метод является достаточно эффективным алгоритмом, показавшим хорошие результаты при решении прикладных задач ЛП, он является алгоритмом с экспоненциальной сложностью.

Причина этого состоит в комбинаторном характере симплекс-метода, последовательно перебирающего вершины многогранника допустимых решений при поиске оптимального решения.

3.Многокритериальная оптимизация и ее применение для решения экономических задач

Эта задачи оптимизации, в которых используется не один, а несколько критериев. На практике такие задачи возникают, когда проектируемый объект не может быть описан однокритериальной зависимостью, или объединить отдельные критерии в единый критерий не представляется возможным. Такое объединение критериев в единый критерий применяется, и оно будет рассмотрено ниже. Но это объединение, как правило, бывает формальным, искусственным. С математической точки зрения не существует идеального способа, метода решения таких задач. Каждый из них имеет преимущества и недостатки. Рассмотрим некоторые методы решения многокритериальных задач оптимизации.

Метод поиска Парето – эффективных решений

Рассмотрим его суть на примере использования двух критериев. Критерии при использовании данного метода являются равнозначными.

Правило. Множество Парето – эффективных оценок P(Y’) представляет собой «северо – восточную» границу множества Y без тех его частей, которые параллельны одной из координатных осей или лежат в «глубоких» провалах.

Для случая, изображенного на рис.9.1, Парето – эффективные оценки состоят из точек кривой (bc), исключая точку (c), и линии (de).

Преимущества метода: 1) Критерии равнозначны; 2) Метод математически объективен.

Недостаток метода: 1) Одно окончательное решение получается только в частном случае, т.е. количество Парето – эффективных решений, как правило, более одного.

Метод решения многокритериальных задач оптимизации с использованием обобщенного (интегрального) критерия

Суть данного метода заключается в том, что частные критерии каким — либо образом объединяются в один интегральный критерий , а затем находится максимум или минимум данного критерия.

Если объединение частных критериев производится, исходя из объектной взаимосвязи частных критериев и критерия обобщенного, то тогда оптимальное решение будет корректно. Но такое объединение осуществить крайне сложно или невозможно, поэтому, как правило, обобщенный критерий есть результат чисто формального объединения частных критериев.

В зависимости от того, каким образом частные критерии объединяются в обобщенный критерий различают следующие виды обобщенных критериев:

Аддитивный критерий;
Мультипликативный критерий;
Максиминный (минимаксный) критерий.

Аддитивный критерий

В них целевая функция получается путем сложения нормированных значений частных критериев. В общем виде целевая функция имеет следующий вид:

где n – количество объединяемых частных критериев;

– весовой коэффициент – го частного критерия;

– числовое значение – го частного критерия;

– – й нормирующий делитель;

– нормированное значение – го частного критерия.

Частные критерии имеют различную физическую природу и поэтому различную размерность. А значит просто суммировать их некорректно. В связи с этим в предыдущей формуле числовые значения частных критериев делятся на некоторые нормирующие делители, которые назначается следующим образом:

В качестве нормирующих делителей принимаются директивные значения параметров или критериев, заданные заказчиком. Считается, что значения параметров, заложенные в техническом задании , являются оптимальными или наилучшими.
В качестве нормирующих делителей принимаются максимальные (минимальные) значения критериев, достигаемые в области допустимых решений.

Размерности самих частных критериев и соответствующих нормирующих делителей одинаковы, поэтому в итоге обобщенный аддитивный критерий получается безразмерной величиной.

Преимущество данного метода: как правило, всегда удается определить единственный оптимальный вариант решения.

Недостатки:

Трудности (субъективизм) в определении весовых коэффициентов.
Аддитивный критерий не вытекает из объектной роли частных критериев и поэтому выступает как формальный математический прием.
В аддитивном критерии происходит взаимная компенсация частных критериев, т.е. уменьшение одного из них может быть компенсировано увеличением другого критерия.

Мультипликативный критерий

Целевая функция здесь записывается следующим образом:

где П – знак произведения;

— весовой коэффициент i-го частного критерия;

— числовое значение i-го частного критерия.

Преимущества мультипликативного критерия:

Не требуется нормирование частных критериев.
Практически всегда определяется одно оптимальное решение.

Недостатки:

Трудности (субъективизм) в определении весовых коэффициентов.
Перемножение разных размерностей.
Взаимная компенсация значений частных критериев.

Максиминный (минимаксный) критерий

Эти критерии работают по принципу компромисса, который основывается на идее равномерности. Сущность принципа максимина заключается в следующем. При проектировании сложных систем, при наличии большого числа частных критериев установить между ними аналитическую взаимосвязь очень сложно. Поэтому стараются найти такие значения переменных (параметров) , при которых нормированные значения всех частных критериев равны между собой:

где — весовой коэффициент i-го частного критерия;

– нормированное значение i-го частного критерия;

K – константа.

При большом количестве частных критериев из-за сложных взаимосвязей добиться выполнения указанного выше соотношения очень сложно. Поэтому на практике так варьируют значениями переменных проектирования

x₁, x₂, … , x_m, при которых последовательно «подтягиваются» те нормированные критерии, численные значения которых в исходном решении оказались наименьшими. Т.к. эта операция производится в области компромисса, подтягивание «отстающего» критерия неизбежно приводит к снижению значений части остальных критериев. Но при проведении ряда шагов можно добиться определенной степени уравновешивания противоречивых частных критериев, что и является целью принципа максимина.

Формально принцип максимина формулируется следующим образом: выбрать такой набор переменных , при котором реализуется максимум из минимальных нормированных значений частных критериев, т.е. .

Такой принцип выбора иногда носит название гарантированного результата.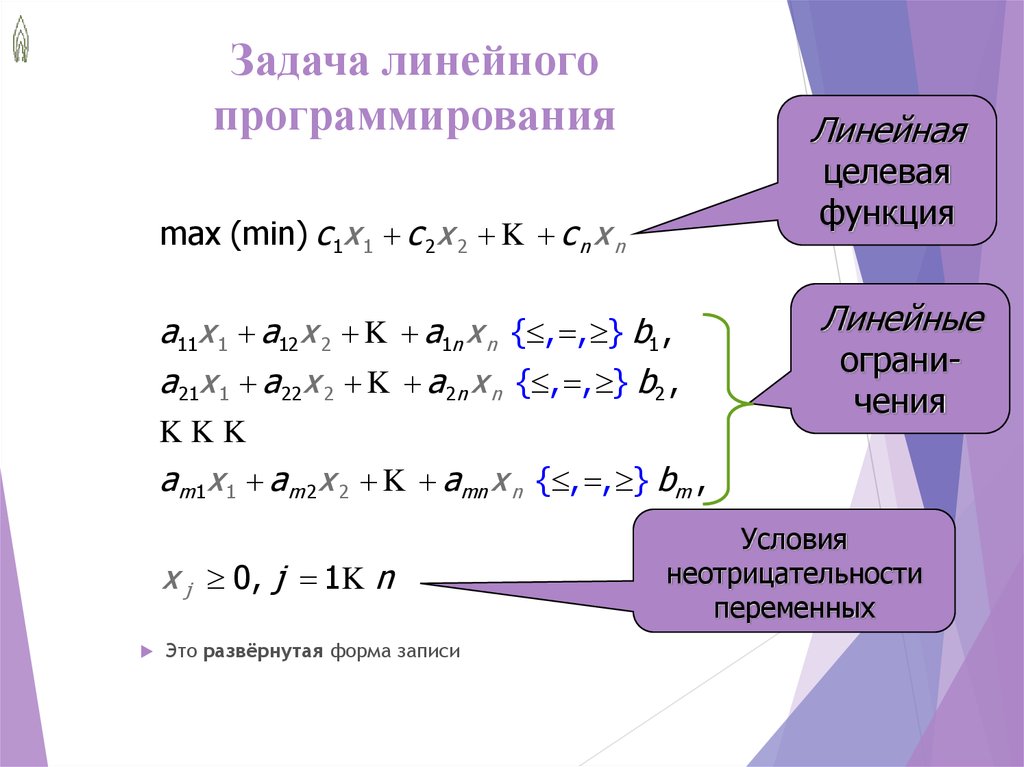 Он заимствован из теории игр, где является основным принципом.

Если частные критерии необходимо минимизировать, то самым отстающим критерием является тот, который принимает максимальное значение. В этом случае применяют принцип минимакса:

Основные принципы выбора критериев оптимальности

Выбор критериев – сложная задача, т.к. цели при проектировании любого объекта, как правило, противоречивы (обеспечение минимальной стоимости и максимальной надежности, максимальной производительности и минимальной энергоемкости и т.д.).

Если требуется оптимизировать один из показателей качества проектируемого объекта при соблюдении ограничительных требований на остальные показатели, то нужно сформировать один частный критерий. Задача оптимизации при этом сводится к задаче максимизации (минимизации) данного критерия с учетом заданных ограничений.

При наличии нескольких критериев выбирают:

а) аддитивный критерий, если существенное значение имеют абсолютные значения критериев при выбранном векторе параметров X;

б) мультипликативный критерий, если существенную роль играет изменение абсолютных значений частных критериев при вариации вектора X;

в) максиминный (минимаксный) критерий, если стоит задача достижения равенства нормированных значений противоречивых (конфликтных) частных критериев.

Линейное программирование | это… Что такое Линейное программирование?

Линейное программирование [linear programming] — область математического программирования, посвященная теории и методам решения экстремальных задач, характеризующихся линейной зависимостью между переменными.

В самом общем виде задачу Л.п. можно записать так. Даны ограничения типа

или в так называемой канонической форме, к которой можно привести все три указанных случая

Требуется найти неотрицательные числа x_j (j = 1, 2, …, n), которые минимизируют (или максимизируют) линейную форму

Неотрицательность искомых чисел записывается так:

Таким образом, здесь представлена общая задача математического программирования с теми оговорками, что как ограничения, так и целевая функция — линейные, а искомые переменные — неотрицательны.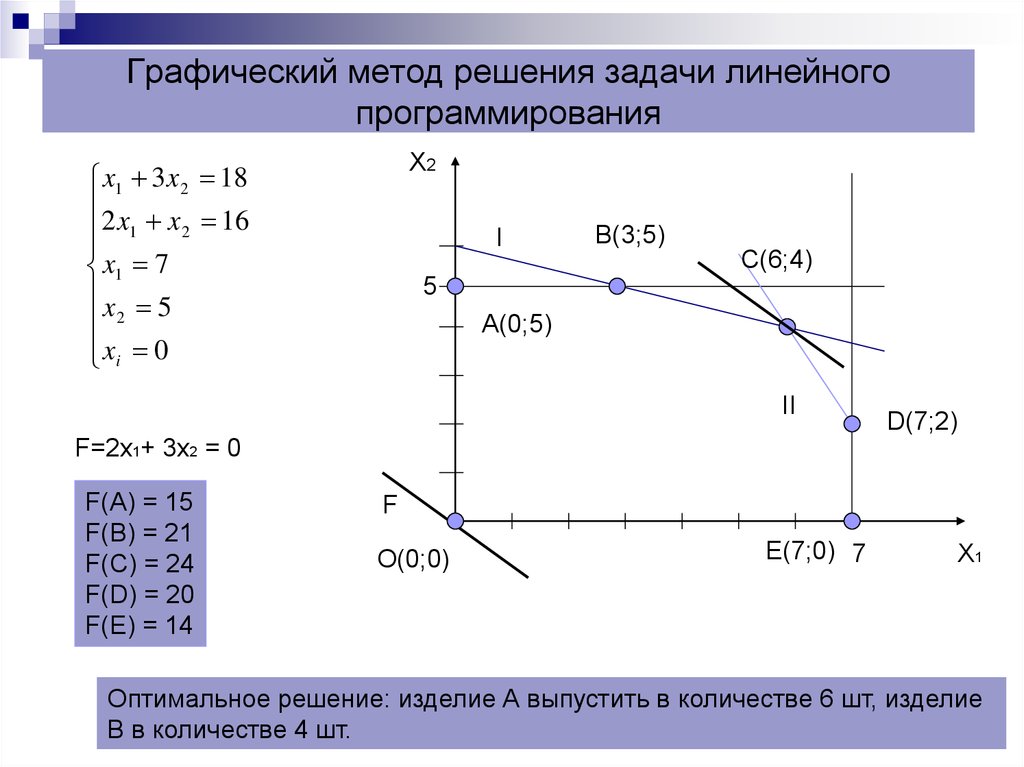 Обозначения можно трактовать следующим образом: b_i — количество ресурса вида i; m — количество видов этих ресурсов; a_ij — норма расхода ресурса вида i на единицу продукции вида j; x_j — количество продукции вида j, причем таких видов — n; c_j — доход (или другой выигрыш) от единицы этой продукции, а в случае задачи на минимум — затраты на единицу продукции; нумерация ресурсов разделена на три части: от 1 до m₁, от m₁ + 1 до m₂ и от m₂ + 1 до m в зависимости от того, какие ставятся ограничения на расходование этих ресурсов; в первом случае — «не больше», во втором — «столько же», в третьем — «не меньше»; Z — в случае максимизации, например, объем продукции или дохода, в случае же минимизации — себестоимость, расход сырья и т.п. Добавим еще одно обозначение, оно появится несколько ниже; v_i — оптимальная оценка i-го ресурса.

Слово «программирование» объясняется здесь тем, что неизвестные переменные, которые отыскиваются в процессе решения задачи, обычно в совокупности определяют программу (план) работы некоторого экономического объекта. Слово, «линейное» отражает факт линейной зависимости между переменными. При этом, как указано, задача обязательно имеет экстремальный характер, т.е. состоит в отыскании экстремума (максимума или минимума) целевой функции.

Следует с самого начала предупредить: предпосылка линейности, когда в реальной экономике подавляющее большинство зависимостей носит более сложный нелинейный характер, есть огрубление, упрощение действительности. В некоторых случаях оно достаточно реалистично, в других же выводы, получаемые с помощью решения задач Л.п. оказываются весьма несовершенными.

Рассмотрим две задачи Л.п. — на максимум и на минимум — на упрощенных примерах. Предположим, требуется разработать план производства двух видов продукции (объем первого — x₁; второго — x₂) с наиболее выгодным использованием трех видов ресурсов (наилучшим в смысле максимума общей прибыли от реализации плана). Условия задачи можно записать в виде таблицы (матрицы):

Вид продукции

Норма затратна единицу

продукции

Прибыль на единицу продукции

Исходя из норм, зафиксированных в таблице, запишем неравенства (ограничения):

a₁₁x₁ + a₁₂x₂≤ b_i

a₂₁x₁ + a₂₂x₂≤ b₂

a₃₁x₁ + a₃₂x₂≤ b₃

Это означает, что общий расход каждого из трех видов ресурсов не может быть больше его наличия. Поскольку выпуск продукции не может быть отрицательным, добавим еще два ограничения:

x₁≥ 0, x₂≥ 0.

Требуется найти такие значения x₁ и x₂, при которых общая сумма прибыли, т.е. величина c₁x₁ + c₂x₂ будет наибольшей, или короче:

Удобно показать условия задачи на графике (рис. Л.2).

Рис. Л.2 Линейное программирование, I (штриховкой окантована область допустимых решений)

Любая точка здесь, обозначаемая координатами x₁ и x₂, составляет вариант искомого плана. Очевидно, что, например, все точки, находящиеся в области, ограниченной осями координат и прямой AA, удовлетворяют тому условию, что не может быть израсходовано первого ресурса больше, чем его у нас имеется в наличии (в случае, если точка находится на самой прямой, ресурс используется полностью). Если то же рассуждение отнести к остальным ограничениям, то станет ясно, что всем условиям задачи удовлетворяет любая точка, находящаяся в пределах области, края которой заштрихованы, — она называется областью допустимых решений (или областью допустимых значений, допустимым множеством).

Остается найти ту из них, которая даст наибольшую прибыль, т.е. максимум целевой функции. Выбрав произвольно прямую c₁x₁ + c₂x₂ = П и обозначив ее MM, находим на чертеже все точки (варианты планов), где прибыль одинакова при любом сочетании x₁ и x₂ (см. Линия уровня). Перемещая эту линию параллельно ее исходному положению, найдем точку, которая в наибольшей мере удалена от начала координат, однако не вышла за пределы области допустимых значений. (Перемещая линию уровня еще дальше, уже выходим из нее и, следовательно, нарушаем ограничения задачи). Точка M₀ и будет искомым оптимальным планом. Она находится в одной из вершин многоугольника. Может быть и такой случай, когда линия уровня совпадает с одной из прямых, ограничивающих область допустимых значений, тогда оптимальным будет любой план, находящийся на соответствующем отрезке.

Координаты точки M₀ (т.е. оптимальный план) можно найти, решая совместно уравнения тех прямых, на пересечении которых она находится.

Противоположна изложенной другая задача Л.п.: поиск минимума функции при заданных ограничениях. Такая задача возникает, например, когда требуется найти наиболее дешевую смесь некоторых продуктов, содержащих необходимые компоненты (см. Задача о диете). При этом известно содержание каждого компонента в единице исходного продукта — a_ij, ее себестоимость — c_j ; задается потребность в искомых компонентах — b_i.

Эти данные можно записать в таблице (матрице), сходной с той, которая приведена выше, а затем построить уравнения как ограничений, так и целевой функции. Предыдущая задача решалась графически. Рассуждая аналогично, можно построить график (рис. Л.3), каждая точка которого — вариант искомого плана: сочетания разных количеств продуктов x₁ и x₂.

Рис.Л.3 Линейное программирование, II

Область допустимых решений здесь ничем сверху не ограничена: нужное количество заданных компонентов тем легче получить, чем больше исходных продуктов. Но требуется найти наиболее выгодное их сочетание. Пунктирные линии, как и в предыдущем примере, — линии уровня. Здесь они соединяют планы, при которых себестоимость смесей исходных продуктов одинакова. Линия, соответствующая наименьшему ее значению при заданных требованиях, — линия MM. Искомый оптимальный план — в точке M₀.

Приведенные крайне упрощенные примеры демонстрируют основные особенности задачи Л.п. Реальные задачи, насчитывающие много переменных, нельзя изобразить на плоскости — для их геометрической интерпретации используются абстрактные многомерные пространства. При этом допустимое решение задачи — точка в n-мерном пространстве, множество всех допустимых решений — выпуклое множество в этом пространстве (выпуклый многогранник).

Задачи Л.п., в которых нормативы (или коэффициенты), объемы ресурсов («константы ограничений«) или коэффициенты целевой функции содержат случайные элементы, называются задачами линейного стохастического программирования; когда же одна или несколько независимых переменных могут принимать только целочисленные значения, то перед нами задача линейного целочисленного программирования. В экономике широко применяются линейно-программные методы решения задач размещения производства (см. Транспортная задача), расчета рационов для скота (см. Задача диеты), наилучшего использования материалов (см. Задача о раскрое), распределения ресурсов по работам, которые надо выполнять (см. Распределительная задача) и т.д.

Разработан целый ряд вычислительных приемов, позволяющих решать на ЭВМ задачи линейного программирования, насчитывающие сотни и тысячи переменных, неравенств и уравнений. Среди них наибольшее распространение приобрели методы последовательного улучшения допустимого решения (см. Симплексный метод, Базисное решение), а также декомпозиционные методы решения крупноразмерных задач, методы динамического программирования и др. Сама разработка и исследование таких методов — развитая область вычислительной математики.

Один из видов решения имеет особое значение для экономической интерпретации задачи Л.п. Он связан с тем, что каждой прямой задаче Л.п. соответствует другая, симметричная ей двойственная задача (подробнее см. также Двойственность в линейном программировании). Если в качестве прямой принять задачу максимизации выпуска продукции (или объема реализации, прибыли и т.д.), то двойственная задача заключается, наоборот, в нахождении таких оценок ресурсов, которые минимизируют затраты. В случае оптимального решения ее целевая функция — сумма произведений оценки (цены) v_i каждого ресурса на его количество b_i— то есть равна целевой функции прямой задачи. Эта цена называется объективно обусловленной, или оптимальной оценкой, или разрешающим множителем. Основополагающий принцип Л.п. состоит в том, что в оптимальном плане и при оптимальных оценках всех ресурсов затраты и результаты равны.

Оценки двойственной задачи обладают замечательными свойствами: они показывают, насколько возрастет (или уменьшится) целевая функция прямой задачи при увеличении (или уменьшении) запаса соответствующего вида ресурсов на единицу. В частности, чем больше в нашем распоряжении данного ресурса по сравнению с потребностью в нем, тем ниже будет оценка, и наоборот. Не решая прямую задачу, по оценкам ресурсов, полученных в двойственной задаче, можно найти оптимальный план: в него войдут все технологические способы, которые оправдывают затраты, исчисленные в этих оценках (см. Объективно обусловленные (оптимальные) оценки).

Первооткрыватель Л.п. — советский ученый, академик, лауреат Ленинской, Государственной и Нобелевской премий Л. В.Канторович. В 1939 г. он решил математически несколько задач: о наилучшей загрузке машин, о раскрое материалов с наименьшими расходами, о распределении грузов по нескольким видам транспорта и др., при этом разработав универсальный метод решения этих задач, а также различные алгоритмы, реализующие его. Л.В.Канторович впервые точно сформулировал такие важные и теперь широко принятые экономико-математические понятия, как оптимальность плана, оптимальное распределение ресурсов, объективно обусловленные (оптимальные) оценки, указав многочисленные области экономики, где могут быть применены экономико-математические методы принятия оптимальных решений. Позднее, в 40—50-х годах, многое сделали в этой области американские ученые — экономист Т.Купманс и математик Дж. Данциг. Последнему принадлежит термин «линейное программирование».

См. также: Ассортиментные задачи, Базисное решение, Блочное программирование, Булево линейное программирование, Ведущий столбец, Ведущая строка, Вершина допустимого многогранника, Вырожденная задача, Гомори способ, Граничная точка, Двойственная задача, Двойственность в линейном программировании, Дифференциальные ренты, Дополняющая нежесткость, Жесткость и нежесткость ограничений ЛП, Задача диеты, Задача о назначениях, Задача о раскрое, Задачи размещения, Исходные уравнения, Куна — Таккера условия, Множители Лагранжа, Область допустимых решений, Опорная прямая, Распределительные задачи, Седловая точка, Симплексная таблица, Симплексный метод, Транспортная задача.

Экономико-математический словарь: Словарь современной экономической науки. — М.: Дело. Л. И. Лопатников. 2003.

Пять областей применения методов линейного программирования

Обновлено 21 мая 2018 г.

Дж. Дайан Дотсон

Линейное программирование используется для получения оптимальных решений для исследования операций. Использование линейного программирования позволяет исследователям найти лучшее и наиболее экономичное решение проблемы со всеми ее ограничениями или ограничениями. Многие области используют методы линейного программирования, чтобы сделать свои процессы более эффективными. К ним относятся продовольствие и сельское хозяйство, машиностроение, транспорт, производство и энергетика.

TL;DR (слишком длинное; не читал)

Линейное программирование предоставляет метод оптимизации операций при определенных ограничениях. Он используется, чтобы сделать процессы более эффективными и экономичными. Некоторые области применения линейного программирования включают продовольствие и сельское хозяйство, машиностроение, транспорт, производство и энергетику.

Обзор линейного программирования

Использование линейного программирования требует определения переменных, нахождения ограничений и нахождения целевой функции или того, что необходимо максимизировать. В некоторых случаях вместо этого используется линейное программирование для минимизации или наименьшего возможного значения целевой функции. Линейное программирование требует создания неравенств, а затем их графического отображения для решения задач. Хотя некоторое линейное программирование можно выполнить вручную, довольно часто переменные и расчеты становятся слишком сложными и требуют использования вычислительного программного обеспечения.

Продовольствие и сельское хозяйство

Фермеры применяют в своей работе методы линейного программирования. Определив, какие культуры они должны выращивать, в каком количестве и как их эффективно использовать, фермеры могут увеличить свои доходы.

В области питания линейное программирование представляет собой мощный инструмент, помогающий планировать диетические потребности. Чтобы обеспечить нуждающихся семей здоровыми и недорогими продуктовыми корзинами, диетологи могут использовать линейное программирование. Ограничения могут включать рекомендации по питанию, рекомендации по питательным веществам, культурную приемлемость или некоторую их комбинацию. Математическое моделирование помогает рассчитать продукты, необходимые для обеспечения питания по низкой цене в целях предотвращения неинфекционных заболеваний. Для таких расчетов необходимы необработанные данные о продуктах питания и ценах, при этом учитываются культурные аспекты типов продуктов питания. Целевой функцией является общая стоимость продуктовой корзины. Линейное программирование также позволяет изменять частоту изготовления таких корзин с едой во времени.

Применение в машиностроении

Инженеры также используют линейное программирование для решения задач проектирования и производства. Например, в аэродинамических сетках инженеры стремятся оптимизировать аэродинамическую форму. Это позволяет снизить коэффициент аэродинамического сопротивления аэродинамического профиля. Ограничения могут включать коэффициент подъемной силы, относительную максимальную толщину, радиус носа и угол задней кромки. Оптимизация формы направлена на создание безударного аэродинамического профиля приемлемой формы. Таким образом, линейное программирование предоставляет инженерам важный инструмент для оптимизации формы.

Оптимизация транспорта

Транспортные системы полагаются на линейное программирование для экономии средств и времени. Автобусные и железнодорожные маршруты должны учитывать расписание, время в пути и количество пассажиров. Авиакомпании используют линейное программирование для оптимизации своей прибыли в соответствии с различными ценами на места и потребительским спросом. Авиакомпании также используют линейное программирование для планирования пилотных полетов и маршрутов. Оптимизация с помощью линейного программирования повышает эффективность авиакомпаний и снижает расходы.

Эффективное производство

Производство требует преобразования сырья в продукты, которые максимизируют доход компании. Каждый этап производственного процесса должен работать эффективно для достижения этой цели. Например, сырье должно проходить через различные машины в течение заданного времени на сборочной линии. Чтобы максимизировать прибыль, компания может использовать линейное выражение количества используемого сырья. Ограничения включают время, затрачиваемое на каждую машину. Любые машины, создающие узкие места, должны быть устранены. Количество произведенной продукции может быть изменено, чтобы максимизировать прибыль в зависимости от сырья и необходимого времени.

Энергетика

Современные энергосистемы включают в себя не только традиционные электрические системы, но и возобновляемые источники энергии, такие как ветряная и солнечная фотоэлектрическая энергия. Для оптимизации требований к электрической нагрузке необходимо учитывать генераторы, линии передачи и распределения, а также накопители. В то же время затраты должны оставаться устойчивыми для получения прибыли. Линейное программирование обеспечивает метод оптимизации конструкции электроэнергетической системы. Это позволяет согласовать электрическую нагрузку по кратчайшему общему расстоянию между выработкой электроэнергии и ее потребностью во времени. Линейное программирование можно использовать для оптимизации согласования нагрузки или оптимизации затрат, что является ценным инструментом для энергетической отрасли.

Линейное программирование и его применение

Оптимизация — это новая потребность нашего времени. Все в этом мире вращается вокруг концепции оптимизации. Он находит свое применение в обычное время производства для решения проблем с цепочкой поставок. Чтобы решить эти проблемы, нам нужны концепции оптимизации. В учебном плане курса по науке о данных оптимизация является одним из таких инструментов, который работает везде. Вы можете выполнять оптимизацию различными способами. В курсе Data Science тема оптимизации является самой важной. Это дает представление о способах оптимизации. Проблема может быть простой и сложной. В обоих случаях оптимизация работает очень эффективно. Существуют различные способы оптимизации. Но линейное программирование — самое простое и легкое.

Это не займет у вас много времени и легко оптимизирует проблемы. Линейное программирование находит применение во всех сферах жизни, как личной, так и профессиональной. Он имеет приложения везде.

Возвращаясь домой, вы выбираете кратчайший путь, чтобы сэкономить время. Вы используете линейные способы программирования, чтобы вернуться домой пораньше. Этот вид программирования также имеет различное применение в проектах школы и колледжа.

Содержание

Что такое линейное программирование?
- Как работает линейное программирование?
- Некоторые известные методы для выполнения линейного программирования
  - 1) Симплексный метод
  - 2) Метод северо -западного углового
  - 3) Метод наименьшего количества
- Применение линейного программирования
- 1). оптимизация
- 3) Производственные единицы
- В заключение

Линейное программирование — самый простой метод оптимизации. Процесс оптимизации варьируется от простых проблем до сложных проблем. Но с этим вы можете решить все проблемы за меньшее время с простотой. Это поможет вам решить все сложные проблемы с помощью упрощенных предположений. Если вы аналитик данных из курса науки о данных, то вы обязаны решать проблемы с помощью этого.

Линейный метод используется в приложениях и на веб-сайтах для решения любой цепочки поставок и решения сложных проблем. Однако этому не уделяется столько внимания, как другим формам в курсе науки о данных. Это не значит, что линейное программирование этого не стоит. Это самый достойный процесс оптимизации; вы когда-нибудь столкнетесь.

В линейных способах программирования проблемы сложных отношений решаются с помощью линейных функций. Это делается для того, чтобы найти оптимальные точки для решения задачи. Здесь изображены сложные проблемы. Реальная проблема может быть более сложной. Тем не менее, используя этот тип программирования, вы можете решить эту проблему.

Видно, что в большинстве случаев такие формы программирования используются для получения подходящих оптимальных решений задачи.

Это делается путем учета ограничений для решения задач. Вам должно быть интересно, как это может решить реальные проблемы. Вопрос нормальный. Но ответ в том, что мы можем решать реальные задачи линейного программирования, используя математическую модель.

Модель содержит целевые функции и линейные неравенства, на которые распространяются заданные ограничения.

Как работает линейное программирование?

В курсе по науке о данных рассматриваются все подобные механизмы программирования для лучшего понимания материи. Как аналитик данных, вы должны много заниматься этой формой программирования, которая приводит вас к простым и оптимальным решениям. Для работы над такими программными моделями и задачами выполняются определенные шаги.

Первый шаг касается выявления проблемы. В нашем мире существует множество применений линейного программирования. Нужен только острый глаз, чтобы его заметить. Внимательно прочитайте о проблеме, прежде чем отправиться в путешествие по программированию. Примите во внимание проблему и отметьте все линейные функции, используемые в процессе линейного программирования.
После идеального анализа сложной проблемы вам необходимо записать все переменные решения и целевые функции. Переменные решения — это тип переменных, которые определяют результат вашей проблемы. Переменные представляют ваше оптимальное решение на последнем этапе этого процесса программирования.

Целевая функция называется функциями для задач, которые необходимо учитывать. Целевые функции помогают сделать процесс этого программирования окончательным.

Учитывайте все переменные и функции для получения оптимальных решений задач.

Обратите внимание на все ограничения изображенной математической модели в процессе программирования. Ограничения определяются как ограничения на переменные решения, которые учитываются при программировании. Для всех таких программ переменные решения должны быть неотрицательными. Он не может принимать отрицательные значения. Это означает, что они должны быть больше или равны нулю.
Теперь, записав все переменные, ограничения и функции, вы можете перейти к процессу решения. В этом типе программирования вы можете решать проблемы различными способами:

Графическими методами
Через R — инструмент с открытым исходным кодом, популярный среди аналитиков данных
Через открытый решатель — другой линейный программатор и оптимизатор с открытым исходным кодом
С помощью симплекс-метода — мощные и популярные методы линейного программирования

Вы можете решить свою сложную проблему любым из этих способов. В хорошем курсе по науке о данных упоминаются все методы решения сложных задач. Выберите один из ваших предпочтений и решите задачи программирования.

Некоторые известные методы линейного программирования

Линейное программирование действительно является простейшей формой программирования в области науки о данных. Некоторые известные методы преобладают в области, которой следуют для выполнения процесса.

Давайте рассмотрим эти известные методы в следующем разделе статьи:

1) Симплексный метод

Как следует из названия, это самый простой метод программирования. Симплексный метод — это мощный метод, который включает в себя итерационные процедуры программирования.

После всей процедуры вы получите реальный результат. Метод включает преобразование значений базовых переменных для получения оптимизированных значений целевой функции.

Ниже приведены шаги процедуры симплекс-метода:

Шаг 1. Сначала определите все переменные решения, как и в любой другой процедуре линейного программирования. Перечислите все переменные вашей проблемы, которые потребуются для решения вашей проблемы с помощью LP.
Шаг 2. Определите цель компании, которая использует этот метод. В этом методе основной задачей компании является максимальное увеличение аудитории. Все цели должны быть определены палачом в симплекс-методе.
Шаг 3. Следующим шагом является перечисление ограничений проблемы. Эти ограничения являются значениями, от которых зависит большинство основных переменных. Ограничения ограничивают значения основных переменных.
Шаг 4: составьте из этого уравнение и решите его соответствующим образом. Сформированное уравнение носит линейный характер и вращается вокруг основного линейного математического процесса.

Симплексный метод очень прост в применении, так как не требует сложного математического аппарата. Многие специалисты по данным используют этот метод для решения задач линейного уравнения.

2) Метод северо-западного угла

Это один из специальных типов методов линейного программирования, которые известны среди специалистов по данным. Здесь задачи переносятся в уравнения линейного программирования для получения приемлемого результата.

Все значения размещаются в верхнем левом углу таблицы уравнений.

Это одна из особенностей метода северо-западного угла. Этот метод находит свое применение в сфере грузоперевозок.

Метод включает следующие компоненты:

Уровень спроса и предложения каждого товара. Это должно быть известно программисту перед выполнением программирования.
Единица транспортировки используется для транспортировки товара от источника к месту назначения. Этот фактор также определяет выполнение процесса линейного программирования.

Этот метод основан на гипотетической теории, согласно которой общий спрос равен общему предложению. Это означает, что модель или уравнение сбалансированы во всех отношениях.

Однако спрос на поставку может исходить из нескольких источников в отрасли.

3) Метод наименьшего счета

Это один из лучших методов решения процедур программирования. Он дает более реальные и точные результаты, чем метод северо-западного угла.

Также используется в транспортной отрасли в производственных подразделениях.

Процедура метода наименьшего количества такая же, как и любого другого метода линейного программирования. Тем не менее, этот метод дает более точные результаты, чем любой другой из перечисленных выше методов.

Применение линейного программирования

Использование линейного программирования имеет множество практических применений. Они используются для оптимизации сложных задач. Многие отрасли внедряют инструменты линейного программирования для получения оптимальных решений. Производственная и обслуживающая отрасли регулярно используют этот метод программирования.

Линейное программирование находит применение в различных отраслях промышленности, где оно используется в процессе цепочки поставок. Как аналитик данных в этих отраслях, вы очень хорошо знаете об использовании этого программирования.

Ниже перечислены отрасли и области, в которых этот тип программирования находит свое применение:

1) Пищевая и сельскохозяйственная промышленность

Все фермеры применяют такие методы программирования в сельском хозяйстве, чтобы знать, какие культуры можно выращивать на земле. Фермеры знают, как использовать линейное программирование, поэтому они используют его для улучшения методов ведения сельского хозяйства. С помощью линейной техники они могут получать больше доходов от своей земли для получения прибыли.

2) Оптимизация транспорта

Транспортная отрасль использует такие методы программирования для экономии средств и времени. Все маршруты автобусов и поездов оптимизированы с помощью методов линейного программирования. В курсе по науке о данных оптимизация транспорта также преподается как отдельный предмет.

3) Производственные единицы

В обрабатывающей промышленности этот тип программирования используется в качестве основного инструмента оптимизации. Промышленность работает над этой техникой, чтобы увеличить прибыль компании. Все виды использования линейного программирования хорошо используются в промышленности.

В заключение

Вы можете найти другие варианты использования линейного программирования в курсе Data Science.

Методы линейного программирования имеют решающее значение для отраслей, упомянутых выше. Большинство работ по оптимизации приходится на линейное программирование для решения сложных задач. Чтобы изучить и освоить линейное программирование, запишитесь на курс по науке о данных прямо сейчас.

В случае каких-либо сомнений относительно линейного программирования, не стесняйтесь спрашивать нас в разделе комментариев.