Аргумент и основание логарифма
Любой логарифм имеет следующую «анатомию»:
Аргумент логарифма обычно пишется на его уровне, а основание — подстрочным шрифтом ближе к знаку логарифма. А читается эта запись так: «логарифм двадцати пяти по основанию пять».
Как вычислить логарифм?
Чтобы вычислить логарифм — нужно ответить на вопрос: в какую степень следует возвести основание, чтобы получить аргумент?
Например, вычислите логарифм: а) \(\log_{4}{16}\) б) \(\log_{3}\)\(\frac{1}{3}\) в) \(\log_{\sqrt{5}}{1}\) г) \(\log_{\sqrt{7}}{\sqrt{7}}\) д) \(\log_{3}{\sqrt{3}}\)
а) В какую степень надо возвести \(4\), чтобы получить \(16\)? Очевидно во вторую. Поэтому:
\(\log_{4}{16}=2\)
б) В какую степень надо возвести \(3\), чтобы получить \(\frac{1}{3}\)? В минус первую, так как именно отрицательная степень «переворачивает дробь» (здесь и далее пользуемся свойствами степени).
\(\log_{3}\)\(\frac{1}{3}\)\(=-1\)
в) В какую степень надо возвести \(\sqrt{5}\), чтобы получить \(1\)? А какая степень делает любое число единицей? Ноль, конечно!
\(\log_{\sqrt{5}}{1}=0\)
г) В какую степень надо возвести \(\sqrt{7}\), чтобы получить \(\sqrt{7}\)? В первую – любое число в первой степени равно самому себе.
\(\log_{\sqrt{7}}{\sqrt{7}}=1\)
д) В какую степень надо возвести \(3\), чтобы получить \(\sqrt{3}\)? Из свойств степени мы знаем, что корень – это дробная степень, и значит квадратный корень — это степень \(\frac{1}{2}\).
\(\log_{3}{\sqrt{3}}=\)\(\frac{1}{2}\)
Пример: Вычислить логарифм \(\log_{4\sqrt{2}}{8}\)
Решение:
|
\(\log_{4\sqrt{2}}{8}=x\) |
Нам надо найти значение логарифма, обозначим его за икс. |
|
|
\(\log_{4}{10}=5x-4\) |
Зеркально перевернем уравнение, чтобы икс был слева |
|
|
\(5x-4=\log_{4}{10}\) |
Перед нами линейное уравнение. Перенесем \(4\) вправо.
И не пугайтесь логарифма, относитесь к нему как к обычному числу. | |
|
\(5x=\log_{4}{10}+4\) |
Поделим уравнение на 5 |
|
|
\(x=\)\(\frac{\log_{4}{10}+4}{5}\) |
|
Вот наш корень. |
Ответ: \(\frac{\log_{4}{10}+4}{5}\)
Десятичный и натуральный логарифмы
Как указано в определении логарифма, его основанием может быть любое положительное число, кроме единицы \((a>0, a\neq1)\). И среди всех возможных оснований есть два встречающихся настолько часто, что для логарифмов с ними придумали особую короткую запись:
Натуральный логарифм: логарифм, у которого основание — число Эйлера \(e\) (равное примерно \(2,7182818…\)), и записывается такой логарифм как \(\ln{a}\).
То есть, \(\ln{a}\) это то же самое, что и \(\log_{e}{a}\), где \(a\) — некоторое число.
Десятичный логарифм: логарифм, у которого основание равно 10, записывается \(\lg{a}\).
То есть, \(\lg{a}\) это то же самое, что и \(\log_{10}{a}\), где \(a\) — некоторое число. {2}=25\)
{2}=25\)
Ответ готов.
Ответ: \(25\)
Как число записать в виде логарифма?
Как уже было сказано выше – любой логарифм это просто число. Верно и обратное: любое число может быть записано как логарифм. Например, мы знаем, что \(\log_{2}{4}\) равен двум. Тогда можно вместо двойки писать \(\log_{2}{4}\).
Но \(\log_{3}{9}\) тоже равен \(2\), значит, также можно записать \(2=\log_{3}{9}\) . Аналогично и с \(\log_{5}{25}\), и с \(\log_{9}{81}\), и т.д. То есть, получается
\(2=\log_{2}{4}=\log_{3}{9}=\log_{4}{16}=\log_{5}{25}=\log_{6}{36}=\log_{7}{49}…\)
Таким образом, если нам нужно, мы можем где угодно (хоть в уравнении, хоть в выражении, хоть в неравенстве) записывать двойку как логарифм с любым основанием – просто в качестве аргумента пишем основание в квадрате.
Точно также и с тройкой – ее можно записать как \(\log_{2}{8}\), или как \(\log_{3}{27}\), или как \(\log_{4}{64}\)… Здесь мы как аргумент пишем основание в кубе:
\(3=\log_{2}{8}=\log_{3}{27}=\log_{4}{64}=\log_{5}{125}=\log_{6}{216}=\log_{7}{343}…\)
И с четверкой:
\(4=\log_{2}{16}=\log_{3}{81}=\log_{4}{256}=\log_{5}{625}=\log_{6}{1296}=\log_{7}{2401}…\)
И с минус единицей:
\(-1=\) \(\log_{2}\)\(\frac{1}{2}\)\(=\) \(\log_{3}\)\(\frac{1}{3}\)\(=\) \(\log_{4}\)\(\frac{1}{4}\)\(=\) \(\log_{5}\)\(\frac{1}{5}\)\(=\) \(\log_{6}\)\(\frac{1}{6}\)\(=\) \(\log_{7}\)\(\frac{1}{7}\)\(…\)
И с одной третьей:
\(\frac{1}{3}\)\(=\log_{2}{\sqrt[3]{2}}=\log_{3}{\sqrt[3]{3}}=\log_{4}{\sqrt[3]{4}}=\log_{5}{\sqrt[3]{5}}=\log_{6}{\sqrt[3]{6}}=\log_{7}{\sqrt[3]{7}}…\)
И так далее.
Любое число \(a\) может быть представлено как логарифм с основанием \(b\): \(a=\log_{b}{b^{a}}\)
Пример: Найдите значение выражения \(\frac{\log_{2}{14}}{1+\log_{2}{7}}\)
Решение:
|
\(\frac{\log_{2}{14}}{1+\log_{2}{7}}\)\(=\) |
Превращаем единицу в логарифм с основанием \(2\): \(1=\log_{2}{2}\) |
|
|
\(=\)\(\frac{\log_{2}{14}}{\log_{2}{2}+\log_{2}{7}}\)\(=\) |
Теперь пользуемся свойством логарифмов: |
|
|
\(=\)\(\frac{\log_{2}{14}}{\log_{2}{(2\cdot7)}}\)\(=\)\(\frac{\log_{2}{14}}{\log_{2}{14}}\)\(=\) |
В числителе и знаменателе одинаковые числа – их можно сократить. |
|
|
\(=1\) |
Ответ готов. |
Ответ: \(1\)
Смотрите также:
Логарифмические уравнения
Логарифмические неравенства
Функция LOG — Служба поддержки Office
В этой статье описаны синтаксис формулы и использование функции LOG в Microsoft Excel.
Описание
Возвращает логарифм числа по заданному основанию.
Синтаксис
LOG(число;[основание])
Аргументы функции LOG описаны ниже.
-
Число Обязательный. Положительное вещественное число, для которого вычисляется логарифм.
-
Основание Необязательный. Основание логарифма. Если аргумент «основание» опущен, предполагается, что он равен 10.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Формула | Описание | Результат |
|---|---|---|
|
=LOG(10) |
Логарифм числа 10. |
1 |
|
=LOG(8; 2) |
Логарифм числа 8 по основанию 2. Результат (3) — степень, в которую необходимо возвести основание, чтобы получить число 8. |
3 |
|
=LOG(86; 2,7182818) |
Логарифм числа 86 по основанию e (приблизительно 2,718). Результат (4,454) — степень, в которую необходимо возвести основание, чтобы получить число 86. |
4,4543473 |
11.
 4.9.6. Формула представления любого числа в виде логарифма.
4.9.6. Формула представления любого числа в виде логарифма.Автор Татьяна Андрющенко На чтение 2 мин. Просмотров 3.1k. Опубликовано
p=logaap Любое число можно представить в виде логарифма по любому основанию.
Под знаком логарифма могут находиться только положительные числа, причем, основание логарифма не равно единице.
Примеры.
I. Представить число 2 в виде логарифма по основанию: 1) 3; 2) 5; 3) 10.
Решение.
1) 2=log33²=log39;
2) 2=log55²=log525;
3) 2=lg10²=lg100.
II. Представить в виде десятичного логарифма числа: 1) -1; 2) -2; 3) -3.
Решение.
1) -1=lg10—1=lg0,1;
2) -2=lg10-2=lg0,01;
3) -3=lg10-3=lg0,001.
Решить уравнение:
1) lg (x-9)+lg (2x-1)=2.
Решение.
lg ((x-9)(2x-1))=lg102; представили сумму логарифмов в виде логарифма произведения и число 2 в правой части равенства записали в виде десятичного логарифма (логарифма с основанием 10).
lg (2x2-18x-x+9)=lg100; упростили выражения под знаками логарифмов.
2x2-19x+9=100; получили после потенцирования.
2x2-19x-91=0. Получили квадратное уравнение вида: ax2+bx+c=0.
a=2, b=-19, c=-91. Решим квадратное уравнение по общей формуле.
D=b2-4ac=(-19)2-4∙2∙(-91)=361+728=1089=332>0; два действительных корня:
Проверка. Значение х=-3,5 не удовлетворяет условию существования логарифма.
Значение х=-3,5 не удовлетворяет условию существования логарифма.
Проверяем данное равенство при х=13.
lg (13-9)+lg (2∙13-1)=2;
lg4+lg25=2;
lg (4∙25)=2;
lg100=2;
2=2.
Ответ: 13.
2) log3(x+1)+log3(x+3)=1.
Решение.
Сумму логарифмов заменим логарифмом произведения, единицу в правой части представим в виде логарифма с основанием 3:
log ((x+1)(x+3))=log33;
log (x2+x+3x+3)=log33. Потенцируем:
x2+4x+3=3;
x2+4x=0;
x (x+4)=0;
x=0 или x+4=0, отсюда x=-4.
Анализируем результаты:
х=-4 не подойдет, так как при этом значении под знаком логарифма окажутся отрицательные числа, что недопустимо.
Проверим значение х=0.
Проверка.
log3(0+1)+log3(0+3)=1;
log31+log33=1;
0+1=1;
1=1.
Ответ: 0.
Натуральный логарифм, формулы и онлайн калькуляторы
Содержание:
Для различного рода теоретических и практических исследований наиболее удобным
основанием логарифма
является иррациональное число $e$. {2 n}}{n}+\ldots, |x| \lt 1$
{2 n}}{n}+\ldots, |x| \lt 1$
Читать дальше: десятичный логарифм.
log3 x 3 2
Вы искали log3 x 3 2? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и лог 3 х 3 2, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «log3 x 3 2».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как log3 x 3 2,лог 3 х 3 2,найдите корень уравнения log 3 x 3 2,найдите корень уравнения log3 3 x 3,найдите корень уравнения log3 x 3 2. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и log3 x 3 2. Просто введите задачу в окошко и нажмите
«решить» здесь (например, найдите корень уравнения log 3 x 3 2).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и log3 x 3 2. Просто введите задачу в окошко и нажмите
«решить» здесь (например, найдите корень уравнения log 3 x 3 2).
Где можно решить любую задачу по математике, а так же log3 x 3 2 Онлайн?
Решить задачу log3 x 3 2 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Рабочая тетрадь по математике. Логарифмы. Свойства логарифмов.
государственное автономное профессиональное образовательное учреждение
Саратовской области
«Саратовский колледж кулинарного искусства»
О. В. Улитина
преподаватель математики ГАПОУ СО СККИ
РАБОЧАЯ ТЕТРАДЬ ПО МАТЕМАТИКЕ
Логарифмы. Свойства логарифмов.
Учебное пособие для студентов ОУ СПО
по учебной дисциплине «Математика» Математика
2017 г
АННОТАЦИЯ
В данном пособии представлен раздел математики 1 курса «Логарифмы.
Свойства логарифмов» в учреждениях среднего профессионального
образования. При изучении данного раздела студентами появляется множество
проблем, которые связаны не только со слабой базовой подготовкой студентов
по основным темам школьного курса, но и с недостаточностью упражнений,
предлагаемых учебниками.
Необходимо увеличить количество упражнений, тестов решаемых
студентами на уроках для лучшего понимания раздела. В данном учебном
пособии представлены упражнения, разработанные по принципу «от простого к
сложному», позволяющие решить проблемы количества упражнений и качества
знаний по данному разделу. Решение задач является одним из видов учебной
работы обучающихся. Поэтому основные цели создания данного пособия:
самостоятельности,
систематизация и закрепление теоретических знаний и практических
умений обучающихся;
углубление и расширение теоретических знаний, формирование умений
использовать справочную документацию и дополнительную литературу;
развитие познавательных способностей и активности обучающихся,
творческой инициативы,
ответственности и
организованности;
формирование самостоятельного мышления.
В. Улитина
преподаватель математики ГАПОУ СО СККИ
РАБОЧАЯ ТЕТРАДЬ ПО МАТЕМАТИКЕ
Логарифмы. Свойства логарифмов.
Учебное пособие для студентов ОУ СПО
по учебной дисциплине «Математика» Математика
2017 г
АННОТАЦИЯ
В данном пособии представлен раздел математики 1 курса «Логарифмы.
Свойства логарифмов» в учреждениях среднего профессионального
образования. При изучении данного раздела студентами появляется множество
проблем, которые связаны не только со слабой базовой подготовкой студентов
по основным темам школьного курса, но и с недостаточностью упражнений,
предлагаемых учебниками.
Необходимо увеличить количество упражнений, тестов решаемых
студентами на уроках для лучшего понимания раздела. В данном учебном
пособии представлены упражнения, разработанные по принципу «от простого к
сложному», позволяющие решить проблемы количества упражнений и качества
знаний по данному разделу. Решение задач является одним из видов учебной
работы обучающихся. Поэтому основные цели создания данного пособия:
самостоятельности,
систематизация и закрепление теоретических знаний и практических
умений обучающихся;
углубление и расширение теоретических знаний, формирование умений
использовать справочную документацию и дополнительную литературу;
развитие познавательных способностей и активности обучающихся,
творческой инициативы,
ответственности и
организованности;
формирование самостоятельного мышления. Содержание учебного пособия соответствует образовательным стандартам
профессионального образования и может быть использовано для различных
специальностей и профессий. В данном пособии представлены упражнения,
тесты, задания, которые автор в течение многих лет использовала на своих
уроках и полученные результаты позволяют сделать следующий вывод:
используемые упражнения помогают студентам восстановить пробелы в знаниях
по темам «Степени», «Корни» и понять темы «Логарифмы», «Свойства
логарифмов». Пособие содержит как небольшой теоретический материал для
изучения тем раздела, так и решенные примеры в качества образца.
.
2 Математика
ЛОГАРИФМ
Операцию нахождения логарифма числа называют логарифмированием. Эта
операция является обратной по отношению к возведению в степень с соответствующим
основанием.
Определение логарифма
Логарифмом числа b по основанию a, где a > 0, a ≠ 1, называется показатель
степени, в которую надо возвести число a, чтобы получить b:
log
a
b
b
a
x
x
при a > 0, a ≠ 1, b > 0.
Содержание учебного пособия соответствует образовательным стандартам
профессионального образования и может быть использовано для различных
специальностей и профессий. В данном пособии представлены упражнения,
тесты, задания, которые автор в течение многих лет использовала на своих
уроках и полученные результаты позволяют сделать следующий вывод:
используемые упражнения помогают студентам восстановить пробелы в знаниях
по темам «Степени», «Корни» и понять темы «Логарифмы», «Свойства
логарифмов». Пособие содержит как небольшой теоретический материал для
изучения тем раздела, так и решенные примеры в качества образца.
.
2 Математика
ЛОГАРИФМ
Операцию нахождения логарифма числа называют логарифмированием. Эта
операция является обратной по отношению к возведению в степень с соответствующим
основанием.
Определение логарифма
Логарифмом числа b по основанию a, где a > 0, a ≠ 1, называется показатель
степени, в которую надо возвести число a, чтобы получить b:
log
a
b
b
a
x
x
при a > 0, a ≠ 1, b > 0. Например:
2
2
5
3
log
25
9
16
log
log
3
2
4
2
25
2
2
16
5
9
4
Задание1: Запишите с помощью логарифма
1
2
1)3
3
3
5
7)32
8)3
2)2
3)4
1
8
16
2;
9;
3
2
1
2
1
5
;
2
1
;
5)9
3;
0
6)7
1
4)5
1
25
;
3
10)81
4
27;
11)32
8;
2
3
9
9)27
12)125
2
3
25
Задание 1
3 Математика
Задание 2: Запишите в виде степенного выражения
1) log
1
81
4)log 16
3
1
2
4;
4;
2) log 256 4;
4
5) log 729 3;
9
3) log 343 3;
7
6) log 1 0;
14
7) log
9
16
3
4
2;
8) log
7
4
7
1
4
;
9) log
13
3
2
13
2
3
;
10) log 32 5
2
Определение логарифма можно записать на математическом языке
следующим образом:
, где
a
,0
a
,1
b
0
.
, где
к
a
,0
a
,1
b
0
к
log
a
b
a
b
Задание 2
, к0
a
log
ba
b
Полученное равенство называется основным логарифмическим тождеством.
Если основное логарифмическое тождество усложнить, то получим формулу:
4 Математика
log 5
12
Задание 3: Найдите значение выражения
1)12
6)9
3) 2
8)7
;
2log 11
2)4
7)11
log 6
;
3log 6
11
4)8
2log 4
log 7
2
7
;
;
;
;
4
9
log 13
8
9)6
;
4log 3
6
5)5
;
5
log 11
;
10)3
5log 2
.
Например:
2
2
5
3
log
25
9
16
log
log
3
2
4
2
25
2
2
16
5
9
4
Задание1: Запишите с помощью логарифма
1
2
1)3
3
3
5
7)32
8)3
2)2
3)4
1
8
16
2;
9;
3
2
1
2
1
5
;
2
1
;
5)9
3;
0
6)7
1
4)5
1
25
;
3
10)81
4
27;
11)32
8;
2
3
9
9)27
12)125
2
3
25
Задание 1
3 Математика
Задание 2: Запишите в виде степенного выражения
1) log
1
81
4)log 16
3
1
2
4;
4;
2) log 256 4;
4
5) log 729 3;
9
3) log 343 3;
7
6) log 1 0;
14
7) log
9
16
3
4
2;
8) log
7
4
7
1
4
;
9) log
13
3
2
13
2
3
;
10) log 32 5
2
Определение логарифма можно записать на математическом языке
следующим образом:
, где
a
,0
a
,1
b
0
.
, где
к
a
,0
a
,1
b
0
к
log
a
b
a
b
Задание 2
, к0
a
log
ba
b
Полученное равенство называется основным логарифмическим тождеством.
Если основное логарифмическое тождество усложнить, то получим формулу:
4 Математика
log 5
12
Задание 3: Найдите значение выражения
1)12
6)9
3) 2
8)7
;
2log 11
2)4
7)11
log 6
;
3log 6
11
4)8
2log 4
log 7
2
7
;
;
;
;
4
9
log 13
8
9)6
;
4log 3
6
5)5
;
5
log 11
;
10)3
5log 2
. 3
Логарифм по основанию 10 называется десятичным логарифмом и обозначается
,
blg
называется натуральным логарифмом и обозначается
логарифм по основанию
( ee
…)7,2
.
bln
Задание 3
5 Математика
При вычислении логарифмов используется таблица степеней:
10
1024
59049
1
2
3
4
5
6
7
8
9
10
2
4
9
16
25
36
49
64
81
10
0
6
64
729
4096
15625
46656
117649
7
128
2187
16 384
78125
279936
823543
3
8
27
64
125
216
343
512
729
1000
8
256
6561
65 536
390625
1679616
5764801
9
512
19683
262 144
1953125
1007696
4035360
7
5
4
32
16
243
81
1024
256
3125
625
1296
7776
2401 16807
2
3
4
5
6
7
8
9
1
0
Степень (результат логарифмирования)
Таблица квадратов
А 11
26
13
А2 121 144 169 196 225 256 289 324 361 400 441 484 529 576 625 676
10 48576
9765625
60466176
282475249
1000 000
100 000
10 000
12
21
22
14
23
24
25
18
19
20
15
16
17
Примеры с решениями
1. Вычислите
.
log 2
1
125,0
Решение.
log
2
1
125,0
log
)5,0(
2
3
log
2
3
1
2
log
2
3
2
log3
2
2
.3
Ответ:
.
log 2
1
125,0
3
2.
3
Логарифм по основанию 10 называется десятичным логарифмом и обозначается
,
blg
называется натуральным логарифмом и обозначается
логарифм по основанию
( ee
…)7,2
.
bln
Задание 3
5 Математика
При вычислении логарифмов используется таблица степеней:
10
1024
59049
1
2
3
4
5
6
7
8
9
10
2
4
9
16
25
36
49
64
81
10
0
6
64
729
4096
15625
46656
117649
7
128
2187
16 384
78125
279936
823543
3
8
27
64
125
216
343
512
729
1000
8
256
6561
65 536
390625
1679616
5764801
9
512
19683
262 144
1953125
1007696
4035360
7
5
4
32
16
243
81
1024
256
3125
625
1296
7776
2401 16807
2
3
4
5
6
7
8
9
1
0
Степень (результат логарифмирования)
Таблица квадратов
А 11
26
13
А2 121 144 169 196 225 256 289 324 361 400 441 484 529 576 625 676
10 48576
9765625
60466176
282475249
1000 000
100 000
10 000
12
21
22
14
23
24
25
18
19
20
15
16
17
Примеры с решениями
1. Вычислите
.
log 2
1
125,0
Решение.
log
2
1
125,0
log
)5,0(
2
3
log
2
3
1
2
log
2
3
2
log3
2
2
.3
Ответ:
.
log 2
1
125,0
3
2. Вычислите
Решение.
3
1,0lg
100
.
1,0lg
3
100
lg(
10
3. Вычислите
13
log13
04,0
.
2
3
1
10
)
lg
10
1
3
lg
10
1
3
1
3
.
Решение.
log
13
04,0
13
4. Вычислите
2
1
log
4
10
10
Решение. Т. к. выражение
1
2
log
13
04,0
13
log
13
04,0
1
2
1
2
04,0
04,0
.2,0
13
.
1
log
4
10
log
log
4
4
10
4
, то решение принимает вид:
4lg
6 Математика
2
1
log
4
10
10
100
4lg
10
100
4
.25
Задание 4: Вычислите, используя таблицу степеней
1)log 1024;
2
2)log
3
1
243
;
3)log
1
5
5)log
4
1
256
;
9)log
4
5
13)log
2
4;
1
2
3
;
4
Задание 4
1
625
1
512
;
;
4)log 512;
2
8)log 216;
6
6
7 ;
12)log
6
3
2
6 ;
6)log 729;
1
3
10)log
3
4
5
3 ;
7)log
1
8
11)log
7
14) log
11
1
11
;
15) log
15
5
1
11
;
16)log
7
1
7
3
.
7 Математика
3
1) log
Задание 5: Выберите номер правильного ответа
81
7)3
) log 3 81;
a
b
) log 81 4;
)log 4 3
c
3
4)8
)log 8 512;
a
b
)log 512 3;
)log
c
8 3
512
3
4
4
4
3
8
512
3
81
4
1
64
64;
64;
3
4
)4
a
b
)3
)64
c
243
5
2)3
)log 3 243;
a
b
)log 243 5;
) log 243 3
c
5
3
5
3)log 216 3
6
)3
a
3
)6
b
216;
216;
6
5
10)2
)log 2 32;
a
b
)log 32 5;
) log 32 2
c
32
5
2
5
21
5) log 441 2
2
441;
)21
a
21
441;
)2
b
c
) 441 21
1
49
49;
49;
1
49
)2
a
2
)7
b
6)log
)7
c
7
;
2
7
2
729;
729;
9
8) log 729 3
9
9
)3
a
3
)9
b
3
)729
c
9) log 144 2
12
144;
)12
a
12
144;
b
)2
) 144 12
c
2
20
11) log 400 2
20
400;
)2
a
400;
b
)20
) 400
20
c
2
Задание 5
8 Математика
1.
Вычислите
Решение.
3
1,0lg
100
.
1,0lg
3
100
lg(
10
3. Вычислите
13
log13
04,0
.
2
3
1
10
)
lg
10
1
3
lg
10
1
3
1
3
.
Решение.
log
13
04,0
13
4. Вычислите
2
1
log
4
10
10
Решение. Т. к. выражение
1
2
log
13
04,0
13
log
13
04,0
1
2
1
2
04,0
04,0
.2,0
13
.
1
log
4
10
log
log
4
4
10
4
, то решение принимает вид:
4lg
6 Математика
2
1
log
4
10
10
100
4lg
10
100
4
.25
Задание 4: Вычислите, используя таблицу степеней
1)log 1024;
2
2)log
3
1
243
;
3)log
1
5
5)log
4
1
256
;
9)log
4
5
13)log
2
4;
1
2
3
;
4
Задание 4
1
625
1
512
;
;
4)log 512;
2
8)log 216;
6
6
7 ;
12)log
6
3
2
6 ;
6)log 729;
1
3
10)log
3
4
5
3 ;
7)log
1
8
11)log
7
14) log
11
1
11
;
15) log
15
5
1
11
;
16)log
7
1
7
3
.
7 Математика
3
1) log
Задание 5: Выберите номер правильного ответа
81
7)3
) log 3 81;
a
b
) log 81 4;
)log 4 3
c
3
4)8
)log 8 512;
a
b
)log 512 3;
)log
c
8 3
512
3
4
4
4
3
8
512
3
81
4
1
64
64;
64;
3
4
)4
a
b
)3
)64
c
243
5
2)3
)log 3 243;
a
b
)log 243 5;
) log 243 3
c
5
3
5
3)log 216 3
6
)3
a
3
)6
b
216;
216;
6
5
10)2
)log 2 32;
a
b
)log 32 5;
) log 32 2
c
32
5
2
5
21
5) log 441 2
2
441;
)21
a
21
441;
)2
b
c
) 441 21
1
49
49;
49;
1
49
)2
a
2
)7
b
6)log
)7
c
7
;
2
7
2
729;
729;
9
8) log 729 3
9
9
)3
a
3
)9
b
3
)729
c
9) log 144 2
12
144;
)12
a
12
144;
b
)2
) 144 12
c
2
20
11) log 400 2
20
400;
)2
a
400;
b
)20
) 400
20
c
2
Задание 5
8 Математика
1. 2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
5
1
3
1
5
1
9
1
8
1
2
3
4
Задание6: Выпишите номера примеров, решенных неверно
1)log 27
3
2
2)log 16
0, 4 2
3) log
4)log 125 3
2
5) log 9
4
0,09 2
1
625
2
11) log 36
7)log 729
8)log 16
9) log
10) log
0,2
4
9
2
3
0,3
5
1
6
12) log
0,5
0,125 3
0, 25 2
0,5
6) log
Задание 6
Задание 7. Найдите логарифмы данных чисел по основанию α:
1)25,
, 5
а
5
2)64,
, 2
а
8
3)16,
1
4
, 2
а
2
4)27,
, 3
а
3
5)2,
,1,0
а
4
Задание 7
Задание 8. Заполни таблицу, используя определение логарифма:
a x
N
log
xNa
log10
1000
3
9
Найти х по заданным условиям
Неизвестное
Условие
х
log 3
1 Математика
log 7 х
2
х
log11
2
2
36,0
log
log х
5
2
1
х
4
625
log
log
2
х
х
4
2
log 6
36
log 8
01
log 3
1
81
4
log 3
х
1
343
х125
log 2,0
log 2
log10
х16
х01,0
7 3
4 3
343
1
64
10 2
01,0
1
32 5
2
2
125 3
25
2,0 3
008,0
1 3
3
27
Задание 9. Используя определение логарифма выберите номер правильного ответа:
ВАРИАНТ 1 ВАРИАНТ 2
10 Математика
4
;
x
1)log
)
b x
)
a x
1
64
3;
1
3
)
c x
3
5
2)3
243
) log 3 243;
a
) log 243 5;
b
) log 243 3
c
3)log 25
2
)
a x
)
b x
3
5
5
;
)
c x
x
5;
5;
1
5
5
)
d x
4)log
x
3
6
)
a x
18;
)
b x
2;
)
c x
216;
9
)
d x
5)log
x
7
14;
)
a x
)
49;
b x
1
49
)
c x
;
2
2
2
6)log 144
12
)12
144;
a
12
144;
)2
b
c
) 144 12
1
225
x
7) log
)
a x
)
b x
15
;
2;
1
2
2
512
3
)
c x
3
8)8
) log 8 512;
a
) log 512 3;
b
)log
c
9)log 64
)
a x
)
b x
8 3
512
2
8
6
;
)
c x
x
8;
8;
1
8
8
)
d x
10) log
x
2
12;
)
a x
)
3;
b x
64;
)
c x
)
8
d x
11) log
x
13
26;
)
a x
)
169;
b x
1
169
)
c x
;
2
12) log 441 2
21
2
441;
)2
a
1
21
441;
)2
b
) 441
21
c
x
2
1) log
3
4
4
;
81
)
b x
)
a x
1
256
4;
1
4
)
c x
4
4
2)3
81
)log 3 81;
a
)log 81 4;
b
) log 4 3
c
3) log 36
x
)
6;
a x
)
6;
b x
1
6
6
)
d x
x
3
4)log
7
21;
)
a x
10;
)
b x
343;
)
c x
5) log
x
11
22;
)
a x
121;
)
b x
1
121
)
c x
)
c x
;
;
2
6)log 243 3
9
9
243;
a
)3
3
2
b
43;
)9
3
)243
c
9
x
;
)
b x
)
a x
7) log
1
5
125
3;
1
3
)
c x
3
5
8)2
32
)log 2 32;
a
)log 32 5;
b
)log 32 2
c
9) log 484
)
a x
)
b x
x
22;
22;
1
22
)
c x
;
5
2
5
2
2
22
)
d x
10)log
x
25
)
a x
27;
)
b x
50;
)
c x
625;
23
)
d x
11)log
x
17
)
a x
34;
)
289;
b x
1
289
)
c x
;
20
12)log 400
20
400;
)2
a
)20
400;
b
) 400
c
20
2
2
2
Ответы запишите в таблицу:
1
5
3
4
2
6
7
8
9
10
11
12
11 Математика
Для всех свойств логарифмов выполняются соответствующие условия:
СВОЙСТВА ЛОГАРИФМОВ
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
5
1
3
1
5
1
9
1
8
1
2
3
4
Задание6: Выпишите номера примеров, решенных неверно
1)log 27
3
2
2)log 16
0, 4 2
3) log
4)log 125 3
2
5) log 9
4
0,09 2
1
625
2
11) log 36
7)log 729
8)log 16
9) log
10) log
0,2
4
9
2
3
0,3
5
1
6
12) log
0,5
0,125 3
0, 25 2
0,5
6) log
Задание 6
Задание 7. Найдите логарифмы данных чисел по основанию α:
1)25,
, 5
а
5
2)64,
, 2
а
8
3)16,
1
4
, 2
а
2
4)27,
, 3
а
3
5)2,
,1,0
а
4
Задание 7
Задание 8. Заполни таблицу, используя определение логарифма:
a x
N
log
xNa
log10
1000
3
9
Найти х по заданным условиям
Неизвестное
Условие
х
log 3
1 Математика
log 7 х
2
х
log11
2
2
36,0
log
log х
5
2
1
х
4
625
log
log
2
х
х
4
2
log 6
36
log 8
01
log 3
1
81
4
log 3
х
1
343
х125
log 2,0
log 2
log10
х16
х01,0
7 3
4 3
343
1
64
10 2
01,0
1
32 5
2
2
125 3
25
2,0 3
008,0
1 3
3
27
Задание 9. Используя определение логарифма выберите номер правильного ответа:
ВАРИАНТ 1 ВАРИАНТ 2
10 Математика
4
;
x
1)log
)
b x
)
a x
1
64
3;
1
3
)
c x
3
5
2)3
243
) log 3 243;
a
) log 243 5;
b
) log 243 3
c
3)log 25
2
)
a x
)
b x
3
5
5
;
)
c x
x
5;
5;
1
5
5
)
d x
4)log
x
3
6
)
a x
18;
)
b x
2;
)
c x
216;
9
)
d x
5)log
x
7
14;
)
a x
)
49;
b x
1
49
)
c x
;
2
2
2
6)log 144
12
)12
144;
a
12
144;
)2
b
c
) 144 12
1
225
x
7) log
)
a x
)
b x
15
;
2;
1
2
2
512
3
)
c x
3
8)8
) log 8 512;
a
) log 512 3;
b
)log
c
9)log 64
)
a x
)
b x
8 3
512
2
8
6
;
)
c x
x
8;
8;
1
8
8
)
d x
10) log
x
2
12;
)
a x
)
3;
b x
64;
)
c x
)
8
d x
11) log
x
13
26;
)
a x
)
169;
b x
1
169
)
c x
;
2
12) log 441 2
21
2
441;
)2
a
1
21
441;
)2
b
) 441
21
c
x
2
1) log
3
4
4
;
81
)
b x
)
a x
1
256
4;
1
4
)
c x
4
4
2)3
81
)log 3 81;
a
)log 81 4;
b
) log 4 3
c
3) log 36
x
)
6;
a x
)
6;
b x
1
6
6
)
d x
x
3
4)log
7
21;
)
a x
10;
)
b x
343;
)
c x
5) log
x
11
22;
)
a x
121;
)
b x
1
121
)
c x
)
c x
;
;
2
6)log 243 3
9
9
243;
a
)3
3
2
b
43;
)9
3
)243
c
9
x
;
)
b x
)
a x
7) log
1
5
125
3;
1
3
)
c x
3
5
8)2
32
)log 2 32;
a
)log 32 5;
b
)log 32 2
c
9) log 484
)
a x
)
b x
x
22;
22;
1
22
)
c x
;
5
2
5
2
2
22
)
d x
10)log
x
25
)
a x
27;
)
b x
50;
)
c x
625;
23
)
d x
11)log
x
17
)
a x
34;
)
289;
b x
1
289
)
c x
;
20
12)log 400
20
400;
)2
a
)20
400;
b
) 400
c
20
2
2
2
Ответы запишите в таблицу:
1
5
3
4
2
6
7
8
9
10
11
12
11 Математика
Для всех свойств логарифмов выполняются соответствующие условия:
СВОЙСТВА ЛОГАРИФМОВ
1. 2.
3.
4.
5.
6.
7.
8.
9.
log aa
1
log a
01
при
при
a
a
;
a
,0
1
;
a
,0
1
при
c
a
при
log
a
bc
(
)
log
b
a
log
a
,0
a
,1
b
,0
c
log
a
b
c
log
a
b
log
a
c
b
a
при
log
a
p
b
p
log
log
b
a
log
log
c
c
b
a
a
,0
a
,1
b
,0
c
при
a
,0
a
,1
b
0
;
a
,0
a
,1
b
,0
c
,0
ñ
0
;
0
;
0
.
Полезно также знать и другие свойства логарифмов:
log
b
a
при
a
,0
a
,1
b
,0
b
1
;
1
log
b
a
log
an
m
b
m
n
log
a
b
при
log
an
b
log
a
b
1
n
при
a
,0
a
,1
b
0
;
a
,0
a
,1
b
0
.
Полезно также знать и «хитрости» свойств логарифмов:
log
a
b
2
log2
b
a
при
a
,0
a
;
0
log
a
bc
(
)
log
a
b
log
a
a
,0
a
,1
b
,0
c
log
a
b
c
log
a
a
c
log
b
c
log
b
a
b
при
log
a
c
a
,0
a
,1
b
,0
c
a
,0
b
,0
b
,0
c
0
.
;
0
.
0
b
,1
при
c
при
Логарифм по основанию 10 называется десятичным логарифмом:
log10
a
lg
a
Десятичным логарифмом называется логарифм по основанию 10.
2.
3.
4.
5.
6.
7.
8.
9.
log aa
1
log a
01
при
при
a
a
;
a
,0
1
;
a
,0
1
при
c
a
при
log
a
bc
(
)
log
b
a
log
a
,0
a
,1
b
,0
c
log
a
b
c
log
a
b
log
a
c
b
a
при
log
a
p
b
p
log
log
b
a
log
log
c
c
b
a
a
,0
a
,1
b
,0
c
при
a
,0
a
,1
b
0
;
a
,0
a
,1
b
,0
c
,0
ñ
0
;
0
;
0
.
Полезно также знать и другие свойства логарифмов:
log
b
a
при
a
,0
a
,1
b
,0
b
1
;
1
log
b
a
log
an
m
b
m
n
log
a
b
при
log
an
b
log
a
b
1
n
при
a
,0
a
,1
b
0
;
a
,0
a
,1
b
0
.
Полезно также знать и «хитрости» свойств логарифмов:
log
a
b
2
log2
b
a
при
a
,0
a
;
0
log
a
bc
(
)
log
a
b
log
a
a
,0
a
,1
b
,0
c
log
a
b
c
log
a
a
c
log
b
c
log
b
a
b
при
log
a
c
a
,0
a
,1
b
,0
c
a
,0
b
,0
b
,0
c
0
.
;
0
.
0
b
,1
при
c
при
Логарифм по основанию 10 называется десятичным логарифмом:
log10
a
lg
a
Десятичным логарифмом называется логарифм по основанию 10. Он обозначается lg ,
т.е. log 10 N = lg N . Логарифмы чисел 10, 100, 1000, … pавны соответственно 1, 2, 3, …, т.е.
имеют столько положительных
единиц, сколько нулей стоит в логарифмируемом числе после единицы. Логарифмы чисел 0.1,
0.01, 0.001, … pавны соответственно –1, –2, –3, …, т.е. имеют столько отрицательных единиц,
сколько нулей стоит в логарифмируемом числе перед единицей ( считая и нуль целых ).
Логарифмы остальных чисел имеют дробную часть, называемую мантиссой. Целая часть
логарифма называется характеристикой. Для практического применения десятичные
логарифмы наиболее удобны.
12 Математика
Натуральным логарифмом называется логарифм по основанию е. Он обозначается ln ,
т.е. log e N = ln N. Число е является иррациональным, его приближённое значение
2.718281828. Оно является пределом, к которому стремится число ( 1 + 1 / n ) n при
неограниченном возрастании n
Логарифм по основанию е называется натуральным логарифмом:
log
ae
ln
a
Примеры с решениями
1.
Он обозначается lg ,
т.е. log 10 N = lg N . Логарифмы чисел 10, 100, 1000, … pавны соответственно 1, 2, 3, …, т.е.
имеют столько положительных
единиц, сколько нулей стоит в логарифмируемом числе после единицы. Логарифмы чисел 0.1,
0.01, 0.001, … pавны соответственно –1, –2, –3, …, т.е. имеют столько отрицательных единиц,
сколько нулей стоит в логарифмируемом числе перед единицей ( считая и нуль целых ).
Логарифмы остальных чисел имеют дробную часть, называемую мантиссой. Целая часть
логарифма называется характеристикой. Для практического применения десятичные
логарифмы наиболее удобны.
12 Математика
Натуральным логарифмом называется логарифм по основанию е. Он обозначается ln ,
т.е. log e N = ln N. Число е является иррациональным, его приближённое значение
2.718281828. Оно является пределом, к которому стремится число ( 1 + 1 / n ) n при
неограниченном возрастании n
Логарифм по основанию е называется натуральным логарифмом:
log
ae
ln
a
Примеры с решениями
1. Найдите значение выражения
log
2
6
log
2
10
2
3
.
log
2,0
75
log
.3
2,0
Решение.
log
2
6
log
10
2
2. Найдите значение выражения
2
3
log
2
6
log
2
32
3
log
2
6
32
3
log
2
64
.6
Решение.
log
2,0
75
log
2,0
3
log
2,0
)3:75(
log
2,0
25
log
1
5
2
1
5
.2
3. Вычислите
Решение.
log 9
.27
log
9
27
log
3
log
27
9
3
log
log
3
3
3
2
3
3
log3
log2
3
3
3
3
3
2
.
4. Известно, что
log 5
a2
. Найдите
log 2
.80
Решение.
log
2
80
log
2
16(
)5
log
16
log
2
2
5
4
5. Найдите значение выражения
log
8
log
2
8 4
4
4
1
log
5
2
5
2
5
5
log
log
.
4
1
a
1
.
4
a
a
Решение.
log
8
log
2
8 4
4
log
8
log
2
32
2
2
log
8
log
2
2
1
16
log
8
1
16
log
8
16
1
log
8
16
6. Найдите
lg
45
log
2
log
2
.
16
4
3
8
, если
3lg
a
2lg,
b
.
13 Математика
5lg
3lg
2
lg
10
2
3lg2
lg
10
2lg
Решение.
lg
45
)59lg(
9lg
Задание 10:
1
2
a
.
b
Используя свойства логарифмов найдите значение выражения:
Вариант 1
Вариант 2
4
4
2) log 5 log
1)log 2 log 32
1
5
1
54
3)log
log
1
2
2
3
2
3
7
7
log
7
log 7
4) log
5
196
5) log 5 log 35
6)3
8) log 9
10)log 36
81
7
3
6
12)6
5log 3
6
14)log
7 3
1
7
2
Задание 10
5
4
7)49
log 3
7
27
3
3log 4
21
9)log
11)21
13)log
5
6
5
5
15)125
log 7
25
1)log 32 log
1
2
2)log 4 log 64
4
4
16
16
1
3
5
log
5
1
75
3)log
3
5
9
7
6
log
4)log
3
180
5)log 4 log 36
6)8
8)log 3
27
49
10)log
log 12
9
8
7
log 5
8
7)64
9)log
11)13
125
13
5
4log 3
12)9
4log 2
9
14)log
6
4
1
6
3
13)log
8
7
3
8
15)625
log
125
4
14 Математика
Задание 11:
ГРУППА А: Найдите значение выражения
log)2
2
5
log
2
log)2
2
22
log
Вариант 1
log)1
2
4
log
4
8
8
5
54
2
196
5
3
3
7
2
7
log)3
log)4
log)5
log
3)6
3
log)8
81
log)10
log)11
8
25
5
64
log
log
3
log
4
35
log
2
2
56
log
25)7
5
3
8
log)9
2
log)12
243
81
Вариант 2
log)1
128
4
log
4
2
2
32
11
45
3
8
5
192
log
3
log
log)3
log)4
log)5
3
8
5
8
log
5
2
log
5
25
4
36)7
log)9
log
6
7
16
4
log)12
81
27
50
log
50)6
log)8
125
log)10
log)11
6
5
49
7
128
16
Задание 11 гр А
15 Математика
ГРУППА Б: Найдите значение выражения
Вариант 1
Вариант 2
16 25
log
4
1
4
764
log)5
5
log
4)6
log2
5
2
3
)7
log
1
2
2
125
4
9
log
5
154
log
16)8
log)10
52
2327
log)9
49
343
8log)11
log
512
1
4
1
7
log)12
25
log
625
7)13
7
7
Математика
log)1
2
7
log
2
14
log)2
3
72
log
3
log2)3
2
6
log
2
log)4
4
5
log
4
63
log
36
2
log
3
18
log
2
35
16
27
35
9
log)1
3
log28
2
log
3
3
log2)2
log)3
5
log)4
4
32
7
22
1
5
log
log
5
256
7
11
log
4
36
log)5
2
12
log
2
5
3
log
2)6
94
)7
log
1
2
log
1
2
9
2
log2
7
10
25
81
4
5
2
4
5
52
log
log
log
8)8
125
2
log)10
327
log)9
216
log)11
4
256
36
log
6)13
1
3
1
6
243
7
3
log)12
9
log
3)14
Задание 11 гр Б
7)14
17 Математика
Задание 12:
Задание 1: Вычислить
Задание 2: Найти х
18 8lg)1
lg
;125
log)2
2
7
log
2
;
lg)4
13
16
log
3
log
4
3
log)8
3,0
lg
lg
16
8lg
3lg
2lg
16,3lg
:
у
)13
;
;
через
4,0lg)10
27
lg
3lg
;
)12
3lg
;
)15
12
)5
log
4
log)3
12
18
8lg
lg
2lg2
3lg
11
log
2
;7,2lg
log)7
lg)9
;
;3
;44
)6
;
2
27
4lg
2lg
15
lg
lg
)11
)14
25
Выразите
lg)1
x
х
y
;1
2
lg5,0
1
3
.
Найдите значение выражения
log
2
6
log
2
10
2
3
.
log
2,0
75
log
.3
2,0
Решение.
log
2
6
log
10
2
2. Найдите значение выражения
2
3
log
2
6
log
2
32
3
log
2
6
32
3
log
2
64
.6
Решение.
log
2,0
75
log
2,0
3
log
2,0
)3:75(
log
2,0
25
log
1
5
2
1
5
.2
3. Вычислите
Решение.
log 9
.27
log
9
27
log
3
log
27
9
3
log
log
3
3
3
2
3
3
log3
log2
3
3
3
3
3
2
.
4. Известно, что
log 5
a2
. Найдите
log 2
.80
Решение.
log
2
80
log
2
16(
)5
log
16
log
2
2
5
4
5. Найдите значение выражения
log
8
log
2
8 4
4
4
1
log
5
2
5
2
5
5
log
log
.
4
1
a
1
.
4
a
a
Решение.
log
8
log
2
8 4
4
log
8
log
2
32
2
2
log
8
log
2
2
1
16
log
8
1
16
log
8
16
1
log
8
16
6. Найдите
lg
45
log
2
log
2
.
16
4
3
8
, если
3lg
a
2lg,
b
.
13 Математика
5lg
3lg
2
lg
10
2
3lg2
lg
10
2lg
Решение.
lg
45
)59lg(
9lg
Задание 10:
1
2
a
.
b
Используя свойства логарифмов найдите значение выражения:
Вариант 1
Вариант 2
4
4
2) log 5 log
1)log 2 log 32
1
5
1
54
3)log
log
1
2
2
3
2
3
7
7
log
7
log 7
4) log
5
196
5) log 5 log 35
6)3
8) log 9
10)log 36
81
7
3
6
12)6
5log 3
6
14)log
7 3
1
7
2
Задание 10
5
4
7)49
log 3
7
27
3
3log 4
21
9)log
11)21
13)log
5
6
5
5
15)125
log 7
25
1)log 32 log
1
2
2)log 4 log 64
4
4
16
16
1
3
5
log
5
1
75
3)log
3
5
9
7
6
log
4)log
3
180
5)log 4 log 36
6)8
8)log 3
27
49
10)log
log 12
9
8
7
log 5
8
7)64
9)log
11)13
125
13
5
4log 3
12)9
4log 2
9
14)log
6
4
1
6
3
13)log
8
7
3
8
15)625
log
125
4
14 Математика
Задание 11:
ГРУППА А: Найдите значение выражения
log)2
2
5
log
2
log)2
2
22
log
Вариант 1
log)1
2
4
log
4
8
8
5
54
2
196
5
3
3
7
2
7
log)3
log)4
log)5
log
3)6
3
log)8
81
log)10
log)11
8
25
5
64
log
log
3
log
4
35
log
2
2
56
log
25)7
5
3
8
log)9
2
log)12
243
81
Вариант 2
log)1
128
4
log
4
2
2
32
11
45
3
8
5
192
log
3
log
log)3
log)4
log)5
3
8
5
8
log
5
2
log
5
25
4
36)7
log)9
log
6
7
16
4
log)12
81
27
50
log
50)6
log)8
125
log)10
log)11
6
5
49
7
128
16
Задание 11 гр А
15 Математика
ГРУППА Б: Найдите значение выражения
Вариант 1
Вариант 2
16 25
log
4
1
4
764
log)5
5
log
4)6
log2
5
2
3
)7
log
1
2
2
125
4
9
log
5
154
log
16)8
log)10
52
2327
log)9
49
343
8log)11
log
512
1
4
1
7
log)12
25
log
625
7)13
7
7
Математика
log)1
2
7
log
2
14
log)2
3
72
log
3
log2)3
2
6
log
2
log)4
4
5
log
4
63
log
36
2
log
3
18
log
2
35
16
27
35
9
log)1
3
log28
2
log
3
3
log2)2
log)3
5
log)4
4
32
7
22
1
5
log
log
5
256
7
11
log
4
36
log)5
2
12
log
2
5
3
log
2)6
94
)7
log
1
2
log
1
2
9
2
log2
7
10
25
81
4
5
2
4
5
52
log
log
log
8)8
125
2
log)10
327
log)9
216
log)11
4
256
36
log
6)13
1
3
1
6
243
7
3
log)12
9
log
3)14
Задание 11 гр Б
7)14
17 Математика
Задание 12:
Задание 1: Вычислить
Задание 2: Найти х
18 8lg)1
lg
;125
log)2
2
7
log
2
;
lg)4
13
16
log
3
log
4
3
log)8
3,0
lg
lg
16
8lg
3lg
2lg
16,3lg
:
у
)13
;
;
через
4,0lg)10
27
lg
3lg
;
)12
3lg
;
)15
12
)5
log
4
log)3
12
18
8lg
lg
2lg2
3lg
11
log
2
;7,2lg
log)7
lg)9
;
;3
;44
)6
;
2
27
4lg
2lg
15
lg
lg
)11
)14
25
Выразите
lg)1
x
х
y
;1
2
lg5,0
1
3
. 2lg
lg
y
y
;
lg)2
x
lg)3
x
Задание 12
4
log
1
3
4,2lg
12
lg2
1
2
50
72
lg
lg
;15
lg
lg
;18
;4lg
;3lg
lg)5
lg)7
x
x
lg)8
x
lg)9
x
1
3
;2lg3
lg
125
1
3
;2lg35lg2
1
2
5lg
3lg
1
2
;5,3lg
Математика
;
7
16
;130
log)1
6
x
lg)2
x
lg
1
2
log3
log5,02
25
6
6
log2
6
;3
5lg
a
lg3
b
lg4
;
c
lg)3
x
lg5
m
lg
n
2
3
1
4
lg
p
;
log29
;40
;10
3,0
log)4
4
x
216
log2
4
10
log4
;3
4
lg)6
x
6,9lg
;4,2lg
lg)10
x
lg)11
x
lg)12
x
19 Математика
Задание 13: Восстановите равенство
log
(…
…
log
2
30(
5,3
8
15
7
9
)5,3
8
15
log
)
9
)…3
log
3
log
log
2
3
21
7
log
…
)7…21(
Вариант 1
log)1
7
14
log
log)2
2
…
log
…
2
21
1
2
log
…
56
7
log
2
log
3
log)4
log)5
2
3)6
25)7
log)8
log)9
5,0
log)10
216
5
196
…5
7
3
125
…
49
…
log
3
log
log
70
2
…
3
…
log
…
)5(
…
log2
log
4
log
2
7
6
216
…
5
)2(
…
5
…
log
625
3
…
…
196
log
…
5(
4….
…
70
log
)56
(….)
20 Математика
Вариант 2
log
).
2lg
lg
y
y
;
lg)2
x
lg)3
x
Задание 12
4
log
1
3
4,2lg
12
lg2
1
2
50
72
lg
lg
;15
lg
lg
;18
;4lg
;3lg
lg)5
lg)7
x
x
lg)8
x
lg)9
x
1
3
;2lg3
lg
125
1
3
;2lg35lg2
1
2
5lg
3lg
1
2
;5,3lg
Математика
;
7
16
;130
log)1
6
x
lg)2
x
lg
1
2
log3
log5,02
25
6
6
log2
6
;3
5lg
a
lg3
b
lg4
;
c
lg)3
x
lg5
m
lg
n
2
3
1
4
lg
p
;
log29
;40
;10
3,0
log)4
4
x
216
log2
4
10
log4
;3
4
lg)6
x
6,9lg
;4,2lg
lg)10
x
lg)11
x
lg)12
x
19 Математика
Задание 13: Восстановите равенство
log
(…
…
log
2
30(
5,3
8
15
7
9
)5,3
8
15
log
)
9
)…3
log
3
log
log
2
3
21
7
log
…
)7…21(
Вариант 1
log)1
7
14
log
log)2
2
…
log
…
2
21
1
2
log
…
56
7
log
2
log
3
log)4
log)5
2
3)6
25)7
log)8
log)9
5,0
log)10
216
5
196
…5
7
3
125
…
49
…
log
3
log
log
70
2
…
3
…
log
…
)5(
…
log2
log
4
log
2
7
6
216
…
5
)2(
…
5
…
log
625
3
…
…
196
log
…
5(
4….
…
70
log
)56
(….)
20 Математика
Вариант 2
log
). ..1
1
2
log)3
)2
log
3
5
log
45
1
3
256
log
2
log
4
256
…
121
log
2
log
2
(…
4
2
32
…
11
log
5
3
….
4
2
log
32
11
log
5(
)
…
log
4
(
256
)2…
)45
log)4
8
96
1
3
log
2
3
log
8
96
log
…
3
log
8
96(
)3…
log
18(
…
25
4
5,4
)
25
4
log)5
5
18
…
log
5
…5,4
log
5
log
13
6
1
169)6
log
36)7
log)8
216
25,0
log)9
3
log)10
7
7
256
…
3
49
…
169
log
…
)6(
…
log
…
169
7
256
…
…
3
)3(
…
log
Задание 13 В
21 Математика
Тренировочные упражнения
Базовый уровень
1. Вычислите
2. Вычислите
3. Вычислите
4. Вычислите
5. Вычислите
6. Вычислите
7. Вычислите
log
2
3
2
.
5,0
2
.
log
3
log 2
.
3
39
82
.
log2
5,0
9
5,0
.
log3
2
27
log 2,0
3
125
.
1
log
5
5,0
.
16
.
Найдите значение выражения
8.
9. Найдите значение выражения
log6
01,0
6
.
25,0
log36
6
10. Найдите значение выражения
.
3lg210
22
11. Найдите значение выражения
.
24
log
1
3
1
3
12. Вычислите
13. Вычислите
14. Вычислите
15.
..1
1
2
log)3
)2
log
3
5
log
45
1
3
256
log
2
log
4
256
…
121
log
2
log
2
(…
4
2
32
…
11
log
5
3
….
4
2
log
32
11
log
5(
)
…
log
4
(
256
)2…
)45
log)4
8
96
1
3
log
2
3
log
8
96
log
…
3
log
8
96(
)3…
log
18(
…
25
4
5,4
)
25
4
log)5
5
18
…
log
5
…5,4
log
5
log
13
6
1
169)6
log
36)7
log)8
216
25,0
log)9
3
log)10
7
7
256
…
3
49
…
169
log
…
)6(
…
log
…
169
7
256
…
…
3
)3(
…
log
Задание 13 В
21 Математика
Тренировочные упражнения
Базовый уровень
1. Вычислите
2. Вычислите
3. Вычислите
4. Вычислите
5. Вычислите
6. Вычислите
7. Вычислите
log
2
3
2
.
5,0
2
.
log
3
log 2
.
3
39
82
.
log2
5,0
9
5,0
.
log3
2
27
log 2,0
3
125
.
1
log
5
5,0
.
16
.
Найдите значение выражения
8.
9. Найдите значение выражения
log6
01,0
6
.
25,0
log36
6
10. Найдите значение выражения
.
3lg210
22
11. Найдите значение выражения
.
24
log
1
3
1
3
12. Вычислите
13. Вычислите
14. Вычислите
15. Вычислите
16. Вычислите
log
18
27
log
.12
18
log
1
2
log
12
.72
1
12
log
2
36
log
29
2
.
log
7
log
256
2
7
.
log
log
6,0
6,0
27
243
.
17. Вычислите
log
1
3
2
log
9
.4
25
.
18.
64
19.
1
Найдите значение выражения
log5,0
4
Найдите значение выражения
1
log
7
2
49
14
. 20. Найдите
log 2
21. Найдите
log 7
6
22. Известно, что
, если
1
81
, если
Найдите
.
lg
175
Тренировочные упражнения
23. Известно, что
2lg
m
7lg,
n
.
Найдите
.
log14
56
24. Вычислите
log
81
25
3
log
5
4
6
.
2
25. Найдите значение выражения
.
4
log
5
2,1
2,1
log
7
3
3
Математика
.
log 2
m3
log 7
5lg
a
7lg,
.
k42
.
b
23 Тесты
Математика
Тест 1
Отметьте номер правильного ответа в заданиях А1 – А7.
А1. Вычислите
.
log
5
1 5
5
1)
;
2) 5;
3)
;
1
5
4) –5.
1
5
1) 0,7;
А2. Найдите значение выражения
.
log3
49,0
3
А3. Найдите значение выражения
.
5
log32
5
2
1) 17;
А4. Найдите
log 5
1)
;
2a
2) 0,07;
2)
;
28,0
2)
;
a
2
25
8
, если известно, что
3) 0,245;
4) 0,2401.
3)
;
25
6
log 5
3)
a7
;
a
5
.
Вычислите
16. Вычислите
log
18
27
log
.12
18
log
1
2
log
12
.72
1
12
log
2
36
log
29
2
.
log
7
log
256
2
7
.
log
log
6,0
6,0
27
243
.
17. Вычислите
log
1
3
2
log
9
.4
25
.
18.
64
19.
1
Найдите значение выражения
log5,0
4
Найдите значение выражения
1
log
7
2
49
14
. 20. Найдите
log 2
21. Найдите
log 7
6
22. Известно, что
, если
1
81
, если
Найдите
.
lg
175
Тренировочные упражнения
23. Известно, что
2lg
m
7lg,
n
.
Найдите
.
log14
56
24. Вычислите
log
81
25
3
log
5
4
6
.
2
25. Найдите значение выражения
.
4
log
5
2,1
2,1
log
7
3
3
Математика
.
log 2
m3
log 7
5lg
a
7lg,
.
k42
.
b
23 Тесты
Математика
Тест 1
Отметьте номер правильного ответа в заданиях А1 – А7.
А1. Вычислите
.
log
5
1 5
5
1)
;
2) 5;
3)
;
1
5
4) –5.
1
5
1) 0,7;
А2. Найдите значение выражения
.
log3
49,0
3
А3. Найдите значение выражения
.
5
log32
5
2
1) 17;
А4. Найдите
log 5
1)
;
2a
2) 0,07;
2)
;
28,0
2)
;
a
2
25
8
, если известно, что
3) 0,245;
4) 0,2401.
3)
;
25
6
log 5
3)
a7
;
a
5
. 4) 19.
4)
.
5a
4) 2,5.
4) 4.
А5. Найдите значение выражения
1) 4,5;
А6. Вычислите
2) 9,5;
.
128
lg
8lg
1)
;
lg
120
А7. Известно, что
2)
;
7
3
lg
m
lg,3
n
8
log
3
72
.8
3
3
log
3) 1;
3)
;
lg
16
. Найдите
1)
;
lg
375
2) 8;
3) 1;
lg
n
1000
m
.
4)
.
8lg
Ответом в заданиях В8 – В10 должно быть целое или записанное в виде десятичной
дроби число.
В8. Вычислите
.
В9. Найдите значение выражения
10
64
log16
81
2lg2
1
log
2 125
8
log
В10. Найдите значение выражения
log
4
3
baa
24
.
3
4
log
3
1
2
, если
.
log ba
14 Математика
Решения заданий В8В10
Тест 2
Базовый уровень
.
5
1. Вычислите
1)
;
5,3
2. Вычислите
1) 2;
Отметьте номер правильного ответа в заданиях А1 – А7.
log 5
125
2)
;
5,1
1,0lg
.
1000
2) –1,5;
.
1
3
log3
12
12
3. Найдите значение выражения
1) –1;
4. Вычислите
1) 2;
5. Вычислите
2)
1
27
;
log
20
.5
20
log
80
2) 400;
log
1
9
log
15
.25
1
15
4)
.
5,2
4)
1
3
.
4)
.
3 3
4) 85.
3)
;6
3) 0,5;
3) 27;
3)
log 20
;85
25
4) 19.
4)
.
5a
4) 2,5.
4) 4.
А5. Найдите значение выражения
1) 4,5;
А6. Вычислите
2) 9,5;
.
128
lg
8lg
1)
;
lg
120
А7. Известно, что
2)
;
7
3
lg
m
lg,3
n
8
log
3
72
.8
3
3
log
3) 1;
3)
;
lg
16
. Найдите
1)
;
lg
375
2) 8;
3) 1;
lg
n
1000
m
.
4)
.
8lg
Ответом в заданиях В8 – В10 должно быть целое или записанное в виде десятичной
дроби число.
В8. Вычислите
.
В9. Найдите значение выражения
10
64
log16
81
2lg2
1
log
2 125
8
log
В10. Найдите значение выражения
log
4
3
baa
24
.
3
4
log
3
1
2
, если
.
log ba
14 Математика
Решения заданий В8В10
Тест 2
Базовый уровень
.
5
1. Вычислите
1)
;
5,3
2. Вычислите
1) 2;
Отметьте номер правильного ответа в заданиях А1 – А7.
log 5
125
2)
;
5,1
1,0lg
.
1000
2) –1,5;
.
1
3
log3
12
12
3. Найдите значение выражения
1) –1;
4. Вычислите
1) 2;
5. Вычислите
2)
1
27
;
log
20
.5
20
log
80
2) 400;
log
1
9
log
15
.25
1
15
4)
.
5,2
4)
1
3
.
4)
.
3 3
4) 85.
3)
;6
3) 0,5;
3) 27;
3)
log 20
;85
25
Найдите значение числового логарифмического выражения – как решать
Формулировка задачи: Найдите значение числового логарифмического выражения.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 5 (Вычисления и преобразования).
Рассмотрим, как решаются подобные задачи на логарифмы на примерах.
Пример задачи 1:
Найдите значение выражения log0,310 – log0,33
Решение:
Разность логарифмов с одинаковым основанием равна логарифму частного:
log0,310 – log0,33 = log0,3(10/3)
Возведем 10/3 в степень -1, вынесем степень из под логарифма (логарифм степени):
log0,3(10/3) = -log0,3(3/10) = -1
Ответ: -1
Пример задачи 2:
Найдите значение выражения log713 / log4913
Решение:
Преобразуем знаменатель: для этого вынесем степень основания из под логарифма:
log4913 = log(7)213 = 1/2 ⋅ log713
Тогда значение выражения равно:
log713 / log4913 = 2 ⋅ log713 / log713 = 2
Ответ: 2
Пример задачи 3:
Найдите значение выражения 9log550 / 9log52
Решение:
Преобразуем выражение:
9log550 / 9log52 = 9log550 – log52
Разность логарифмов с одинаковыми основаниями равна логарифму частного:
log550 – log52 = log5(50/2) = log525 = 2
Тогда значение выражения равно:
Ответ: 81
Пример задачи 4:
Найдите значение выражения 6log7∛7
Решение:
Вынесем корень за пределы логарифма:
6log7∛7 = 6 ⋅ 1/3 ⋅ log77 = 2
Ответ: 2
Пример задачи 5:
Найдите значение выражения log35 / log37 + log70,2
Решение:
Преобразуем частное с помощью формулы перехода от логарифма в одном основании к логарифму при другом основании:
Сумма логарифмов с одним основанием равна логарифму произведения:
log75 + log70,2 = log71 = 0
Ответ: 0
Пример задачи 6:
Найдите значение выражения log0,83 ⋅ log31,25
Решение:
Преобразуем второй множитель и приведем его к тому же основанию:
log31,25 = log3(5/4) = -log3(4/5) = -log30,8 = -1 / log0,83
И найдем значение выражения:
log0,83 ⋅ log31,25 = -log0,83 / log0,83 = -1
Ответ: -1
Пример задачи 7:
Найдите значение выражения 5log2549
Решение:
Вынесем степень основания логарифма за его пределы:
Внесем ее обратно как логарифм корня:
1/2 ⋅ log549 = log5(49)1/2 = log57
И воспользуемся основным логарифмическим тождеством:
Ответ: 7
Пример задачи 8:
Найдите значение выражения log4(log216)
Решение:
Вычислим значение выражения в скобках:
Тогда значение выражения равно:
Ответ: 1
Пример задачи 9:
Найдите значение выражения log42 + log0,258
Решение:
Найдем значения каждой части выражения и получим результат:
log42 =1/2 ⋅ log22 = 1/2 ⋅ 1 = 0,5
log0,258 = log1/48 = 1/2 ⋅ log1/28 = 1/2 ⋅ log1/223 = 1/2 ⋅ (-3) = -1,5
Тогда значение выражения равно:
log42 + log0,258 = 0,5 – 1,5 = -1
Ответ: -1
Пример задачи 10:
Найдите значение выражения 2log26 – 3
Решение:
Разложим число на множители:
2log26 – 3 = 2log26 ⋅ 2–3
Применим основное логарифмическое тождество к первому множителю и выполним оставшиеся вычисления:
2log26 ⋅ 2-3 = 6 ⋅ 1/8 = 0,75
Ответ: 0,75
Пример задачи 11:
Найдите значение выражения 7–2log72
Решение:
Вынесем множитель перед логарифмом в степень, чтобы избавиться от него:
–2log72 = log72–2 = log70,25
И применим основное логарифмическое тождество:
7–2log72 = 7log70,25 = 0,25
Ответ: 0,25
Пример задачи 12:
Найдите значение выражения (3log23)log32
Решение:
Если мы возведем число сначала в степень log32, а потом уже в степень log23, то сможем применить основное логарифмическое тождество:
(3log23)log32 = (3log32)log23 = 2log23 = 3
Ответ: 3
Пример задачи 13:
Найдите значение выражения (1 – log212) ⋅ (1 – log612)
Решение:
Преобразуем логарифмы:
log212 = log2(2 ⋅ 6) = log22 + log26 = 1 + log26
log612 = log6(2 ⋅ 6) = log62 + log66 = log62 + 1
Подставим полученные значения в выражение:
(1 – (1 + log26)) ⋅ (1 – (log62 + 1)) = (1 – 1 – log26) ⋅ (1 – log62 – 1) = – log26 ⋅ (– log62) = log26 ⋅ log62
Преобразуем второй множитель, чтобы логарифмы имели одинаковые основания, и выполним остальные действия:
log26 ⋅ log62 = log26 ⋅ 1/log26 = 1
Ответ: 1
Пример задачи 14:
Найдите значение выражения log318 / (2 + log32)
Решение:
Преобразуем 2 в знаменателе в логарифм с основанием 3 (возведем 3 в степень 2 и получим число под логарифмом):
Сумма логарифмов с одним основанием в знаменателе равна логарифму произведения:
2 + log32 = log39 + log32 = log3(9 ⋅ 2) = log318
Осталось сократить числитель и знаменатель:
Ответ: 1
База логарифма 2 Калькулятор Log2
База логарифма 2 Калькулятор Log2 Калькулятор логарифма 2 находит результат функции логарифма по основанию 2. Вычислить логарифм по основанию 2 числа.
Вычислить логарифм по основанию 2 числа.
журнал 2 (x) = y
x: — действительное число, x> 0
журнал 2 (x) = y и x = 2 y
База логарифмических данных 2 таблицы значений
Список журналов 2 таблицы значений функций , база 2 чисел.
| log 2 (x) | Обозначение | Значение |
|---|---|---|
| log 2 (1) | фунтов (1) | 0 |
| log 2 (2) | фунтов (2) | 1 |
| log 2 (3) | фунтов (3) | 1,584963 |
| log 2 (4) | фунтов (4) | 2 |
| журнал 2 (5) | фунтов (5) | 2. 321928 321928 |
| log 2 (6) | фунтов (6) | 2,584963 |
| log 2 (7) | фунтов (7) | 2,807355 |
| log 2 ( 8) | фунтов (8) | 3 |
| log 2 (9) | фунтов (9) | 3,169925 |
| log 2 (10) | фунтов (10) | 3.321928 |
| log 2 (11) | фунтов (11) | 3.459432 |
| log 2 (12) | фунтов (12) | 3,584963 |
| log 2 (13) | фунтов (13) | 3.70044 |
| log 2 ( 14) | фунтов (14) | 3.807355 |
| log 2 (15) | фунтов (15) | 3.1 |
| log 2 (16) | фунтов (16) | 4 |
| log 2 (17) | фунтов (17) | 4.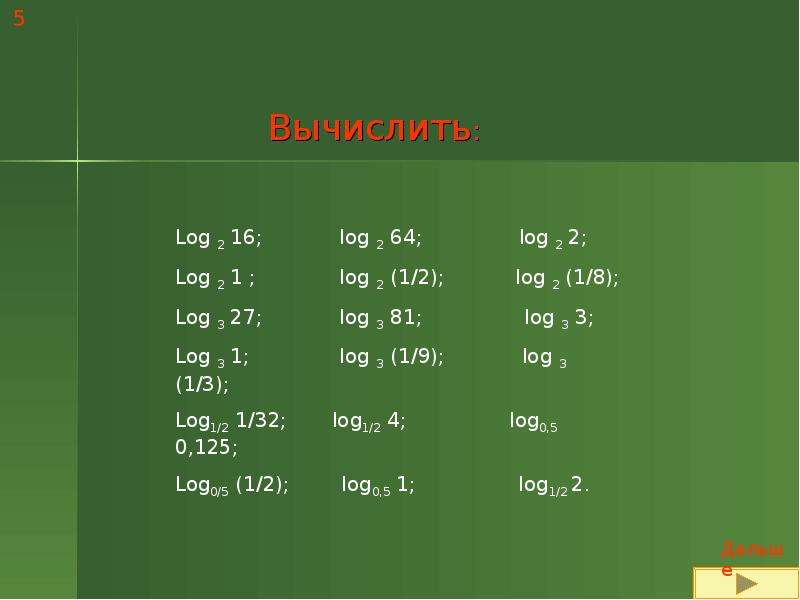 087463 087463 |
| log 2 (18) | фунтов (18) | 4,169925 |
| log 2 (19) | фунтов (19) | 4.247928 |
| log 2 ( 20) | фунтов (20) | 4,321928 |
| log 2 (21) | фунтов (21) | 4,3 |
| log 2 (22) | фунтов (22) | 4.459432 |
| log 2 (23) | фунтов (23) | 4.523562 |
| log 2 (24) | фунтов (24) | 4.584963 |
| log 2 (25) | фунтов (25) | 4.643856 |
| log 2 ( 26) | фунтов (26) | 4,70044 |
| log 2 (27) | фунтов (27) | 4,754888 |
| log 2 (28) | фунтов (28) | 4.807355 |
| log 2 (29) | фунтов (29) | 4.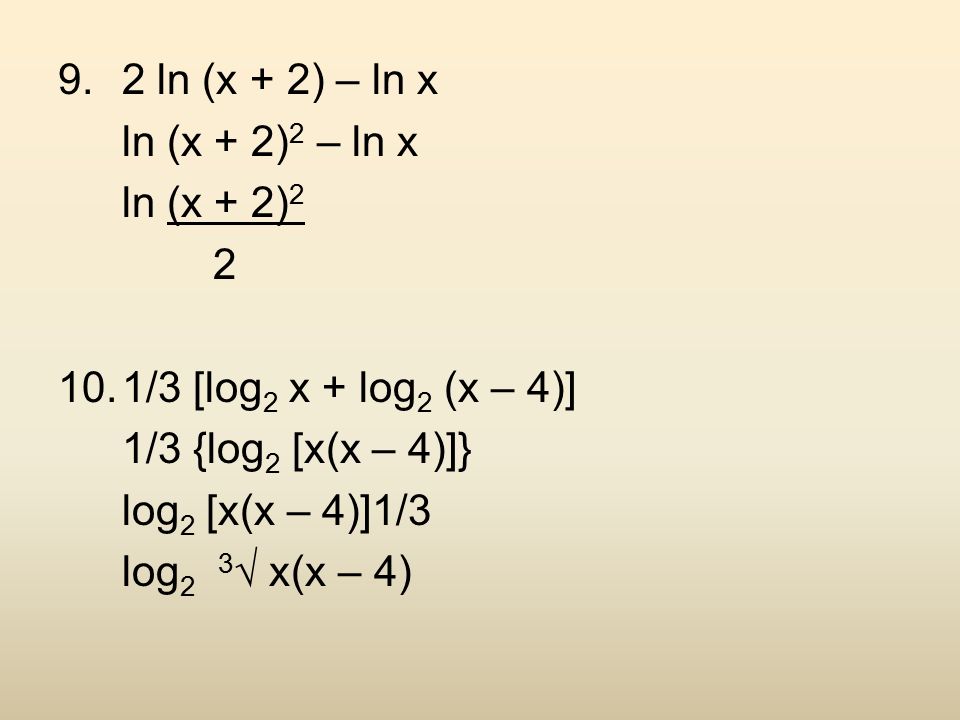 857981 857981 |
| log 2 (30) | фунтов (30) | 4,1 |
| log 2 (31) | фунтов (31) | 4.954196 |
| log 2 ( 32) | фунтов (32) | 5 |
| log 2 (33) | фунтов (33) | 5.044394 |
| log 2 (34) | фунтов (34) | 5,087463 |
| журнал 2 (35) | фунтов (35) | 5.129283 |
| log 2 (36) | фунтов (36) | 5,169925 |
| log 2 (37) | фунтов (37) | 5.209453 |
| log 2 ( 38) | фунтов (38) | 5.247928 |
| log 2 (39) | фунтов (39) | 5.285402 |
| log 2 (40) | фунтов (40) | 5,321928 |
| log 2 (41) | фунтов (41) | 5. 357552 357552 |
| log 2 (42) | фунтов (42) | 5,3 |
| log 2 (43) | фунтов (43) | 5.426265 |
| log 2 ( 44) | фунтов (44) | 5,459432 |
| log 2 (45) | фунтов (45) | 5,4 |
| log 2 (46) | фунтов (46) | 5.523562 |
| log 2 (47) | фунтов (47) | 5.554589 |
| log 2 (48) | фунтов (48) | 5.584963 |
| log 2 (49) | фунтов (49) | 5.61471 |
| log 2 ( 50) | фунтов (50) | 5,643856 |
| log 2 (51) | фунтов (51) | 5,672425 |
| log 2 (52) | фунтов (52) | 5.70044 |
| log 2 (53) | фунтов (53) | 5. 72792 72792 |
| log 2 (54) | фунтов (54) | 5,754888 |
| log 2 (55) | фунтов (55) | 5,78136 |
| log 2 ( 56) | фунтов (56) | 5.807355 |
| log 2 (57) | фунтов (57) | 5,83289 |
| log 2 (58) | фунтов (58) | 5,857981 |
| log 2 (59) | фунтов (59) | 5.882643 |
| log 2 (60) | фунтов (60) | 5.1 |
| log 2 (61) | фунтов (61) | 5.7 |
| log 2 ( 62) | фунтов (62) | 5.954196 |
| log 2 (63) | фунтов (63) | 5.97728 |
| log 2 (64) | фунтов (64) | 6 |
| log 2 (65) | фунтов (65) | 6. 022368 022368 |
| log 2 (66) | фунтов (66) | 6.044394 |
| log 2 (67) | фунтов (67) | 6.066089 |
| log 2 ( 68) | фунтов (68) | 6.087463 |
| log 2 (69) | фунтов (69) | 6,108524 |
| log 2 (70) | фунтов (70) | 6,129283 |
| log 2 (71) | фунтов (71) | 6.149747 |
| log 2 (72) | фунтов (72) | 6,169925 |
| log 2 (73) | фунтов (73) | 6,189825 |
| log 2 ( 74) | фунтов (74) | 6.209453 |
| log 2 (75) | фунтов (75) | 6.228819 |
| log 2 (76) | фунтов (76) | 6.247928 |
| log 2 (77) | фунтов (77) | 6. 266787 266787 |
| log 2 (78) | фунтов (78) | 6.285402 |
| log 2 (79) | фунтов (79) | 6.303781 |
| log 2 ( 80) | фунтов (80) | 6.321928 |
| log 2 (81) | фунтов (81) | 6.33985 |
| log 2 (82) | фунтов (82) | 6.357552 |
| log 2 (83) | фунтов (83) | 6.375039 |
| log 2 (84) | фунтов (84) | 6.3 |
| log 2 (85) | фунтов (85) | 6.409391 |
| log 2 ( 86) | фунтов (86) | 6.426265 |
| log 2 (87) | фунтов (87) | 6.442943 |
| log 2 (88) | фунтов (88) | 6.459432 |
| log 2 (89) | фунтов (89) | 6. 475733 475733 |
| log 2 (90) | фунтов (90) | 6.4 |
| log 2 (91) | фунтов (91) | 6.507795 |
| log 2 ( 92) | фунтов (92) | 6.523562 |
| log 2 (93) | фунтов (93) | 6.539159 |
| log 2 (94) | фунтов (94) | 6.554589 |
| log 2 (95) | фунтов (95) | 6.569856 |
| log 2 (96) | фунтов (96) | 6.584963 |
| log 2 (97) | фунтов (97) | 6.599913 |
| log 2 ( 98) | фунтов (98) | 6,61471 |
| log 2 (99) | фунтов (99) | 6,629357 |
| log 2 (100) | фунтов (100) | 6.643856 |
| log 2 (x) | Обозначение | Значение | |
|---|---|---|---|
| log 2 (101) | фунтов (101) | 6. 658211 658211 | |
| log 2 (102) | фунтов (102) | 6,672425 | |
| log 2 (103) | фунтов (103) | 6.686501 | |
| log 2 ( 104) | фунтов (104) | 6.70044 | |
| log 2 (105) | фунтов (105) | 6,714246 | |
| log 2 (106) | фунтов (106) | 6.72792 | |
| log 2 (107) | фунтов (107) | 6.741467 | |
| log 2 (108) | фунтов (108) | 6,754888 | |
| log 2 (109) | фунтов (109) | 6.768184 | |
| log 2 ( 110) | фунтов (110) | 6,78136 | |
| log 2 (111) | фунтов (111) | 6,794416 | |
| log 2 (112) | фунтов (112) | 6.807355 | |
| log 2 (113) | фунтов (113) | 6. 820179 820179 | |
| log 2 (114) | фунтов (114) | 6,83289 | |
| log 2 (115) | фунтов (115) | 6.84549 | |
| log 2 ( 116) | фунтов (116) | 6,857981 | |
| log 2 (117) | фунтов (117) | 6,870365 | |
| log 2 (118) | фунтов (118) | 6,882643 | |
| log 2 (119) | фунтов (119) | 6.894818 | |
| log 2 (120) | фунтов (120) | 6.1 | |
| log 2 (121) | фунтов (121) | 6. | 3 |
| log 2 ( 122) | фунтов (122) | 6.7 | |
| log 2 (123) | фунтов (123) | 6.942515 | |
| log 2 (124) | фунтов (124) | 6.954196 | |
| log 2 (125) | фунтов (125) | 6. 965784 965784 | |
| log 2 (126) | фунтов (126) | 6.97728 | |
| log 2 (127) | фунтов (127) | 6.988685 | |
| log 2 ( 128) | фунтов (128) | 7 | |
| log 2 (129) | фунтов (129) | 7.011227 | |
| log 2 (130) | фунтов (130) | 7.022368 | |
| log 2 (131) | фунтов (131) | 7.033423 | |
| log 2 (132) | фунтов (132) | 7.044394 | |
| log 2 (133) | фунтов (133) | 7.055282 | |
| log 2 ( 134) | фунтов (134) | 7.066089 | |
| log 2 (135) | фунтов (135) | 7.076816 | |
| log 2 (136) | фунтов (136) | 7.087463 | |
| log 2 (137) | фунтов (137) | 7. 098032 098032 | |
| log 2 (138) | фунтов (138) | 7.108524 | |
| log 2 (139) | фунтов (139) | 7.118941 | |
| log 2 ( 140) | фунтов (140) | 7,129283 | |
| log 2 (141) | фунтов (141) | 7,139551 | |
| log 2 (142) | фунтов (142) | 7.149747 | |
| log 2 (143) | фунтов (143) | 7.159871 | |
| log 2 (144) | фунтов (144) | 7.169925 | |
| log 2 (145) | фунтов (145) | 7.179909 | |
| log 2 ( 146) | фунтов (146) | 7,189825 | |
| log 2 (147) | фунтов (147) | 7,199672 | |
| log 2 (148) | фунтов (148) | 7. 209453 209453 | |
| log 2 (149) | фунтов (149) | 7.219169 | |
| log 2 (150) | фунтов (150) | 7.228819 | |
| log 2 (151) | фунтов (151) | 7.238405 | |
| log 2 ( 152) | фунтов (152) | 7,247928 | |
| log 2 (153) | фунтов (153) | 7,257388 | |
| log 2 (154) | фунтов (154) | 7.266787 | |
| log 2 (155) | фунтов (155) | 7.276124 | |
| log 2 (156) | фунтов (156) | 7.285402 | |
| log 2 (157) | фунтов (157) | 7.294621 | |
| log 2 ( 158) | фунтов (158) | 7.303781 | |
| log 2 (159) | фунтов (159) | 7. 312883 312883 | |
| log 2 (160) | фунтов (160) | 7.321928 | |
| log 2 (161) | фунтов (161) | 7.330917 | |
| log 2 (162) | фунтов (162) | 7.33985 | |
| log 2 (163) | фунтов (163) | 7.348728 | |
| log 2 ( 164) | фунтов (164) | 7,357552 | |
| log 2 (165) | фунтов (165) | 7,366322 | |
| log 2 (166) | фунтов (166) | 7.375039 | |
| log 2 (167) | фунтов (167) | 7.383704 | |
| log 2 (168) | фунтов (168) | 7,3 | |
| log 2 (169) | фунтов (169) | 7.400879 | |
| log 2 ( 170) | фунтов (170) | 7,409391 | |
| log 2 (171) | фунтов (171) | 7,417853 | |
| log 2 (172) | фунтов (172) | 7,426265 | |
| log 2 (173) | фунтов (173) | 7. 434628 434628 | |
| log 2 (174) | фунтов (174) | 7,442943 | |
| log 2 (175) | фунтов (175) | 7,451211 | |
| log 2 ( 176) | фунтов (176) | 7,459432 | |
| log 2 (177) | фунтов (177) | 7,467606 | |
| log 2 (178) | фунтов (178) | 7,475733 | |
| log 2 (179) | фунтов (179) | 7.483816 | |
| log 2 (180) | фунтов (180) | 7,4 | |
| log 2 (181) | фунтов (181) | 7,499846 | |
| log 2 ( 182) | фунтов (182) | 7,507795 | |
| log 2 (183) | фунтов (183) | 7,5157 | |
| log 2 (184) | фунтов (184) | 7.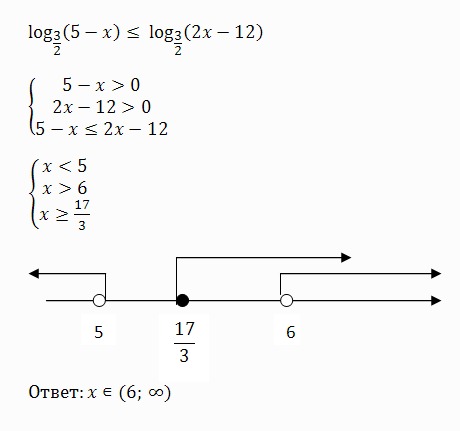 523562 523562 | |
| log 2 (185) | фунтов (185) | 7.531381 | |
| log 2 (186) | фунтов (186) | 7,539159 | |
| log 2 (187) | фунтов (187) | 7.546894 | |
| log 2 ( 188) | фунтов (188) | 7,554589 | |
| log 2 (189) | фунтов (189) | 7,562242 | |
| log 2 (190) | фунтов (190) | 7,569856 | |
| log 2 (191) | фунтов (191) | 7.577429 | |
| log 2 (192) | фунтов (192) | 7,584963 | |
| log 2 (193) | фунтов (193) | 7,5 | |
| log 2 ( 194) | фунтов (194) | 7,599913 | |
| log 2 (195) | фунтов (195) | 7. 60733 60733 | |
| log 2 (196) | фунтов (196) | 7,61471 | |
| log 2 (197) | фунтов (197) | 7.622052 | |
| log 2 (198) | фунтов (198) | 7,629357 | |
| log 2 (199) | фунтов (199) | 7,636625 | |
| log 2 ( 200) | фунтов (200) | 7,643856 |
| log 2 (x) | Обозначение | Значение | |
|---|---|---|---|
| log 2 (201) | фунтов (201) | 7,651052 | |
| log 2 (202) | фунтов (202) | 7.658211 | |
| log 2 (203) | фунтов (203) | 7,665336 | |
| log 2 (204) | фунтов (204) | 7,672425 | |
| log 2 ( 205) | фунтов (205) | 7,67948 | |
| log 2 (206) | фунтов (206) | 7,686501 | |
| log 2 (207) | фунтов (207) | 7. 6 6 | |
| log 2 (208) | фунтов (208) | 7.70044 | |
| log 2 (209) | фунтов (209) | 7.707359 | |
| log 2 (210) | фунтов (210) | 7.714246 | |
| log 2 ( 211) | фунтов (211) | 7,721099 | |
| log 2 (212) | фунтов (212) | 7,72792 | |
| log 2 (213) | фунтов (213) | 7,73471 | |
| log 2 (214) | фунтов (214) | 7.741467 | |
| log 2 (215) | фунтов (215) | 7,748193 | |
| log 2 (216) | фунтов (216) | 7,754888 | |
| log 2 ( 217) | фунтов (217) | 7,761551 | |
| log 2 (218) | фунтов (218) | 7,768184 | |
| log 2 (219) | фунтов (219) | 7. 774787 774787 | |
| log 2 (220) | фунтов (220) | 7.78136 | |
| log 2 (221) | фунтов (221) | 7,787903 | |
| log 2 (222) | фунтов (222) | 7.794416 | |
| log 2 ( 223) | фунтов (223) | 7.8009 | |
| log 2 (224) | фунтов (224) | 7.807355 | |
| log 2 (225) | фунтов (225) | 7.813781 | |
| log 2 (226) | фунтов (226) | 7.820179 | |
| log 2 (227) | фунтов (227) | 7,826548 | |
| log 2 (228) | фунтов (228) | 7,83289 | |
| log 2 ( 229) | фунтов (229) | 7,839204 | |
| log 2 (230) | фунтов (230) | 7,84549 | |
| log 2 (231) | фунтов (231) | 7,851749 | |
| log 2 (232) | фунтов (232) | 7. 857981 857981 | |
| log 2 (233) | фунтов (233) | 7,864186 | |
| log 2 (234) | фунтов (234) | 7.870365 | |
| log 2 ( 235) | фунтов (235) | 7,876517 | |
| log 2 (236) | фунтов (236) | 7,882643 | |
| log 2 (237) | фунтов (237) | 7.888743 | |
| log 2 (238) | фунтов (238) | 7.894818 | |
| log 2 (239) | фунтов (239) | 7. | |
| log 2 (240) | фунтов (240) | 7.1 | |
| log 2 ( 241) | фунтов (241) | 7. | |
| log 2 (242) | фунтов (242) | 7. | 3 |
| log 2 (243) | фунтов (243) | 7. | |
| log 2 (244) | фунтов (244) | 7.7 | |
| log 2 (245) | фунтов (245) | 7.8 | |
| log 2 (246) | фунтов (246) | 7.942515 | |
| log 2 ( 247) | фунтов (247) | 7,948367 | |
| log 2 (248) | фунтов (248) | 7,954196 | |
| log 2 (249) | фунтов (249) | 7.960002 | |
| log 2 (250) | фунтов (250) | 7.965784 | |
| log 2 (251) | фунтов (251) | 7.971544 | |
| log 2 (252) | фунтов (252) | 7.97728 | |
| log 2 ( 253) | фунтов (253) | 7.982994 | |
| log 2 (254) | фунтов (254) | 7.988685 | |
| log 2 (255) | фунтов (255) | 7. 994353 994353 | |
| log 2 (256) | фунтов (256) | 8 | |
| log 2 (257) | фунтов (257) | 8.005625 | |
| log 2 (258) | фунтов (258) | 8.011227 | |
| log 2 (259) | фунтов (259) | 8.016808 | |
| log 2 ( 260) | фунтов (260) | 8,022368 | |
| log 2 (261) | фунтов (261) | 8,027906 | |
| log 2 (262) | фунтов (262) | 8.033423 | |
| log 2 (263) | фунтов (263) | 8.038919 | |
| log 2 (264) | фунтов (264) | 8.044394 | |
| log 2 (265) | фунтов (265) | 8.049849 | |
| log 2 ( 266) | фунтов (266) | 8.055282 | |
| log 2 (267) | фунтов (267) | 8. 060696 060696 | |
| log 2 (268) | фунтов (268) | 8.066089 | |
| log 2 (269) | фунтов (269) | 8.071462 | |
| log 2 (270) | фунтов (270) | 8.076816 | |
| log 2 (271) | фунтов (271) | 8.082149 | |
| log 2 ( 272) | фунтов (272) | 8,087463 | |
| log 2 (273) | фунтов (273) | 8,0 | |
| log 2 (274) | фунтов (274) | 8.098032 | |
| log 2 (275) | фунтов (275) | 8.103288 | |
| log 2 (276) | фунтов (276) | 8.108524 | |
| log 2 (277) | фунтов (277) | 8.113742 | |
| log 2 ( 278) | фунтов (278) | 8. 118941 118941 | |
| log 2 (279) | фунтов (279) | 8.124121 | |
| log 2 (280) | фунтов (280) | 8.129283 | |
| log 2 (281) | фунтов (281) | 8.134426 | |
| log 2 (282) | фунтов (282) | 8.139551 | |
| log 2 (283) | фунтов (283) | 8.144658 | |
| log 2 ( 284) | фунтов (284) | 8.149747 | |
| log 2 (285) | фунтов (285) | 8.154818 | |
| log 2 (286) | фунтов (286) | 8.159871 | |
| log 2 (287) | фунтов (287) | 8.164907 | |
| log 2 (288) | фунтов (288) | 8.169925 | |
| log 2 (289) | фунтов (289) | 8. 174926 174926 | |
| log 2 ( 290) | фунтов (290) | 8,179909 | |
| log 2 (291) | фунтов (291) | 8,184875 | |
| log 2 (292) | фунтов (292) | 8.189825 | |
| log 2 (293) | фунтов (293) | 8.194757 | |
| log 2 (294) | фунтов (294) | 8.199672 | |
| log 2 (295) | фунтов (295) | 8.204571 | |
| log 2 ( 296) | фунтов (296) | 8.209453 | |
| log 2 (297) | фунтов (297) | 8,214319 | |
| log 2 (298) | фунтов (298) | 8.219169 | |
| log 2 (299) | фунтов (299) | 8.224002 | |
| журнал 2 (300) | фунтов (300) | 8,228819 |
© 2019-2021 www.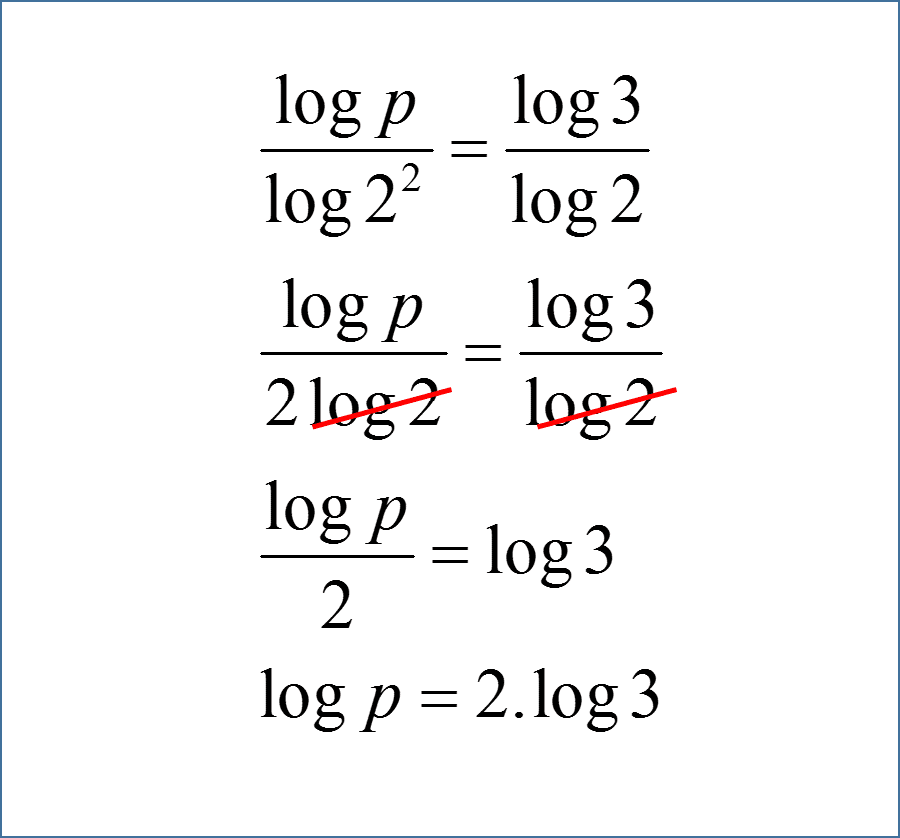 logcalculator.net
logcalculator.net
Базовые правила журнала и расширяющиеся выражения журнала
Purplemath
Вы изучили различные правила для управления и упрощения выражений с показателями, например, правило, которое гласит, что x 3 × x 5 равно x 8 , потому что вы можете складывать экспоненты.Аналогичные правила для логарифмов.
Правила журнала:
1) журнал b ( mn ) = журнал b ( m ) + журнал b ( n )
2) бревно b ( м / n ) = бревно b ( м ) — бревно b ( n )
3) бревно b ( м n ) = n · лог b ( м )
MathHelp.
 com
comМенее формально правила журнала могут быть выражены как:
1) Умножение внутри журнала можно превратить в сложение вне журнала, и наоборот.
2) Деление внутри журнала можно превратить в вычитание вне журнала, и наоборот.
3) Показатель степени для всего, что находится внутри бревна, можно переместить вперед как множитель, и наоборот.
Предупреждение: как и в случае с экспонентами, приведенные выше правила работают только , если основания совпадают. Например, выражение «log d ( m ) + log b ( n )» нельзя упростить, потому что основания («d» и «b») не совпадают, просто как x 2 × y 3 нельзя упростить, потому что основания ( x и y ) не совпадают.
Расширяющиеся логарифмы
Правила журнала могут использоваться для упрощения (или, точнее, для «уплотнения») выражений, для «расширения» выражений или для поиска значений. Начнем с расширения.
Когда в инструкциях говорится «расширить», они означают, что они дали мне одно выражение журнала с большим количеством информации внутри него, и они хотят, чтобы я использовал правила журнала, чтобы разбить журнал на множество отдельных терминов журнала, каждый из которых имеет только одна вещь внутри его конкретного журнала.То есть они дали мне один журнал с сложным аргументом , и они хотят, чтобы я преобразовал это в много журналов , каждый с простым аргументом .
В данном случае у меня внутри журнала есть «2 x ». Поскольку «2 x » — это умножение, я могу разделить это выражение в соответствии с первым из приведенных выше правил журнала и превратить его в сложение вне журнала:
журнал 3 (2 x ) = журнал 3 (2) + журнал 3 ( x )
Тогда ответ, который они ищут:
Примечание: не пытайтесь вычислить «журнал 3 (2)» в вашем калькуляторе. Хотя вы будете правы, если скажете, что «log 3 (2)» — это просто число (и позже мы увидим, как преобразовать это выражение во что-то, что вы можете оценить на своем калькуляторе), что они? На самом деле мы ищем здесь «точную» форму журнала, как показано выше, а не десятичное приближение из вашего калькулятора.
Хотя вы будете правы, если скажете, что «log 3 (2)» — это просто число (и позже мы увидим, как преобразовать это выражение во что-то, что вы можете оценить на своем калькуляторе), что они? На самом деле мы ищем здесь «точную» форму журнала, как показано выше, а не десятичное приближение из вашего калькулятора.
Если вы дадите «ответ» в виде десятичного приближения, вы должны ожидать потерю баллов.
У меня внутри журнала деление.Согласно второму правилу журнала, приведенному выше, его можно разделить на части как вычитание вне журнала, так:
журнал 4 ( 16 / x ) = журнал 4 (16) — журнал 4 ( x )
Первый член в правой части приведенного выше уравнения можно упростить до точного значения, применив основное определение логарифма. В этом случае я использую тот факт, что мощность, необходимая на 4 для создания 16, равна 2; другими словами, поскольку 4 2 = 16, то:
В этом случае я использую тот факт, что мощность, необходимая на 4 для создания 16, равна 2; другими словами, поскольку 4 2 = 16, то:
Затем исходное выражение полностью раскрывается как:
журнал 4 ( 16 / x ) = 2 — журнал 4 ( x )
Всегда не забывайте находить время, чтобы проверить, можно ли упростить какие-либо термины в вашем расширении (например, журнал 4 (16) выше).
Показатель внутри бревна можно вынести как множитель:
log 5 ( x 3 ) = 3 · log 5 ( x ) = 3log 5 ( x )
Приведенные выше примеры представляют собой очень простое использование правил журнала применительно к раскрытию выражений журнала. На следующей странице мы рассмотрим, какие упражнения вы будете выполнять в своем домашнем задании и на следующем тесте.
На следующей странице мы рассмотрим, какие упражнения вы будете выполнять в своем домашнем задании и на следующем тесте.
URL: https://www.purplemath.com/modules/logrules.htm
База логарифма 3 из 62 преобразователей
Используйте форму ниже, чтобы выполнить преобразование.
| Бревно 3 10 2 3 4 5 6 7 8 9 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | знак равно | ||
| Ответ преобразования Log 3 62 = 3.75667961083 |
Решение Шаг 1 Журнал 3 62 = Журнал (62) ÷ Журнал (3) Лог (62) = 1,7923 |
|
Другие преобразования системы счисления для проверки
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
Преобразование системы счисления — это числа от 1 до 32, где числа 2-9 представлены простыми цифрами, а числа 11-32 представлены буквами A-Z. {\ displaystyle 3})}} {3-3}
{\ displaystyle 3})}} {3-3}
$ = \ dfrac {\ log_ {2} {(9-8)}} {0}
$$ = \ dfrac {\ log_ {2} {(1)}} {0}
$$ = \ dfrac {0} {0}
$Следовательно, значение выражения в левой части неопределенно при $ x $ равно $ 3 $.Следовательно, $ x \ ne 3 $, но $ x = 0 $ является только решением логарифмического уравнения и математически является необходимым решением этой логарифмической задачи.
Расширяющиеся логарифмы — ChiliMath
Когда вас просят развернуть логарифмические выражения , ваша цель состоит в том, чтобы выразить одно логарифмическое выражение на множество отдельных частей или компонентов. Этот процесс прямо противоположен сжатию логарифмов, потому что вы сжимаете кучу лог-выражений в более простое.
Лучший способ проиллюстрировать эту концепцию — показать множество примеров. В этом уроке восемь решенных задач.
Ключ к успешному расширению логарифмов — это осторожное применение правил логарифмов. Найдите время, чтобы изучить правила и понять, что они пытаются «сказать».
Найдите время, чтобы изучить правила и понять, что они пытаются «сказать».
Например, правило 1 называется правилом продукта . Что он делает, так это разбивает произведение выражений на сумму лог-выражений. См. Остальные описания ниже.
Правила логарифмов
Изучите описание каждого правила, чтобы получить его интуитивное понимание.
Описание правил логарифмирования
Правило 1: Правило продукта
Логарифм произведения чисел — это сумма логарифмов отдельных чисел.
Правило 2: Правило частного
Логарифм частного числа — это разность логарифма отдельных чисел.
Правило 3: Правило силы
Логарифм экспоненциального числа — это показатель степени, умноженный на логарифм основания.
Правило 4: Правило нуля
Логарифм 1, где b> 0, но b \ ne 1, равен нулю.
Правило 5: Правило идентификации
Логарифм числа, равного его основанию, равен 1. Поскольку число также является основанием, b, это означает, что b> 0, но b \ ne 1.
Поскольку число также является основанием, b, это означает, что b> 0, но b \ ne 1.
Правило 6: Журнал экспоненты Правило
Логарифм экспоненциального числа, основание которого совпадает с основанием журнала, равно экспоненте.
Правило 7: Экспонент логарифма Правило
Возведение логарифма числа по основанию равняется числу.
Примеры раскрытия логарифмов
Пример 1 : развернуть логарифмическое выражение.
Заглянув в круглые скобки, мы видим произведение числа и переменных. Правило продукта не говорит, что внутри должно быть только два фактора, на самом деле их может быть больше. Хорошо, поэтому мы разделим основное логарифмическое выражение как сумму четырех журналов.
Пример 2 : развернуть логарифмическое выражение.
Внутри скобок — дробь, означающая, что сначала я буду применять правило частных. Поскольку числитель является произведением 7 и x, я использую правило произведения, чтобы разбить его.
Пример 3 : развернуть логарифмическое выражение.
Хорошо, это тоже дробная форма, поэтому правило частных — это первый шаг, который мы собираемся применить.
Итак, в этой проблеме есть что-то «новое».То есть числитель содержит переменную с показателем степени. Это должно быть легко, поскольку с этим легко справятся Правило 3 или Правило мощности. Просто опустите экспоненту влево, вот и все!
Кроме того, в знаменателе стоит радикальное выражение. Помните, что радикал можно выразить дробной степенью. Поскольку этот радикал является квадратным корнем, это означает, что степень просто \ large {1 \ over 2}.
Кроме того, мы впервые видим в действии Правило 5 или Правило логарифма идентичности.Ожидайте, что это правило будет применяться чаще, потому что оно чрезвычайно полезно в процессе упрощения.
Пример 4 : развернуть логарифмическое выражение.
Пусть вас не пугает квадратный корень. Просто представьте это как степень или показатель \ large {1 \ over 2}. Таким образом, эта проблема сводится к расширению лог-выражения со степенью \ large {1 \ over 2}. Здесь правило мощности опускает показатель \ large {1 \ over 2} слева от журнала, а затем вы расширяете остальную часть, как обычно.
Просто представьте это как степень или показатель \ large {1 \ over 2}. Таким образом, эта проблема сводится к расширению лог-выражения со степенью \ large {1 \ over 2}. Здесь правило мощности опускает показатель \ large {1 \ over 2} слева от журнала, а затем вы расширяете остальную часть, как обычно.
Пример 5 : развернуть логарифмическое выражение.
Эта задача довольно интересна, потому что все выражение возводится в некоторую степень. Кроме того, наличие квадратного корня в числителе добавляет некоторого уровня сложности.
Однако, если мы будем придерживаться основ, тщательно применяя правила экспонент на каждом этапе, у нас не должно возникнуть проблем с решением этой проблемы! Давай спланируем наши действия, хорошо?
Уменьшите показатель степени 4, используя Правило мощности.Затем используйте правило частного, чтобы выразить дробь как разность логарифмических выражений. И, наконец, не забывайте, что квадратный корень — это всего лишь дробный показатель от \ large {1 \ over 2}.
Я распределил 4 по символу группировки, чтобы избавиться от дроби \ large {1 \ over 2}. Также можно оставить 4 за пределами символа группировки, что означает, что нам не нужно распределять 4 по выражениям внутри квадратных скобок. Любой из двух ответов должен быть правильным.
Пример 6 : развернуть логарифмическое выражение.
Это просто кубический корень из некоторого рационального выражения. Замените символ корня куба дробной степенью \ large {1 \ over 3}. Этот показатель степени \ large {1 \ over 3} можно уменьшить, используя правило логарифма степени. Теперь нам нужно разобраться с рациональным выражением, используя правило частных, а затем завершить его, используя правило продукта.
Не отвлекайтесь на разные типы групповых символов. Идея состоит в том, чтобы убедиться, что мы правильно применяем правила логарифмирования на каждом этапе, который мы предпринимаем, без совершения алгебраических ошибок, таких как распределение -1 в символе группировки. 3}. Обработайте квадратные корни, заменив их дробной степенью, а затем используйте правило логарифмов мощности, чтобы уменьшить его перед символом журнала в качестве множителя.
3}. Обработайте квадратные корни, заменив их дробной степенью, а затем используйте правило логарифмов мощности, чтобы уменьшить его перед символом журнала в качестве множителя.
Пример 8 : развернуть логарифмическое выражение.
Основное питание 3 может быть размещено в качестве множителя с помощью правила мощности. Правило Quotient должно иметь дело с дробными выражениями, записывая их как разность журналов. Теперь замените символ квадратного корня на показатель степени \ large {1 \ over 2}.Аналогичным образом замените символ корня куба на показатель степени \ large {1 \ over 3}.
Практика с рабочими листами
Возможно, вас заинтересует:
Уплотняющие логарифмы
Объяснение логарифма
Правила логарифмирования
Решение логарифмических уравнений
Брайс Райнер бросает Гарвард-Вестлейк в чемпионский матч
Первокурсник Брайс Райнер, 15 лет, стоял на холме в начале седьмого иннинга жарким днем вторника в Энсино. У Orange Lutheran были бегуны на втором и третьем местах с двумя аутами в полуфинальной игре Южного дивизиона 1. Он бросил 95 ударов. Тренеры Гарвард-Вестлейк отказались подтолкнуть его к команде. Кэтчер Джейкоб Гэллоуэй коротко с ним ободрял.
У Orange Lutheran были бегуны на втором и третьем местах с двумя аутами в полуфинальной игре Южного дивизиона 1. Он бросил 95 ударов. Тренеры Гарвард-Вестлейк отказались подтолкнуть его к команде. Кэтчер Джейкоб Гэллоуэй коротко с ним ободрял.
«Вот оно. Это последний парень. Давай сделаем это.»
Поле № 96 в пользу пинч-нападающего из лютеранской команды Orange Ричарда Техады в результате фол с кривой мячом. Поле № 97 было быстрым и пропущенным. Поле № 98 было высоким фастболом, требовавшим третьего удара.Товарищи по команде выскочили из блиндажа, чтобы отпраздновать победу со счетом 3: 2, в результате которой Росомахи, занявшие второе место (28-4), вышли в финал первого дивизиона против Сан-Хуана Капистрано Джсерры, занявшего первое место.
«Он не потерял свои вещи», — сказал тренер по питанию Джо Гюнц о Райнере, который улучшился до 9: 0, выбив девять, отказавшись от четырех ударов и два шага. «Он атаковал. Когда у вас есть особенный ребенок, вы должны ему доверять. Он быстро вырос ».
Он быстро вырос ».
Беннетт Маркинсон сделал первый тайм хоум-ран для Гарвард-Вестлейк.Оранжевый лютеранский ас Луи Родригес был удален во втором иннинге после синглов RBI Дэвида Лозано и Джорджа Купера. Крис Кэнэда не допускал Гарвард-Вестлейк до конца игры, но уланам так и не удалось решить проблему с Райнером, который вывел их из равновесия с помощью своего слайдера и кривой. Только в седьмом они оказали давление, получив сингл RBI от Макса Андила.
Райнер никогда не менял выражения лица. Он был методичен, уравновешен и невозмутим до финального удара.
JSerra 11, Ayala 4: Коди Шриер, Колин Бланшар и Люк Джуэтт совершили хоум-раны, чтобы сплотить Львов в полуфинале Дивизиона 1.Джуэтт пошел три из трех. У Джейкоба Бадави было три удара для Айалы.
Таузенд-Оукс 10, Бонита 3: Мэтт Манси совершил хоумран с тремя ранами, его 12-е место в сезоне, а Рок Риджио сделал свой 13-й хоум-ран, чтобы помочь «Уланам 28-1» выйти в чемпионат Дивизиона 2. .
.
Royal 4, Paraclete 1: Тревор Хансен вычеркнул шесть и забросил полную игру, а Р. Дж. Фейгенбаум пошел три на три, чтобы помочь Royal выйти в чемпионат Дивизиона 4. Роял сыграет с Ранчо Кукамонга, победившим Мурриету Меса со счетом 2: 0.
Лонг-Бич Милликен 2, Харт 1: Милликен расстроил индейцев номер 1 в полуфинале Дивизиона 3. «Рэмс» сыграют с «Риверсайд Арлингтон» со счетом 7-6 над Палосом Вердесом.
Citrus Valley 14, Laguna Hills 13: Трэвис Уильямс сделал три дубля в полуфинале пятого дивизиона. Цитрус Вэлли сыграет с Кахоном, победив со счетом 5: 4 над Северным Торрансом в восьми подачах.
Баскетбол для мальчиков
Сьерра-Каньон 94, Бирмингем 74: Амари Бейли набрал 28 очков в пользу команды Trailblazers, которая примет Этиванду в полуфинале открытого дивизиона в четверг.
Дэмиен 102, Санта-Мария-Сент-Джозеф 71: Малик Томас, летевший в USC, финишировал с 33 очками. В четверг Дэмиен сыграет с Торри Пайнсом с лучшим посевом.
West Hills Chaminade 79, Clovis North 76: Кейт Хиггинс набрал 29 очков, а Кей Джей Симпсон и Колин Уимс добавили по 20 очков в первом дивизионе 1-A.
Гарвард-Вестлейк 78, Мемориал Сан-Хоакина 70: Кэмерон Троуэр набрал 19 очков за «Росомаху».
Нарбонна 67, Лонг-Бич Поли 65: Гаучо опрокинули верхних сеяных Джекрэббитс в открытии 2-А.Девин Уильямс набрал 24 очка, а Брайс Адамс вернулся после травмы стопы и набрал 20 очков.
Баскетбол для девочек
Corona Centennial 79, La Jolla Country День 44: Хаски выиграли свой первый региональный плей-офф в Открытом дивизионе. Лондин Джонс набрал 25 очков, а Джайда Карри — 18 очков.
Софтбол
Эль Камино Реал 6, Карсон 0: Джиллиан Келли вывела конкистадоров в игру чемпионата открытого дивизиона городской секции. Конкистадоры казнили овсянками и полагались на качки Келли.
Гранада Хиллз 8, Сан-Педро 7: Элла Ладден провела полную игру, чтобы организовать матч чемпионата открытого дивизиона лиги Западной долины.
Гольф
Юсон Чой из Анахайма Дискавери Кристиан забил на поле для гольфа Brookside на семь очков меньше номинала и выиграл чемпионат Южной Калифорнии по гольфу среди юношей CIF / SCGA. Командный титул выиграла Анахайм Сервите.
Эмико Свердук из Лонг-Бич Уилсон выиграла личный титул среди девушек со счетом до 68. Фуллертон Трой стал командным титулом.
Сенсационное выступление Дюранта выводит Нетс вперед 3: 2 — Солсбери Пост
БРАЙАН МАХОНИ
AP Баскетбольный писатель
НЬЮ-ЙОРК (AP) — Кевин Дюрант набрал 49 очков, 17 подборов и 10 передач в одном из самых зрелищных выступлений в истории постсезонных матчей, вернув «Бруклин Нетс» в лидеры в полуфинале Восточной конференции со счетом 114-108 побед над командой Милуоки Бакс в пятой игре во вторник вечером.
Джеймс Харден вернулся, но не обиделся, а Кайри Ирвинг покинул поле. Дюрант отыграл все 48 минут и бросил 16 из 23 с поля.Он набрал 20 очков в четвертой четверти, пожалуй, самый крупный бросок — трехочковый за 50 секунд до конца и «Нетс», сохранив преимущество в одно очко.
«Он положил нас на спину и нес нас всю игру», — сказал нападающий Джефф Грин.
Двукратный MVP финала НБА стал первым игроком в истории НБА, набравшим не менее 45 очков, 15 подборов и 10 передач в матче плей-офф.
«Историческое, историческое выступление», — сказал тренер Нетс Стив Нэш.
Харден сыграл впервые с 43 секунды после начала серии с напряжением правой подколенной сухожилия.Он бросил всего 1 из 10 и пропустил все восемь трехочковых, но сделал восемь передач и шесть подборов, играя 46 минут.
Грин сделал семь трехочковых и набрал 27 очков для «Нетс», которые упали в 17-очковую брешь после двух поражений в «Милуоки», прежде чем Дюрант отыграл их. Блейк Гриффин прибавил 17 очков.
Шестая игра состоится в четверг в Милуоки, где «Бакс» в этом сезоне сыграют 4-0 против «Нетс».
Яннис Антетокунмпо набрал 34 очка и 12 подборов, а Крис Миддлтон прибавил 25 очков.
«Бакс» набрал обороты после победы в двух играх в Милуоки, когда Ирвинг вывихнул лодыжку во второй четверти игры 4. Похоже, что Дюрант будет единственным из трех суперзвезд, сыгравших во вторник, учитывая его манеру игры. , в любом случае могло быть достаточно.
Похоже, что Дюрант будет единственным из трех суперзвезд, сыгравших во вторник, учитывая его манеру игры. , в любом случае могло быть достаточно.
Нетс изначально исключили Хардена в понедельник, а затем повысили его во вторник сначала до сомнительного, а затем и до сомнительного. Он тренировался перед игрой и, казалось, хорошо двигался, бегая с корта в туннель после разминки, прежде чем его допустили к игре.
Но, похоже, у него не было полной силы в ноге, из-за чего прыгуны были короткими, и он редко кого-нибудь обыгрывал при ведении мяча.
Дюрант убедился, что это не имеет значения.
«Его особенное выступление», — сказал тренер Бакс Майк Буденхольцер. «Благодарность ему, несколько сложных моментов, так что мы должны взглянуть на это, выяснить, как стать лучше».
«Нетс» были 4 из 20 в первой четверти, 2 из 13 при трехочковых, а трехочковая игра Миддлтона за 33 секунды до конца дала «Милуоки» преимущество 29: 1 после одного.
Корзина Дюранта снизила счет до 42-33, прежде чем Антетокунмпо сделал трехочковый и следовал еще двумя корзинами, чтобы увеличить преимущество до 16, что было по-прежнему, когда Бакс повели 59-43 на половину поля.
«Бакс» по-прежнему лидировали в счете 16 в середине третьей четверти, отвечая каждый раз, когда «Нетс», казалось, имели какой-то импульс. Но Дюрэнт тогда стал горячим и так и не остыл.
Он сделал все четыре броска и набрал 11 очков в последних 6:18 третьего матча, когда «Нетс» потянули до 87-81 в его трехочковой игре за 31 секунду до конца.
Дюрант продолжал открывать четвёртый счет, с его 3-мя очками за 8:36 до игры 94-93, первое преимущество Бруклина после 2: 0.
TIP-INS
баксов: Антетокунмпо был единственным игроком, получившим голоса за первую команду All-NBA по всем 100 бюллетеням, заработав свой третий подряд выбор за первую команду. … Джру Холидей набрал 19 очков.
Нетс: Ирвинг был выбран в третью команду Все-НБА, это был первый выбор в НБА для Нетс с тех пор, как Джейсон Кидд был выбран в первую команду в сезоне 2003-04 гг.… The Nets отдали дань уважения диктору Марву Альберту, который называл игру кортом для TNT.

 {b}=c\) \(\Leftrightarrow\) \(\log_{a}{c}=b\)
{b}=c\) \(\Leftrightarrow\) \(\log_{a}{c}=b\)
 Да, выглядит непривычно, но ответ не выбирают.
Да, выглядит непривычно, но ответ не выбирают.
 Так как второй аргумент (основание) опущен, предполагается, что он равен 10. Результат (1) — степень, в которую необходимо возвести основание, чтобы получить число 10.
Так как второй аргумент (основание) опущен, предполагается, что он равен 10. Результат (1) — степень, в которую необходимо возвести основание, чтобы получить число 10. 75667961083
75667961083