Log a 1 вычислить: 1.Вычислить: а) log(1/2)16; б) 5 в степени 1+log(5)3; в)log(3)135-log(3)20+2log(3)2 2)Сравнить числа: log(1/2)3/4 и log(1/2)4/5 …

alexxlab / / Разное

Свойства логарифмов — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Определение

Логарифмом положительного числа b
по основанию a, где а>0, а≠1
называется показатель степени, в
которую надо возвести число а,
чтобы получить b.
log a b x, a b,
x
a 0, a 1, b 0

2. Вычислить устно:

3. Вычислить устно:

1) log 2 64
2) log 4 16
3) log 1 3
1
4) log 5
25
3
5) log 6 36
6) log 25 5
7) log
8) log 3
2
2
9) log 2 64 log 4 16
10) log 2 12 log 2 3
27

4.

Свойства логарифмов

5. Основное логарифмическое тождество

По определению логарифма
а
loga b
b
a)2
б)
log2 13
70
2
7
log2 5
log7 13
13
70
14
5
13 1
в)
0,25
52
52 4
.
Вычислите:
3 log 3 18;
3 5log 3 2;
5 log 5 16;
0,3 2log 0,3 6;
10 log 10 2;
(1/4) log(1/4) 6;
8 log 2 5;
9 log 3 12.

8. Решить устно:

9. Вычислить устно:

10. 1. Логарифм произведения равен сумме логарифмов множителей:

log x ab log x a log x b
Пример :
log 72 log 3 log6 (72 3) log 216 3
6
6
6
a ) log 12 4 log 12 36 log 12 (4 36)
log 12 144 log 12 12 2 2 log 12 12 2 1 2

11. Вычислите:

1. log18 2 + log18 9
2. log4 8 + log4 32
3. log32 2 + log32 2
4. lg 40 + lg 25
1)
2)
3)
4)
1
4
0,2
3
2. Логарифм частного равен логарифмов
делимого без логарифма делителя:
a
log x log x a log x b
b
Пример:
log 48 log 4
12
12
48
log
12 4
log 12
12
1

13.

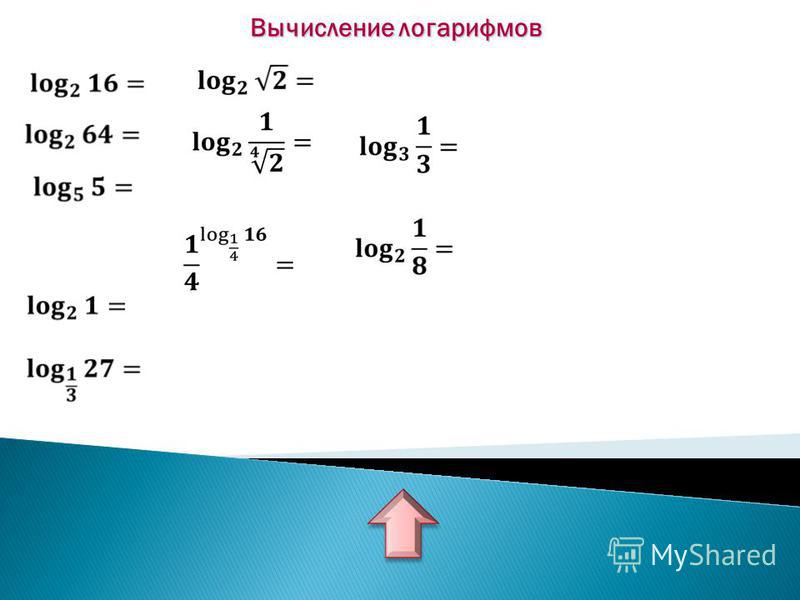3. Логарифм степени равен произведению показателя степени на логарифм ее основания:log x a m log x a
m
Пример
log 125 log 125
5
5
1
2
1
log 5125 1,5
2
log 2 32 log 2 2 5 log 2 2 5 1 5
5
4. Основание логарифма в степени
log a k
1
x log a x, a 0, x 0, a 1
k
Пример
1
1
1
log 16 2 log 24 2 log 2 2 1 0,25
4
4
4
5. Переход от одного основания к другому
log b x
1
log a x
log a x
log b a
log x a

16. Свойства логарифмов

1
log
log 3 7
3 7
1
a) log
log 3 81 log 3 34 4 log 3 3 4 1 4
3 81

17. Свойства логарифмов

log 113 log 3 11 1

18. Частные свойства:

1)log a 1 = 0;
2) log a a = 1;
3) log a (1/a) = — 1;
4) log a a m = m;
5) log a m a = 1/m.

19. Упражнение № 1. Вычислить

20. Решаем из учебника:

№290-294 (четные номера)

21. Домашняя работа:

• П.16, (выучить свойства
логарифмов)
• №290-294 (нечетные номера)

English     Русский Правила

Алгебра 10-11 класс.

Свойства логарифмов. Логарифмические вычисления — math200.ru Skip to content

Алгебра 10-11 класс. Свойства логарифмов. Логарифмические вычисленияadmin2022-11-02T20:37:49+03:00

Скачать файл в формате pdf.


Алгебра 10-11 класс. Свойства логарифмов. Логарифмические вычисления
Задача 1. Вычислите    \({\log _3}9 — {\log _{\sqrt 6 }}36 + {\log _5}125\) 

Ответ

ОТВЕТ: 1.

Задача 2. Вычислите    \({\log _2}8 + {\log _{\sqrt 3 }}27 — {\log _7}343\)

Ответ

ОТВЕТ: 6.

Задача 3. Вычислите    \({\log _{\frac{1}{3}}}27 + {\log _{\frac{3}{2}}}\frac{9}{4} + {\log _{2,5}}1\)

Ответ

ОТВЕТ: -1.

Задача 4. Вычислите    \(3\,{\log _8}2 — {\log _{1,2}}1,44 + {\log _{1,2}}1\)

Ответ

ОТВЕТ: -1.

Задача 5. { — x}} = 34\)

Ответ

ОТВЕТ: 6.

 

Реклама

Поддержать нас

Точно вычислять log(1+x) для небольших значений x

Перейти к содержимому

Основное содержание

Точное вычисление log(1+x) для малых значений x +х)

, компенсация округления в 1+x . log1p(x) есть точнее, чем log(1+x) для малых значений Икс. Для малых х , log1p(x) есть приблизительно x , тогда как log(1+x) может быть нулем.

Расширенные возможности


Расчет с массивами, в которых больше строк, чем помещается в памяти.

Эта функция полностью поддерживает длинные массивы. За дополнительную информацию см. в разделе Длинные массивы.

Генерация кода C/C++


Генерация кода C и C++ с помощью MATLAB® Coder™.

Генерация кода графического процессора


Генерация кода CUDA® для графических процессоров NVIDIA® с помощью GPU Coder™.
Запустите код в фоновом режиме с помощью MATLAB® backgroundPool или ускорьте код с помощью Parallel Computing Toolbox™ ThreadPool .

Эта функция полностью поддерживает среды на основе потоков. За дополнительную информацию смотрите в разделе «Выполнение функций MATLAB в среде с потоками».


Ускорьте выполнение кода, запустив его на графическом процессоре (GPU) с помощью Parallel Computing Toolbox™.

Замечания по использованию и ограничения:

  • Если выходные данные функции, работающей на графическом процессоре, могут быть сложными, то вы должны явно указать ее входные аргументы как сложные. Дополнительные сведения см. в разделе Работа с комплексными числами на графическом процессоре (Parallel Computing Toolbox).

Для получения дополнительной информации см. Запуск функций MATLAB на графическом процессоре (Parallel Computing Toolbox).


Разделите большие массивы по объединенной памяти вашего кластера с помощью Parallel Computing Toolbox™.

Эта функция полностью поддерживает распределенные массивы. Для большего информацию смотрите в разделе Запуск функций MATLAB с распределенными массивами (Parallel Computing Toolbox).

История версий

Представлено до R2006a

См.

также

журнал | опыт1

Выберите веб-сайт, чтобы получить переведенный контент, где он доступен, и ознакомиться с местными событиями и предложениями. В зависимости от вашего местоположения мы рекомендуем вам выбрать: .

Вы также можете выбрать веб-сайт из следующего списка:

Европа

Свяжитесь с местным офисом

  • Пробная версия ПО
  • Пробная версия ПО
  • Обновления продукта
  • Обновления продукта
Функция журнала

— RDocumentation

Описание

log вычисляет логарифмы, по умолчанию натуральные логарифмы, log10 вычисляет десятичные логарифмы и log2 вычисляет двоичные (т. е. по основанию 2) логарифмы. Общая форма log(x, base)

вычисляет логарифмы по основанию база .

log1p(x) точно вычисляет \(\log(1+x)\) также для \(|x| \ll 1\).

exp вычисляет экспоненциальную функцию.

expm1(x) точно вычисляет \(\exp(x) — 1\) также для \(|x| \ll 1\).

Использование 

 log(x, base = exp(1))
logb(x, база = exp(1))
лог10(х)
лог2(х) 
 log1p(x) 
 
 exp(x)
expm1(x)

Аргументы

x

Числовой или комплексный вектор.

основание

положительное или комплексное число: основание, относительно которого вычисляются логарифмы. По умолчанию \(e\)= exp(1) .

Значение

Вектор той же длины, что и x , содержащий преобразованный значения. log(0) дает -Inf и log(x) для отрицательные значения x равно

NaN . exp(-Inf) равно 0 .

Для сложных входных данных функций журнала значение представляет собой комплексное число. с мнимой частью в диапазоне \([-\pi, \pi]\): что конец диапазона может зависеть от платформы.

Методы S4

exp , expm1 , log , log10 , log2 и log1p являются общими для S4 и являются членами Math универсальная группа.

Обратите внимание, что это означает, что универсальный S4 для журнала имеет подпись только с одним аргументом, x , но эта база может передаваться методам (но не будет использоваться для выбора метода). На с другой стороны, если вы установите метод только для группы Math общий, то аргумент

base log будет игнорироваться для твой класс.

Детали

Все, кроме logb , являются общими функциями: методы могут быть определены для них индивидуально или через Математика групповой универсальный.

log10 и log2 — это только удобные обертки, но журналы к основаниям 10 и 2 (независимо от того, вычислено ли через log или обертки) будут вычисляться более эффективно и точно, если это поддерживается операционной системой.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *