Матрица ab ba: Действия с матрицами

Реферат «Произведение матриц»: annaalex95 — LiveJournal

?

Произведением матрицы на матрицу называется матрица такая, что элемент матрицы , стоящий в -ой строке и -ом столбце, т.е. элемент , равен сумме произведений элементов -ой строки матрицы на соответствующие элементы -ого столбца матрицы .
Умножать матрицы можно тогда и только тогда, когда количество столбцов первой матрицы равно количеству строк второй матрицы.
Если матрица A содержит m строк, а матрица B содержит n-столбцов, то произведение AB представляет собой матрицу С размера m × n. Элемент , стоящий в i-ой строке и j-ом столбце матрицы AB, вычисляется по правилу умножения строки на столбец: i-ая строка матрицы A умножается на j-ый столбец матрицы B.
Операция матричного умножения определена только для матриц, удовлетворяющих определенным условиям:
1)Произведение AB определено, если число столбцов матрицы A совпадает с числом строк матрицы B. (Другими словами, число элементов в строке матрицы A должно совпадать с числом элементов в столбце матрицы B.)
2)Произведение BA определено, если число столбцов матрицы B совпадает с числом строк матрицы A.
Отметим, что в общем случае произведение матриц некоммутативно, то есть AB ≠ BA. Более того,
1)Существование одного из произведений (AB или BA) не влечет за собой существование другого.
2)Если определено каждое из таких произведений, то размеры матриц AB и BA не обязательно совпадают друг с другом. Например, результатом умножения матрицы A размера 1×n на матрицу B размера n×1 является число (то есть матрица размера 1×1), тогда как произведение BA представляет собой квадратную матрицу n-го порядка.
3)Если матрицы A и B являются квадратными маирицами n-го, то и их произведения AB и BA являются матрицами такого же порядка. Однако даже для таких матриц их произведения в одном и другом порядках равны только в некоторых частных случаях.

4)Произведение нескольких матриц, расположенных в определенном порядке, однозначно определено, если число столбцов каждой матрицы равно числу строк соседней матрицы справа. 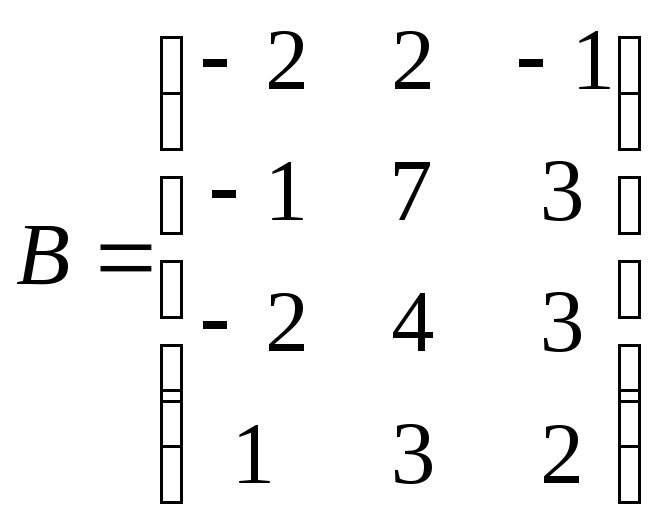В этом случае для нахождения произведения матриц можно использовать произвольный порядок расстановки скобок.
Разность AB – BA произведений квадратных матриц одного и того же порядка называется коммутатором матриц.
Сумма AB + BA произведений квадратных матриц одного и того же порядка называется антикоммутатором матриц.

Символическая записьозначает произведение двух одинаковых квадратных матриц:
Аналогичным образом определяются другие целые положительные степени квадратной матрицы:

Правило (1) матричного умножения сохраняет свой вид и в том случае, когда элементами матриц A и B являются другие матрицы. Пусть, например, матрицы A и B представлены в виде

где Ai j и Bi j – некоторые матрицы, размеры которых таковы, что соответствующие матричные произведения определены.

Тогда

Источники:http://portal.tpu.ru/SHARED/k/KONVAL/Sites/Russian_sites/1/04.htm

Tags: реферат

Subscribe

Photo

Hint http://pics. livejournal.com/igrick/pic/000r1edq

НОУ ИНТУИТ | Лекция | Матрицы. Основные определения и виды матриц. Действия над матрицами. Понятие ранга матрицы. Операции над матрицами. Понятие и нахождение обратной матрицы

< Лекция 10 || Лекция 3: 123

Аннотация: В лекции рассказывается о матрицах – как об одном из самых популярных инструментов высшей математики, позволяющем определять возможность получения решения системы линейных уравнений и находить его

Ключевые слова: таблица, матрица, натуральное число, решение системы линейных уравнений, ранг, детерминант, определитель, вывод, операции, Произведение, умножение, равенство, перемножение матриц, EA, Алгебраическим дополнением, алгоритм, алгебраические

Матрицы. Основные определения и типы матриц

Определение 1. Матрицей A называется любая прямоугольная таблица, составленная из чисел a_ij, которые называют элементами матрицы и обозначается

( 2. 1)

Заметим, что элементами матрицы могут быть не только числа. Представим себе, что вы описываете книги, которые стоят на вашей книжной полке. Пусть у вас на полке порядок и все книги стоят на строго определенных местах. Таблица, которая будет содержать описание вашей библиотеки (по полкам и следованию книг на полке), тоже будет матрицей. Но такая матрица будет не числовой. Другой пример. Вместо чисел стоят разные функции, объединенные между собой некоторой зависимостью. Полученная таблица также будет называться матрицей. Иными словами, Матрица, это любая прямоугольная таблица, составленная из однородных элементов. Здесь и далее мы будем говорить о матрицах, составленных из чисел.

Вместо круглых скобок для записи матриц применяют квадратные скобки или прямые двойные вертикальные линии

( 2. 1*)

Определение 2. Если в выражении (1) m = n, то говорят о квадратной матрице, а если , то о прямоугольной.

В зависимости от значений m и n различают некоторые специальные виды матриц:

1. Матрица — строка (или строковая матрица), состоящая из одной строки. Это прямоугольная матрица размером 1 x n.

   A=(a11  a12  ...  an).
2. Матрица — столбец ( столбцевая матрица), состоящая только из одного столбца. Это также прямоугольная матрица размером m x 1
3. Матрица, состоящая из одного элемента. A=(a₁₁)_1×1=a₁₁.
4. ru/2010/edi»> Нулевая матрица, состоящая из одних нулей, в матричной алгебре играет роль 0, обозначается V.
5. Единичная матрица, состоящая из нулей, кроме главной диагонали, на которой стоят единицы. Обозначается E и играет роль единицы в матричной алгебре
6. Диагональная матрица, квадратная порядка n, состоящая из нулей и на главной диагонали стоят не равные нулю элементы (не обязательно единицы)

Важнейшей характеристикой квадратной матрицы является ее определитель или детерминант, который составляется из элементов матрицы и обозначается

Очевидно, что D_E=1 ; .

Определение 3. Если , то матрица A называется невырожденной или не особенной.

Определение 4. Если detA = 0, то матрица A называется вырожденной или особенной.

Определение 5. Две матрицы A и B называются равными и пишут A = B, если они имеют одинаковые размеры и их соответствующие элементы равны, т.е

.

Например, матрицы и равны, т.к. они равны по размеру и каждый элемент одной матрицы равен соответствующему элементу другой матрицы. А вот матрицы и нельзя назвать равными, хотя детерминанты обеих матриц равны, и размеры матриц одинаковые, но не все элементы , стоящие на одних и тех же местах равны. Матрицы и разные, так как имеют разный размер. Первая матрица имеет размер 2х3, а вторая 3х2. Хотя количество элементов одинаковое – 6 и сами элементы одинаковые 1, 2, 3, 4, 5, 6, но они стоят на разных местах в каждой матрице. А вот матрицы и равны, согласно определению 5.

Определение 6. Если зафиксировать некоторое количество столбцов матрицы A и такое же количество ee строк, тогда элементы, стоящие на пересечении указанных столбцов и строк образуют квадратную матрицу

n — го порядка, определитель которой называется минором k – го порядка матрицы A.

Пример. Выписать три минора второго порядка матрицы

Решение. .

Дальше >>

< Лекция 10 || Лекция 3: 123

Видео с вопросами: Определение условий равенства двух матриц

Стенограмма видео

Рассмотрите показанные матрицы. Матрица 𝐴 равна единице, двум, трем, четыре. А матрица 𝐵 равна единице, двум, три, 𝑘. Можно ли выбрать 𝑘 такой что 𝐴𝐵 равно 𝐵𝐴? Если да, то чему должно быть равно 𝑘 к?

Итак, в этой задаче первым делом мы собираемся посмотреть, как мы перемножаем матрицы вместе. Так что у нас есть два на два матрицы. Итак, как бы мы умножили два матрицы два на два? Что ж, давайте посмотрим на этот. У нас есть 𝑎, 𝑏, 𝑐, 𝑑 один матрица, а 𝑒, 𝑓, 𝑔, ℎ — другая матрица. Теперь, если мы посмотрим на первый элемент, у нас есть 𝑎𝑒 плюс 𝑏𝑔. Итак, что мы делаем, так это умножаем первый элемент первой строки первой матрицы на первый элемент первой столбец второй матрицы. А потом добавляем второй элемент первой строки первой матрицы, умноженный на второй элемент первый столбец второй матрицы. И тогда то, что мы делаем, завершено этот образец для других элементов нашей матрицы.

Хорошо, отлично. Итак, теперь нам нужно работать выяснить, возможно ли, чтобы 𝐴𝐵 было равно 𝐵𝐴, если у нас есть значение 𝑘. Ну, при первом осмотре вы может подумать, что 𝐴𝐵 будет таким же, как 𝐵𝐴, потому что если мы просто умножим вещи, неважно, в каком они направлении.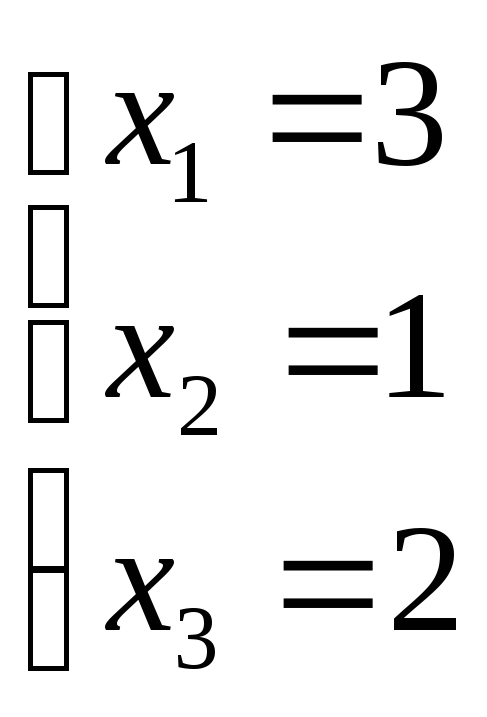

Тем не менее, это похоже на уже показанное когда мы имеем дело с матрицами. Теперь есть два пути решения Эта проблема. Прежде всего, просто взглянув в наших двух матрицах мы, вероятно, могли видеть, каким должно быть значение 𝑘. Потому что, просто взглянув на наши матрицы, мы видим, что 𝑘 будет равно четырем. И почему так? Ну, причина, по которой 𝑘 будет равно четырем, потому что если 𝑘 равно четырем, то матрица 𝐴 и матрица 𝐵 равны идентичный. Поэтому, если мы умножим их вместе, либо 𝐴𝐵, либо 𝐵𝐴, это не повлияет на результат.

Но сейчас мы просто докажите это, заполнив 𝐴𝐵 и 𝐵𝐴. Ну, если у нас есть 𝐴𝐵, это 𝐴 умножить на 𝐵. Итак, у нас есть один, два, три, четыре умножить на один, два, три, 𝑘. Итак, если мы воспользуемся правило умножения, которое мы показали ранее, то для первого элемента мы получили бы единицу. умножить на один плюс два умножить на три, то второй элемент, один умножить на два плюс два 𝑘. Тогда у нас было бы три, умноженное на один плюс четыре умножить на три, а затем три умножить на два плюс четыре 𝑘. Таким образом, мы можем сказать, что 𝐴𝐵 будет равно матрице два на два семь, два плюс два 𝑘, 15, шесть плюс четыре 𝑘.

Итак, теперь мы можем перейти к 𝐵𝐴. Ну, 𝐵𝐴 будет матрицей один, два, три, 𝑘 умножить на матрицу один, два, три, четыре. Тогда это будет равно единице умножить на один плюс два умножить на три, затем один умножить на два плюс два умножить на четыре, затем три умножить на один плюс три 𝑘 и, наконец, три умножить на два плюс четыре 𝑘. Таким образом, результат будет была матрицей два на два семь, 10, три плюс три 𝑘 и шесть плюс четыре 𝑘.

Хорошо, отлично. Так что бы мы сделали сейчас? Ну, что мы можем сделать, так это найти 𝑘 по приравнивая соответствующие элементы, а затем подставляя это обратно, чтобы увидеть, дает ли это получим тот же результат для 𝐴𝐵 и 𝐵𝐴. Ну, если мы начнем с два плюс два 𝑘 равно 10, а затем вычтем два из каждой части уравнения, мы получим два 𝑘 равно восьми. Делим на два, получаем 𝑘 равняется четырем. Ладно, верно. Так что теперь, если мы заменим 𝑘 равно четыре в другие элементы, все мы получим то же самое для 𝐴𝐵 и 𝐵𝐴. Ну, а если мы посмотрим на нижний левый элемент 𝐵𝐴, тогда у нас будет три плюс три 𝑘, что то же самое, что три плюс три, умноженное на четыре, если 𝑘 равно четырем, что будет равно 15. Отлично, вот что у нас получилось 𝐴𝐵.

И для нижнего правого элемента 𝐴𝐵 и 𝐵𝐴, у нас есть шесть плюс четыре 𝑘, так что в любом случае одинаково. Но если бы мы хотели работать, мы могли бы получить шесть плюс четыре, умноженное на четыре, то есть шесть плюс 16, то есть 22. Следовательно, если 𝑘 было равно четыре, результатом для 𝐴𝐵 и 𝐵𝐴 будет матрица два на два семь, 10, 15, 22. Таким образом, ответ на вопрос «можно ли выбрать 𝑘 так, чтобы 𝐴𝐵 равнялось 𝐵𝐴», — да. И значение 𝑘 которое бы сделать это возможным — четыре.

Как доказать, что AB=BA тогда и только тогда, когда AB также симметричен?

Last updated date: 15th Feb 2023

•

Total views: 234.3k

•

Views today: 5.22k

Answer

Verified

234.3k+ views

Hint: $AB=BA $ тогда и только тогда, когда $AB$ также симметрична, является заданным утверждением, которое необходимо доказать. Симметричная матрица равна транспонированию той же матрицы. Чтобы доказать утверждение, нам нужно использовать метод транспонирования матриц. При использовании транспонирования измененная матрица будет симметричной. Транспонирование происходит только для квадратной матрицы, потому что и строки, и столбцы будут равны в квадратной матрице. 9{Т}}=B$.