8 бит, 10 бит, 8+2 frc. что такое битность матрицы современного телевизора?
При подборе телевизора разные люди по-разному выбирают ту или иную марку и модель. У кого-то главным критерием подбора будет личный опыт пользования, и обращать внимание на ньюансы примененных технологий он не будет. Другой же человек, выбирая себе будущий экран, прошерстит весь интернет в поисках отзывов о модели, размерах каждого болтика и химической формуле использованного пластика, и подчас может быть технически подкован (хотя зачастую только он так и считает) поболее чем представители компании-производителя. :-). Но и те и другие, наверняка будут обращать внимание на технические характеристики. Конечно, их в таблицах немало, но, если быть честными, обращать внимание при сравнении и выборе надо не на все. Что касательно характеристик непосредственно экрана (матрицы, ЛСД-панели — как будет угодно) — то при подборе телевизора стоит обращать внимание не на размер или разрешение. Первое — это выбор не технический, а эстетически-дизайнерский, и выбирается по потребности, а второе — ну… вообще все современные телевизоры… ну почти все — 4К. А вот такие вещи как контрастность, яркость или частота обновления — это то, на что стоит обращать внимание. Но если с ними более чем ясно — они встречались и раньше, и нам понятны, то такой параметр как разрядность матрицы, или как еще его называют — битность матрицы многих ставит в тупик. Разберемся что это такое, и насколько это важно для современного телевизора. И может, если данная тематика будет интересна читателям, затронем и другие загадочные характеристики, на которые стоит обращать внимание.
А вот такие вещи как контрастность, яркость или частота обновления — это то, на что стоит обращать внимание. Но если с ними более чем ясно — они встречались и раньше, и нам понятны, то такой параметр как разрядность матрицы, или как еще его называют — битность матрицы многих ставит в тупик. Разберемся что это такое, и насколько это важно для современного телевизора. И может, если данная тематика будет интересна читателям, затронем и другие загадочные характеристики, на которые стоит обращать внимание.
Итак, что же значат эти самые загадочные значения Матрица 8 бит, Матрица 10 бит, или матрица 8+2 бит FRC?
Битность матрицы, она же разрядность матрицы — параметр, отвечающий за глубину цвета, а именно — какое количество отображаемых цветов может дать эта самая матрица.
Немножко теории.
Источником цвета в современном LCD-экране является пиксель. Собственно, сам пиксель состоит из трех субпикселей — красного, зеленого и синего цвета. Именно их английские название и формирует эту самую часто встречающуюся аббревиатуру RGB. Каждый цветной субпиксель открываясь -приоткрываясь изменяемый выдаваемый цвет в виде оттенков. Значение матрицы 8 бит говорит о том, что, каждый субпиксель может давать 2 в 8 степени оттенков — а именно 2х2х2х2х2х2х2х2 = 256 цветов. Но поскольку каждый пиксель состоит из 3 субпикселей разного цвета — то их комбинации выдают 256х256х256 = 16777216 цветов. То есть 8-ми битная матрица показывает на очи наши ясные 16,7 млн цветов. Соответственно 10-ти битная матрица — это 1.07 млрд цветов. Существуют так же 6-битные и даже 12-ти битные матрицы. И если первые успешно уходят в небытие, то вторые — очень редко встречаются из-за своей дороговизны и узкости применения.
Именно их английские название и формирует эту самую часто встречающуюся аббревиатуру RGB. Каждый цветной субпиксель открываясь -приоткрываясь изменяемый выдаваемый цвет в виде оттенков. Значение матрицы 8 бит говорит о том, что, каждый субпиксель может давать 2 в 8 степени оттенков — а именно 2х2х2х2х2х2х2х2 = 256 цветов. Но поскольку каждый пиксель состоит из 3 субпикселей разного цвета — то их комбинации выдают 256х256х256 = 16777216 цветов. То есть 8-ми битная матрица показывает на очи наши ясные 16,7 млн цветов. Соответственно 10-ти битная матрица — это 1.07 млрд цветов. Существуют так же 6-битные и даже 12-ти битные матрицы. И если первые успешно уходят в небытие, то вторые — очень редко встречаются из-за своей дороговизны и узкости применения.
Страшные буковки FRC
Очень часто в характеристиках определенных моделей телевизоров и мониторов встречается такое обозначение, как 8+2 бит FRC. Не надо их боятся. Например, видеокарта компьютера или просто источник сигнала (скажем фильм) имеет-выдает изображение с глубиной цвета 10 бит. А матрица монитора или телевизора может отобразить только 8-ми битный цвет. И для решения таких сложностей используется методы сглаживания (дизиринга) или технология FRC (Frame rate control). Эти все ухищрения позволяет отобразить недостающие цвета с помощью имеющейся палитры. Ну как отобразить… Конечно, данная технология делает цветовые переходы не настолько плавными в сравнении с честной 10-битной палитрой. Но однозначно лучше, чем при 8-ми битах. Так что эти самые буквы весьма желательны. Не нужно думать, что с FRC 8+2 возьмет 8-ми битную картинку и сделает ее 10 битной. Нет, это не улучшалка в чистом виде. Эта технология нужна именно для того, чтобы 10-ти битная картинка не выглядела на 8-ми битной матрице совсем нехорошо и криво.
А матрица монитора или телевизора может отобразить только 8-ми битный цвет. И для решения таких сложностей используется методы сглаживания (дизиринга) или технология FRC (Frame rate control). Эти все ухищрения позволяет отобразить недостающие цвета с помощью имеющейся палитры. Ну как отобразить… Конечно, данная технология делает цветовые переходы не настолько плавными в сравнении с честной 10-битной палитрой. Но однозначно лучше, чем при 8-ми битах. Так что эти самые буквы весьма желательны. Не нужно думать, что с FRC 8+2 возьмет 8-ми битную картинку и сделает ее 10 битной. Нет, это не улучшалка в чистом виде. Эта технология нужна именно для того, чтобы 10-ти битная картинка не выглядела на 8-ми битной матрице совсем нехорошо и криво.
Теперь о практике
И, пожалуй, два самых важных вопроса: видит ли человеческий глаз разницу между битностью цвета 8 и 10, а также стоит ли переплачивать за телевизор с 10-битной матрицей. Да, человеческий глаз эту разницу видит.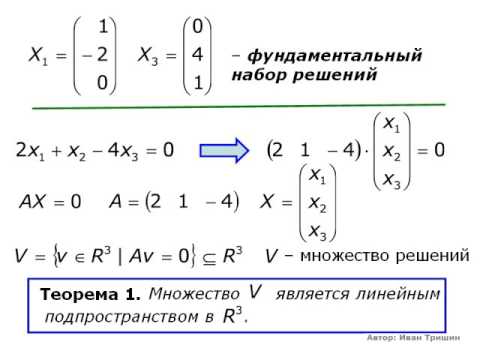 Но — не каждый. Да да, много людей не воспринимают цветовое разнообразие и плавность этих самых переходов. Особенно это касается мужчин, ведь представительницы женской части планеты как известно изначально лучше различают оттенки. Но факт остается фактом — в общем массе разницу между 16.7 млн и 1,07 млрд цветов видно. Но — это еще не все. Тут важнее как эта разница заметна на экране монитора или телевизора. А выглядит это скорее всего похоже, как вот так.
Но — не каждый. Да да, много людей не воспринимают цветовое разнообразие и плавность этих самых переходов. Особенно это касается мужчин, ведь представительницы женской части планеты как известно изначально лучше различают оттенки. Но факт остается фактом — в общем массе разницу между 16.7 млн и 1,07 млрд цветов видно. Но — это еще не все. Тут важнее как эта разница заметна на экране монитора или телевизора. А выглядит это скорее всего похоже, как вот так.
То есть плавность переходов, особенно при динамической картинке и быстрых изменениях — вещь важная, особенно для видеофилов и перфекционистов. Ну и конечно, важный вопрос — стоит ли платить за 10 бит, или все же стоит перетерпеть с 8+2 FRC. Разница в цене может быть немалая — правда нам не известно, сколько из этой разницы отдается именно за битность матрицы. Ведь даже для примера тот же Samsung Q70 в отличие от Q60 в размере 55 и выше дюймов кроме десятибитности еще имеет весьма недешевую технологическую штуку под названием система локального затемнения, она же Localdimming. Так что понять, за что конкретно отстегиваем кровные весьма сложно, но давайте просто считать, что комплексно платим за технологичный продукт с более широкими возможностями.
Так что понять, за что конкретно отстегиваем кровные весьма сложно, но давайте просто считать, что комплексно платим за технологичный продукт с более широкими возможностями.
Но, наиболее выразительный плюс в пользу 10-бит кроется в ином месте. Есть такая очень популярная нынче шутка, которую пихают в каждый телевизор, как Расширенный динамический диапазон изображения, в простонародье HDR.
А там все построено именно на 10-битном цвете. Также есть такая себе технологическая войнушка между HDR10+ и Dolby Vision (который, кстати, уже на 12-битах), и конечно все эти заварушки и противостояния технологий нам, рядовым пользователям только на пользу. Все зависит от двух моментов — сколько есть на данный момент контента (читай кино) в HDR, и конечно, насколько позволяет такую покупку Ваш кошелек. Первое — а именно контента в HDR — ну… становиться все больше и больше. Со вторым — ну, тут остается Вам пожелать, чтобы там тоже был прогресс, и чем больше — тем лучше.
Стоит ли расстраиваться, что в Вашем телевизоре 8+2frc а не честные 10 бит? Нет! Покупка телевизора должна быть соизмерима с финансовыми возможностями, без тотального фанатизма и неразумных трат. Все равно за всеми новыми технологиями угнаться невозможно.
3.7. Диагонализация матрицы линейного оператора
Пусть линейный оператор . Рассмотрим в произвольный базис . Пусть в этом базисе линейному оператору соответствует матрица . Существует ли такой базис в пространстве , в котором матрица линейного оператора была бы диагональной?
Очевидно, если такой базис существует, то по Свойству 1 (п. 3.6) диагонализация матрицы произойдет в результате преобразование подобия.
Имеет место следующая
Теорема. Если в существует базис из собственных векторов линейного оператора то матрица линейного оператора будет диагональной в этом базисе.
Выясним, при каких условиях существует базис из собственных векторов линейного оператора.
Пусть – собственные значения линейного оператора кратностей , причём . Если для каждого существует собственных векторов – решений ФСР соответствующей однородной СЛАУ, то существует базис из собственных векторов, а значит, матрицу линейного оператора можно привести к диагональному виду. В частности, если , т. е. спектр линейного оператора простой, то базис из собственных векторов существует. Однако, если среди корней характеристического уравнения найдётся хотя бы одна пара комплексно-сопряжённых, то в вещественном линейном пространстве не существует базиса из собственных векторов.
Покажем, например, что, если спектр простой, то матрица линейного оператора в базисе из собственных векторов будет диагональной.
Рассмотрим квадратную матрицу , в столбцах которой стоят координаты собственных векторов , соответствующих собственным значениям . Это означает, что матрица является матрицей перехода к базису из собственных векторов. Очевидно, в этом случае , т. е. матрица – невырожденная, и для неё существует обратная – Из определения собственных векторов линейного оператора следует, что
(16)
Где – векторы-столбцы, соответствующие собственным векторам линейного оператора .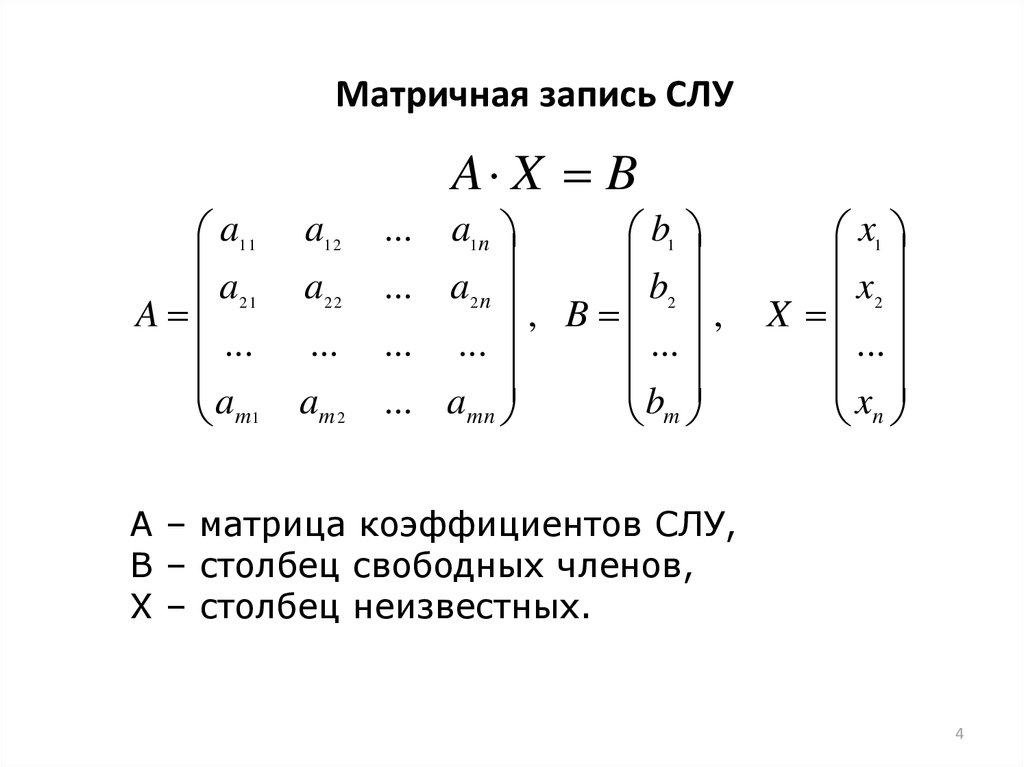 Равенство (16) можно записать в более компактной форме:
Равенство (16) можно записать в более компактной форме:
(17)
Где – диагональная матрица, у которой на главной диагонали расположены собственные числа т. е.
Умножим обе части равенства (17) слева на матрицу :
или (18)
Это означает, что матрица линейного оператора при переходе к базису из собственных векторов станет диагональной в результате преобразования подобия (18).
Пример 14. Найти собственные значения и собственные векторы линейного оператора , заданного в некотором базисе матрицей . Построить, если это возможно, базис из собственных векторов линейного оператора и найти матрицу линейного оператора в этом базисе. Выполнить проверку.
Решение. Составим характеристическое уравнение:
Найдём собственные векторы линейного оператора:
;
Т. е.
Собственные значения линейного оператора различны, значит, собственные векторы линейно независимы, т. е. образуют базис. В этом базисе матрица линейного оператора будет диагональной:
.
Матрица перехода к базису из собственных векторов .
Проверим правильность проведенных вычислений. По формуле (7) Найдём :
.
Тогда
Ответ: .
Пример 15. Линейный оператор в некотором базисе задан матрицей Существует ли базис из собственных векторов линейного оператора ?
Решение. Составим характеристическое уравнение:
Собственные значения линейного оператора Найдём соответствующие им собственные векторы: Т. е. . Все остальные собственные векторы имеют вид . Это означает, что базис из собственных векторов не существует.
Пример 16. Найти собственные векторы и собственные значения линейного оператора , заданного в некотором базисе матрицей . Можно ли привести матрицу к диагональному виду?
Решение. Составим характеристическое уравнение:
Т. е.
Или
Собственные значения линейного оператора Найдём собственные векторы:
Эта система эквивалентна следующей:
Т. е. ФСР этой системы состоит из одного решения, например, Собственным значениям и соответствует собственный вектор . Другие собственные векторы, соответствующие собственным значениям и , могут быть получены из умножением на произвольное вещественное число. Например, .
е. ФСР этой системы состоит из одного решения, например, Собственным значениям и соответствует собственный вектор . Другие собственные векторы, соответствующие собственным значениям и , могут быть получены из умножением на произвольное вещественное число. Например, .
Так как , то значит,
линейно зависимы, значит, совокупность собственных векторов также линейно зависима, т. е. собственные векторы линейного оператора не образуют базис в . Поэтому матрица не может быть приведена к диагональному виду.
Литература: [3, 4, 5, 7, 10].
| < Предыдущая | Следующая > |
|---|
Матричный массив ThruMode
+ Нажмите, чтобы открыть полный размер
Этот массив из 160 ячеек измерения силы, 10 рядов и 16 столбцов, позволяет пользователю одновременно измерять силу каждой ячейки одновременно. С активной площадью 2 x 3 дюйма этот планшет можно использовать в качестве мультисенсорного пользовательского устройства ввода, музыкального контроллера или даже для измерения распределения силы объектов.
С активной площадью 2 x 3 дюйма этот планшет можно использовать в качестве мультисенсорного пользовательского устройства ввода, музыкального контроллера или даже для измерения распределения силы объектов.
Конструкция ThruMode позволяет измерять малые значения усилия.
Как это работает?
Если вы только начинаете работать с матричными массивами, мы предоставили несколько примеров схем и кода Arduino в нашем учебном пособии по матричным массивам.
Инструменты и решения для разработки
(Сторонние поставщики)Необходимо ускорить проектирование или оценку датчика? Ниже приведены рекомендуемые продукты от Sensitronics Partners.
| Поставщик | Продукт | Описание/применение | Совместим с |
| Китроникс | Сноуборд |
|
|
Характеристики датчика
| Собственность | Значение | Примечания |
| Диапазон размеров | Активная область 2 x 3 дюйма | Габаритные размеры см.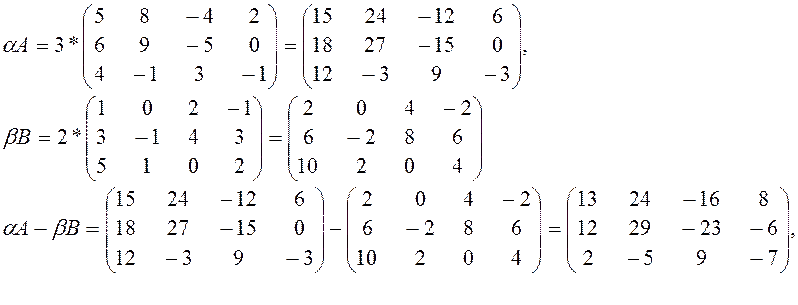 на линейной схеме. на линейной схеме. |
| Диапазон чувствительности к силе | от 0,25 до 12,5 фунтов. | Сила распределяется на площади 0,5 дюйма. |
| Диапазон чувствительности к давлению | от 0,5 до 25 фунтов на кв. дюйм | Зависит от механического интерфейса |
| Повторяемость усилия от детали к детали | ок. +/- 15% от среднего сопротивления | С последовательным срабатыванием |
| Максимальный ток | ,5 мА | |
| Повторяемость усилия одной детали | +/- 5% установленного номинального сопротивления | С последовательным срабатыванием |
| Принудительное разрешение | 1% полной шкалы | |
| Противостояние | 10 МОм или больше | |
| Переключатель хода | . 005″ 005″ | |
| Время нарастания устройства | 15 кГц или выше | |
| Жизненный цикл | 1 миллион плюс срабатывания | |
| Диапазон температур | от -15°F до +200°F | |
| Толщина устройства | 0,017″ | |
| Гибкость |
Как работает резистор, чувствительный к силе (FSR)?
В последние годы печатные, тонкие и гибкие датчики вызвали настоящий ажиотаж в инженерном сообществе. Во многом это связано с бумом умных, легких и энергоэффективных технологий, которые прочно вошли в нашу повседневную жизнь. Естественно, при разработке этих компактных, но мощных устройств и продуктов встроенные компоненты, которые делают их революционными инновациями, также должны обладать теми же характеристиками.
Резисторы, чувствительные к силе (AKA, печатные датчики силы или резисторы, чувствительные к силе) представляют собой большую и растущую группу встроенных компонентов, при этом в последние годы появилось много новых типов датчиков. Однако резисторы, чувствительные к силе, вовсе не являются новой технологией. Фактически, резисторы измерения усилия использовались в качестве встроенных компонентов на протяжении десятилетий.
В этой статье рассказывается об основах технологии резисторов измерения усилия, о том, как они работают и как их можно использовать для регистрации измерений силы в качестве встроенного компонента внутри устройства.
Как резисторы, чувствительные к силе, измеряют силу?
Рис. 1. Когда к резистору, чувствительному к силе, прикладывается сила, реакция проводимости как функция силы является линейной. Большинство инженеров усвоили, что формула силы представляет собой массу объекта, умноженную на его ускорение (или F=M*A). , или приложенное давление, умноженное на площадь контакта (F=P*площадь). Есть несколько инженерных единиц для представления «F» в этих уравнениях, таких как ньютоны (Н), фунт-сила (фунт-сила) и другие.
Есть несколько инженерных единиц для представления «F» в этих уравнениях, таких как ньютоны (Н), фунт-сила (фунт-сила) и другие.
Сами по себе резисторы для измерения силы не калибруются предварительно для соотнесения показаний силы с известными техническими единицами. Однако выходной сигнал измерения усилия, полученный датчиком силы, может быть соотнесен с приложенной силой с помощью процедуры калибровки.
Резисторы, чувствительные к силе, представляют собой пьезорезистивную технологию измерения. Это означает, что они являются пассивными элементами, которые функционируют как переменный резистор в электрической цепи. Как показано на рис. 1 , в ненагруженном состоянии датчик имеет высокое сопротивление (порядка мегаом (МОм)), которое падает при приложении силы (обычно порядка килоом (КОм)). Когда вы рассматриваете обратную зависимость сопротивления (проводимости), реакция проводимости как функция силы является линейной в пределах установленного диапазона силы датчика.
Как откалибровать резистор, чувствительный к силе?
Из-за их линейной зависимости сопротивления/проводимости резисторы, чувствительные к силе, можно калибровать с двумя-тремя известными нагрузками. В этой статье подробно объясняется пошаговый процесс калибровки.
Кроме того, если ваша схема разработана с регулируемыми компонентами, чувствительность датчика можно отрегулировать для оптимальной работы в вашем конкретном диапазоне усилия. В этой статье приведены дополнительные сведения о значении регулируемой чувствительности.
Как изготавливаются резисторы, чувствительные к силе?
Резисторы, чувствительные к силе, состоят из полупроводящего материала или полупроводящих чернил, заключенных между двумя тонкими подложками. Как показано на рис. 2 , существует два различных типа технологии резисторов измерения силы – шунтирующий режим и сквозной режим.
Рис. 2. На этом рисунке показаны различия между технологиями резисторов, чувствительных к силе, в шунтирующем и сквозном режимах.
Шунтирующие резисторы для измерения силы представляют собой полимерные толстопленочные устройства, состоящие из двух мембран, разделенных тонким воздушным зазором. Одна мембрана имеет два набора встречно-штыревых дорожек, которые электронно изолированы друг от друга, а другая мембрана покрыта специальной текстурированной резистивной краской.
Резисторы для измерения силы сквозного режима представляют собой гибкие печатные схемы, в которых в качестве двух внешних подложек используется полиэфирная пленка. Серебряные круги со следами расположены над и под чувствительным к давлению слоем, за которым следует проводящий полимер. Клейкий слой используется для ламинирования двух слоев подложки вместе.
Матричные или одноточечные резисторы для измерения силы
Рисунок 3: Примеры различных технологий резисторов, чувствительных к силе. Резисторы, чувствительные к силе, могут быть спроектированы как одноточечные датчики силы или в виде матрицы, что позволяет пользователю фиксировать распределение давления в заданной области. Матрицы резисторов, чувствительные к силе, обычно называют технологией картирования давления.
Матрицы резисторов, чувствительные к силе, обычно называют технологией картирования давления.
Датчики FlexiForce™ от Tekscan представляют собой разновидность резисторов для измерения силы в сквозном режиме. Гибкость этой технологии в сочетании с их операционными возможностями и их способностью работать на простых схемах делают их отличным вариантом для встраивания в интеллектуальные устройства с ограниченным пространством и ограничениями по мощности. Датчики FlexiForce также легко настраиваются. Форма, размер, чувствительность, электрическое подключение и рабочая температура могут быть адаптированы к конкретным потребностям вашего приложения.
В этой статье рассматриваются некоторые различия в характеристиках датчиков с шунтирующим и сквозным режимами, в том числе их сравнение по линейности, дрейфу, точности и другим ключевым факторам.
Как используются резисторы, чувствительные к силе?
Несмотря на то, что каждый день открываются новые области применения технологии резисторов, чувствительных к силе, большинство приложений, как правило, подпадают под четыре различные категории использования:
- Обнаружение или измерение скорости изменения силы
- Обнаружение или измерение относительного изменения силы
- Обнаружение контакта и/или прикосновения
- Обнаружение пороговых значений силы для запуска какого-либо действия (например, приложений IoT)
В этом коротком видеоролике представлен более наглядный контекст этих различных вариантов использования резисторов для измерения усилия, в частности резисторов для измерения усилия FlexiForce:
