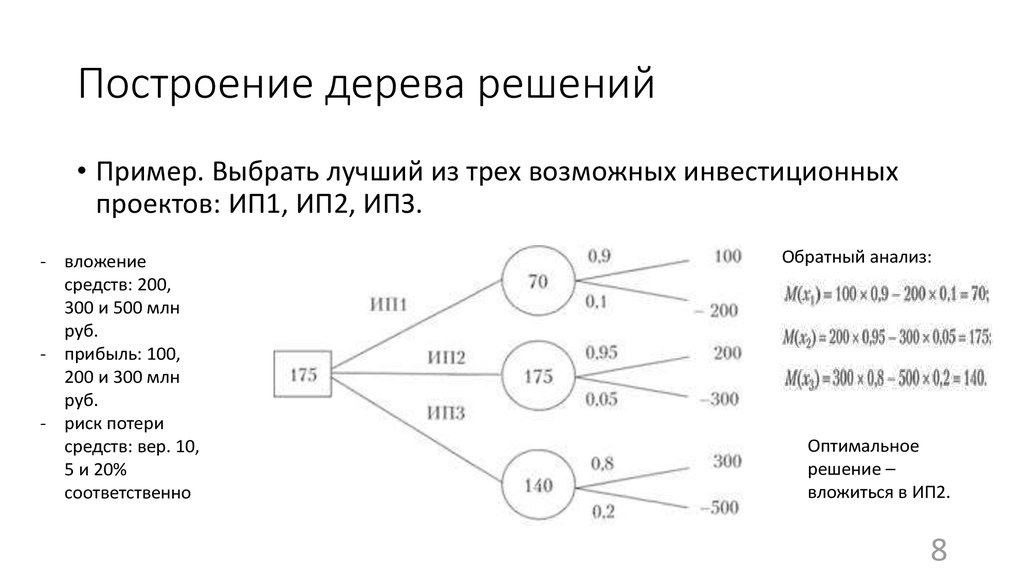
понятие, алгоритм работы, сферы применения метода
Что это такое? Дерево решений является весьма эффективной методикой, применяемой для анализа больших массивов данных. Инструмент работает по четкому алгоритму и в соответствии со строго определенными принципами.
Где применяется? Дерево решений как способ обработки имеющейся информации и одно из средств предсказательной аналитики используется во многих сферах человеческой деятельности: банковской и медицинской, предпринимательской и промышленной. Часто инструмент бывает полезен в машинном обучении.
В статье рассказывается:
- Общее описание метода дерева решений
- Алгоритм работы инструмента
- Задачи, решаемые с помощью дерева методики
- Сферы применения инструмента
- Дерево решений в машинном обучении
- Этапы построения дерева решений
- Преимущества и недостатки методики
-
Пройди тест и узнай, какая сфера тебе подходит:
айти, дизайн или маркетинг.
Бесплатно от Geekbrains
Общее описание метода дерева решений
Сама идея создания и дальнейшего развития моделей дерева решений появилась в середине XX века после исследований вероятного человеческого поведения киберсистемами. Работы К. Ховеленда «Компьютерное моделирование мышления» и Е. Ханта «Эксперименты по индукции» сыграли ведущую роль в развитии этого направления.
Дальнейшее увеличение популярности этому методу обеспечили работы Джона Р. Куинлена, который разработал алгоритм ID3 и его усовершенствованные модификации С4.5 и С5.0, а также Лео Бреймана, предложившего алгоритм CART и метод случайного леса.
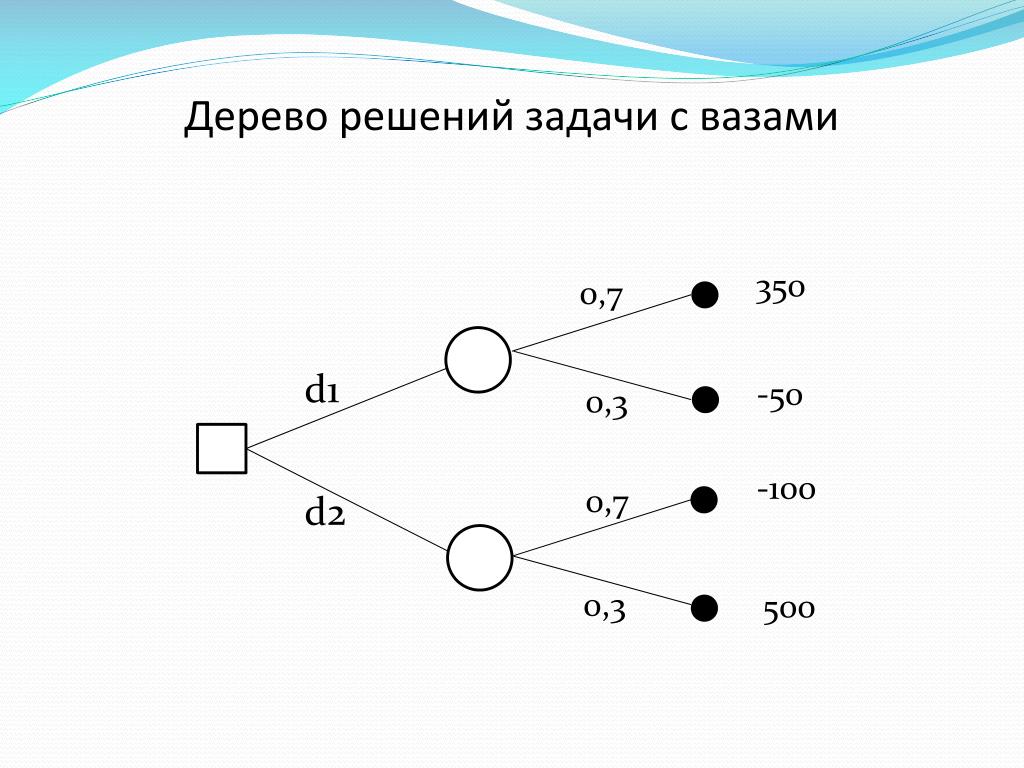
Если говорить простыми словами, то дерево решений представляет собой задачу с несколькими вариантами действий. На карте прорабатываются возможные результаты каждого шага, а также следующие на них реакции. Этот метод особенно актуален в тех ситуациях, в которых нужно сделать вывод о ряде последовательных решений, ведущих к оптимальному исходу.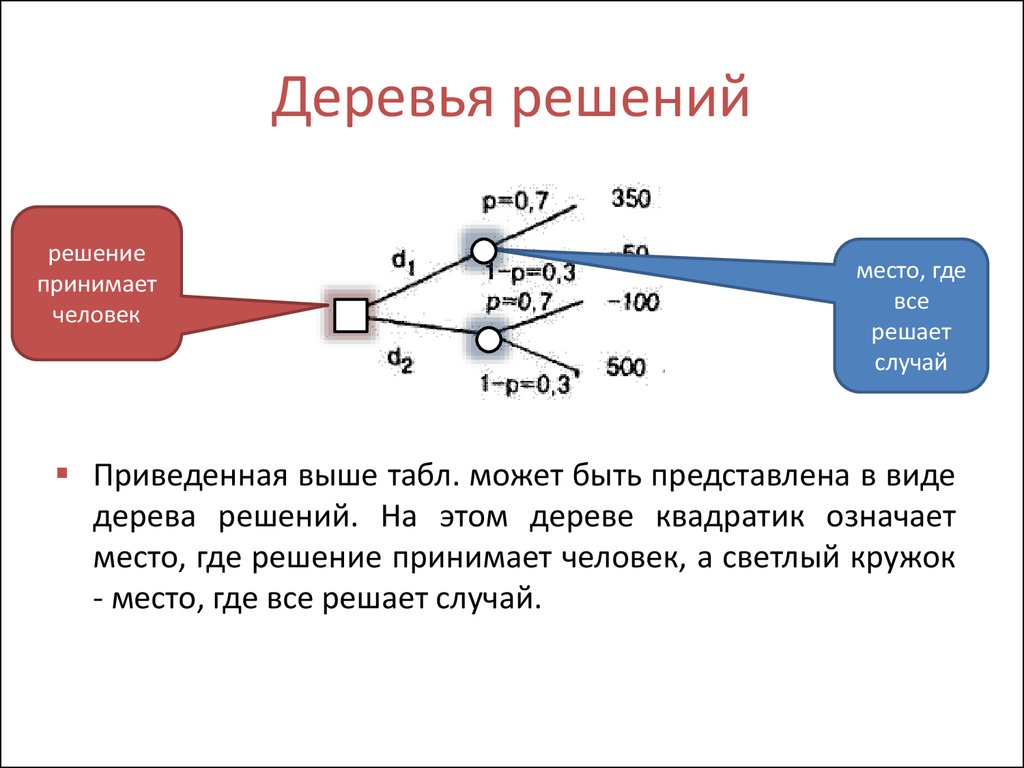
Алгоритм работы инструмента
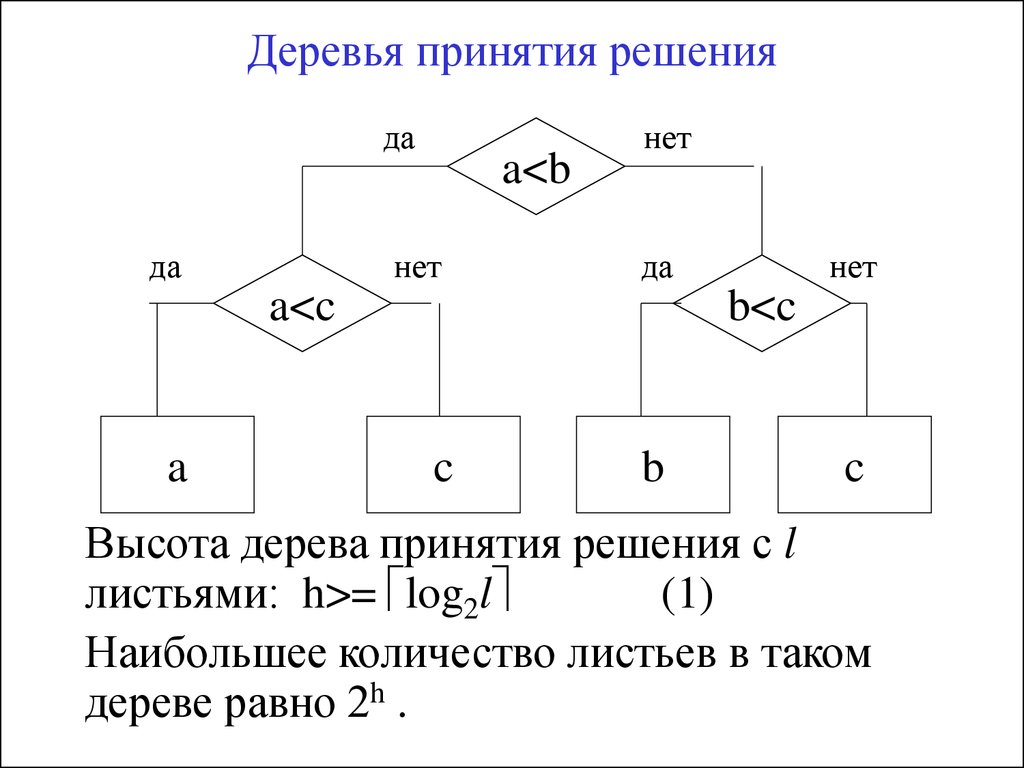
Дерево принятия решений — это метод, дающий представление о действиях и их последствиях в виде упорядоченной иерархии. Оно включает в себя элементы двух типов: узлы (node) и листья (leaf). Узлы представляют собой совокупность решающих правил и осуществляют проверку гипотетических ситуаций на соответствие выбранным показателям.
Если говорить проще, то примеры, которые попадают в узел, после прохождения проверки разделяются на два типа:
- Первый — те, которые подходят под назначенные правила.
- Второй — те, которые не подходят под назначенные правила.
Затем к каждому подтипу опять применяется правило, и процедура повторяется до тех пор, пока не произойдёт остановка алгоритма дерева решений. Последний узел, который больше не нуждается в проверке и разделении на подмножество, становится листом.
Лист представляет собой решение для примера, который в нём находится. Таким образом, там содержится не одно общее правило, а подмножество объектов, которые удовлетворяют всем правилам данной ветви.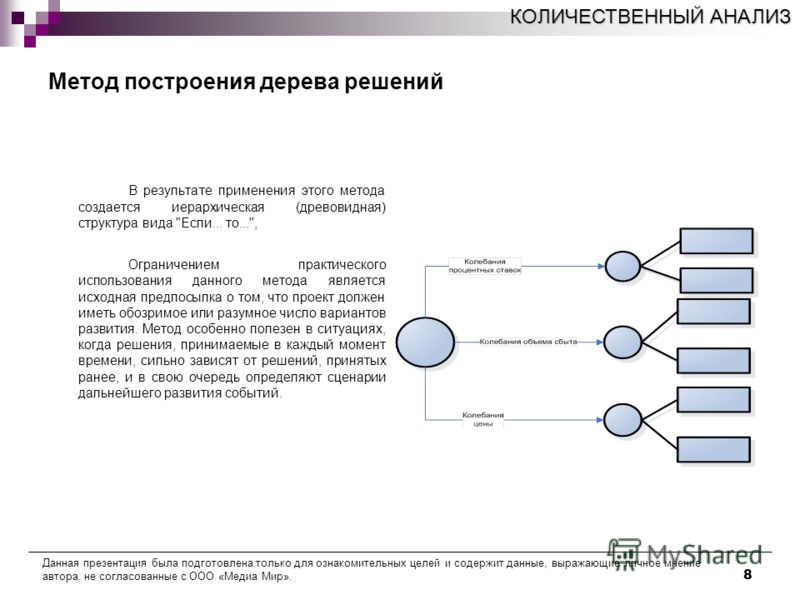 Ведь пример оказывается в листе, только если будет соответствовать всем установленным критериям на пути к нему. Очевидно, что к каждому листу ведёт только одна «дорога», что предполагает единственное верное решение и следование одному оптимальному алгоритму.
Ведь пример оказывается в листе, только если будет соответствовать всем установленным критериям на пути к нему. Очевидно, что к каждому листу ведёт только одна «дорога», что предполагает единственное верное решение и следование одному оптимальному алгоритму.
Задачи, решаемые с помощью методики
Задачи составления дерева решений заключаются в следующем:
- Классификация. Анализ предложенных объектов и решение о соответствии их определённому классу из заявленных ранее. При этом целевая переменная имеет дискретные задачи.
- Регрессия (численное предсказание). Прогнозирование конкретного числового значения независимой переменной для заданного вектора.
- Описание объектов. Позволяет ёмко и лаконично описывать объекты при помощи использования ряда конкретных правил.
Сферы применения
Огромное количество аналитических платформ включают в себя различные модули для построения деревьев решений. Этот метод анализа данных является очень удобным и позволяет выявить оптимальный алгоритм действий для решения заданной проблемы.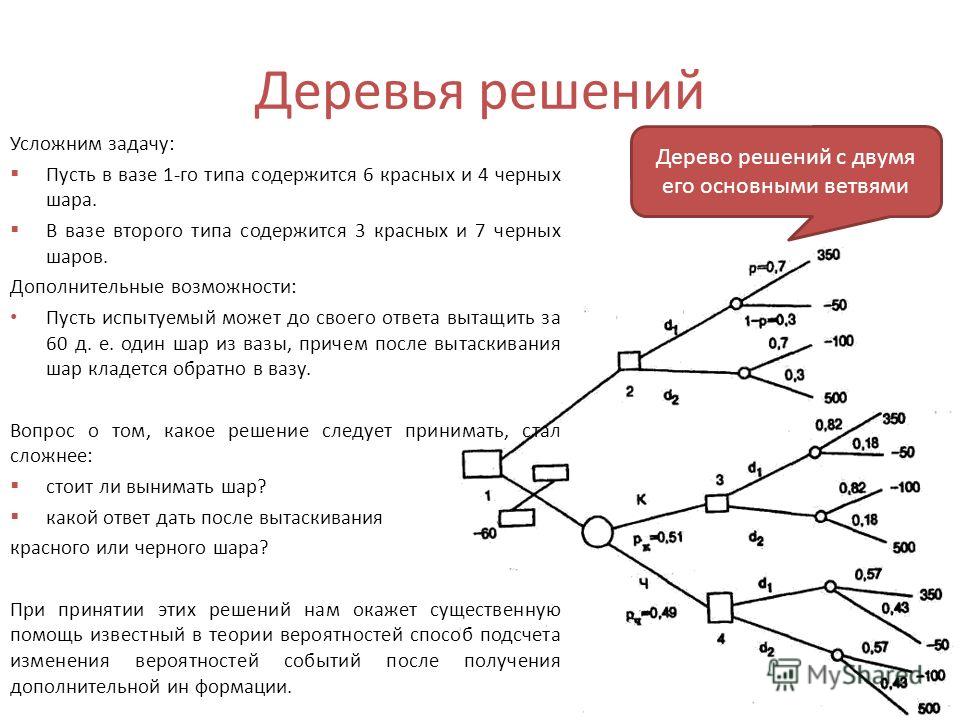 Дерево решений, например, используется для составления готовых скриптов для общения с потребителями в сфере продаж товаров и услуг.
Дерево решений, например, используется для составления готовых скриптов для общения с потребителями в сфере продаж товаров и услуг.
Рассмотрим следующую ситуацию: пользователь захотел оплатить услугу через приложение банка. Операция была отклонена. После этого клиент написал в службу поддержки банка для выяснения обстоятельств. Сотрудник, который ответит ему в чате, будет следовать определённому алгоритму. Для начала он спросит у клиента идентификатор платежа. В дальнейшем, согласно дереву решений, варианты общения будут разветвляться в зависимости от ответа на этот вопрос.
Отдел продаж также пользуется деревьями решений: менеджер задает клиенту вопросы и выстраивает своё дальнейшее общение с ним в зависимости от его ответов.
В общем, практически в любой службе поддержки или работы с клиентами пользуются деревьями решений, будь то интернет-провайдер или отдел претензий к качеству товара.
В статистике данный инструмент также очень полезен, ведь с его помощью можно прогнозировать ситуации и описывать данные, разделяя их на взаимосвязанные группы. Самой простой и популярной задачей, которая ставится перед деревом решений, является бинарная классификация. Она представляет собой деление заявленных примеров на два типа, один из которых является положительным (успех), а второй — отрицательным (неудача).
Самой простой и популярной задачей, которая ставится перед деревом решений, является бинарная классификация. Она представляет собой деление заявленных примеров на два типа, один из которых является положительным (успех), а второй — отрицательным (неудача).
Топ-30 самых востребованных и высокооплачиваемых профессий 2023
Поможет разобраться в актуальной ситуации на рынке труда
Подборка 50+ ресурсов об IT-сфере
Только лучшие телеграм-каналы, каналы Youtube, подкасты, форумы и многое другое для того, чтобы узнавать новое про IT
ТОП 50+ сервисов и приложений от Geekbrains
Безопасные и надежные программы для работы в наши дни
pdf 3,7mb
doc 1,7mb
Уже скачали 20583
Например, метеорологам требуется составить прогноз о том, будет ли завтра дождь. Для анализа предлагаются данные о предшествующих пятидесяти днях. Чтобы составить дерево решений, нужно разделить все эти дни на две группы, которые будут соответствовать следующим значениям: 1 — на следующий день шёл дождь, 0 — на следующий день дождя не было.
Кроме того, анализируются все сопутствующие условия: влажность, атмосферное давление, направление ветра, средняя температура и т. д. Использование алгоритма дерева решений дает возможность выявить в общем объёме информации те условия, которые позволят разделить дни на предложенные два типа. Таким образом, будет выявлена ситуация, позволяющая максимально верно составить прогноз на следующий день.
Дерево решений в машинном обучении
Этот инструмент используется и при составлении автоматизированных моделей прогнозирования. Они активно применяются в машинном обучении. Применение дерева решений даёт возможность предсказать вероятную ценность объекта с учётом всей известной о нём информации.
Дерево решений в машинном обученииЭтот тип называется «дерево классификации». В данной схеме узлы представляют собой данные, а не решение. Каждая ветвь такого дерева содержит определённый набор правил, которые соответствуют выбранному классу.
Такие правила принятия решений обычно выражаются в условии соответствия, которое кратко можно описать формулой «если — то».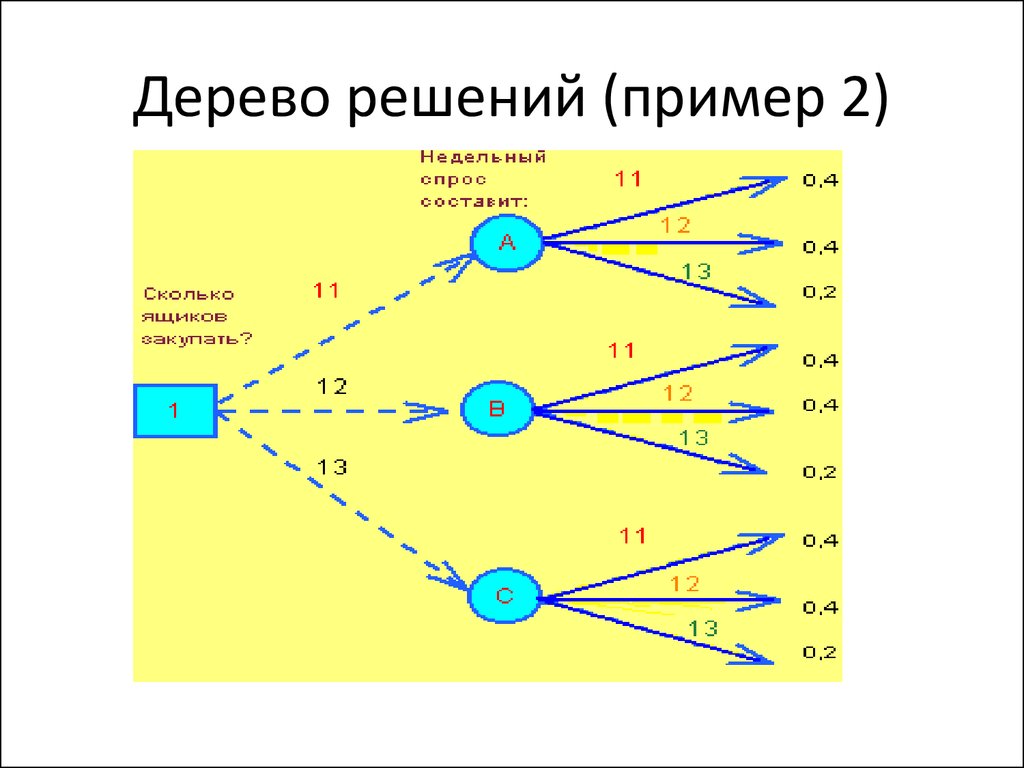
Любая дополнительная информация увеличивает достоверность прогнозирования того, насколько выбранный объект соответствует заявленным условиям. Полученные данные могут быть использованы для составления более масштабного дерева решений в выбранной области.
Только до 4.05
Скачай подборку тестов, чтобы определить свои самые конкурентные скиллы
Список документов:
Тест на определение компетенций
Чек-лист «Как избежать обмана при трудоустройстве»
Инструкция по выходу из выгорания
Чтобы получить файл, укажите e-mail:
Подтвердите, что вы не робот,
указав номер телефона:
Уже скачали 7503
Иногда применяется сразу несколько видов деревьев решений. Это позволяет наиболее точно предсказать результат и выявить оптимальный алгоритм для достижения желаемого итога. В качестве комбинированного подхода используются следующие методы:
Это позволяет наиболее точно предсказать результат и выявить оптимальный алгоритм для достижения желаемого итога. В качестве комбинированного подхода используются следующие методы:
- Бэггинг. Включает в себя создание нескольких деревьев решений для анализа повторной выборки исходных данных. На основе полученных результатов формулируется единое решение заданного вопроса.
- Метод случайного леса. В данном случае несколько деревьев применяются для увеличения количества успешно классифицированных объектов.
- Бустинг. Используется в отношении регрессионных и классификационных деревьев.
- Ротационный лес
Идеально составленное дерево решений должно выдавать максимум информации при минимальном количестве уровней.
Дерево решений в машинном обученииВ машинном обучении модель дерева решений используется особенно часто, так как она дает множество преимуществ.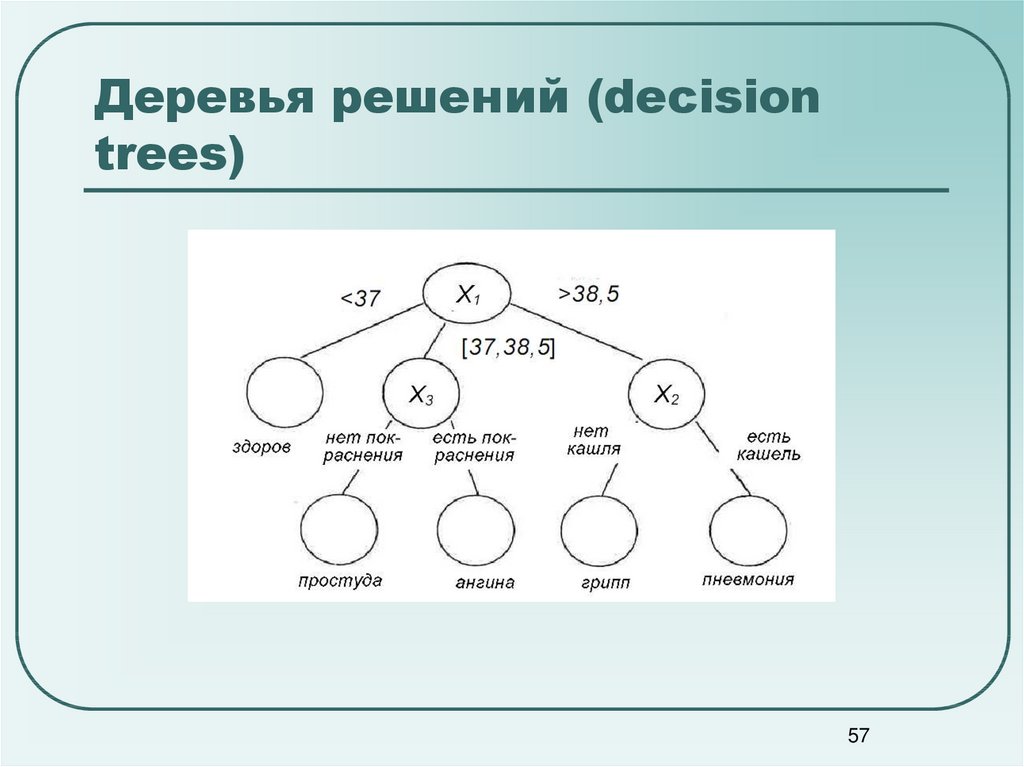 Этот инструмент экономически выгоден, так как затраты на его использование уменьшаются с каждой дополнительной точкой данных. Деревья решений позволяют анализировать как числовые, так и категориальные данные.
Этот инструмент экономически выгоден, так как затраты на его использование уменьшаются с каждой дополнительной точкой данных. Деревья решений позволяют анализировать как числовые, так и категориальные данные.
Кроме того, данный метод даёт возможность формировать вопросы с несколькими вероятными ответами. Он даёт максимально точные результаты даже при искажении предпосылок исходных данных.
Этапы построения дерева решений
Составление деревьев решений для машинного обучения и анализа давно автоматизировано. Для этого можно воспользоваться специальными библиотеками, созданными при помощи двух языков программирования: R и Python. В рамках Python существует бесплатная библиотека стандартных моделей машинного обучения scikit-learn, которая активно используется аналитиками для решения задач. В ней также существует возможность использования предподготовленного кода.
Для того чтобы составить дерево решений с помощью предподготовленного кода, необходимо выполнить следующие действия:
Сбор данных и их анализ
Сначала аналитики оценивают исходные данные и ищут в них общие закономерности. Затем они формируют ответ на вопрос о том, почему для решения данной задачи должен использоваться именно такой инструмент. Кроме того, на этом этапе вычисляются факторы, которые оказывают влияние на зависимую переменную.
Затем они формируют ответ на вопрос о том, почему для решения данной задачи должен использоваться именно такой инструмент. Кроме того, на этом этапе вычисляются факторы, которые оказывают влияние на зависимую переменную.
Проведение предподготовки
На этом этапе специалисты очищают данные от аномалий. Это действие необходимо для того, чтобы представить информацию в нужном формате. Существуют специализированные алгоритмы для данной работы:
- Заполнение пропусков средними значениями.
- Нормирование показателей относительно друг друга.
- Удаление аномалий.
- Категоризация переменных данных.
Формирование отложенной выборки
Некоторую часть представленных данных необходимо проанализировать самостоятельно, чтобы определить ожидаемое значение для итогового результата. Это позволяет проверить качество работы алгоритма дерева решений при анализе ситуации, с которыми обученная модель ранее не сталкивалась.
Составление дерева решений и начало обучение модели
Специалисты загружают в библиотеку необходимые данные и условия задачи. На основе представленной информации происходит автоматическая генерация правил работы дерева решений.
На основе представленной информации происходит автоматическая генерация правил работы дерева решений.
Сравнение результатов на обучающей и на отложенной выборке
Если результаты совпадают, значит, модель дерева решений обучена верно и пригодна для дальнейшей работы. В этом случае можно сохранить код обученной модели и применять его в будущем.
Преимущества и недостатки методики
Преимущества метода дерева решений:
- Правила создания таких моделей просты и понятны, а интерпретировать полученные результаты легко.
- Есть возможность работать с разными видами переменных.
- Деревья решений допускают пропуски данных и способны заполнять их наиболее вероятным в данной ситуации значением.
- Этот инструмент помогает выявить, какие данные наиболее важны для достижения нужного результата.
- Деревья решений способны самостоятельно формировать правила в малознакомых специалисту областях.
- Их легко визуализировать, что позволяет воспринимать не только модель в целом, но и прогнозировать результат для отдельных субъектов в дереве.

- Не требуют большого количества изначально заданных параметров.
- Способны работать с категориальными и числовыми идентификаторами.
- Позволяют быстро решить проблему благодаря качественному прогнозированию результата.
Но данный метод имеет не только преимущества, но и недостатки, которые тоже необходимо учитывать при работе с ним:
- В задачах на классификацию объектов существует вероятность ошибок. Это связано с большим количеством классов при маленьком числе обучающих примеров.
- Важно учитывать то, что изменения параметров в одном узле дерева решений может привести к полному изменению всей его структуры.
- Составление дерева решений может быть весьма трудоёмким. Это связано с тем, что в каждом узле каждый элемент должен анализироваться до тех пор, пока не станет возможным принятие наилучшего возможного в данной ситуации решения.
Несмотря на ряд недостатков, создание дерева решений является очень востребованной методикой. Она актуальна в различных ситуациях и способна сослужить хорошую службу. Если вы являетесь новичком в данной сфере, то попробуйте начать с небольших задач. Постепенно вы наберетесь опыта и сможете грамотно использовать этот инструмент для работы с более глобальными вопросами.
Она актуальна в различных ситуациях и способна сослужить хорошую службу. Если вы являетесь новичком в данной сфере, то попробуйте начать с небольших задач. Постепенно вы наберетесь опыта и сможете грамотно использовать этот инструмент для работы с более глобальными вопросами.
Продвижение блога — Генератор продаж
Рейтинг: 3
( голосов 2 )
Поделиться статьей
1.10. Деревья решений — scikit-learn
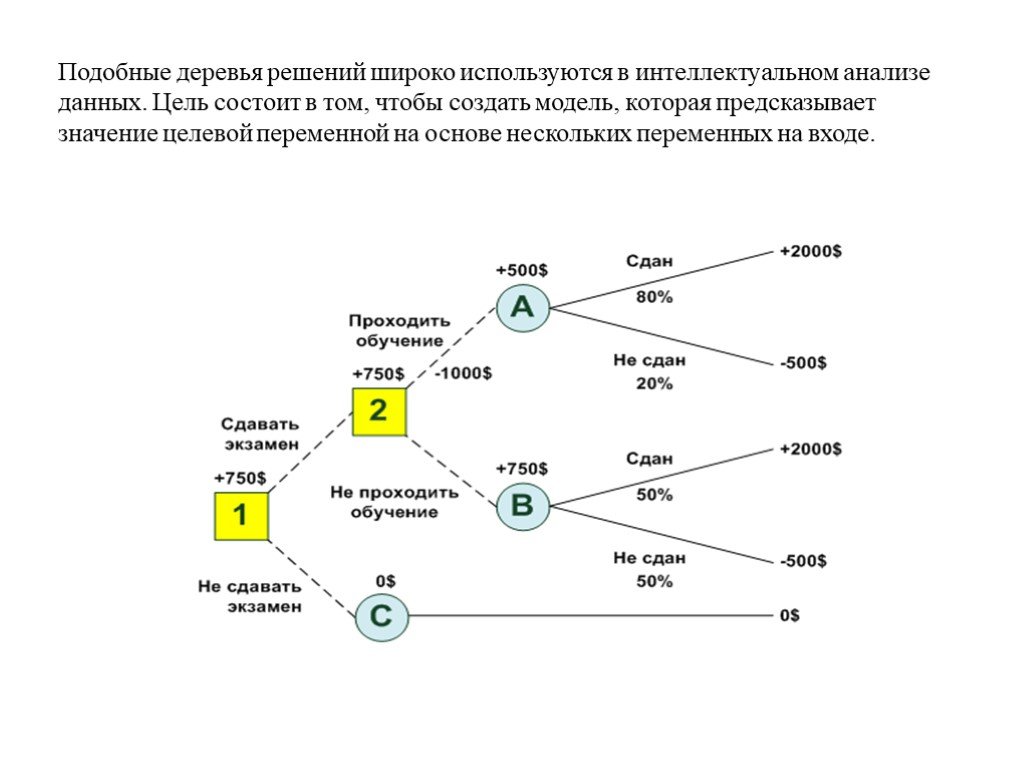
Деревья решений (DT) — это непараметрический контролируемый метод обучения, используемый для классификации и регрессии .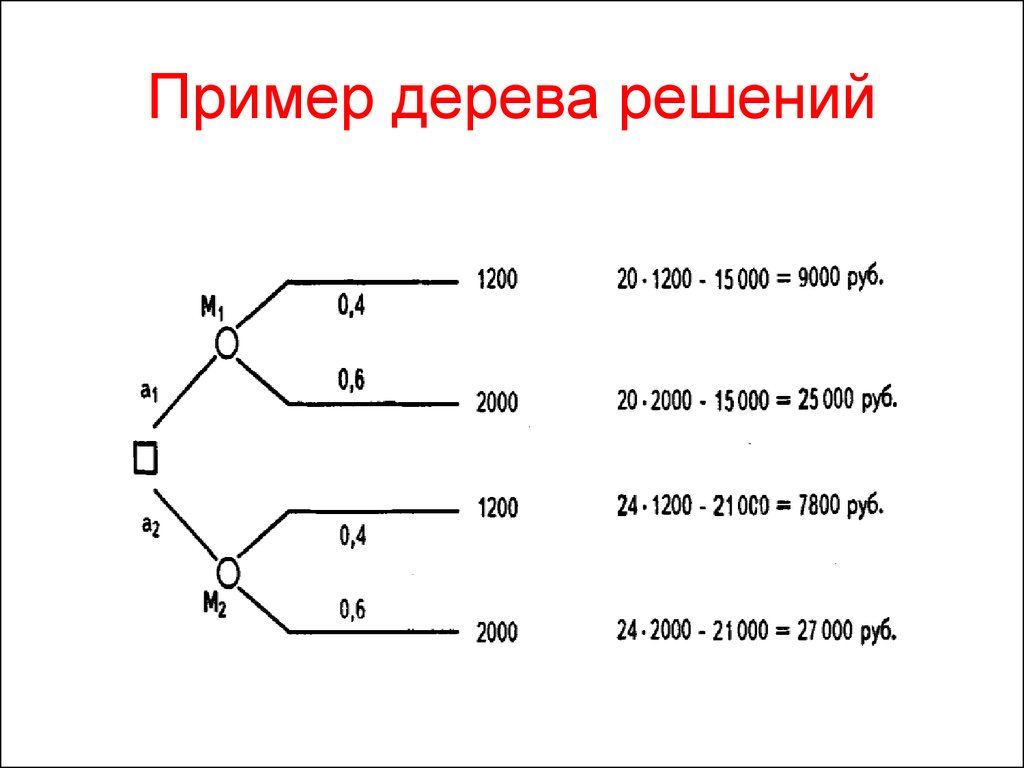 Цель состоит в том, чтобы создать модель, которая предсказывает значение целевой переменной, изучая простые правила принятия решений, выведенные из характеристик данных. Дерево можно рассматривать как кусочно-постоянное приближение.
Цель состоит в том, чтобы создать модель, которая предсказывает значение целевой переменной, изучая простые правила принятия решений, выведенные из характеристик данных. Дерево можно рассматривать как кусочно-постоянное приближение.
Например, в приведенном ниже примере деревья решений обучаются на основе данных, чтобы аппроксимировать синусоидальную кривую с набором правил принятия решений «если-то-еще». Чем глубже дерево, тем сложнее правила принятия решений и тем лучше модель.
Некоторые преимущества деревьев решений:
- Просто понять и интерпретировать. Деревья можно визуализировать.
- Требуется небольшая подготовка данных. Другие методы часто требуют нормализации данных, создания фиктивных переменных и удаления пустых значений. Однако обратите внимание, что этот модуль не поддерживает отсутствующие значения.
- Стоимость использования дерева (т. Е. Прогнозирования данных) является логарифмической по количеству точек данных, используемых для обучения дерева.

- Может обрабатывать как числовые, так и категориальные данные. Однако реализация scikit-learn пока не поддерживает категориальные переменные. Другие методы обычно специализируются на анализе наборов данных, содержащих только один тип переменных. См. Алгоритмы для получения дополнительной информации.
- Способен обрабатывать проблемы с несколькими выходами.
- Использует модель белого ящика. Если данная ситуация наблюдаема в модели, объяснение условия легко объяснить с помощью булевой логики. Напротив, в модели черного ящика (например, в искусственной нейронной сети) результаты могут быть труднее интерпретировать.
- Возможна проверка модели с помощью статистических тестов. Это позволяет учитывать надежность модели.
- Работает хорошо, даже если его предположения несколько нарушаются истинной моделью, на основе которой были сгенерированы данные.
К недостаткам деревьев решений можно отнести:
- Обучающиеся дереву решений могут создавать слишком сложные деревья, которые плохо обобщают данные.
 Это называется переобучением. Чтобы избежать этой проблемы, необходимы такие механизмы, как обрезка, установка минимального количества выборок, необходимых для конечного узла, или установка максимальной глубины дерева.
Это называется переобучением. Чтобы избежать этой проблемы, необходимы такие механизмы, как обрезка, установка минимального количества выборок, необходимых для конечного узла, или установка максимальной глубины дерева. - Деревья решений могут быть нестабильными, поскольку небольшие изменения в данных могут привести к созданию совершенно другого дерева. Эта проблема смягчается за счет использования деревьев решений в ансамбле.
- Как видно из рисунка выше, предсказания деревьев решений не являются ни гладкими, ни непрерывными, а являются кусочно-постоянными приближениями. Следовательно, они не годятся для экстраполяции.
- Известно, что проблема обучения оптимальному дереву решений является NP-полной с точки зрения нескольких аспектов оптимальности и даже для простых концепций. Следовательно, практические алгоритмы обучения дереву решений основаны на эвристических алгоритмах, таких как жадный алгоритм, в котором локально оптимальные решения принимаются в каждом узле. Такие алгоритмы не могут гарантировать возврат глобального оптимального дерева решений.
 Это можно смягчить путем обучения нескольких деревьев в учащемся ансамбля, где функции и образцы выбираются случайным образом с заменой.
Это можно смягчить путем обучения нескольких деревьев в учащемся ансамбля, где функции и образцы выбираются случайным образом с заменой. - Существуют концепции, которые трудно изучить, поскольку деревья решений не выражают их легко, например проблемы XOR, четности или мультиплексора.
- Ученики дерева решений создают предвзятые деревья, если некоторые классы доминируют. Поэтому рекомендуется сбалансировать набор данных перед подгонкой к дереву решений.
1.10.1. Классификация
DecisionTreeClassifier — это класс, способный выполнять мультиклассовую классификацию набора данных.
Как и в случае с другими классификаторами, DecisionTreeClassifier принимает в качестве входных данных два массива: массив X, разреженный или плотный, формы (n_samples, n_features), содержащий обучающие образцы, и массив Y целочисленных значений, формы (n_samples,), содержащий метки классов для обучающих образцов:
>>> from sklearn import tree >>> X = [[0, 0], [1, 1]] >>> Y = [0, 1] >>> clf = tree.DecisionTreeClassifier() >>> clf = clf.fit(X, Y)
После подбора модель можно использовать для прогнозирования класса образцов:
>>> clf.predict([[2., 2.]]) array([1])
В случае, если существует несколько классов с одинаковой и самой высокой вероятностью, классификатор предскажет класс с самым низким индексом среди этих классов.
В качестве альтернативы выводу определенного класса можно предсказать вероятность каждого класса, которая представляет собой долю обучающих выборок класса в листе:
>>> clf.predict_proba([[2., 2.]]) array([[0., 1.]])
DecisionTreeClassifier поддерживает как двоичную (где метки — [-1, 1]), так и мультиклассовую (где метки — [0,…, K-1]) классификацию.
Используя набор данных Iris, мы можем построить дерево следующим образом:
>>> from sklearn.datasets import load_iris >>> from sklearn import tree >>> iris = load_iris() >>> X, y = iris.data, iris.target >>> clf = tree.DecisionTreeClassifier() >>> clf = clf.fit(X, y)
После обучения вы можете построить дерево с помощью plot_tree функции:
>>> tree.plot_tree(clf)
Мы также можем экспортировать дерево в формат Graphviz с помощью export_graphviz экспортера. Если вы используете Conda менеджер пакетов, то Graphviz бинарные файлы и пакет питон может быть установлен conda install python-graphviz.
В качестве альтернативы двоичные файлы для graphviz можно загрузить с домашней страницы проекта graphviz, а оболочку Python установить из pypi с помощью pip install graphviz.
Ниже приведен пример экспорта graphviz вышеуказанного дерева, обученного на всем наборе данных радужной оболочки глаза; результаты сохраняются в выходном файле iris.pdf:
>>> import graphviz >>> dot_data = tree.export_graphviz(clf, out_file=None) >>> graph = graphviz.Source(dot_data) >>> graph.render("iris")
Экспортер export_graphviz также поддерживает множество эстетических вариантов, в том числе окраски узлов их класс (или значение регрессии) и используя явные имена переменных и классов , если это необходимо. Блокноты Jupyter также автоматически отображают эти графики встроенными:
>>> dot_data = tree.export_graphviz(clf, out_file=None, ... feature_names=iris.feature_names, ... class_names=iris.target_names, ... filled=True, rounded=True, ... special_characters=True) >>> graph = graphviz.Source(dot_data) >>> graph
В качестве альтернативы дерево можно также экспортировать в текстовый формат с помощью функции export_text. Этот метод не требует установки внешних библиотек и более компактен:
>>> from sklearn.datasets import load_iris >>> from sklearn.tree import DecisionTreeClassifier >>> from sklearn.tree import export_text >>> iris = load_iris() >>> decision_tree = DecisionTreeClassifier(random_state=0, max_depth=2) >>> decision_tree = decision_tree.fit(iris.data, iris.target) >>> r = export_text(decision_tree, feature_names=iris['feature_names']) >>> print(r) |--- petal width (cm) <= 0.80 | |--- class: 0 |--- petal width (cm) > 0.80 | |--- petal width (cm) <= 1.75 | | |--- class: 1 | |--- petal width (cm) > 1.75 | | |--- class: 2
Примеры
- Постройте поверхность принятия решений дерева решений на наборе данных радужной оболочки глаза
- Понимание структуры дерева решений
1.10.2. Регрессия
Деревья решений также могут применяться к задачам регрессии с помощью класса DecisionTreeRegressor .
Как и в настройке классификации, метод fit будет принимать в качестве аргументов массивы X и y, только в этом случае ожидается, что y будет иметь значения с плавающей запятой вместо целочисленных значений:
>>> from sklearn import tree >>> X = [[0, 0], [2, 2]] >>> y = [0.5, 2.5] >>> clf = tree.DecisionTreeRegressor() >>> clf = clf.fit(X, y) >>> clf.predict([[1, 1]]) array([0.5])
Пример:
- Регрессия дерева решений
1.10.3. Проблемы с несколькими выходами
Задача с несколькими выходами — это проблема контролируемого обучения с несколькими выходами для прогнозирования, то есть когда Y — это 2-й массив формы (n_samples, n_outputs).
Когда нет корреляции между выходами, очень простой способ решить эту проблему — построить n независимых моделей, то есть по одной для каждого выхода, а затем использовать эти модели для независимого прогнозирования каждого из n выходов. Однако, поскольку вполне вероятно, что выходные значения, относящиеся к одному и тому же входу, сами коррелированы, часто лучшим способом является построение единой модели, способной прогнозировать одновременно все n выходов. Во-первых, это требует меньшего времени на обучение, поскольку строится только один оценщик. Во-вторых, часто можно повысить точность обобщения итоговой оценки.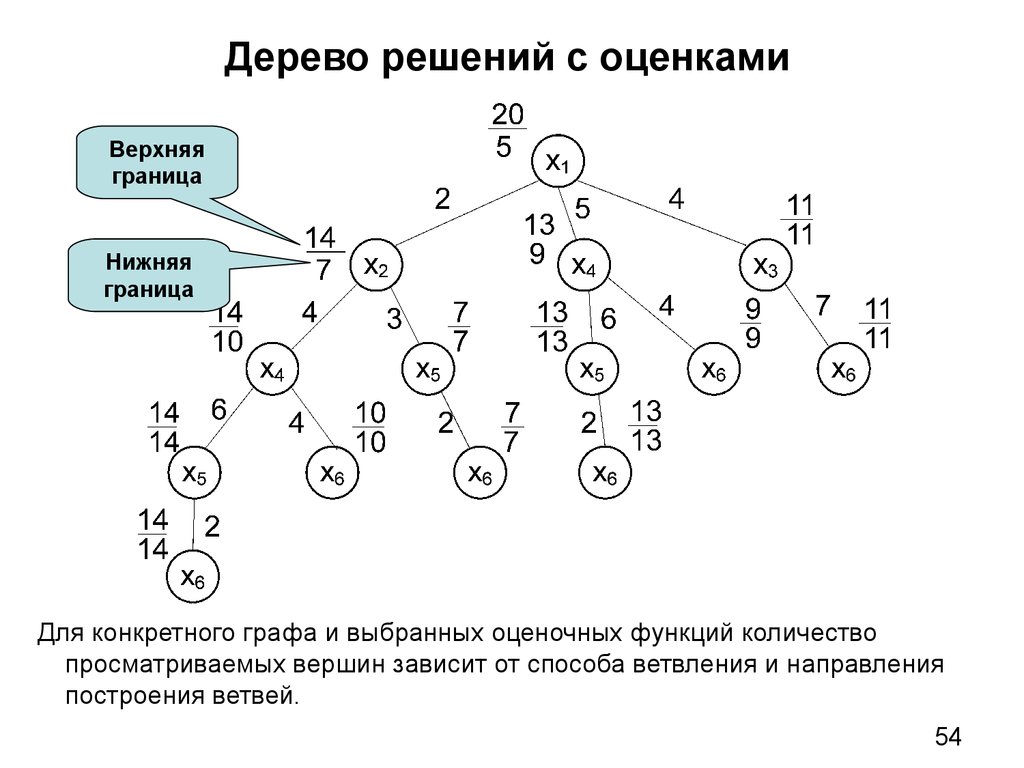
Что касается деревьев решений, эту стратегию можно легко использовать для поддержки задач с несколькими выходами. Для этого требуются следующие изменения:
- Сохранять n выходных значений в листьях вместо 1;
- Используйте критерии разделения, которые вычисляют среднее сокращение для всех n выходов.
Этот модуль предлагает поддержку для задач с несколькими выходами, реализуя эту стратегию как в, так DecisionTreeClassifier и в DecisionTreeRegressor. Если дерево решений соответствует выходному массиву Y формы (n_samples, n_outputs), то итоговая оценка будет:
- Вывести значения n_output при
predict; - Выведите список массивов n_output вероятностей классов на
predict_proba.
Использование деревьев с несколькими выходами для регрессии продемонстрировано в разделе «Регрессия дерева решений с несколькими выходами» . В этом примере вход X — это одно действительное значение, а выходы Y — синус и косинус X.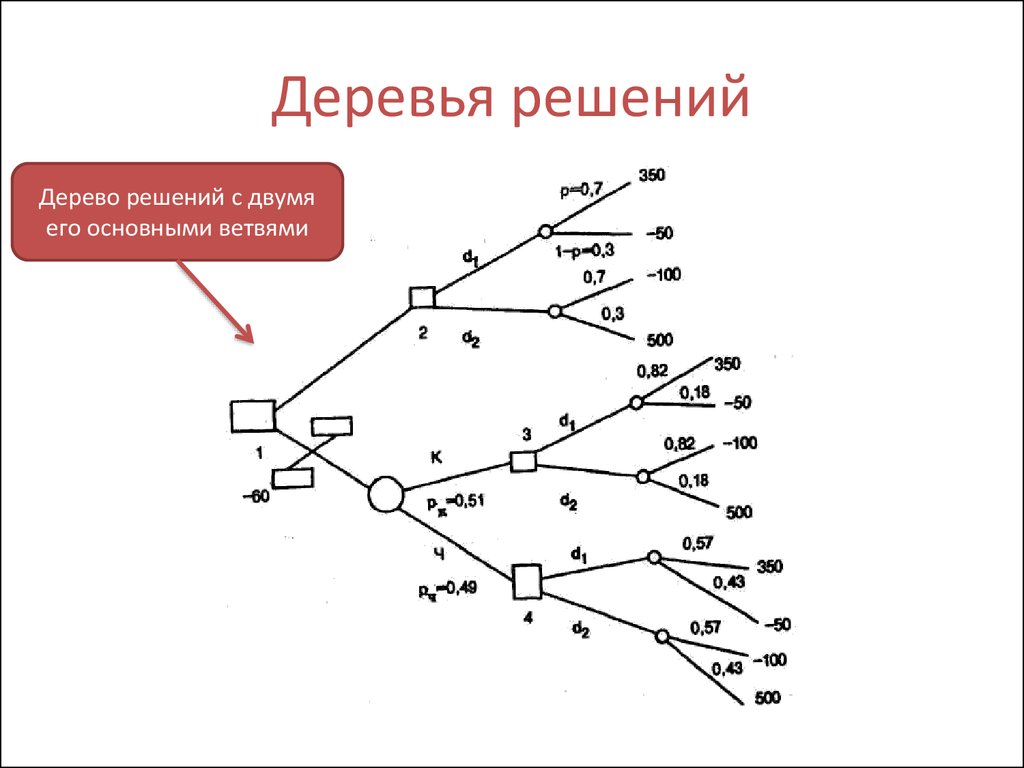
Использование деревьев с несколькими выходами для классификации демонстрируется в разделе «Завершение лица с оценками с несколькими выходами» . В этом примере входы X — это пиксели верхней половины граней, а выходы Y — пиксели нижней половины этих граней.
Примеры:
- Регрессия дерева решений с несколькими выходами
- Завершение лица с помощью многовыходных оценщиков
Рекомендации:
- М. Дюмон и др., Быстрая мультиклассовая аннотация изображений со случайными подокнами и множественными выходными рандомизированными деревьями , Международная конференция по теории и приложениям компьютерного зрения, 2009 г.
1.10.4. Сложность
В общем, время выполнения для построения сбалансированного двоичного дерева составляет $O(n_{samples}n_{features}\log(n_{samples}))$ и время запроса $O(\log(n_{samples}))$. Хотя алгоритм построения дерева пытается генерировать сбалансированные деревья, они не всегда будут сбалансированными. Предполагая, что поддеревья остаются примерно сбалансированными, стоимость на каждом узле состоит из перебора $O(n_{features})$ найти функцию, обеспечивающую наибольшее снижение энтропии.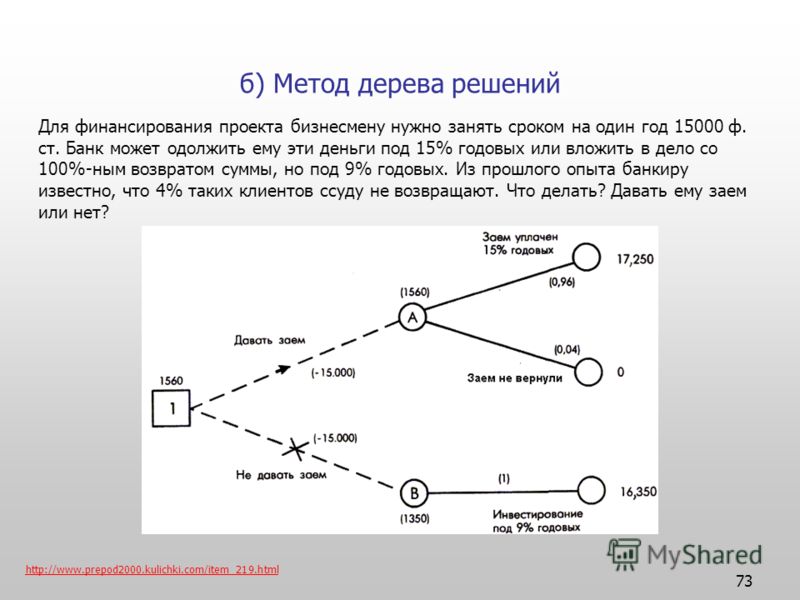 {2}\log(n_{samples}))$
{2}\log(n_{samples}))$
1.10.5. Советы по практическому использованию
- Деревья решений имеют тенденцию чрезмерно соответствовать данным с большим количеством функций. Получение правильного соотношения образцов к количеству функций важно, поскольку дерево с небольшим количеством образцов в многомерном пространстве, скорее всего, переоборудуется.
- Предварительно рассмотрите возможность уменьшения размерности (PCA, ICA, или Feature selection), чтобы дать вашему дереву больше шансов найти отличительные признаки.
- Понимание структуры дерева решений поможет лучше понять, как дерево решений делает прогнозы, что важно для понимания важных функций данных.
- Визуализируйте свое дерево во время тренировки с помощью
exportфункции. Используйтеmax_depth=3в качестве начальной глубины дерева, чтобы понять, насколько дерево соответствует вашим данным, а затем увеличьте глубину. - Помните, что количество образцов, необходимых для заполнения дерева, удваивается для каждого дополнительного уровня, до которого дерево растет.
 Используйте
Используйте max_depthдля управления размером дерева во избежание переобучения. - Используйте
min_samples_splitили,min_samples_leafчтобы гарантировать, что несколько выборок информируют каждое решение в дереве, контролируя, какие разделения будут учитываться. Очень маленькое число обычно означает, что дерево переоборудуется, тогда как большое число не позволяет дереву изучать данные. Попробуйтеmin_samples_leaf=5в качестве начального значения. Если размер выборки сильно различается, в этих двух параметрах можно использовать число с плавающей запятой в процентах. В то время какmin_samples_splitможет создавать произвольно маленькие листья,min_samples_leafгарантирует, что каждый лист имеет минимальный размер, избегая малодисперсных, чрезмерно подходящих листовых узлов в задачах регрессии. Для классификации с несколькими классамиmin_samples_leaf=1это часто лучший выбор.Обратите внимание, что
min_samples_splitвыборки рассматриваются напрямую и независимо от нихsample_weight, если они предусмотрены (например, узел с m взвешенными выборками по-прежнему обрабатывается как имеющий ровно m выборок). Рассмотрим
Рассмотрим min_weight_fraction_leafилиmin_impurity_decreaseесли учет образцов весов требуются при расколах. - Перед обучением сбалансируйте набор данных, чтобы дерево не смещалось в сторону доминирующих классов. Балансировка классов может быть выполнена путем выборки равного количества выборок из каждого класса или, предпочтительно, путем нормализации суммы весов выборок (
sample_weight) для каждого класса к одному и тому же значению. Также обратите внимание, что критерии предварительного отсечения на основе веса, такие какmin_weight_fraction_leaf, будут менее смещены в сторону доминирующих классов, чем критерии, которые не знают весов выборки, напримерmin_samples_leaf. - Если выборки взвешены, будет проще оптимизировать древовидную структуру, используя основанный на весе критерий предварительной отсечения, например
min_weight_fraction_leaf, который гарантирует, что конечные узлы содержат по крайней мере часть общей суммы весов выборки.
- Все деревья решений
np.float32внутренне используют массивы. Если данные обучения не в этом формате, будет сделана копия набора данных. - Если входная матрица X очень разреженная, рекомендуется преобразовать ее в разреженную
csc_matrixперед вызовом соответствия и разреженнуюcsr_matrixперед вызовом предсказания. Время обучения может быть на порядки меньше для входной разреженной матрицы по сравнению с плотной матрицей, когда функции имеют нулевые значения в большинстве выборок.
1.10.6. Алгоритмы дерева: ID3, C4.5, C5.0 и CART
Что представляют собой различные алгоритмы дерева решений и чем они отличаются друг от друга? Какой из них реализован в scikit-learn?
ID3 (Iterative Dichotomiser 3) был разработан Россом Куинланом в 1986 году. Алгоритм создает многостороннее дерево, находя для каждого узла (т. Е. Жадным образом) категориальный признак, который даст наибольший информационный выигрыш для категориальных целей. Деревья вырастают до максимального размера, а затем обычно применяется этап обрезки, чтобы улучшить способность дерева обобщать невидимые данные.
Деревья вырастают до максимального размера, а затем обычно применяется этап обрезки, чтобы улучшить способность дерева обобщать невидимые данные.
C4.5 является преемником ID3 и снял ограничение, что функции должны быть категориальными, путем динамического определения дискретного атрибута (на основе числовых переменных), который разбивает непрерывное значение атрибута на дискретный набор интервалов. C4.5 преобразует обученные деревья (т. Е. Результат алгоритма ID3) в наборы правил «если-то». Затем оценивается точность каждого правила, чтобы определить порядок, в котором они должны применяться. Удаление выполняется путем удаления предусловия правила, если без него точность правила улучшается.
C5.0 — это последняя версия Quinlan под частной лицензией. Он использует меньше памяти и создает меньшие наборы правил, чем C4.5, но при этом является более точным.
CART (Classification and Regression Trees — деревья классификации и регрессии) очень похож на C4.5, но отличается тем, что поддерживает числовые целевые переменные (регрессию) и не вычисляет наборы правил.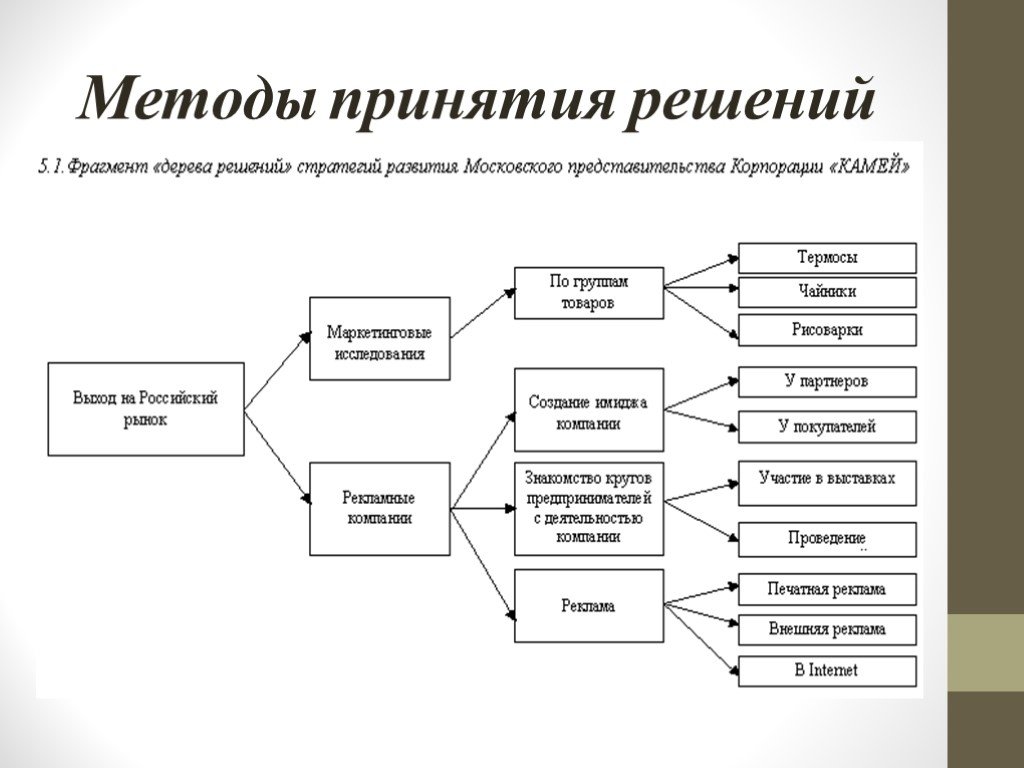 *)$ пока не будет достигнута максимально допустимая глубина, $N_m < \min_{samples}$ или же $N_m = 1$.
*)$ пока не будет достигнута максимально допустимая глубина, $N_m < \min_{samples}$ или же $N_m = 1$.
1.10.7.1. Критерии классификации
Если целью является результат классификации, принимающий значения 0,1,…, K-1, для узла m, позволять
$$p_{mk} = 1/ N_m \sum_{y \in Q_m} I(y = k)$$
быть пропорцией наблюдений класса k в узле m. Еслиmявляется конечным узлом, predict_proba для этого региона установлено значение $p_{mk}$. Общие меры примеси следующие.
Джини:
$$H(Q_m) = \sum_k p_{mk} (1 — p_{mk})$$
Энтропия:
$$H(Q_m) = — \sum_k p_{mk} \log(p_{mk})$$
Неверная классификация:
$$H(Q_m) = 1 — \max(p_{mk})$$
1.10.7.2. Критерии регрессии
Если целью является непрерывное значение, то для узла m, общими критериями, которые необходимо минимизировать для определения местоположений будущих разделений, являются среднеквадратичная ошибка (ошибка MSE или L2), отклонение Пуассона, а также средняя абсолютная ошибка (ошибка MAE или L1). 2$$
2$$
Половинное отклонение Пуассона:
$$H(Q_m) = \frac{1}{N_m} \sum_{y \in Q_m} (y \log\frac{y}{\bar{y}_m} — y + \bar{y}_m)$$
Настройка criterion="poisson" может быть хорошим выбором, если ваша цель — счетчик или частота (количество на какую-то единицу). В любом случае, y>=0 является необходимым условием для использования этого критерия. Обратите внимание, что он подходит намного медленнее, чем критерий MSE.
Средняя абсолютная ошибка:
$$median(y)m = \underset{y \in Q_m}{\mathrm{median}}(y)$$
$$H(Q_m) = \frac{1}{N_m} \sum{y \in Q_m} |y — median(y)_m|$$
Обратите внимание, что он подходит намного медленнее, чем критерий MSE.
1.10.8. Обрезка с минимальными затратами и сложностью
Сокращение с минимальными затратами и сложностью — это алгоритм, используемый для сокращения дерева во избежание чрезмерной подгонки, описанный в главе 3 [BRE] . Этот алгоритм параметризован $\alpha\ge0$ известный как параметр сложности. Параметр сложности используется для определения меры затрат и сложности, $R_\alpha(T)$ данного дерева $T$:
$$R_\alpha(T) = R(T) + \alpha|\widetilde{T}|$$
где $|\widetilde{T}|$ количество конечных узлов в $T$ а также $R(T)$ традиционно определяется как общий коэффициент ошибочной классификации конечных узлов.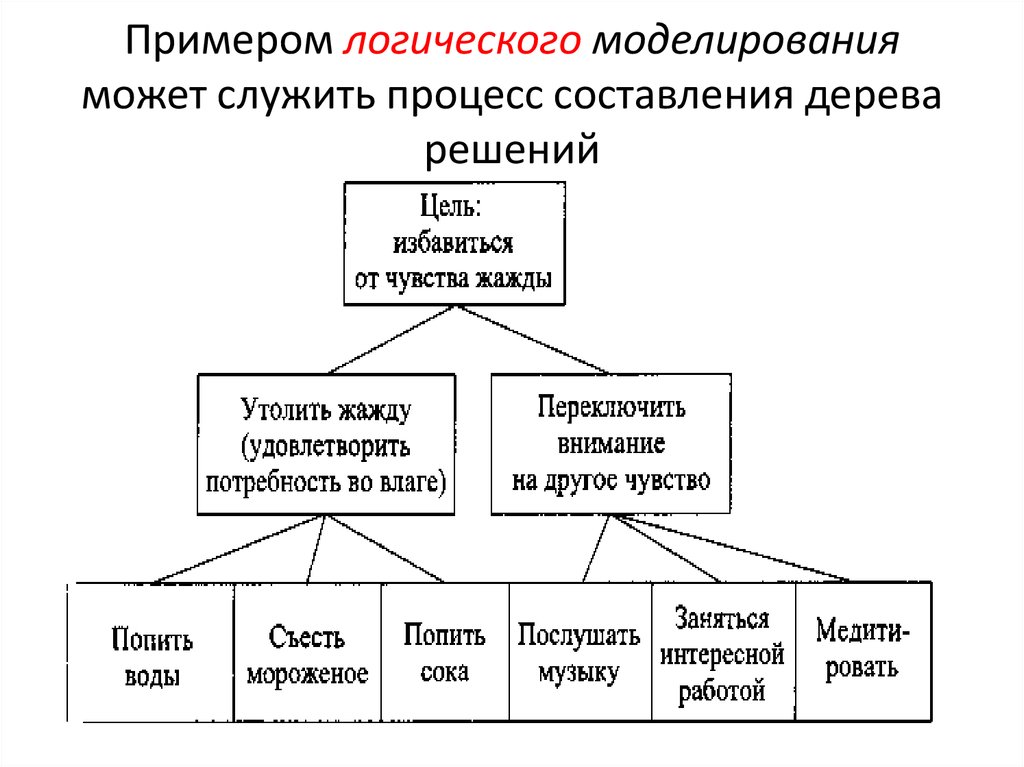 В качестве альтернативы scikit-learn использует взвешенную общую примесь конечных узлов для $R(T)$. Как показано выше, примесь узла зависит от критерия. Обрезка с минимальными затратами и сложностью находит поддеревоT что сводит к минимуму $R_\alpha(T)$.
В качестве альтернативы scikit-learn использует взвешенную общую примесь конечных узлов для $R(T)$. Как показано выше, примесь узла зависит от критерия. Обрезка с минимальными затратами и сложностью находит поддеревоT что сводит к минимуму $R_\alpha(T)$.
Оценка сложности стоимости одного узла составляет $R_\alpha(t)=R(t)+\alpha$. Ответвление $T_t$, определяется как дерево, в котором узел $t$ это его корень. В общем, примесь узла больше, чем сумма примесей его конечных узлов, $R(T_t)<R(t)$. Однако мера стоимости и сложности узла, $t$, и его ветвь, $T_t$, может быть равным в зависимости от $\alpha$. Определяем эффективныйα узла быть значением, где они равны, $R_\alpha(T_t)=R_\alpha(t)$ или же $\alpha_{eff}(t)=\frac{R(t)-R(T_t)}{|T|-1}$. Нетерминальный узел с наименьшим значением $\alpha_{eff}$ является самым слабым звеном и будет удалено. Этот процесс останавливается, когда обрезанное дерево минимально $\alpha_{eff}$ больше ccp_alpha параметра.
Примеры:
- Публикация деревьев решений об обрезке с сокращением сложности затрат
Рекомендации:
- BRE Л.
 Брейман, Дж. Фридман, Р. Олшен и К. Стоун. Деревья классификации и регрессии. Уодсворт, Белмонт, Калифорния, 1984.
Брейман, Дж. Фридман, Р. Олшен и К. Стоун. Деревья классификации и регрессии. Уодсворт, Белмонт, Калифорния, 1984. - https://en.wikipedia.org/wiki/Decision_tree_learning
- https://en.wikipedia.org/wiki/Predictive_analytics
- JR Quinlan. C4. 5: программы для машинного обучения. Морган Кауфманн, 1993.
- Т. Хасти, Р. Тибширани и Дж. Фридман. Элементы статистического обучения, Springer, 2009.
Что такое дерево решений
Деревья решений
Дерево решений — это непараметрический контролируемый алгоритм обучения, который используется как для задач классификации, так и для задач регрессии. Он имеет иерархическую древовидную структуру, которая состоит из корневого узла, ветвей, внутренних узлов и конечных узлов.
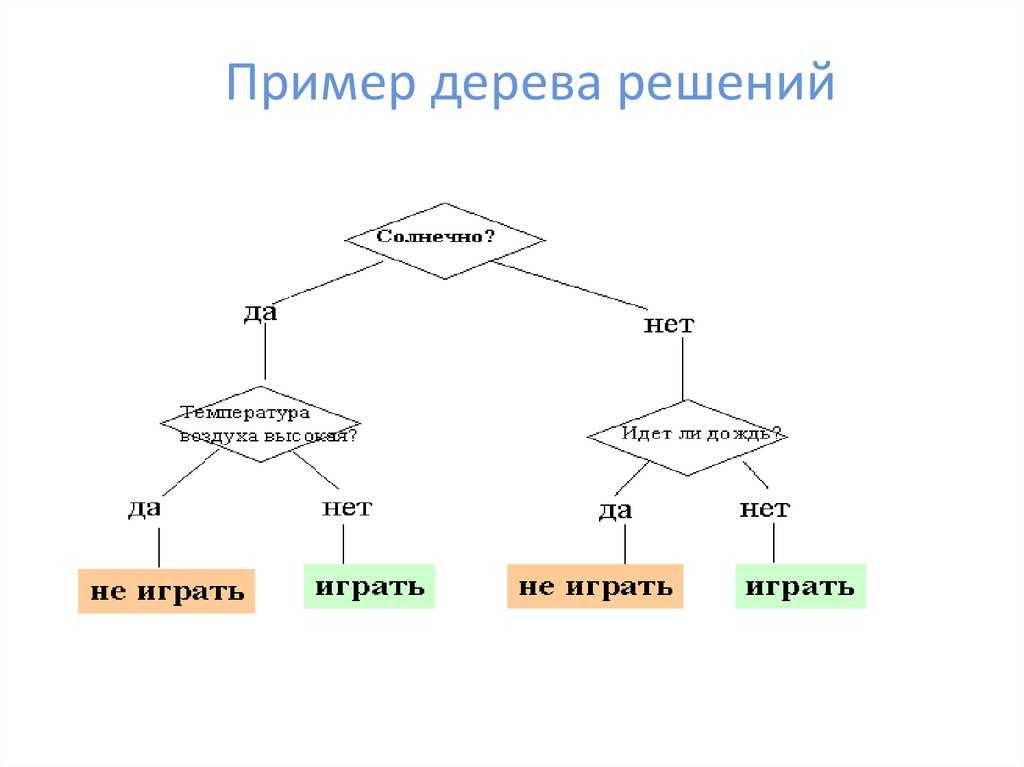
Как видно из диаграммы выше, дерево решений начинается с корневого узла, который не имеет входящих ветвей. Исходящие ветви от корневого узла затем направляются во внутренние узлы, также известные как узлы принятия решений.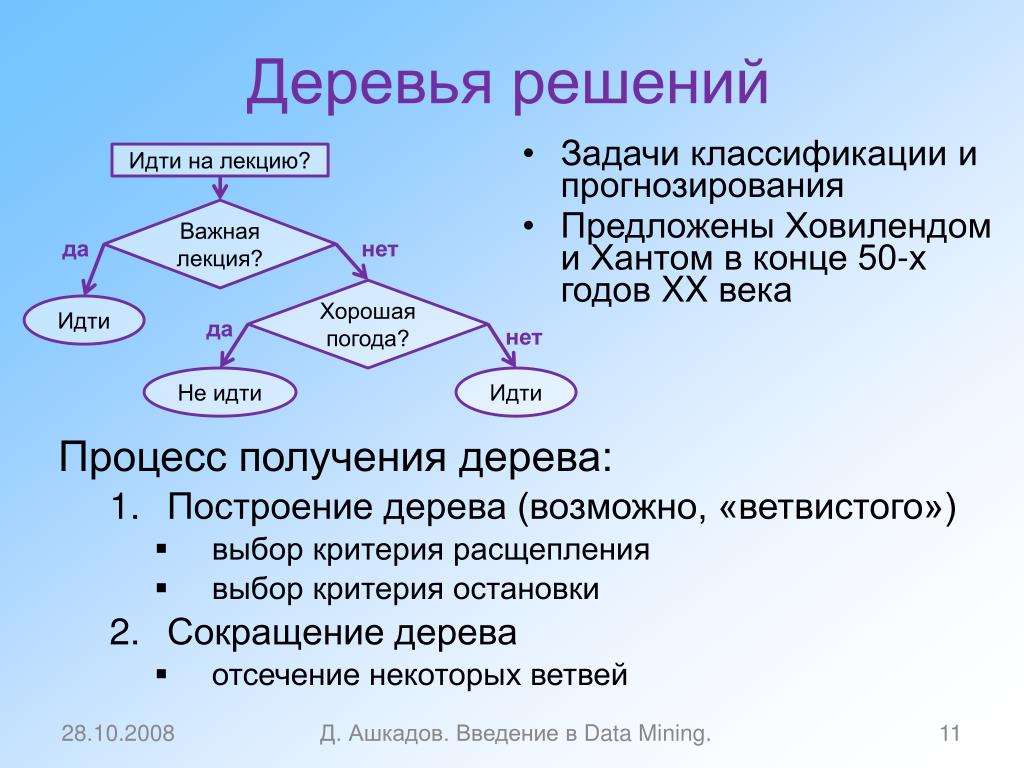 На основе доступных функций оба типа узлов выполняют оценку для формирования однородных подмножеств, которые обозначаются конечными узлами или конечными узлами. Листовые узлы представляют все возможные результаты в наборе данных. В качестве примера, давайте представим, что вы пытаетесь оценить, стоит ли вам заниматься серфингом, вы можете использовать следующие правила принятия решений, чтобы сделать выбор:
На основе доступных функций оба типа узлов выполняют оценку для формирования однородных подмножеств, которые обозначаются конечными узлами или конечными узлами. Листовые узлы представляют все возможные результаты в наборе данных. В качестве примера, давайте представим, что вы пытаетесь оценить, стоит ли вам заниматься серфингом, вы можете использовать следующие правила принятия решений, чтобы сделать выбор:
Этот тип структуры блок-схемы также создает легкое для восприятия представление о принятии решений, позволяя различным группам в организации лучше понять, почему было принято решение.
Изучение дерева решений использует стратегию «разделяй и властвуй» путем проведения жадного поиска для определения оптимальных точек разделения в дереве. Затем этот процесс разделения повторяется рекурсивно сверху вниз до тех пор, пока все или большинство записей не будут отнесены к определенным меткам классов. Классифицируются ли все точки данных как однородные наборы, во многом зависит от сложности дерева решений. Меньшие деревья легче могут получить чистые листовые узлы, т.е. точки данных в одном классе. Однако по мере роста дерева становится все труднее поддерживать эту чистоту, и это обычно приводит к тому, что в данное поддерево попадает слишком мало данных. Когда это происходит, это называется фрагментацией данных и часто может привести к переоснащению. В результате деревья решений отдают предпочтение маленьким деревьям, что согласуется с принципом экономии в бритве Оккама; то есть «сущности не должны умножаться сверх необходимости». Иными словами, деревья решений должны усложнять только в случае необходимости, поскольку самое простое объяснение часто является лучшим. Чтобы уменьшить сложность и предотвратить переоснащение, обычно используется обрезка; это процесс, который удаляет ветви, разделяющиеся на объекты с низкой важностью. Затем соответствие модели можно оценить в процессе перекрестной проверки. Другой способ, которым деревья решений могут поддерживать свою точность, — это формирование ансамбля с помощью алгоритма случайного леса; этот классификатор предсказывает более точные результаты, особенно когда отдельные деревья не коррелируют друг с другом.
Меньшие деревья легче могут получить чистые листовые узлы, т.е. точки данных в одном классе. Однако по мере роста дерева становится все труднее поддерживать эту чистоту, и это обычно приводит к тому, что в данное поддерево попадает слишком мало данных. Когда это происходит, это называется фрагментацией данных и часто может привести к переоснащению. В результате деревья решений отдают предпочтение маленьким деревьям, что согласуется с принципом экономии в бритве Оккама; то есть «сущности не должны умножаться сверх необходимости». Иными словами, деревья решений должны усложнять только в случае необходимости, поскольку самое простое объяснение часто является лучшим. Чтобы уменьшить сложность и предотвратить переоснащение, обычно используется обрезка; это процесс, который удаляет ветви, разделяющиеся на объекты с низкой важностью. Затем соответствие модели можно оценить в процессе перекрестной проверки. Другой способ, которым деревья решений могут поддерживать свою точность, — это формирование ансамбля с помощью алгоритма случайного леса; этот классификатор предсказывает более точные результаты, особенно когда отдельные деревья не коррелируют друг с другом.
Типы деревьев решений
Алгоритм Ханта, разработанный в 1960-х годах для моделирования человеческого обучения в психологии, формирует основу многих популярных алгоритмов дерева решений, таких как: является сокращением от «Итеративный дихотомайзер 3». Этот алгоритм использует энтропию и прирост информации в качестве метрик для оценки расщеплений-кандидатов. Некоторые из исследований Куинлана по этому алгоритму от 1986 можно найти здесь (PDF, 1,4 МБ) (ссылка находится за пределами ibm.com).
— C4.5: Этот алгоритм считается более поздней итерацией ID3, который также был разработан Куинланом. Он может использовать прирост информации или коэффициент усиления для оценки точек разделения в деревьях решений.
— CART: Термин CART является аббревиатурой для «деревьев классификации и регрессии» и был введен Лео Брейманом. Этот алгоритм обычно использует примесь Джини для определения идеального атрибута для разделения. Примесь Джини измеряет, как часто случайно выбранный атрибут неправильно классифицируется. При оценке с использованием примеси Джини более низкое значение является более идеальным.
Примесь Джини измеряет, как часто случайно выбранный атрибут неправильно классифицируется. При оценке с использованием примеси Джини более низкое значение является более идеальным.
Как выбрать лучший атрибут в каждом узле
Хотя существует несколько способов выбора наилучшего атрибута в каждом узле, два метода, прирост информации и примесь Джини, действуют как популярные критерии разделения для моделей дерева решений. Они помогают оценить качество каждого условия тестирования и то, насколько хорошо оно сможет классифицировать образцы по классам.
Энтропия и прирост информации
Трудно объяснить получение информации без обсуждения энтропии. Энтропия — это концепция, вытекающая из теории информации, которая измеряет нечистоту выборочных значений. Он определяется по следующей формуле, где:
- S представляет набор данных, для которого рассчитывается энтропия
- c представляет классы в наборе, S
- p(c) представляет долю точек данных, принадлежащих классу c, к общему количеству точек данных в наборе, S
Значения энтропии могут находиться в диапазоне от 0 до 1. Если все выборки в наборе данных S принадлежат одному классу, то энтропия будет равна нулю. Если половина выборок относится к одному классу, а другая половина — к другому классу, энтропия будет максимальной, равной 1. Чтобы выбрать лучший признак для разделения и найти оптимальное дерево решений, атрибут с наименьшим следует использовать количество энтропии. Прирост информации представляет собой разницу в энтропии до и после разделения по данному атрибуту. Атрибут с наибольшим приростом информации даст наилучшее разделение, поскольку он лучше всего справляется с классификацией обучающих данных в соответствии с его целевой классификацией. Прирост информации обычно представляется следующей формулой, где:
Если все выборки в наборе данных S принадлежат одному классу, то энтропия будет равна нулю. Если половина выборок относится к одному классу, а другая половина — к другому классу, энтропия будет максимальной, равной 1. Чтобы выбрать лучший признак для разделения и найти оптимальное дерево решений, атрибут с наименьшим следует использовать количество энтропии. Прирост информации представляет собой разницу в энтропии до и после разделения по данному атрибуту. Атрибут с наибольшим приростом информации даст наилучшее разделение, поскольку он лучше всего справляется с классификацией обучающих данных в соответствии с его целевой классификацией. Прирост информации обычно представляется следующей формулой, где:
- a представляет определенный атрибут или метку класса
- Entropy(S) — энтропия набора данных, S
- |Зв|/ |С| представляет пропорцию значений в S и к количеству значений в наборе данных, S
- Энтропия (S v ) — энтропия набора данных, S v
Давайте рассмотрим пример, чтобы закрепить эти понятия.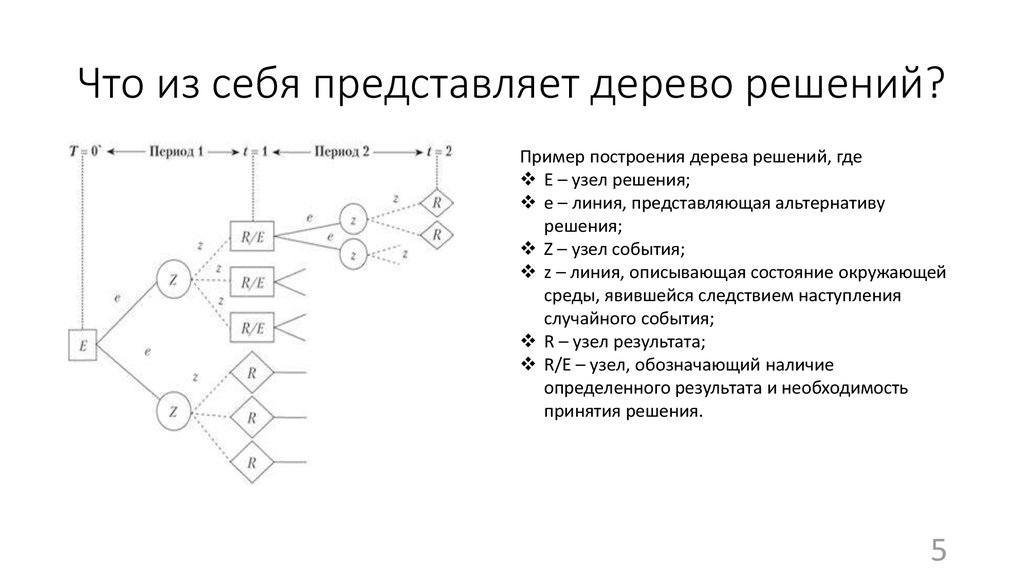 Представьте, что у нас есть следующий произвольный набор данных:
Представьте, что у нас есть следующий произвольный набор данных:
Для этого набора данных энтропия равна 0,94. Это можно рассчитать, найдя долю дней, когда «Играть в теннис» — «Да», что составляет 9/14, и долю дней, когда «Играть в теннис» — «Нет», что составляет 5/14. Затем эти значения можно подставить в приведенную выше формулу энтропии.
Энтропия (теннис) = -(9/14) log2(9/14) – (5/14) log2 (5/14) = 0,94
Затем мы можем вычислить прирост информации для каждого из атрибутов в отдельности. Например, прирост информации для атрибута «Влажность» будет следующим:
Коэффициент усиления (теннис, влажность) = (0,94)-(7/14)*(0,985) – (7/14)*(0,592) = 0,151 доля значений, где влажность равна «высокой», к общему количеству значений влажности. В этом случае количество значений, в которых влажность равна «высокой», равно количеству значений, в которых влажность равна «нормальной».
— 0,985 — энтропия при влажности = «высокая»
— 0,59 — энтропия при влажности = «нормальная»
Затем повторите расчет прироста информации для каждого атрибута в приведенной выше таблице и выберите атрибут с наибольшим приростом информации в качестве первой точки разделения в дереве решений. В этом случае Outlook дает наибольший прирост информации. Оттуда процесс повторяется для каждого поддерева.
В этом случае Outlook дает наибольший прирост информации. Оттуда процесс повторяется для каждого поддерева.
Примесь Джини
Примесь Джини — это вероятность неправильной классификации случайных точек данных в наборе данных, если они были помечены на основе распределения классов набора данных. Подобно энтропии, если набор S является чистым, т.е. принадлежащий одному классу), то его примесь равна нулю. Это обозначается следующей формулой:
Преимущества и недостатки деревьев решений
Хотя деревья решений можно использовать в различных случаях, другие алгоритмы обычно превосходят алгоритмы деревьев решений. Тем не менее, деревья решений особенно полезны для задач интеллектуального анализа данных и поиска знаний. Давайте рассмотрим основные преимущества и проблемы использования деревьев решений ниже:
Преимущества — Простота интерпретации: Булева логика и визуальное представление деревьев решений упрощают их понимание и использование.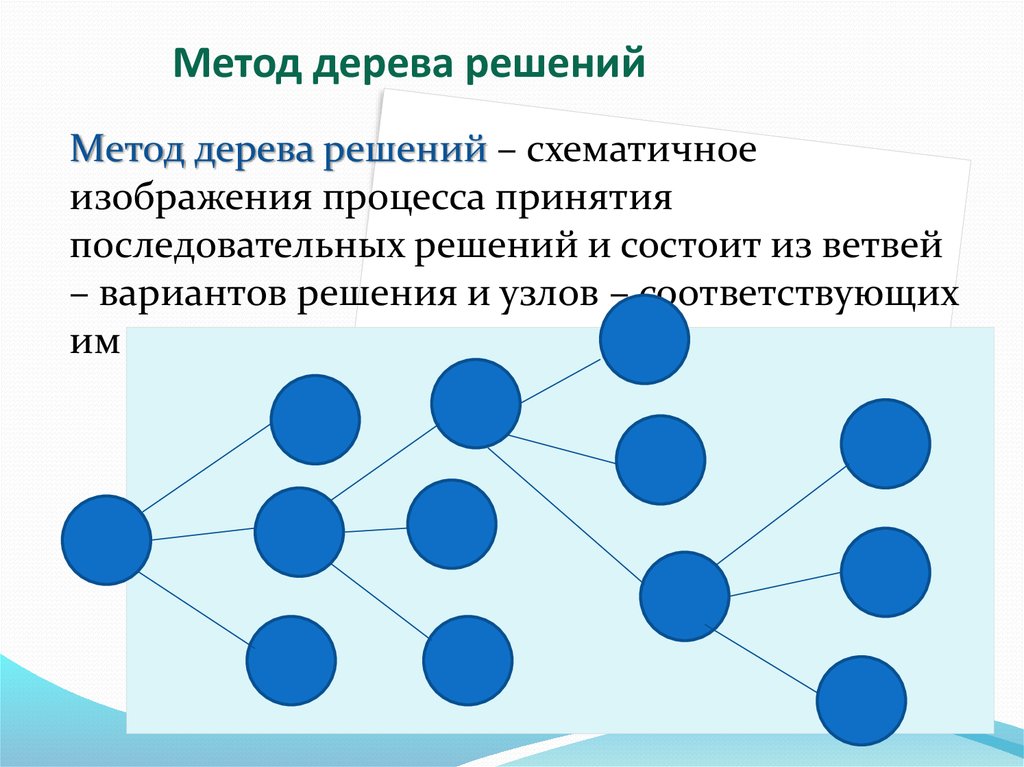 Иерархическая природа дерева решений также позволяет легко увидеть, какие атрибуты являются наиболее важными, что не всегда понятно с другими алгоритмами, такими как нейронные сети.
Иерархическая природа дерева решений также позволяет легко увидеть, какие атрибуты являются наиболее важными, что не всегда понятно с другими алгоритмами, такими как нейронные сети.
— Подготовка данных практически не требуется: Деревья решений обладают рядом характеристик, которые делают его более гибким, чем другие классификаторы. Он может обрабатывать различные типы данных, т.е. дискретные или непрерывные значения, а непрерывные значения могут быть преобразованы в категориальные значения с помощью порогов. Кроме того, он также может обрабатывать значения с отсутствующими значениями, что может быть проблематичным для других классификаторов, таких как наивный байесовский метод.
— Более гибкий: Деревья решений можно использовать как для задач классификации, так и для задач регрессии, что делает его более гибким, чем некоторые другие алгоритмы. Он также нечувствителен к лежащим в основе отношениям между атрибутами; это означает, что если две переменные сильно коррелированы, алгоритм выберет только одну из функций для разделения.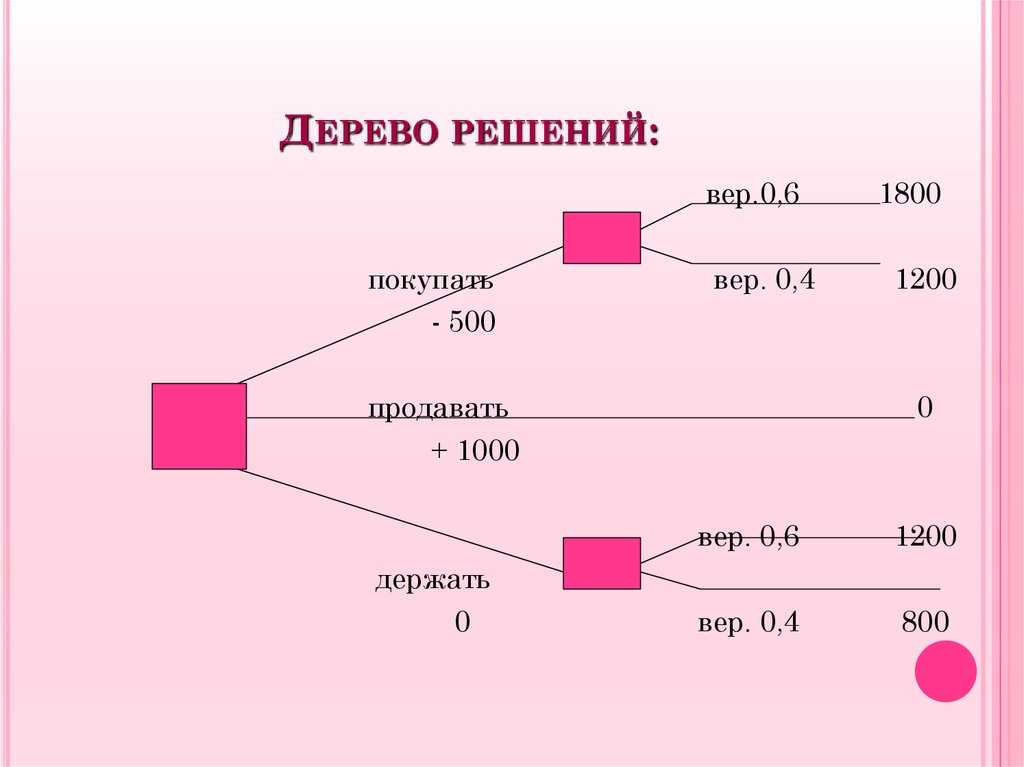
— Склонность к переоснащению: Сложные деревья решений склонны к переоснащению и плохо обобщают новые данные. Этого сценария можно избежать с помощью процессов предварительной обрезки или последующей обрезки. Предварительная обрезка останавливает рост дерева при недостатке данных, а постобрезка удаляет поддеревья с неадекватными данными после построения дерева.
— Оценщики с высокой дисперсией: Небольшие вариации в данных могут привести к совершенно другому дереву решений. Бэггинг или усреднение оценок может быть методом уменьшения дисперсии деревьев решений. Однако этот подход ограничен, поскольку он может привести к сильно коррелированным предикторам.
— Дороже: Учитывая, что деревья решений используют жадный поиск во время построения, их обучение может быть более дорогим по сравнению с другими алгоритмами.
— Не полностью поддерживается в scikit-learn: Scikit-learn — это популярная библиотека машинного обучения на основе Python.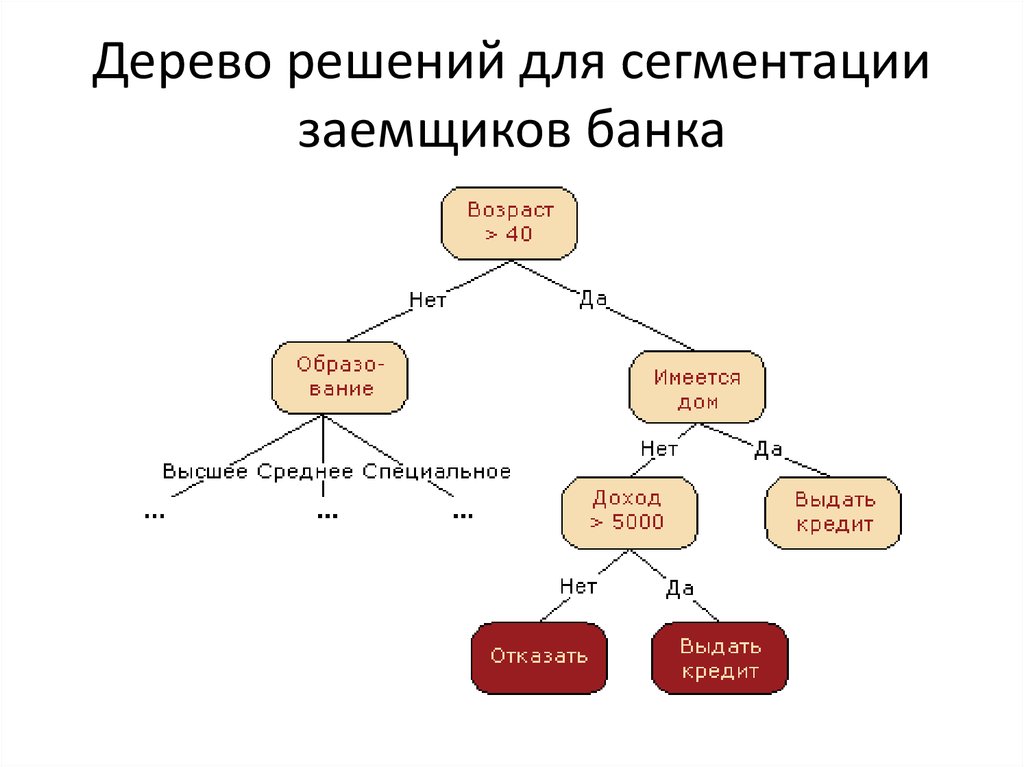 Хотя в этой библиотеке есть модуль дерева решений (DecisionTreeClassifier, ссылка находится за пределами ibm.com), текущая реализация не поддерживает категориальные переменные.
Хотя в этой библиотеке есть модуль дерева решений (DecisionTreeClassifier, ссылка находится за пределами ibm.com), текущая реализация не поддерживает категориальные переменные.
Деревья решений и IBM
IBM SPSS Modeler — это инструмент интеллектуального анализа данных, который позволяет разрабатывать прогностические модели для развертывания их в бизнес-операциях. Разработанный на основе модели CRISP-DM, являющейся отраслевым стандартом, IBM SPSS Modeler поддерживает весь процесс интеллектуального анализа данных, от обработки данных до улучшения бизнес-результатов.
Деревья решений IBM SPSS содержат визуальную классификацию и деревья решений, которые помогают вам представлять результаты по категориям и более четко объяснять анализ нетехнической аудитории. Создавайте модели классификации для сегментации, стратификации, прогнозирования, сокращения данных и скрининга переменных.
Чтобы получить дополнительную информацию об инструментах и решениях IBM для интеллектуального анализа данных, подпишитесь на IBMid и создайте учетную запись IBM Cloud сегодня.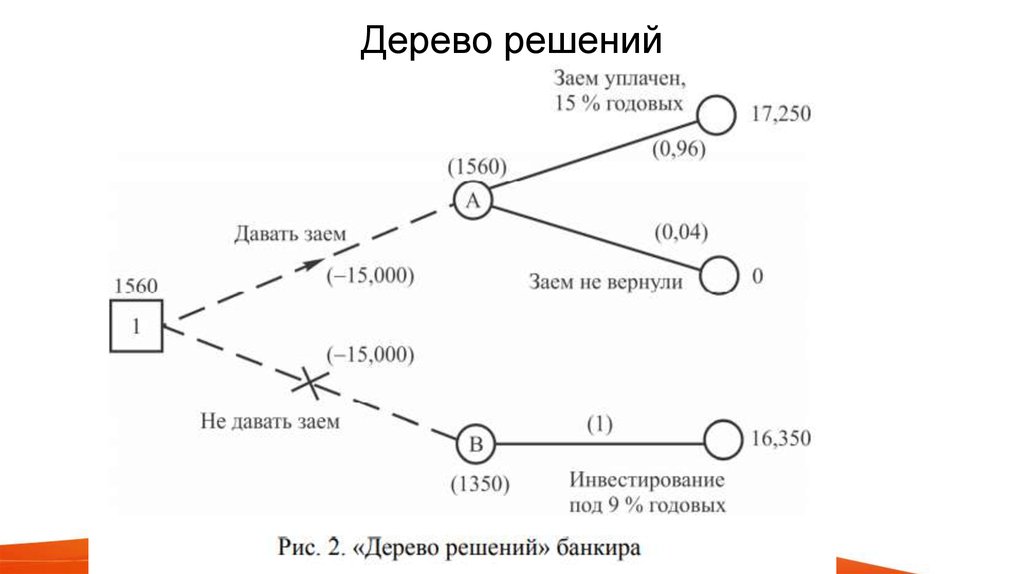
IBM SPSS Modeler — это инструмент интеллектуального анализа данных, который позволяет разрабатывать прогностические модели для развертывания их в бизнес-операциях. Разработанный на основе модели CRISP-DM, являющейся отраслевым стандартом, IBM SPSS Modeler поддерживает весь процесс интеллектуального анализа данных, от обработки данных до улучшения бизнес-результатов.
Деревья решений IBM SPSSДеревья решений IBM SPSS содержат визуальную классификацию и деревья решений, которые помогают вам представлять результаты по категориям и более четко объяснять анализ нетехнической аудитории. Создавайте модели классификации для сегментации, стратификации, прогнозирования, сокращения данных и скрининга переменных.
Узнайте больше о решениях IBM для интеллектуального анализа данных
Чтобы получить дополнительную информацию об инструментах и решениях IBM для интеллектуального анализа данных, подпишитесь на IBMid и создайте учетную запись IBM Cloud уже сегодня.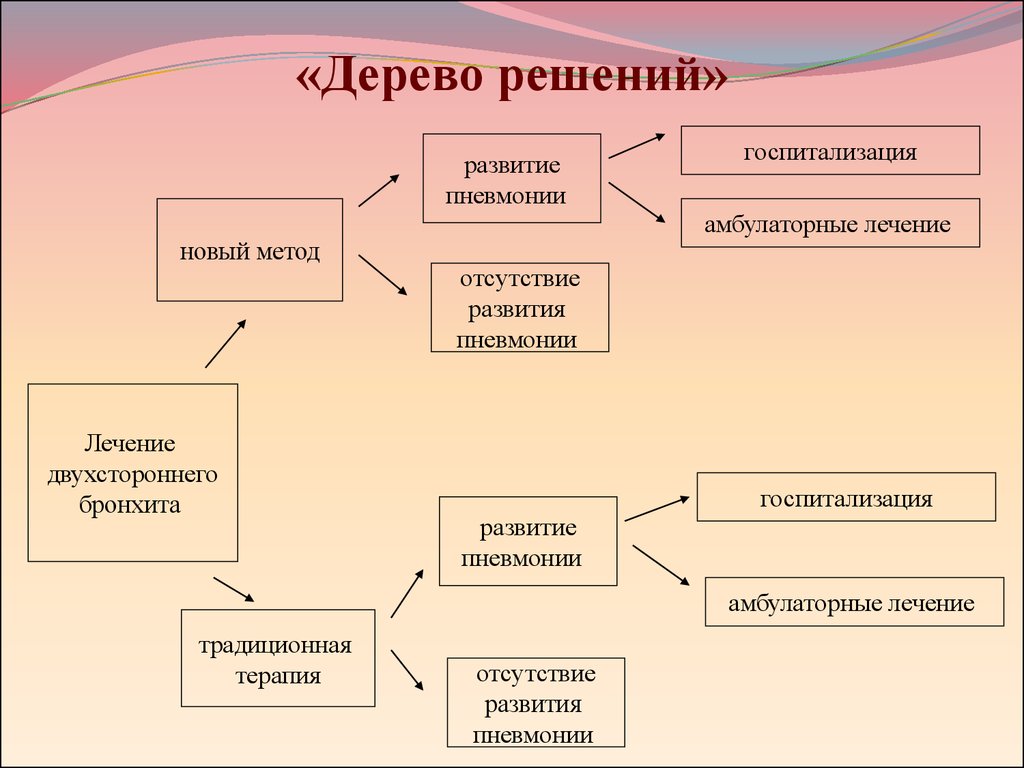 Завести аккаунт
Завести аккаунтОбъяснение алгоритма дерева решений — KDnuggets
Введение
Классификация — это двухэтапный процесс машинного обучения: этап обучения и этап прогнозирования. На этапе обучения модель разрабатывается на основе заданных обучающих данных. На этапе прогнозирования модель используется для прогнозирования ответа на заданные данные. Дерево решений — один из самых простых и популярных алгоритмов классификации для понимания и интерпретации.
Алгоритм дерева решений
Алгоритм дерева решений принадлежит к семейству алгоритмов обучения с учителем. В отличие от других алгоритмов обучения с учителем, алгоритм дерева решений можно использовать для решения0018 проблемы регрессии и классификации тоже.
Целью использования дерева решений является создание обучающей модели, которая может использоваться для прогнозирования класса или значения целевой переменной путем изучения простых правил принятия решений, полученных из предыдущих данных (данные для обучения).
В деревьях решений для прогнозирования метки класса для записи мы начинаем с корня дерева. Мы сравниваем значения корневого атрибута с атрибутом записи. На основе сравнения мы следуем по ветке, соответствующей этому значению, и переходим к следующему узлу.
Типы деревьев решений
Типы деревьев решений основаны на типе имеющейся у нас целевой переменной. Оно может быть двух типов:
- Дерево решений категориальной переменной: Дерево решений , которое имеет категориальную целевую переменную, затем называется деревом решений категориальной переменной .
- Дерево решений с непрерывной переменной: Дерево решений имеет непрерывную целевую переменную, тогда оно называется Дерево решений с непрерывной переменной.
Пример: — Допустим, у нас есть проблема, чтобы предсказать, будет ли клиент платить свой взнос за продление со страховой компанией (да/нет).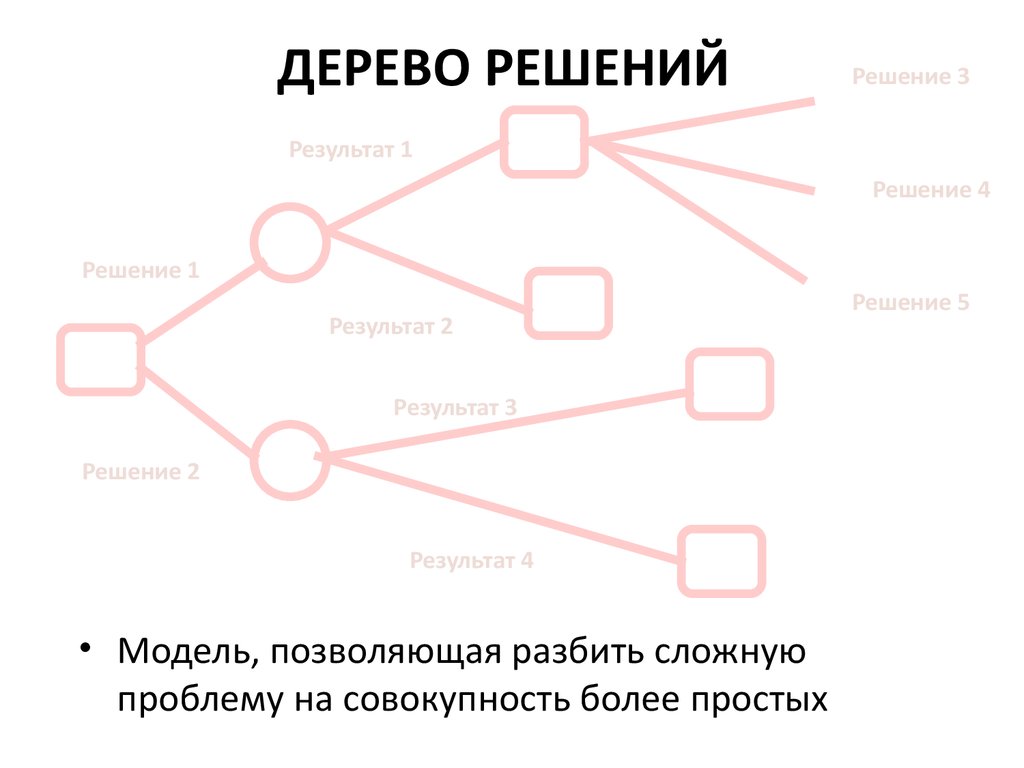 Здесь мы знаем, что доход клиентов является существенной переменной, но страховая компания не располагает подробной информацией о доходах всех клиентов. Теперь, когда мы знаем, что это важная переменная, мы можем построить дерево решений для прогнозирования доходов клиентов на основе рода занятий, продукта и различных других переменных. В этом случае мы прогнозируем значения для непрерывных переменных.
Здесь мы знаем, что доход клиентов является существенной переменной, но страховая компания не располагает подробной информацией о доходах всех клиентов. Теперь, когда мы знаем, что это важная переменная, мы можем построить дерево решений для прогнозирования доходов клиентов на основе рода занятий, продукта и различных других переменных. В этом случае мы прогнозируем значения для непрерывных переменных.
Важная терминология, связанная с деревьями решений
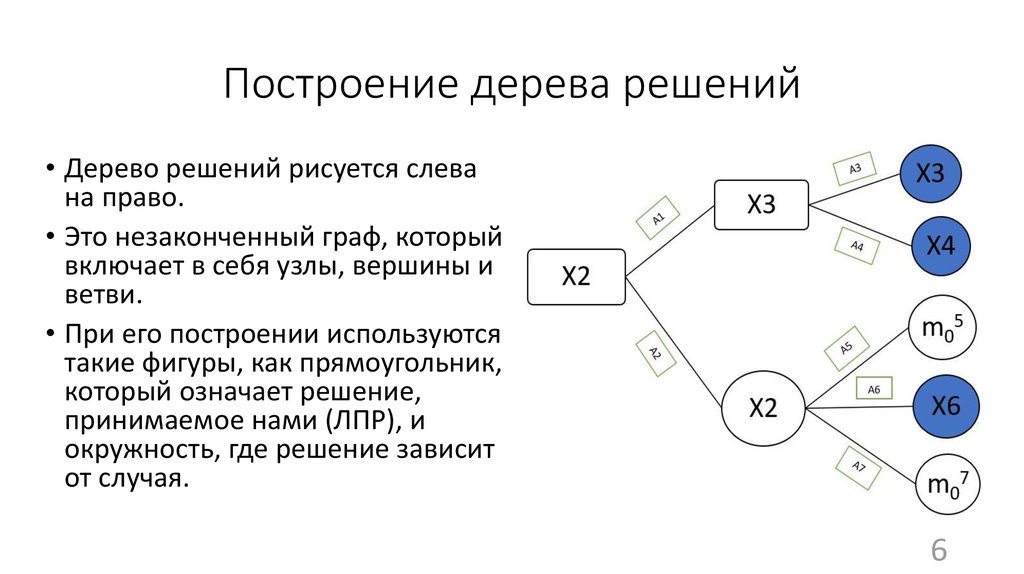
- Корневой узел: Он представляет всю совокупность или выборку, которая далее делится на два или более однородных набора.
- Разделение: Это процесс разделения узла на два или более подузлов.
- Узел принятия решения: Когда подузел разделяется на дополнительные подузлы, он называется узлом принятия решения.
- Листовой/терминальный узел: Узлы, которые не разделяются, называются конечными или конечными узлами.

- Сокращение: Когда мы удаляем подузлы узла принятия решений, этот процесс называется сокращением. Можно сказать обратный процесс расщепления.
- Ветвь/поддерево: Подраздел всего дерева называется ветвью или поддеревом.
- Родительский и дочерний узел: Узел, который разделен на подузлы, называется родительским узлом подузлов, тогда как подузлы являются дочерними по отношению к родительскому узлу.
Деревья решений классифицируют примеры, сортируя их вниз по дереву от корня до некоторого листового/конечного узла, при этом листовой/конечный узел обеспечивает классификацию примера.
Каждый узел в дереве действует как тестовый пример для некоторого атрибута, и каждое ребро, спускающееся с узла, соответствует возможным ответам на тестовый пример. Этот процесс носит рекурсивный характер и повторяется для каждого поддерева с корнем в новом узле.
Предположения при создании дерева решений
Ниже приведены некоторые предположения, которые мы делаем при использовании дерева решений:
- Вначале вся обучающая выборка рассматривается как корень.

- Предпочтительно, чтобы значения признаков были категориальными. Если значения непрерывны, то перед построением модели они дискретизируются.
- Записи распределяются рекурсивно на основе значений атрибутов.
- Порядок размещения атрибутов в качестве корневого или внутреннего узла дерева выполняется с использованием некоторого статистического подхода.
Деревья решений следуют представлению Сумма продукта (СОП) r . Сумма произведения (SOP) также известна как Дизъюнктивная нормальная форма . Для класса каждая ветвь от корня дерева к конечному узлу, имеющему тот же класс, является конъюнкцией (произведением) значений, разные ветви, оканчивающиеся в этом классе, образуют дизъюнктуру (сумму).
Основная проблема при реализации дерева решений состоит в том, чтобы определить, какие атрибуты нам нужно рассматривать как корневой узел и каждый уровень. Обработка этого должна быть известна как выбор атрибутов. У нас есть различные меры выбора атрибутов для определения атрибута, который можно рассматривать как корневую ноту на каждом уровне.
У нас есть различные меры выбора атрибутов для определения атрибута, который можно рассматривать как корневую ноту на каждом уровне.
Как работают деревья решений?
Решение о стратегическом разделении сильно влияет на точность дерева. Критерии принятия решений различаются для деревьев классификации и регрессии.
Деревья решений используют несколько алгоритмов для принятия решения о разделении узла на два или более подузлов. Создание подузлов повышает однородность результирующих подузлов. Другими словами, мы можем сказать, что чистота узла увеличивается по отношению к целевой переменной. Дерево решений разбивает узлы на все доступные переменные, а затем выбирает разбиение, в результате которого получаются наиболее однородные подузлы.
Выбор алгоритма также зависит от типа целевых переменных. Давайте рассмотрим некоторые алгоритмы, используемые в деревьях решений:
ID3 → (расширение D3)
C4.5 → (преемник ID3)
CART → (Дерево классификации и регрессии)
ЧАЙД → (автоматическое обнаружение взаимодействия методом хи-квадрат. Выполняет многоуровневое разбиение при вычислении деревьев классификации)
Выполняет многоуровневое разбиение при вычислении деревьев классификации)
MARS → (многомерные адаптивные регрессионные сплайны)
Алгоритм ID3 строит деревья решений, используя подход жадного поиска сверху вниз в пространстве возможных ветвей без возврата. Жадный алгоритм, как следует из названия, всегда делает выбор, который кажется лучшим в данный момент.
Шаги в алгоритме ID3:
- Он начинается с исходного набора S в качестве корневого узла.
- На каждой итерации алгоритм перебирает очень неиспользуемый атрибут множества S и вычисляет Энтропия (H) и Прирост информации (IG) этого атрибута.
- Затем он выбирает атрибут с наименьшей энтропией или наибольшим приростом информации.
- Затем набор S разбивается по выбранному атрибуту для создания подмножества данных.
- Алгоритм продолжает повторяться для каждого подмножества, учитывая только никогда не выбранные ранее атрибуты.

Меры по выбору атрибутов
Если набор данных состоит из N атрибутов, а затем решить, какой атрибут разместить в корне или на разных уровнях дерева в качестве внутренних узлов, — сложный шаг. Простой случайный выбор любого узла в качестве корня не может решить проблему. Если мы будем следовать случайному подходу, это может дать нам плохие результаты с низкой точностью.
Для решения этой проблемы выбора атрибутов исследователи работали и разработали несколько решений. Они предложили использовать некоторые критериев , например:
Энтропия ,
Прирост информации,
Индекс Джини,
Коэффициент усиления,
Уменьшение дисперсии
Хи-квадрат
 е. атрибут с большим значением (в случае прироста информации) помещается в корень.
е. атрибут с большим значением (в случае прироста информации) помещается в корень. При использовании прироста информации в качестве критерия мы предполагаем, что атрибуты являются категориальными, а для индекса Джини предполагается, что атрибуты непрерывны.
Энтропия
Энтропия — это мера случайности обрабатываемой информации. Чем выше энтропия, тем сложнее делать какие-либо выводы из этой информации. Подбрасывание монеты является примером действия, которое предоставляет информацию, которая является случайной.
Из приведенного выше графика совершенно очевидно, что энтропия H(X) равна нулю, когда вероятность равна 0 или 1. Энтропия максимальна, когда вероятность равна 0,5, потому что она отражает идеальную случайность данных и это не шанс, если полностью определяет результат.
ID3 следует правилу — ветвь с нулевой энтропией является конечным узлом, а ветвь с энтропией больше нуля требует дальнейшего разделения.

Математически энтропия для 1 атрибута представлена как:
Где S → Текущее состояние, а Pi → Вероятность события i состояния S или Процент класса i 9003 5 в узле состояния S
Математически энтропия для нескольких атрибутов представлена как:
где T→ текущее состояние и X → выбранный атрибут
получение информации статистическое свойство, которое измеряет, насколько хорошо данный атрибут разделяет обучающие примеры в соответствии с их целевая классификация. Построение дерева решений сводится к поиску атрибута, который дает наибольший прирост информации и наименьшую энтропию.
Получение информации
Прирост информации – это уменьшение энтропии. Он вычисляет разницу между энтропией до разделения и средней энтропией после разделения набора данных на основе заданных значений атрибутов. Алгоритм дерева решений ID3 (итеративный дихотомайзер) использует прирост информации.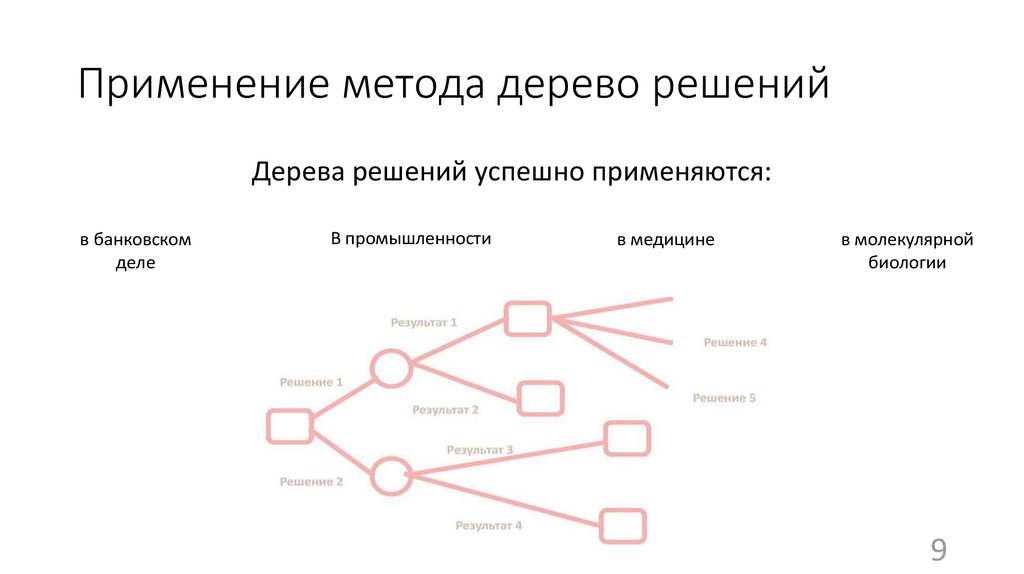
Математически IG представляется как:
Гораздо проще можно заключить, что:
Прирост информации
Где «до» — набор данных до разделения, K — количество сгенерированных подмножеств расщеплением, а (j, after) является подмножеством j после расщепления.
Индекс Джини
Индекс Джини можно понимать как функцию стоимости, используемую для оценки разделения в наборе данных. Он рассчитывается путем вычитания суммы квадратов вероятностей каждого класса из единицы. Он предпочитает более крупные разделы и прост в реализации, тогда как прирост информации предпочитает меньшие разделы с разными значениями.
Индекс Джини
Индекс Джини работает с категориальной целевой переменной «Успех» или «Неудача». Он выполняет только двоичные расщепления.
Более высокое значение индекса Джини означает более высокое неравенство, более высокую неоднородность.
Этапы расчета индекса Джини для разделения
- Вычислить Джини для подузлов, используя приведенную выше формулу для успеха (p) и отказа (q) (p²+q²).

- Рассчитайте индекс Джини для разделения, используя взвешенную оценку Джини для каждого узла этого разделения.
CART (Дерево классификации и регрессии) использует метод индекса Джини для создания точек разделения.
Коэффициент усиления
Прирост информации смещен в сторону выбора атрибутов с большим количеством значений в качестве корневых узлов. Это означает, что он предпочитает атрибут с большим количеством различных значений.
C4.5, усовершенствование ID3, использует коэффициент усиления, который является модификацией усиления информации, которая уменьшает его смещение и обычно является лучшим вариантом. Коэффициент усиления преодолевает проблему с получением информации, принимая во внимание количество ветвей, которые возникнут до разделения. Он корректирует прирост информации, принимая во внимание внутреннюю информацию разделения.
Давайте рассмотрим, есть ли у нас набор данных, в котором есть пользователи и их предпочтения в жанрах фильмов, основанные на таких переменных, как пол, возрастная группа, рейтинг и т.
д. С помощью прироста информации вы разделитесь на «Пол» (при условии, что он имеет самый высокий прирост информации), и теперь переменные «Возрастная группа» и «Рейтинг» могут быть одинаково важны, и с помощью коэффициента прироста он будет наказывать переменная с более четкими значениями, которые помогут нам определить разделение на следующем уровне.
Gain Ratio
Где «до» — это набор данных до разделения, K — количество подмножеств, созданных при разделении, а (j, после) — это подмножество j после разделения.
Уменьшение дисперсии
Уменьшение дисперсии — это алгоритм, используемый для непрерывных целевых переменных (задачи регрессии). Этот алгоритм использует стандартную формулу дисперсии для выбора наилучшего разделения. Разделение с более низкой дисперсией выбрано в качестве критерия для разделения населения:
Над чертой X указано среднее значение значений, X — фактическое значение, а n — количество значений.
Шаги для расчета дисперсии:
- Рассчитать дисперсию для каждого узла.
- Рассчитать дисперсию для каждого разделения как средневзвешенную дисперсию каждого узла.
Хи-квадрат
Аббревиатура CHAID расшифровывается как Хи -квадрат Автоматический детектор взаимодействия. Это один из старейших методов классификации деревьев. Он определяет статистическую значимость различий между подузлами и родительским узлом. Мы измеряем его суммой квадратов стандартизированных различий между наблюдаемой и ожидаемой частотами целевой переменной.
Работает с категориальной целевой переменной «Успех» или «Неудача». Он может выполнять два или более шпагата. Чем выше значение хи-квадрата, тем выше статистическая значимость различий между подузлом и родительским узлом.
Генерирует дерево CHAID (детектор автоматических взаимодействий хи-квадрат).
Математически хи-квадрат представляется как:
Шаги для расчета хи-квадрат для разделения:
- Вычисление хи-квадрат для отдельного узла путем расчета отклонения для успеха и неудачи
- Расчет хи-квадрата разделения с использованием суммы всех хи-квадратов успеха и отказа каждого узла разделения
Как избежать/противодействовать переобучению в деревьях решений?
Общая проблема с деревьями решений, особенно с таблицей, полной столбцов, они много помещаются. Иногда кажется, что дерево запомнило обучающий набор данных. Если для дерева решений не установлено ограничение, это даст вам 100% точность в наборе обучающих данных, потому что в худшем случае для каждого наблюдения будет создан 1 лист. Таким образом, это влияет на точность прогнозирования выборок, не входящих в обучающую выборку.
Иногда кажется, что дерево запомнило обучающий набор данных. Если для дерева решений не установлено ограничение, это даст вам 100% точность в наборе обучающих данных, потому что в худшем случае для каждого наблюдения будет создан 1 лист. Таким образом, это влияет на точность прогнозирования выборок, не входящих в обучающую выборку.
Вот два способа устранения переобучения:
- Сокращение деревьев решений.
- Случайный лес
Обрезка деревьев решений
Процесс разделения приводит к полностью выращенным деревьям, пока не будут достигнуты критерии остановки. Но полностью выросшее дерево, скорее всего, будет соответствовать данным, что приведет к плохой точности невидимых данных.
Отсечение в действии
В отсечении вы отсекаете ветви дерева, т. е. удаляете узлы решений, начиная с конечного узла, так, чтобы общая точность не нарушалась. Это делается путем разделения фактического обучающего набора на два набора: набор обучающих данных, D, и набор проверочных данных, V. Подготовьте дерево решений, используя отдельный набор обучающих данных, D. Затем продолжайте обрезать дерево соответствующим образом, чтобы оптимизировать точность набор проверочных данных, версия
Подготовьте дерево решений, используя отдельный набор обучающих данных, D. Затем продолжайте обрезать дерево соответствующим образом, чтобы оптимизировать точность набор проверочных данных, версия
Сокращение
На приведенной выше диаграмме атрибут «Возраст» в левой части дерева был сокращен, поскольку он имеет большее значение в правой части дерева, что устраняет переоснащение.
Случайный лес
Случайный лес — это пример ансамблевого обучения, в котором мы объединяем несколько алгоритмов машинного обучения для повышения эффективности прогнозирования.
Почему название «Случайный»?
Две ключевые концепции, которые дают ему название random:
- Случайная выборка обучающего набора данных при построении деревьев.
- Случайные подмножества объектов, учитываемые при разделении узлов.
Техника, известная как бэггинг, используется для создания ансамбля деревьев, в котором несколько обучающих наборов генерируются с заменой.
В методе бэггинга набор данных делится на N выборок с использованием рандомизированной выборки. Затем с помощью единого алгоритма обучения строится модель на всех выборках. Позже полученные прогнозы объединяются с помощью голосования или параллельного усреднения.
Случайный лес в действии
Что лучше: линейная или древовидная модели?
Ну, это зависит от того, какую проблему вы решаете.
- Если взаимосвязь между зависимыми и независимыми переменными хорошо аппроксимируется линейной моделью, линейная регрессия превзойдет древовидную модель.
- Если существует высокая нелинейность и сложная взаимосвязь между зависимыми и независимыми переменными, древовидная модель превзойдет классический метод регрессии.
- Если вам нужно построить модель, которую легко объяснить людям, модель дерева решений всегда будет лучше, чем линейная модель. Модели деревьев решений даже проще интерпретировать, чем линейную регрессию!
Построение классификатора дерева решений в Scikit-learn
Набор данных, который у нас есть, представляет собой данные супермаркета, которые можно скачать отсюда.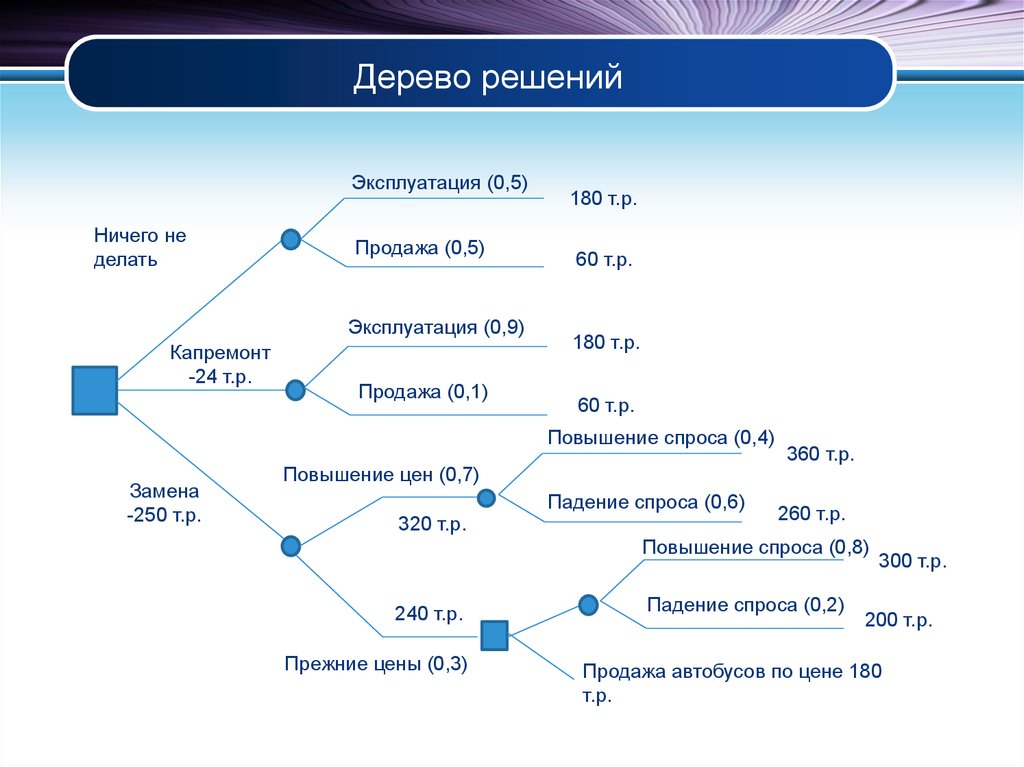
Загрузить все основные библиотеки.
импортировать numpy как np импортировать matplotlib.pyplot как plt импортировать панд как pd
Загрузите набор данных. Он состоит из 5 функций: UserID , Пол , Возраст , Расчетная зарплата и Покупки .
данные = pd.read_csv('/Users/ML/DecisionTree/Social.csv')
data.head() Набор данных
Мы возьмем только Age и EstimatedSalary в качестве независимых переменных 9 0618 X из-за других функций, таких как Пол и Идентификатор пользователя не имеют значения и не влияют на покупательную способность человека. Purchased — это наша зависимая переменная y .
feature_cols = ['Возраст','Расчетная зарплата']X = data.iloc[:,[2,3]].values y = data.iloc[:,4].values
Следующим шагом является разделение набора данных на обучающий и тестовый.
из sklearn.model_selection импорта train_test_split X_train, X_test, y_train, y_test = train_test_split (X, y, test_size = 0,25, random_state = 0)
Выполнить масштабирование признаков
#масштабирование признаков из sklearn.preprocessing импортировать StandardScaler sc_X = Стандартный масштаб() X_train = sc_X.fit_transform(X_train) X_test = sc_X.transform(X_test)
Подгонка модели в классификаторе дерева решений.
из импорта sklearn.tree DecisionTreeClassifier классификатор = DecisionTreeClassifier() classifier = classifier.fit(X_train,y_train)
Делайте прогнозы и проверяйте точность.
#прогноз
y_pred = classifier.predict(X_test)#Точность
from sklearn import metricsprint('Оценка точности:', metrics.accuracy_score(y_test,y_pred))
Классификатор дерева решений дал точность 91%.
Матрица путаницы
из sklearn.metrics импорта путаницы_матрицы
cm = матрица_замешательства (y_test, y_pred) Вывод:
массив([[64, 4],
[ 2, 30]])
Это означает, что 6 наблюдений классифицированы как ложные.
Давайте сначала визуализируем результаты предсказания модели.
из импорта matplotlib.colors ListedColormap
X_set, y_set = X_тест, y_тест
X1, X2 = np.meshgrid(np.arange(начало = X_set[:,0].min()-1, стоп= X_set[:,0].max()+1, шаг = 0,01),np.arange (начало = X_set[:,1].min()-1, стоп= X_set[:,1].max()+1, шаг = 0,01))
plt.contourf(X1,X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape), альфа=0,75, cmap = ListedColormap(( "красный", "зеленый")))plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())для i,j в перечислении(np.unique(y_set)):
plt.scatter(X_set[y_set==j,0],X_set[y_set==j,1], c = ListedColormap(("красный","зеленый"))(i),метка = j)
plt.title("Дерево решений(Тестовый набор)")
plt.xlabel("Возраст")
plt.ylabel("Ориентировочная зарплата")
plt.legend()
plt.show()
Давайте также визуализируем дерево:
Вы можете использовать функцию export_graphviz Scikit-learn для отображения дерева в блокноте Jupyter.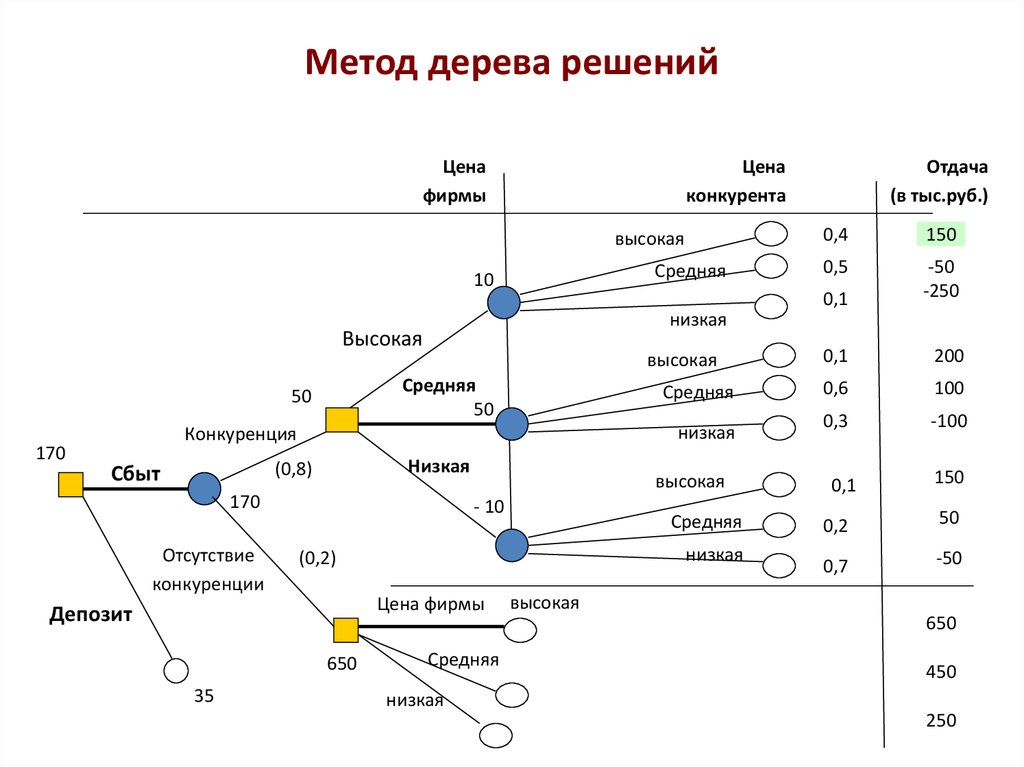 Для построения деревьев вам также необходимо установить Graphviz и pydotplus.
Для построения деревьев вам также необходимо установить Graphviz и pydotplus.
conda install python-graphviz
pip install pydotplus
export_graphviz функция преобразует классификатор дерева решений в точечный файл, а pydotplus преобразует этот точечный файл в png или отображаемую форму на Jupy тер.
из sklearn.tree import export_graphviz
из sklearn.externals.six импортировать StringIO
из IPython.display импортировать изображение
импортировать pydotplusdot_data = StringIO()
export_graphviz (классификатор, out_file = dot_data,
заполнено = верно, округлено = верно,
special_characters=True,feature_names = feature_cols,class_names=['0','1'])
график = pydotplus.graph_from_dot_data(dot_data.getvalue())
Изображение(graph.create_png())
Дерево решений.
В диаграмме дерева решений каждый внутренний узел имеет правило принятия решения, которое разделяет данные.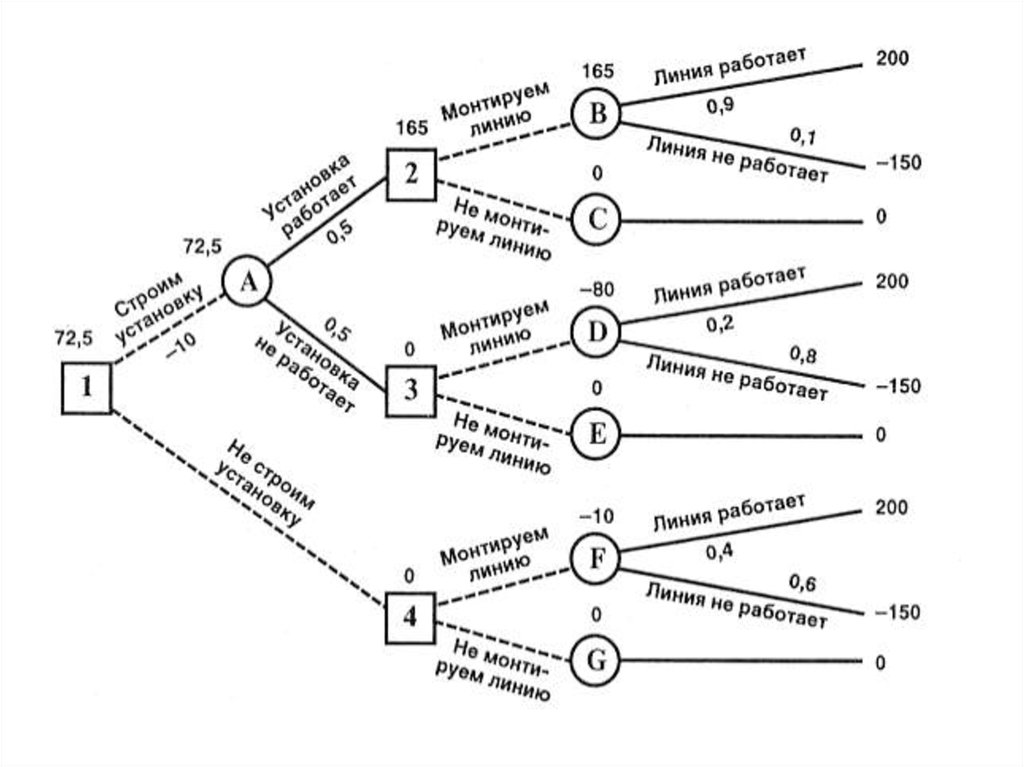 Джини называют коэффициентом Джини, который измеряет загрязненность узла. Вы можете сказать, что узел чистый, когда все его записи принадлежат одному и тому же классу, такие узлы известны как конечные узлы.
Джини называют коэффициентом Джини, который измеряет загрязненность узла. Вы можете сказать, что узел чистый, когда все его записи принадлежат одному и тому же классу, такие узлы известны как конечные узлы.
Здесь результирующее дерево не обрезано. Это необрезанное дерево необъяснимо и нелегко понять. В следующем разделе давайте оптимизируем его путем обрезки.
Оптимизация классификатора дерева решений
критерий : необязательный (по умолчанию = «джини») или Выбрать меру выбора атрибута: этот параметр позволяет нам использовать меру выбора различных атрибутов. Поддерживаемые критерии: «джини» для индекса Джини и «энтропия» для получения информации.
splitter : строка, необязательная (по умолчанию = «best») или Split Strategy: этот параметр позволяет нам выбрать стратегию разделения. Поддерживаемые стратегии: «лучшие» для выбора наилучшего разделения и «случайные» для выбора наилучшего случайного разделения.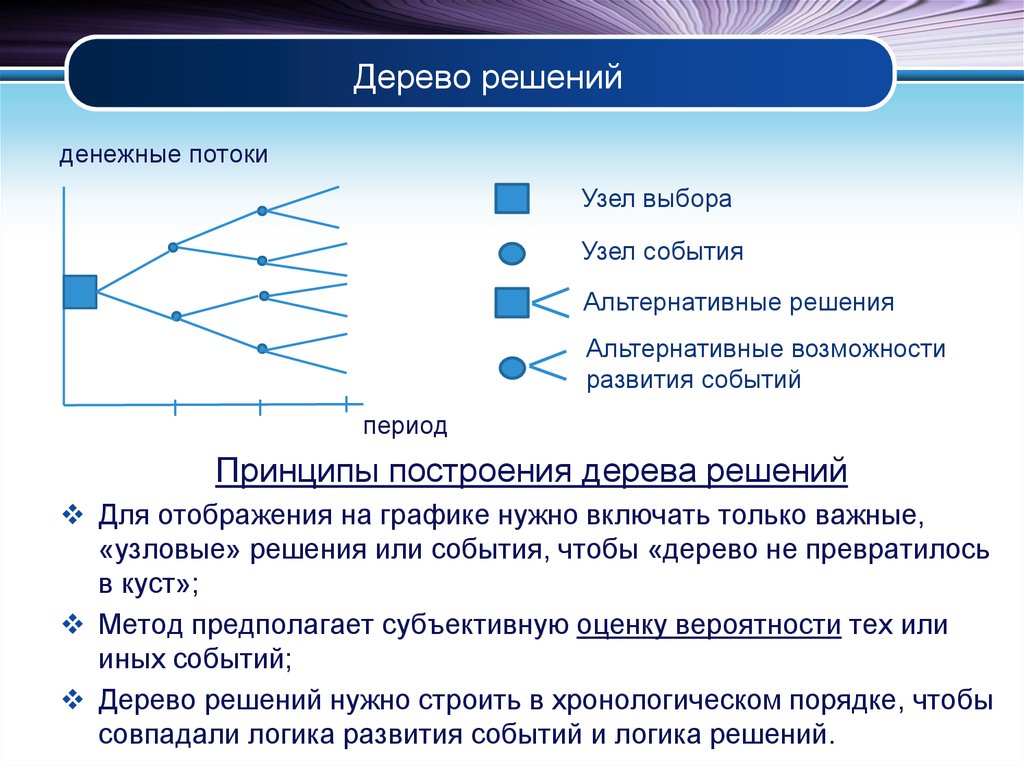
max_depth : int или None, необязательно (по умолчанию = None) или Максимальная глубина дерева: максимальная глубина дерева. Если None, то узлы расширяются до тех пор, пока все листья не будут содержать выборок меньше, чем min_samples_split. Более высокое значение максимальной глубины вызывает переоснащение, а более низкое значение — недостаточное (Источник).
В Scikit-learn оптимизация классификатора дерева решений выполняется только путем предварительной обрезки. Максимальная глубина дерева может использоваться как управляющая переменная для предварительной обрезки.
# Создать объект классификатора дерева решений
classifier = DecisionTreeClassifier(criterion="entropy", max_depth=3)# Обучить классификатор дерева решений
classifier = classifier.fit(X_train,y_train)#Предсказать ответ для тестового набора данных
y_pred = classifier.predict(X_test)# Точность модели, как часто классификатор верен?
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
Ну, скорость классификации увеличилась до 94%, что лучше, чем в предыдущей модели.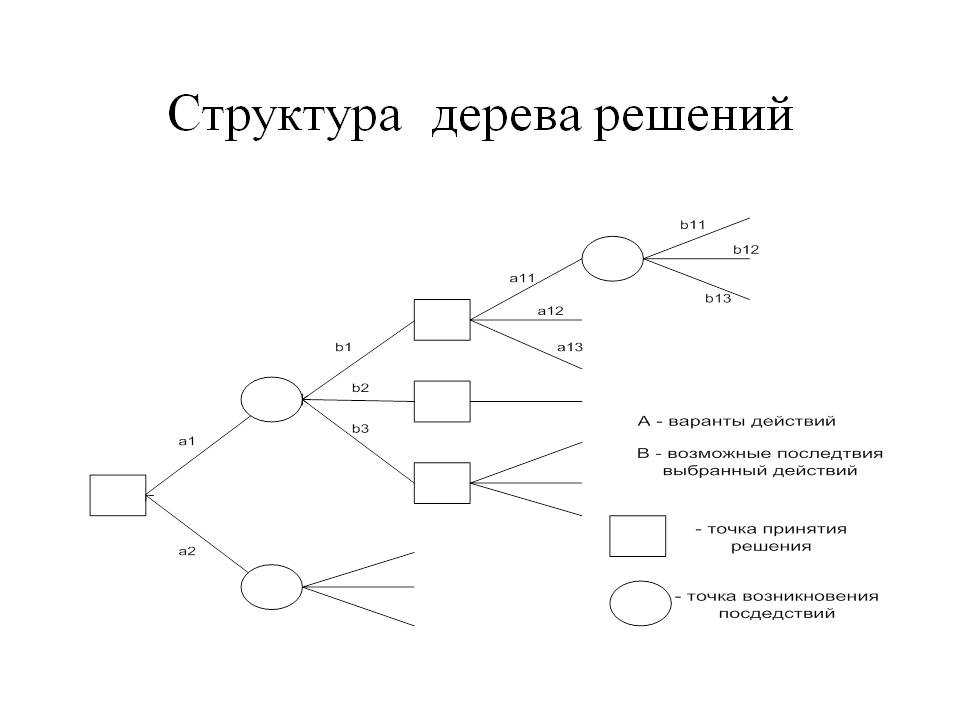
Теперь давайте снова визуализируем обрезанное дерево решений после оптимизации.
точка_данных = StringIO()
export_graphviz (классификатор, out_file = dot_data,
заполнено = верно, округлено = верно,
special_characters = True, feature_names = feature_cols, class_names = ['0','1'])
график = pydotplus.graph_from_dot_data(dot_data.getvalue())
Image(graph.create_png())
Дерево решений после обрезки
Эта сокращенная модель менее сложна, объяснима и проста для понимания, чем предыдущий график модели дерева решений.
Заключение
В этой статье мы подробно рассмотрели дерево решений; Это работает, меры выбора атрибутов, такие как получение информации, коэффициент усиления и индекс Джини, построение модели дерева решений, визуализация и оценка набора данных супермаркета с использованием пакета Python Scikit-learn и оптимизация производительности дерева решений с помощью настройки параметров.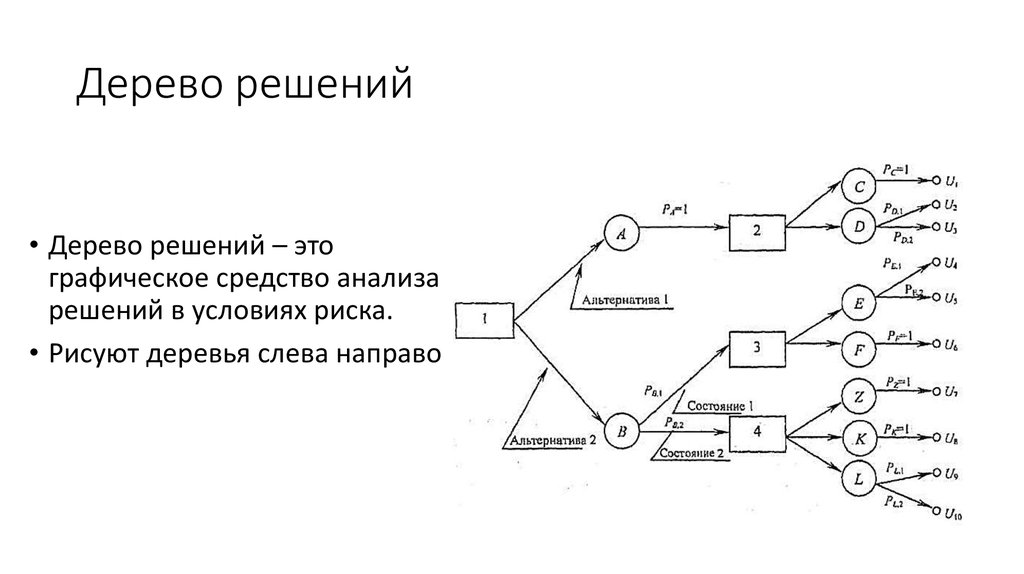


 Это называется переобучением. Чтобы избежать этой проблемы, необходимы такие механизмы, как обрезка, установка минимального количества выборок, необходимых для конечного узла, или установка максимальной глубины дерева.
Это называется переобучением. Чтобы избежать этой проблемы, необходимы такие механизмы, как обрезка, установка минимального количества выборок, необходимых для конечного узла, или установка максимальной глубины дерева. Это можно смягчить путем обучения нескольких деревьев в учащемся ансамбля, где функции и образцы выбираются случайным образом с заменой.
Это можно смягчить путем обучения нескольких деревьев в учащемся ансамбля, где функции и образцы выбираются случайным образом с заменой. DecisionTreeClassifier()
>>> clf = clf.fit(X, Y)
DecisionTreeClassifier()
>>> clf = clf.fit(X, Y)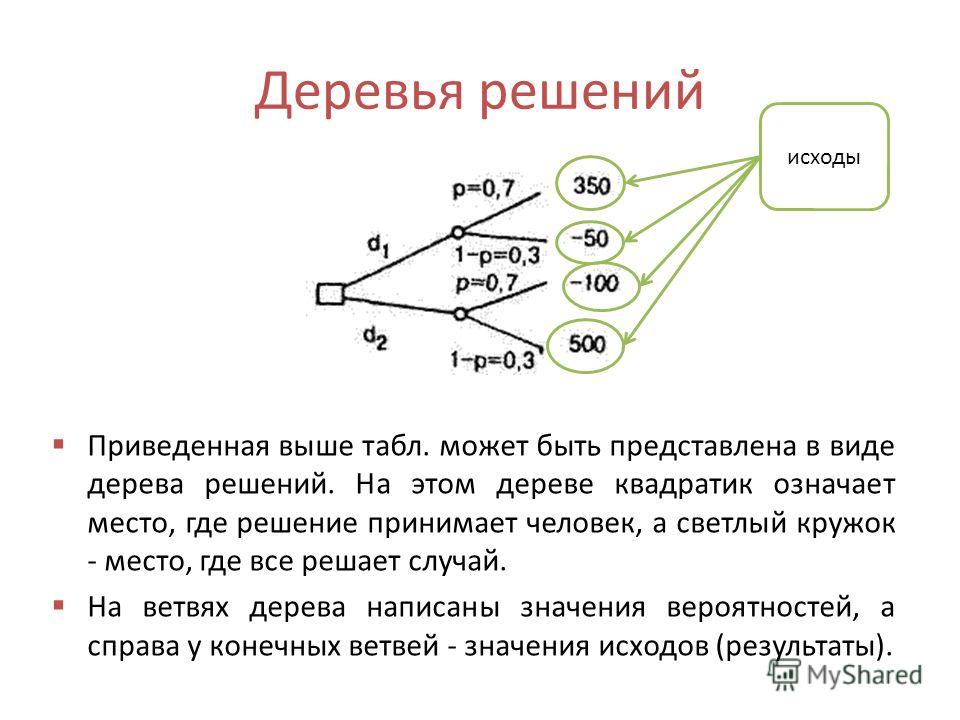 predict_proba([[2., 2.]])
array([[0., 1.]])
predict_proba([[2., 2.]])
array([[0., 1.]]) plot_tree(clf)
plot_tree(clf)  export_graphviz(clf, out_file=None)
>>> graph = graphviz.Source(dot_data)
>>> graph.render("iris")
export_graphviz(clf, out_file=None)
>>> graph = graphviz.Source(dot_data)
>>> graph.render("iris")  .. special_characters=True)
>>> graph = graphviz.Source(dot_data)
>>> graph
.. special_characters=True)
>>> graph = graphviz.Source(dot_data)
>>> graph 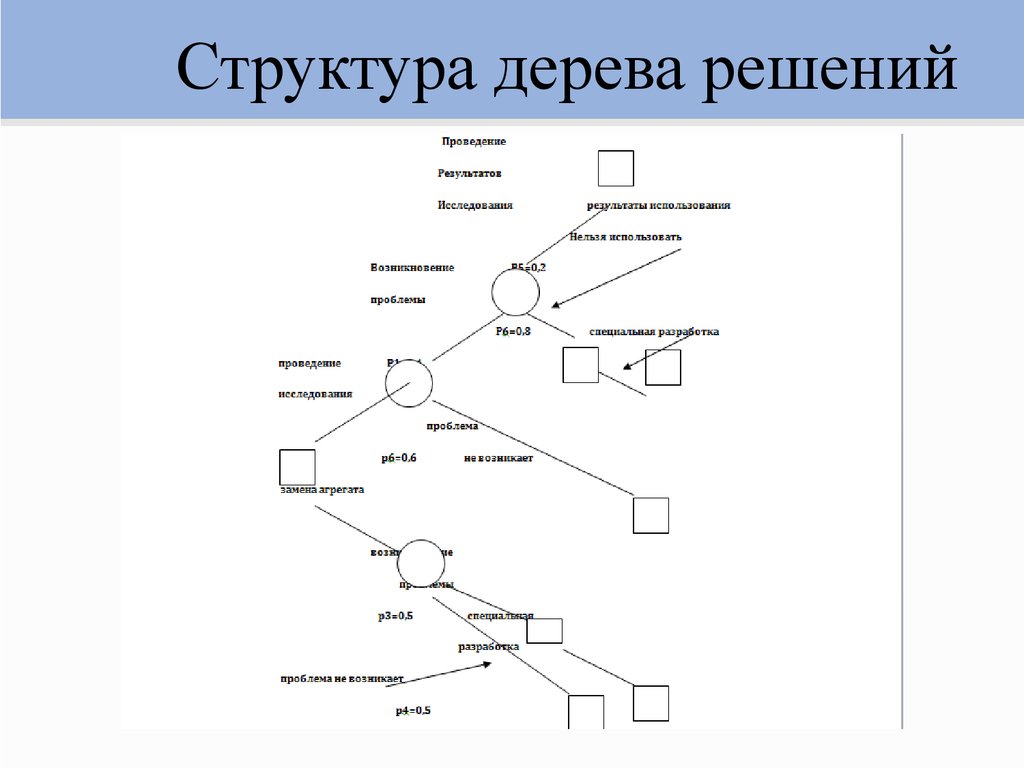 80
| |--- class: 0
|--- petal width (cm) > 0.80
| |--- petal width (cm) <= 1.75
| | |--- class: 1
| |--- petal width (cm) > 1.75
| | |--- class: 2
80
| |--- class: 0
|--- petal width (cm) > 0.80
| |--- petal width (cm) <= 1.75
| | |--- class: 1
| |--- petal width (cm) > 1.75
| | |--- class: 2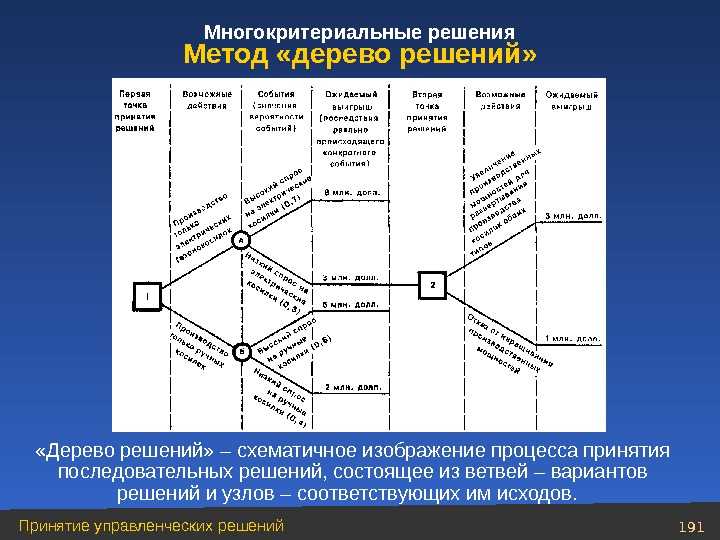 5, 2.5]
>>> clf = tree.DecisionTreeRegressor()
>>> clf = clf.fit(X, y)
>>> clf.predict([[1, 1]])
array([0.5])
5, 2.5]
>>> clf = tree.DecisionTreeRegressor()
>>> clf = clf.fit(X, y)
>>> clf.predict([[1, 1]])
array([0.5])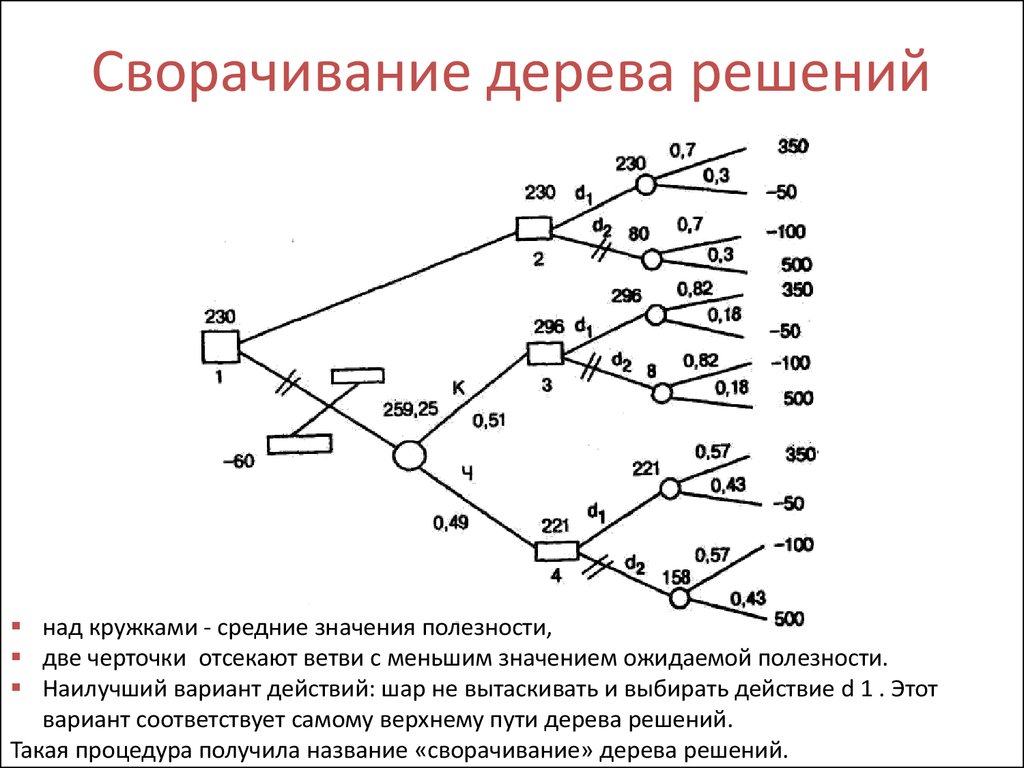 Используйте
Используйте 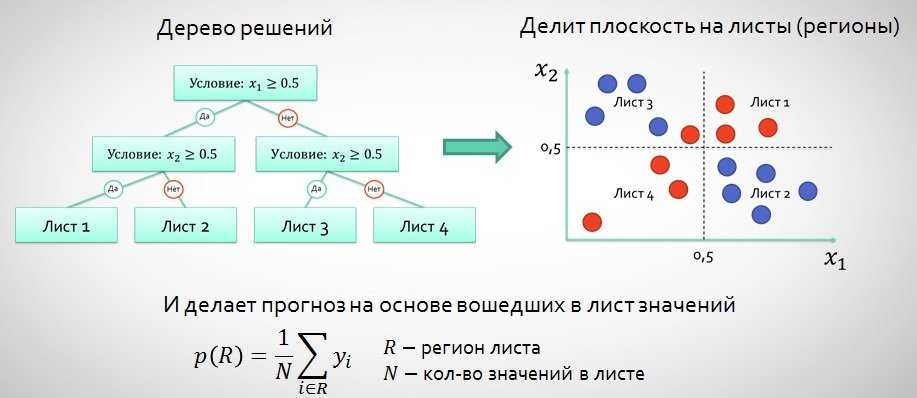 Рассмотрим
Рассмотрим 
 Брейман, Дж. Фридман, Р. Олшен и К. Стоун. Деревья классификации и регрессии. Уодсворт, Белмонт, Калифорния, 1984.
Брейман, Дж. Фридман, Р. Олшен и К. Стоун. Деревья классификации и регрессии. Уодсворт, Белмонт, Калифорния, 1984.
 д. С помощью прироста информации вы разделитесь на «Пол» (при условии, что он имеет самый высокий прирост информации), и теперь переменные «Возрастная группа» и «Рейтинг» могут быть одинаково важны, и с помощью коэффициента прироста он будет наказывать переменная с более четкими значениями, которые помогут нам определить разделение на следующем уровне.
д. С помощью прироста информации вы разделитесь на «Пол» (при условии, что он имеет самый высокий прирост информации), и теперь переменные «Возрастная группа» и «Рейтинг» могут быть одинаково важны, и с помощью коэффициента прироста он будет наказывать переменная с более четкими значениями, которые помогут нам определить разделение на следующем уровне.