Метод гаусса решения систем линейных уравнений примеры: Решение систем линейных уравнений методом Гаусса

alexxlab / / Разное

Метод Гаусса. Примеры

Метод Гаусса заключается в последовательном исключении переменных и преобразовании системы линейных алгебраических уравнений

к треугольному виду

Предположим, что в системе коэффициент . Если это условие не выполняется, то на первое место переносим уравнение, которое ее удовлетворяет. С помощью первого уравнения исключим из остальных уравнений.

Для этого делят первую строчку на , обозначим

.

Дальше второй строки вычитаем первую строку, умноженную на ;от третьего первую строчку, умноженный на ; и так далее до последней строки. Получим таблицу коэффициентов:

Для неизвестных имеем систему уравнений. Выполняя, как и раньше, исключим из всех уравнений, начиная с третьего. Для этого сначала разделим вторую строчку на .

Если коэффициент , то переставим уравнения так, чтобы выполнялось условие .

Обозначив

,

от третьей строки вычтем вторую строчку, умноженный на ;

от четвертой строки вычтем вторую строчку, умноженный на и т. д. Получим таблицу коэффициентов:

Продолжая процесс исключения неизвестных получим таблицу:

Таблица коэффициентов при неизвестных сводится к треугольному виду. Все главной диагонали элементы . Запишем соответствующую систему уравнений:

Переход от первой системы уравнений до последней называется прямым ходом метода Гаусса. Обратный ход метода Гаусса начинается с последней системы уравнений. Ее решают с конца до начала. Из последнего уравнения находят . Подставив это значение в предпоследнее — находят и т.д. Из первого уравнения находят .

Если система уравнений с неизвестными имеет единственное решение, то эта система всегда может быть преобразована к треугольному виду. Для студентов не всегда требуют, чтобы диагональные элементы были равны единице. Достаточно просто свести систему линейных уравнений к верхней треугольной.

———————————————

Пример 1.

Дана система трех линейных уравнений с тремя неизвестными. Решить систему методом Гаусса.

Решение.

Исключим неизвестную из второго и третьего уравнения. Для этого от них вычтем первое умноженное на

Видим, что наше уравнение в таком виде можно решать обратным ходом метода Гаусса. Для этого из последнего уравнения выразим

Подставим полученное значение в предыдущее уравнение и найдем

Из первого уравнения находим

Решение данной системы равен

——————————————

В случаях систем больших размеров, а также для удобства, часто на практике используют другую схему решения. Вместо преобразований над системой выполняют соответствующие преобразования над матрицей, составленной из коэффициентов при неизвестных и столбца из свободных членов, который для удобства выделяют вертикальной линией. Такую матрицу называют расширенной матрицей системы.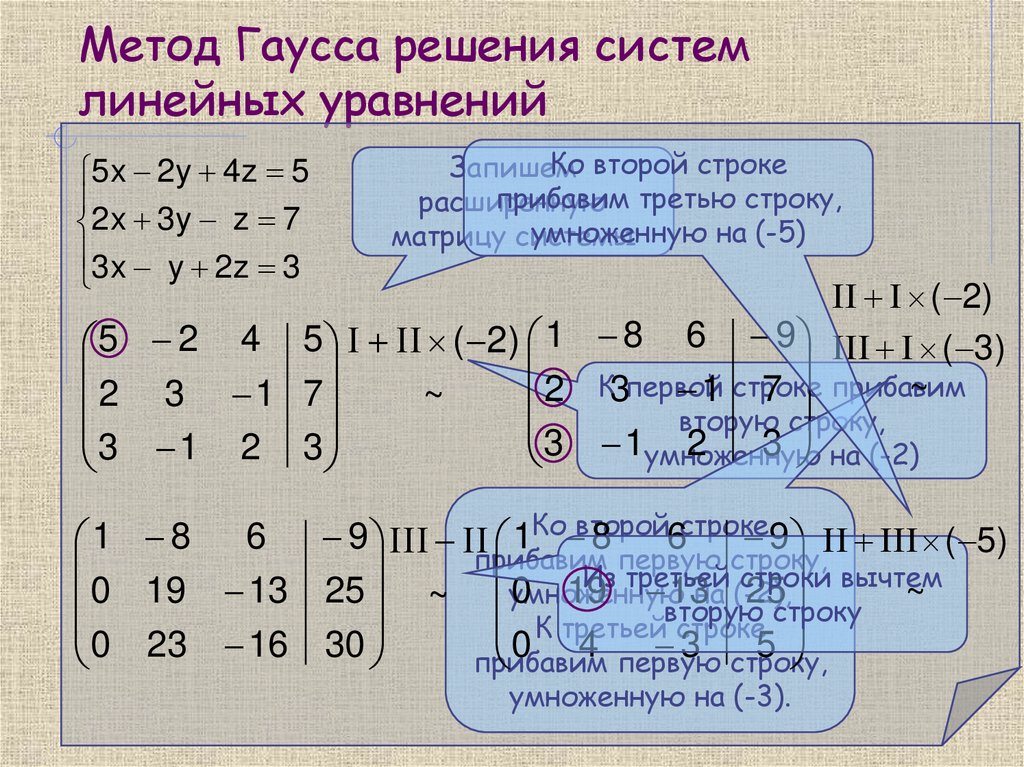

——————————————

Пример 2.

Решить систему четырех линейных алгебраических уравнений методом Гаусса.

Решение.

Выпишем расширенную матрицу для данной системы

Сведем ее к треугольному виду с помощью элементарных преобразований.

1.Поменяем местами первый и второй строки.

2. Добавим к элементам второго, третьего и четвертого строк элементы первой строки, умноженные соответственно на

3. Поменяем местами второй и третий строки. Добавим к элементам третьего и четвертого строк элементы второй строки, умноженные соответственно на

4. От четвертого уравнения умноженного на вычитаем третье уравнение умноженное на

Такой расширенной матрицы соответствует следующая система уравнений

С четвертого уравнения находим и подставляем в третье уравнение

Найденные значения подставляем во второе уравнение

Из первого уравнения находим первую неизвестную

Система полностью решена и – ее решение.

——————————————————

Посмотреть материалы:

  • Матричный метод решения системы линейных уравнений
  • Метод Крамера
  • Решение методом Крамера СЛАУ 3-4-го порядка
  • Решение СЛАУ 3-4 порядка матричным методом
  • Решение методом Гаусса СЛАУ 3-5-ого порядка

Решение систем линейных уравнений методом гаусса

Содержание

  1. Введение                                                                                                     2        
  2. Понятие матрицы                                                                                       5
  3. Немного из биографии Гаусса                                                                  6
  4. Решение систем линейных уравнений методом Гаусса                         7
  5. Проведение обучающего  эксперимента                                                  12                                            
  6. Заключение                                                                                                  14                                                                                                  
  7. Список используемой литературы                                                            15                                                              

ВВЕДЕНИЕ

Увлечение математикой начинается с размышления над какой-то интересной задачей или проблемой.

Часто на уроках математики мы решаем различные уравнения. Многие теоретические и практические вопросы приводят не к одному уравнению, а к целой системе уравнений с несколькими неизвестными. Особенно важен случай системы линейных алгебраических уравнений. Способы  решения систем линейных уравнений – очень интересная и важная тема. В седьмом  классе на уроках алгебры мы использовали такие способы, как сложение, подстановка и графический.

Нужно  заметить,  что  не  всегда  системы  линейных  уравнений  удобно решать  данными  способами. Мы решили выяснить существуют  ли  другие  методы решения систем линейных уравнений. Изучив данную тему, мы выяснили, что существуют такие методы,  как:  метод  Крамара,  метод Гаусса, метод обратной матрицы.

Одним из самых распространенных методов решения систем линейных уравнений является метод Гаусса. Выдающегося немецкого математика Карла Фридриха Гаусса (1777–1855) современники называли «королём математики». Ещё в раннем детстве он проявлял незаурядные математические способности.

На примерах был изучен и исследован алгоритм решения систем линейных уравнений методом Гаусса. Этот метод (который также называют методом последовательного исключения неизвестных) известен в различных вариантах уже более 2000 лет.

Процесс решения по методу Гаусса состоит из двух этапов, называемых прямым и обратным ходом. На первом этапе система приводится к треугольному виду, а на втором (обратный ход) идет последовательное определение неизвестных из указанной треугольной системы.

Метод Гаусса — один из основных результатов линейной алгебры и аналитической геометрии, к нему сводятся множество других теорем и методов линейной алгебры. Поэтому поиск решения системы линейных уравнений методом Гаусса имеет не только важное значение, но и является частью алгоритма решения многих задач, что позволяет говорить об актуальности изучения метода Гаусса. В отличие от матричного метода и метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных.  

Актуальность:

Системы линейных алгебраических уравнений имеют широкое применение в решении многих задач практического приложения математики. Данная тема в школьном курсе алгебры не изучается, чтобы изучить  данную тему, необходимо познакомиться с понятиями матрицы, матрица системы и расширенная матрица системы. Получение новых знаний и нового опыта способствует развитию личности, формирует некоторые особенности мышления и оказывает влияние на отношение к миру.

Цель работы:

Научиться решать системы уравнений с помощью метода Гаусса

и применять этот метод на практике,  ознакомить и научить одноклассников решать системы уравнений методом Гаусса.

Задачи исследования

1. Познакомиться с понятием «матрица» и «матрица системы».

2. Изучить метод Гаусса.

3. Научиться применять метод Гаусса на практике.

Объект(изучения):     Метод Гаусса

Предмет:  Системы линейных уравнений с двумя и более переменными. 

Методы исследования: анализ, обобщение, эксперимент, опрос.

Гипотезы:  С помощью данного метода увеличивается скорость решения систем линейных уравнений. Метод Гаусса можно изучать на уроках       алгебры в 7 — 8 классах как дополнительный метод решения систем уравнений с двумя и более переменными.

 

Глава I

ПОНЯТИЕ МАТРИЦЫ

Матрицей  размера mn, где m — число строк, n — число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются aij, где i — номер строки, а j — номер столбца

 Матрица может состоять как из одной строки, так и из одного столбца. Вообще говоря, матрица может состоять даже из одного элемента.

Если число столбцов матрицы равно числу строк (m=n), то матрица называется квадратной.

Матрица системы – это матрица, составленная только из коэффициентов при неизвестных.

                

Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае.  

        

НЕМНОГО ИЗ БИОГРАФИИ ГАУССА

Иога́нн Карл Фри́дрих Га́усс (1777 — 1855) — немецкий математик, механик, физик, астроном и геодезист. Считается одним из величайших математиков всех времён, «королём математиков».

С именем Гаусса связаны фундаментальные исследования почти во всех основных областях математики: в алгебре, теории чисел, дифференциальной и неевклидовой геометрии, теории вероятностей, а также в механике, астрономии, физике и геодезии.

Гаусс чрезвычайно строго относился к своим печатным трудам и никогда не публиковал даже выдающиеся результаты, если считал свою работу над этой темой незавершённой.  Изучение архива Гаусса показало, что он медлил с публикацией ряда своих открытий, и в результате его опередили другие математики. Вот неполный перечень упущенных им трудов.

  • Неевклидова геометрия
  • Эллиптические функции
  • Метод наименьших квадратов
  • Закон распределения простых чисел

РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДОМ ГАУССА

Метод Гаусса представляет собой специальный алгоритм последовательного исключения неизвестных из уравнений системы. В этом алгоритме обычно различают два этапа:

Первый этап называется прямой ход,

Второй этап – обратный ход.

Цель прямого хода метода Гаусса заключается в приведение матрицы системы к треугольному виду, когда в результате некоторых элементарных преобразований уравнений системы на главной диагонали матрицы системы будут располагаться ненулевые элементы, а все элементы ниже главной диагонали будут равны нулю. В результате наших преобразований должна получаться система, равносильная исходной системе линейных уравнений. Преобразования, которые позволяют свести исходную систему к треугольной, сохраняя равносильность, называются элементарными. Что будем понимать под элементарными преобразованиями?

Определение. Элементарными преобразованиями уравнений системы называют следующие преобразования:

1) перестановка местами двух любых уравнений;

2) умножение обеих частей какого-либо уравнения на любое число, не равное нулю;

3) прибавление к обеим частям одного из уравнений соответствующих частей любого другого уравнения;

4) перестановка (перенумерация) неизвестных системы.

Примем без доказательства, что все перечисленные преобразования приводят к системам, которые равносильны (эквивалентны) исходной системе линейных уравнений.

Удобно в методе Гаусса работать не с самой системой линейных уравнений, а с основой системы – расширенной матрицей.

Элементарным преобразованиям системы соответствуют следующие элементарные преобразования расширенной матрицы:
1. умножение произвольной строки на любое число, отличное от нуля;
2.  прибавление к произвольной строке матрицы любой другой строки матрицы;

3. перестановка местами любых двух строк;

4. перестановка местами любых двух столбцов матрицы системы;

5. транспонирование.

Решение системы уравнений с двумя переменными

Пример 1. Решим систему:

Решение:

 

                         Ответ: (-4; 1)

Решение системы уравнений с тремя переменными

Пример 2. Решим систему:  

Решение:

                

        

                                             

                                                                                                       Ответ: (-3; 8; 0)                         

Пример 3. Решим систему:

Решение:

     

 

                                                                                                                   

        Ответ: (1; 2; 3).

Пробуем применять изученное к решению задач:

Кондитерская фабрика производит продукцию трех видов: торты, пирожные и рулеты. Для их производства используется сырье трех типов: мука 1 кг, сахар 1 кг, молоко 1 л. Нормы расхода каждого из них на одну продукцию и объем расхода сырья на один день заданы таблицей:

Найти ежедневный объем выпуска каждого вида продукции.

Решение. Пусть ежедневно фабрика выпускает х1 тортов, х2 пирожных и х3 рулетов. Составим систему уравнений.

Составим расширенную матрицу системы :

        

Ответ: фабрика выпускает ежедневно 50 тортов, 200 пирожных и 95 рулетов.

Глава II

Проведение обучающего  эксперимента

Одной из целей моего проекта является научить одноклассников решать системы уравнений методом Гаусса, для чего на спецкурсе по математике я показала и рассказала им о своей работе и предложила  совместно решить несколько систем, состоящих из двух строк, методом Гаусса. Ребят заинтересовал данный метод, они с интересом слушали меня, а потом совместно решали системы уравнений данным методом.  Далее ребятам были предложены системы уравнений и заданы следующие вопросы: 

   Ответ:     Ответ:  

    Ответ:          Ответ:  

 Ответ:             Ответ:

   Ответ:

1. Знакомы ли вы с методом Гаусса?

2. Применяете и вы этот метод?

3. Хотите ли вы что б этот метод был в школьной программе ?

4. Будете ли вы решать системы этим методом?

5. Считаете ли вы этот метод простым ?

Ответы на которые вы можете видеть на диаграмме.

        

Заключение.

Метод Гаусса позволяет решать любые системы линейных уравнений и существенно сократить время нахождения решений систем линейных уравнений. Метод Гаусса доступен для его изучения учащимся 7 — 8 классов при решении систем линейных уравнений  

У меня получилось самой освоить данный метод и передать свои знания одноклассникам. Таким образом,  поставленные мною цели и задачи выполнены. И ещё метод Гаусса прост тем, как мне кажется, что для его освоения не требуется много знаний. А также для матриц ограниченного размера метод Гаусса менее трудоёмкий по сравнению с другими методами, поэтому в будущем я планирую его активно применять при решении систем уравнений.

ЛИТЕРАТУРА

  1. Основы высшей математики: Учеб. пособие для вузов/В.С. Шипачев; под ред.акад. А.Н. Тихонова. —5-е изд.,стер. — М. Высш. Шк., 2003. — 279с.
  2. Высшая математика для экономистов: учебное пособие для студентов экономических специальностей высших учебных заведений /Н.Ш Кремер, Б.А. Путко. — М.: Банки и биржи ЮНИТИ, 1997. – 239с.
  3. Математика. Задачник : учеб. Пособие для образоват. Учреждений нач. и сред. Проф. образования / М. И. Башмаков. — 3-е изд., стер. — М.: Издательский центр «Акадения», 2013. —416с.
  4. http://mathprofi.ru/metod_gaussa_dlya_chainikov.html 
  5. https://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%93%D0%B0%D1%83%D1%81%D1%81%D0%B0 
  6. https://ru.wikipedia.org/wiki/%D0%93%D0%B0%D1%83%D1%81%D1%81,_%D0%9A%D0%B0%D1%80%D0%BB_%D0%A4%D1%80%D0%B8%D0%B4%D1%80%D0%B8%D1%85 
  7. https://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D1%82%D1%80%D0%B8%D1%86%D0%B0 

ИСКЛЮЧЕНИЕ ГАУССА: РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ: ПРИМЕРЫ И РЕШЕННЫЕ ЗАДАЧИ: ВЫСШАЯ ШКОЛА

Содержание этой страницы:

Введение

система уравнений (линейная) представляет собой группу (линейных) ar) уравнения с различные неизвестные факторы. Вообще говоря, неизвестные факторы появляются в различных уравнениях.

Уравнение с различными неизвестными множителями связывает их друг с другом.

Решение системы состоит в нахождении значения неизвестных факторов способом, который проверяет все уравнений, составляющих систему.

  • Если существует единственное решение (по одному значению для каждого неизвестного фактора), мы будем говорить, что система Согласованная независимая система (СНГ) .

  • Если существуют различные решения (система имеет бесконечно много решений), мы говорим, что система является Согласованная зависимая система (CDS).

    .

  • Если решения нет, а это произойдет, если их два или несколько уравнений, которые не могут быть проверены одновременно, мы говорим, что это несогласованная система (IS) . Например, следующая система уравнений

    $$ \begin{cases} \begin{array}{lcl} y & = & 0 \\ 2x + y & = & 0 \\ 2x + y & = & 2 \end{array} \end{cases}$ $

    несовместимо, потому что мы получаем решение x = 0 из второго уравнения и из третьего x = 1 .

В этом разделе мы собираемся решать системы, используя метод исключения Гаусса , который состоит в простом выполнении элементарных операций в строке или столбце расширенной матрицы для получить его эшелон формы или его

уменьшенный эшелон форма (Гаусс-Джордан).

Метод разрешения

  1. Мы применяем Gauss-Jordan Метод исключения : мы получаем уменьшенный эшелон строки из из расширенной матрицы систему уравнений, выполняя элементарные операции в строках (или столбцах).

  2. Получив матрицу, мы применяем теорему Руше-Капелли для определения тип системы и получить решение (решения), такие как:

    Пусть A·X = B будет системой m линейных уравнений с n неизвестно множители, m и n натуральные числа (не нуль):

    • AX = B соответствует тогда и только тогда, когда

      $$ ранг(A)=ранг(A|B) $$

    • AX = B является непротиворечивым независимым

      тогда и только тогда, когда

      $$ ранг(A)=n=ранг(A|B) $$

Примечание: Элементарные операции в строках или столбцах позволяют получить системы эквивалентные исходной, но с видом, упрощающим получение решений (если они есть). Также есть более быстрые инструменты для отработки решений в СНГ, вроде правила Крамера.

Система 1

Показать решение


Система 2

Показать решение


Система 3

Показать решение


Система 4

Показать решение


Система 5

Показать решение


Система 6

Показать решение


Система 7

Показать решение


Система 8

Показать решение


Система 9

Показать решение


Система 10

Показать решение


Matesfacil. com J. Llopis имеет лицензию творческий Commons Attribution-NonCommercial 4.0 Международная лицензия.


Исключение Гаусса | математика | Британика

  • Развлечения и поп-культура
  • География и путешествия
  • Здоровье и медицина
  • Образ жизни и социальные вопросы
  • Литература
  • Философия и религия
  • Политика, право и правительство
  • Наука
  • Спорт и отдых
  • Технология
  • Изобразительное искусство
  • Всемирная история
  • В этот день в истории
  • Викторины
  • Подкасты
  • Словарь
  • Биографии
  • Резюме
  • Популярные вопросы
  • Инфографика
  • Демистификация
  • Списки
  • #WTFact
  • Товарищи
  • Галереи изображений
  • Прожектор
  • Форум
  • Один хороший факт
  • Развлечения и поп-культура
  • География и путешествия
  • Здоровье и медицина
  • Образ жизни и социальные вопросы
  • Литература
  • Философия и религия
  • Политика, право и правительство
  • Наука
  • Спорт и отдых
  • Технология
  • Изобразительное искусство
  • Всемирная история
  • Britannica объясняет
    В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы.
  • Britannica Classics
    Посмотрите эти ретро-видео из архивов Encyclopedia Britannica.
  • Demystified Videos
    В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы.
  • #WTFact Видео
    В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти.
  • На этот раз в истории
    В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории.
  • Студенческий портал
    Britannica — это главный ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д.
  • Портал COVID-19
    Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня.
  • 100 женщин
    Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю.

    No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *