Метод гаусса слау калькулятор: Онлайн калькулятор. Решение систем линейных уравнений. Метод Гаусса

Содержание

Схема гаусса

Чтобы сразу же понять суть метода Гаусса, остановите ненадолго взгляд на анимации ниже. Почему одни буквы постепенно исчезают, другие окрашиваются в зелёный цвет, то есть становятся известными, а числа сменяются другими числами? Подсказка: из последнего уравнения совершенно точно известно, чему равна переменная z. В такой системе, называемой трапециевидной, последнее уравнение содержит только одну переменную и её значение можно однозначно найти. Затем значение этой переменной подставляют в предыдущее уравнение обратный ход метода Гаусса , далее — просто обратный ход , из которого находят предыдущую переменную, и так далее. Метод Гаусса, называемый также методом последовательного исключения неизвестных, состоит в следующем.

Поиск данных по Вашему запросу:

Схемы, справочники, даташиты:

Прайс-листы, цены:

Обсуждения, статьи, мануалы:

Дождитесь окончания поиска во всех базах.

По завершению появится ссылка для доступа к найденным материалам.

Содержание:

Метод Гаусса. Схема единственного деления

Метод Гаусса. Метод последовательного исключения неизвестных

Онлайн калькулятор. Решение систем линейных уравнений методом Гаусса.

Метода Гаусса: примеры решения СЛАУ

Метод Гаусса онлайн

Решение СЛАУ методом Гаусса

ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Математика без Ху%!ни. Метод Гаусса. Метод Жордано-Гаусса.

Метод Гаусса.

Схема единственного деления

Метод Гаусса — последовательное исключение неизвестных. Этот метод используется для решения квадратных систем линейных алгебраических уравнений. Хотя уравнения при помощи метода Гаусса решаются легко, но всё же студенты часто не могут найти правильное решение, так как путаются в знаках плюсы и минусы. Поэтому во время решения СЛАУ необходимо быть предельно внимательным и только тогда можно легко, быстро и правильно решить даже самое сложное уравнение.

У систем линейных алгебраических уравнений есть несколько преимуществ: уравнение не обязательно заранее на совместность; можно решать такие системы уравнений, в которых число уравнений не совпадает с количеством неизвестных переменных или определитель основной матрицы равняется нулю; есть возможность при помощи метода Гаусса приводить к результату при сравнительно небольшом количестве вычислительных операций.

Как уже говорилось, метод Гаусса вызывает у студентов некоторые сложности. Однако, если выучить методику и алгоритм решения, сразу же приходит понимание в тонкостях решения. В первых двух случаях СЛАУ называется совместимой, а в третьем случае — несовместима. Если система имеет одно решение, она называется определённой, а если решений больше одного, тогда система называется неопределённой. Метод Крамера и матричный способ не подходят для решения уравнений, если система имеет бесконечное множество решений.

Вот поэтому нам и нужен метод Гаусса, который поможет нам в любом случае найти правильное решение. К элементарным преобразованиям относятся:. Коэффициенты и свободные члены уравнения можно называть его элементами. Система, которую мы написали выше имеет координатную форму. Если её переделать в матричную форму, тогда система будет выглядеть так:. Если к основной матрице добавить в качестве — ого столбца матрицу-столбец свободных членов, тогда получится расширенная матрица систем линейных уравнений.

Как правило, расширенная матрица обозначается буквой , а столбец свободных членов желательно отделить вертикальной линией от остальных столбцов.

То есть, расширенная матрица выглядит так:. Если квадратная матрица равна нулю, она называется вырожденная , а если — матрица невырожденная. Если с системой уравнений:. Мы рассмотрели основные определения и уже понимаем, чем нам поможет метод Гаусса в решении системы. Теперь давайте рассмотрим простую систему уравнений. Для этого возьмём самое обычное уравнение, где и используем решение методом Гаусса:. Из данной матрицы видно, по какому принципу она записана.

Вертикальную черту не обязательно ставить, но просто так удобнее решать систему. В матрице строки можно переставлять местами. Например, в нашей матрице спокойно можно переставить первую и вторую строки:. Если в матрице имеются или появились пропорциональные строки одинаковые , тогда необходимо оставить всего лишь одну строку, а остальные убрать удалить.

Если в ходе преобразований в матрице появилась строка, где находятся одни нули, тогда такую строку тоже нужно удалять. Строку матрицы можно умножать делить на любое число, которое отличное от нуля. Такое действие желательно проделывать, так как в будущем проще преобразовывать матрицу. Сейчас рассмотрим преобразование, которое больше всего вызывает затруднение у студентов.

Для этого возьмём изначальную нашу матрицу:. Теперь ко второй строке прибавляем первую строку, которую умножали на Вот что у нас получается:. Теперь для проверки можно разделить все коэффициенты первой строки на те же и вот что получается:. Первую строку делим на и преобразовалась нижняя строка:. И верхнюю строку поделили на то же самое число :. Как вы можете убедиться, в итоге строка, которую мы прибавляли ни капельки не изменилась, а вот вторая строка поменялась.

Мы расписали в таких подробностях, чтобы было вам понятно, откуда какая цифра взялась. На практике, например, на контрольной или экзамене матрица так подробно не расписывается. Как правило, в задании решение матрицы оформляется так:. После того, как мы рассмотрели простейшие преобразования, в которых на помощь пришёл метод Гаусса, можем вернуться к нашей системе, которую уже разложили по полочкам и пошагово распишем:.

Как мы привели вторую строку в первом столбце к нулю описано выше. Напомним, что первую строку умножали на и вторую строку прибавили к первой , умноженной на. Верхнюю строку делим на и приводим матрицу к ступенчатому виду:. Хотя в учебниках и другой литературе нет такого понятия, как ступенчатый вид.

Как правило, математики такой вид называют трапециевидным или треугольным. Теперь систему нужно решить в обратном направлении, то есть обратным ходом, начиная с последней строки. После находим :. Как мы уже упоминали, невырожденная матрица бывает тогда, когда. Разберём систему уравнений невырожденной матрицы, где уравнений по количеству столько же, сколько и неизвестных. Эту систему уравнений решим другим способом. Для начала нужно решить первое уравнение системы относительно неизвестной переменной.

Далее подставим полученное выражение сначала во второе уравнение, а затем в третье, чтобы исключить из них эту переменную. Теперь переходим ко второму уравнению системы относительно и полученный результат подставим в третье уравнение. . Это нужно для того, чтобы исключить неизвестную переменную :.

Из последнего, третьего уравнения мы видим, что. Из второго уравнения находим. И последнее, находим первое уравнение. Итак, мы нашли все три неизвестных при помощи последовательного исключения. Такой процесс называют — прямой ход метода Гаусса. Когда последовательно находятся неизвестные переменные, начиная с последнего уравнения, называется обратным ходом метода Гаусса. Когда выражается через и в первом уравнении, а затем подставляется полученное выражение во второе или третье уравнения, тогда, чтобы привести в к такому же результату, необходимо проделать такие действия:.

И действительно, благодаря такой процедуре у нас есть возможность исключать неизвестную переменную со второго и третьего уравнения системы:. Возникают нюансы с исключением неизвестных переменных тогда, когда в уравнении системы нет каких-либо неизвестных переменных. Рассмотрим такую систему:. В этой системе в первом уравнении нет переменной и поэтому у нас нет возможности решить первое уравнение системы относительно , чтобы исключить данную переменную из остальных уравнений.

В таком случае выход есть. Нужно всего лишь уравнения переставить местами. Так как мы описываем уравнения системы, в которых определитель основных матриц отличен от нуля, тогда всегда есть такое уравнение, в котором есть необходимая нам переменная и это уравнение мы можем поставить туда, куда нам нужно. В примере, который мы рассматриваем, достаточно всего лишь поменять местами первое и второе уравнение. Теперь мы можем спокойно разрешить первое уравнение относительно переменной и убрать исключить из остальных уравнений в системе.

Вот и весь принцип работы с такими, на первый взгляд, сложными системами. Метод Гаусса помогает решать системы уравнений, у которых основная матрица прямоугольная или квадратная, но основная вырожденная матрица может совсем не иметь решений, иметь бесконечное множество решений или иметь всего лишь одно единственное решение.

Рассмотрим, как при помощи метода Гаусса устанавливается совместность или несовместность систем линейных уравнений. В случае, если есть совместность определим все решения или одно решение.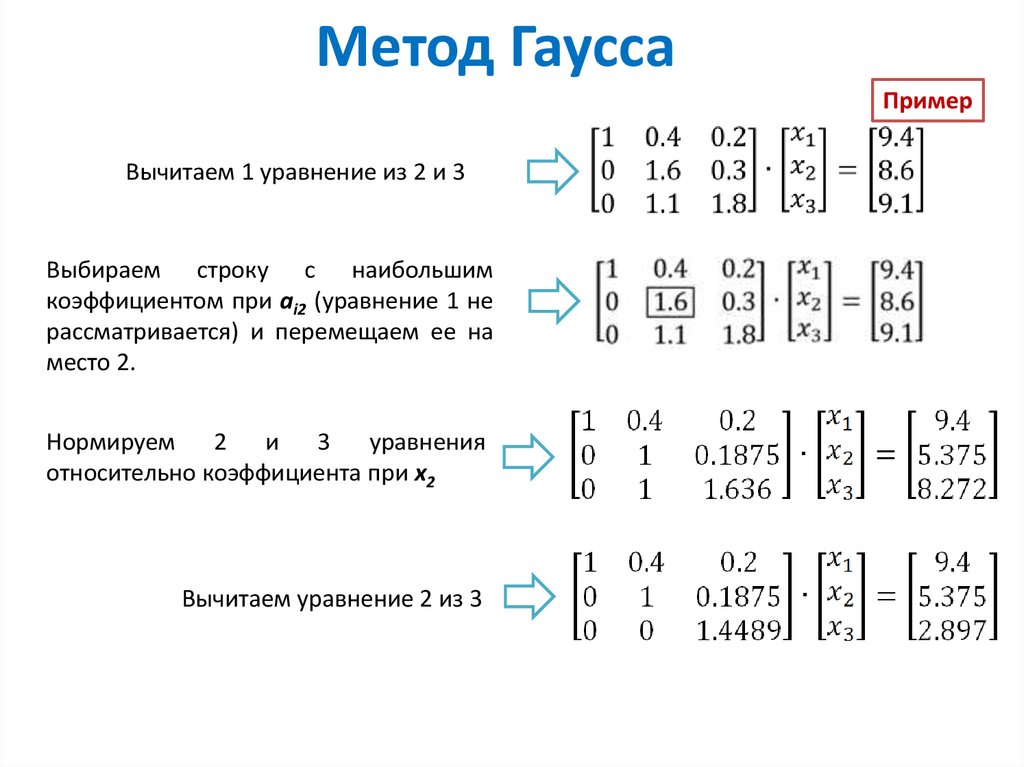

В принципе, исключать неизвестные переменные можно точно так, как описано выше. Однако, есть некоторые непонятные ситуации, которые могут возникнуть в ходе решения:.

На некоторых этапах в момент исключения неизвестных переменных некоторые уравнения могут обратиться в тождества. В данном случае такие уравнения лишние в системе и их можно смело полностью убирать, а затем продолжать решать уравнение методом Гаусса. Как видим, второе уравнение. Соответственно, данное уравнение мы можем из системы удалить, так как оно без надобности. Дальше можно продолжать решение системы линейных алгебраических уравнений уравнений традиционным методом Гаусса.

При решении уравнений прямым ходом методом Гаусса могут принять не только одно, но и несколько уравнений такой вид: , где — число, которое отличное от нуля. Это говорит о том, что такое уравнение никогда не сможет превратиться в тождество даже при любых значениях неизвестных переменных.

То есть, можно выразить по-другому. Рассмотрим на примере:. Для начала необходимо исключить неизвестную переменную из всех уравнений данной системы, начиная со второго уравнения. Для этого нужно прибавить к левой и правой частям второго, третьего, четвёртого уравнения части левую и правую первого уравнения, которые соответственно, умножаются на -1 , -2 , В третьем уравнении получилось равенство.

Оно не подходит ни для каких значений неизвестных переменных , и , и поэтому, у данной системы нет решений. То есть, говорится, что система не имеет решений. Допустим, что при выполнении прямого хода методом Гаусса нам нужно исключить неизвестную переменную , и ранее, на каком-то этапе у нас уже исключалась вместе с переменной. Как вы поступите в таком случае? При таком положении нам нужно перейти к исключению переменной. Вы наверное уже обратили внимание, что вместе с исключились и.

Поэтому решение методом Гаусса продолжаем исключением переменной из всех уравнений системы, а начнём мы с третьего уравнения:. Чтобы завершить уравнение прямым ходом метода Гаусса, необходимо исключить последнюю неизвестную переменную из последнего уравнения:.

Метод Гаусса. Метод последовательного исключения неизвестных

Пусть дана система 5. Для ее решения нужно выполнить следующие действия. Выяснить, совместна система или нет. Процесс решения завершен. Процесс решения продолжается. Для этого при помощи элементарных преобразований над строками добиваемся того, чтобы в каждом столбце, входящем в базисный минор, все элементы были равны нулю, за исключением одного, равного единице.

Метод Гаусса прекрасно подходит для решения систем линейных алгебраических уравнений (СЛАУ). Он обладает рядом преимуществ по сравнению с.

Онлайн калькулятор. Решение систем линейных уравнений методом Гаусса.

Сегодня разбираемся с методом Гаусса для решения систем линейных алгебраических уравнений. О том, что это за системы, можно почитать в предыдущей статье, посвященной решению тех же СЛАУ методом Крамера. Метод Гаусса не требует каких-то специфических знаний, нужна лишь внимательность и последовательность. Несмотря на то что с точки зрения математики для его применения хватит и школьной подготовки, у студентов освоение этого метода часто вызывает сложности. В этой статье попробуем свести их на нет! В отличие от рассмотренного ранее метода Крамера , он подходит не только для систем, имеющих единственное решение, но и для систем, у которых решений бесконечное множество. Здесь возможны три варианта. Итак, у нас есть система пусть у нее будет одно решение , и мы собираемся решать ее методом Гаусса. Как это работает?

Метода Гаусса: примеры решения СЛАУ

Наиболее распространённым приёмом решения системы линейных уравнений является метод Гаусса или метод последовательного исключения неизвестных. Выбираем ведущий элемент. Поделив первое уравнение на , получаем. Исключаем переменную из всех последующих уравнений, начиная со второго, путём вычитания уравнения 2, умноженного на коэффициент, стоящий при в соответствующем уравнении. Выбираем ведущий элемент во втором уравнении.

В линейной алгебре рассматриваются четыре класса основных задач: решение систем линейных алгебраических уравнений СЛАУ , вычисление определителей, нахождение обратных матриц, определение собственных значений и собственных векторов матриц. Все эти задачи имеют важное прикладное значение при решении различных проблем науки и техники.

Метод Гаусса онлайн

Придумано много различных видоизменений схемы Гаусса, дающих те или иные преимущества. Приведем одну такую схему. Рассмотрим сначала систему четырех уравнений общего вида: Исходные данные, промежуточные и окончательные результаты будем записывать в следующую схему: Верхнюю половину схемы мы отводим для коэффициентов и свободных членов исходной системы, а в нижней половине будут помещаться промежуточные и окончательные результаты. Верхний индекс показывает порядок получения промежуточных и окончательных результатов. Величины просто совпадают с соответствующими величинам и выписываются здесь лишь для удобства пользования схемой. Величины вычисляем по формулам При этом уравнение эквивалентно первому уравнению исходной системы.

Решение СЛАУ методом Гаусса

Целью данной лабораторной работы является разработка параллельной программы, которая выполняет решение системы линейных уравнений методом Гаусса. Выполнение лабораторной работы включает:. Системы линейных уравнений возникают при решении многих прикладных задач. Матрицы коэффициентов систем линейных уравнений могут иметь различные структуру и свойства. Мы будем полагать, что решаемая система имеет плотную матрицу высокого порядка. Линейная система n уравнений с n неизвестными x0, x1, …, xn-1 может быть представлена в виде:. Под задачей решения системы линейных уравнений для заданных матрицы А и вектора b обычно понимается нахождение значения вектора неизвестных x , при котором выполняются все уравнения системы.

Метод Гаусса — это метод, который применяется при решении систем Дальнейшие преобразования происходит по такой схеме: все элементы во.

Войдите , пожалуйста. Хабр Geektimes Тостер Мой круг Фрилансим. Войти Регистрация.

Содержание [скрыть] [показать]. Дана система линейных алгебраических уравнений СЛАУ с неизвестными. Требуется решить эту систему: определить, сколько решений она имеет ни одного, одно или бесконечно много , а если она имеет хотя бы одно решение, то найти любое из них.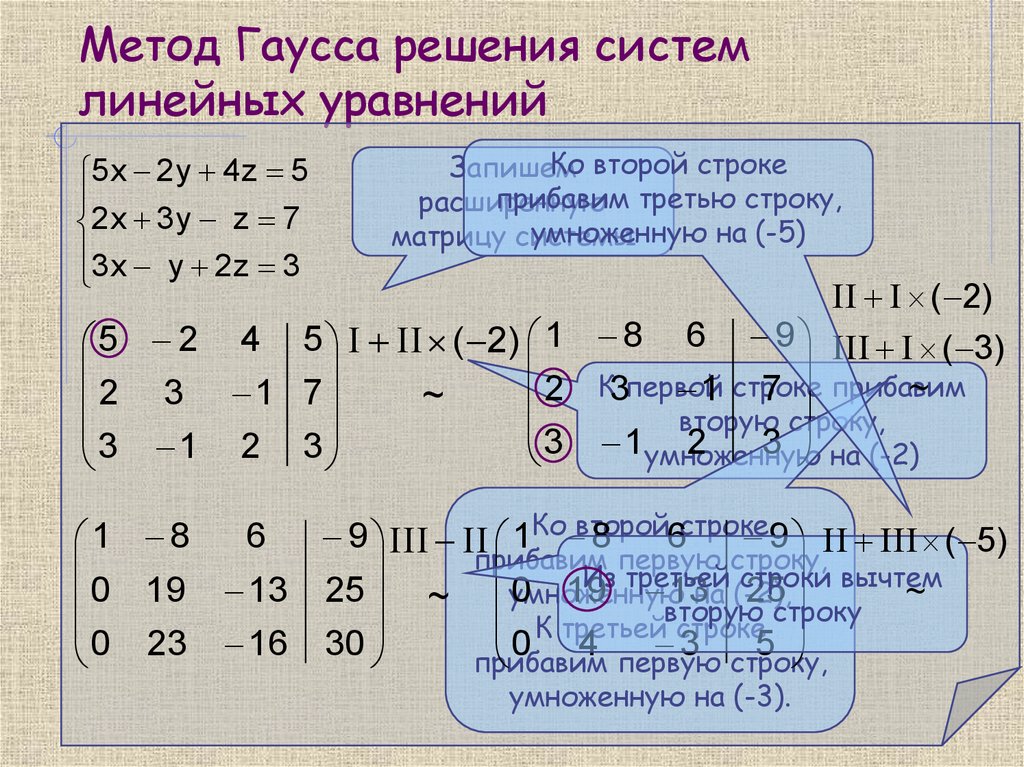 Формально задача ставится следующим образом: решить систему:.

Используя этот онлайн калькулятор для решения систем линейных уравнений СЛУ методом Гаусса , вы сможете очень просто и быстро найти решение системы. Воспользовавшись онлайн калькулятором для решения систем линейных уравнений методом Гаусса, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на решения систем линейных уравнений, а также закрепить пройденный материал.

Вопрос возник по этой заметке , где реализованы прямые и итерационные методы решения систем линейных алгебраических уравнений СЛАУ в Mathcad. Для сходимости как метода Якоби, так и модификации Гаусса-Зейделя, следует приводить матрицу к виду с диагональным преобладанием , это можно всегда сделать, применяя элементарные преобразования над строками и столбцами матрицы. Приложенный документ содержит модификацию итерационного метода Якоби, известную как метод Гаусса-Зейделя и показывает, как привести матрицу к виду с диагональным преобладанием : Исходя из определения , достаточно, чтобы модуль элемента главной диагонали был больше остальных элементов своей строки. Поэтому для исходной матрицы, показанной на скрине, мы поменяли местами первую и вторую строки, а затем вычли из третьей строки вторую бывшую первую. То же самое не забыли сделать для вектора правой части b , на практике лучше работать с расширенной матрицей системы, в которую последним столбцом дописан вектор правой части b.

Он обладает рядом преимуществ по сравнению с другими методами:. Далее опишем алгоритм метода Гаусса для простейшего случая, то есть, для систем линейных алгебраических уравнений, количество уравнений в которых совпадает с количеством неизвестных переменных и определитель основной матрицы системы не равен нулю. При решении таких систем уравнений наиболее отчетливо видна суть метода Гаусса, которая заключается в последовательном исключении неизвестных переменных. Поэтому метод Гаусса также называют методом последовательного исключения неизвестных.

Метод Гаусса. Примеры

Метод Гаусса заключается в последовательном исключении переменных и преобразовании системы линейных алгебраических уравнений

к треугольному виду

Предположим, что в системе коэффициент . Если это условие не выполняется, то на первое место переносим уравнение, которое ее удовлетворяет. С помощью первого уравнения исключим из остальных уравнений.

Для этого делят первую строчку на , обозначим

Дальше второй строки вычитаем первую строку, умноженную на ;от третьего первую строчку, умноженный на ; и так далее до последней строки. Получим таблицу коэффициентов:

Для неизвестных имеем систему уравнений. Выполняя, как и раньше, исключим из всех уравнений, начиная с третьего. Для этого сначала разделим вторую строчку на .

Если коэффициент , то переставим уравнения так, чтобы выполнялось условие .

Обозначив

от третьей строки вычтем вторую строчку, умноженный на ;

от четвертой строки вычтем вторую строчку, умноженный на и т.д. Получим таблицу коэффициентов:

Продолжая процесс исключения неизвестных получим таблицу:

Таблица коэффициентов при неизвестных сводится к треугольному виду. Все главной диагонали элементы . Запишем соответствующую систему уравнений:

Переход от первой системы уравнений до последней называется прямым ходом метода Гаусса. Обратный ход метода Гаусса начинается с последней системы уравнений. Ее решают с конца до начала. Из последнего уравнения находят . Подставив это значение в предпоследнее — находят и т.д. Из первого уравнения находят .

Если система уравнений с неизвестными имеет единственное решение, то эта система всегда может быть преобразована к треугольному виду. Для студентов не всегда требуют, чтобы диагональные элементы были равны единице. Достаточно просто свести систему линейных уравнений к верхней треугольной.

———————————————

Пример 1.

Дана система трех линейных уравнений с тремя неизвестными. Решить систему методом Гаусса.

Решение.

Исключим неизвестную из второго и третьего уравнения. Для этого от них вычтем первое умноженное на

Видим, что наше уравнение в таком виде можно решать обратным ходом метода Гаусса. Для этого из последнего уравнения выразим

Подставим полученное значение в предыдущее уравнение и найдем

Из первого уравнения находим

Решение данной системы равен

——————————————

В случаях систем больших размеров, а также для удобства, часто на практике используют другую схему решения. Вместо преобразований над системой выполняют соответствующие преобразования над матрицей, составленной из коэффициентов при неизвестных и столбца из свободных членов, который для удобства выделяют вертикальной линией. Такую матрицу называют расширенной матрицей системы.