Методом интервалов решите неравенство: Метод интервалов: примеры, решения

Метод интервалов — материалы для подготовки к ЕГЭ по Математике

Метод интервалов – простой способ решения дробно-рациональных неравенств. Так называются неравенства, содержащие рациональные (или дробно-рациональные) выражения, зависящие от переменной.

1. Рассмотрим, например, такое неравенство

Метод интервалов позволяет решить его за пару минут.

В левой части этого неравенства – дробно-рациональная функция. Рациональная, потому что не содержит ни корней, ни синусов, ни логарифмов – только рациональные выражения. В правой – нуль.

Метод интервалов основан на следующем свойстве дробно-рациональной функции.

Дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует.

Найдем нули функции в левой части нашего неравенства. Для этого разложим числитель на множители. (Если вы не помните, что такое нули функции и знак функции на промежутке – смотрите статью «Исследование графика функции»).

Напомним, как раскладывается на множители квадратный трехчлен, то есть выражение вида .

, где и — корни квадратного уравнения .

Получим:

Рисуем ось и расставляем точки, в которых числитель и знаменатель обращаются в нуль.

Нули знаменателя и — выколотые точки, так как в этих точках функция в левой части неравенства не определена (на нуль делить нельзя). Нули числителя и — закрашены, так как неравенство нестрогое. При и наше неравенство выполняется, так как обе его части равны нулю.

Эти точки разбивают ось на промежутков.

Определим знак дробно-рациональной функции в левой части нашего неравенства на каждом из этих промежутков. Мы помним, что

дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Это значит, что на каждом из промежутков между точками, где числитель или знаменатель обращаются в нуль, знак выражения в левой части неравенства будет постоянным — либо «плюс», либо «минус».

И поэтому для определения знака функции на каждом таком промежутке мы берем любую точку, принадлежащую этому промежутку. Ту, которая нам удобна.
. Возьмем, например, и проверим знак выражения в левой части неравенства. Каждая из «скобок» отрицательная. Левая часть имеет знак .

$\left( + \right)$

Следующий промежуток: . Проверим знак при . Получаем, что левая часть поменяла знак на .

$\left( - \right)$

. Возьмем . При выражение положительно — следовательно, оно положительно на всем промежутке от до .

При левая часть неравенства отрицательна.

1<x<7

И, наконец, . Подставим и проверим знак выражения в левой части неравенства. Каждая «скобочка» положительна. Следовательно, левая часть имеет знак .

$\left( + \right)$

Мы нашли, на каких промежутках выражение положительно. Осталось записать ответ:

Ответ: .

Обратите внимание: знаки на промежутках чередуются. Это произошло потому, что при переходе через каждую точку ровно один из линейных множителей поменял знак, а остальные сохранили его неизменным

Мы видим, что метод интервалов очень прост. Чтобы решить дробно-рациональное неравенство методом интервалов, приводим его к виду:

, или , или , или .

(в левой части — дробно-рациональная функция, в правой — нуль).

Затем — отмечаем на числовой прямой точки, в которых числитель или знаменатель обращаются в нуль.
Эти точки разбивают всю числовую прямую на промежутки, на каждом из которых дробно-рациональная функция сохраняет свой знак.
Остается только выяснить ее знак на каждом промежутке.
Мы делаем это, проверяя знак выражения в любой точке, принадлежащей данному промежутку. После этого — записываем ответ. Вот и всё.

Но возникает вопрос: всегда ли знаки чередуются? Нет, не всегда! Надо быть внимательным и не расставлять знаки механически и бездумно.

Ты нашел то, что искал? Поделись с друзьями!

2. Рассмотрим еще одно неравенство.

Снова расставляем точки на оси . Точки и — выколотые, поскольку это нули знаменателя. Точка — тоже выколота, поскольку неравенство строгое.

При числитель положителен, оба множителя в знаменателе отрицательны. Это легко проверить, взяв любое число с данного промежутка, например, . Левая часть имеет знак :

$\left( + \right)$

При числитель положителен; первый множитель в знаменателе положителен, второй множитель отрицателен. Левая часть имеет знак :

$\left( - \right)$

При ситуация та же! Числитель положителен, первый множитель в знаменателе положителен, второй отрицателен. Левая часть имеет знак :

$\left( - \right)$

Наконец, при все множители положительны, и левая часть имеет знак :
$\left( + \right)$

Ответ: .

Почему нарушилось чередование знаков? Потому что при переходе через точку «ответственный» за неё множитель не изменил знак. Следовательно, не изменила знак и вся левая часть нашего неравенства.

Вывод: если линейный множитель стоит в чётной степени (например, в квадрате), то при переходе через точку знак выражения в левой части не меняется. В случае нечётной степени знак, разумеется, меняется.

3. Рассмотрим более сложный случай. От предыдущего отличается тем, что неравенство нестрогое:

Левая часть та же, что и в предыдущей задаче. Та же будет и картина знаков:

$\genfrac{}{}{}{0}{\displaystyle \left( x-2 \right)^2}{\displaystyle \left( x-1 \right)\left( x-3 \right)} \geqslant 0$

Может, и ответ будет тем же? Нет! Добавляется решение Это происходит потому, что при и левая, и правая части неравенства равны нулю — следовательно, эта точка является решением.

Ответ: .

В задаче на ЕГЭ по математике такая ситуация встречается часто. Здесь абитуриенты попадают в ловушку и теряют баллы. Будьте внимательны!

4. Что делать, если числитель или знаменатель не удается разложить на линейные множители? Рассмотрим такое неравенство:

Квадратный трехчлен на множители разложить нельзя: дискриминант отрицателен, корней нет. Но ведь это и хорошо! Это значит, что знак выражения при всех одинаков, а конкретно — положителен. Подробнее об этом можно прочитать в статье о свойствах квадратичной функции.

И теперь мы можем поделить обе части нашего неравенства на величину , положительную при всех . Придём к равносильному неравенству:

— которое легко решается методом интервалов.

Обратите внимание — мы поделили обе части неравенства на величину, о которой точно знали, что она положительна. Конечно, в общем случае не стоит умножать или делить неравенство на переменную величину, знак которой неизвестен.

5. Рассмотрим еще одно неравенство, на вид совсем простое:

Так и хочется умножить его на . Но мы уже умные, и не будем этого делать. Ведь может быть как положительным, так и отрицательным. А мы знаем, что если обе части неравенства умножить на отрицательную величину — знак неравенства меняется.

Мы поступим по другому — соберём всё в одной части и приведём к общему знаменателю. В правой части останется нуль:

И после этого — применим метод интервалов.

Содержание

Метод интервалов, решение неравенств

Решение неравенств

Метод интервалов

Перенос знаков

Выбор точек

Система и совокупность

Точка знакопостоянства

Что нельзя делать в неравенстве, даже под пытками:

1) Домножать на знаменатель.

2) Умножать/делить на отрицательное число, не меняя знак.

3) Убирать бездумно логарифм или основание.

Начнем с простого:

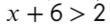
Линейные уравнения решаются обычным переносом. Икс в одной части оставим, а числа перенесем в другую:

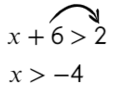
А само значение −4 нам подходит?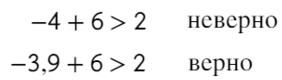

Нет, поэтому ставим круглые скобочки ()

Ответ: x ∈ ( −4; +oo).

Разберемся со скобками:

Когда мы включаем точку (корень числителя), или стоят знаки нестрогие (≥, ≤), ставим «[ ]» — квадратные скобки. Если не включаем (корень знаменателя), или знак строгий (>, <), скобки круглые «( )».

Если же возьмем пример, где придется делить или умножать на отрицательное число, то знак поменяется:

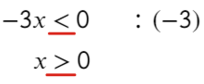Ответ: x ∈ ( 0; +oo).

Следующий пример уже с дробью:

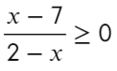
Приравняем числитель к нулю и скажем, что знаменатель не равен нулю:

к.ч. (корни числителя)

к.з. (корни знаменателя)

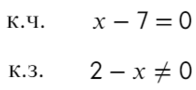
Расставляем корни числителя и знаменателя на одной прямой (сколько решаем неравенств, столько же чертим прямых). Попробуем подставить х = 0, чтобы определить знаки:

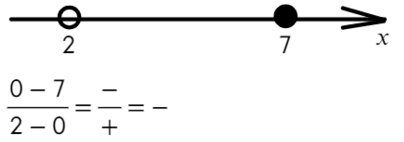
Там, где «0» (перед двойкой), ставим знак «−», а дальше знаки чередуем:

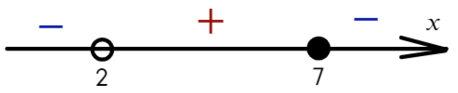
Из-за того, что знаком неравенства был «≥», нам подходят промежутки со знаком «+» и закрашенная точка:

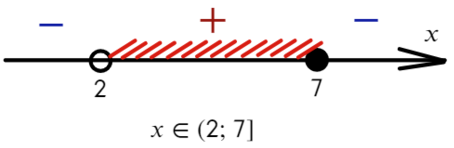
Когда мы включаем точку (корень числителя), или стоят знаки (≥, ≤), ставим «[ ]» — квадратные скобки. Если не включаем (корень знаменателя), или знак строгий (>, <), скобки круглые «( )».

Ответ: x ∈ (2; 7].

Данный пример можно решить по-другому. Подумаем, когда дробь больше нуля? Конечно, когда числитель и знаменатель — положительные значения или когда оба отрицательные. Поэтому данное неравенство можно разбить на две системы в совокупности:

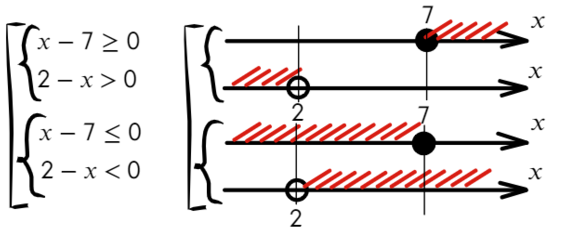
Отметим на прямой решение каждого неравенства.

Решением системы «{» является тот участок, который подходит обоим неравенствам.

Решением совокупности «[» является тот участок, который включен хотя бы в одно неравенство.

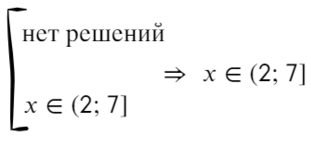
Мой любимый пример:

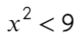
Покажу мастер-класс, как делать не надо. Дома не повторять!

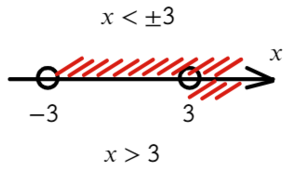
А теперь через метод интервалов разберемся, как сделать правильно:

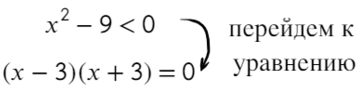
Там, где ноль, ставим знак «−», рисуем прямую и отмечаем корни каждой скобки. А дальше чередуем:

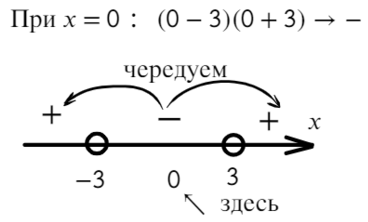
В данном неравенстве знак меньше, поэтому записываем в ответ промежуток, где знак «−».

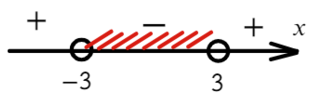
Ответ: x ∈ (−3; 3).

Перейдем к квадратному уравнению:

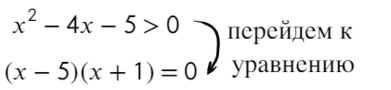
Разложим на множители и подставим x = 10, чтобы определить знак:

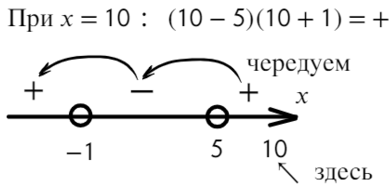
Нам требуются положительные значения:

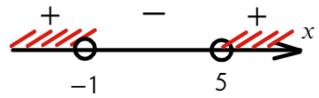
Второй способ разложить на множители:

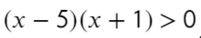
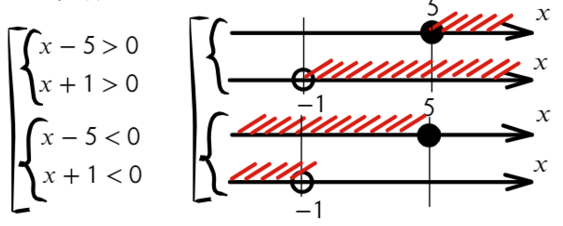
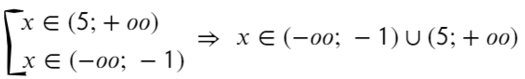
Ответ: x ∈ (−oo; −1) ∪ (5; +oo).

А теперь простой, но крайне показательный пример:

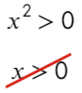
Убирать квадрат ни в коем случае нельзя. Простенький контрпример:

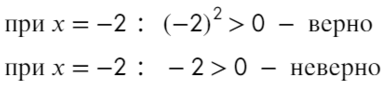
Надеюсь, убедил. Вместо знака больше поставим знак равно и попробуем решить методом интервалов:

Если корень повторяется четное количество раз, то в этой точке знак меняться не будет. Отмечать будем такую точку восклицательным знаком (а внутри него ±, чуть ниже объясню, зачем это).

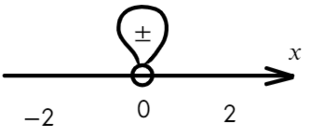
Проверим это:

В данном неравенстве знак больше, тогда отметим те промежутки, где стоит знак «+».

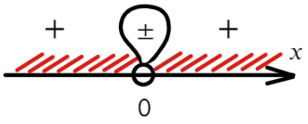
Только точка «0» не подходит, 0 > 0 — неверно!

Ответ: x ∈ R \ {0} или x ∈ (−oo; 0) ∪ (0; +oo).

Переходим на новый уровень:

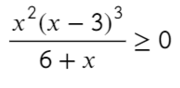
Все говорят, что домножать на знаменатель нельзя, а я говорю, что буду! (joke)

По методу координат найдем корни числителя и знаменателя:

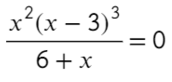
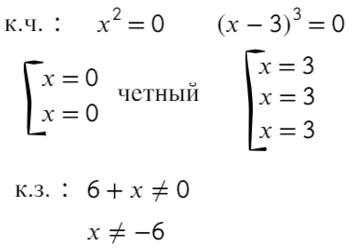
Отметим все корни на одной прямой (сколько неравенств, столько же и прямых). Ноль — корень четной кратности, над ним рисуем восклицательный знак! Если это корень числителя, то точка будет закрашена, если знаменателя — выколота (на ноль делить нельзя).

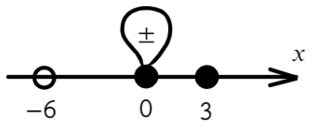
Требуется найти промежутки, где выражение больше или равно нулю. Нам подойдут все «промежутки», где знак плюс. Для этого подставим значение x = 1 и с промежутка [0; 3] начнем расставлять знаки. Там же находится единица.

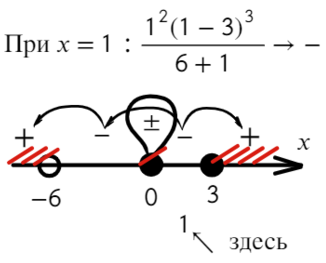
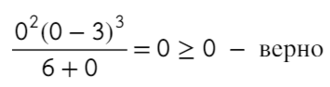
Вот для чего ставят в восклицательном знаке ±: чтобы не потерять отдельные точки, в данном случае 0.

Ответ: (−oo; − 6) ∪ {0} ∪ [ 3; +oo).

Дальше интереснее:

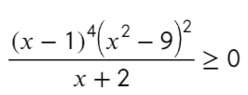
По той же схеме корни числителя и знаменателя:

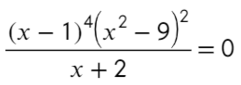
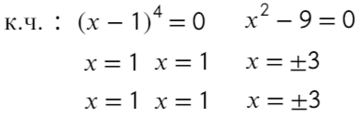
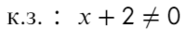
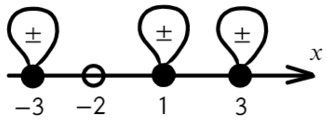
Определим знак при x = 10 и расставим знаки с промежутка, где присутствует 10:

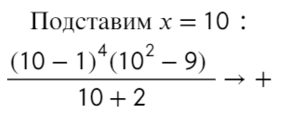
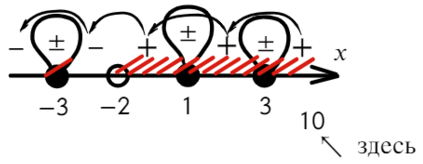
Все точки от − 2 закрашены, значит эти промежутки можно объединить в один.

Ответ: {−3} ∪ (−2; +oo).

Закрепляем последовательность:

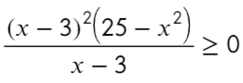
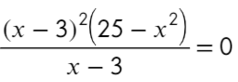
Точка x = 3 встречается 3 раза (2 раза в числителе и 1 раз в знаменателе), знак через нее меняться будет! А также эта точка будет выколота, проверь это, подставив в уравнение x = 3. На ноль же делить нельзя?

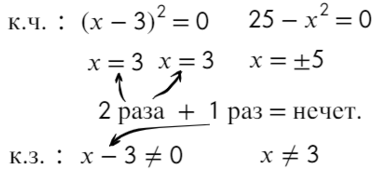
Подставим x = 10 и расставим знаки:

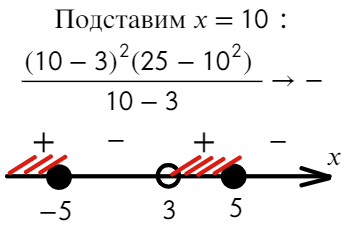
Ответ: [ −oo; −5) ∪ [ 3; 5).

Все скользкие моменты разобрали, стало понятнее?

Резюме:

Если знак строгий (>, <), все точки выколотые (в круглые скобки).
Если знак нестрогий (≥, ≤), корни числителя закрашенные, точки знаменателя выколотые [в квадратные скобки].
Если корень является решением уравнения четное кол-во раз (2, 4, 6, 8), то в этой точке знак меняться не будет.
Отдельная точка записывается {в фигурных скобках}.

Нашел ошибку/опечатку — напиши.

Группа с полезной информацией и легким математическим юмором.

Метод интервалов. Учебник по ЕГЭ и ГИА

Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».

Этот метод тебе просто необходимо понять и знать его как свои пять пальцев! Хотя бы потому, что он применяется для решения рациональных неравенств и потому, что, зная этот метод как следует, решать эти неравенства на удивление просто. Чуть позже раскрою тебе пару секретов, как сэкономить время на решении этих неравенств. Ну что, заинтриговал? Тогда поехали!

Суть метода в разложении неравенства на множители (повтори тему «Разложение на множители») и определении ОДЗ и знака сомножителей, сейчас все поясню. Возьмем самый простенький пример: .

Области допустимых значений (ОДЗ) здесь писать не надо, поскольку деления на переменную нет, и радикалов (корней) здесь не наблюдается. На множители здесь все и так разложено за нас. Но не расслабляйся, это все, чтоб напомнить азы и понять суть!

Допустим, ты не знаешь метода интервалов, как бы ты стал решать это неравенство? Подойди логически и опирайся на то, что уже знаешь. Во-первых, левая часть будет больше нуля если оба выражения в скобках либо больше нуля, либо меньше нуля, т.к. «плюс» на «плюс» дает «плюс» и «минус» на «минус» дает «плюс», так? А если знаки у выражений в скобках разные, то в итоге левая часть будет меньше нуля. А что же нам нужно, чтоб узнать те значения , при которых выражения в скобках будут отрицательными или положительными?

Нам нужно решить уравнение, оно точно такое же как неравенство, только вместо знака будет знак , корни этого уравнения и позволят определить те пограничные значения, при отступлении от которых множители и будут больше или меньше нуля.

А теперь сами интервалы. Что такое интервал? Это некий промежуток числовой прямой, то есть все возможные числа, заключенные между двумя какими-то числами – концами интервала. Эти промежуткив голове представить не так просто, поэтому интервалы принято рисовать, сейчас научу.

Рисуем ось , на ней располагается весь числовой ряд от и до . На ось наносятся точки, те самые так называемые нули функции, значения, при которых выражение равняется нулю. Эти точки «выкалываются» что означает, что они не относятся к числу тех значений, при которых неравенство верно. В данном случае, они выкалываются т.к. знак в неравенстве а не, то есть строго больше а не больше или равно.

Хочу сказать, что ноль отмечать не обязательно, он без кружочков тут, а так, для понимания и ориентации по оси. Ладно, ось нарисовали, точки (точнее кружочки) поставили, дальше что, как мне это поможет в решении? – спросишь ты. Теперь просто возьми значение для икса из интервалов по порядку и подставь их в свое неравенство и смотри, какой знак будет в результате умножения.

Короче, просто берем например, подставляем его сюда , получится , а , значит на всем промежутке (на всем интервале) от до , из которого мы брали , неравенство будет справедливо. Иными словами если икс от до , то неравенство верно.

То же самое делаем и с интервалом от до , берем или , например, подставляем в , определяем знак, знак будет «минус». И так же делаем с последим, третьим интервалом от до , где знак получится «плюс». Такая куча текста вышла, а наглядности мало, правда?

Взгляни еще раз на неравенство .

Теперь все на ту же ось наносим еще и знаки, которые получатся в результате. Ломаной линией, в моем примере,обозначаем положительные и отрицательные участки оси.

Смотри на неравенство – на рисунок, опять на неравенство – и снова на рисунок, что-нибудь понятно? Постарайся теперь сказать на каких промежутках икса, неравенство будет верно. Правильно, от до неравенство будет справедливо и от до , а на промежутке от до неравенство нуля и нас этот промежуток мало интересует, ведь у нас в неравенстве знак стоит.

Ну, раз ты с этим разобрался, то дело за малым – записать ответ! В ответ пишем те промежутки, при которых левая часть больше нуля, , что читается, как икс принадлежит промежутку от минус бесконечности до минус одного и от двух до плюс бесконечности. Стоит пояснить, что круглые скобки означают, что значения, которыми ограничен интервал не являются решениями неравенства, то есть они не включены в ответ, а лишь говорят о том, что до , например, но не есть решение.

Теперь пример, в котором тебе придется не только интервал рисовать:

Как думаешь, что надо сделать, прежде, чем точки на ось наносить? Ага, на множители разложить:

Рисуем интервалы и расставляем знаки, заметь точки у нас выколотые, потому, что знак строго меньше нуля:

Пришло время раскрыть тебе один секрет, который я обещал еще в начале этой темы! А что если я скажу тебе, что можно не подставлять значения из каждого интервала для определения знака, а можно определить знак в одном из интервалов, а в остальных просто чередовать знаки!

Таким образом, мы сэкономили немного времени на проставлении знаков – думаю, это выигранное время на ЕГЭ не помешает!

Пишем ответ:

Теперь рассмотрим пример дробно-рационального неравенства – неравенство, обе части которого являются рациональными выражениями (см. «Рациональные уравнения»).

Что можешь сказать про это неравенство? А ты взгляни на него как на дробно-рациональное уравнение, что делаем в первую очередь? Сразу видим, что корней нет, значит точно рациональное, но тут же дробь, да еще и с неизвестным в знаменателе!

Верно, ОДЗ надо!

ОДЗ

Так, дальше поехали, здесь все множители кроме одного имеют переменную первой степени, но есть множитель , где икс имеет вторую степень. Обычно знак у нас менялся после перехода через одну из точек, в которой левая часть неравенства принимает нулевое значение, для чего мы определяли чему должен быть равен икс в каждом множителе. А тут , так оно же всегда положительно, т.к. любое число в квадрате > нуля и положительное слагаемое .

Как думаешь, повлияет на значение неравенства ? Правильно – не повлияет! Смело можем поделить на обе части неравенства и тем самым убрать этот множитель, чтоб глаза не мозолил.

Имеем:

пришло время интервалы рисовать, для этого нужно определить те пограничные значения, при отступлении от которых множители и будут больше и меньше нуля. Но обрати внимание, что здесь знак , значит точку, в которой левая часть неравенства принимает нулевое значение, выкалывать не будем, она ведь входит в число решений, такая точка у нас одна, это точка, где икс равен одному. А точку, где знаменатель равен нулю, закрасим? – Конечно, нет!

Знаменатель не должен быть равен нулю, поэтому интервал будет выглядеть так:

По этой схеме ты уже без труда сможешь написать ответ, скажу только, что теперь у тебя в распоряжении есть новый тип скобки – квадратный! Вот такая скобка

[ говорит, что значение входит в интервал решений, т.е. является частью ответа, эта скобка соответствует закрашенной (не выколотой) точке на оси.

Вот, – у тебя такой же ответ получился?

Чем дальше в лес, тем больше дров! Лови еще примерчик!

Раскладываем на множители и переносим все в одну сторону, нам ведь справа только ноль надо оставить, чтоб с ним сравнивать:

Обращаю твое внимание, что в последнем преобразовании, дабы получить в числителе как и в знаменателе, умножаю обе части неравенства на . Помни, что при умножении обеих частей неравенства на , знак неравенства меняется на противоположный!!!

Пишем ОДЗ:

, иначе знаменатель обратится в ноль, а на ноль, как ты помнишь, делить нельзя!

Согласись, в получившемся неравенства так и подмывает сократить в числителе и знаменателе! Этого делать нельзя, можно потерять часть решений или ОДЗ!

Теперь попробуй сам нанести точки на ось. Замечу лишь, что при нанесении точек надо обратить внимание на то, что точка со значением , которая исходя из знака , казалось бы, должна быть нанесена на ось как закрашенная, закрашенной не будет, она будет выколота! Почему спросишь ты? А ты ОДЗ вспомни, не собираешься же ты на ноль делить так?

Запомни, ОДЗ превыше всего! Если все неравенство и знаки равенства говорят одно, а ОДЗ – другое, доверяй ОДЗ, великой и могучей! Ну что, ты построил интервалы, я уверен, что ты воспользовался моей подсказкой по поводу чередования и у тебя получилось вот так (см. рисунок ниже) А теперь зачеркни, и не повторяй эту ошибку больше! Какую ошибку? – спросишь ты.

Дело в том, что в данном неравенстве множитель повторялся дважды (помнишь, как ты его еще сократить порывался?). Так вот, если какой-то множитель повторяется в неравенстве четное количество раз, то при переходе через точку на оси, которая обращает этот множитель в ноль (в данном случае точка ), знак меняться не будет, если нечетное, то знак меняется!

Верным будет следующая ось с интервалами и знаками:

И, обрати внимание, что знак нас интересует не тот, который был в начале (когда мы только увидели неравенство, знак был ), после преобразований, знак сменился на , значит, нас интересуют промежутки со знаком .

Ответ:

Скажу так же, что бывают ситуации, когда есть корни неравенства, которые не входят в какой-либо промежуток, в ответ они записываются в фигурных скобках, вот так, например: . Подробнее о таких ситуациях можешь прочитать «Метод интервалов» средний уровень.

Давай подведем итоги того, как решать неравенства методом интервала:

Переносим все в левую часть, справа оставляем только ноль;
Находим ОДЗ;
Наносим на ось все корни неравенства;
Берем произвольный из одного из промежутков и определяем знак в интервале к которому относится корень, чередуем знаки, обращая внимание на корни, повторяющиеся в неравенстве несколько раз, от четности или нечетности количества раз их повторения зависит, меняется знак при прохождении через них или нет;
В ответ пишем интервалы, соблюдая выколотые и не выколотые точки (смотри ОДЗ), ставя необходимые виды скобок между ними.

Ну и наконец, наша любимая рубрика, «сделай сам»!

Примеры:

;
;
.

Ответы:

;
;
.

МЕТОД ИНТЕРВАЛОВ. СРЕДНИЙ УРОВЕНЬ

Линейная функция

Линейной называется функция вида . Рассмотрим для примера функцию . Она положительна при и отрицательна при . Точка – нуль функции ( ). Покажем знаки этой функции на числовой оси:

Говорим, что «функция меняет знак при переходе через точку ».

Видно, что знаки функции соответствуют положению графика функции: если график выше оси , знак « », если ниже – « ».

Если обобщить полученное правило на произвольную линейную функцию, получим такой алгоритм:

Находим нуль функции;
Отмечаем его на числовой оси;
Определяем знак функции по разные стороны от нуля.

Квадратичная функция

Надеюсь, ты помнишь, как решаются квадратные неравенства? Если нет, прочти тему «Квадратные неравенства». Напомню общий вид квадратичной функции: .

Теперь вспомним, какие знаки принимает квадратичная функция. Ее график – парабола, и функция принимает знак « » при таких , при которых парабола выше оси , и « » – если парабола ниже оси :

Если у функции есть нули (значения , при которых ), парабола пересекает ось в двух точках – корнях соответствующего квадратного уравнения. Таким образом ось разбивается на три интервала, а знаки функции попеременно меняются при переходе через каждый корень.

А можно ли как-нибудь определить знаки, не рисуя каждый раз параболу?

Вспомним, что квадратный трехчлен можно разложить на множители:

Например: .

Отметим корни на оси:

Мы помним, что знак функции может меняться только при переходе через корень. Используем этот факт: для каждого из трех интервалов, на которые ось разбивается корнями, достаточно определить знак функции только в одной произвольно выбранной точке: в остальных точках интервала знак будет таким же.

В нашем примере: при оба выражения в скобках положительны (подставим, например : ). Ставим на оси знак « »:

Далее, (подставь в выражение любой корень из этого интервала, например, ). Первая скобка положительна, а вторая отрицательна. Значит, все произведение отрицательно: ставим на оси знак « »:

Ну и, при (подставь, например, ) обе скобки отрицательны, значит, произведение положительно:

Это и есть метод интервалов: зная знаки сомножителей на каждом интервале, определяем знак всего произведения.

Рассмотрим также случаи, когда нулей у функции нет, или он всего один.

Если их нет, то и корней нет. А значит, не будет и «перехода через корень». А значит, функция на всей числовой оси принимает только один знак. Его легко определить, подставив в функцию .

Если корень только один, парабола касается оси , поэтому знак функции не меняется при переходе через корень. Какое правило придумаем для таких ситуаций?

Если разложить такую функцию на множители, получатся два одинаковых множителя:

А любое выражение в квадрате неотрицательно! Поэтому знак функции и не меняется. В таких случаях будем выделять корень, при переходе через который знак не меняется, обведя его квадратиком:

Такой корень будем называть кратным.

Метод интервалов в неравенствах

Теперь любое квадратное неравенство можно решать без рисования параболы. Достаточно только расставить на оси знаки квадратичной функции, и выбрать интервалы в зависимости от знака неравенства. Например:

Отмерим корни на оси и расставим знаки:

Нам нужна часть оси со знаком « »; так как неравенство нестрогое, сами корни тоже включаются в решение:

Теперь рассмотрим рациональное неравенство – неравенство, обе части которого являются рациональными выражениями (см. «Рациональные уравнения»).

Пример:

Все множители кроме одного – – здесь «линейные», то есть, содержат переменную только в первой степени. Такие линейные множители нам и нужны для применения метода интервалов – знак при переходе через их корни меняется. А вот множитель вообще не имеет корней. Это значит, что он всегда положительный (проверь это сам), и поэтому не влияет на знак всего неравенства. Значит, на него можно поделить левую и правую часть неравенства, и таким образом избавиться от него:

Теперь все так же, как было с квадратными неравенствами: определяем, в каких точках каждый из множителей обращается в нуль, отмечаем эти точки на оси и расставляем знаки. Обращаю внимание очень важный факт:

Корни знаменателя всегда выколоты, то есть на рисунке они выглядят как незакрашенные кружочки, и в ответ они

Метод интервалов

Метод интервалов — это специальный алгоритм, предназначенный для решения сложных неравенств вида f(x) > 0. Алгоритм состоит из 5 шагов:

Решить уравнение f(x) = 0. Таким образом, вместо неравенства получаем уравнение, которое решается намного проще;
Отметить все полученные корни на координатной прямой. Таким образом, прямая разделится на несколько интервалов;
Найти кратность корней. Если корни четной кратности, то над корнем рисуем петлю. (Корень считается кратным, если существует четное количество одинаковых решений)
Выяснить знак (плюс или минус) функции f(x) на самом правом интервале. Для этого достаточно подставить в f(x) любое число, которое будет правее всех отмеченных корней;
Отметить знаки на остальных интервалах, чередуя их.

После этого останется лишь выписать интервалы, которые нас интересуют. Они отмечены знаком «+», если неравенство имело вид f(x) > 0, или знаком «−», если неравенство имеет вид f(x) < 0.

В случае с нестрогими неравенствами( ≤ , ≥) необходимо включить в интервалы точки, которые являются решением уравнения f(x) = 0;

Пример 1:

Решить неравенство:

(x — 2)(x + 7) < 0

Работаем по методу интервалов.

Шаг 1: заменяем неравенство уравнением и решаем его:

(x — 2)(x + 7) = 0

Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю:

x — 2 = 0 => x = 2

x + 7 = 0 => x = -7

Получили два корня.

Шаг 2: отмечаем эти корни на координатной прямой. Имеем:

Шаг 3: находим знак функции на самом правом интервале (правее отмеченной точки x = 2). Для этого надо взять любое число, которое больше числа x = 2. Например, возьмем x = 3 (но никто не запрещает взять x = 4, x = 10 и даже x = 10 000).

Получим:

f(x) = (x — 2)(x + 7)

x = 3

f(3)=(3 — 2)(3 + 7) = 1*10 = 10

Получаем, что f(3) = 10 > 0 (10 – это положительное число), поэтому в самом правом интервале ставим знак плюс.

Шаг 4: нужно отметить знаки на остальных интервалах. Помним, что при переходе через каждый корень знак должен меняться. Например, справа от корня x = 2 стоит плюс (мы убедились в этом на предыдущем шаге), поэтому слева обязан стоять минус. Этот минус распространяется на весь интервал (−7; 2), поэтому справа от корня x = −7 стоит минус. Следовательно, слева от корня x = −7 стоит плюс. Осталось отметить эти знаки на координатной оси.

Вернемся к исходному неравенству, которое имело вид:

(x — 2)(x + 7) < 0

Итак, функция должна быть меньше нуля. Значит, нас интересует знак минус, который возникает лишь на одном интервале: (−7; 2). Это и будет ответ.

Пример 2:

Решить неравенство:

(9x²— 6x + 1)(x — 2) ≥ 0

Решение:

Для начала необходимо найти корни уравнения

(9x²— 6x + 1)(x — 2) = 0

Свернем первую скобку, получим:

(3x — 1)²(x — 2) = 0

Отсюда:

x — 2 = 0; (3x — 1)² = 0

Решив эти уравнения получим:

x₁= 2; x₂= ; x₃= ;

Нанесем точки на числовую прямую:

Т.к. x₂и x₃– кратные корни, то на прямой будет одна точка и над ней “петля”.

Возьмем любое число меньшее самой левой точки и подставим в исходное неравенство. Возьмем число -1.

(9*(-1)²— 6*(-1) + 1)(-1 — 2) = -12

Т.к. решение уравнения при x = -1 отрицательное (-12), то на графике в крайнем левом интервале пишем -, и далее чередуя знак записываем его в следующие интервалы:

Далее выбираем отрицательные интервалы, т.к. знак нашего неравенства ≤.

Не забываем включать решение уравнения (найденные X), т.к. наше неравенство нестрогое.

Ответ: {} U [2;+∞)

Пример 3:

Решить неравенство:

(9x²— 6x + 1)(x — 2) > 0

Все, чем данное неравенство отличается от предыдущего – вместо нестрогого неравенства (≥) стоит строгое (>). Как ни странно, решение данного неравенства будет иным.

Найдем корни уравнения (9x²— 6x + 1)(x — 2) ≠ 0 (знак ≠ означает, что найденные корни не могут быть решениями нашего неравенства, т.к. оно строгое). Проделав все этапы, что и в предыдущем примере получим:

x₁= 2; x_2,3 =;

Вынесем наши решения на числовую прямую (обратите внимания, что данные точки не включены, т.к. неравенство строгое, т.е. левая часть неравенства не равна нулю)

Обратите внимание, что корни x₂ и x₃ совпадают, корень “” является кратным. Соответственно, в данной точке на числовой прямой рисуем петлю.

Возьмем число -1.

(9*(-1)²— 6*(-1) + 1)(-1 — 2) = -12

Далее выбираем отрицательные интервалы, т.к. знак нашего неравенства <.

Найденные корни не включаем в ответ.

Ответ: (2;+∞).

Метод интервалов в рациональных неравенствах. Примеры, тест

Чтобы оценить все могущество метода интервалов, давайте сначала решим несложное неравенство так, как если бы мы его решали, ~~не зная метода интервалов~~. + показать

Решим неравенство .

Как мы будем рассуждать?

Произведение двух множителей дает знак «+», когда

1) оба множителя положительны;

2) оба множителя отрицательны.

Поэтому предстоит решить совокупность двух систем неравенств:

$\left[ \begin{gathered} \begin{cases} x+6>0,& &x-5>0; \end{cases}& &\begin{cases} x+6<0,& &x-5<0;\end{cases} \end{gathered} \right$

Решение первой системы:

yugh

$x\in(5; +\infty)$

Решение второй системы:

3qwas

$x\in(-\infty;-6)$

Итак, нам осталось объединить решения первой и второй систем:

Ответ: $x\in(-\infty;-6)\cup(5; +\infty)$

А теперь представьте, если бы у нас было не два множителя, как выше, а три-четыре, а если бы при этом множители представляли из себя многочлены второй степени, например.

Представляете, сколько было бы перебора различных ситуаций?

Метод интервалов для рациональных неравенств

Метод интервалов выручит! Избавит нас от рутины! + показать

Мы ведь понимаем, что любое число – либо отрицательное (-), либо положительное (+), либо ноль. Где «переход» из одной зоны (+или – ) в другую (- или +)? В нуле!

На рисунке 1 функция обращается в нуль в точках -2; 1; 5 и 7. Именно при переходе через них она и меняет свой знак с одного на другой.

Функция может также коснуться оси (ох), и «не перескочить» в другую зону (как на рисунке 2). В данном случае точка x=-2 – корень четной кратности (мы еще поговорим об этом).

В любом случае, если функция попала из одной «зоны» («+,-») в другую («-,+»), – значит она в какой-то точке должна была обратиться в ноль.

Поэтому-то нули функции и помогут нам!

Итак, давайте выработаем алгоритм, которого будем придерживаться при решении рациональных неравенств.

Алгоритм решения рациональных неравенств

Пусть нам дано неравенство вида $f(x)\vee0$ , где $\vee$ – один из знаков $<,\leq,>,\geq$ .

1. Раскладываем на множители (если это возможно*).

2. Находим нули .

3. Отмечаем корни (нули) функции на оси в порядке возрастания. Эти числа разбивают числовую ось на интервалы. На каждом из этих интервалов выражение сохраняет знак, а, переходя через отмеченные точки, меняет знак на противоположный (или не меняет, если корень – четной кратности, например, в неравенстве x=1 – корень четной кратности, корень x=0 – обычный).

4. Расставляем знаки на интервалах, начиная от крайнего правого. Советую брать «миллиончик» – не промахнетесь (шучу). Нам не важно само значение функции в выбранной точке, но только ЗНАК в ней, поэтому не утруждайте себя подсчетами – только грубая прикидка.

5. Выбираем подходящие нам промежутки, записываем ответ. Например, если неравенство со знаком «>», то берем интервалы со знаком «+», если неравенство со знаком «<», то берем интервалы со знаком «-», если неравенство со знаком $\leq$ ( $\geq$ ), то берем промежутки со знаком «+» («-») c закрытыми концами.

Практика

Пример 1.

Решить неравенство:

Решение: + показать

1) Разложим вторую скобку неравенства на множители по формуле «разность квадратов»:

2) Нули: $2; \pm3$

wer

4) Взяв «миллиончик» и «подставив» в , конечно же будем иметь знак «-». Далее знаки чередуются.

5) Выбираем подходящие нам промежутки, записываем ответ:

Ответ: $x\in (-3;2)\cup(3;+\infty)$ .

Пример 2.

Решить неравенство:

Решение: + показать

1) Попадаем в ситуацию (*) – на множители-то не раскладывается, так как D<0 .

2) –

3) А отмечать-то нечего на оси 🙁

4) Так значит, меняться знаку негде! Он – либо «+» либо «-» всюду! Берем любое число, например, 0 и смотрим, какой знак в нем принимает выражение . Очевидно, это «+». Поэтому

5) Ответ: $x\in R$ .

Пример 3.

Решить неравенство: $(x^3-27)(x+5)^2\geq 0$

Решение: + показать

1) Раскладываем первую скобку на множители по формуле разность кубов:

$(x-3)(x^2+3x+9)(x+5)^2\geq 0$ . Заметим, дальше на множители не раскладывается, так как D<0 для этого квадратного трехчлена. А значит, эта скобка несет в себе только один знак (не трудно понять, что «+»). То есть, вообще говоря, мы можем поделить обе части исходного неравенства на . Полученное тогда неравенство $(x-3)(x+5)^2\geq 0$ равносильно исходному.

Будем дальше решать именно это неравенство:

$(x-3)(x+5)^2\geq 0$

2) Нули: $3;\;-5$ .

3)-4) Обратите внимание: корень x=-5 – четной кратности, при переходе через него не будет происходить смена знаков! Ну действительно, знак неравенства определяется только выражением x-3 , ведь (x+5)^2 принимает только «+» (то есть не влияет на знак произведения) или обращается в ноль.

Обратите внимание – в ответ пойдет и точка {-5}! Так как знак неравенства нестрогий, мы должны взять и все точки, лежащие на оси.

5) Ответ: $x\in$ {} $\cup[3;+\infty]$ .

Пример 4.

Решить неравенство: $(x^3-4x)(x^2+2x-8)(x^2+7x+10)\leq 0$

Решение: + показать

Пример 5.

Решить неравенство:

Решение: + показать

Надеюсь, у вас не возникает желания разложить на множители каждую из скобок? Ни в коем случае! Должен быть «0» справа!

Поэтому, первое, что нужно сделать, – перенести «-5» в левую сторону. Но раскрывать скобки и выходить на 4-ю степень не хотелось бы.

Замечаем, что есть одинаковые компоненты ( x^2-x ) в скобках, поэтому, можно сделать замену переменной. Обозначим x^2-x-1 за . Тогда получаем следующее неравенство: .

Далее: .

1) Раскладываем на множители:

2) Нули: 1; 5

3)-5) Ось у нас будет называться :

ujk

$t\in (1;5)$ .

Теперь нам предстоит сделать обратную замену: .

Перепишем двойное неравенство в виде системы:

$\begin{cases} x^2-x-1<5,& &x^2-x-1>1; \end{cases}$

$\begin{cases} x^2-x-6<0,& &x^2-x-2>0; \end{cases}$

Нам предстоит решить два неравенства, а потом пересечь их решения.

Решаем первое неравенство:

Раскладываем на множители: .

wsdfu

Решение первого неравенства: $x\in (-2;3)$

Решаем второе неравенство:

Раскладываем на множители:

op;l

Решение второго неравества: $x\in(-\infty;-1)\cup(2;+\infty)$ .

Пересекаем решения неравенств:

Ответ: $x\in(-2;-1)\cup(2;3)$ .

Пример 6.

Решить неравенство: .

Решение: + показать

Введем переменную: , заметим, при этом $t\geq 0$ .

$t\in[0;3)\cup(7;+\infty)$

Или, что тоже самое:

Обратная замена:

Тогда (как раскрывать модуль)

Ответ: $x\in(-\infty;-7)\cup(-3;3)\cup(7;+\infty)$ .

! Возможно, вам будет интересно ВИДЕО по данной теме.

А также смотри это видео

Здесь предлагаю ознакомиться с решением дробно-рациональных неравенств методом интервалов.

Вы можете пройти тест тест по теме «Метод интервалов для рациональных неравенств»

Метод интервалов. Как решать неравенства с помощью метода интервалов

Метод интервалов применяется при решении огромного количества самых разных неравенств – квадратных, дробно-рациональных, показательных, логарифмических…

Примеры неравенств, которые удобно решать методом интервалов:

$(2x-5)(x+3)≤0$	$\frac{-14}{x^2+2x-15}$$≤0$
$x^2<361$	$\frac{x^2-6x+8}{x-1}$$-$$\frac{x-4}{x^2-3x+2}$$≤0$
$\frac{x-2}{3-x}$$≤0$	$\frac{2}{5^x-1}$$+$$\frac{5^x-2}{5^x-3}$$≥2$
$x^2 (-x^2-64)≤64(-x^2-64)$	$\frac{5\log^2_{2}⁡x-100}{\log^2_{2}⁡x-25}$$≥4$

Как решать неравенства методом интервалов (алгоритм с примерами)

Равносильными преобразованиями приведите неравенство к виду: $\frac{(x-x_1 )^n (x-x_2 )^k…}{(x-x_3 )^l (x-x_4 )^m…}$$∨0$ или $(x-x_1 )^n (x-x_2 )^k…∨0$ ($∨$ — любой знак сравнения; $n,k,l,m$ – любые натуральные числа большие нуля, в том числе и $1$)

Пример:

$(2x+5)(x-2)>5$
$2x^2-4x+5x-10-5>0$
$2x^2+x-15>0$
$D=1-4 \cdot 2 \cdot (-15)=121=11^2$
$x_1=\frac{-1-11}{2 \cdot 2}=-3;$ $x_2=\frac{-1+11}{2 \cdot 2}=\frac{5}{2}$
$2(x-\frac{5}{2})(x+3)>0$ $|:2$
$(x-\frac{5}{2})(x+3)>0$

Отметим, что здесь применено разложение на множители квадратного трехчлена.
Найдите корни числителя и знаменателя (т.е. такие значения икса, которые превратят их в ноль).

$x=\frac{5}{2}; x=-3$
Нанесите найденные значения на числовую ось.

Если неравенство строгое, то корни числителя обозначьте «выколотой» точкой, если нет — закрашенной. Корни знаменателя «выколоты» всегда, независимо от строгости знака сравнения.

Расставьте знаки на интервалах числовой оси. Напомню правила расстановки знаков:

— В крайнем правом интервале ставим знак плюс;

— Дальше двигаемся влево;

— Переходя через число:

— меняем знак, если скобка с этим числом была в нечетной степени (1, 3, 5…)

— не меняем знак, если скобка с этим числом была в четной степени (2, 4, 6…)

Выделите нужные промежутки.
Если есть отдельно стоящий корень, то отметьте его флажком, чтоб не забыть внести этот корень в ответ (такая ситуация рассмотрена в одном из примеров ниже).
Запишите в ответ выделенные промежутки и корни, отмеченные флажком (если они есть).

Ответ: $(-∞;-3)∪(\frac{5}{2};∞)$

Почему алгоритм метода интервалов работает именно так?

+5 видео-примеров решения

Пример. (задание из ОГЭ) Решите неравенство методом интервалов $(x-7)^2< \sqrt{11}(x-7)$

Решение:

$(x-7)^2< \sqrt{11}(x-7)$		Чтобы в неравенстве справа был $0$, перенесем выражение из правой части в левую.
$(x-7)^2- \sqrt{11}(x-7)<0$		Вынесем за скобку $(x-7)$.
$(x-7)(x-7-\sqrt{11})<0$		Находим корни.
$x=7;$ $x=7+\sqrt11$		Расставляем на числовой оси корни, затем знаки и закрашиваем нужные интервалы
		Записываем ответ

Ответ: $(7;7+\sqrt{11})$

Пример. Решите неравенство методом интервалов $\frac{(4-x)^3 (x+6)(6-x)^4}{(x+7,5)}$$≥0$
Решение:

$\frac{(4-x)^3 (x+6)(6-x)^4}{(x+7,5)}$$≥0$		Здесь на первый взгляд все кажется нормальным, а неравенство изначально приведенным к нужному виду. Но это не так – ведь в первой и третьей скобке числителя икс стоит со знаком минус. Преобразовываем скобки, с учетом того, что четвертая степень — четная (т.е. уберет знак минус), а третья – нечетная (т.е. не уберет). $(4-x)^3=(-x+4)^3=(-(x-4))^3=-(x-4)^3$ $(6-x)^4=(-x+6)^4=(-(x-6))^4=(x-6)^4$ Вот так. Теперь возвращаем скобки «на место» уже преобразованными.
$\frac{-(x-4)^3 (x+6)(x-6)^4}{(x+7,5)}$$≥0$		Теперь все скобки выглядят как надо (первым идет иск без знака и только потом число). Но перед числителем появился минус. Убираем его, умножая неравенство на $-1$, не забыв при этом перевернуть знак сравнения
$\frac{(x-4)^3 (x+6)(x-6)^4}{(x+7,5)}$$≤0$		Готово. Вот теперь неравенство выглядит как надо. Можно применять метод интервалов.
$x=4;$ $x=-6;$ $x=6;$ $x=-7,5$		Расставим точки на оси, знаки и закрасим нужные промежутки.
		В промежутке от $4$ до $6$, знак не надо менять, потому что скобка $(x-6)$ в четной степени (см. пункт 4 алгоритма). Флажок будет напоминанием о том, что шестерка — тоже решение неравенства. Запишем ответ.

Ответ: $(-∞;7,5]∪[-6;4]∪\left\{6\right\}$

Пример. (Задание из ОГЭ) Решите неравенство методом интервалов $x^2 (-x^2-64)≤64(-x^2-64)$
Решение:

$x^2 (-x^2-64)≤64(-x^2-64)$		Слева и справа есть одинаковые выражения – это явно не случайно. Первое желание – поделить на $-x^2-64$, но это ошибка, т.к. есть шанс потерять корень. Вместо этого перенесем $64(-x^2-64)$ в левую сторону
$x^2 (-x^2-64)-64(-x^2-64)≤0$		Вынесем за скобку общий множитель.
$(-x^2-64)(x^2-64)≤0$		Вынесем минус в первой скобки и разложим на множители вторую
$-(x^2+64)(x-8)(x+8)≤0$		Обратите внимание: $x^2$ либо равно нулю, либо больше нуля. Значит, $x^2+64$ – однозначно положительно при любом значении икса, то есть это выражение никак не влияет на знак левой части. Поэтому можно смело делить обе части неравенства на это выражение. Поделим неравенство так же на $-1$ , чтобы избавиться от минуса.
$(x-8)(x+8)≥0$		Теперь можно применять метод интервалов
$x=8;$ $x=-8$		Запишем ответ

Ответ: $(-∞;-8]∪[8;∞)$

Смотрите также:
Квадратные неравенства
Дробно-рациональные неравенства

Скачать статью

Неравенства методом интервалов

Рассмотрим, как решать неравенства методом интервалов, на конкретных примерах.

Используем алгоритм метода интервалов. Приравниваем к нулю левую часть:

Полученные точки отмечаем на числовой прямой:

Для проверки знака берем 0 (желательно на числовой прямой отметить взятую точку, чтобы потом не забыть, куда ставить знак). Подставляем 0 в последнее неравенство: (2∙0-14)(5∙0+25)= -14∙25, то есть (-)∙(+)= -. Таким образом, в промежуток, из которого взяли нуль, ставим знак «-«, остальные знаки чередуем в шахматном порядке. Поскольку решаем неравенство ≥0, выбираем промежутки со знаком «+» и записываем ответ.

Ответ:

Приравниваем к нулю левую часть:

Полученные точки отмечаем на числовой прямой:

Для проверки знака берем 0 и подставляем его в последнее неравенство. По знакам получаем:

В промежуток, которому принадлежит 0, ставим «+», остальные знаки расставляем в шахматном порядке. Поскольку решаем неравенство ≤0, в ответ выбираем промежутки со знаком «-«. (Не забываем, когда точки закрашенные, а когда — выколотые. Те точки, в которых знаменатель обращается в нуль, выколотые всегда).

Ответ:

Приравниваем к нулю левую часть:

По теореме, обратной теореме Виета

Полученные точки отмечаем на числовой прямой:

Для определения знака берем 0 и подставляем его в последнее неравенство. Получает (-)/(-)=(+). Остальные знаки расставляем в шахматном порядке. Поскольку решаем неравенство ≥0, выбираем промежутки со знаком «+» и записываем ответ.

Ответ:

Переносим все слагаемые в левую часть, приводим к наименьшему общему знаменателю и упрощаем:

После упрощения решаем неравенство методом интервалов.

Приравниваем к нулю левую часть:

Точек, в которых числитель обращается в нуль, нет. На числовой прямой отмечаем только одну точку:

Для проверки берем нуль. Подставляя его в последнее неравенство, получаем «+». На другом интервале — «-«. Нам нужен интервал с «-«.

Ответ:

Как решать более сложные неравенства методом интервалов, рассмотрим в следующий раз.

Решение полиномиальных неравенств

Решение Полиномиальные Неравенства (страница 1 из 2)

Первый шаг в решении полиномиальное неравенство состоит в том, чтобы найти нули полинома (его x -интервет).Между любыми двумя последовательными нулями полином будет либо положительным или отрицательный. Поскольку неравенство требует позитива («больше чем ноль «) или отрицательность (» меньше нуля «), находя Перехват («равно нулю») — это способ начать. если ты думать о проблеме графически, нули, где многочлен пересекает ось х ; между любыми двумя последовательными точками пересечения полином будет быть выше оси (и, следовательно, положительной) или ниже (и, следовательно, отрицательной).

Найти решение:
( x + 4) ( x 2) ( x 7)> 0

Так как они уже учтены этот многочлен, большая часть моей работы уже выполнена. Так что я пойду прямо чтобы найти нули:

x + 4 = 0, поэтому x = 4
x 2 = 0, поэтому x = 2
x 7 = 0, поэтому x = 7

Эти три нуля делят ось x на четыре интервала: (бесконечность, 4), (4, 2), (2, 7), и (7, + бесконечность).Мне нужно выяснить, на каком из этих интервалов график полинома выше оси x . Если бы я умножил факторы, я бы получил положительный куб полином, и я знать что такое куб выглядит так: начинается слева, подходит к ось, и в конечном итоге масштабируется вверх справа с небольшим изгибом посередине примерно так:

Из этого знания я знать, что многочлен может быть выше оси («больше нуля») только на втором и четвертом интервале, поэтому я могу идти прямо к решение:

Как видите, будучи знакомым с полиномами и их формами может сделать вашу жизнь проще для некоторых из этих проблем.Но что, если вы не узнали об их формах, или если полином более сложный, или если вам нужно «показать ваши рассуждения «? Ваша книга наверняка болтала о» тесте точки «, но этот метод требует много вычислений, поэтому я предпочитаю более простой метод. Я пересмотрю вышеупомянутое упражнение, используя «фактор метод «.

Найти решение: ( x + 4) ( x 2) ( x 7)> 0

Факторы дают мне нули многочлена, и нули дают мне следующие интервалы позитивности и негатива: (бесконечность, 4), (4, 2), (2, 7), и (7, + бесконечность).Мне просто нужно выяснить, какие инверсии являются положительными, а какие отрицательный. У меня есть три фактора, поэтому я составлю таблицу факторов с интервалы отмечены:

В этой таблице есть строка для каждого из факторов, строка для числовой линии и строка для многочлен. Каждая строка разделена на столбцы, каждый столбец соответствует с интервалом между нулями на числовой линии.

Теперь я выясню, где каждый фактор положительный. (Каждый фактор будет отрицательным, где бы он ни положительный.)

я отмечу в таблице интервалы, в которых каждый из факторов является положительным:

… а потом я Марк факторы как отрицательные везде:

Факторы множатся вместе, чтобы создать многочлен; признаки факторов умножаются вместе, чтобы дать знак многочлена.Так что я умножу знаки факторов на каждом интервале, чтобы найти общий знак полинома на этом интервале:

В первом интервале от отрицательной бесконечности до 4, было три знака «минус» и произведение трех негативов это негатив. Во втором интервале от 4 до 2, было два знака «минус» и произведение двух негативов это позитив.И так далее.

Теперь я могу прочитать решение со стола. Мне нужны интервалы, где полином положителен, поэтому я выберу интервалы, в которых есть знак «плюс» в нижнем ряду моего стола:

Самый простой метод решения для полиномиальных неравенств использовать то, что вы знаете о полиномиальных формах, но формы не всегда достаточно, чтобы дать вам ответ.Контрольная точка метод из вашей книги даст вам ответ в конце концов, но это может быть много работы. Метод таблицы факторов быстрее, чем контрольные точки и, поскольку не требуется никаких вычислений, он менее подвержен ошибкам. Так если ваш инструктор не настаивает на том, чтобы вы использовали метод контрольной точки, попробуйте изучить метод таблицы факторов. Это сделает вашу жизнь намного проще.

Топ | 1 | 2 | Возвращение Индексировать Далее >>

Цитировать эту статью как:

Stapel, Елизавета.«Решение полиномиальных неравенств». Purplemath . Доступно с
https://www.purplemath.com/modules/ineqpoly.htm . Доступ [Дата] [Месяц] 2016

Устранение неравенств: обзор

Решение Неравенство: обзор (страница 3 из 3)

Разделы: Линейный неравенства, квадратные неравенства, Другие неравенства

Общие полиномиальные неравенства

Решить x ⁵ + 3 x ⁴ 23 x ³ 51 x ² + 94 x + 120 > 0.

Во-первых, я фактор, чтобы найти нули:

x ⁵ + 3 x ⁴ 23 x ³ 51 x ² + 94 x + 120

… так x = 5, 3, 1, 2, и 4 являются нули этого многочлена.(Обзор как решить многочлены, если вы не уверены, как получить это решение.)

Решить тест-точкой Метод, я бы выбрал точку выборки в каждом интервале, интервалы существо (отрицательное бесконечность, 5), (5, 3), (3, 1), (1, 2), (2, 4) и (4, положительная бесконечность). Как вы можете видеть, если ваша полиномиальная или рациональная функция имеет много факторов, Метод Test-Point может стать довольно трудоемким.

Решить Фактором Метод, я бы решил каждый фактор для его положительности: х + 5> 0 для x > 5; x + 3> 0 для x > 3; x + 1> 0 для x > 1; x 2> 0 для x > 2; и х 4> 0 для x > 4.Тогда я рисую сетка:

… и заполните:

… и решить:

Тогда решение (вспоминая включить конечные точки, потому что это «или равно» неравенство) — это набор значений x в интервалах [5, 3], [1, 2], и [4, положительная бесконечность] .

Как видите, если ваш полиномиальная или рациональная функция имеет много факторов, факторный метод может быть намного быстрее

Рациональное неравенство

Прежде всего, я должен помните, что я не могу начать решать, пока у меня не будет неравенства в «= 0 «формат.

Теперь мне нужно конвертировать к общему знаменателю:

Два фактора: x + 6 и x 3.Обратите внимание, что x не может равняться 3, иначе я бы разделил на ноль, что недопустимо. Первый фактор, х + 6, равно нулю когда х = 6. Другой фактор, x 3, равно нулю когда х = 3. Теперь х на самом деле не может быть равен 3, поэтому эта конечная точка не будет включена ни в один интервал решения (даже хотя это неравенство «или равно»), но мне нужно значение для того, чтобы выяснить, каковы мои интервалы.В этом случае мой интервалы (отрицательная бесконечность, 3), (3, 6], и [6, положительная бесконечность). Обратите внимание на использование скобок, чтобы указать, что 6 можно включить в решение, но это 3 не может.

Использование контрольной точки Метод, я бы выбрал точку в каждом интервале и проверил на знак на результат. Я мог бы использовать, скажем, x = 0, х = 4 и x = 7

Используя Факторный Метод, Я решаю каждый фактор: х + 6> 0 для x > 6 или x <6; x 3> 0 для x > 3. Тогда я делаю сетку:

… заполните знаки по факторам:

..и решить для знак рациональной функции:

Так что решение все х в интервалах (отрицательный бесконечность, 3 ) и [6 , положительная бесконечность).

Есть еще один способ решить неравенства.Вам все еще нужно найти нули ( x -интервет) сначала, но потом вы график функции и просто посмотрите: где график выше оси x , функция положительная; где бы это ни было ниже оси, функция отрицательно. Например, для первого квадратичное упражнение, и = x ² 3 x + 2> 0, мы нашли нули в х = 1 и x = 2Теперь посмотрим на график:

На графике решение очевидно: вы бы взяли два интервала (но не конечные точки интервала) где линия выше оси x .

Или этот огромный полином мы сделали в верхней части этой страницы: x ⁵ + 3 x ⁴ 23 x ³ 51 x ² + 94 x + 120 > 0.Мы нашли нули полинома, будучи x = 5, x = 3, x = 1, x = 2 и x = 4. Теперь посмотрим на графике:

На картинке решение очевидно: взять три интервала (вместе с конечными точками интервала) где линия выше оси x .

Как вы можете догадаться, графический калькулятор может сэкономить вам много времени на эти неравенства если ты понимаешь что делаешьВы все еще должны показать свою работу и рассуждения, но не стесняйтесь использовать картинки для подтверждения алгебры.

<< Предыдущая Топ | 1 | 2 | 3 | Возвращение к индексу

Цитировать эту статью как:

Stapel, Елизавета. «Устранение неравенства: обзор.» Purplemath . Доступно с
https://www.purplemath.com/modules/ineqsolv3.htm . Доступ [Дата] [Месяц] 2016

Устранение линейных неравенств: введение и форматирование

Решение Линейные Неравенства:
Введение и форматирование (страница 1 из 3)

Разделы: Введение и форматирование, Элементарные примеры, Продвинутый примеры

Решение линейных неравенств почти так же, как решение линейных уравнений.

Если бы они дали мне « x + 3 = 0», я бы Я знал, как решить: я бы вычел 3 с обеих сторон. Я могу сделать то же самое здесь:

Тогда решение:

Форматирование выше Ответ называется «обозначение неравенства», потому что решение написано как неравенство.Это, наверное, самое простое решение нотации, но есть три других, с которыми вам может понадобиться знакомый. авторское право © Elizabeth Stapel 2002-2011 Все права защищены.

«Набор обозначение» записывает решение в виде набора точек. Вышеупомянутое решение будет написано в обозначении набора как «{ x | x является реальным номер x
<–3} ", который произносится как «множество всех значений x , такой, что х является действительным числом, и x меньше, чем минус три «.Более простая форма этой записи будет быть чем-то вроде «{ x | x
<–3} ", который произносится как «все х , так что х меньше, чем минус три».

«Интервальная запись» записывает решение как интервал (то есть как отрезок или длину вдоль номерная строка). Вышеупомянутое решение, « x <–3», будет быть написано как "", который произносится как «интервал от отрицательной бесконечности до минус три "или просто" от минус бесконечности до минус три ".интервал нотация легче написать, чем произнести, из-за неоднозначности относительно того, включены ли конечные точки в интервал. (Для Обозначим, например, « x < –3», интервал будет написан «», который будет произносится как «минус бесконечность до (не просто «до») минус три «или» минус бесконечность до минус три включительно «, что означает, что -3 будет включен.Правая скобка в случае « x <–3» указал, что -3 не был включен; правая скобка в « x < –3» дело указывает, что это так.)

Последняя «запись» это больше иллюстрация. Вы можете быть направлены на «график» решение. Это означает, что вы нарисуете номерную линию, а затем выделите часть, которая включена в решение.Во-первых, вы бы отметили край интервала решения, в данном случае –3. Поскольку –3 не входит в решение (это «меньше чем», помните, не «меньше или равно»), вы бы отметили эту точку открытая точка или открытая скобка, указывающая в направлении интервал остальной части решения:

..или

Тогда вы бы затенили соответствующая сторона:

… или:

Почему тень слева? Потому что они хотят, чтобы все значения, которые на меньше, чем -3, и эти значения находятся слева от граничной точки.Если бы они хотели точки «больше чем» вы бы заштриховали вправо.

Всего мы увидели четыре способов, с помощью пары вариантов, обозначить решение вышеуказанного неравенства:

нотация	формат	произношение
неравенство	x <–3	x меньше, чем минус три
набор	я) { x \| x — действительное число, x <–3} ..или ii) { x \| x <–3}	я) набор всего х , такой, что x является реальным число и х меньше, чем минус три ii) все x , так что x меньше, чем минус три
интервал		интервал от минус бесконечности до минус три
график	либо из следующих графиков:

Вот еще один пример, наряду с различными форматами ответов:

Если бы они дали мне « x — 4 = 0», то Я бы решил, добавив четыре к каждой стороне.Я могу сделать то же самое здесь:

Тогда решение будет: x > 4

Как и прежде, это решение может быть представлен любым из четырех следующих способов:

нотация	формат	произношение
неравенство	x > 4	x больше или равно четырем
набор	я) { x \| x — действительное число, x > 4} ..или ii) { x \| x > 4}	я) набор всего х , такой, что x — это действительное число, и х больше чем или равно четырем ii) все x , так что x равно больше или равно четырем
интервал		интервал от четырех до бесконечности, включая четыре
график	либо из следующих графиков:

Относительно графиков решение, обозначение в квадратных скобках идет с обозначением в скобках, и нотация закрытой (заполненной) точки идет с нотацией открытой точки.Хотя ваш нынешний учебник может потребовать, чтобы вы знали только один или два из приведенных выше форматов для ваших ответов, эта тема неравенств имеет тенденцию возникать в других контекстах в других книгах для других курсов. С вами может понадобиться позже, чтобы иметь возможность понять другие форматы, убедитесь, что сейчас что ты их всех знаешь. Тем не менее, до конца этого урока я буду использовать только обозначение «неравенства»; Мне нравится это больше всего.

Топ | 1 | 2 | 3 | Вернуться к оглавлению Следующая >>

Цитировать эту статью как:

Stapel, Елизавета.«Решение линейных неравенств: введение и форматирование». Purplemath . Доступен с
https://www.purplemath.com/modules/ineqlin.htm . Доступ [Дата] [Месяц] 2016

Интервалы

Интервал: все числа между двумя заданными числами.

Пример: все числа от 1 до 6 — это интервал

Все номера?

Да. Все действительные числа, которые лежат между этими двумя значениями.

Пример: интервал от 2 до 4 включает такие числа, как:

2,1

2,1111

2.5

2,75

2.80001

№

⁷/₂

3.7937

И многое другое!

Включая числа на каждом конце?

Ааа … может быть да, а может и нет … мы должны сказать!

Пример: «допускаются коробки весом до 20 кг»

Если ваш ящик , то точно 20 кг … это будет разрешено или нет?

Это не совсем понятно.

Давайте посмотрим, как быть точным об этом в каждом из трех популярных методов:

Неравенство
Номерная линия
Интервальная нотация

Неравенство

С неравенством мы используем:

> больше, чем
≥ больше или равно
<менее
≤ меньше или равно

Нравится:

Пример: x ≤ 20

Говорит: «х меньше или равно 20»

А означает: до включительно 20

включительно

Интервальная запись

В «Interval Notation» мы просто записываем начальные и конечные числа интервала и используем:

[] квадратная скобка, когда мы хотим, чтобы включали конечное значение, или
() круглая скобка, когда мы не

Нравится:

Пример: (5, 12]

Значения от 5 до 12, , но не включают 5, но и включают 12

Номерная строка

С помощью числовой линии мы рисуем толстую линию, чтобы показать значения, которые мы включаем, и:

заполненный круг, когда мы хотим включить конечное значение, или
открытый круг, когда мы не

Нравится:

Пример:

означает, что все числа от 0 до 20, , кроме , включают 0, но до , включают 20

Все три метода вместе

Вот удобная таблица, показывающая все 3 метода (интервал от 1 до 2):

	от 1		до 2
	в том числе 1	Не Включая 1	Не Включая 2	в том числе 2
Неравенство:	x ≥ 1 «больше чем или равно «	х> 1 «больше чем»	х <2 «меньше чем»	x ≤ 2 «меньше чем или равно «
Номерная строка:
Интервальная запись:	[1	(1	2)	2]

Пример: до включают 1 , а не включают 2 :

Неравенство:

x ≥ 1 и x <2

или вместе: 1 ≤ x <2

Номерная строка:

Интервальная запись:

[1, 2)

Дополнительные примеры

Пример 1: «Продажа за $ 10»

Это означает от до долларов США включительно.

И справедливо сказать, что все цены превышают 0,00 долларов.

В качестве неравенства мы показываем это как:

Цена ≤ 10 и Цена> 0

На самом деле мы могли бы объединить это в:

0 <Цена ≤ 10

На номерной линии это выглядит так:

И используя интервальную нотацию это просто:

(0, 10]

Пример 2: «Участникам должно быть от 14 до 18 лет»

Итак, 14 включено, и «быть 18» идет вплоть до (но не включая) 19.

Как неравенство это выглядит так:

14 ≤ Возраст <19

На числовой линии это выглядит так:

И используя интервальную запись это просто:

[14, 19)

Разве не смешно, как мы измеряем возраст совершенно иначе, чем что-либо еще? Мы остаемся 18 до тех пор, пока нам не исполнится 19. Мы не говорим, что нам 19 (до ближайшего года) с 18½ года .

Открыто или Закрыто

Термины «Открытый» и «Закрытый» иногда используются, когда конечное значение включено или нет:

(а, б)	а <х	открытый интервал
[а, б)	a ≤ x	закрыто слева, открыто справа
(а, б)	a	открыто слева, закрыто справа
[a, b]	a ≤ x ≤ b	закрытый интервал

Это интервалы конечной длины.У нас также есть интервалы бесконечной длины.

до бесконечности (но не дальше!)

Мы часто используем бесконечность в интервальной записи.

Бесконечность — это , а не действительное число , в данном случае это просто означает «продолжить …»

Пример: х больше или равно 3:

[3, + ∞)

Обратите внимание, что мы используем круглую скобку с бесконечностью, потому что мы не достигаем ее!

Существует 4 возможных «бесконечных конца»:

Интервал	Неравенство
(a, + ∞)	х>	«больше, чем»
[a, + ∞)	x ≥	«больше или равно»
(-∞, а)	х <	«меньше чем»
(-∞, а)	х ≤ а	«меньше или равно»

Мы могли бы даже показать без ограничений , используя эту запись: (-∞, + ∞)

Два интервала

Мы можем иметь два (или более) интервала.

Пример: x ≤ 2 или x> 3

На числовой линии это выглядит так:

И интервальная запись выглядит так:

(-∞, 2] U (3, + ∞)

Мы использовали «U», чтобы обозначить Союз (соединение двух наборов).

Примечание: будьте осторожны с неравенствами, подобными этому.
Не пытайтесь объединить это в одно неравенство:

2 ≥ x> 3 неправильно!

, что не имеет смысла (вы не можете быть меньше 2
и больше 3 одновременно).

Союз и пересечение

Мы только что увидели, как объединить два набора, используя «Союз» (и символ 000 ).

Существует также «Пересечение», что означает «должен быть в обоих». Подумайте, «где они перекрываются?».

Символ пересечения — это перевернутая буква «U», например: ∩

Пример: (-∞, 6] ∩ (1, ∞)

Первый интервал идет до (включая) 6

Второй интервал начинается с (но не включая) 1 и далее.

Пересечение (или перекрытие) этих двух наборов идет от 1 до 6 (не включая 1, включая 6):

(1, 6]

Заключение

Интервал — это все числа между двумя заданными числами.
Показывает, включены ли начальный и конечный номер важно
Существует три основных способа отображения интервалов: неравенства, номерная линия и интервальная запись.

Сноска: геометрия, алгебра и множества

Возможно, вы этого не заметили … но мы на самом деле использовали:

все в одной теме. Разве математика не удивительна?

\((2x-5)(x+3)≤0\)	\(\frac{-14}{x^2+2x-15}\)\(≤0\)
\(x^2<361\)	\(\frac{x^2-6x+8}{x-1}\)\(-\)\(\frac{x-4}{x^2-3x+2}\)\(≤0\)
\(\frac{x-2}{3-x}\)\(≤0\)	\(\frac{2}{5^x-1}\)\(+\)\(\frac{5^x-2}{5^x-3}\)\(≥2\)
\(x^2 (-x^2-64)≤64(-x^2-64)\)	\(\frac{5\log^2_{2}⁡x-100}{\log^2_{2}⁡x-25}\)\(≥4\)

\((x-7)^2< \sqrt{11}(x-7)\)		Чтобы в неравенстве справа был \(0\), перенесем выражение из правой части в левую.
\((x-7)^2- \sqrt{11}(x-7)<0\)		Вынесем за скобку \((x-7)\).
\((x-7)(x-7-\sqrt{11})<0\)		Находим корни.
\(x=7;\) \(x=7+\sqrt11\)		Расставляем на числовой оси корни, затем знаки и закрашиваем нужные интервалы
		Записываем ответ

\(\frac{(4-x)^3 (x+6)(6-x)^4}{(x+7,5)}\)\(≥0\)		Здесь на первый взгляд все кажется нормальным, а неравенство изначально приведенным к нужному виду. Но это не так – ведь в первой и третьей скобке числителя икс стоит со знаком минус. Преобразовываем скобки, с учетом того, что четвертая степень — четная (т.е. уберет знак минус), а третья – нечетная (т.е. не уберет). \((4-x)^3=(-x+4)^3=(-(x-4))^3=-(x-4)^3\) \((6-x)^4=(-x+6)^4=(-(x-6))^4=(x-6)^4\) Вот так. Теперь возвращаем скобки «на место» уже преобразованными.
\(\frac{-(x-4)^3 (x+6)(x-6)^4}{(x+7,5)}\)\(≥0\)		Теперь все скобки выглядят как надо (первым идет иск без знака и только потом число). Но перед числителем появился минус. Убираем его, умножая неравенство на \(-1\), не забыв при этом перевернуть знак сравнения
\(\frac{(x-4)^3 (x+6)(x-6)^4}{(x+7,5)}\)\(≤0\)		Готово. Вот теперь неравенство выглядит как надо. Можно применять метод интервалов.
\(x=4;\) \(x=-6;\) \(x=6;\) \(x=-7,5\)		Расставим точки на оси, знаки и закрасим нужные промежутки.
		В промежутке от \(4\) до \(6\), знак не надо менять, потому что скобка \((x-6)\) в четной степени (см. пункт 4 алгоритма). Флажок будет напоминанием о том, что шестерка — тоже решение неравенства. Запишем ответ.

\(x^2 (-x^2-64)≤64(-x^2-64)\)		Слева и справа есть одинаковые выражения – это явно не случайно. Первое желание – поделить на \(-x^2-64\), но это ошибка, т.к. есть шанс потерять корень. Вместо этого перенесем \(64(-x^2-64)\) в левую сторону
\(x^2 (-x^2-64)-64(-x^2-64)≤0\)		Вынесем за скобку общий множитель.
\((-x^2-64)(x^2-64)≤0\)		Вынесем минус в первой скобки и разложим на множители вторую
\(-(x^2+64)(x-8)(x+8)≤0\)		Обратите внимание: \(x^2\) либо равно нулю, либо больше нуля. Значит, \(x^2+64\) – однозначно положительно при любом значении икса, то есть это выражение никак не влияет на знак левой части. Поэтому можно смело делить обе части неравенства на это выражение. Поделим неравенство так же на \(-1\) , чтобы избавиться от минуса.
\((x-8)(x+8)≥0\)		Теперь можно применять метод интервалов
\(x=8;\) \(x=-8\)		Запишем ответ

Метод интервалов, решение неравенств

<img decoding="async" src="/800/600/https/ik-study.ru/uploads/s/v/d/w/vdwu9qwztel6/img/hgsT8tKi.jpg" />Решение неравенств

Метод интервалов

Перенос знаков

Выбор точек

Система и совокупность

Точка знакопостоянства

Ответ: [ −oo; −5) ∪ [ 3; 5).

Метод интервалов. Учебник по ЕГЭ и ГИА

МЕТОД ИНТЕРВАЛОВ. СРЕДНИЙ УРОВЕНЬ

Линейная функция

Квадратичная функция

Метод интервалов в неравенствах

Метод интервалов

Пример 1:

Пример 2:

Пример 3:

Метод интервалов для рациональных неравенств

Алгоритм решения рациональных неравенств

Практика

Как решать неравенства методом интервалов (алгоритм с примерами)

Почему алгоритм метода интервалов работает именно так?

Неравенства методом интервалов

Решение полиномиальных неравенств

Устранение неравенств: обзор

Интервалы

Все номера?

Пример: интервал от 2 до 4 включает такие числа, как:

Включая числа на каждом конце?

Пример: «допускаются коробки весом до 20 кг»

Неравенство

Пример: x ≤ 20

Интервальная запись

Пример: (5, 12]

Номерная строка

Все три метода вместе

Дополнительные примеры

Пример 1: «Продажа за $ 10»

Пример 2: «Участникам должно быть от 14 до 18 лет»

Открыто или Закрыто

до бесконечности (но не дальше!)

Пример: х больше или равно 3:

Два интервала

Пример: x ≤ 2 или x> 3

Союз и пересечение

Пример: (-∞, 6] ∩ (1, ∞)

Заключение

Сноска: геометрия, алгебра и множества

Добавить комментарий Отменить ответ

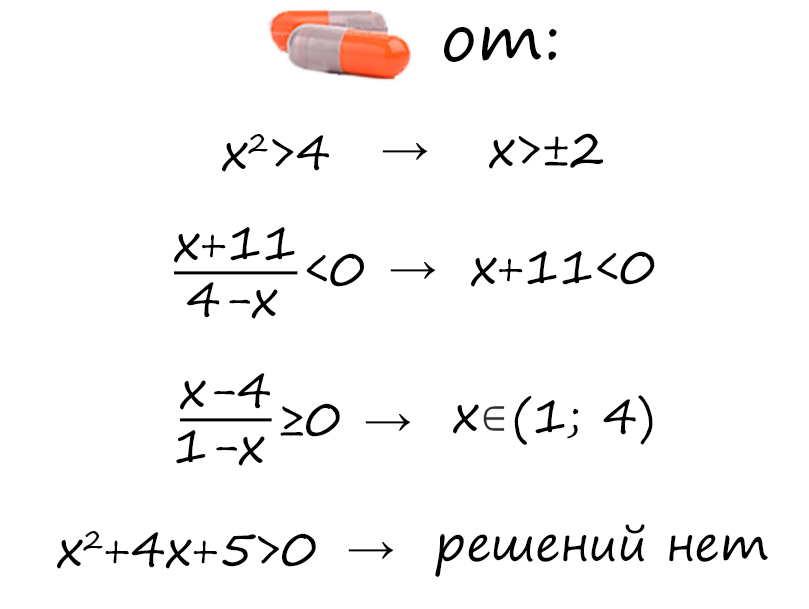Решение неравенств