Методы решения квадратных неравенств: Методы решения квадратных неравенств. Алгебра, 8 класс: уроки, тесты, задания.

МБОУ «ЦО № 19»

Размер шрифта

Межбуквенный интервал

Межстрочный интервал

Директор

Данилин Сергей Викторович

Дата основания: 1 сентября 1979 г

(школа переименована в центр образования 07.09.2015 г.)
Адрес: 300045, г. Тула, ул.Кауля д.9 кор.4
Телефоны:
373-111 — секретарь, директор
373-808 — учительская
e-mail: [email protected]

Мероприятия 15 марта, 07:52

Призеров Всероссийской олимпиады за 3 года

Медали за особые успехи в учении в 2021 году

Средний балл на ЕГЭ по Русскому языку в 2021 году

Выпускников поступивших в ВУЗы в 2021 году

Средний балл на ЕГЭ по профильной математике в 2021 году

Средняя оценка по ОГЭ (Русский язык)

Средняя оценка по ОГЭ (Математика)

Добро пожаловать на наш образовательный сайт!

Он создан для ознакомления всех, кого объединяют наши образовательные учреждения.

В нашем центре объединены детские сады и школы, поэтому мы можем подойти к развитию детей комплексно. 

Мы стремимся обеспечить наших учеников полноценным, качественным образованием, сделать обучение максимально комфортным, дать каждому из воспитанников необходимые знания, навыки и компетенции.

Ждем Вас в нашем центре!!  

Приказ об утверждении графика приема граждан в МБОУ ЦО № 19

Столовая

В текущем учебном году 462 человека из числа учащихся получают горячие завтраки, 176 человек — горячие обеды.

Библиотека

Библиотека подразделения «средняя школа» имеет два помещения: абонемент, совмещенный с читальным залом, и книгохранилище. На 1 января 2020 г. Основной фонд библиотеки составляет 7651 экземпляр, из них 102 экземпляра ЭОР. Учебный фонд «ЦО № 19» – 14300 экземпляров, из них 13737 учебников.

Информация о питании и меню

Чтобы пользоваться услугой «Электронный дневник школьника», вы и ваш ребенок должны быть зарегистрированы на сайте gosuslugi. ru

Для регистрации в электронном дневнике авторизуйтесь на сайте «Сетевой город» и заполните онлайн-форму, указав необходимые данные. Для перехода на сайт нажмите кнопку ниже. Заполнение формы не займет много времени.

Инструкция по регистрации в системе

Получить электронную услугу

Информация и условия для поступления в школу

Закрепленные территории:

1. Приложение к приказу с адресами Центральный район
2. Приложение к приказу с адресами Советский район
3. Приложение к приказу с адресами Привокзальный район
4. Приложение к приказу с адресами Зареченский район
5. Приложение к приказу с адресами Пролетарский район

Свяжитесь с нами удобным для Вас способом:

Телефон: +8 (4872) 373-111
Электронная почта: [email protected]

Тренажер для решения квадратных неравенств

Главная / Старшие классы / Алгебра

Скачать

130. 32 КБ, 687811.docx Автор: Захарова Людмила Владимировна, 31 Мар 2015

Тренажер для решения квадратных неравенств содержит девять варианов. по десять неравенств в каждом.

Автор: Захарова Людмила Владимировна

Похожие материалы

Тип	Название материала	Автор	Опубликован
документ	Тренажер для решения квадратных неравенств	Захарова Людмила Владимировна	31 Мар 2015
презентация, документ	Алгоритм решения квадратных неравенств	Иванова Светлана Борисовна	21 Мар 2015
презентация	Графический метод решения квадратных неравенств. Алгебра. 8 класс.	Николаева Елена Владимировна	1 Апр 2015
презентация	Презентация на тему «Методика решения линейных, квадратных и дробно-рациональных неравенств при подготовке учащихся к ГИА и ЕГЭ».	Шибанова Наталья Николаевна	21 Мар 2015
презентация, документ	Открытый урок по теме ,,Графический способ решения квадратных неравенств»	Михайлова Лариса Валентиновна	20 Фев 2016
документ	Пособие для учащихся «Примеры решения неполных квадратных уравнений»	Кузнецова В. К.	16 Ноя 2015
разное	Применение метода рационализации для решения неравенств	Юрьева Ольга Александровна	31 Мар 2015
презентация	Презентация «Применение метода интервалов для решения неравенств»	Устинова Алевтина Ивановна	6 Дек 2015
презентация	Тренажер для решения задач по математике	Палилова Ирина Николаевна	18 Дек 2015
разное	Способы решения квадратных уравнений	Алейникова Марина Анатольевна	22 Окт 2015
презентация	Решение квадратных неравенств	Луценко Ирина Владимировна	31 Мар 2015
презентация, документ	Урок по теме: “Применение метода интервалов для решения неравенств” 9 класс	Руднева Елена Сергеевна	21 Мар 2015
документ	Рабочая программа курсов по выбору для 9 класса «Самый простой способ решения непростых неравенств»	Габбасова Расима Расимовна	31 Мар 2015
презентация	Презентация «Метод интервалов для решения уравнений и неравенств, содержащих модуль»	Зайцева Ольга Александровна	1 Апр 2015
документ	Методика построения графика квадратичной функции и использование графика для решения неравенств. (развивающее обучение)	Охрименко Марина Михайловна	1 Апр 2015
презентация, документ	Применение метода интервалов для решения неравенств. Урок 9 класс. Диск	Чудаева Елена Владимировна	1 Апр 2015
разное	РАЗЛИЧНЫЕ СПОСОБЫ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ	Лесных Марина Владимировна	21 Мар 2015
разное	Видеоурок «Способы решения квадратных уравнений»	Кисельман Надежда Юрьевна	25 Авг 2015
	«Некоторые приемы решения квадратных уравнений»	Карманова Светлана Сергеевна	10 Ноя 2018
разное	Методы решения неравенств	Грязева Галина Сергеевна	21 Мар 2015
разное	Эффективные методы решения неравенств с одной переменной	Юрьева Ольга Александровна	31 Мар 2015
документ	Технологическая карта урока «Решение квадратных неравенств»	Полякова Ольга Лаврентьевна	21 Мар 2015
документ	«Решение квадратных неравенств с параметром»	Буреева Людмила Алексеевна	21 Мар 2015
документ	План урока «Решение квадратных неравенств»	Попова Татьяна Викторовна	31 Мар 2015
презентация	«Решение квадратных неравенств»	Анцупова Юлия Владимировна	25 Авг 2015
презентация, документ	Открытый урок на тему: «Решение квадратных неравенств»	Стенина Татьяна Леонидовна	20 Сен 2015
документ	Урок по теме: «Решение квадратных неравенств »	Аюпова Зульфия Салихзяновна	15 Окт 2015
документ	Решение квадратных неравенств в 9-ом классе	Бабенко Наталья Валерьевна	6 Дек 2015
документ	Методические рекомендации к изучению темы: « Решение квадратных уравнений» с применением теоремы Виета для решения приведенного квадратного уравнения и полного квадратного уравнени	смаглий лариса викторовна	5 Апр 2015
разное	тренажер по решению всех видов квадратных уравнений	Валентина Викторовна Ласкутова	7 Ноя 2015
презентация	Устные методы решения квадратных уравнений	Ярцева Ксения Юрьевна	21 Мар 2015
презентация	11 способов решения квадратных уравнений	Гатауллина Сария Рустемовна	21 Мар 2015
презентация	Презентация по теме » решения квадратных уравнений»	Камаева Ольга Юрьевна	21 Мар 2015
презентация	Открытый урок в 8 классе. Методы решения квадратных уравнений.	Логинова Ольга Викторовна	21 Мар 2015
документ	Различные способы решения квадратных уравнений	Шакуло Елена Викторовна	21 Мар 2015
документ	РАЗЛИЧНЫЕ СПОСОБЫ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ	Лесных Марина Владимировна	21 Мар 2015
разное	Эффективное решение квадратных уравнений. Приемы устного решения.	Полищук Ольга Владимировна	21 Мар 2015
документ	Формирование умения решения квадратных уравнений в 8 классе.	Николаева Галина Анатольевна	31 Мар 2015
презентация	Алгоритм решения квадратных уравнений	Костерина Елена Владимировна	31 Мар 2015
документ	Методический материал «Частные случаи решения квадратных уравнений»	Гавриш Марина Юрьевна	31 Мар 2015

{2} – 3x + 8 \gt 0$?

Решение квадратных неравенств состоит из двух шагов. В этой статье вы узнаете, как решать квадратные неравенства.

Разница между уравнением и неравенством (неравенством)

Уравнение — это оператор, поддерживающий равенство значений двух математических выражений. Неравенство, с другой стороны, представляет собой утверждение, в котором используются символы $\gt$ для обозначения больше или $\lt$ для обозначения меньшего, чтобы обозначить, что одна величина больше или меньше по значению, чем другая.

Например, $5x – 7 = 0$ является уравнением, тогда как $5x – 7 \lt 0$ является неравенством.

Ниже приведены основные различия между уравнением и неравенством.

• В уравнении используется символ $=$, а в неравенстве используются такие символы, как $\lt$ и $\gt$.
• Уравнение — это математическое утверждение, показывающее равное значение двух выражений, а неравенство — это математическое утверждение, показывающее, что одно выражение больше или меньше другого. 9{2} – 5x + 6 = 0$ равно $x = 2$ и $x = 3$.

  Теперь начертите числовую линию и отметьте эти две точки ($x = 2$ и $x = 3$).

  Вы видите, что точки $x = 2$ и $x = 3$ делят числовую прямую на три области:

  • Область 1: $ \left( – \infty, 2 \right)$
  • Область 2: $ \left(2, 3 \right)$
  • Область 3: $ \left( 3, \infty \right) $

  Далее рассмотрим случайную точку в каждой из этих областей. {2} – 5 \times 0 + 6 \lt 0 => 6 \lt 0 $ (ложь). Следовательно, $ \left( – \infty, 2 \right)$ не может быть решением. 92+’, б, ‘х+’, в) # Добавляем ярлыки plt.xlabel(«ось X») plt.ylabel(«ось Y») # Отображать plt.show()

  Попробуй!

  Заключение

  Квадратное неравенство не решается с помощью нормального метода, используемого с линейными неравенствами. Чтобы решить квадратное неравенство, первым шагом является нахождение решений соответствующего квадратного уравнения, а затем эти решения используются для решения квадратного неравенства.

  Практические задачи

  Решите следующие квадратные неравенства: 9{2} + x – 528 \gt 0$

Рекомендуемое чтение

• Что вы выберете: две 5-дюймовые пиццы или одну 9-дюймовую пиццу?
• Разница между десятичным логарифмом и натуральным логарифмом
• Что означает e (константа Эйлера) в математике?

Изображение предоставлено: вектор школьных канцелярских принадлежностей, созданный upklyak – www.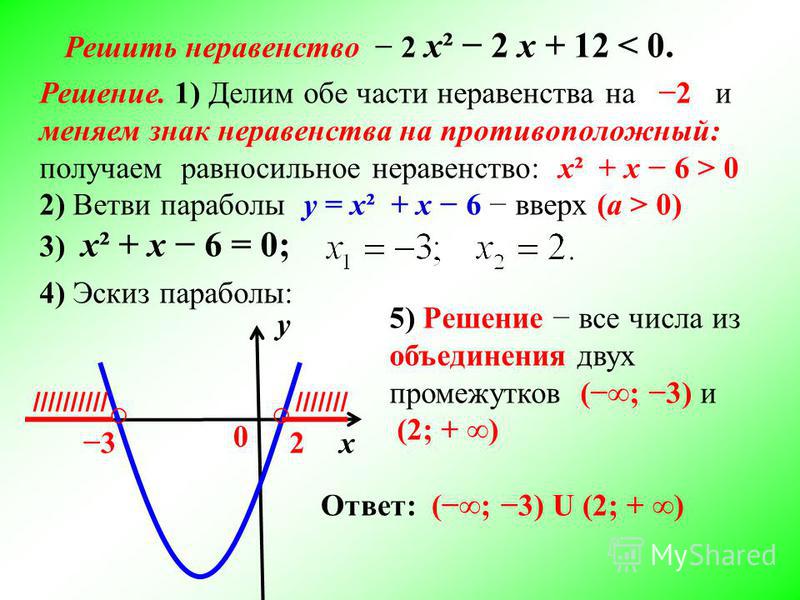 freepik.com

Вам также может понравиться

Геометрическая прогрессия – значение, формулы и примеры

Содержание Что такое геометрическая прогрессия? Примеры геометрической прогрессии

Читать далее

Арифметическая прогрессия – значение, формулы и примеры

Содержание Что такое арифметическая прогрессия? Примеры арифметической прогрессии Член

Читать далее

Последовательность и серия – типы, различия и формулы

Содержание Что такое последовательность и серия? Сигма-нотация серии General

Читать далее

Предварительное исчисление по алгебре — Решение квадратных неравенств

спросил 6 лет, 6 месяцев назад

Изменено 2 года, 7 месяцев назад

Просмотрено 642 раза

$\begingroup$

У меня есть квадратное неравенство. Я на полпути к решению, но не могу понять суть. $$3+\frac{4-x}x>0$$ Я пока понимаю, что, не зная, положительно ли x, мне нужно было бы возвести его в квадрат, но я не знаю, что будет дальше.

• алгебра-предварительное исчисление
• неравенство
• квадратика

$\endgroup$

1

$\begingroup$

Имеем

$$3+\frac{4-x}{x} >0$$

$$\frac{3x+4-x}{x} >0$$

$$\frac{ 2x+4}{x} >0$$

Разделить обе стороны на $2$

$$\frac{x+2}{x} >0$$

Теперь используем метод волнистой кривой

$- \infty+++++ (-2)——(0)++++++ \infty$

Как мы хотим L.H.S. положительно, поэтому мы получаем

$x \in (-\infty, -2) \cup (0, \infty)$

Редактировать 1

Позвольте мне объяснить вам, как я определил знаки.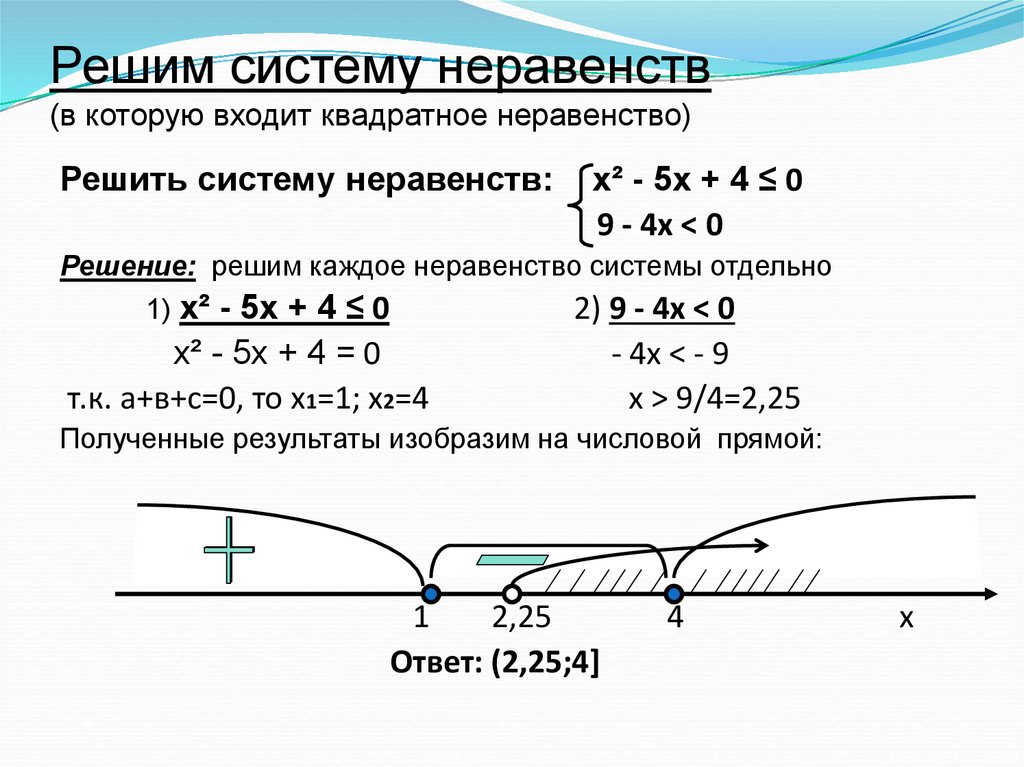

Когда $x>0$, то $x+2>0$ и $x>0$, следовательно, $\frac{x+2}{x}$ будет положительным.

Опять же, когда $x<-2$, тогда $x+2<0$ и $x<0$, следовательно, $\frac{x+2}{x}$ будет положительным.

Когда $-20$, но $x<0$, следовательно, $\frac{x+2}{x}$ будет отрицательным.

Вот так я решил знак.

$\endgroup$

4 9*$$ $$2+\frac4x>0$$ $$\frac4x>-2$$ $$\frac1x>-\frac12$$ $$x<-2\text{ или }x>0$$ *Поскольку мы берем $\frac xx=1$, мы должны исключить случай $x=0$, поскольку он приводит к неопределенной форме.

$\endgroup$

2

$\begingroup$

Мы хотим найти все решения $3 + \frac{4-x}{x} >0$.

Сначала мы должны провести различие между (i) $x>0$ и (ii) $x<0$. Поскольку $x=0$ невозможен, все возможные значения $x$ охватываются этим различием.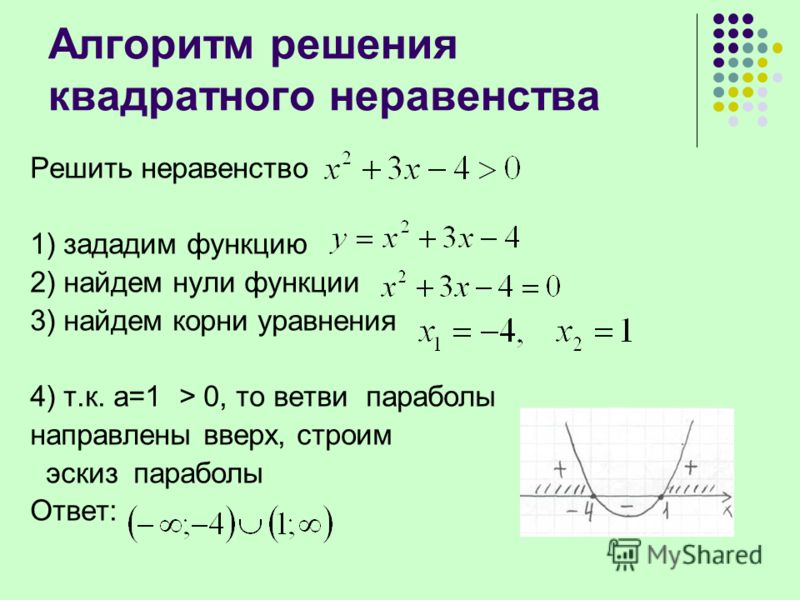

(i) Умножаем неравенство на $x$. Поскольку $x$ положителен, «>» остается «>»:

$$3x + 4 — x > 0 \Longleftrightarrow 2x > -4 \Longleftrightarrow x>-2.$$

(ii) Умножаем неравенство на $x$. Поскольку $x$ отрицательно, на этот раз «>» заменяется на «<":

$$3x + 4 — x < 0 \Longleftrightarrow 2x < -4 \Longleftrightarrow x<-2.$$

Вывод: Множество «L» всех растворов можно записать в виде Союза

$$L = \{x>0, x>-2\} \cup \{x<0,x<-2\} = \{x>0\} \cup \{x<-2\} = (-\infty,-2) \cup (0, \infty).$$

$\endgroup$

2

$\begingroup$

Мы можем использовать следующие

$\frac{A}{B}>0$ и $B\not=0$ тогда и только тогда, когда $AB>0$.

Это верно для остальных знаков неравенства ($<$, $\leq$ и т.д.). Тривиально это верно и для $=$.

Таким образом, получив следующее,

$$\frac{x+2}{x}>0$$

, где $x\not=0$, мы можем переписать его как

$$x(x+ 2)>0$$

Поскольку в другом ответе это называется методом «волнистой кривой», нарисуйте числовую линию с нулями $x(x+2)$ и определите знак $x(x+2)$ на каждом интервале.