Минус на минус дает знак плюс: Что будет если плюс на плюс. Действия с минусом

Деление 6 класс онлайн-подготовка на Ростелеком Лицей

Введение

 

Деление на положительное число эквивалентно умножению на обратное ему число. Например,  или .

 

Но у любого отрицательного числа тоже есть обратное. И деление на отрицательное число тоже можно заменить умножением на обратное:  или .

Давайте вспомним определение. Два числа называются взаимно обратными, если их произведение равное единице: если , то  и  – взаимно обратные числа.

Но это значит, что взаимно обратные числа всегда имеют один и тот же знак. Если бы они были разных знаков, то их произведение получилось бы отрицательным.

 

Правила деления

 

 

Отрицательное число можно представить как произведение  на противоположное положительное число: . Этот факт и позволяет получить правила умножения чисел с разными знаками. Например:  Но при делении получается такая же ситуация: 

 

То есть правило деления чисел с разными знаками аналогично правилу умножения. Их даже можно объединить в одно правило: выполнять умножение или деление двух чисел нужно, не обращая внимания на знаки. Если числа были одного знака, то результат будет положительным, а если разного – то отрицательным.

 

Примеры

 

 

1) .

 

Делим, не обращая внимания на знак. Так как числа разных знаков, то в ответе ставим минус: .

2) .

Делим  на , так как числа оба отрицательные, то ответ положительный: .

3) 

Делим  на , так как знаки у чисел разные, в ответе минус: .

Часто, чтобы понять, какой знак получится, правило запоминают так: «минус на минус дает плюс, плюс на минус дает минус». Это верно и для умножения и для деления.

4) 

Делимое и делитель можно умножить на . Так как числа разных знаков, то в ответе ставим минус: .

5) .

Знак ответа минус, его можно сразу поставить впереди, т.к. у чисел разные знаки. Деление заменяем умножением. Сокращаем и получаем ответ: .

6) .

Сразу определяем знак. Минус на минус дают плюс. Запишем смешанную дробь в виде неправильной и сократим на , деление на  означает умножение на . Выделяем целую часть и получаем ответ: .

7) .

Дробь – это тоже деление. Минус на минус дают плюс. Сокращаем дробь на  и на . Можно записать в виде десятичной дроби: .

8) .

Если в выражении несколько операций умножения и деления, то правило то же самое. Два первых минуса дают плюс. Остается один. В ответе минус. Или так: всего три минуса. Нечетное количество минусов дает минус: .

 

Заключение

 

 

Деление можно считать умножением. Поэтому правило умножения чисел с разными знаками подходит и для деления. Заключается правило в следующем: чтобы выполнить действия с несколькими умножениями и делениями, нужно выполнить действия, не обращая внимания на знаки. Четное количество минусов в исходном выражении даст плюс в ответе, нечетное – минус.

 

Если мы умножаем всего два числа или делим одно число на другое, то правило звучит проще: минус на минус дает плюс, плюс на минус дает минус.

Тот факт, что деление можно заменить умножением на обратное число, мы использовали, чтобы объяснить, почему правило умножения подходит и для деления.

При расчетах такую замену делать совсем не обязательно. Все зависит от конкретного примера. В примере  это в самом деле удобно сделать: . А в примере , если заменить деление умножением, то удобнее не станет, поэтому считаем так, как есть: .

 

Список рекомендованной литературы

1. Зубарева И.И., Мордкович А.Г. Математика. 6 класс. М.: ИОЦ «Мнемозина», 2014.
2. Дорофеев Г.В., Петерсон Л.Г. Математика. 6 класс. Учебник в 3 частях. М. «Просвещение», 2010.
3. Виленкин Н.Я. и др. Математика. Учебник для 6 класса. М.: ИОЦ «Мнемозина», 2013.

 

Рекомендованные ссылки на ресурсы сети Интернет

1. Yaklass.ru (Источник).
2. Math-prosto.ru (Источник).
3. Mathematics-repetition.com (Источник).

 

Домашнее задание

• Определите знак частного:

а) ;

б) ;

в) .

• Выполните деление: .

Найдите значение выражения:

 

Как поставить знак плюс-минус в Ворде

Оглавление

• Вставка знака «плюс-минус» через «Символы»
• Добавление символа «плюса над минусом» посредством кода

Пользователям текстового редактора Word часто приходится использовать разные символы и всевозможные знаки препинания. Всем известный способ вставки того или иного знака посредством функции «Символ» является самым простым. К примеру, обычный знак плюс-минус также можно поставить через вкладку «Вставка». Существует еще несколько вариантов, как можно быстро включить в статью или уравнение данный символ.

Вставка знака «плюс-минус» через «Символы»

Чтобы поставить плюс над минусом следует воспользоваться следующими шагами:

1. Указать курсором место в тексте, где необходим значок «±»;
2. Перейти во вкладку «Вставка» и нажать на всем знакомую кнопку «Символ»;
3. Далее нажать на «Другие символы»;
4. В появившемся окне необходимо установить некоторые параметры. В подразделе «Набор» нужно выбрать «Дополнительную латиницу-1»;
5. Следующее действие это найти значок плюс над минусом, нажать по нему и вставить.

Добавление символа «плюса над минусом» посредством кода

Любой математический символ имеет индивидуальный кодовый знак. С помощью данного кода и сочетания клавиш можно ускорить вставку любого знака, в том числе и плюса над минусом. Существует два вида кода, только работать с каждым из них нужно по-разному. Разберем подробности немного ниже.

Способ 1: Клавиша «Num lk»

Сделать плюс над минусом можно посредством комбинации клавиш и основной кнопки «Num lk». Установите указатель мыши в нужное место в тексте или в формуле, где необходим символ плюс-минус. Включите кнопку «Num lk» она относится к цифровой панели. В случае если Num lk не будет включен, данный способ не сработает. Итак, теперь задержите кнопку «Alt» и наберите число 0177 на цифровой панели.

Способ 2: Комбинация клавиш «Alt+X»

Данный способ также поможет написать плюс над минусом. Поставьте курсор в нужное место, где будет располагаться значок плюс-минус. Далее нужно переключиться с русского метода ввода букв на английский. Если забыли комбинацию то, Shift+Alt переключит на английскую раскладку клавиатуры. Теперь введите этот код 00B1(В – английская буква) и зажмите последовательно сочетание клавиш Alt и X, где Х – тоже английская буква.

Примечание. Буква «В» может быть прописной «b». Способ сработает вне зависимости от регистра буквы.

Из данной статьи пользователь для себя может выбрать самый легкий и удобный способ написания значка плюса над минусом и применить в нужный момент.

Оцените статью: 

Поделиться

Как вставить символы плюс-минус и минус-плюс в Word

Символ плюс-минус

± (также известный как знак плюс или минус ) помещается перед выражением и означает, что следующее значение может быть как положительным, так и отрицательным, большим или меньшим. Этот символ часто обозначает:

• пределы изменения параметров
• инструментальная погрешность измерений физической величины
• ожидаемый разброс статистически оцененных значений параметра
• интервал результата в приближенных математических расчетах.

Например, фраза «масса нетто 200 ± 5% г» означает, что масса нетто продукта находится в диапазоне от 190 до 210 г.

Символ минус-плюс ∓ (также известный как знак минус-или-плюс ) используется с одним или несколькими знаками плюс-минус и означает, что знак плюс

в плюсе -минус в одном выражении строго соответствует минус в минус-плюс и наоборот, например:

символ говорит о том, что у черных есть преимущество.

Существует несколько способов вставки символов плюс-минус или минус-плюс в документ Word:

   I.  Использование уравнения:

   1.    Поместите курсор туда, куда вы хотите вставить символ плюс-минус или символ минус-плюс , затем нажмите Alt+= , чтобы вставить блок экватора:

   2.   В блоке верховой езды без дополнительных усилий можно ввести некоторые математические символы, набрав \+Имя символа :

,

   II. Использование автозамены по математике:

При работе с большим количеством документов и часто нужно вставить один специальный символ, вы можете не хотеть вставлять уравнение каждый раз. Microsoft Word предлагает полезную функцию под названием

AutoCorrect . Параметры AutoCorrect в Microsoft Word предлагают два разных способа быстрого добавления любого специального символа или даже большие куски текста:

• Использование в Заменить текст при вводе Функция Автозамены Опции.
• Использование Math AutoCorrect опции:

Используя этот метод, вы можете использовать параметры Math AutoCorrect без вставки уравнения. Чтобы включить или выключить AutoCorrect символов Math , выполните следующие действия:

   1.   На вкладке Файл нажмите Параметры :

   2.   В диалоговом окне Параметры Word на Вкладка Правописание щелкните Параметры автозамены… 9кнопка 0004:

   3.   В диалоговом окне AutoCorrect на вкладке Math AutoCorrect выберите параметр Использовать правила Math AutoCorrect за пределами математических областей :

После нажатия OK вы можете использовать любое из перечисленных Имен символов , и Microsoft Word заменит их соответствующими символами:

, , , .

Примечание : Если вам не нужна последняя замена, нажмите Ctrl+Z для отмены.

   III. Использование сочетания клавиш:

Microsoft Word предлагает предопределенные сочетания клавиш для некоторых символов, таких как знак плюс-минус и знак минус-плюс :

• Тип 00b1

  (неважно, прописные или строчные) и сразу нажмите

  Alt+X , чтобы вставить символ плюс-минус : ±
• Тип 2213 и нажмите Alt+X , чтобы вставить символ минус-плюс : ∓

Примечание : Комбинацию можно увидеть в поле Код символа в диалоговом окне Символ (см.

ниже).

   IV. Использование диалогового окна «Символ»:

Чтобы открыть диалоговое окно « Symbol », на вкладке Insert в группе Symbols выберите Symbol , а затем нажмите More Symbols… :

В диалоговом окне Symbol выберите символ и нажмите кнопку Insert :

Чтобы выбрать символ минус-плюс , в Список шрифтов , выберите шрифт Segoe UI Symbol и символ:

Знак плюс-минус | Энциклопедия MDPI

Знак плюс-минус (±) — это математический символ с несколькими значениями. Знак обычно произносится как «плюс или минус». В математике это обычно указывает на выбор ровно двух возможных значений, одно из которых является отрицанием другого. В экспериментальных науках знак обычно указывает на доверительный интервал или ошибку измерения, часто на стандартное отклонение или стандартную ошибку. Знак также может представлять включающий диапазон значений, которые может иметь показание. В технике знак указывает на допуск, который представляет собой диапазон значений, которые считаются приемлемыми, безопасными или соответствующими какому-либо стандарту или контракту. ^{В ботанике используется в морфологических описаниях для обозначения «более или менее». В химии этот знак используется для обозначения рацемической смеси. В шахматах знак указывает на явное преимущество белого игрока; дополнительный знак ∓ указывает на такое же преимущество черного игрока.}

1. История

Вариант знака, включающий также французское слово или («или»), был использован в его математическом значении Альбертом Жираром в 1626 году, а знак в его современном виде использовался еще в 9 Уильяма Отреда0252 Clavis Mathematicae (1631). ^[1]

2. Применение

2.1. В математике

В математических формулах символ ± может использоваться для обозначения символа, который может быть заменен символами + или -, что позволяет формуле представлять два значения или два уравнения.

Например, для уравнения x ² = 9 можно дать решение как x = ±3. Это указывает на то, что уравнение имеет два решения, каждое из которых может быть получено заменой этого уравнения одним из двух уравнений 92-4ас}}{2а}. }[/математика]

, описывающее два решения квадратного уравнения x ²  +  bx  +  c  = 0. ) = \sin(A) \cos(B) \pm \cos(A) \sin(B). }[/математика]

можно интерпретировать как сокращение двух уравнений: одно с «+» с обеих сторон уравнения, а другое с «-» с обеих сторон. Обе копии знака ± в этом тождестве должны быть заменены одинаковым образом: недопустимо заменять одну из них на «+», а другую на «-». В отличие от примера с квадратичной формулой, оба уравнения, описываемые этим тождеством, справедливы одновременно. 9{2n+1} + \cdots. }[/математика]

Здесь знак «плюс» или «минус» указывает на то, что знаки терминов чередуются, где (начиная с 0) термины с четным индексом n добавляются, а термины с нечетным индексом вычитаются. Более строгое представление той же формулы будет умножать каждый член на коэффициент (-1) ⁿ , что дает +1, когда n четно, и -1, когда n нечетно.

2.2. В статистике

Использование ⟨±⟩ для приближения чаще всего встречается при представлении числового значения величины вместе с ее допуском или статистической погрешностью. ^[2] Например, «5,7±0,2» может находиться в диапазоне от 5,5 до 5,9 включительно. В научном использовании это иногда относится к вероятности попадания в указанный интервал, обычно соответствующей 1 или 2 стандартным отклонениям (вероятность 68,3% или 95,4% при нормальном распределении).

Проценты также могут использоваться для указания предела погрешности. Например, 230 ± 10 % В относится к напряжению в пределах 10 % от любой стороны от 230 В (от 207 В до 253 В включительно). Можно также использовать отдельные значения для верхней и нижней границ. Например, чтобы указать, что значение, скорее всего, равно 5,7, но может достигать 5,9. или всего 5,6, можно написать 5,7 + 0,2
-0,1.

2.3. В шахматах

Символы ± и ∓ используются в шахматной системе обозначений для обозначения преимущества белых и черных соответственно. Однако более распространенными шахматными обозначениями будут только + и -. ^[3] Если есть разница, символы + и — обозначают большее преимущество, чем ± и ∓.

3. Знак минус-плюс

Знак минус-плюс (∓) обычно используется в сочетании со знаком «±» в таких выражениях, как «x ± y ∓ z», что можно интерпретировать как значение x +

y — z »и/или« x — y + z », но Not » x + 51 + 51 + 51 + 5 + 5 + 5 + 5 + 51 + 51 + 1 + 1 + 1 + 1 + 51 + 1 + 5. − y − z «. Верхний «-» в «∓» считается связанным с «+» в «±» (и аналогично для двух нижних символов), даже если нет визуальной индикации зависимости.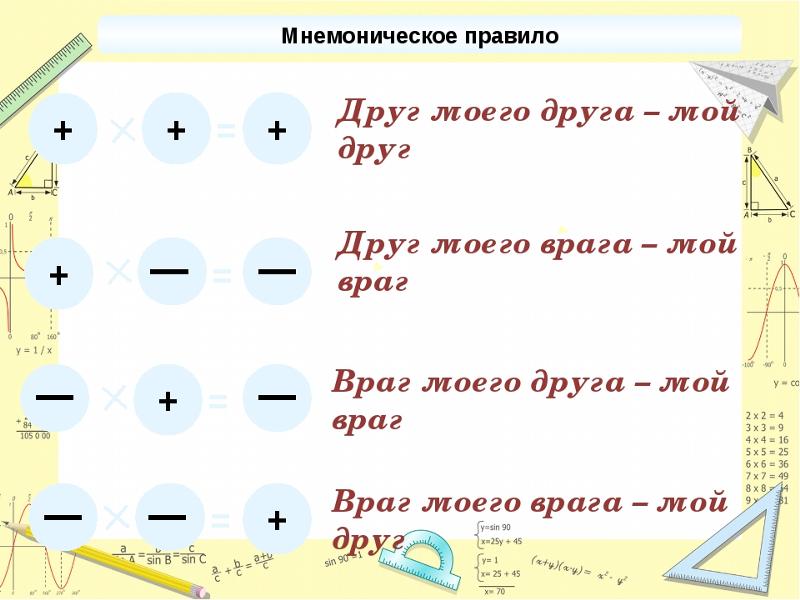 (Однако знак «±» обычно предпочтительнее знака «∓», поэтому, если они оба появляются в уравнении, можно с уверенностью предположить, что они связаны. С другой стороны, если есть два экземпляра знака «±» в выражении, по одному лишь обозначению невозможно сказать, является ли предполагаемая интерпретация двумя или четырьмя различными выражениями.) Исходное выражение можно переписать как « x ± ( y − z )», чтобы избежать путаницы, но такие случаи, как тригонометрическое тождество

[math]\displaystyle{ \cos(A \pm B) = \cos(A) \cos (B) \mp \sin(A) \sin(B) }[/math]

лучше всего писать с использованием знака «∓». Таким образом, приведенное выше тригонометрическое уравнение представляет два уравнения:

[math]\displaystyle{ \begin{align} \cos(A + B) &= \cos(A)\cos(B) — \sin(A) \ sin(B) \\ \cos(A — B) &= \cos(A)\cos(B) + \sin(A) \sin(B) \end{align} }[/math] 92 \mp x + 1\справа) }[/math]

, который представляет собой два уравнения.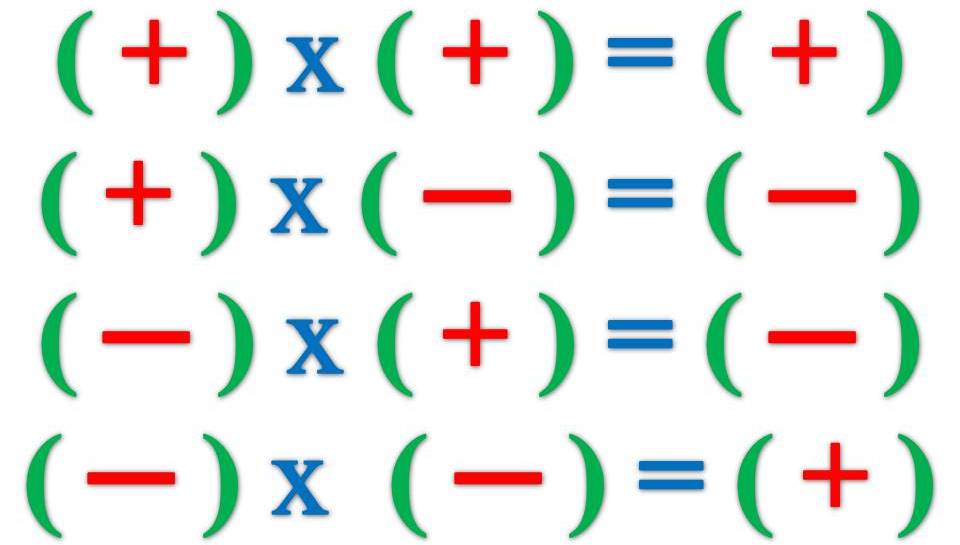

4. Кодировки

• В Unicode: U+00B1 ± ЗНАК ПЛЮС-МИНУС (HTML ±   · + )
• В ISO 8859-1, -7, -8, -9, -13, -15 и -16 символ плюс-минус задается кодом 0xB1 _hex Поскольку первые 256 кодовых точек Unicode идентичны к содержимому ISO-8859-1 этот символ также находится в кодовой точке Unicode U+00B1.
• Символ также имеет HTML-представление сущности ± .
• Более редкий знак минус-плюс (∓) обычно не встречается в устаревших кодировках и не имеет именованного объекта HTML, но доступен в Unicode с кодовой точкой U+2213 и поэтому может использоваться в HTML с использованием ∓ или ∓ .
• В TeX символы «плюс-или-минус» и «минус-или-плюс» обозначаются \pm и \mp соответственно.
• Эти символы также могут быть представлены в виде подчеркнутого или надчеркнутого символа + ( +  или + ), но будьте осторожны, форматирование может быть удалено позднее, что изменит значение.

  No related posts.