Минус пи на окружности где находится: где находится промежуток [-2п п] на тригонометрическом круге

alexxlab / / Разное

Где на окружности находится.

Главная » Математика

Автор Admin На чтение 3 мин Просмотров 57 Опубликовано

Сегодня мы посмотрим на крысиные бега в математике. Где на окружности находится 7пи/2? Очень интересный вопрос. Подобные вопросы любят задавать злобные математики. Точнее, их это заставляет делать учебная программа, составленная по сочинениям безмозглых математиков. Почему безмозглых? Измерять вращение математиков никто не научил, а собственные мозги у них отсутствуют. Вот математики и носятся со своими «пи», как дурни со ступой.

Один полный оборот математики обозначают как 2 пи. Что это значит? Вот вы стоите перед входом в школу. Поворачиваетесь на минус 90 градусов (что равно минус пи/2), то есть по часовой стрелке, и бежите вокруг школы в положительном направлении (против часовой стрелки).

Когда вы снова окажетесь напротив школьного входа, значит вы пробежали угол величиной в 2 пи. Если вы повернетесь на плюс 90 градусов (что равно плюс пи/2) и побежите в противоположном направлении, вы пробежите угол в минус 2 пи. Сколько бы кругов вы не наматывали вокруг школы, вы всегда будете попадать в ту же точку, с которой начинались ваши крысиные бега. Почему бега называют крысиными? Наверное потому, что сколько не бегай, а никуда не убежишь.

План эвакуации

Приблизительно так будет выглядеть план эвакуации, разработанный и утвержденный математиками. И так, бег по кругу — это самое бессмысленное занятие, которое можно придумать. Естественно, если этот бег по кругу не связан со спортом или укреплением собственного здоровья. Здесь у кругового бега одно существенное преимущество — бегая, вы всегда остаетесь практически на месте, не зависимо от того, какое расстояние пробежали.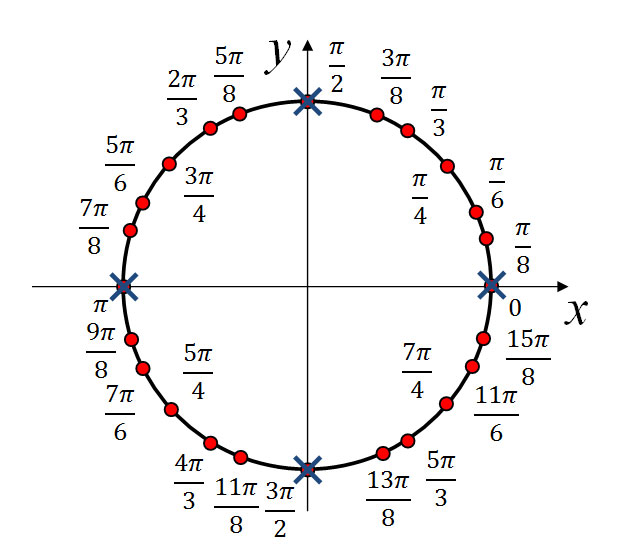

Попробуйте пробежать назад 10 километров, если вы только что закончили забег на 10 километров вперед. А по кругу — пробежал 10 километров и хватит.

Но вернемся к нашей задаче. Как узнать, где на окружности находится 7 пи, деленное пополам? Для начала, нужно выбросить всю дурь не только с головы, но и со значения угла. Если размер дури в других науках определить довольно проблематично, то в математике она имеет вполне конкретное выражение — два пи или 360 градусов. Вот их и нужно выбросить из наших 7пи/2. Вспоминаем вычитание дробей. Чтобы зловредная буква пи нам не мешала, вынесем её за скобки.

Вычисление угла

Про сокращение дробей помните? Точно так же мы выполнили сокращение угла. Сколько бы дури размером в 2 пи (360 градусов) не содержалось в наших углах, всю её необходимо выбросить. Это обычный математический мусор, который, как святыню, хранят церковно-приходские математики.

После сокращения угла можно взять окружность и показать на ней точку, соответствующую углу в 3/2 пи.

Окружность градусов и радиан

Как видно из картинки, угол в 3/2 пи или 270 градусов находится на границе третьей и четвертой четвертей окружности. Хотя, благодаря Интернету и путину, понятие «граница» сегодня весьма размыто.

Не следует забывать, что «пи» — это не единица измерения радиан, а загадочное число 3,1415… Угол в 3/2 пи равен 4,7122… радиан. По умолчанию, математики не пишут возле значения угла единицу измерения «радиан». Чем всех нас запутывают и сами путаются.

Кстати, на сокращении дробей построены пропорции. На сокращении углов такой фокус не возможен — на идиотизме пропорцию не построишь.

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )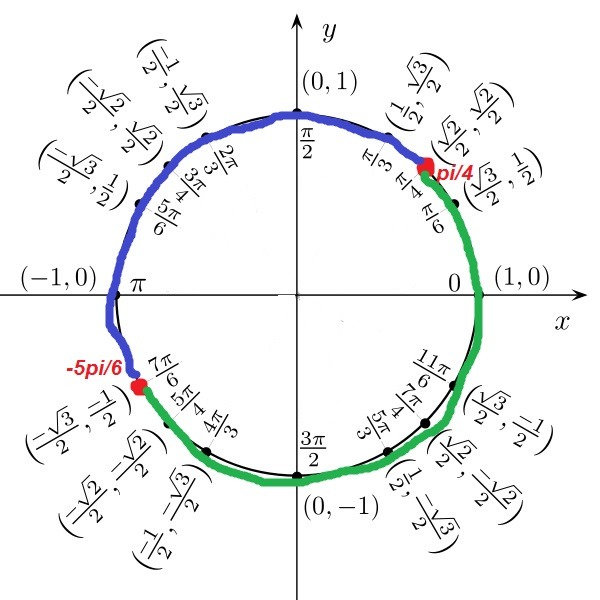
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8Найти точное значениеcos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значение
cos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15Найти точное значениеcsc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25
Найти точное значение		sec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значениеsin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )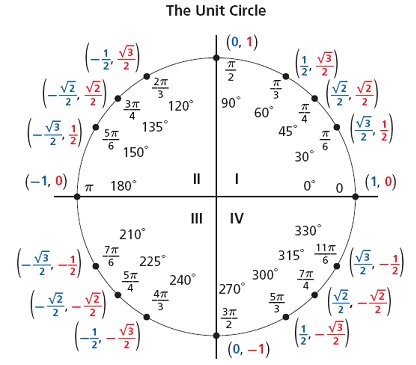
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значениеsin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

геометрия — Почему $\pi$ оказывается отрицательным

Задавать вопрос

спросил

Изменено 5 лет, 1 месяц назад

Просмотрено 87 раз

$\begingroup$

Я сделал следующее, чтобы получить значение $\pi$, вы можете взять карандаш и лист бумаги:

Представьте единичный круг с точкой в ​​центре $b$ и двумя точками $a$ и $c $ на окружности такой, что треугольник $abc$ тупоугольный. вы можете видеть, что если $\theta$ обозначает угол $\angle acb$, то $0<\theta<90$ и что угол сектора $abc$ равен $180 -2\theta$, поэтому площадь сектора $abc $ равно $\frac{180-2\theta}{360}\pi = \frac{90-\theta}{180}\pi$. Если мы расширим радиус $bc$ до диаметра $D$, то угол между прямыми $ab$ и $D$ будет равен $180-(180-2\theta) = 2\theta$; поэтому, если мы определим расстояние между точкой $a$ и линией $D$ как $h$, мы получим $h = \sin(2\theta)$. Это позволяет нам получить площадь треугольника $abc$ как $\frac{1}{2}sin(2\theta)$. Площадь отрезка $ac$ равна площади сектора abc - площади треугольника abc: $$ \фракция{90-\theta}{180}\pi - \frac{1}{2}\sin(2\theta) $$ Мы можем видеть, что по мере того, как $\theta$ приближается к 0, площадь сегмента ac приближается к половине площади круга, равной $\frac{\pi}{2}$ $$ \lim_{\theta\to 0} \frac{90-\theta}{180}\pi - \frac{1}{2}\sin(2\theta) = \frac{\pi}{2} $$ $$ \lim_{\theta \to 0} \frac{90-\theta}{90}\pi - \sin(2\theta) = \pi $$ $$ \lim_{\theta\to 0} \pi\Big[\frac{90-\theta}{90} - 1\Big] = \lim_{\theta\to 0} \sin(2\theta) $$ $$ \lim_{\theta\to 0} -\frac{\theta\pi}{90} = \lim_{\theta\to 0} \sin(2\theta) $$ $$ \pi = -\lim_{\theta\to 0} \frac{90\sin(2\тета)}{\тета} $$ Однако этот предел приближается к -3,1415.

..

  • геометрия
  • пределы
  • пи
$\endgroup$

$\begingroup$

$$\lim_{\theta\to 0} -\frac{\theta\pi}{90} = \lim_{\theta \to 0} \sin(2\theta) $$

Вышеупомянутое верно, но не подразумевает следующую строку:

$$\pi = -\lim_{\theta \to 0} \frac{90\sin(2\theta)}{\theta}$$

Заблуждение здесь состоит в том, что предполагается (или махается рукой), что $\displaystyle \,\lim_{\theta \to 0} f(\theta) = \lim_{\theta \to 0} g(\theta) \implies \lim_ {\ theta \ to 0} \ frac {f (\ theta)} {g (\ theta)} = 1 \, $, но это последнее следствие не обязательно верно, когда оба предела равны $ \, 0 \, $.

Сравните, например, с $\displaystyle\,\lim_{\theta \to 0} \theta + \lim_{\theta \to 0} \theta = 0 \подразумевает \lim_{\theta \to 0} \theta = -\lim_{\theta\to 0} \theta\имеет 1 = -\lim_{\theta\to 0} \dfrac{\theta}{\theta}=-1\,$.

$\endgroup$

$\begingroup$

Ваша математика хороша до

$$\lim_{\theta \to 0} -\frac{\theta\pi}{90} = \lim_{\theta \to 0} \sin(2\theta) $$, что просто $$0=0$$, то же самое, что и $$-0=0$$

Вы хотите манипулировать $$0=0$$, разделив обе стороны на $0$, чтобы получить неопределенное значение $$0/ 0$$ и получить отрицательное значение для $\pi $

Хорошо, если заметить $$\lim_{\theta \to 0} -\frac{\theta\pi}{90}= \lim_{\theta \to 0 } \ гидроразрыва {\ тета \ пи} {93 6 Решить для ? cos(x)=1/2 7 Найдите x sin(x)=-1/2 8 Преобразование градусов в радианы 225 9 Решить для ? cos(x)=(квадратный корень из 2)/2 10 Найдите x cos(x)=(квадратный корень из 3)/2 11 Найдите x sin(x)=(квадратный корень из 3)/2 92=9 14 Преобразование градусов в радианы 120 градусов 15 Преобразование градусов в радианы 180 16 Найти точное значение желто-коричневый(195) 92-4 38 Найти точное значение грех(255) 39 Оценить лог база 27 из 36 40 Преобразовать из радианов в градусы 2 шт.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *