Множество и его элементы. подмножество. пустое множество. — Информатика, информационные технологии
Понятие множества – одно из основных понятий математики. Под множеством понимают совокупность объектов (предметов или понятий), которая рассматривается как единое целое. Например, можно говорить о множестве натуральных чисел, о множестве букв на данной странице, о множестве корней данного уравнения и т. п. Понятие множества принимается как исходное, первичное, т. е. несводимое к другим понятиям. Объекты, входящие в состав множества, называются его элементами. Обычно множества обозначаются большими печатными буквами английского алфавита, например, множество А; а его элементы маленькими прописными буквами, например, элемент а.
Запись означает, что элемент а принадлежит множеству А. Запись — наоборот, Что элемент а множеству А не принадлежит. Знак называют знаком принадлежности.
Определение 1. Два множества А и В называются равными и пишут А=В, если множества А и В содержат одни и те же элементы.
Например: {2, 4, 6} = {4, 2, 6} – равные множества.
Определение 2. Множество называется непустым, если содержит хотя бы один элемент.
Определение 3. Множество А является подмножеством множества В, если каждый элемент множества А принадлежит множеству В.
В этом случае пишут , знак называют знаком включения.
Например: {2, 4,} {4, 2, 6}
Рассмотрим свойства отношения включения.
рефлексивно, т.е любое множество является подмножеством самому себе.
транзитивно, т. е. для любых множеств А, В и С, если множество А является подмножеством множества В и множество В является подмножеством множества С, то из этого следует, что множество А является подмножеством множества С.
антисимметрично, т. е. для любых множеств А и В следует, что, если множество А является подмножеством множества В и в то же время множество В является подмножеством множества А, то множества А и В равны.
Определение 4. Множество, не содержащее ни одного элемента, называется пустыммножеством.
Пустое множество обозначают
Пустое множество является подмножеством любого множества.
Определение 5. Множество всех подмножеств множества A называется множеством-степенью и обозначается P(A).
В дальнейшем будем пользоваться следующим утверждением:
Утверждение 1. Число всех подмножеств конечного множества равно 2n.
Пример. Выделим все подмножества множества А ={2, 4, 6}.
Р(А)={2, 4, 6}, {2, 4}, {4, 6}, {2, 6}, {2}, {4 }, {6}, — всего 23=8.
Операции над множествами
Объединением множеств А и В называется множество, состоящее из тех элементов, которые принадлежат одному из множеств А или В.
Для обозначения объединения множеств используют знак .
Пример. , ,
Пересечением множеств А и В называются такое множество, элементы которого принадлежат как множеству А, так и множеству В.
Для обозначения пересечения множеств используют знак .
Пример. , ,
Разностью множеств А и В называется множество, элементы которого являются элементами множества А, не принадлежащие множеству В.
Для обозначения разности множеств используют знак /.
Пример. , ,
Перечислим основные свойства операций над множествами:
1) идемпотентность объединения
2) идемпотентность пересечения
3) коммутативность объединения
4) коммутативность пересечения
5) ассоциативность объединения
6) ассоциативность пересечения
7) дистрибутивность объединения относительно пересечения
8) дистрибутивность пересечения относительно объединения
Универсальное множество. Дополнение множества.
Во многих приложениях теории множеств рассматриваются только такие множества, которые содержатся в некотором фиксированном множестве. Например, в геометрии мы имеем дело с множеством точек данного пространства, в арифметике – с множеством целых чисел. Такое фиксированное множество называют универсальным.Для его обозначения используют букву U.
Определение 6. Множество U/А называется дополнением множества А и обозначается (или ).
Дополнение U/ множества обозначается
Справедливы следующие формулы:
=
— закон инволюции.
Теорема. Если множество А является подмножеством множества В, то дополнение множества А будет являться подмножеством дополнения множества В.
Доказательство.
Пусть множество А является подмножеством множества В, , необходимо доказать, что для каждого элемента х из универсального множества U выполняется следующее условие: если элемент х принадлежит множеству , то он принадлежит и множеству .
.
Действительно, если х принадлежит множеству , то он не принадлежит множеству В, а т. к. множество А является подмножеством множества В, то элемент х не принадлежит и множеству А, а это означает его принадлежность множеству .
Теорема. Имеют место следующие тождества
— Законы де Моргана для множеств
Приведем краткое доказательство первого утверждения.
Второе утверждение докажите самостоятельно.
Диаграммы Эйлера-Венна.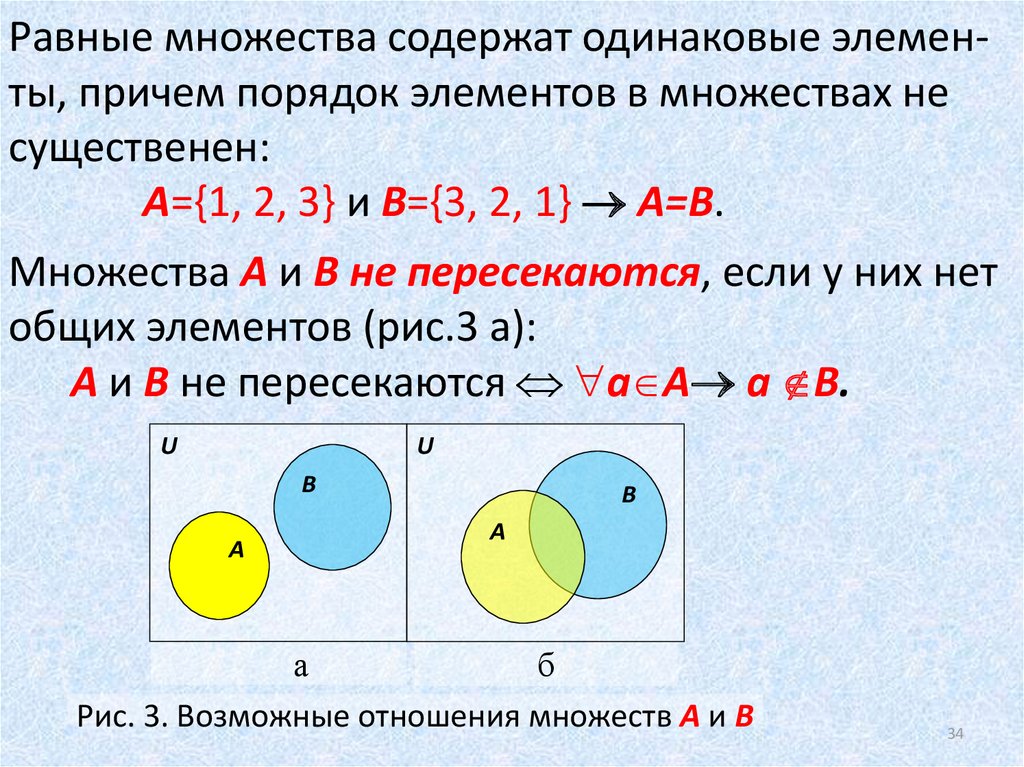
Для графического изображения множеств и их свойств используются так называемые диаграммы Эйлера-Венна.
Объединение множеств Пересечение множеств
Разность множеств Подмножество
Универсальное множество Дополнение
Понятие множества. Элементы множества. Пустое множество. Принадлежность элементов.
Множество. Элементы множества. Способы задания множества. Пустое множество. Подмножество.Операции над множествами.
Тема урока: Множество. Элементы множества. Способы задания множества. Пустое множество. Подмножество.Операции над множествами.
Цель
урока: изучить понятия множество, подмножество,
элементы множества, пустое множество и операций над
множествами: пересечение, объединение; проводить несложные систематизации;
приводить примеры различных множеств и подмножеств, правильно проводить
логические рассуждения.
Воспитание аккуратности
при работе в тетради, самостоятельности, грамотной математической речи. Развитие
мышления учащихся (в ходе выполнения заданий актуализации и на протяжении всего
урока). внимания учащихся (выполнение заданий на нахождение соответствия).
Развитие памяти учащихся
СТРУКТУРА УРОКА
1.Организационный момент
2.Устный счет
3. Изучение нового материала
4.Закрепление
5.Подведение итогов
6.Рефлексия
7.Домашнее задание
Ход урока
1.Организационный момент
Вступительное слово учителя
2. Устный счет
1) 52 + 32 2)67 – 25 3) 51:10 4) 47 -3 : 2
3. Изучение нового материала
Часть 1
Эпиграф:
Множество возникает путем объединения
отдельных предметов в единое целое.
Оно есть множественность мыслимая как единое.
Ф. Хаусдорф
Множество представляет собой объединение некоторых объектов или предметов в единую совокупность по каким-либо общим свойствам или законам.Обозначают А,В,Р,…
Например:
- множество зверей,
- множество учеников;
- множество столов;
- множество стульев;
Предметы, составляющие данное множество, называются его элементами.
Обозначают .
Если множество А состоит из элементов a , c , k , то записывают это так: А = { a , c , k }.
Например, множество дней недели состоит из элементов: понедельник, вторник, среда, четверг, пятница, суббота, воскресенье.
Множество месяцев – из элементов: январь, февраль, март, апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь, декабрь.
Множество арифметических действий — из элементов: сложение, вычитание, умножение, деление.
Множества, состоящие из чисел, называют числовыми множествами.
N – множество натуральных чисел,
Z – множество целых чисел.
Виды множеств
Подмножество
Если каждый элемент множества В является элементом множества А, то множество В называется подмножеством множества А.
Пустое множество, по определению, считают подмножеством всякого множества.Обозначают Ø
Если два множества состоят из одних и тех же элементов, то они называются равными.
Например, А = { a , c , k , m , n } и В = { m , n , a , c , k }, А = В.
Множество является заданным, т.е. известным, если ясно, какие у него элементы. Поэтому, чтобы задать множество, можно просто перечислить все его элементы.
Круги́
Э́йлера[—
геометрическая схема, с помощью которой можно изобразить отношения междуподмножествами, для
наглядного представления.
При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов.
Однако, этим методом ещё до Эйлера пользовался выдающийся немецкий философ и математик Готфрид Вильгельм Лейбниц (1646—1716). Практическая работа
Задание1
1. Перечислите множество фруктов
2. Перечислите множество овощей
3. Перечислите множество школьных предметов учеников 6 класса
Задание 2
Начертите три круга изображающие круги Эйлера. В самом маленьком круге напишите, те знания и умения которые вы приобрели в дошкольном возрасте (множества А), во втором круге – чем пополнились ваши знания в начальной школе (множества В) и в самом большом круге чему вы научились в 5-6 классах (множество С). В каком отношении находятся эти множества? (ответ А подмножества множества В и в – подмножества множества С)
1.Дано
множество {11; 34; 60; 16; 90}. Принадлежит ли этому множеству число, которое
получится при сложении 60 и 30, при вычитании 9 из 17, при делении 72 на 8, при
вычитании И из 48, при умножении 20 на 3? [да; нет; нет; да; да].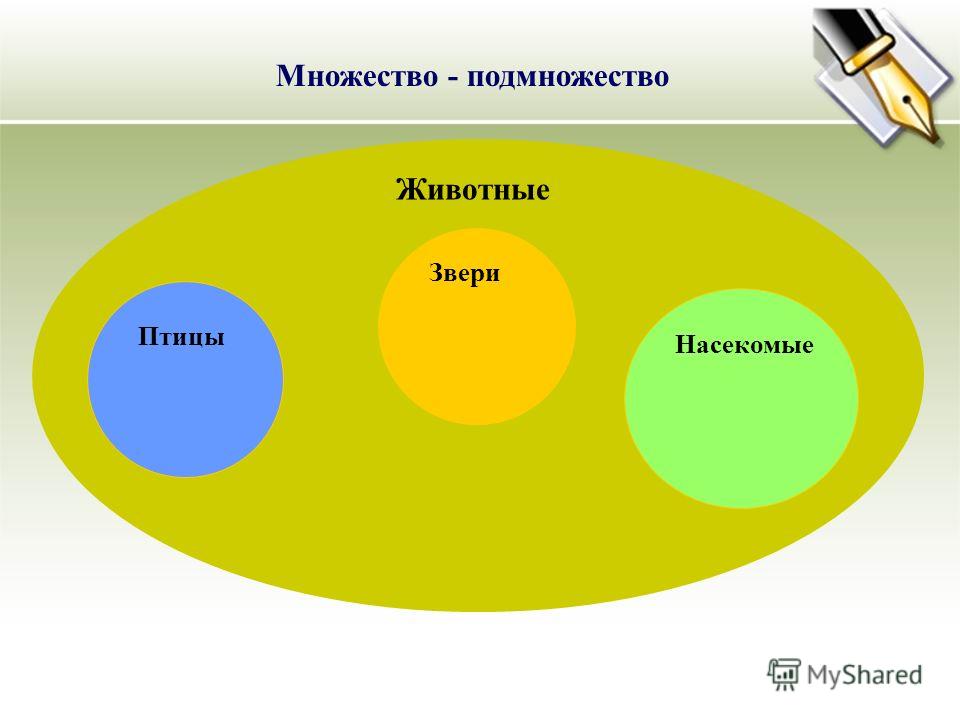
2.По какому признаку составлено множество {зима, весна, лето, осень}, {11. 13, 15, 17, 19}? [времена года, [нечетные числа большие 10 и меньшие 20].
3.По какому признаку составлено множество {6,3,5,2,4}? [Множество чисел, больших 1 и меньших 7. Является ли это мно жество подмножеством натуральных чисел? [Да].
4.Назовите множество дней одной недели; множество месяцев одного года. Является ли множество дней одной недели подмно жеством множества дней одного месяца? [Да].
5.Даны следующие множества:
А — множество учеников данной школы;
В — множество учеников пятых классов данной школы;
С — множество учащихся всех школ данного города;
Д — множество учащихся пятых классов, посещающих кружковые занятия по математике;
Е — множество всех учащихся школ России.
[ Д ВАСЕ].
Перечислить буквы, обозначающие множества, так, чтобы каждая буква (кроме последней) обозначала подмножество следующего множества.
6.Даны множества:
А — множество натуральных чисел;
В — множество четных чисел;
С — множество нечетных чисел;
Д — множество чисел, делящихся на 5;
Е
— множество чисел, делящихся на 10.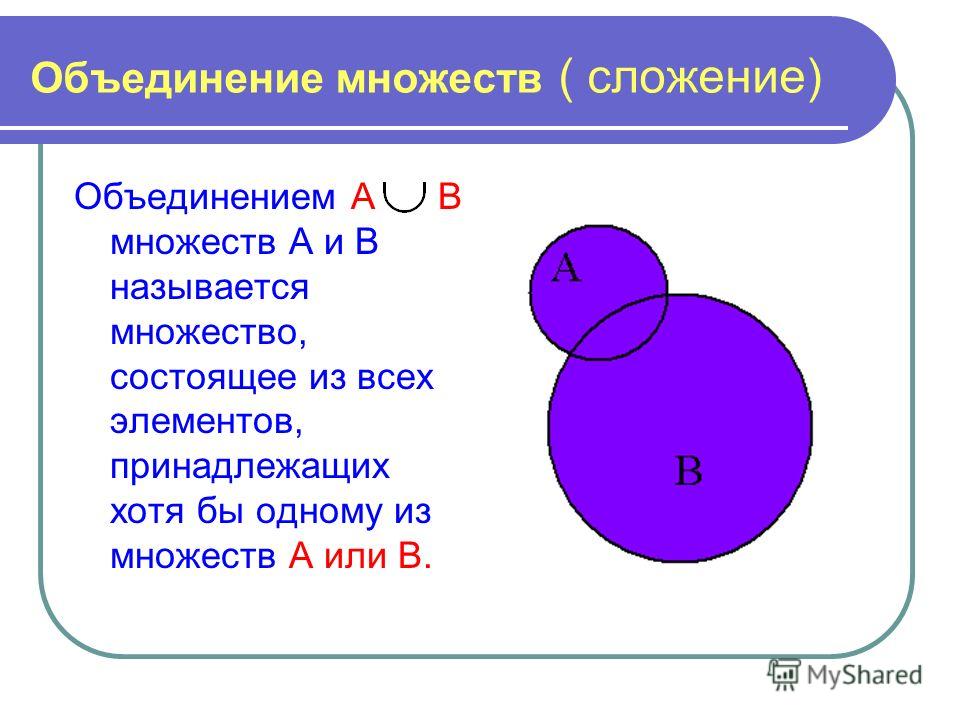
[ВА, СА, ДА, ЕА, ДС, ЕВ, ДЕ].
Указать, какие из данных множеств являются подмножествами других данных множеств.
7.Назовите множество натуральных чисел, расположенных между числами 21 и 22.
[Ø]
(Объяснение учителя).
Часть 2.Решим ЗАДАЧУ № 1.
«В пятых классах школы училось 70 человек. Им было предложено записаться в 3 кружка: по математике, литературе и истории. Староста подсчитал число учащихся, желающих участвовать во внеклассной работе, и получил такие результаты. В кружок по математике записалось 51 человек, по литературе — 40, по истории — 22. 6 человек решили заниматься во всех кружках, математикой и литературой решили заниматься 32 человека, одновременно заниматься математикой и историей решили 11 человек, а литера турой и историей 8 человек. Получив результаты, староста сказал: «Можно подумать, что у нас в 5-х классах обучается не 70 человек, а 170. Все хотят заниматься в кружках».
Однако
один из любителей математики сказал: «Что ты, у нас есть ученики, которые не
любят ни математику, ни литературу, ни исто рию.
Я даже могу сказать, сколько
их». Как он узнал?»
Введем обозначения:
В — множество всех учащихся;
М — множество учащихся (кружковцев), увлекающихся мате матикой;
JI — множество учащихся (кружковцев), увлекающихся лите ратурой;
И — множество учащихся (кружковцев), увлекающихся историей.
Из условия задачи следует, что все условия пересекаются.
Для составления схемы воспользуемся «кругами Эйлера».
Пересечение множеств М, JI и Д содержит 6 элементов (МЛИ|=6 это следует из условия задачи).
Пересечение множеств М и Л содержит 32 элемента (|MЛ|=32), но 6 элементов принадлежат множеству И (смотри рисунок).
Можно определить, сколько человек записать в кружки по мате матике и литературе (32-6=26 человек).
Пересечение множеств М и И содержит 11 элемента (|МИ|=11), но 6 элементов принадлежат множеству JI; следовательно в кружки по математике и истории записалось 11-6=5 человек.
ЛИ
содержит 8 человек (|ЛИ|=8), но 6 элементов принадлежат множеству М, значит в
кружки по литературе и истории записалось 8-6=2 человека.
Теперь легко определить сколько учащихся посещают только один кружок:
· по математике — 51-(6+26+5)= 14 человек;
· по литературе — 40-(6+26+2)=6 человек;
· по истории — 22-(6+5+2)=9 человек;
· всего записалось — 14+6+9+26+5+6+2=68 человек;
· не записалось — 70-68=2 человека.
Решим ЗАДАЧУ № 2.
«В классе 40 человек. Играют в баскетбол 26 человек, занимаются плаванием — 25, ходят на лыжах — 27. Одновременно занимаются плаванием и баскетболом — 15, баскетболом и лыжами — 16, пла ванием и лыжами — 18. Один человек освобожден от занятий по физ культуре. Сколько человек занимается всеми указанными видами спорта? Сколько человек занимается только в одной спортивной секции?».
Введем обозначения:
Л — множество лыжников;
Б — множество баскетболистов;
П — множество пловцов.
По
условию задачи все три множества пересекаются. Число эле ментов пересечения
трёх множеств обозначим через X.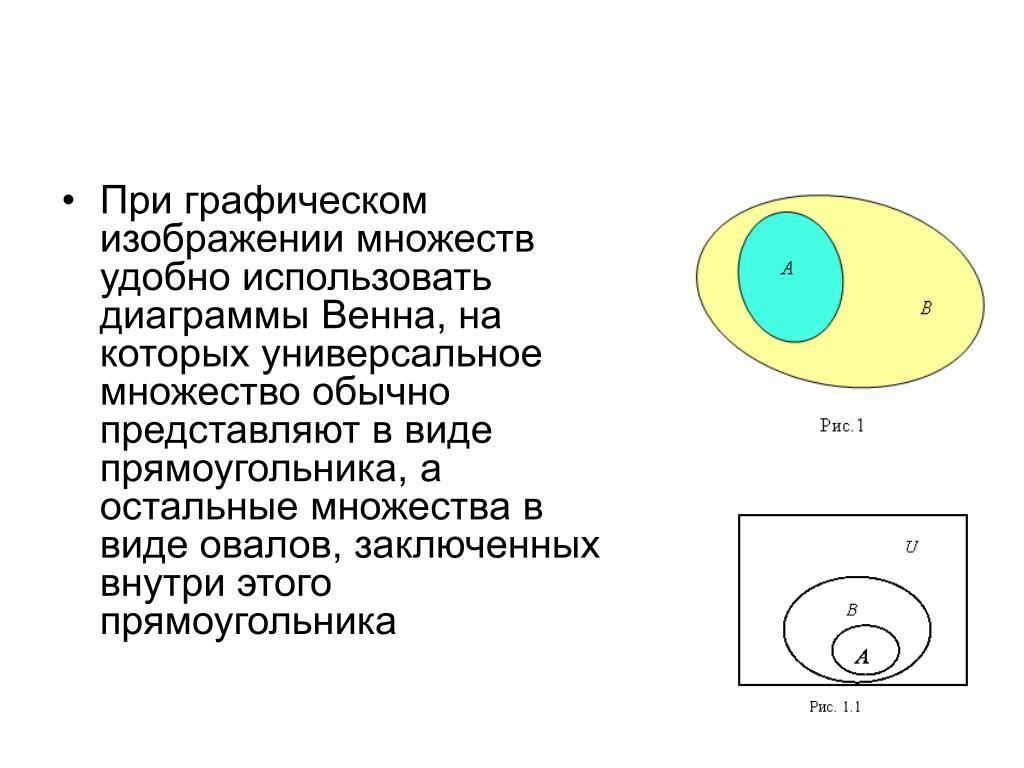
Пересечение множеств Б и П (БП) содержит 15 человек (|БП| = 15), но X человек принадлежат множеству Л. Можно определить, сколько человек занимаются баскетболом и плава нием: 15-Х (чел.).
Пересечение множеств JI и П (ЛП) содержит 18 человек (|ЛП|=18), но X человек принадлежат множеству Б. Можно определить, сколько человек занимаются лыжами и плаванием: 18-Х (чел.).
Пересечение множеств Б и JI (БЛ) содержит 16 человек (|БЛ|= 16), но X человек принадлежат множеству П. Можно определить, сколько человек занимаются баскетболом и лыжами: 16-Х (чел.).
Теперь легко определить, сколько учащихся занимаются только баскетболом:
26-(16-Х+Х+15-Х)=26-(31 -X).
Сколько учащихся занимаются только плаванием:
25-(18-Х+Х+15-Х)=25-(33-Х).
Сколько учащихся занимаются только лыжами:
27-(16-Х+Х+18-Х)=27-(34-Х).
По условию задачи известно, что в классе 40 человек и один чело век освобожден от занятий по физкультуре. Следовательно, можно составить уравнение:
25-(33-Х)+27-(34-Х)+26-(31
-Х)+15-X+l 8-Х+16-Х+Х+1 =40.
Отсюда, Х= 10, т. е. 10 человек одновременно занимаются баскет болом, плаванием и лыжами.
26-(31-10)=5 (чел.) занимаются только баскетболом.
3 (чел.) занимаются только лыжами.
25-(33-10)=2 (чел.) занимаются только плаванием.
Задача № 3
Из 40 учащихся класса выписывают газету, 21 – журнал, 15 учащихся – и газету и журнал. Сколько учащихся не выписывают ни журнала, ни газеты?
1. 32-15=17 (чел.) — выписывают только газету.
2. 21-15=6 (чел.) — выписывают только журнал.
3. 40—(15+17+6)=2 (чел.).
Ответ: 2 человека не выписывают ни газеты, ни журнала.
Задача №4
В классе 35 учеников. 20 человек посещают математический кружок, 11 – биологический. 10 человек не посещают кружков. Сколько биологов увлекается математикой?
1. 35-10=25 (чел.) — посещают кружки.
2. Пусть
X чел. посещают и биологический, и математический кружки, тогда 20-Х (чел.) —
посещают математический кружок, а 11 -X (чел.
) — посещают биологический кружок.
Известно, что всего в кружках занимаются 25 человек. Следо вательно, можно составить уравнение:
20-Х+11-Х+Х=25
Х=6
Ответ: 6 биологов увлекаются математикой.
ЗАДАЧА №5.
Из 100 человек 85 знают английский язык, 80 – испанский, 75 – немецкий. Все владеют по крайней мере одним иностранным языком. Среди них нет таких, которые знают только два иностранных языка, но есть владеющие тремя языками. Сколько человек знают три иностранных языка?
Пусть X чел. владеют тремя языками, тогда (85-Х) чел. Владе ют только английским языком,(80-Х) чел. — только испанским, (75-Х) чел. — только немецким. По условию задачи известно, что среди 100 человек нет таких, которые знают только два иностранных языка, но все владеют по крайней мере одним иностранным языком. Следовательно, можно составить уравнение:
85-Х+Х+80-Х+75-Х=100
Х=70.
Ответ: 70 человек знают три иностранных языка.
Между двумя множествами
существует несколько видов отношений.
Если множества А
и В не имеют общих элементов, то говорят, что эти множества не пересекаются и
записывают этот факт в виде А∩В =∅ . Например, А = { a , c , k }, В = { d , e , m , n }, общих элементов у этих
множеств нет, поэтому множества не пересекаются.
Если множества А и В имеют общие элементы, т.е. элементы, принадлежащие одновременно А и В, то говорят, что эти множества пересекаются и записывают А∩В≠∅ . Например, множества А = { a , c , k } и В = { c , k , m , n } пересекаются, т. к. у них есть общие элементы c , k .
Множество В является подмножеством множества А, если каждый элемент множества В является также элементом множества А. Пустое множество является подмножеством любого множества. Само множество является подмножеством самого себя. (пишут В⊂ А)
Существует пять случаев
отношений между двумя множествами. Их можно наглядно представить при помощи
особых чертежей, которые называются кругами
или диаграммами Эйлера-Венна.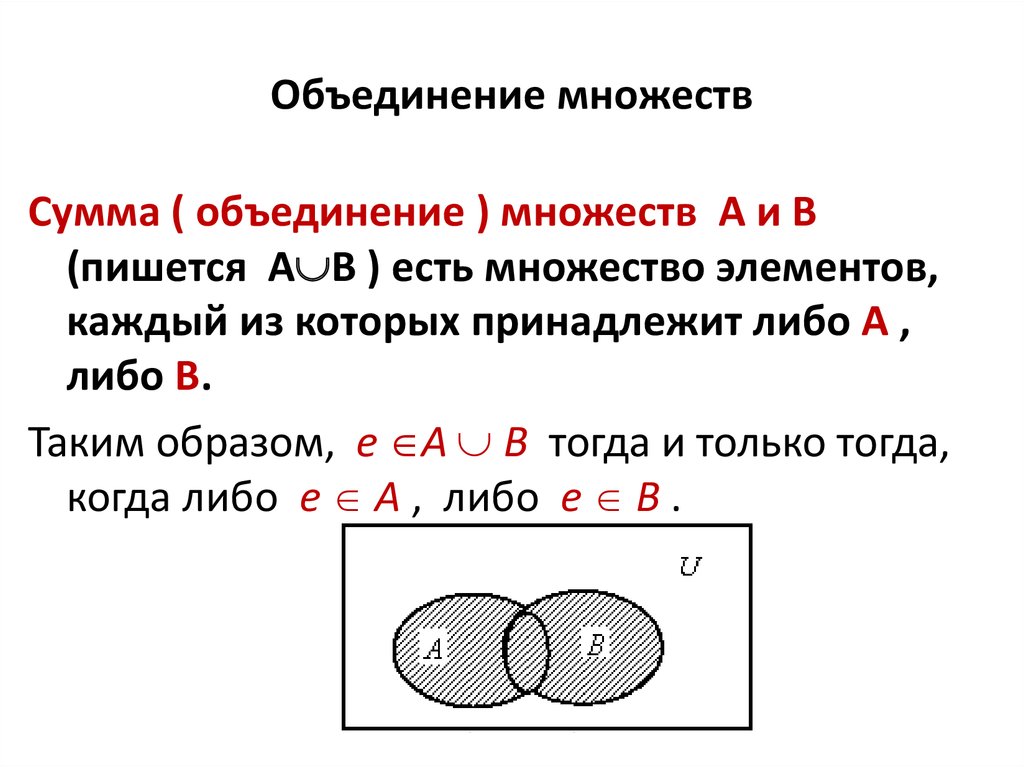
а) б) в) г) д)
Определение. Пересечением множеств А и В называется множество, содержащее все элементы, которые принадлежат множеству А и множеству В.
Пересечение множеств А и В обозначают А∩ В. Таким образом, по определению, А ∩ В = { х | х ∈ А и х ∈ В}.
Например, если А = { a , c , k , m , n } и В = { a , b , c , d , e }, то А ∩ В = { a , c }.
Если изобразить множества А и В при помощи кругов Эйлера-Венна, то пересечением данных множеств является заштрихованная область (рис. 3).
Для пересечения множеств выполняются следующие свойства.
1) Переместительное или коммутативное свойство: А ∩ В = В ∩ А.
2)
Сочетательное или ассоциативное свойство:(А ∩ В) ∩ С = А ∩ (В ∩ С).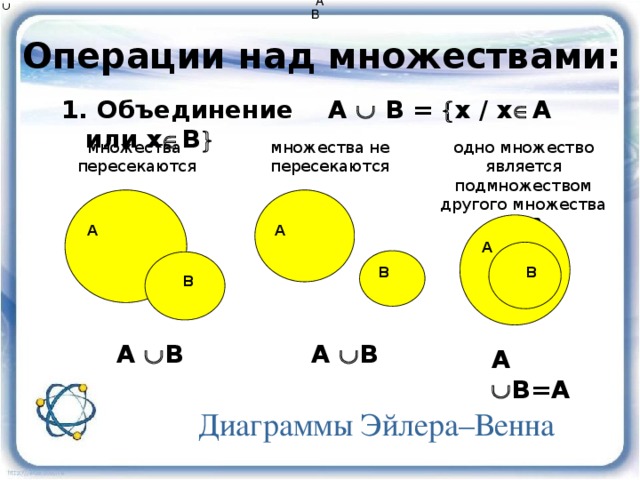
3) А ∩ ∅ = ∅ (пустое множество является поглощающим элементом).
4) А ∩ U = А (универсальное множество является нейтральным элементом).
5) Если В ⊂А, то А∩В = В
Определение. Объединением множеств А и В называется множество, содержащее все элементы, которые принадлежат множеству А или множеству В.
Объединение множеств А и В обозначают А∪ В. Таким образом, по определению, А ∪ В = { х | х ∈А или х∈В}.
Например, если А = { a , c , k , m , n } и В = { a , b , c , d , e }, то А ∪ В = { a , c , k , m , n , b , d , e }.
Если изобразить А и В при помощи кругов Эйлера-Венна, то объединением данных множеств является заштрихованная область
Для объединения множеств выполняются следующие свойства.
1) Переместительное или коммутативное свойство: А ∪ В = В ∪ А.
2) Сочетательное или ассоциативное свойство:(А ∪ В)∪ С = А ∪ (В ∪ С).
3) А ∪ ∅= А (пустое множество является нейтральным элементом).
4) А ∪ U = U (универсальное множество является поглощающим элементом).
5) Если В ⊂А, то А∪В = В
Операции объединения и пересечения множеств связаны законами дистрибутивности или иначе распределительными свойствами:
(А ∪ В) ∩С = (А∩С) ∪ (В∩С) и (А∩В) ∪ С = (А ∪ С) ∩(В ∪ С).
П р и м е р 1. Пусть А – множество различных букв в слове «математика», а В – множество различных букв в слове «стереометрия». Найти пересечение и объединение множеств А и В.
Р е ш е н и е. Запишем
множества А и В, перечислив их элементы: А = { м, а, т, е, и, к }, В = { с, т, е, р, о, м, и, я }. Буквы м, т, е, и принадлежат и множеству А, и
множеству В, поэтому они войдут в пересечение этих множеств: А∩В = { м, т, е, и }. В объединение этих множеств
войдут все элементы множества А и несовпадающие с ними элементы из множества В:
А ∪ В = { м, а, т, е, и, к, с, р, о, я }.
П р и м е р 2 . В классе английский язык изучают 25 человек, а немецкий – 27 человек, причем 18 человек изучают одновременно английский и немецкий языки. Сколько всего человек в классе изучают эти иностранные языки? Сколько человек изучают только английский язык? Только немецкий язык?
Р е ш е н и е.
Через А обозначим множество школьников, изучающих английский язык, через В –
множество школьников, изучающих
немецкий язык. Изобразим эту ситуацию с помощью диаграммы. Два языка изучают 18
школьников, поставим это число в пересечение множеств А и В. Английский язык
изучают 25 человек, но среди них 18 человек изучают и немецкий язык, значит,
только английский язык изучают 7 человек, укажем это число на диаграмме.
Рассуждая аналогично, получим, что только немецкий язык изучают 27 – 18 = 9
человек. Поместим и это число на диаграмму. Теперь известно количество
элементов в каждой части множеств, изображенных на диаграмме. Чтобы
ответить на главный вопрос задачи, нужно сложить все числа: 7 + 18 + 9 =
34.
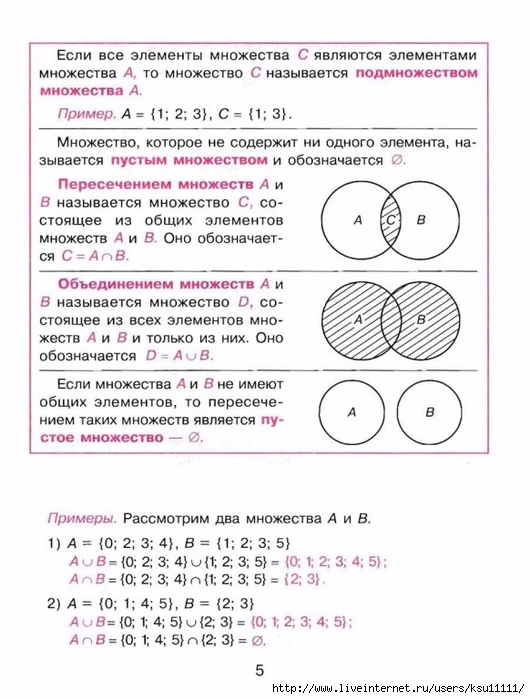Ответ: 34 человека в классе изучают иностранные языки.
Определение. Разностью множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству А и не принадлежат множеству В.
Разность множеств А и В обозначают А \ В. Таким образом, по определению разности А \ В = { х | х ∈ А и х ∉В}.
Например, если А = { a , c , k , m , n } и В = { a , b , c , d , e }, то А \ В = { k , m , n }.
Если изобразить А и В при помощи кругов Эйлера-Венна, то разность данных множеств является заштрихованная область (рис. 5).
Определение. Пусть В является подмножеством
множества А. В этом случае разность множеств А и В называют дополнением подмножества В до множества А и
обозначают В’А. Дополнение
можно изобразить как показано на рис. 5. Если В – подмножество универсального
множества U, то дополнение подмножества В до U обозначают В’.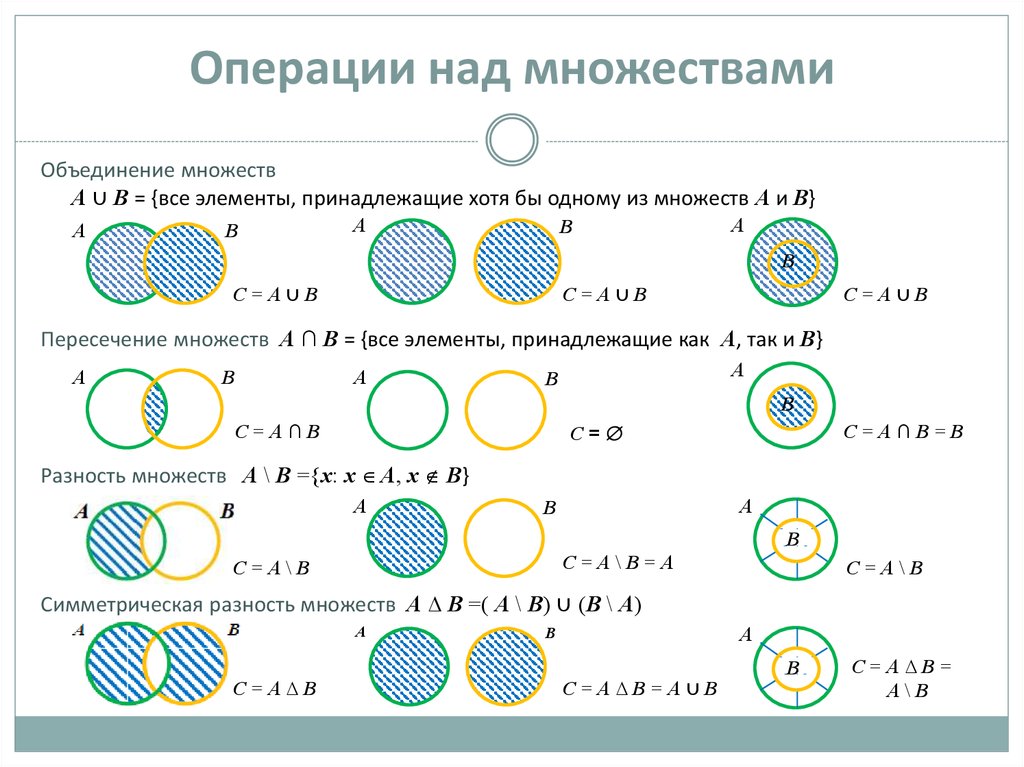
Например, если В – множество однозначных натуральных чисел, то В’– множество неоднозначных натуральных чисел, если С – множество равнобедренных треугольников, то С’ – множество треугольников, у которых все стороны имеют разную длину.
Разность множеств и дополнение к подмножеству обладают рядом свойств.
1) (А \ В) \ С = (А \ С) \ В.
2) (А∪В) \ С = (А \ С) ∪ (В \ С).
3) (А \ В) ∩ С = (А ∩С) \ (В ∩ С).
4) (А ∪ В)’ = А’ ∩ В’.
5) (А ∩ В)’ = А’ ∪В’.
Четвертое свойство формулируется так: дополнение к объединению двух множеств равно пересечению дополнений к этим множествам. Пятое свойство формулируется аналогично.
П р и м е р 1. А – множество натуральных чисел, кратных 3, В – множество натуральных чисел, кратных 5. Задать описанием характеристического свойства множество А \ В и назвать три числа, принадлежащих этому множеству.
Р е ш е н и е. По
определению разность данных множеств состоит из натуральных чисел, кратных 3 и
не кратных 5.
Поэтому разности множеств А и В принадлежат числа 9, 24, 33.
Задания для самостоятельной работы по теме :
1. Приведите примеры множеств А, В, С, если отношения между ними таковы:
2. Образуйте все подмножества множества букв в слове «крот». Сколько подмножеств получилось?
3. Даны множества А = { a , b , c , d , e , f , k } и В = { a , c , e , k , m , p }. Найдите А ∪ В , А ∩ В , А \ В , В \ А .
4. Из множества N выделили два
подмножества: А – подмножество натуральных
чисел, кратных 3, и В – подмножество натуральных
чисел, кратных 5. Постройте круги Эйлера для множеств N , A , B ; установите, на сколько
попарно непересекающихся множеств произошло разбиение множества N ; укажите характеристические
свойства этих множеств.
5. Имеется множество блоков, различающихся по цвету (красные, желтые, зеленые), форме (круглые, треугольные, прямоугольные), размеру (большие, маленькие). На сколько классов разбивается множество, если в нем выделены подмножества: А – круглые блоки, В – зеленые блоки, С – маленькие блоки? Сделайте диаграмму Эйлера и охарактеризуйте каждый класс.
6. Известно, что А – множество спортсменов класса, В – множество отличников класса. Сформулируйте условия, при которых: а) А ∩В=Ø б)А U В=А
7. Пусть Х= { x N/ 1 x 15}. Задайте с помощью перечисления следующие его подмножества:
А – подмножество всех четных чисел;
В – подмножество всех нечетных чисел;
С – подмножество всех чисел, кратных 3;
D – подмножество всех чисел, являющихся квадратами;
E – подмножество всех простых чисел.
В каких отношениях они находятся?
6. Рефлексия
- Мне больше всего удалось…
- Для меня было открытием то, что …
- За что ты можешь себя похвалить?
- Что на ваш взгляд не удалось? Почему? Что учесть на будущее?
- Мои
достижения на уроке.
Раздаточный материал
ЗАДАЧа № 1.
«В пятых классах школы училось 70 человек. Им было предложено записаться в 3 кружка: по математике, литературе и истории. Староста подсчитал число учащихся, желающих участвовать во внеклассной работе, и получил такие результаты. В кружок по математике записалось 51 человек, по литературе — 40, по истории — 22. 6 человек решили заниматься во всех кружках, математикой и литературой решили заниматься 32 человека, одновременно заниматься математикой и историей решили 11 человек, а литера турой и историей 8 человек. Получив результаты, староста сказал: «Можно подумать, что у нас в 5-х классах обучается не 70 человек, а 170. Все хотят заниматься в кружках».
Однако один из любителей математики сказал: «Что ты, у нас есть ученики, которые не любят ни математику, ни литературу, ни исто рию. Я даже могу сказать, сколько их». Как он узнал?»
ЗАДАЧа № 2.
«В
классе 40 человек.
Играют в баскетбол 26 человек, занимаются плаванием — 25,
ходят на лыжах — 27. Одновременно занимаются плаванием и баскетболом — 15,
баскетболом и лыжами — 16, пла ванием и лыжами — 18. Один человек освобожден от
занятий по физ культуре. Сколько человек занимается всеми указанными видами
спорта? Сколько человек занимается только в одной спортивной секции?».
Задача № 3
Из 40 учащихся класса выписывают газету, 21 – журнал, 15 учащихся – и газету и журнал. Сколько учащихся не выписывают ни журнала, ни газеты?
Задача №4
В классе 35 учеников. 20 человек посещают математический кружок, 11 – биологический. 10 человек не посещают кружков. Сколько биологов увлекается математикой?
ЗАДАЧА №5.
Из 100 человек 85 знают английский язык, 80 – испанский, 75 – немецкий. Все владеют по крайней мере одним иностранным языком. Среди них нет таких, которые знают только два иностранных языка, но есть владеющие тремя языками. Сколько человек знают три иностранных языка?
Основы набора
Основы набораКомплект
Основы набора
Предметы для изучения
- равенство множеств
- подмножество, правильное подмножество
- пустой набор
- универсальный набор
- блок питания
Содержимое
Определение (Равенство множеств): Два множества равны равно тогда и только тогда, когда у них одни и те же элементы.
Более формально, для любых наборов A и Б , А = В тогда и только тогда, когда х [ х А х В ].
Таким образом, например, { 1, 2, 3 } = { 3, 2, 1 } , то есть порядок элементов не имеет значения, и { 1, 2, 3 } = { 3, 2, 1, 1 } , то есть дублирования не происходит не имеет значения для наборов.
Определение (подмножество): Набор А является
подмножество набора B тогда и только тогда, когда
все в A есть и в B .
Более формально, для любых наборов A и B , A является подмножеством B и обозначается как А B , тогда и только тогда, когда х [ х А х В ].
Если А Б ,
а также А Б ,
тогда A называется правильное подмножество B и обозначается А Б .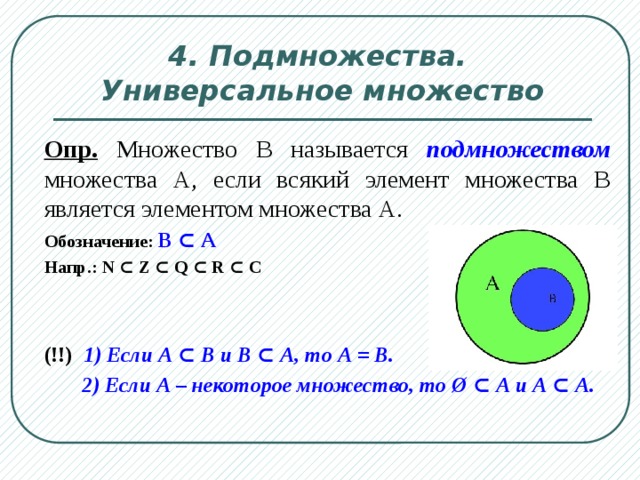
Например { 1, 2 } { 3, 2, 1 } .
Также { 1, 2 } { 3, 2, 1 } .
Определение (мощность): Если набор S имеет n различные элементы для некоторого натурального числа n , n мощность (размер) S и S является конечным множеством . Мощность S обозначается как | С | .
Например, мощность набора { 3, 1, 2 } равна 3 .
Определение (Пустой набор): Набор, который не имеет элементов, называется
пустой набор.
Более формально, пустой набор , обозначаемый , представляет собой набор, который удовлетворяет следующему:
х х .
Определение (Универсальный набор): Набор, содержащий все элементы
Вселенная дискурса называется
универсальный набор.
Более формально, универсальный набор , обозначаемый У , представляет собой набор, который удовлетворяет следующему:
х х У .
Три отношения подмножества, включающие пустой набор и универсальный набор, перечислены ниже. как теорема без доказательства. Их доказательства найдены в другом месте.
Теорема 1: Для произвольного множества A А У .
Теорема 2: Для произвольного множества A А .
Теорема 3: Для произвольного набора A А А .
Определение (силовой набор): Набор всех подмножеств набора A называется набором мощности из A и обозначается 2 А или ( А ) .
Например, для A = { 1, 2 } , ( А )
знак равно
,
{ 1 },
{ 2 },
{ 1, 2 } } .
Для B = {{ 1, 2 }, {{ 1 }, 2}, } , ( Б ) знак равно , {{ 1, 2 }}, {{{ 1 }, 2}}, {}, {{ 1, 2 }, {{ 1 }, 2}}, {{ 1, 2 }, }, { {{ 1 }, 2}, }, {{ 1, 2 }, {{ 1 }, 2}, } } .
Теорема 4: Для произвольного набора A , количество подмножеств A составляет 2 |А| .
Проверьте свое понимание базовых концепций набора
Далее — Математическое мышление
Вернуться к расписанию
Вернуться к оглавлению
Урок по подмножествам | Математические вкусности
Форма поиска
Поиск
Пример 1: Учитывая A = {1, 2, 4} и B = {1, 2, 3, 4, 5}, какова связь между этими множествами?
Мы говорим, что A является подмножеством B , поскольку каждый элемент A также входит в B .
Это обозначается:
Диаграмма Венна для отношения между этими множествами показана справа.
Ответ: A является подмножеством B .
Другой способ определить подмножество: A является подмножеством B , если каждый элемент A 9002 содержится в Оба определения показаны на приведенной выше диаграмме Венна.
Пример 2: Учитывая X = {a, r, e} и Y = {r, e, a, d}, какова связь между этими множествами?
We say that X is a subset of Y , since every element of X is also in Y. This is denoted by:
A Venn diagram for the связь между этими наборами показана справа.
Ответ: X является подмножеством Y .
Пример 3: Учитывая P = {1, 3, 4} и Q = {2, 3, 4, 5, 6}, какова связь между этими множествами?
, мы говорим, что P не является подмножеством Q S Ince Не каждый элемент P не содержится в Q.
. Например, мы можем видеть, что 1 Q . Утверждение «P не является подмножеством Q» обозначается:
Обратите внимание, что эти множества имеют некоторые общие элементы. Пересечение этих множеств показано на диаграмме Венна ниже.
Ответ: P не является подмножеством Q .
Обозначения для подмножеств показаны ниже.
| Символ | Значение |
| является подмножеством | .|
| не является подмножеством |
Пример 4: Учитывая A = {1, 2, 3, 4, 5} и B = {3, 1, 2, 5, 4}, какова связь между A и B ?
Анализ: Напомним, что порядок, в котором элементы появляются в наборе, не важен.
Глядя на элементы этих множеств, становится ясно, что:
Ответ: A и B эквивалентны.
Определение: Для любых двух наборов, если A B и B A, , то 9A = B.0030 Таким образом, A и B эквивалентны.
Пример 5: Список всех подмножеств набора C = {1, 2, 3}.
Ответ:
| Подмножество | Список всех возможных комбинаций элементов … |
| Д = {1} | по одному |
| E = {2} | по одному |
| Ф = {3} | по одному |
| Г = {1, 2} | два за раз |
| M = {1, 3} | два за раз |
| N = {2, 3} | два за раз |
| P = {1, 2, 3} | три за раз |
| Ø | Пустой набор не содержит элементов. |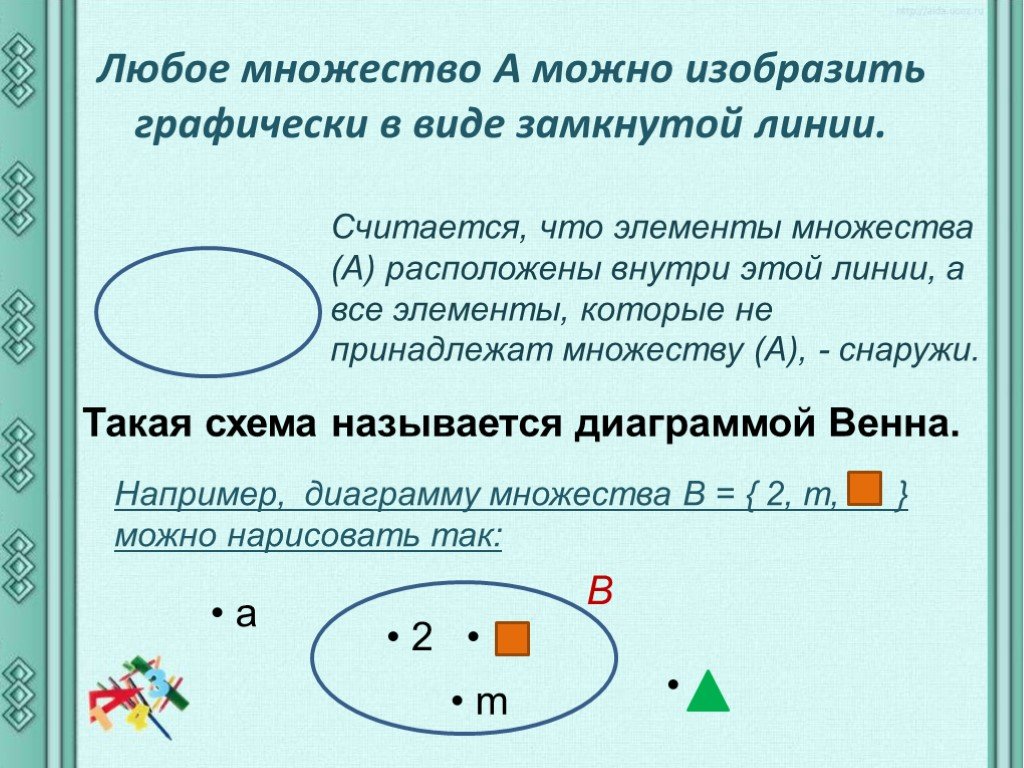
Глядя на пример 5, вы можете удивиться, почему нулевой набор указан как подмножество C. В нулевом наборе нет элементов, поэтому в нулевом наборе не может быть элементов, не содержащихся в полный комплект. Следовательно, нулевой набор является подмножеством каждого набора. Вам также может быть интересно: является ли множество подмножеством самого себя? Ответ положительный: любое множество содержит себя как подмножество. Обозначается:
A A.
Подмножество, которое меньше полного набора, называется правильным подмножеством . Таким образом, набор {1, 2} является правильным подмножеством набора {1, 2, 3}, поскольку элемент 3 не входит в первый набор. В примере 5 видно, что G является правильным подмножеством C . На самом деле каждое подмножество, указанное в примере 5, является правильным подмножеством C, , кроме P . Это связано с тем, что P и C являются эквивалентными множествами ( P = C ) .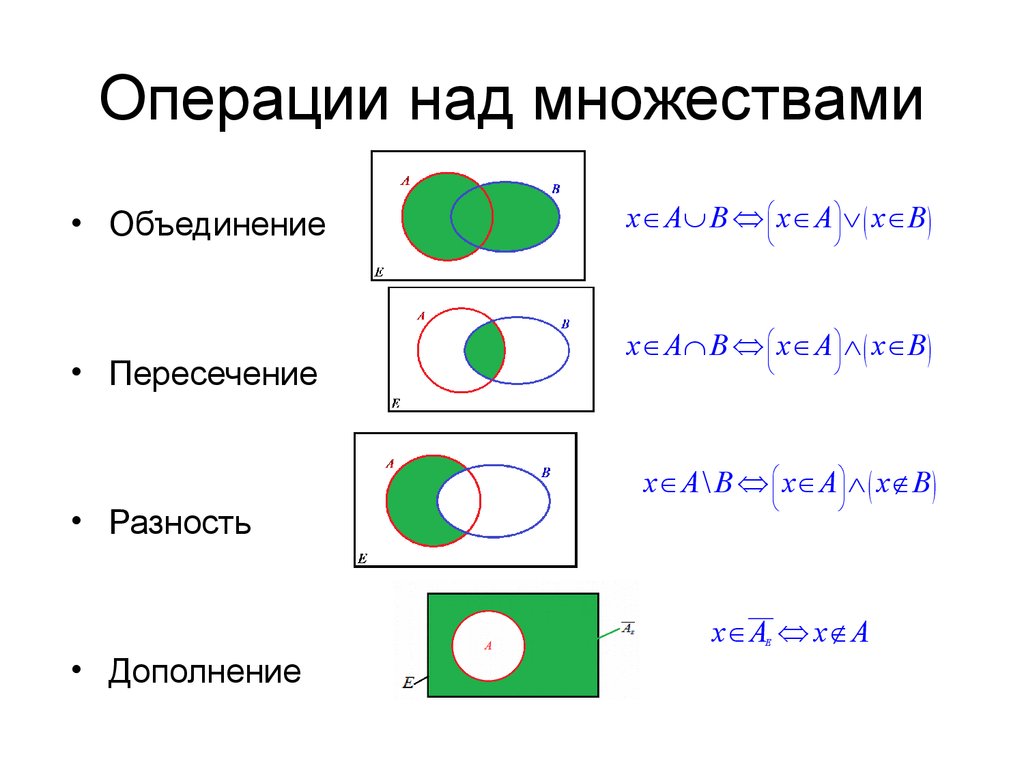
Некоторые математики используют символ для обозначения подмножества и символ для обозначения правильного подмножества, при этом определение правильных подмножеств выглядит следующим образом:
называется собственным подмножеством B и обозначается как A B .
Хотя важно указать на приведенную выше информацию, она может немного запутать. Итак, давайте думать о подмножествах и правильных подмножествах следующим образом:
| Подмножества и собственные подмножества |
| Множество {1, 2} является правильным подмножеством множества {1, 2, 3}. |
| Множество {1, 2, 3} не является правильным подмножеством множества {1, 2, 3}. |
Видите ли вы закономерность в приведенных ниже примерах?
Пример 6: Список всех подмножеств набора R = {x, y, z}.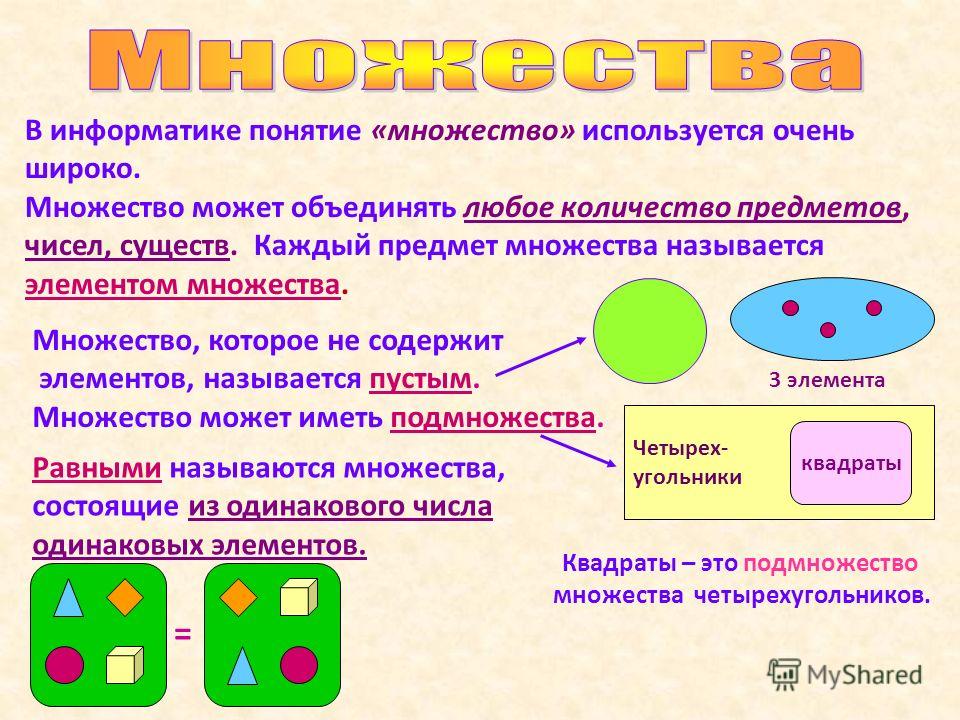
Сколько их там?
| Подмножества |
| D = {х} |
| E = {г} |
| F = {z} |
| G = {х, у} |
| Н = {х, г} |
| J = {у, г} |
| К = {х, у, г} |
| Ø |
Ответ: Существует восемь подмножеств множества R = {x, y, z}.
Пример 7: Список всех подмножеств набора C = {1, 2, 3, 4}. Сколько их там?
| Подмножества | |
| Д = {1} | М = {2, 4} |
| E = {2} | N = {3, 4} |
| Ф = {3} | О = {1, 2, 3} |
| Г = {4} | P = {1, 2, 4} |
| Н = {1, 2} | Q = {1, 3, 4} |
| J = {1, 3} | Ч = {2, 3, 4} |
| К = {1, 4} | S = {1, 2, 3, 4} |
| Л = {2, 3} | Ø |
Ответ: Существует 16 подмножеств множества C = {1, 2, 3, 4}.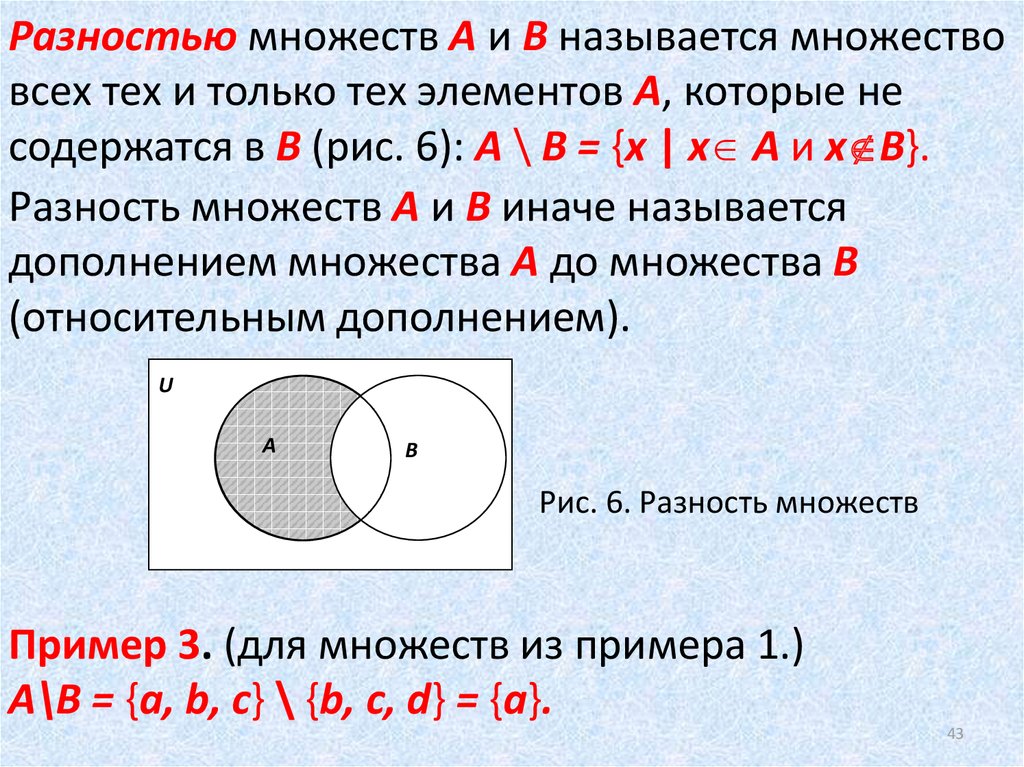
В примере 6 набор R состоит из трех (3) элементов и восьми (8) подмножеств. В примере 7 набор C состоит из четырех (4) элементов и 16 подмножеств. Чтобы найти количество подмножеств множества из n элементов, возведите 2 в n-ю степень: То есть:
Количество подмножеств в множестве A равно 2 n , где n — количество элементов в множестве A.
Краткое содержание урока
Подмножество: A является подмножеством B: , если каждый элемент A содержится в B . Это обозначается A B.
Эквивалентные наборы: для любых двух наборов, если A B и B A, Then A = B. B. 44444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444. A . Нулевой набор: Нулевой набор является подмножеством каждого набора.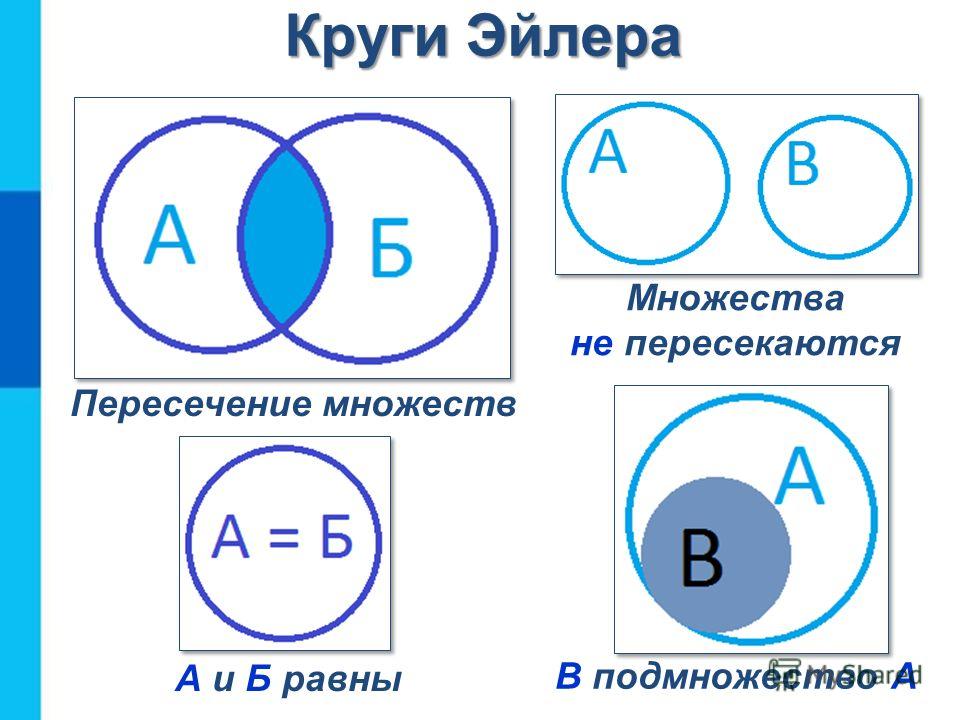
Наборы и подмножества: Любой набор содержит себя как подмножество. Обозначается A A.
Правильные подмножества: , если A B и A ≠ B , затем A , как говорят, является правильной суббот. обозначается A B .
Количество подмножеств: Количество подмножеств в наборе A равно 2 n , где n – количество элементов в наборе A.
Упражнения Указания: Прочитайте каждое ниже. Выберите свой ответ, нажав на его кнопку. Обратная связь по вашему ответу представлена в ОКНО РЕЗУЛЬТАТЫ. Если вы допустили ошибку, обдумайте свой ответ еще раз, а затем выберите другую кнопку.
| 1. | Что из следующего является подмножеством множества G? G = {d, a, r, e} |
| X = {e, a, r} Y = {e, r, a} Z = {r, e, d} Все вышеперечисленное.  ОКНО РЕЗУЛЬТАТОВ: |
| 2. | Какое из следующих утверждений верно? |
| {гласные} {согласные} {согласные} {гласные} {гласные} {алфавит} Ничего из вышеперечисленного. ОКНО РЕЗУЛЬТАТОВ: |
| 3. | Что из нижеперечисленного НЕ является подмножеством набора A? А = {2, 3, 5, 7, 11} |
| B = {3, 5, 2, 7} C = {2, 3, 7, 9} D = {7, 2, 3, 11} Все вышеперечисленное. ОКНО РЕЗУЛЬТАТОВ: |
4. |