|
Пожалуйста активируйте JavaScript в настройках браузера.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Отношение синуса угла к его косинусу это тест — Тестирование
Отношение синуса угла к его косинусу это тест
Тесты по геометрии 9 класс. Тема: «Синус, косинус, тангенс»
Тема: «Синус, косинус, тангенс»
Правильный вариант ответа отмечен знаком +
1. Как называется раздел математики, изучающий функции синуса, косинуса, тангенса и их применение?
2. Тригонометрические функции синуса и косинуса называются… тригонометрическими функциями. Вставьте пропущенное слов:
3. Выберите производную тригонометрическую функцию из предложенных:
4. С помощью какой фигуры определяются тригонометрические функции для острого угла?
5. Что такое синус острого угла?
— произведение двух прилежащих сторон в равностороннем треугольнике
+ отношение противолежащего катета в прямоугольном треугольнике к гипотенузе
— отношение прилежащего катета в прямоугольном треугольнике к гипотенузе
— отношение прилежащей стороны в параллелограмме к высоте, опущенной на эту сторону
6. Если в единичной полуокружности провести луч, который будет пересекать полуокружность в точке K.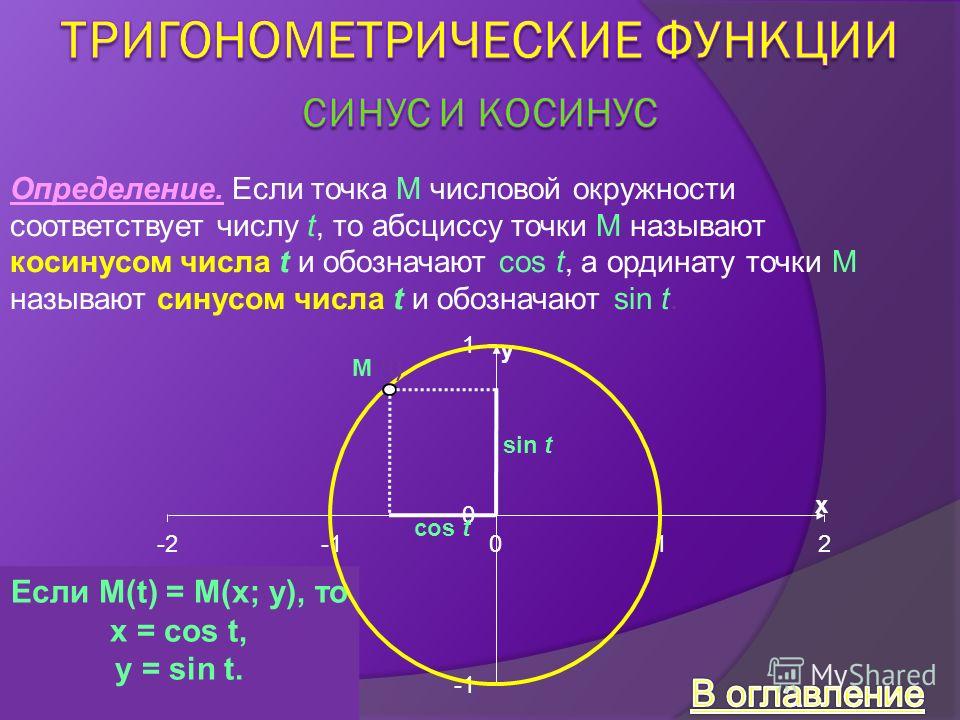 Чему будет равен синус угла, образованного лучом и осью абсцисс?
Чему будет равен синус угла, образованного лучом и осью абсцисс?
— абсциссе точки K
+ ординате точки K
7. В каких пределах располагается значение синуса острога угла?
8. Может ли синус угла быть равен 0?
— может, если угол тупой
+ может, если угол равен 0° или 180°
— может, если угол равен 90°
9. Дан треугольник FBK. Известно, что FB=14 см, BK=7 см. Найдите синус угла BFK.
Тест 10. На рисунке изображен треугольник DNL, у которого известны три стороны. Найдите синус угла DNL.
11. На рисунке изображен ромб KEUT, диагонали которого пересекаются в точке O. Известно, что длина меньшей диагонали равна 6 см, большей диагонали – 8 см. Необходимо найти синус угла KET.
12. Отношение прилежащего катета к гипотенузе в прямоугольном треугольнике называется… Закончите утверждение.
— котангенсом острого угла
— арккосинусом острого угла
+ косинусом острого угла
— арксинусом острого угла
13.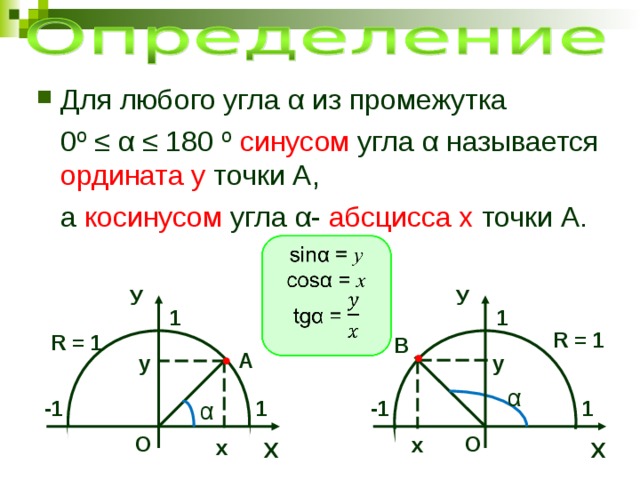 Может ли косинус быть отрицательным?
Может ли косинус быть отрицательным?
— может, если угол прямой
— может, если угол равен 0°
+ может, если угол тупой
14. Чему равен косинус прямого угла?
15. В прямоугольном треугольнике прилежащий к углу α катет равен 2 см, противолежащий – 1 см, а гипотенуза равна 5 см. Чему равен косинус угла α?
16. На рисунке изображена координатная плоскость с единичной полуокружностью. Координаты точки F равны (-0,7; 0,5). Найдите косинус угла α.
— невозможно определить, так как косинус вычисляется только для острых углов в прямоугольном треугольнике
17. Выберите верную тригонометрическую формулу приведения:
+ все перечисленные формулы являются формулами приведения
18. Косинус какого угла равен синусу 30°?
19. Синус какого угла равен синусу 170°?
— синус не вычисляется для тупых углов
Тест-20. Что такое тангенс острого угла в прямоугольном треугольнике?
— отношение прилежащего катета к противолежащему
+ отношение противолежащего катета к прилежащему
— отношение прилежащего катета к гипотенузе
— отношение противолежащего катета к гипотенузе
21.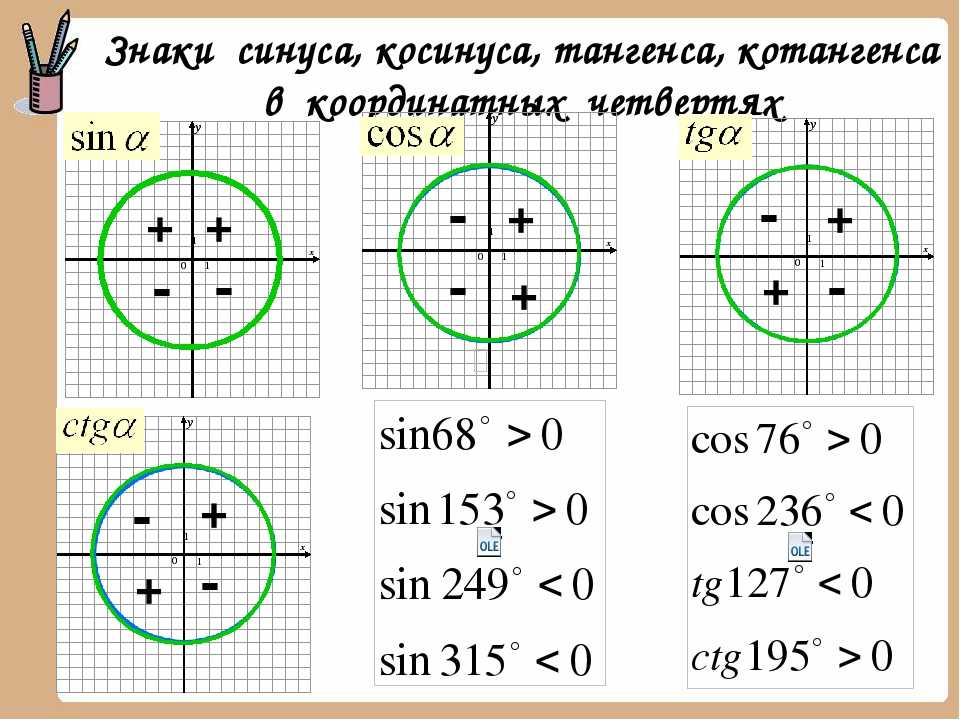 Как иначе можно найти тангенс угла?
Как иначе можно найти тангенс угла?
— через отношение единицы к синусу угла
— через отношение косинуса угла к синусу
+ через отношение синуса угла к косинусу
— через отношение единицы к косинусу угла
22. С помощью какой таблицы можно определить значения основных тригонометрических функций?
— таблицы простых чисел
23. Известно, что FBXC – квадрат со стороной 17 см. Найдите тангенс угла XFB.
24. Известно, что косинус угла равен 0,5. Определите тангенс этого угла.
25. Выберите формулу основного тригонометрического тождества?
26. Найдите, чему равно значение выражения 4sin(90°)α +3cos(0°).
27. Дан прямоугольный треугольник, в котором синус одного из углов равен 0,6. Найдите косинус этого угла.
Выберите формулу основного тригонометрического тождества.
Testua. ru
12.07.2017 6:23:35
2017-07-12 06:23:35
Источники:
Https://testua. ru/geometriya/204-testy-po-geometrii-9-klass/2215-testy-sinus-kosinus-tangens-9-klass-s-otvetami. html
ru/geometriya/204-testy-po-geometrii-9-klass/2215-testy-sinus-kosinus-tangens-9-klass-s-otvetami. html
Синус, косинус, тангенс и котангенс в тригонометрии: определения, формулы, примеры, угол поворота » /> » /> .keyword { color: red; }
Отношение синуса угла к его косинусу это тест
Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Синус, косинус, тангенс и котангенс. Определения
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.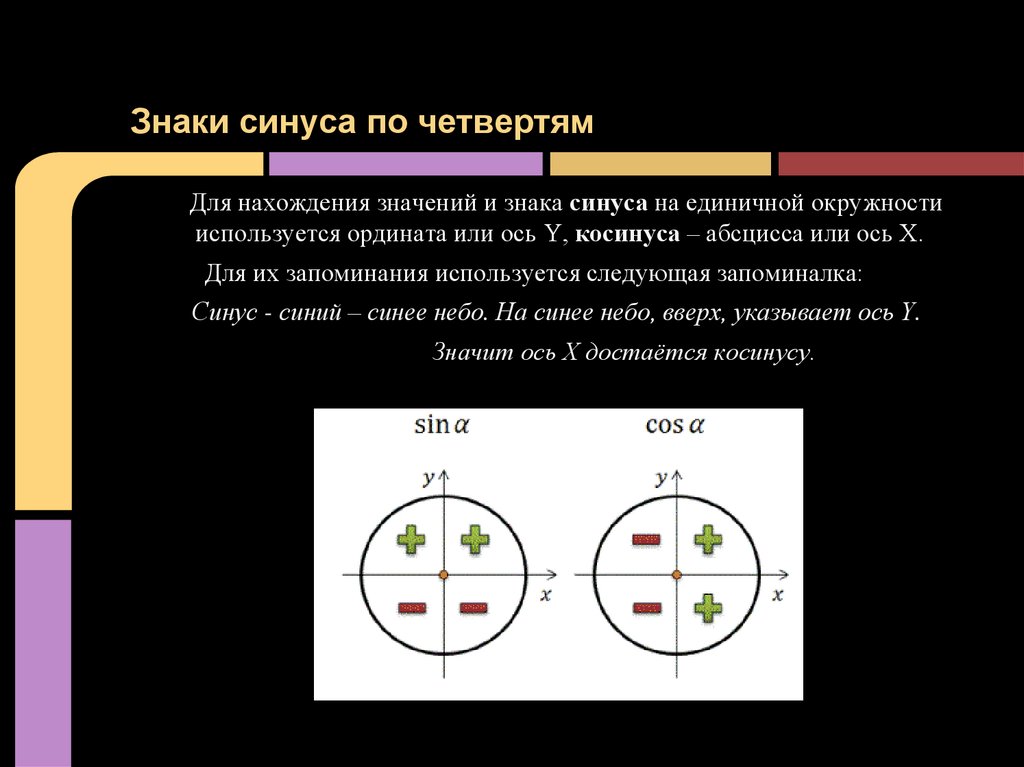
Определения тригонометрических функций
Синус угла ( sin α ) — отношение противолежащего этому углу катета к гипотенузе.
Косинус угла ( cos α ) — отношение прилежащего катета к гипотенузе.
Тангенс угла ( t g α ) — отношение противолежащего катета к прилежащему.
Котангенс угла ( c t g α ) — отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.
Угол поворота
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов. Угол поворота в градусах или радианах выражается любым действительным числом от — ∞ до + ∞ .
Угол поворота в градусах или радианах выражается любым действительным числом от — ∞ до + ∞ .
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Начальная точка A с координатами ( 1 , 0 ) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A 1 . Определение дается через координаты точки A 1 ( x, y ).
Синус (sin) угла поворота
Синус угла поворота α — это ордината точки A 1 ( x, y ). sin α = y
Косинус угла поворота α — это абсцисса точки A 1 ( x, y ). cos α = х
Тангенс угла поворота α — это отношение ординаты точки A 1 ( x, y ) к ее абсциссе. t g α = y x
Котангенс угла поворота α — это отношение абсциссы точки A 1 ( x, y ) к ее ординате. c t g α = x y
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле.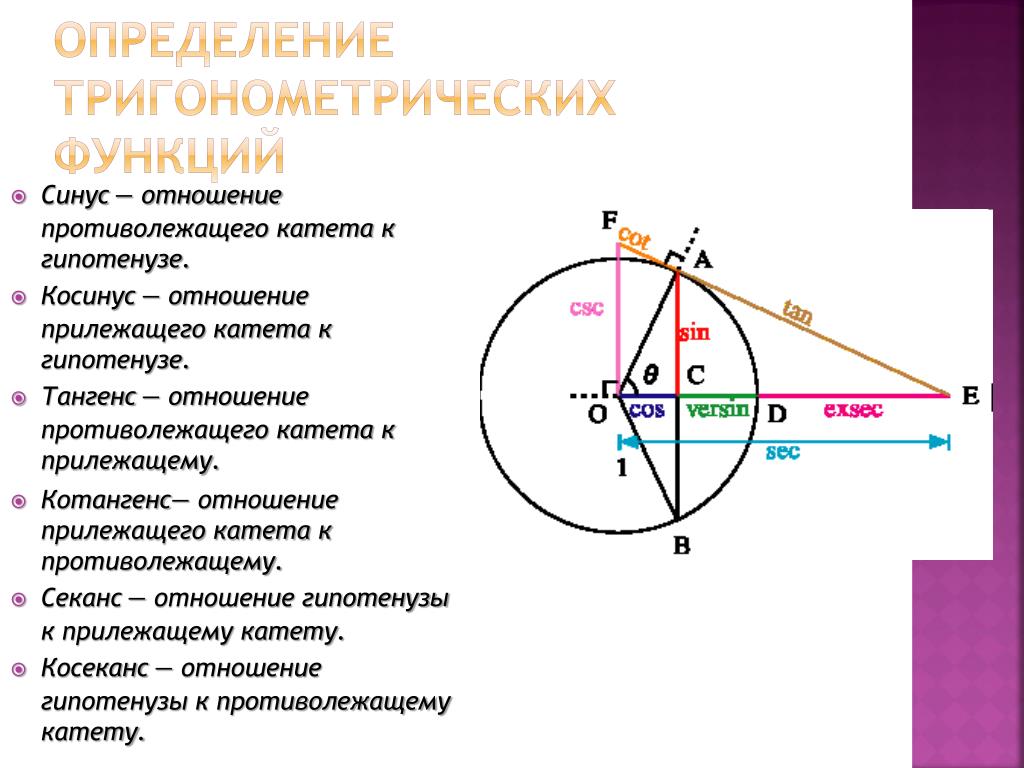 Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой ( 0 , 1 ) и ( 0 , — 1 ). В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой ( 0 , 1 ) и ( 0 , — 1 ). В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Синус и косинус определены для любых углов α.
Тангенс определен для всех углов, кроме α = 90 ° + 180 ° · k, k ∈ Z ( α = π 2 + π · k, k ∈ Z )
Котангенс определен для всех углов, кроме α = 180 ° · k, k ∈ Z ( α = π · k, k ∈ Z )
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа T называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в T радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу T ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности — точка A c координатами ( 1 , 0 ).
Положительному числу T соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.
Отрицательному числу T соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус (sin) числа t
Синус числа T — ордината точки единичной окружности, соответствующей числу T. sin t = y
Косинус числа T — абсцисса точки единичной окружности, соответствующей числу T. cos t = x
Тангенс числа T — отношение ординаты к абсциссе точки единичной окружности, соответствующей числу T. t g t = y x = sin t cos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу T, совпадает с точкой, в которую переходит начальная точка после поворота на угол T радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α, отличным от α = 90 ° + 180 ° · k, k ∈ Z ( α = π 2 + π · k, k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α, кроме α = 180 ° · k, k ∈ Z ( α = π · k, k ∈ Z ).
Котангенс, как сказано выше, определен для всех α, кроме α = 180 ° · k, k ∈ Z ( α = π · k, k ∈ Z ).
Можно сказать, что sin α, cos α, t g α, c t g α — это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу T соответствует определенное значение синуса или косинуса числа T. Всем числам, отличным от π 2 + π · k, k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k, k ∈ Z.
Основные функции тригонометрии
Синус, косинус, тангенс и котангенс — основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A ( 1 , 0 ) на угол величиной до 90 градусов и проведем из полученной точки A 1 ( x, y ) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α, длина катета O H равна абсциссе точки A 1 ( x, y ) . Длина катета, противолежащего углу, равна ординате точки A 1 ( x, y ) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
Sin α = A 1 H O A 1 = y 1 = y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α, при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Угол поворота в градусах или радианах выражается любым действительным числом от — до.
Zaochnik. com
22.09.2018 10:18:08
2018-01-29 11:43:53
Источники:
Https://zaochnik. com/spravochnik/matematika/trigonometrija/sinus-kosinus-tangens-i-kotangens/
Синус, косинус, тангенс острого угла в прямоугольном треугольнике » /> » /> .keyword { color: red; }
Отношение синуса угла к его косинусу это тест
Внимание! Все тесты в этом разделе разработаны пользователями сайта для собственного использования. Администрация сайта не проверяет возможные ошибки, которые могут встретиться в тестах.
Тест состоит из 11 вопросов по теме «Синус, косинус, тангенс острого угла в прямоугольном треугольнике»
Список вопросов теста
Вопрос 1
Выберите правильный ответ.
Дан треугольник АВС, в котором угол С прямой. Для угла А противолежащим катетом является:
Для угла А противолежащим катетом является:
Варианты ответов
- катет АС катет ВС
Вопрос 2
Выберите правильный ответ.
Дан треугольник АВС, в котором угол С прямой. Для угла А прилежащим катетом является:
Варианты ответов
- катет АС катет ВС
Вопрос 3
Выберите правильный ответ.
Дан треугольник АВС, в котором угол С прямой. Для угла В прилежащим катетом является:
Варианты ответов
- катет АС катет ВС
Вопрос 4
Выберите правильный ответ.
Дан треугольник АВС, в котором угол С прямой. Для угла В противолежащим катетом является:
Варианты ответов
- катет АС катет ВС
Вопрос 5
Выберите правильный ответ.
Дан прямоугольный треугольник. Отношение каких сторон треугольника называется синусом острого угла.
Варианты ответов
- Катета к гипотенузе Гипотенузы к противолежащему катету Прилежащего катета к гипотенузе Противолежащего катета к гипотенузе
Вопрос 6
Выберите правильный ответ.
Дан прямоугольный треугольник. Отношение каких сторон треугольника называется косинусом острого угла.
Варианты ответов
- Катета к гипотенузе Гипотенузы к противолежащему катету Прилежащего катета к гипотенузе Противолежащего катета к гипотенузе
Вопрос 7
Выберите правильный ответ.
Дан прямоугольный треугольник. Отношение каких сторон треугольника называется тангенсом острого угла.
Противолежащего катета к гипотенузе.
Videouroki. net
03.12.2019 14:12:41
2019-12-03 14:12:41
Источники:
Https://videouroki. net/tests/ploshchadi-3.html
Угол положительный и отрицательный. Отрицательный угол
Отсчёт углов на тригонометрическом круге.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Он почти такой, как в предыдущем уроке. Есть оси, окружность, угол, всё чин-чинарём. Добавлены номера четвертей (в уголках большого квадрата) — от первой, до четвёртой.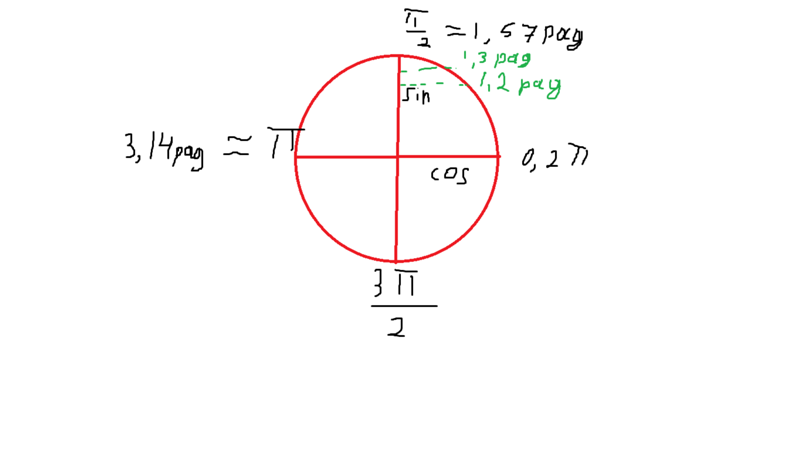 А то вдруг кто не знает? Как видите, четверти (их ещё называют красивым словом «квадранты») нумеруются против хода часовой стрелки. Добавлены значения угла на осях. Всё понятно, никаких заморочек.
А то вдруг кто не знает? Как видите, четверти (их ещё называют красивым словом «квадранты») нумеруются против хода часовой стрелки. Добавлены значения угла на осях. Всё понятно, никаких заморочек.
И добавлена зелёная стрелка. С плюсом. Что она означает? Напомню, что неподвижная сторона угла всегда прибита к положительной полуоси ОХ. Так вот, если подвижную сторону угла мы будем крутить по стрелке с плюсом , т.е. по возрастанию номеров четвертей, угол будет считаться положительным. Для примера на картинке показан положительный угол +60°.
Если будем откладывать углы в обратную сторону, по ходу часовой стрелки, угол будет считаться отрицательным. Наведите курсор на картинку (или коснитесь картинки на планшете), увидите синюю стрелку с минусом. Это — направление отрицательного отсчёта углов. Для примера показан отрицательный угол (- 60°). А ещё вы увидите, как поменялись циферки на осях… Я их тоже перевёл в отрицательные углы. Нумерация квадрантов не меняется.
Вот тут, обычно, начинаются первые непонятки. Как так!? А если отрицательный угол на круге совпадёт с положительным!? Да и вообще, получается что, одно и то же положение подвижной стороны (или точки на числовой окружности) можно обозвать как отрицательным углом, так и положительным!?
Да. Именно так. Скажем, положительный угол 90 градусов занимает на круге точно такое же положение, что и отрицательный угол в минус 270 градусов. Положительный угол, к примеру, +110° градусов занимает точно такое же положение, что и отрицательный угол -250°.
Не вопрос. Всяко правильно.) Выбор положительного или отрицательного исчисления угла зависит от условия задания. Если в условии ничего не сказано открытым текстом про знак угла, (типа «определить наименьший положительный угол» и т.д.), то работаем с удобными нам величинами.
Исключением (а как без них?!) являются тригонометрические неравенства, но там мы эту фишку освоим.
А теперь вопрос вам. Как я узнал, что положение угла 110° совпадает с положением угла -250°?
Как я узнал, что положение угла 110° совпадает с положением угла -250°?
Намекну, что это связано с полным оборотом. В 360°… Непонятно? Тогда рисуем круг. Сами рисуем, на бумаге. Отмечаем угол примерно 110°. И считаем , сколько остается до полного оборота. Останется как раз 250°…
Уловили? А теперь — внимание! Если углы 110° и -250° занимают на круге одно и то же положение, то что? Да то, что у углов 110° и -250° совершенно одинаковые синус, косинус, тангенс и котангенс!
Т.е. sin110° = sin(-250°), ctg110° = ctg(-250°) и так далее. Вот это уже действительно важно! И само по себе — есть масса заданий, где надо упростить выражения, и как база для последующего освоения формул приведения и прочих премудростей тригонометрии.
Понятное дело, 110° и -250° я взял наобум, чисто для примера. Всё эти равенства работают для любых углов, занимающих одно положение на круге. 60° и -300°, -75° и 285°, ну и так далее. Отмечу сразу, что углы в этих парочках — разные. А вот тригонометрические функции у них — одинаковые.
А вот тригонометрические функции у них — одинаковые.
Думаю, что такое отрицательные углы вы поняли. Это совсем просто. Против хода часовой стрелки — положительный отсчёт. По ходу — отрицательный. Считать угол положительным, или отрицательным зависит от нас . От нашего желания. Ну, и ещё от задания, конечно… Надеюсь, вы поняли и как переходить в тригонометрических функциях от отрицательных углов к положительным и обратно. Нарисовать круг, примерный угол, да посмотреть, сколько недостаёт до полного оборота, т.е. до 360°.
Углы больше 360°.
Займемся углами которые больше 360°. А такие бывают? Бывают, конечно. Как их нарисовать на круге? Да не проблема! Допустим, нам надо понять, в какую четверть попадёт угол в 1000°? Легко! Делаем один полный оборот против хода часовой стрелки (угол-то нам дали положительный!). Отмотали 360°. Ну и мотаем дальше! Ещё оборот — уже получилось 720°. Сколько осталось? 280°. На полный оборот не хватает… Но угол больше 270° — а это граница между третьей и четвёртой четвертью.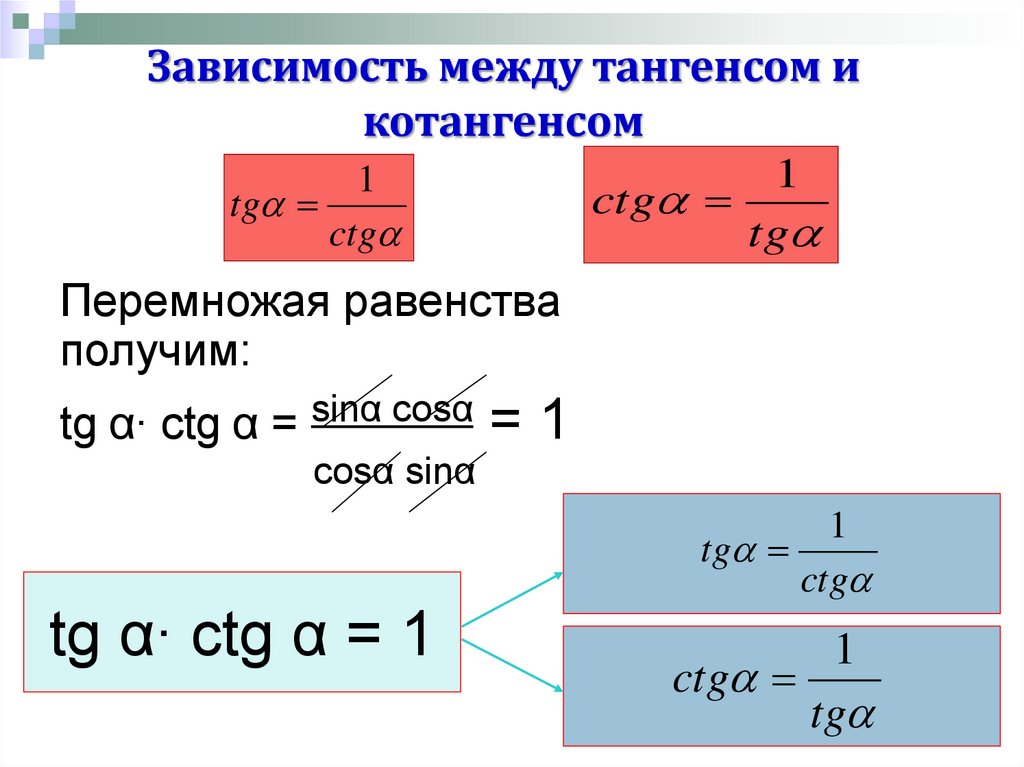 Стало быть наш угол в 1000° попадает в четвёртую четверть. Всё.
Стало быть наш угол в 1000° попадает в четвёртую четверть. Всё.
Как видите, это совсем просто. Ещё раз напомню, что угол 1000° и угол 280°, который мы получили путём отбрасывания «лишних» полных оборотов — это, строго говоря, разные углы. Но тригонометрические функции у этих углов совершенно одинаковые ! Т.е. sin1000° = sin280°, cos1000° = cos280° и т.д. Если бы я был синусом, я бы не заметил разницы между этими двумя углами…
Зачем всё это нужно? Зачем нам переводить углы из одного в другой? Да всё за тем же.) С целью упрощения выражений. Упрощение выражений, собственно, главная задача школьной математики. Ну и, попутно, голова тренируется.)
Ну что, потренируемся?)
Отвечаем на вопросы. Сначала простые.
1. В какую четверть попадает угол -325° ?
2. В какую четверть попадает угол 3000° ?
3. В какую четверть попадает угол -3000° ?
Есть проблемы? Или неуверенность? Идём в Раздел 555, Практическая работа с тригонометрическим кругом. Там, в первом уроке этой самой «Практической работы…» всё подробненько… В таких вопросах неуверенности быть не должно!
Там, в первом уроке этой самой «Практической работы…» всё подробненько… В таких вопросах неуверенности быть не должно!
4. Какой знак имеет sin555° ?
5. Какой знак имеет tg555° ?
Определили? Отлично! Сомневаетесь? Надо в Раздел 555… Кстати, там научитесь рисовать тангенс и котангенс на тригонометрическом круге. Очень полезная штучка.
А теперь вопросы помудрёнее.
6. Привести выражение sin777° к синусу наименьшего положительного угла.
7. Привести выражение cos777° к косинусу наибольшего отрицательного угла.
8. Привести выражение cos(-777°) к косинусу наименьшего положительного угла.
9. Привести выражение sin777° к синусу наибольшего отрицательного угла.
Что, вопросы 6-9 озадачили? Привыкайте, на ЕГЭ и не такие формулировочки встречаются… Так и быть, переведу. Только для вас!
Слова «привести выражение к…» означают преобразовать выражение так, чтобы его значение не изменилось, а внешний вид поменялся в соответствии с заданием. Так, в задании 6 и 9 мы должны получить синус, внутри которого стоит наменьший положительный угол. Всё остальное — не имеет значения.
Так, в задании 6 и 9 мы должны получить синус, внутри которого стоит наменьший положительный угол. Всё остальное — не имеет значения.
Ответы выдам по порядку (в нарушение наших правил). А что делать, знака всего два, а четверти всего четыре… Не разбежишься в вариантах.
6. sin57°.
7. cos(-57°).
8. cos57°.
9. -sin(-57°)
Предполагаю, что ответы на вопросы 6 -9 кое-кого смутили. Особенно -sin(-57°) , правда?) Действительно, в элементарных правилах отсчёта углов есть место для ошибок… Именно поэтому пришлось сделать урок: «Как определять знаки функций и приводить углы на тригонометрическом круге?» В Разделе 555. Там задания 4 — 9 разобраны. Хорошо разобраны, со всеми подводными камнями. А они тут есть.)
В следующем уроке мы разберёмся с загадочными радианами и числом «Пи» . Научимся легко и правильно переводить градусы в радианы и обратно. И с удивлением обнаружим, что этой элементарной информации на сайте уже хватает , чтобы решать некоторые нестандартные задачки по тригонометрии!
Если Вам нравится этот сайт. ..
.. Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
В прошлом уроке мы с вами успешно освоили (или повторили – кому как) ключевые понятия всей тригонометрии. Это тригонометрический круг , угол на круге , синус и косинус этого угла , а также освоили знаки тригонометрических функций по четвертям . Освоили подробно. На пальцах, можно сказать.
Но этого пока мало. Для успешного практического применения всех этих простых понятий нам необходим ещё один полезный навык. А именно – правильная работа с углами в тригонометрии. Без этого умения в тригонометрии – никак. Даже в самых примитивных примерах. Почему? Да потому, что угол – ключевая действующая фигура во всей тригонометрии! Нет, не тригонометрические функции, не синус с косинусом, не тангенс с котангенсом а именно сам угол . Нет угла – нету и тригонометрических функций, да…
Нет угла – нету и тригонометрических функций, да…
Как правильно работать с углами на круге? Для этого нам надо железно усвоить два пункта.
1) Как отсчитываются углы на круге?
2) В чём они считаются (измеряются)?
Ответ на первый вопрос – и есть тема сегодняшнего урока. С первым вопросом мы детально разберёмся прямо здесь и сейчас. Ответ на второй вопрос здесь не дам. Ибо достаточно развёрнутый он. Как и сам второй вопрос очень скользкий, да.) Вдаваться в подробности пока не буду. Это – тема следующего отдельного урока.
Приступим?
Как отсчитываются углы на круге? Положительные и отрицательные углы.
У прочитавших название параграфа, возможно, уже волосы встали дыбом. Как так?! Отрицательные углы? Разве такое вообще возможно?
К отрицательным числам мы с вами уже попривыкли. На числовой оси их изображать умеем: справа от нуля положительные, слева от нуля отрицательные. Да и на градусник за окном поглядываем периодически. Особенно зимой, в мороз.) И денежки на телефоне в «минус» (т.е. долг ) иногда уходят. Это всё знакомо.
Особенно зимой, в мороз.) И денежки на телефоне в «минус» (т.е. долг ) иногда уходят. Это всё знакомо.
А что же с углами? Оказывается, отрицательные углы в математике тоже бывают! Всё зависит от того, как отсчитывать этот самый угол… нет, не на числовой прямой, а на числовой окружности! То бишь, на круге. Круг – вот он, аналог числовой прямой в тригонометрии!
Итак, как же отсчитываются углы на круге? Ничего не поделать, придётся нам для начала этот самый круг нарисовать.
Я нарисую вот такую красивую картинку:
Она очень похожа на картинки из прошлого урока. Есть оси, есть окружность, есть угол. Но есть и новая информация.
Также я добавил циферки 0°, 90°, 180°, 270° и 360° на осях. Вот это уже поинтереснее.) Что это за циферки? Правильно! Это значения углов, отсчитанные от нашей неподвижной стороны, которые попадают на координатные оси. Вспоминаем, что неподвижная сторона угла у нас всегда крепко-накрепко привязана к положительной полуоси ОХ. И любой угол в тригонометрии отсчитывается именно от этой полуоси. Это базовое начало отсчёта углов надо держать в голове железно. А оси – они же под прямым углом пересекаются, верно? Вот и прибавляем по 90° в каждой четверти.
И любой угол в тригонометрии отсчитывается именно от этой полуоси. Это базовое начало отсчёта углов надо держать в голове железно. А оси – они же под прямым углом пересекаются, верно? Вот и прибавляем по 90° в каждой четверти.
И ещё добавлена красная стрелочка. С плюсом. Красная – это специально, чтобы в глаза бросалась. И в память хорошенько врезалась. Ибо это надо запомнить надёжно.) Что же означает эта стрелочка?
Так вот оказывается, если наш угол мы будем крутить по стрелочке с плюсом (против часовой стрелки, по ходу нумерации четвертей), то угол будет считаться положительным! В качестве примера на рисунке показан угол +45°. Кстати, обратите внимание, что осевые углы 0°, 90°, 180°, 270° и 360° также отмотаны именно в плюс! По красной стрелочке.
А теперь посмотрим на другую картинку:
Здесь почти всё то же самое. Только углы на осях пронумерованы в обратную сторону. По часовой стрелке. И имеют знак «минус».) Ещё нарисована синяя стрелочка.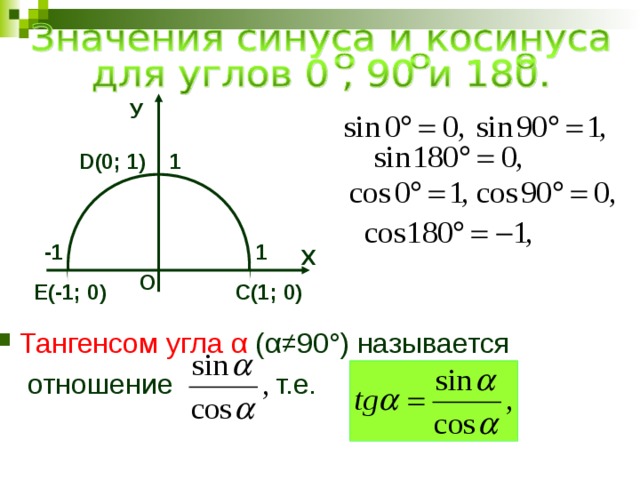 Также с минусом. Эта стрелочка – направление отрицательного отсчёта углов на круге. Она нам показывает, что, если мы будем откладывать наш угол по ходу часовой стрелки , то угол будет считаться отрицательным. Для примера я показал угол -45°.
Также с минусом. Эта стрелочка – направление отрицательного отсчёта углов на круге. Она нам показывает, что, если мы будем откладывать наш угол по ходу часовой стрелки , то угол будет считаться отрицательным. Для примера я показал угол -45°.
Кстати, прошу заметить, что нумерация четвертей никогда не меняется! Неважно, в плюс или в минус мы мотаем углы. Всегда строго против часовой стрелки.)
Запоминаем:
1. Начало отсчёта углов – от положительной полуоси ОХ. По часам – «минус», против часов – «плюс».
2. Нумерация четвертей всегда против часовой стрелки вне зависимости от направления исчисления углов.
Кстати говоря, подписывать углы на осях 0°, 90°, 180°, 270°, 360°, каждый раз рисуя круг – вовсе не обязаловка. Это чисто для понимания сути сделано. Но эти циферки обязательно должны присутствовать в вашей голове при решении любой задачи по тригонометрии. Почему? Да потому, что эти элементарные знания дают ответы на очень многие другие вопросы во всей тригонометрии! Самый главный вопрос – в какую четверть попадает интересующий нас угол? Хотите верьте, хотите нет, но правильный ответ на этот вопрос решает львиную долю всех остальных проблем с тригонометрией. Этим важным занятием (распределением углов по четвертям) мы займёмся в этом же уроке, но чуть позже.
Этим важным занятием (распределением углов по четвертям) мы займёмся в этом же уроке, но чуть позже.
Величины углов, лежащих на осях координат (0°, 90°, 180°, 270° и 360°), надо запомнить! Запомнить накрепко, до автоматизма. Причём как в плюс, так и в минус.
А вот с этого момента начинаются первые сюрпризы. И вместе с ними и каверзные вопросы в мой адрес, да…) А что будет, если отрицательный угол на круге совпадёт с положительным? Выходит, что одну и ту же точку на круге можно обозначить как положительным углом, так и отрицательным???
Совершенно верно! Так и есть.) Например, положительный угол +270° занимает на круге то же самое положение , что и отрицательный угол -90°. Или, например, положительный угол +45° на круге займёт то же самое положение , что и отрицательный угол -315°.
Смотрим на очередной рисунок и всё видим:
Точно так же положительный угол +150° попадёт туда же, куда и отрицательный угол -210°, положительный угол +230° – туда же, куда и отрицательный угол -130°. И так далее…
И так далее…
И что теперь делать? Как именно считать углы, если можно и так и сяк? Как правильно?
Ответ: по-всякому правильно! Ни одно из двух направлений отсчёта углов математика не запрещает. А выбор конкретного направления зависит исключительно от задания. Если в задании ничего не сказано прямым текстом про знак угла (типа «определите наибольший отрицательный угол» и т.п.), то работаем с наиболее удобными нам углами.
Конечно, например, в таких крутых темах, как тригонометрические уравнения и неравенства направление исчисления углов может колоссально влиять на ответ. И в соответствующих темах мы эти подводные камни рассмотрим.
Запоминаем:
Любую точку на круге можно обозначить как положительным, так и отрицательным углом. Любым! Каким хотим.
А теперь призадумаемся вот над чем. Мы выяснили, что угол 45° в точности совпадает с углом -315°? Как же я узнал про эти самые 315
°
? Не догадываетесь? Да! Через полный оборот. ) В 360°. У нас есть угол 45°. Сколько не хватает до полного оборота? Отнимаем 45
°
от 360
°
– вот и получаем 315
°
. Мотаем в отрицательную сторону – и получаем угол -315°. Всё равно непонятно? Тогда смотрим на картинку выше ещё раз.
) В 360°. У нас есть угол 45°. Сколько не хватает до полного оборота? Отнимаем 45
°
от 360
°
– вот и получаем 315
°
. Мотаем в отрицательную сторону – и получаем угол -315°. Всё равно непонятно? Тогда смотрим на картинку выше ещё раз.
И так надо поступать всегда при переводе положительных углов в отрицательные (и наоборот) – рисуем круг, отмечаем примерно заданный угол, считаем, сколько градусов не хватает до полного оборота, и мотаем получившуюся разность в противоположную сторону. И всё.)
Чем ещё интересны углы, занимающие на круге одно и то же положение, как вы думаете? А тем, что у таких углов совершенно одинаковые синус, косинус, тангенс и котангенс! Всегда!
Например:
Sin45° = sin(-315°)
Cos120° = cos(-240°)
Tg249° = tg(-111°)
Ctg333° = ctg(-27°)
А вот это уже крайне важно! Зачем? Да всё за тем же!) Для упрощения выражений. Ибо упрощение выражений – ключевая процедура успешного решения любых заданий по математике. И по тригонометрии в том числе.
И по тригонометрии в том числе.
Итак, с общим правилом отсчёта углов на круге разобрались. Ну а коли мы тут заикнулись про полные обороты, про четверти, то пора бы уже покрутить и порисовать эти самые углы. Порисуем?)
Начнём пока с положительных углов. Они попроще в рисовании будут.
Рисуем углы в пределах одного оборота (между 0° и 360°).
Нарисуем, например, угол 60°. Тут всё просто, никаких заморочек. Рисуем координатные оси, круг. Можно прямо от руки, безо всякого циркуля и линейки. Рисуем схематично : у нас не черчение с вами. Никаких ГОСТов соблюдать не надо, не накажут.)
Можно (для себя) отметить значения углов на осях и указать стрелочку в направлении против часов. Ведь мы же в плюс откладывать собираемся?) Можно этого и не делать, но в голове держать всяко надо.
И теперь проводим вторую (подвижную) сторону угла. В какой четверти? В первой, разумеется! Ибо 60 градусов – это строго между 0° и 90°. Вот и рисуем в первой четверти.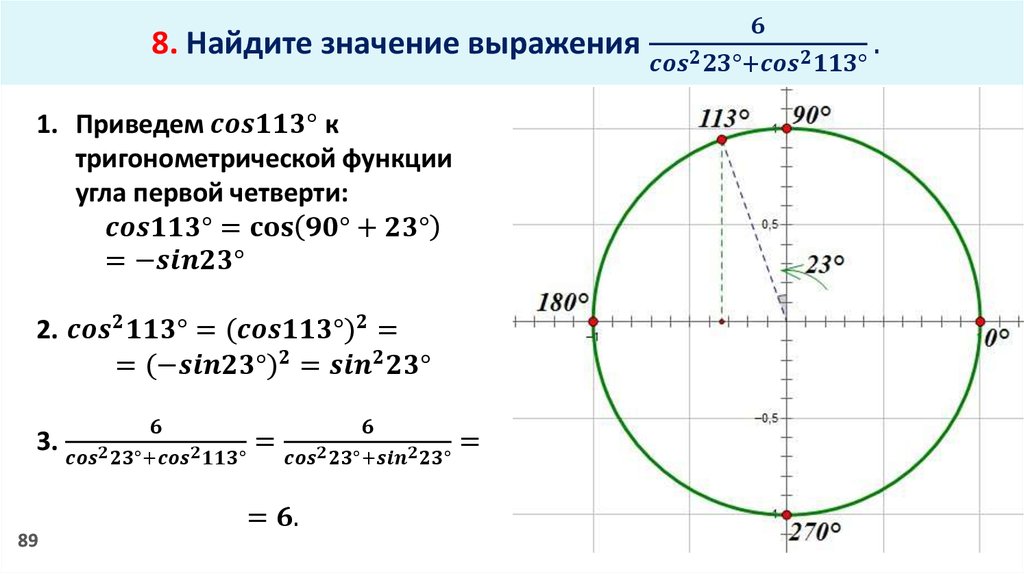 Под углом примерно 60 градусов к неподвижной стороне. Как отсчитать примерно 60 градусов без транспортира? Легко! 60° – это две трети от прямого угла! Делим мысленно первую чертвертинку круга на три части, забираем себе две трети. И рисуем… Сколько у нас там по факту получится (если приложить транспортир и померить) – 55 градусов или же 64 – неважно! Важно, что всё равно где-то около 60° .
Под углом примерно 60 градусов к неподвижной стороне. Как отсчитать примерно 60 градусов без транспортира? Легко! 60° – это две трети от прямого угла! Делим мысленно первую чертвертинку круга на три части, забираем себе две трети. И рисуем… Сколько у нас там по факту получится (если приложить транспортир и померить) – 55 градусов или же 64 – неважно! Важно, что всё равно где-то около 60° .
Получаем картинку:
Вот и всё. И инструментов не понадобилось. Развиваем глазомер! В задачах по геометрии пригодится.) Этот неказистый рисунок бывает незаменим, когда надо нацарапать круг и угол на скорую руку, не особо задумываясь о красоте. Но при этом нацарапать правильно , без ошибок, со всей необходимой информацией. Например, как вспомогательное средство при решении тригонометрических уравнений и неравенств.
Нарисуем теперь угол, например, 265°. Прикидываем, где он может располагаться? Ну, ясное дело, что не в первой четверти и даже не во второй: они на 90 и на 180 градусов оканчиваются.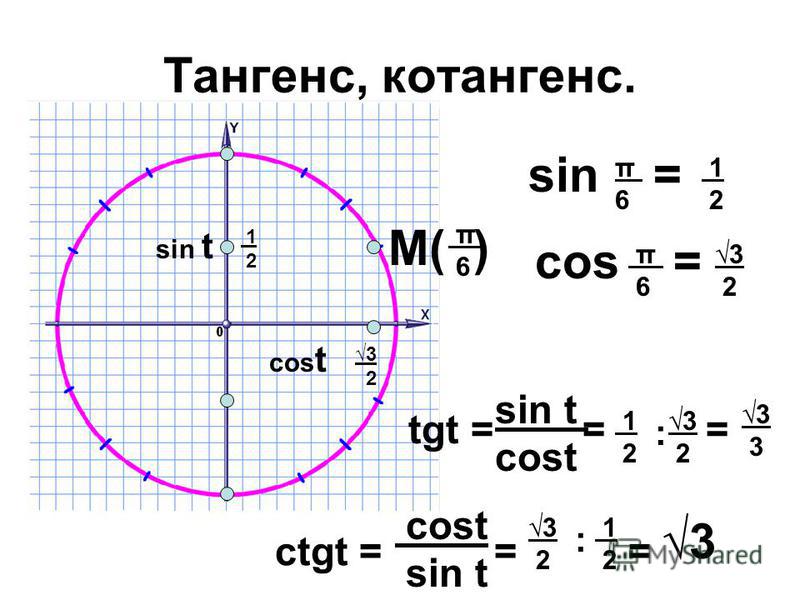 Можно сообразить, что 265° — это 180° плюс ещё 85°. То есть, к отрицательной полуоси ОХ (там, где 180°) надо добавить примерно 85°. Или, что ещё проще, догадаться, что 265° не дотягивает до отрицательной полуоси OY (там, где 270°) каких-то несчастных 5°. Одним словом, в третьей четверти будет этот угол. Очень близко к отрицательной полуоси OY, к 270 градусам, но всё-таки в третьей!
Можно сообразить, что 265° — это 180° плюс ещё 85°. То есть, к отрицательной полуоси ОХ (там, где 180°) надо добавить примерно 85°. Или, что ещё проще, догадаться, что 265° не дотягивает до отрицательной полуоси OY (там, где 270°) каких-то несчастных 5°. Одним словом, в третьей четверти будет этот угол. Очень близко к отрицательной полуоси OY, к 270 градусам, но всё-таки в третьей!
Рисуем:
Повторюсь, абсолютная точность здесь не требуется. Пускай в реальности этот угол получился, скажем 263 градуса. Но на самый главный вопрос (какая четверть?) мы ответили безошибочно. Почему этот вопрос самый главный? Да потому, что любая работа с углом в тригонометрии (неважно, будем мы рисовать этот угол или не будем) начинается с ответа именно на этот вопрос! Всегда. Если этот вопрос проигнорировать или пробовать на него ответить мысленно, то ошибки почти неизбежны, да… Оно вам надо?
Запоминаем:
Любая работа с углом (в том числе и рисование этого самого угла на круге) всегда начинается с определения четверти, в которую попадает этот угол.
Теперь, я надеюсь, вы уже безошибочно изобразите углы, например, 182°, 88°, 280°. В правильных четвертях. В третьей, первой и четвёртой, если что…)
Четвёртая четверть заканчивается углом 360°. Это один полный оборот. Ясен перец, что этот угол занимает на круге то же самое положение, что и 0° (т.е. начало отсчёта). Но углы на этом не заканчиваются, да…
Что делать с углами, большими 360°?
«А такие разве бывают?» – спросите вы. Бывают, ещё как! Бывает, например, угол 444°. А бывает, скажем, угол 1000°. Всякие углы бывают.) Просто визуально такие экзотические углы воспринимаются чуть сложнее, чем привычные нам углы в пределах одного оборота. Но рисовать и просчитывать такие углы тоже надо уметь, да.
Для правильного рисования таких углов на круге необходимо всё то же самое – выяснить, в какую четверть попадает интересующий нас угол. Здесь умение безошибочно определять четверть куда более важно, чем для углов от 0° до 360°! Сама процедура определения четверти усложняется всего одним шагом. Каким, скоро увидите.
Каким, скоро увидите.
Итак, например, нам надо выяснить, в какую четверть попадает угол 444°. Начинаем крутить. Куда? В плюс, разумеется! Угол-то нам дали положительный! +444°. Крутим, крутим… Крутанули на один оборот – дошли до 360°.
Сколько там осталось до 444°? Считаем оставшийся хвостик:
444°-360° = 84°.
Итак, 444° — это один полный оборот (360°) плюс ещё 84°. Очевидно, это первая четверть. Итак, угол 444° попадает в первую четверть. Полдела сделано.
Осталось теперь изобразить этот угол. Как? Очень просто! Делаем один полный оборот по красной (плюсовой) стрелке и добавляем ещё 84°.
Вот так:
Здесь я уж не стал загромождать рисунок – подписывать четверти, рисовать углы на осях. Это всё добро уже давно в голове быть должно.)
Зато я «улиткой» или спиралькой показал, как именно складывается угол 444° из углов 360° и 84°. Пунктирная красная линия – это один полный оборот. К которому дополнительно прикручиваются 84° (сплошная линия).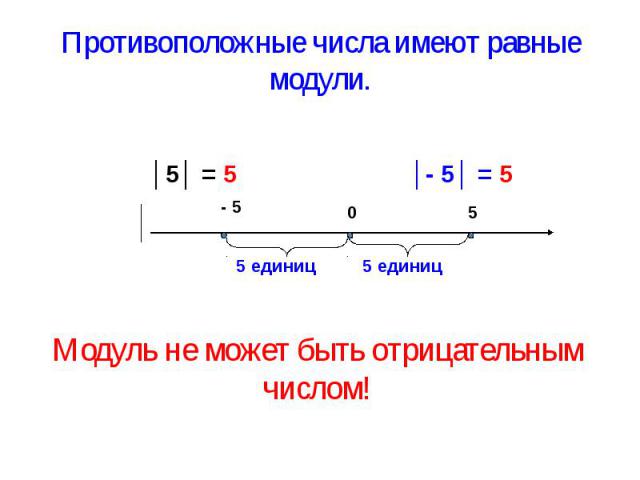 Кстати, обратите внимание, что, если этот самый полный оборот отбросить, то это никак не повлияет на положение нашего угла!
Кстати, обратите внимание, что, если этот самый полный оборот отбросить, то это никак не повлияет на положение нашего угла!
А вот это важно! Положение угла 444° полностью совпадает с положением угла 84°. Никаких чудес нет, так уж получается.)
А можно ли отбросить не один полный оборот, а два или больше?
А почему – нет? Если угол здоровенный, то не просто можно, а даже нужно! Угол-то не изменится! Точнее, сам-то угол по величине, конечно же, изменится. А вот его положение на круге – никак нет!) На то они и полные обороты, что сколько экземпляров ни добавляй, сколько ни убавляй, всё равно будешь в одну и ту же точку попадать. Приятно, правда?
Запоминаем:
Если к углу прибавить (отнять) любое целое число полных оборотов, положение исходного угла на круге НЕ изменится!
Например:
В какую четверть попадает угол 1000°?
Никаких проблем! Считаем, сколько полных оборотов сидит в тысяче градусов.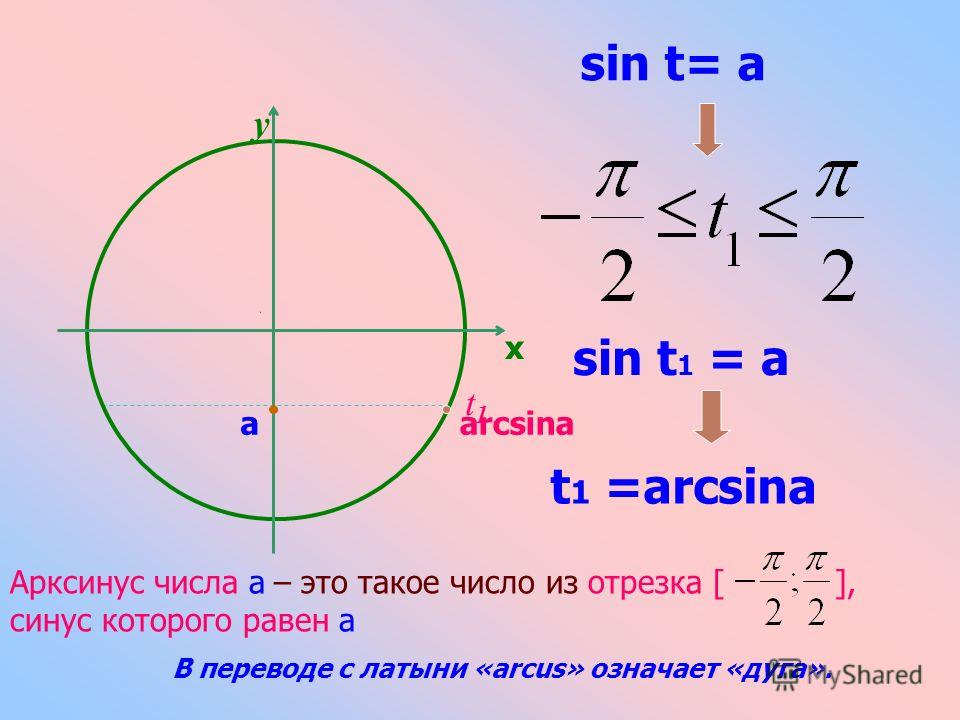 Один оборот — это 360°, ещё один – уже 720°, третий — 1080°… Стоп! Перебор! Значит, в угле 1000° сидит два полных оборота. Выбрасываем их из 1000° и считаем остаток:
Один оборот — это 360°, ещё один – уже 720°, третий — 1080°… Стоп! Перебор! Значит, в угле 1000° сидит два полных оборота. Выбрасываем их из 1000° и считаем остаток:
1000° — 2 ·360° = 280°
Значит, положение угла 1000° на круге то же самое , что и у угла 280°. С которым работать уже гораздо приятнее.) И куда же попадает этот угол? В четвёртую четверть он попадает: 270° (отрицательная полуось OY) плюс ещё десяточка.
Рисуем:
Здесь я уже не рисовал пунктирной спиралькой два полных оборота: уж больно длинная она получается. Просто нарисовал оставшийся хвостик от нуля , отбросив все лишние обороты. Как будто бы их и не было вовсе.)
И ещё раз. По-хорошему, углы 444° и 84°, а также 1000° и 280° – разные. Но для синуса, косинуса, тангенса и котангенса эти углы – одинаковые!
Как вы видите, для того чтобы работать с углами, большими 360°, надо определить, сколько полных оборотов сидит в заданном большом угле.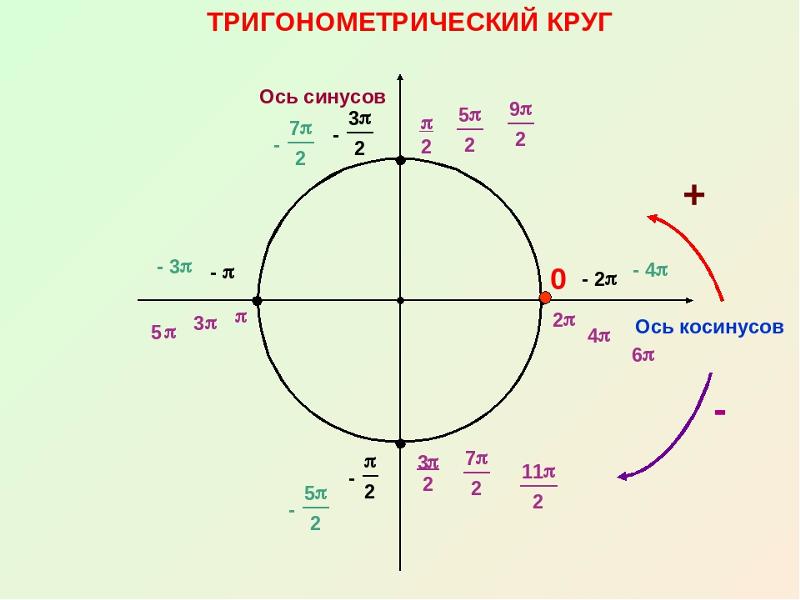 Это и есть тот самый дополнительный шаг, который обязательно надо предварительно проделывать при работе с такими углами. Ничего сложного, правда?
Это и есть тот самый дополнительный шаг, который обязательно надо предварительно проделывать при работе с такими углами. Ничего сложного, правда?
Отбрасывание полных оборотов, конечно, занятие приятное.) Но на практике при работе с совсем уж кошмарными углами случаются и затруднения.
Например:
В какую четверть попадает угол 31240° ?
И что же, будем много-много раз прибавлять по 360 градусов? Можно, если не горит особо. Но мы же не только складывать можем.) Ещё и делить умеем!
Вот и поделим наш большущий угол на 360 градусов!
Этим действием мы как раз и узнаем, сколько полных оборотов запрятано в наших 31240 градусах. Можно уголком поделить, можно (шепну на ушко:)) на калькуляторе.)
Получим 31240:360 = 86,777777….
То, что число получилось дробным – не страшно. Нас же только целые обороты интересуют! Стало быть, до конца делить и не надо.)
Итак, в нашем лохматом угле сидит аж 86 полных оборотов. Ужас…
Ужас…
В градусах это будет 86·360° = 30960°
Вот так. Именно столько градусов можно безболезненно выкинуть из заданного угла 31240°. Останется:
31240° — 30960° = 280°
Всё! Положение угла 31240° полностью идентифицировано! Там же, где и 280°. Т.е. четвёртая четверть.) Кажется, мы уже изображали этот угол ранее? Когда угол 1000° рисовали?) Там мы тоже на 280 градусов вышли. Совпадение.)
Итак, мораль сей басни такова:
Если нам задан страшный здоровенный угол, то:
1. Определяем, сколько полных оборотов сидит в этом угле. Для этого делим исходный угол на 360 и отбрасываем дробную часть.
2. Считаем, сколько градусов в полученном количестве оборотов. Для этого умножаем число оборотов на 360.
3. Отнимаем эти обороты от исходного угла и работаем с привычным углом в пределах от 0° до 360°.
Как работать с отрицательными углами?
Не вопрос! Точно так же, как и с положительными, только с одним единственным отличием.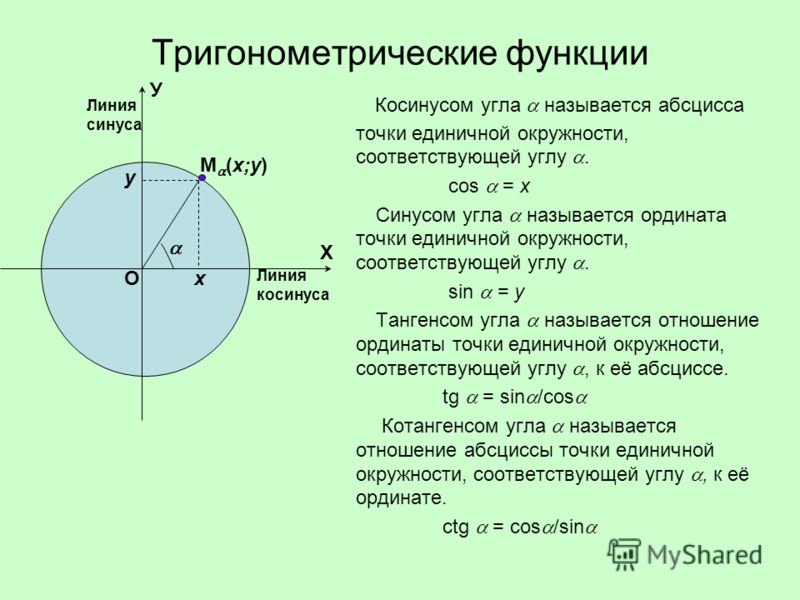 Каким? Да! Крутить углы надо в обратную сторону , в минус! По ходу часовой стрелки.)
Каким? Да! Крутить углы надо в обратную сторону , в минус! По ходу часовой стрелки.)
Нарисуем, например, угол -200°. Сначала всё как обычно для положительных углов – оси, круг. Ещё синюю стрелочку с минусом изобразим да углы на осях по-другому подпишем. Их, естественно, также придётся отсчитывать в отрицательном направлении. Это будут всё те же самые углы, шагающие через 90°, но отсчитанные в обратную сторону, в минус: 0°, -90°, -180°, -270°, -360°.
Картинка станет вот такой:
При работе с отрицательными углами часто возникает чувство лёгкого недоумения. Как так?! Получается, что одна и та же ось – это одновременно, скажем, и +90° и -270°? Неее, что-то тут нечисто…
Да всё чисто и прозрачно! Мы ведь же уже в курсе, что любую точку на круге можно обозвать как положительным углом, так и отрицательным! Совершенно любую. В том числе и на какой-то из координатных осей. В нашем случае нам нужно отрицательное исчисление углов. Вот и отщёлкиваем в минус все углы.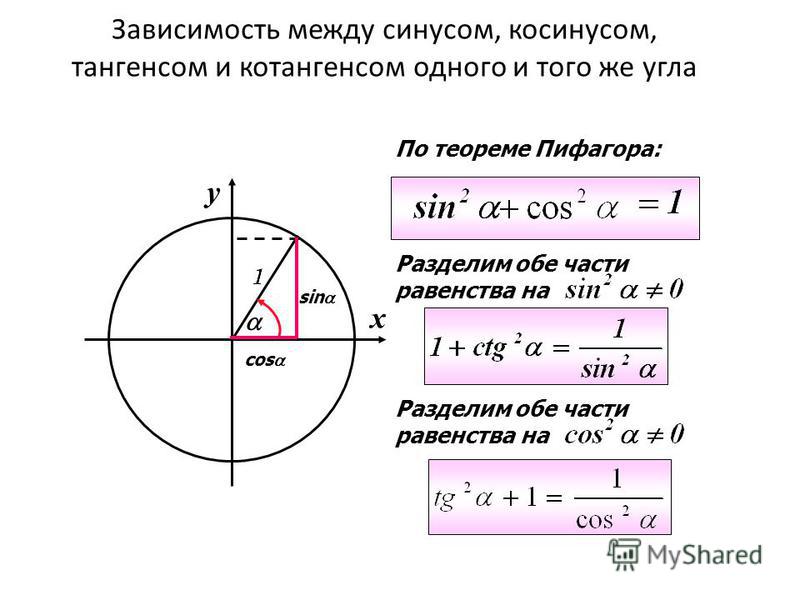 )
)
Теперь нарисовать правильно угол -200° никакого труда не составляет. Это -180° и минус ещё 20°. Начинаем мотать от нуля в минус: четвёртую четверть пролетаем, третью тоже мимо, доходим до -180°. Куда мотать оставшуюся двадцатку? Да всё туда же! По часам.) Итого угол -200° попадает во вторую четверть.
Теперь вы понимаете, насколько важно железно помнить углы на осях координат?
Углы на осях координат (0°, 90°, 180°, 270°, 360°) надо помнить именно для того, чтобы безошибочно определять четверть, куда попадает угол!
А если угол большой, с несколькими полными оборотами? Ничего страшного! Какая разница, куда эти самые полные обороты крутить – в плюс или в минус? Точка-то на круге не изменит своего положения!
Например:
В какую четверть попадает угол -2000°?
Всё то же самое! Для начала считаем, сколько полных оборотов сидит в этом злом угле. Чтобы не косячить в знаках, оставим минус пока в покое и просто поделим 2000 на 360.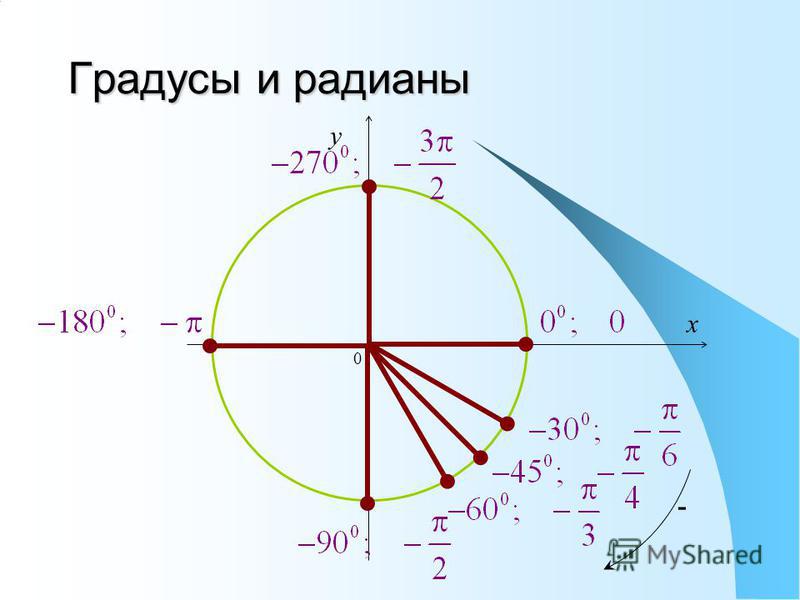 Получим 5 с хвостиком. Хвостик нас пока не волнует, его чуть позже сосчитаем, когда рисовать угол будем. Считаем пять полных оборотов в градусах:
Получим 5 с хвостиком. Хвостик нас пока не волнует, его чуть позже сосчитаем, когда рисовать угол будем. Считаем пять полных оборотов в градусах:
5·360° = 1800°
Воот. Именно столько лишних градусов можно смело выкинуть из нашего угла без ущерба для здоровья.
Считаем оставшийся хвостик:
2000° – 1800° = 200°
А вот теперь можно и про минус вспомнить.) Куда будем мотать хвостик 200°? В минус, конечно же! Нам же отрицательный угол задан.)
2000° = -1800° — 200°
Вот и рисуем угол -200°, только уже без лишних оборотов. Только что его рисовали, но, так уж и быть, накалякаю ещё разок. От руки.
Ясен перец, что и заданный угол -2000°, так же как и -200°, попадает во вторую четверть.
Итак, мотаем себе на кру… пардон… на ус:
Если задан очень большой отрицательный угол, то первая часть работы с ним (поиск числа полных оборотов и их отбрасывание) та же самая, что и при работе с положительным углом. Знак «минус» на данном этапе решения не играет никакой роли. Учитывается знак лишь в самом конце, при работе с углом, оставшимся после удаления полных оборотов.
Знак «минус» на данном этапе решения не играет никакой роли. Учитывается знак лишь в самом конце, при работе с углом, оставшимся после удаления полных оборотов.
Как видите, рисовать отрицательные углы на круге ничуть не сложнее, чем положительные.
Всё то же самое, только в другую сторону! По часам!
А вот теперь — самое интересное! Мы рассмотрели положительные углы, отрицательные углы, большие углы, маленькие — полный ассортимент. Также мы выяснили, что любую точку на круге можно обозвать положительным и отрицательным углом, отбрасывали полные обороты… Нету никаких мыслей? Должно отложиться…
Да! Какую точку на круге ни возьми, ей будет соответствовать бесконечное множество углов! Больших и не очень, положительных и отрицательных — всяких! И разница между этими углами будет составлять целое число полных оборотов. Всегда! Так уж тригонометрический круг устроен, да…) Именно поэтому обратная задача — найти угол по известным синусу/косинусу/тангенсу/котангенсу — решается неоднозначно .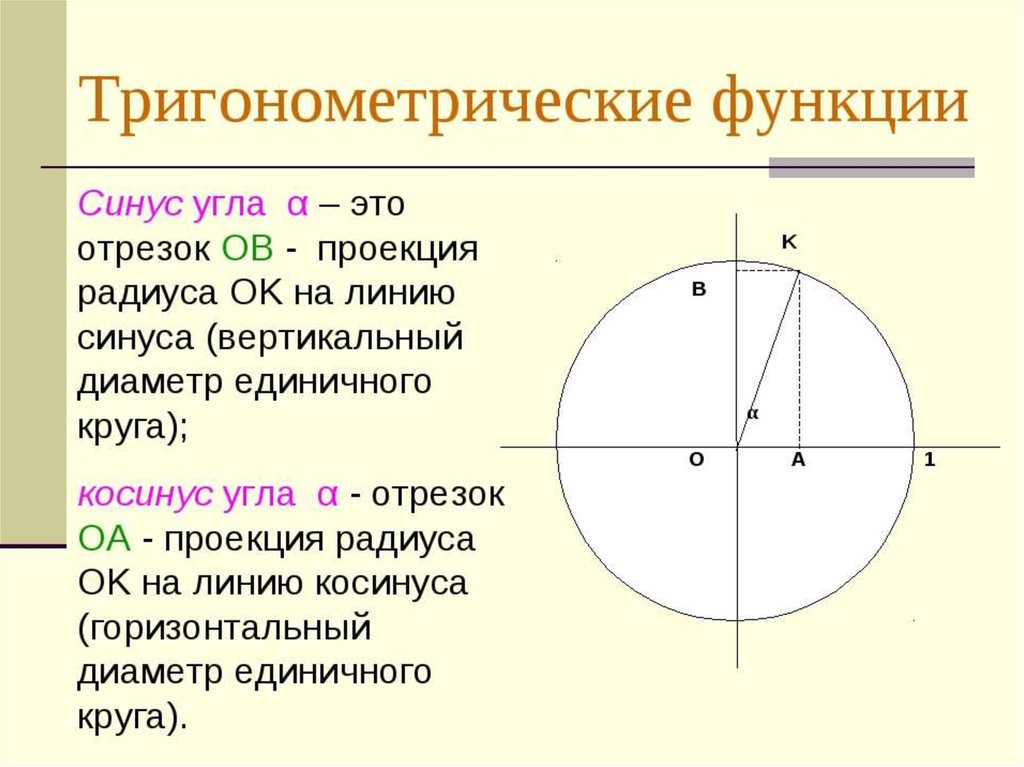 И куда сложнее. В отличие от прямой задачи — по заданному углу найти весь набор его тригонометрических функций. И в более серьёзных темах тригонометрии (арки , тригонометрические уравнения и неравенства ) мы с этой фишкой будем сталкиваться постоянно. Привыкаем.)
И куда сложнее. В отличие от прямой задачи — по заданному углу найти весь набор его тригонометрических функций. И в более серьёзных темах тригонометрии (арки , тригонометрические уравнения и неравенства ) мы с этой фишкой будем сталкиваться постоянно. Привыкаем.)
1. В какую четверть попадает угол -345°?
2. В какую четверть попадает угол 666°?
3. В какую четверть попадает угол 5555°?
4. В какую четверть попадает угол -3700°?
5. Какой знак имеет cos 999°?
6. Какой знак имеет ctg 999°?
И это получилось? Прекрасно! Есть проблемы? Тогда вам .
Ответы:
1. 1
2. 4
3. 2
4. 3
5. «+»
6. «-»
В этот раз ответы выданы по порядку в нарушение традиций. Ибо четвертей всего четыре, а знаков так и вовсе два. Особо не разбежишься…)
В следующем уроке мы с вами поговорим про радианы, про загадочное число «пи», научимся легко и просто переводить радианы в градусы и обратно. И с удивлением обнаружим, что даже этих простых знаний и навыков нам будет уже вполне достаточно для успешного решения многих нетривиальных задачек по тригонометрии!
И с удивлением обнаружим, что даже этих простых знаний и навыков нам будет уже вполне достаточно для успешного решения многих нетривиальных задачек по тригонометрии!
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Пара различных лучей Оа и Оb, выходящих из одной точки О, называется углом и обозначается символом (а, b). Точка О называется вершиной угла, а лучи Оа u Оb — сторонами угла. Если А и В — две точки лучей Оа и Оb, то (а, b) обозначается также символом АОВ (рис. 1.1).
Точка О называется вершиной угла, а лучи Оа u Оb — сторонами угла. Если А и В — две точки лучей Оа и Оb, то (а, b) обозначается также символом АОВ (рис. 1.1).
Угол (а, Ь) называют развернутым, если лучи Оа и Ob, выходящие из одной точки, лежат на одной прямой и не совпадают (т. е. противоположно направлены).
Рис.1.1
Два угла считаются равными, если один угол можно наложить на другой так, чтобы стороны углов совпадали. Биссектрисой угла называется луч с началом в вершине угла, делящий угол на два равных угла.
Говорят, что луч ОС, исходящий из вершины угла АОВ, лежит между его сторонами, если он пересекает отрезок АВ (рис. 1.2). Говорят, что точка С лежит между сторонами угла, если через эту точку можно провести луч с началом в вершине угла, лежащий между сторонами угла. Множество всех точек плоскости, лежащих между сторонами угла, образует внутреннюю область угла (рис. 1.3). Множество точек плоскости, не принадлежащих внутренней области и сторонам угла, образует внешнюю область угла.
Угол (а, b) считают больше угла (c, d), если угол (с, d) можно наложить на угол (а, b) так, что после совмещения одной пары сторон вторая сторона угла (с, d) будет лежать между сторонами угла (а, b). На рис. 1.4 АОВ больше АОС.
Пусть луч с лежит между сторонами угла (а, b) (рис. 1.5). Пары лучей а, с и с, b образуют два угла. Об угле (а, b) говорят, что он является суммой двух углов (а, с) и (с, b), и пишут: (а, b) = (а, с) + (с, b).
Рис.1.3
Обычно в геометрии имеют дело с углами, меньшими развернутого. Однако в результате сложения двух углов может получиться угол, больший развернутого. В этом случае ту часть плоскости, которая считается внутренней областью угла, отмечают дугой. На рис. 1.6 внутренняя часть угла АОВ, полученного в результате сложения углов АОС и СОВ и большего развернутого, отмечена дугой.
Рис.1.5
Существуют также углы большие 360°. Такие углы образуются, например, вращением пропеллера самолета, вращением барабана, на который наматывается канат, и т. д.
д.
В дальнейшем при рассмотрении каждого угла условимся считать одну из сторон этого угла его начальной стороной, а другую — конечной стороной.
Любой угол, например угол АОВ (рис. 1.7), можно получить в результате вращения подвижного луча вокруг вершины О от начальной стороны угла (ОА) до его конечной стороны (ОВ). Мы будем измерять этот угол, учитывая полное количество оборотов, сделанных при этом вокруг точки О, а также и направление, в котором происходило вращение.
Положительные и отрицательные углы.
Пусть мы имеем угол, образованный лучами ОА и ОВ (рис.1.8). Подвижный луч, вращаясь вокруг точки О от своего начального положения (ОА), может занять конечное положение (ОВ) при двух различных направлениях вращения. Эти направления показаны на рисунке 1.8 соответствующими стрелками.
Рис.1.7
Подобно тому, как на числовой оси одно из двух направлений считается положительным, а другое отрицательным, различают и два различных направления вращения подвижного луча. Условились считать положительным направлением вращения то направление, которое противоположно направлению вращения часовой стрелки. Направление вращения, совпадающее с направлением вращения часовой стрелки, считается отрицательным.
Условились считать положительным направлением вращения то направление, которое противоположно направлению вращения часовой стрелки. Направление вращения, совпадающее с направлением вращения часовой стрелки, считается отрицательным.
В соответствии с этими определениями углы также подразделяются на положительные и отрицательные.
Положительным углом называется угол, образованный вращением подвижного луча вокруг начальной точки в положительном направлении.
На рисунке 1.9 даны некоторые положительные углы. (Направление вращения подвижного луча показано на чертежах стрелками.)
Отрицательным углом называется угол, образованный вращением подвижного луча вокруг начальной точки в отрицательном направлении.
На рисунке 1.10 изображены некоторые отрицательные углы. (Направление вращения подвижного луча показано на чертежах стрелками.)
Но два совпадающих луча могут также образовать и углы +360°п и -360°п (п = 0,1,2,3,…). Обозначим через б наименьший возможный неотрицательный угол поворота, переводящий луч ОА в положение ОВ. Если теперь луч ОВ совершит дополнительно полный оборот вокруг точки О, то получим другую величину угла, а именно: АВО = б + 360°.
Если теперь луч ОВ совершит дополнительно полный оборот вокруг точки О, то получим другую величину угла, а именно: АВО = б + 360°.
Измерение углов дугами окружности. Единицы измерения дуг и углов
В ряде случаев оказывается удобным измерять углы при помощи дуг окружности. Возможность такого измерения основа на известном предложении планиметрии о том, что в одном круге (или в равных кругах) центральные углы и соответствующие им дуги находятся в прямой пропорциональной зависимости.
Пусть некоторая дуга данной окружности принята за единицу измерения дуг. Соответствующий этой дуге центральный угол примем за единицу измерения углов. При таком условии любая дуга окружности и соответствующий этой дуге центральный угол будут содержать одно и то же число единиц измерения. Поэтому, измеряя дуги окружности, можно определять и величину соответствующих этим дугам центральных углов.
Рассмотрим две наиболее распространенные системы измерения дуг и углов.
Градусная мера измерения углов
При градусном измерении углов в качестве основной единицы измерения углов (эталонного угла, с которым сравниваются различные углы) берется угол в один градус (обозначается 1?). Угол в один градус — это угол, равный 1/180 части развернутого угла. Угол, равный 1/60 части угла в 1°, — это угол в одну минуту (обозначается 1″). Угол, равный 1/60 части угла в одну минуту,— это угол в одну секунду (обозначается 1″).
Угол в один градус — это угол, равный 1/180 части развернутого угла. Угол, равный 1/60 части угла в 1°, — это угол в одну минуту (обозначается 1″). Угол, равный 1/60 части угла в одну минуту,— это угол в одну секунду (обозначается 1″).
Радианная мера измерения углов
Наряду с градусной мерой измерения углов в геометрии и тригонометрии употребляется и другая мера измерения углов, называемая радианной. Рассмотрим окружность радиуса R с центром О. Проведем два радиуса О А и ОВ так, чтобы длина дуги АВ была равна радиусу окружности (рис. 1.12). Получившийся при этом центральный угол АОВ будет углом в один радиан. Угол в 1 радиан принимается за единицу измерения радианной меры измерения углов. При радианном измерении углов развернутый угол равен р радиан.
Градусная и радианная единицы измерения углов связаны равенствами:
1 радиан =180?/р57° 17″ 45″; 1?=р/180 радиана0,017453радиана;
1″=р/180*60 радиана0,000291 радиана;
1″»=р/180*60*60 радиана0,000005 радиана.
Градусную (или радианную) меру угла также называют величиной угла. Величину угла АОВ иногда обозначают /
Классификация углов
Угол, равный 90°, или в радианной мере р/2, называется прямым углом; его часто обозначают буквой d. Угол, меньший 90°, называется острым; угол, больший 90°, но меньший 180°, называется тупым.
Два угла, имеющие одну общую сторону и в сумме составляющие 180°, называются смежными углами. Два угла, имеющие одну общую сторону и в сумме составляющие 90°, называются дополнительными углами.
тригонометрия — Почему $\cos(-\theta)$ дает положительные значения, а в случае синуса отрицательные?
Спросил
Изменено 1 месяц назад
Просмотрено 74k раз
$\begingroup$
Почему $\cos(-\theta)$ дает положительные значения, а в случае синуса отрицательные?
Я имею в виду
$\cos(-\theta) = +\cos(\theta)$
$\sin(-\theta) = -\sin(\theta)$
$\tan(-\theta) = -\tan(\theta)$
и, пожалуйста, объясните общие углы в простых мирах?
- тригонометрия
$\endgroup$
11
$\begingroup$
Изменение знака $\theta$ соответствует обходу в другом направлении. Поскольку $\theta$ отсчитывается от положительной оси $x$, все, что нужно сделать, это перевернуть конечную точку по оси $x$, как показано ниже.
Поскольку $\theta$ отсчитывается от положительной оси $x$, все, что нужно сделать, это перевернуть конечную точку по оси $x$, как показано ниже.
Поскольку косинус — это $x$-компонента $P$, а синус — это $y$-компонента, переворот по оси $x$ сведет на нет $\sin\theta$, но не $\cos\ тета$. Надеюсь, это проясняет, почему синус и косинус ведут себя именно так. 95/5!\pm…$
Обратите внимание, что изменение знака для cos не имеет значения (поскольку у нас есть все четные степени x), но изменение знака для sin имеет значение (поскольку у нас есть все нечетные степени x ).
Также $\tan (-\theta)=\frac {sin (-\theta)}{cos (-\theta)}\frac {-sin (\theta)}{cos (\theta)}=-tan (\тета)$.
$\endgroup$
$\begingroup$
Функция $f(x)$ называется четной, если $f(-x) = f(x)$. С другой стороны, функция $g(x)$ называется нечетной, если $g(-x) = -g(x)$. Таким образом, мы хотим знать, почему $cos(x)$ — четная функция, а $sin(y)$ — нечетная. Теперь мы можем представить, как синус и косинус зависят от угла тета ($θ$), используя единичный круг в декартовых координатах. Нарисуйте любой радиус единичной окружности, образуя угол $θ$ с положительной половиной оси x. Точка на окружности, где пересекается этот радиус, будет иметь координаты x и y как $\cos(θ)$ и $\sin(θ)$ соответственно. Это естественное следствие того, что гипотенуза соответствующего прямоугольного треугольника равна 1 (любой радиус единичного круга по определению будет равен 1).
Радиус единичной окружности как гипотенуза прямоугольного треугольника
Теперь при изменении угла $\theta$ мы получаем различные значения $sinθ$ и $cosθ$. Они были нанесены на следующий график:
Графики $\cos(x)$ и $\sin(y)$
Теперь мы можем представить, как синус и косинус зависят от угла тета ($θ$), используя единичный круг в декартовых координатах. Нарисуйте любой радиус единичной окружности, образуя угол $θ$ с положительной половиной оси x. Точка на окружности, где пересекается этот радиус, будет иметь координаты x и y как $\cos(θ)$ и $\sin(θ)$ соответственно. Это естественное следствие того, что гипотенуза соответствующего прямоугольного треугольника равна 1 (любой радиус единичного круга по определению будет равен 1).
Радиус единичной окружности как гипотенуза прямоугольного треугольника
Теперь при изменении угла $\theta$ мы получаем различные значения $sinθ$ и $cosθ$. Они были нанесены на следующий график:
Графики $\cos(x)$ и $\sin(y)$
Как видите, график косинуса симметричен относительно оси y, что означает, что для каждого $x$ $\cos(x) = \cos(-x)$. Сделать косинус четной функцией. С другой стороны, если вы посмотрите на график синуса, вы заметите, что $|\sin(x)|$ = $|\sin(-x)|$, но знак противоположный.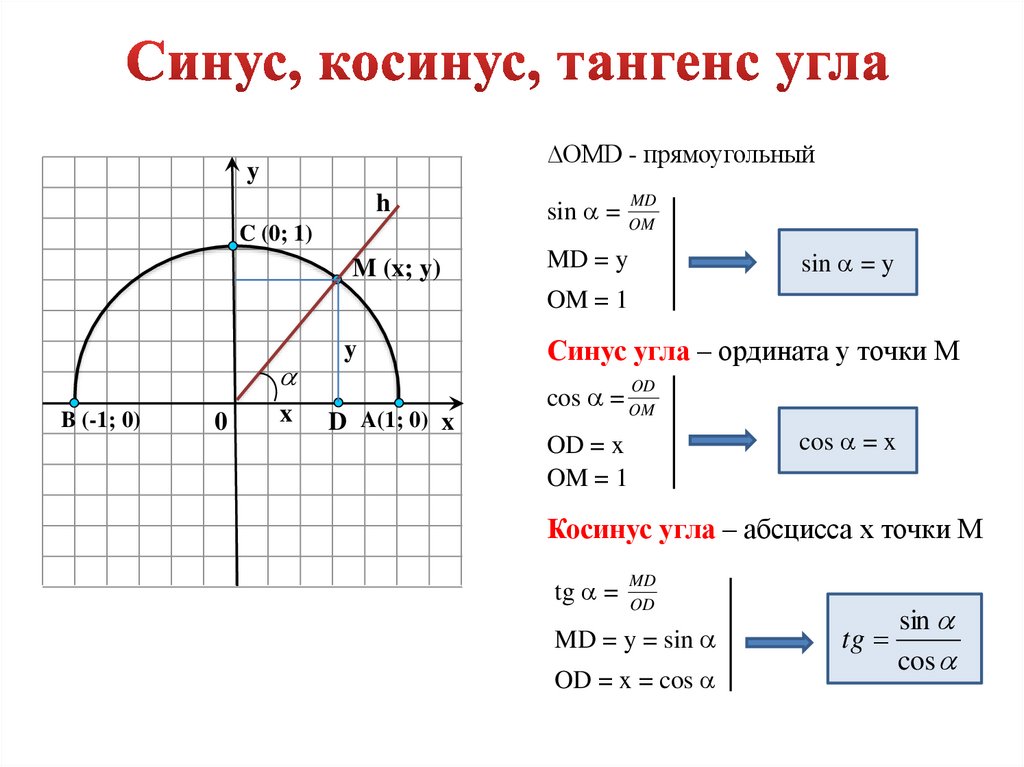 То есть абсолютное значение совпадает с пересечением оси $y$, но с обратным направлением. Сделать синус нечетной функцией.
То есть абсолютное значение совпадает с пересечением оси $y$, но с обратным направлением. Сделать синус нечетной функцией.
$\endgroup$
$\begingroup$
Косинус принимает значения от 1 до -1 в интервале $[0,\pi]$, тогда как синус принимает значения от 0 до 1. Я не знаю, что вы имеете в виду под общими углами простыми словами. 92-2bc\cos\альфа. $$ Аналогичное рассуждение, основанное на законе синусов, дает понять, что синус тупого угла должен быть таким же, как и синус дополнительного угла.
Синусы и косинусы позже были определены для любого угла; расширение можно обосновать тригонометрическим кругом, и стало ясно, что их нужно определить так, чтобы $$ \sin(-\alpha)=-\sin\alpha,\qquad \cos(-\alpha)=\cos\alpha $$ просто глядя на тригонометрический круг.
$\endgroup$
$\begingroup$
92-2bc\cos\альфа. $$ Аналогичное рассуждение, основанное на законе синусов, дает понять, что синус тупого угла должен быть таким же, как и синус дополнительного угла.
$$ Аналогичное рассуждение, основанное на законе синусов, дает понять, что синус тупого угла должен быть таким же, как и синус дополнительного угла.
Синусы и косинусы позже были определены для любого угла; расширение можно оправдать тригонометрическим кругом, и стало ясно, что их нужно определить так, чтобы $$ \sin(-\alpha)=-\sin\alpha,\qquad \cos(-\alpha)=\cos\ alpha $$ просто взглянув на тригонометрический круг.
$\endgroup$
$\begingroup$
$\cos(-\theta)=\cos(0-\theta)=\cos0\cos\theta+\sin0\sin\theta=\cos(\theta)$.
$\sin(-\theta)=\sin(0-\theta)=\sin0\cos\theta-\cos0\sin\theta=-\sin(\theta)$.
$\tan(-\theta)=\frac {\sin(-\theta)}{\cos(-\theta)}=-\tan(\theta)$. (Используя два приведенных выше равенства.)
$\endgroup$
$\begingroup$
Помните, что углы отсчитываются от положительной оси $x$.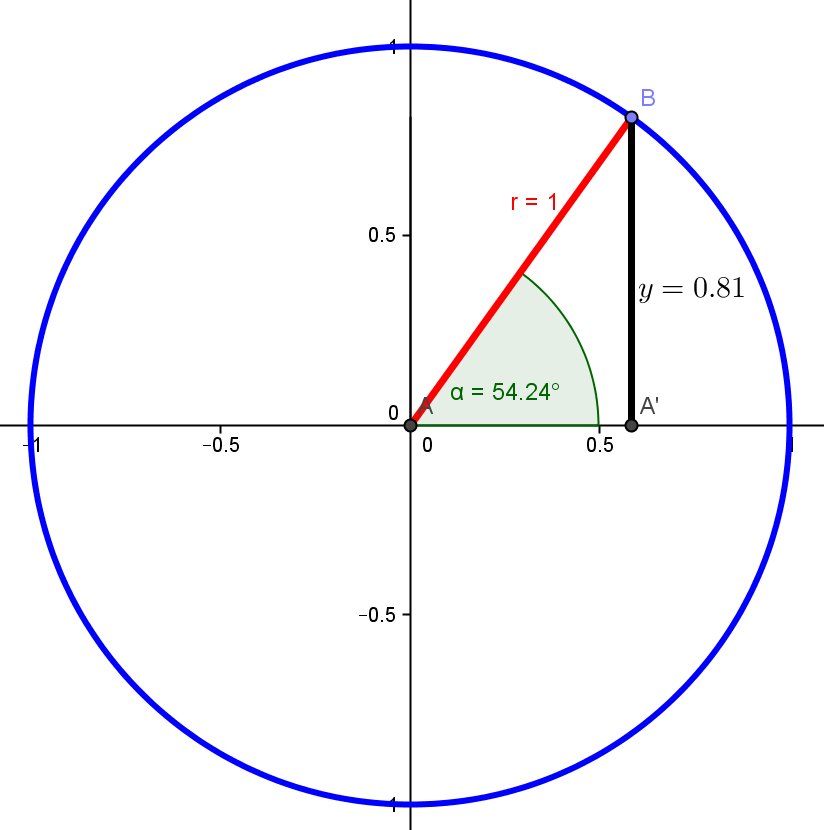 Нарисуйте линию, образующую угол $\theta$ с положительной осью $x$. Эта прямая пересекает единичную окружность в точке $(\cos\theta,\sin\theta)$ и имеет уравнение $y=x\tan\theta$.
Нарисуйте линию, образующую угол $\theta$ с положительной осью $x$. Эта прямая пересекает единичную окружность в точке $(\cos\theta,\sin\theta)$ и имеет уравнение $y=x\tan\theta$.
Для угла $\alpha=-\theta$ все зеркально отражается вокруг оси $x$. Отражением точки $(x,y)$ относительно оси $x$ является точка $(x,-y)$. Таким образом, отражение нашей исходной линии относительно оси $x$ пересечет единичный круг в точке $(\cos\theta,-\sin\theta)$ и будет иметь формулу $y=-x\tan\theta$.
Таким образом, если прямая, образующая угол $\alpha$, пересекает единичную окружность в точке $(\cos\alpha,\sin\alpha)$ и имеет уравнение $y=x\tan\alpha$, мы имеем
$$ \cos\alpha=\cos(-\theta)=\cos\theta$$ $$\sin\alpha=\sin(-\theta)=-\sin\theta$$ $$\tan\alpha=\tan(-\theta)=-\tan\theta$$
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
. Тригонометрия
Тригонометрия. Почему гипотенуза в тригонометрической системе всегда положительна независимо от квадранта?
За исключением опорных углов (которые всегда неотрицательны, острые и измеряются от ближайшей части оси $x$), все значения на этих диаграммах являются значениями со знаком. В частности,
- Метки стандартных позиционных углов начинаются с положительной оси $x$ и положительны для против часовой стрелки и (хотя на приведенных диаграммах нет примеров этого) отрицательны для по часовой стрелке.
- Метки ветвей, идущих вдоль оси $x$, представляют собой длины со знаком, положительные вправо и отрицательные влево.
- Метки для вертикальных ножек представляют собой длину со знаком, положительную для верха и отрицательную для низа.
- Метки гипотенуз представляют собой расстояния со знаком от начала координат, положительные для радиально наружу.
Конечно, поскольку в радиальном направлении нет другого направления, кроме «наружу», все гипотенузы неотрицательны.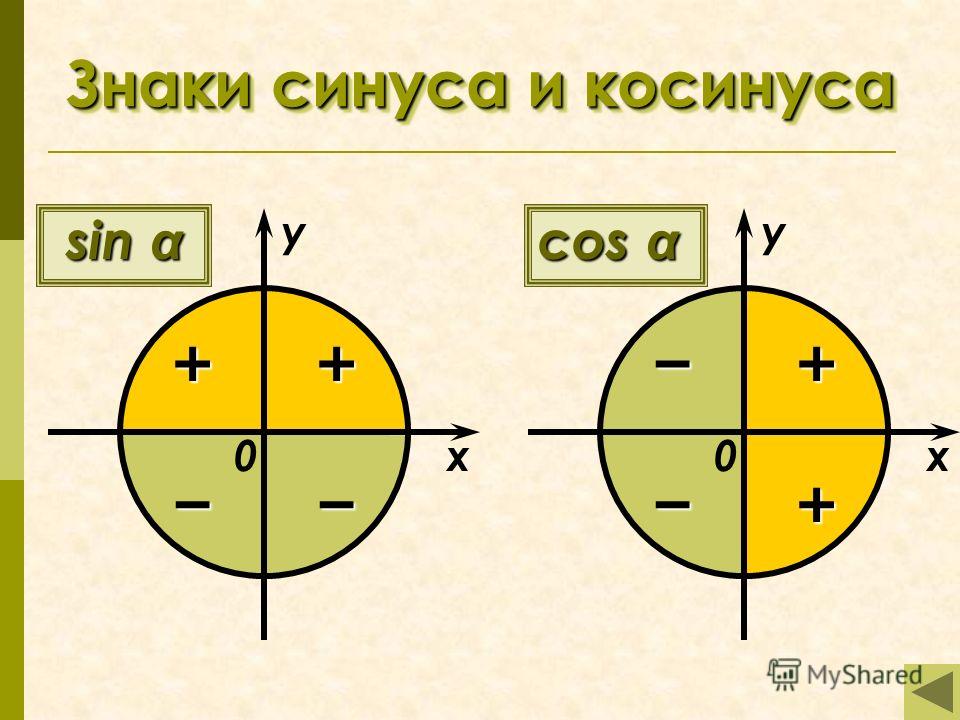
(Если вы продолжите изучать полярные координаты, будет введен некоторый смысл отрицательных радиусов. Метод помещает копию действительной оси через начало координат вдоль луча заданного угла с неотрицательной половиной оси совпадает с лучом угла. В некотором смысле замена «расстояния от начала координат» на «расстояние от начала координат со знаком» аналогично расширению тригонометрии из первого квадранта путем замены «длины катета» на «длину катета со знаком». Таким образом, в дополнение ко всем котерминальным псевдонимам для точек на плоскости, все они дублируются, чтобы включить новые псевдонимы для отрицательных радиусов.Для точки, имеющей координаты $(r,\theta)$, котерминальные псевдонимы $(r,\theta + 2 \pi k)$ для любого целого числа $k$ и новые псевдонимы $(-r, \theta + \pi + 2 \pi k)$ для любого целого числа $k$.)
Совершенно неуместно обсуждать тригонометрию с использованием треугольников или единичной окружности. Начинают с геометрических треугольников, все длины положительны.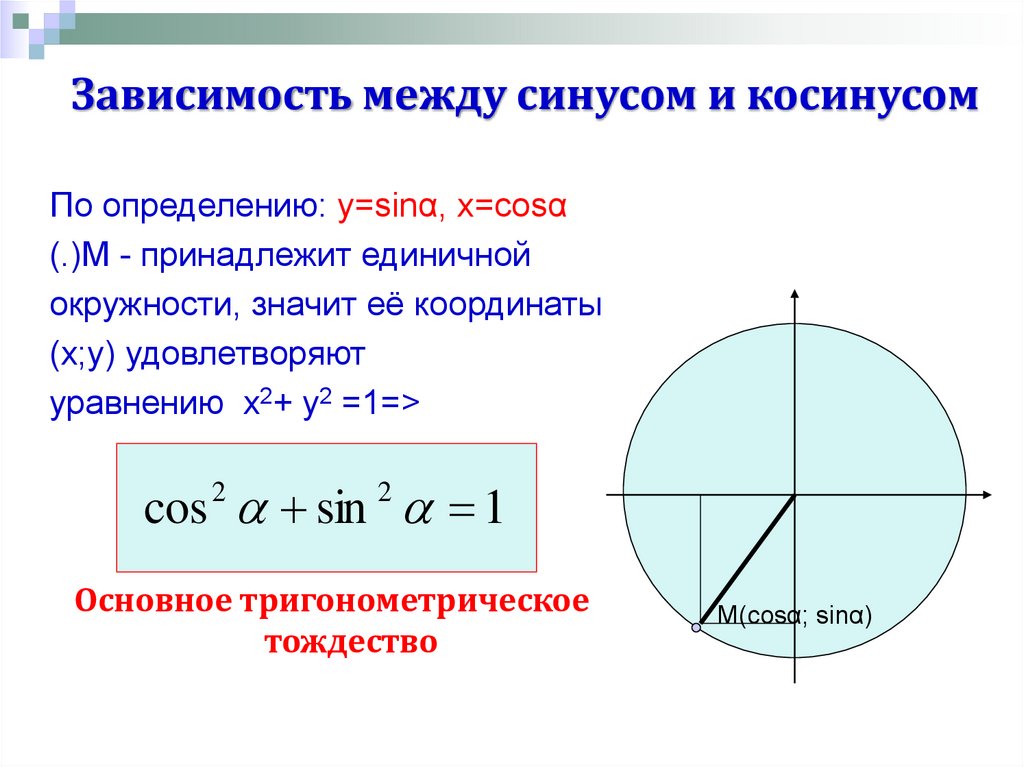 Но поскольку вы начинаете с прямоугольных треугольников, два других угла всегда острые. Если вы когда-нибудь захотите поговорить об угле измерения, превышающем $\pi/2$, вам придется как-то обобщить. (И говорить об углах, превышающих $\pi/2$, необходимо. Не все углы острые.) Мы вводим тригонометрические отношения, когда говорим о геометрических треугольниках, и понимаем, что эти отношения не зависят от масштаба — мы могли бы бросить любой геометрический треугольник на фотокопировальном устройстве масштабируйте его вверх или вниз, и коэффициенты не изменятся. Это означает, что мы можем выбрать некоторую длину, которая будет постоянной во всех наших треугольниках, и изучить нормализованное подмножество всех треугольников, но все же понять их все путем масштабирования. При подготовке к следующему шагу удобно масштабировать все гипотенузы до единицы.
Но поскольку вы начинаете с прямоугольных треугольников, два других угла всегда острые. Если вы когда-нибудь захотите поговорить об угле измерения, превышающем $\pi/2$, вам придется как-то обобщить. (И говорить об углах, превышающих $\pi/2$, необходимо. Не все углы острые.) Мы вводим тригонометрические отношения, когда говорим о геометрических треугольниках, и понимаем, что эти отношения не зависят от масштаба — мы могли бы бросить любой геометрический треугольник на фотокопировальном устройстве масштабируйте его вверх или вниз, и коэффициенты не изменятся. Это означает, что мы можем выбрать некоторую длину, которая будет постоянной во всех наших треугольниках, и изучить нормализованное подмножество всех треугольников, но все же понять их все путем масштабирования. При подготовке к следующему шагу удобно масштабировать все гипотенузы до единицы.
Когда мы понимаем, что любой прямоугольный треугольник можно масштабировать так, чтобы его гипотенуза имела длину один, мы берем все геометрические треугольники, делаем с ними то же самое и сводим их вместе с «углом интереса» (тот, который мы продолжаем вводить в синус, косинус и тангенс) в стандартном положении в начале координат. Получаем единичную четверть окружности в первом квадранте. Это прямое следствие теоремы Пифагора/евклидова расстояния. Что ж, мы определенно достаточно хитры, чтобы продолжить этот круг на квадранты со второго по четвертый. Когда мы делаем это, все гипотенузы имеют длину один; мы не получаем никаких отрицательных длин гипотенузы. Но ноги указывают влево и вправо, вверх и вниз. На самом деле это координаты точки на единичной окружности, через которую проходит конечный луч угла в стандартном положении. Если мы расширим наше определение «длины стороны, примыкающей к углу» и «длины стороны, противоположной углу», чтобы разрешить положительные и отрицательные значения, мы получим расширение косинуса и синуса, соответственно, из первого квадранта в три других. .
Получаем единичную четверть окружности в первом квадранте. Это прямое следствие теоремы Пифагора/евклидова расстояния. Что ж, мы определенно достаточно хитры, чтобы продолжить этот круг на квадранты со второго по четвертый. Когда мы делаем это, все гипотенузы имеют длину один; мы не получаем никаких отрицательных длин гипотенузы. Но ноги указывают влево и вправо, вверх и вниз. На самом деле это координаты точки на единичной окружности, через которую проходит конечный луч угла в стандартном положении. Если мы расширим наше определение «длины стороны, примыкающей к углу» и «длины стороны, противоположной углу», чтобы разрешить положительные и отрицательные значения, мы получим расширение косинуса и синуса, соответственно, из первого квадранта в три других. .
Что в этом хорошего? Теперь наши тригонометрические функции сообщают нам обо всех точках окружности, а не только о точках в первом квадранте. Мы можем сказать вам, где точка крепления соединительных стержней находится на всем протяжении вращения колеса паровой машины, без необходимости устанавливать новую систему координат в каждом квадранте. Когда точка соединения находится над осью колеса, вертикальная координата, заданная синусом, положительна, а когда ниже — отрицательна. Аналогичное наблюдение относится и к косинусу. Есть два основных механических движения — линейное и круговое. Моделирование линейного движения с помощью математики было в нашей рубрике с тех пор, как мы изучали параметризованные линейные уравнения в алгебре. Теперь, когда у нас есть параметризация (по углу) окружностей, мы можем моделировать круговое движение.
Когда точка соединения находится над осью колеса, вертикальная координата, заданная синусом, положительна, а когда ниже — отрицательна. Аналогичное наблюдение относится и к косинусу. Есть два основных механических движения — линейное и круговое. Моделирование линейного движения с помощью математики было в нашей рубрике с тех пор, как мы изучали параметризованные линейные уравнения в алгебре. Теперь, когда у нас есть параметризация (по углу) окружностей, мы можем моделировать круговое движение.
Но мы еще не закончили. Нам нужно еще одно обобщение. Мы начали с тригонометрических функций, которые могли принимать только острые углы. Мы обобщили тригонометрические функции, которые могут принимать любой угол от $0$ до $2\pi$ радиан. Но колеса не катятся один раз, а затем останавливаются. Они продолжают идти. И идут назад. (Скорее всего, идея отрицательных углов, больших положительных углов и того, что каждый угол имеет бесконечно много котерминальных углов, была объяснена, когда был определен термин «угол». ) Нам нужно расширить наши тригонометрические функции, чтобы обрабатывать все этих углов. Как мы делаем это? Расширяя единичный круг, чтобы двигаться по кругу как против часовой стрелки, так и по часовой стрелке. Это как если бы у нас была спираль бесконечного единичного радиуса с осевым периодом $2\pi$, но мы видим ее только в параллельной проекции вдоль ее оси на плоскость (поэтому мы «видим» точку, совершающую бесконечное число оборотов по единичной окружности). ).
) Нам нужно расширить наши тригонометрические функции, чтобы обрабатывать все этих углов. Как мы делаем это? Расширяя единичный круг, чтобы двигаться по кругу как против часовой стрелки, так и по часовой стрелке. Это как если бы у нас была спираль бесконечного единичного радиуса с осевым периодом $2\pi$, но мы видим ее только в параллельной проекции вдоль ее оси на плоскость (поэтому мы «видим» точку, совершающую бесконечное число оборотов по единичной окружности). ).
На этом мы завершаем расширение наших тригонометрических соотношений от геометрических треугольников (острых углов) до энциклопедии значений синуса и косинуса (единичная окружность для углов в $[0,2\pi)$) и, наконец, до все возможные реальные углы.
Значит, вы не объясняете тригонометрические функции в терминах треугольников или единичных окружностей. Чтобы сначала определить, а затем обобщить, вам нужно и то, и другое. Но тогда у вас есть оба инструмента в вашем наборе инструментов в будущем.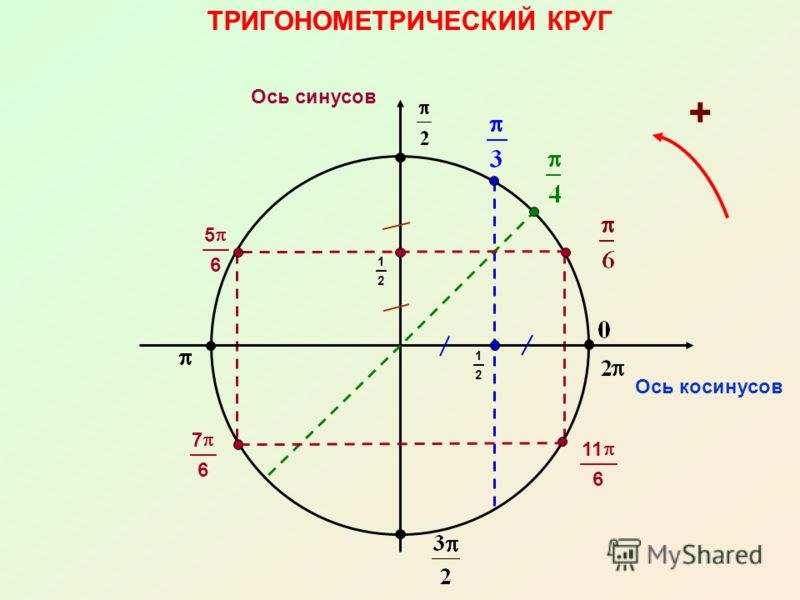 Если к конкретной проблеме лучше всего подходить с помощью геометрического треугольника, вы можете это сделать. Если лучше подойти с единичным кругом, вы тоже можете это сделать. И в обоих случаях вы знаете, как связаны эти два подхода, поэтому можете переключаться между ними по мере необходимости.
Если к конкретной проблеме лучше всего подходить с помощью геометрического треугольника, вы можете это сделать. Если лучше подойти с единичным кругом, вы тоже можете это сделать. И в обоих случаях вы знаете, как связаны эти два подхода, поэтому можете переключаться между ними по мере необходимости.
Понимание знаков 6 тригонометрических функций в каждом квадранте
Все ресурсы по тригонометрии
6 Диагностические тесты 155 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Тригонометрия Помощь » Тригонометрические функции и графики » Тригонометрические функции » Поймите знаки 6 тригонометрических функций в каждом квадранте
Если косинус угла отрицателен, а тангенс положителен, в каком(их) квадранте(ах) лежит этот угол?
Возможные ответы:
Квадранты 3 и 4
Квадрант 3
Квадрант 2
Квадраты 2 и 3
Квадрант 4
Правильный ответ:
Квадрат 3
. Объяснение:
Объяснение:
Тангенс положителен в двух квадрантах: квадрантах 1 и 3 (где синус и косинус имеют одинаковые знаки)
Косинус отрицателен в двух квадрантах: квадрантах 2 и 3 (левых квадрантах, где x отрицательно).
Единственным квадрантом, обладающим обоими качествами, является квадрант 3.
Сообщить об ошибке
Что из следующего является положительным?
Возможные ответы:
Правильный ответ:
Объяснение:
При проведении из начала координат линия на 45 градусов выше (против часовой стрелки) положительной оси x лежит в квадранте I. Косинус определяется как отношение между прилежащей стороной треугольника и гипотенузой треугольника. Прямоугольный треугольник можно нарисовать в квадранте I, состоящем из любой точки на этой линии, начала координат и точки на оси x. Гипотенуза этого треугольника считается длиной и поэтому положительна. Прилегающая сторона этого треугольника лежит вдоль положительной оси x. Поскольку смежная сторона и гипотенуза представлены положительными числами, дробь A/H положительна. Следовательно, cos 45 положителен.
Гипотенуза этого треугольника считается длиной и поэтому положительна. Прилегающая сторона этого треугольника лежит вдоль положительной оси x. Поскольку смежная сторона и гипотенуза представлены положительными числами, дробь A/H положительна. Следовательно, cos 45 положителен.
Сообщить об ошибке
Что из перечисленного является положительным?
Возможные ответы:
Правильный ответ:
Объяснение:
При проведении из начала координат линия на 135 градусов против часовой стрелки от положительной оси x лежит в квадранте II. Синус определяется как отношение между противолежащей стороной треугольника и гипотенузой треугольника. Прямоугольный треугольник можно нарисовать в квадранте II, состоящем из любой точки на этой линии, начала координат и точки на оси x. Гипотенуза этого треугольника считается длиной и поэтому положительна. Противоположная сторона этого треугольника лежит над осью x и поэтому представлена положительным числом. Поскольку противоположная сторона и гипотенуза представлены положительными числами, дробь O/H положительна. Следовательно, sin 135 положителен.
Противоположная сторона этого треугольника лежит над осью x и поэтому представлена положительным числом. Поскольку противоположная сторона и гипотенуза представлены положительными числами, дробь O/H положительна. Следовательно, sin 135 положителен.
Сообщить об ошибке
Что из следующего является отрицательным?
Возможные ответы:
Правильный ответ:
Объяснение:
При проведении из начала координат линия на 135 градусов против часовой стрелки от положительной оси x лежит в квадранте II. Тангенс определяется как отношение между противолежащей и прилежащей сторонами треугольника. Прямоугольный треугольник можно нарисовать в квадранте II, состоящем из любой точки на этой линии, начала координат и точки на оси x. Противоположная сторона этого треугольника лежит над осью x и поэтому представлена положительным числом.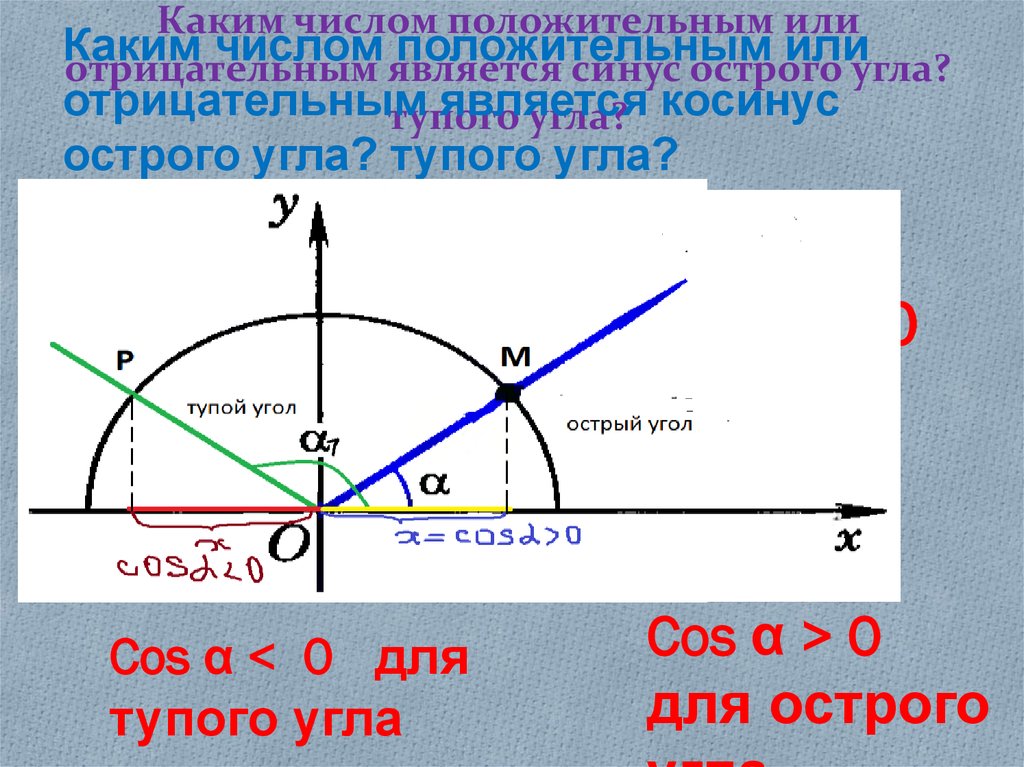 Прилегающая сторона этого треугольника лежит на отрицательной оси x и поэтому представлена отрицательным числом. Поскольку противолежащая сторона и прилежащая сторона имеют противоположные знаки, дробь O/A отрицательна. Следовательно, тангенс 135 отрицательный.
Прилегающая сторона этого треугольника лежит на отрицательной оси x и поэтому представлена отрицательным числом. Поскольку противолежащая сторона и прилежащая сторона имеют противоположные знаки, дробь O/A отрицательна. Следовательно, тангенс 135 отрицательный.
Сообщить об ошибке
Что из следующего является отрицательным?
Возможные ответы:
Правильный ответ:
Объяснение:
При проведении из начала координат линия на 225 градусов против часовой стрелки от положительной оси x лежит в квадранте III. Косинус определяется как отношение между прилежащей стороной треугольника и гипотенузой треугольника. Прямоугольный треугольник можно нарисовать в квадранте III, состоящем из любой точки на этой линии, начала координат и точки на оси x. Гипотенуза этого треугольника считается длиной и поэтому положительна. Прилегающая сторона этого треугольника лежит на отрицательной оси x и поэтому представлена отрицательным числом. Поскольку противолежащий катет и гипотенуза имеют противоположные знаки, дробь A/H отрицательна. Следовательно, cos 225 отрицателен.
Прилегающая сторона этого треугольника лежит на отрицательной оси x и поэтому представлена отрицательным числом. Поскольку противолежащий катет и гипотенуза имеют противоположные знаки, дробь A/H отрицательна. Следовательно, cos 225 отрицателен.
Сообщить об ошибке
Что из следующего является отрицательным?
Возможные ответы:
Правильный ответ:
Объяснение:
При проведении из начала координат линия на 225 градусов против часовой стрелки от положительной оси x лежит в квадранте III. Синус определяется как отношение между прилежащей стороной треугольника и гипотенузой треугольника. Прямоугольный треугольник можно нарисовать в квадранте III, состоящем из любой точки на этой линии, начала координат и точки на оси x. Гипотенуза этого треугольника считается длиной и поэтому положительна. Противоположная сторона этого треугольника лежит ниже оси x и поэтому представлена отрицательным числом.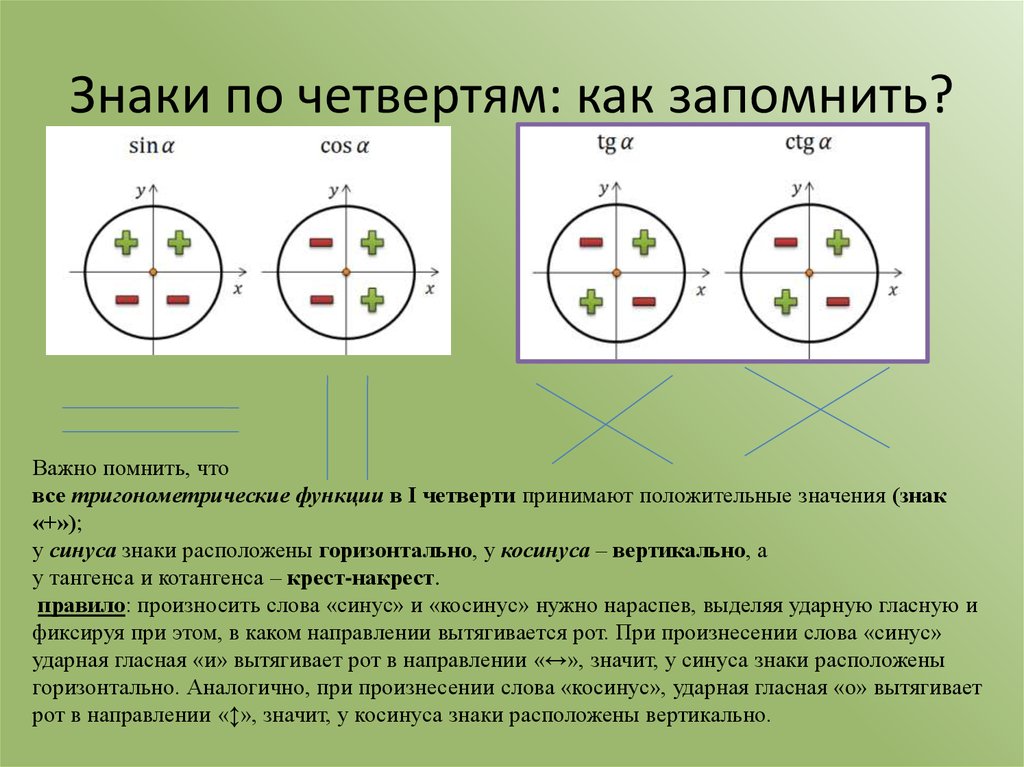 Поскольку противолежащий катет и гипотенуза имеют противоположные знаки, дробь O/H отрицательна. Следовательно, sin 225 является отрицательным.
Поскольку противолежащий катет и гипотенуза имеют противоположные знаки, дробь O/H отрицательна. Следовательно, sin 225 является отрицательным.
Сообщить об ошибке
Что из перечисленного является положительным?
Возможные ответы:
Правильный ответ:
Объяснение:
При проведении из начала координат линия на 225 градусов против часовой стрелки от положительной оси x лежит в квадранте II. Тангенс определяется как отношение между противолежащей и прилежащей сторонами треугольника. Прямоугольный треугольник можно нарисовать в квадранте III, состоящем из любой точки на этой линии, начала координат и точки на оси x. Противоположная сторона этого треугольника лежит ниже оси x и поэтому представлена отрицательным числом. Прилегающая сторона этого треугольника лежит на отрицательной оси x и поэтому представлена отрицательным числом.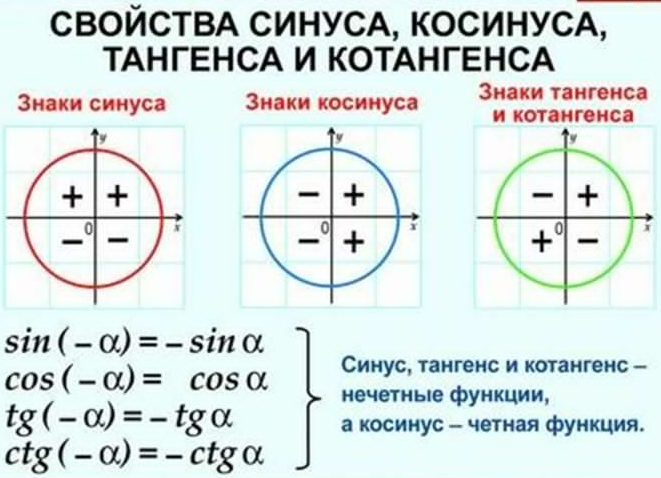 Так как противолежащая сторона и примыкающая сторона имеют один и тот же знак, дробь O/A положительна. Следовательно, тангенс 225 положительный.
Так как противолежащая сторона и примыкающая сторона имеют один и тот же знак, дробь O/A положительна. Следовательно, тангенс 225 положительный.
Сообщить об ошибке
Что из перечисленного является положительным?
Возможные ответы:
Правильный ответ:
Объяснение:
При проведении из начала координат линия на 45 градусов выше (против часовой стрелки) положительной оси x лежит в квадранте I. Косинус определяется как отношение между прилежащей стороной треугольника и гипотенузой треугольника. Секанс определяется как величина, обратная косинусу; следовательно, косинус и секанс угла имеют один и тот же знак. Прямоугольный треугольник можно нарисовать в квадранте I, состоящем из любой точки на этой линии, начала координат и точки на оси x. Гипотенуза этого треугольника считается длиной и поэтому положительна. Прилегающая сторона этого треугольника лежит вдоль положительной оси x. Поскольку смежная сторона и гипотенуза представлены положительными числами, дробь A/H положительна. Следовательно, cos 45 положителен, как и его обратная величина, sec 45.
Прилегающая сторона этого треугольника лежит вдоль положительной оси x. Поскольку смежная сторона и гипотенуза представлены положительными числами, дробь A/H положительна. Следовательно, cos 45 положителен, как и его обратная величина, sec 45.
Сообщить об ошибке
Что из перечисленного является положительным?
Возможные ответы:
Правильный ответ:
Объяснение:
При проведении из начала координат линия на 135 градусов против часовой стрелки от положительной оси x лежит в квадранте II. Синус определяется как отношение между противолежащей стороной треугольника и гипотенузой треугольника. Косеканс определяется как величина, обратная синусу, поэтому синус и косеканс угла должны иметь один и тот же знак. Прямоугольный треугольник можно нарисовать в квадранте II, состоящем из любой точки на этой линии, начала координат и точки на оси X. Гипотенуза этого треугольника считается длиной и поэтому положительна. Противоположная сторона этого треугольника лежит над осью x и поэтому представлена положительным числом. Поскольку противоположная сторона и гипотенуза представлены положительными числами, дробь O/H положительна. Таким образом, sin 135 положителен, как и его обратная величина, csc 135.
Гипотенуза этого треугольника считается длиной и поэтому положительна. Противоположная сторона этого треугольника лежит над осью x и поэтому представлена положительным числом. Поскольку противоположная сторона и гипотенуза представлены положительными числами, дробь O/H положительна. Таким образом, sin 135 положителен, как и его обратная величина, csc 135.
Сообщить об ошибке
Что из перечисленного является положительным?
Возможные ответы:
Правильный ответ:
Объяснение:
При проведении из начала координат линия на 225 градусов против часовой стрелки от положительной оси x лежит в квадранте II. Тангенс определяется как отношение между противолежащей и прилежащей сторонами треугольника. Котангенс определяется как величина, обратная тангенсу, поэтому тангенс и котангенс угла должны иметь один и тот же знак.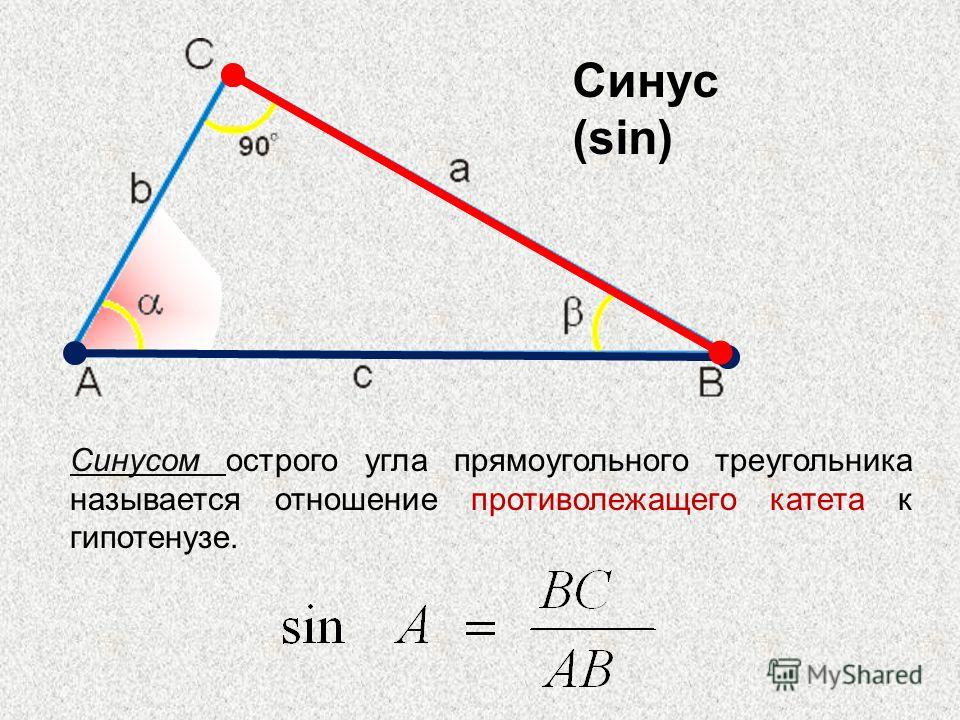

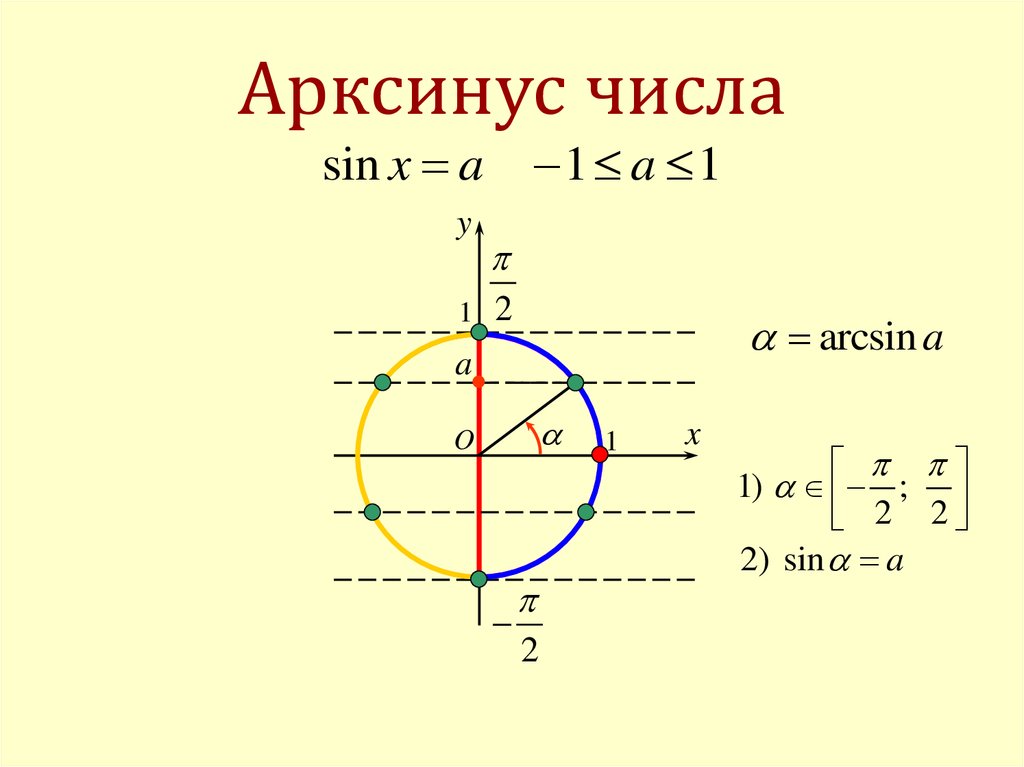 01.2008
01.2008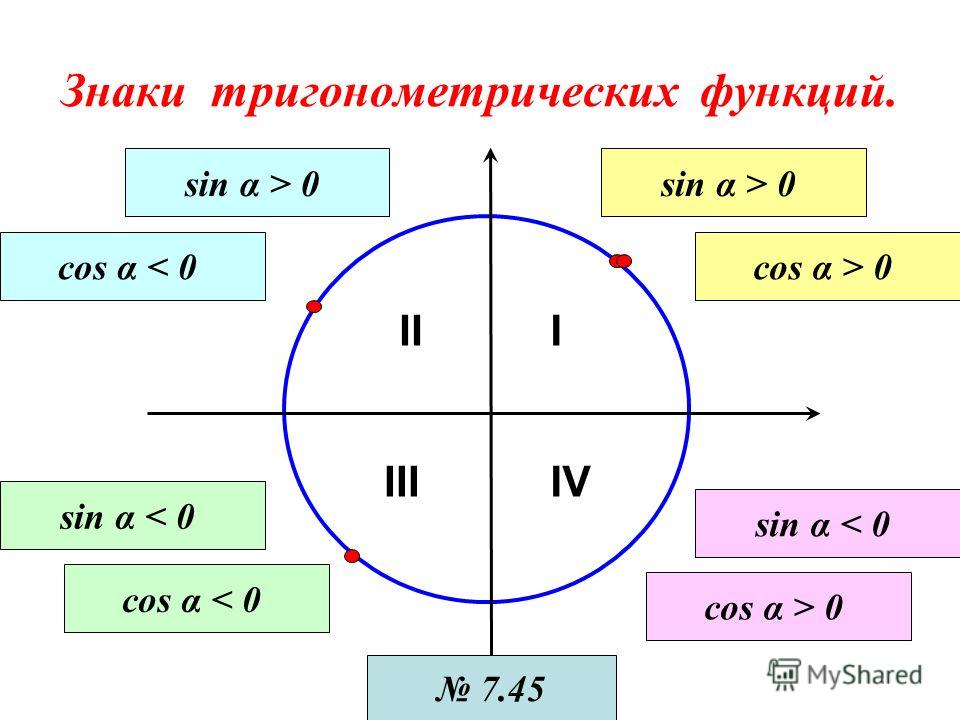
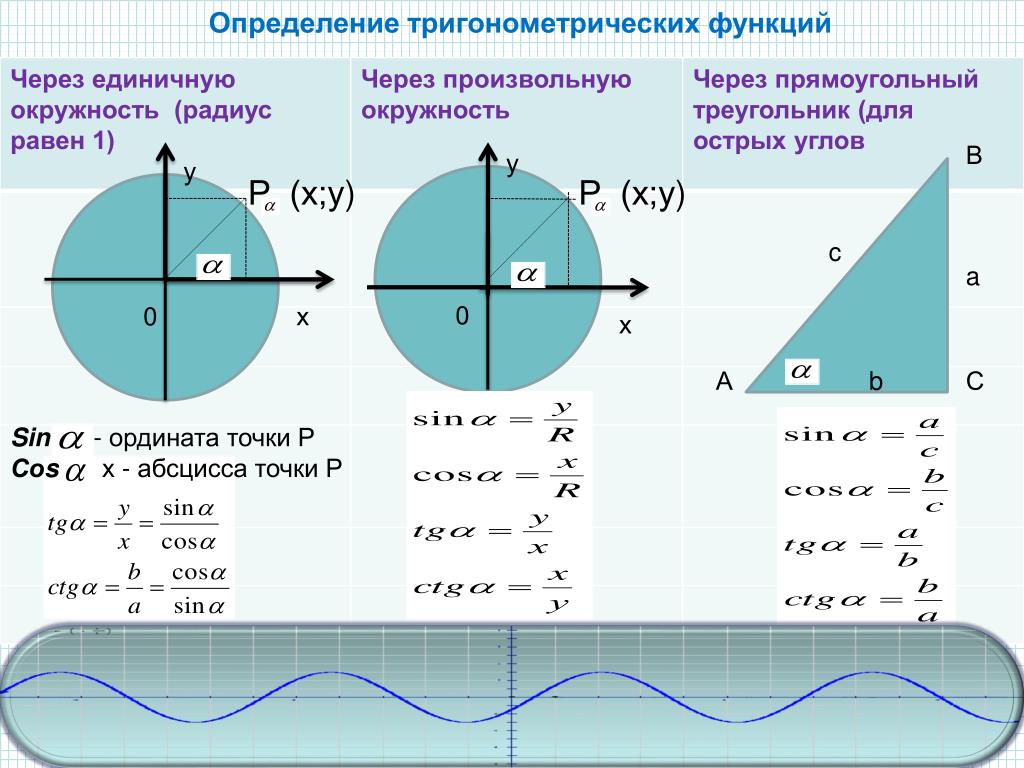 Если исходить из теоремы Пифогора то гипотенуза в системе координат какой знак будет иметь?
Если исходить из теоремы Пифогора то гипотенуза в системе координат какой знак будет иметь?
 08.2008
08.2008 Словом, надо посмотреть действительно в теххарактеристиках (или стандартах), что показывает знак cosφ в приборе. Я уверен, что направление активной мощности (в противном случае это будет театр абсурда).
Словом, надо посмотреть действительно в теххарактеристиках (или стандартах), что показывает знак cosφ в приборе. Я уверен, что направление активной мощности (в противном случае это будет театр абсурда).
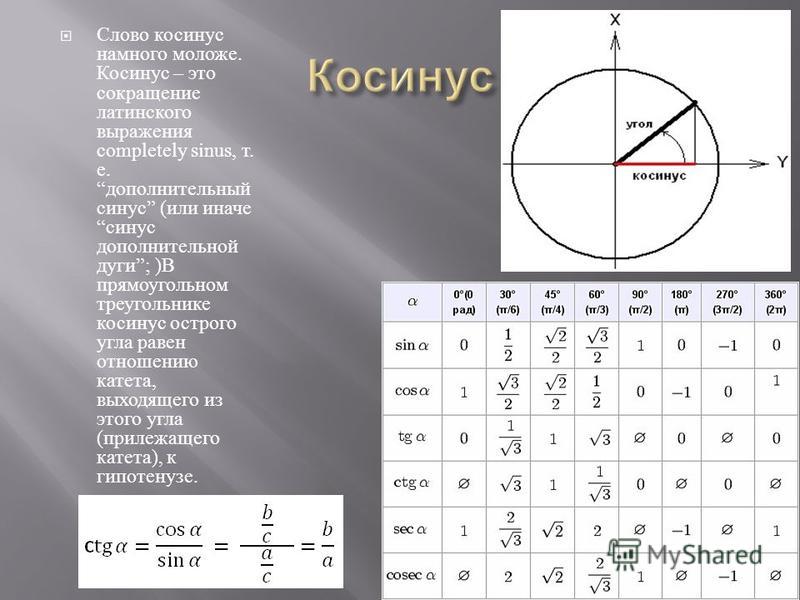 ТТ подключены «Полярниками» к источнику.
ТТ подключены «Полярниками» к источнику.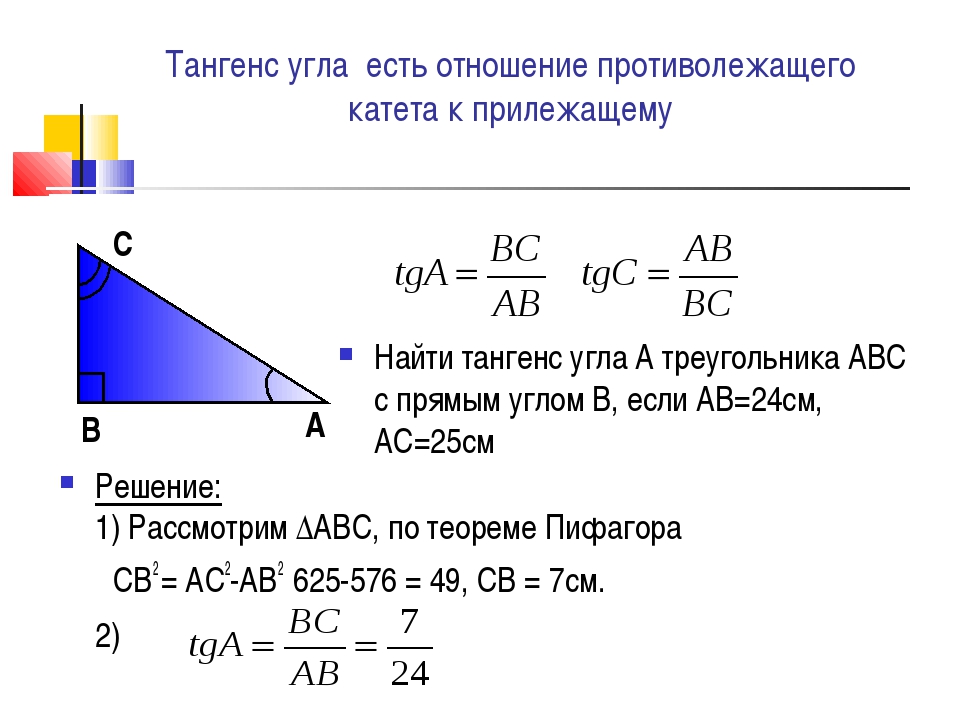 Котлеты отдельно? (-) к косинусу никакого отношения не имеет. Просто рядом стояли?
Котлеты отдельно? (-) к косинусу никакого отношения не имеет. Просто рядом стояли?
 08.2008
08.2008
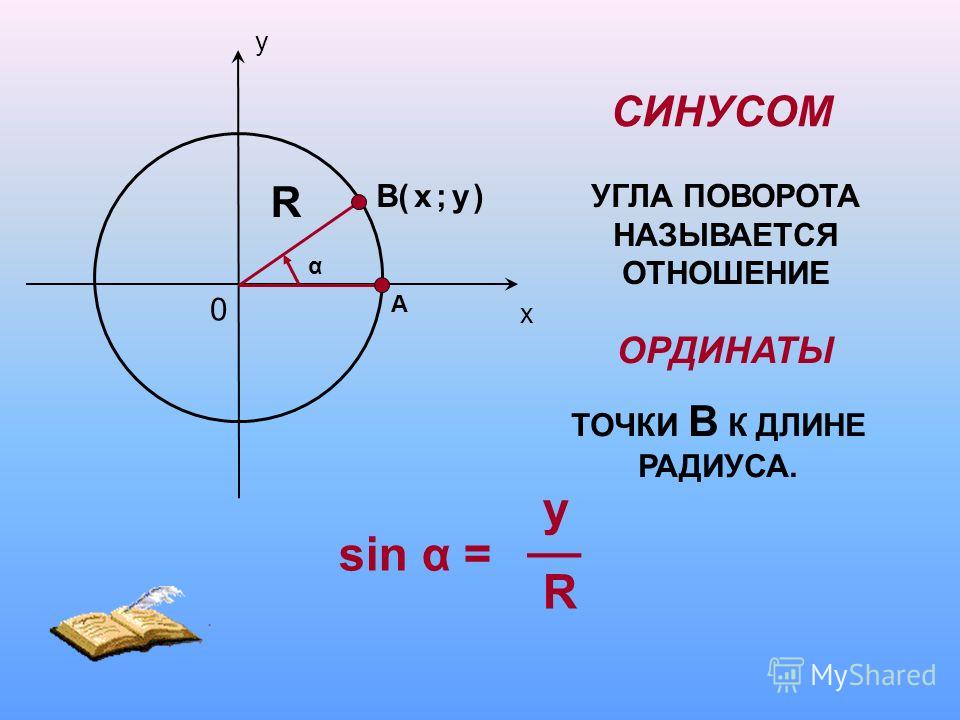 11.2010 13:38
11.2010 13:38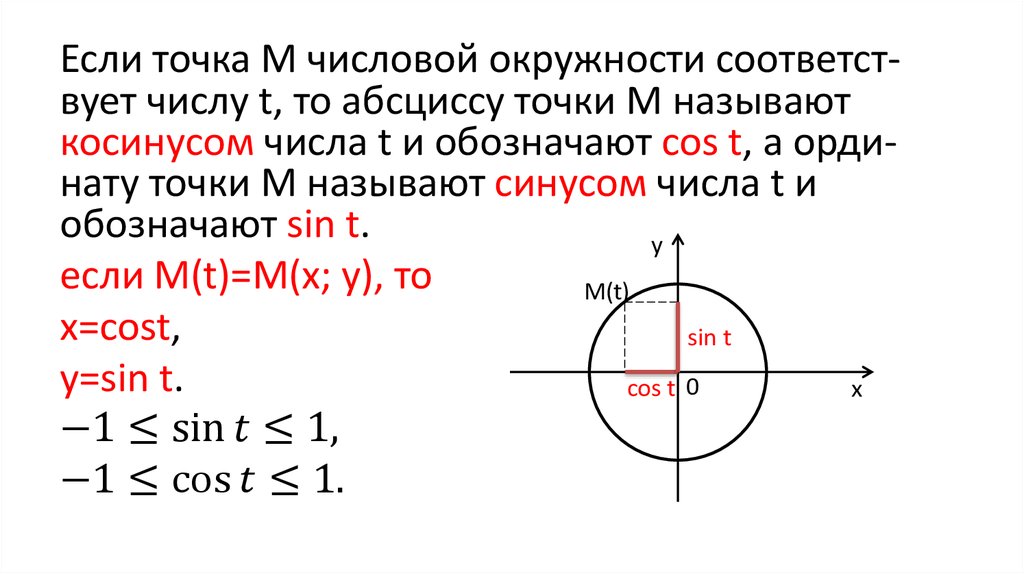 08.2007
08.2007 д.
д.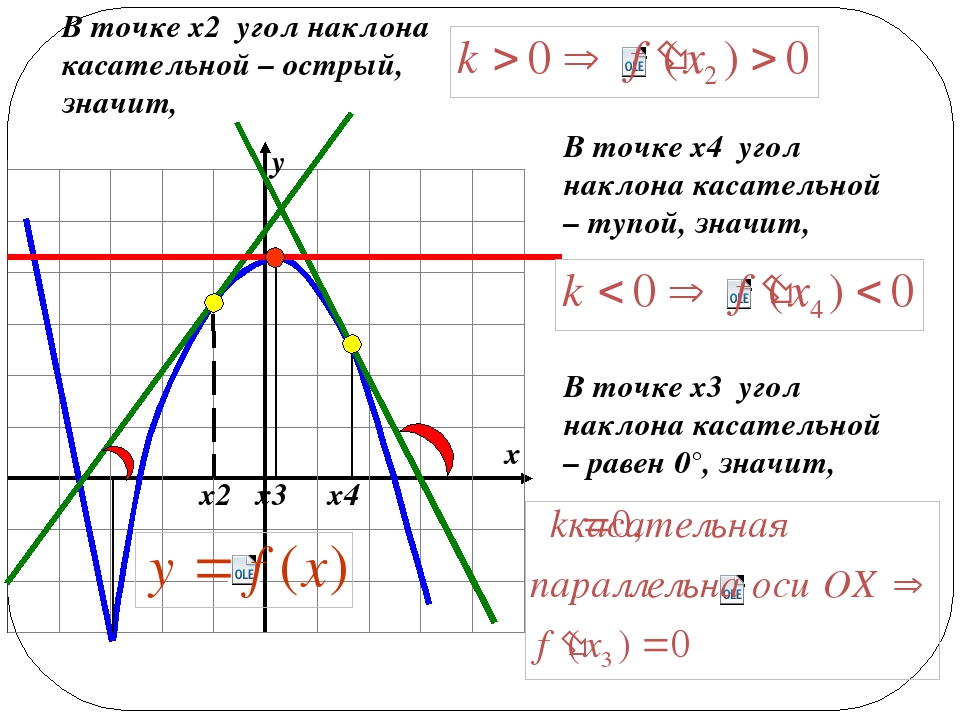 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.