Можно ли прибавить к матрице число: Как складывать матрицы разных размеров. Действия с матрицами

Сообщество Экспонента

• вопрос
• 24.04.2023

Системы управления, Электропривод и силовая электроника, Другое, Автоматизация испытаний

Необходимо рассмотреть различные режимы работы энергосистемы в зависимости от загрузки двигателей,но в схеме это просто мощность,активная и реактивная соответсвенно. Так же для этих параметеров рассчи…

Необходимо рассмотреть различные режимы работы энергосистемы в зависимости от загрузки двигателей,но в схеме это просто мощность,активная и реактивная соответсвенно. Так же для этих параметеров рассчи…

1 Ответ

• Simulink

24.04.2023

• вопрос
• 23.04.2023

ПЛИС и СнК

Здравствуйте! Требуется помощь в написании кода на verilog. Генератор импульсной последовательности с заданными параметрами реализован в виде блок-схемы. Результат этого проектирования, временные диаг…

Здравствуйте! Требуется помощь в написании кода на verilog.

Генератор импульсной последовательности с заданными параметрами реализован в виде блок-схемы. Результат этого проектирования, временные диаг…

1 Ответ

• вопрос
• 19.04.2023

Изображения и видео, Цифровая обработка сигналов, Математика и статистика

Вроде как схема у меня получилась но при добавлении зависимости от температуры и старения возникли проблемы кто-нибудь знает как сделать по красоте?

Вроде как схема у меня получилась но при добавлении зависимости от температуры и старения возникли проблемы кто-нибудь знает как сделать по красоте?

• вопрос
• 14.04.2023

Глубокое и машинное обучение(ИИ), Математика и статистика, Системы управления

Прошу помощи в создании модели газотранспортной системы в Simulink/Simscape. Спасибо

Прошу помощи в создании модели газотранспортной системы в Simulink/Simscape. Спасибо

4 Ответа

• Simulink
• modeling
• газ

14. 04.2023

• вопрос
• 12.04.2023

Математика и статистика, Робототехника и беспилотники, Системы связи, Цифровая обработка сигналов

Всем привет. Мне нужно собрать схему FSK-модема для моей научной работы в университете. Требования:1. Модулятор в передатчике должен быть реализован на GMSK или 4-FSK (желательно не брать библиотечный…

Всем привет. Мне нужно собрать схему FSK-модема для моей научной работы в университете. Требования:1. Модулятор в передатчике должен быть реализован на GMSK или 4-FSK (желательно не брать библиотечный…

2 Ответа

• вопрос
• 06.04.2023

Цифровая обработка сигналов

Добрый день, уважаемые участники форума! Подскажите, пожалуйста, как можно забрать те данные, по которым был построен график спектра сигнала? Они мне нужны для дальнейшей нормировки в excel.

Добрый день, уважаемые участники форума! Подскажите, пожалуйста, как можно забрать те данные, по которым был построен график спектра сигнала? Они мне нужны для дальнейшей нормировки в excel.

1 Ответ

• вопрос
• 04.04.2023

Цифровая обработка сигналов

  End

  End

3 Ответа

• вопрос
• 02.04.2023

Другое

Добрый день/вечер! подскажите, пожалуйста, как настроить матлаб чтобы можно было работать с ним удаленно. то есть он развернут на одной ПЭВМ, а мне нужно подключится с другой ПЭВМ, но не к виндоус чер…

Добрый день/вечер! подскажите, пожалуйста, как настроить матлаб чтобы можно было работать с ним удаленно. то есть он развернут на одной ПЭВМ, а мне нужно подключится с другой ПЭВМ, но не к виндоус чер…

• Публикация
• 29.03.2023

Глубокое и машинное обучение(ИИ)

Но давайте будем честными, для не технических менеджеров продуктов, дизайнеров и предпринимателей, внутреннее устройство ChatGPT может показаться как волшебный черный ящик. Не волнуйтесь! В этой статье я постараюсь объяснить технологию и модель, лежащие в осно. ..

Это перевод статьи: https://bootcamp.uxdesign.cc/how-chatgpt-really-works-explained-for-non-technical-people-71efb078a5c9

Автор: Guodong (Troy) Zhao

Выход ChatGPT, созданного OpenAI в конце прошлого года, был явлением феноменальным — даже моя бабушка спрашивает об этом. Его возможности генерировать язык, похожий на человеческий, вдохновляют людей экспериментировать с его потенциалом в различных продуктах. Его крайне успешный запуск даже поставил давление на гигантов технологической отрасли, таких как Google, чтобы спешить выпустить свою собственную версию ChatGPT.

• ИИ
• ChatGPT
• OpenAI
• Искусственный интеллект
• NLP
• GPT

29.03.2023

• вопрос
• 27.03.2023

Цифровая обработка сигналов, Системы связи, Математика и статистика, Автоматизация испытаний, Встраиваемые системы, Радиолокация, Другое, Изображения и видео

Прошу помочь в реализации программы написанной в AppDesigner.   оптический волновод , входные параметры, законы геометрической оптики , построение мод (волн) учитывая вышеперечисленные параметры,…

Прошу помочь в реализации программы написанной в AppDesigner.  оптический волновод , входные параметры, законы геометрической оптики , построение мод (волн) учитывая вышеперечисленные параметры,…

• оптика
• Оптические системы
• Волоконная оптика

27.03.2023

Матрицы, определители, системы линейных уравнений (Лекция №12)

ОПРЕДЕЛЕНИЕ МАТРИЦЫ. ВИДЫ МАТРИЦ

Матрицей размером m×n называется совокупность m·n чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов. Эту таблицу обычно заключают в круглые скобки. Например, матрица может иметь вид:

Для краткости матрицу можно обозначать одной заглавной буквой, например, А или В.

В общем виде матрицу размером m×n записывают так

.

Числа, составляющие матрицу, называются элементами матрицы. Элементы матрицы удобно снабжать двумя индексами a_ij: первый указывает номер строки, а второй – номер столбца. Например, a₂₃ – элемент стоит во 2-ой строке, 3-м столбце.

Если в матрице число строк равно числу столбцов, то матрица называется квадратной, причём число ее строк или столбцов называется порядком матрицы. В приведённых выше примерах квадратными являются вторая матрица – её порядок равен 3, и четвёртая матрица – её порядок 1.

Матрица, в которой число строк не равно числу столбцов, называется прямоугольной. В примерах это первая матрица и третья.

Различаются также матрицы, имеющие только одну строку или один столбец.

Матрица, у которой всего одна строка , называется матрицей – строкой (или строковой), а матрица, у которой всего один столбец,

матрицей – столбцом.

Матрица, все элементы которой равны нулю, называется нулевой и обозначается (0), или просто 0. Например,

.

Главной диагональю квадратной матрицы назовём диагональ, идущую из левого верхнего в правый нижний угол.

Квадратная матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю, называется треугольной матрицей.

.

Квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю, называется диагональной матрицей. Например, или .

Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной матрицей и обозначается буквой E. Например, единичная матрица 3-го порядка имеет вид .

ДЕЙСТВИЯ НАД МАТРИЦАМИ

Равенство матриц. Две матрицы A и B называются равными, если они имеют одинаковое число строк и столбцов и их соответствующие элементы равны a_ij = b_ij. Так если и , то A=B, если a₁₁ = b₁₁, a₁₂ = b₁₂, a₂₁ = b₂₁ и a₂₂ = b₂₂.

Транспонирование. Рассмотрим произвольную матрицу A из m строк и n столбцов. Ей можно сопоставить такую матрицу B из n строк и m столбцов, у которой каждая строка является столбцом матрицы A с тем же номером (следовательно, каждый столбец является строкой матрицы A с тем же номером). Итак, если , то .

Эту матрицу B называют транспонированной матрицей

A, а переход от A к B транспонированием.

Таким образом, транспонирование – это перемена ролями строк и столбцов матрицы. Матрицу, транспонированную к матрице A, обычно обозначают A^T.

Связь между матрицей A и её транспонированной можно записать в виде .

Например. Найти матрицу транспонированную данной.

Сложение матриц. Пусть матрицы A и B состоят из одинакового числа строк и одинакового числа столбцов, т. е. имеют одинаковые размеры. Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах. Таким образом, суммой двух матриц A и B называется матрица C, которая определяется по правилу, например,

или

Примеры. Найти сумму матриц:

1. .
2. — нельзя, т.к. размеры матриц различны.
3. .

Легко проверить, что сложение матриц подчиняется следующим законам: коммутативному A+B=B+A и ассоциативному (A+B)+C=A+(B+C).

Умножение матрицы на число. Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число. Таким образом, произведение матрицы A на число k есть новая матрица, которая определяется по правилу или .

Для любых чисел a и b и матриц A и B выполняются равенства:

3. .

Примеры.

1. .
2. Найти 2A-B, если , .

   .

3. Найти C=–3A+4B.

   Матрицу C найти нельзя, т.к. матрицы A и B имеют разные размеры.

Умножение матриц. Эта операция осуществляется по своеобразному закону. Прежде всего, заметим, что размеры матриц–сомножителей должны быть согласованы. Перемножать можно только те матрицы, у которых число столбцов первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки первой равна высоте столбца второй). Произведением матрицы A не матрицу B называется новая матрица C=AB, элементы которой составляются следующим образом:

.

Таким образом, например, чтобы получить у произведения (т. е. в матрице C) элемент, стоящий в 1-ой строке и 3-м столбце c₁₃, нужно в 1-ой матрице взять 1-ую строку, во 2-ой – 3-й столбец, и затем элементы строки умножить на соответствующие элементы столбца и полученные произведения сложить. И другие элементы матрицы-произведения получаются с помощью аналогичного произведения строк первой матрицы на столбцы второй матрицы.

В общем случае, если мы умножаем матрицу A = (a_ij) размера m×n на матрицу B = (b_ij) размера n×p, то получим матрицу C размера m×p, элементы которой вычисляются следующим образом: элемент c_ij получается в результате произведения элементов i-ой строки матрицы A на соответствующие элементы j-го столбца матрицы B и их сложения.

Из этого правила следует, что всегда можно перемножать две квадратные матрицы одного порядка, в результате получим квадратную матрицу того же порядка. В частности, квадратную матрицу всегда можно умножить саму на себя, т.е. возвести в квадрат.

Другим важным случаем является умножение матрицы–строки на матрицу–столбец, причём ширина первой должна быть равна высоте второй, в результате получим матрицу первого порядка (т.е. один элемент). Действительно,

.

Примеры.

1. Пусть

   Найти элементы c₁₂, c₂₃ и c₂₁ матрицы C.

2. Найти произведение матриц.

   .

3. .
4. — нельзя, т.к. ширина первой матрицы равна 2-м элементам, а высота второй – 3-м.
5. Пусть

   Найти АВ и ВА.

6. Найти АВ и ВА.

   , B·A – не имеет смысла.

Таким образом, эти простые примеры показывают, что матрицы, вообще говоря, не перестановочны друг с другом, т.е. A∙B ≠ B∙A. Поэтому при умножении матриц нужно тщательно следить за порядком множителей.

Можно проверить, что умножение матриц подчиняется ассоциативному и дистрибутивному законам, т.е. (AB)C=A(BC) и (A+B)C=AC+BC.

Легко также проверить, что при умножении квадратной матрицы A на единичную матрицу E того же порядка вновь получим матрицу A, причём AE=EA=A.

Можно отметить следующий любопытный факт. Как известно произведение 2-х отличных от нуля чисел не равно 0. Для матриц это может не иметь места, т.е. произведение 2-х не нулевых матриц может оказаться равным нулевой матрице.

Например, если , то

.

ПОНЯТИЕ ОПРЕДЕЛИТЕЛЕЙ

Пусть дана матрица второго порядка – квадратная матрица, состоящая из двух строк и двух столбцов .

Определителем второго порядка, соответствующим данной матрице, называется число, получаемое следующим образом: a₁₁a₂₂ – a₁₂a₂₁.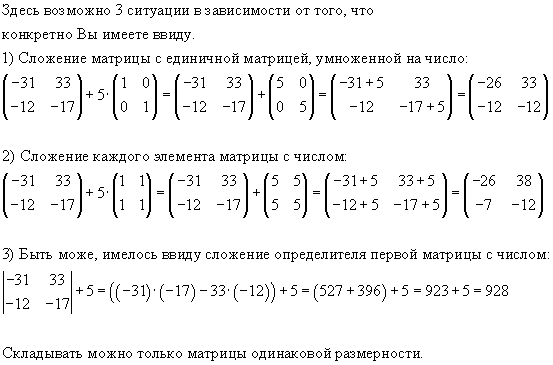

Определитель обозначается символом .

Итак, для того чтобы найти определитель второго порядка нужно из произведения элементов главной диагонали вычесть произведение элементов по второй диагонали.

Примеры. Вычислить определители второго порядка.

2. .
3. Вычислить определитель матрицы D, если D= -А+2В и

Аналогично можно рассмотреть матрицу третьего порядка и соответствующий ей определитель.

Определителем третьего порядка, соответствующим данной квадратной матрице третьего порядка, называется число, обозначаемое и получаемое следующим образом:

.

Таким образом, эта формула даёт разложение определителя третьего порядка по элементам первой строки a₁₁, a₁₂, a₁₃ и сводит вычисление определителя третьего порядка к вычислению определителей второго порядка.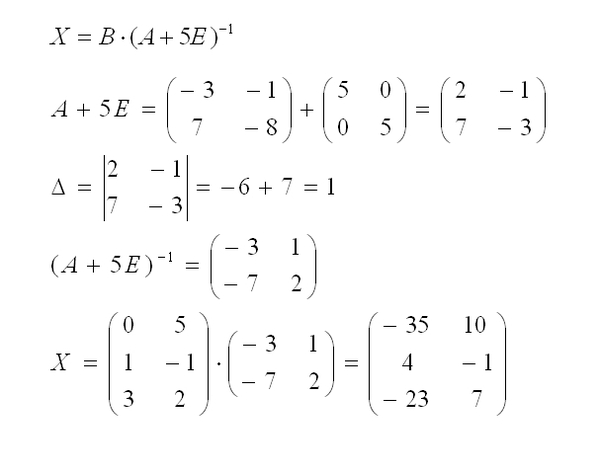

Примеры. Вычислить определитель третьего порядка.

1. .
2. .
3. Решите уравнение..

   .

   (x+3)(4x-4-3x)+4(3x-4x+4)=0.

   (x+3)(x-4)+4(-x+4)=0.

   (x-4)(x-1)=0.

   x₁ = 4, x₂ = 1.

Аналогично можно ввести понятия определителей четвёртого, пятого и т.д. порядков, понижая их порядок разложением по элементам 1-ой строки, при этом знаки «+» и «–» у слагаемых чередуются.

Итак, в отличие от матрицы, которая представляют собой таблицу чисел, определитель это число, которое определённым образом ставится в соответствие матрице.

матриц. Можете ли вы добавить скаляр к матрице?

спросил 7 лет, 8 месяцев назад

Изменено 3 года, 5 месяцев назад

Просмотрено 52к раз

$\begingroup$

Если я добавлю скаляр к каждому элементу матрицы, например. для матрицы $2\times2$

$$ \begin{pmatrix}a_{11} & a_{12} \\ a_{21} & a_{22}\end{pmatrix} + b \overset{?}{=} \begin{pmatrix}a_ {11}+b & a_{12}+b \\ a_{21}+b & a_{22}+b\end{pmatrix},$$

, где $b$ — скаляр, тогда какое обозначение правильное ? Сложение и вычитание матриц определены только для матриц одинакового размера. Однако кажется утомительным сначала умножать $b$ на матрицу из единиц, чтобы сложить две матрицы одинакового размера:

$$ J_2 = \begin{pmatrix} 1 & 1 \\ 1 & 1\end{pmatrix} .$$

Таким образом, записать:

$$ \begin{pmatrix}a_{11} & a_{12} \\ a_{21} & a_{22}\end{pmatrix} + bJ_2 = \begin{pmatrix}a_{ 11}+b & a_{12}+b \\ a_{21}+b & a_{22}+b\end{pmatrix}.$$

Вы всегда пишете $A+bJ_d$ (с $d$ размеры $A$)? Другим обозначением будет $A+\mathbf{b}$ (жирный шрифт $b$), подразумевающий матрицу размера $A$. Однако это обозначение также используется для умножения $b$ на единичную матрицу $bI_d$, которая отличается и, следовательно, сбивает с толку.

Почему прибавление скаляра к матрице не определяется просто как скалярное умножение, то есть операция над каждым элементом матрицы? Примером, где это разрешено , является язык MATLAB, где вы можете добавить скаляр к матрице $A$ просто путем добавления: например. А+3 . Мне кажется, это логичный выбор. Добавление скаляра к матрице может быть определено как $A+b = A+bJ_d$, где $d$ размерность $A$. Это коммутативно и ассоциативно, как обычное сложение матриц. Тогда $A+\mathbf{b}$ будет сложением $A$ и $bI_d$, а $A+B$ — сложением матриц в известном нам виде, действительным только для матриц одинаковой размерности. Почему это не определения?

• матрицы
• обозначения
• арифметика

$\endgroup$

1

$\begingroup$

Вероятно, это потому, что это не имеет геометрического смысла; линейное преобразование, матрица которого в одном базисе равна всем единицам, имеет другую матрицу в другом базисе.

Всякий раз, когда я встречал обозначение $A+b$ в математике, оно означало $A+bI$ (где $A$ — квадратичная матрица, а $I$ — единичная матрица того же размера). Например, некоторые пишут $\det(A-\lambda)$ для характеристического многочлена.

$\endgroup$

2

$\begingroup$

Пояснение:

$I$ Обычно относится к идентификационной матрице https://en.wikipedia.org/wiki/Identity_matrix

$I=\begin{bmatrix}1&0&\cdots&0\\0&1&\cdots&0\\ \vdots&\vdots&\ddots&\vdots\\0&0&\cdots&1\end{bmatrix}$

$J$ встречается реже и обычно относится к матрице всех единиц https://en.wikipedia.org/wiki/Matrix_of_ones

$J=\begin{bmatrix}1&1&\cdots&1\\1&1&\cdots&1\\\vdots&\vdots&\ddots&\vdots\\1&1&\cdots&1\end{bmatrix}$

Имеет ли это смысл?

Да, это так. Одним из примеров является алгоритм PageRank https://epubs. T}}$$

Правильно?

Точно не знаю. В любом случае я бы не стал использовать в документе $A+\lambda$, где A — матрица, а $\lambda$ — скаляр, потому что мне лично кажется, что это выглядит странно и труднее увидеть, как уравнение работает с измерениями.

Тем не менее, он отлично работает в Matlab, например:

 magic(3) + 1
ответ =
       9 2 7
       4 6 8
       5 10 3
 

Рекомендация:

9 таджикских доллара

$A+\лямбда J$

В обоих случаях вам, вероятно, потребуется объяснить, что $e$ — это вектор-столбец всех единиц или что $J$ — это матрица всех единиц. Подразумевая, что $I$ или $J$ имеют правильную размерность, это нормально, лично мне не нравятся ни $I_\text{dim}$, ни $J_\text{dim}.$

$\endgroup$

2

$\begingroup$

матричное скалярное сложение математически неверно. выглядит не так, как вы написали.

в numpy или matlab:

$a[2×2] + b = a[2×2] + b\cdot I[2×2]$

$ \begin{pматрица} а_{11} и а_{12}\\ а_{21} и а_{22} \end{pmatrix} + b \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} а_{11} + 1 и а_{12}\\ а_{21} и а_{22} +1 \end{pматрица} $

В [1]: a = np.matrix('1 , 2; 3, 4') + 1

В [2]: a

matrix([[2, 3], [4, 5]])

$\endgroup$

1

$\begingroup$

Я не думаю, что добавление скаляра к матрице имеет большой смысл. Однако было бы разумно добавить вектор-столбец: поскольку матрицы представляют собой линейные преобразования, такое выражение будет представлять собой аффинное преобразование.

$\endgroup$

матрицы — Сложение/умножение матриц разных размеров

$\begingroup$

У меня есть следующие две матрицы:

$$A=\begin{pmatrix}1 & -2\\3 & 1\end{pmatrix}\text{ и }B=\begin{pmatrix}1 & 3 & 2\\-1 & 0 & 2\end{pmatrix}$$

Итак, у меня есть две матрицы разных размеров. Несколько источников говорят мне, что я не могу выполнять умножение или сложение с матрицами разных размеров. Так что я немного смущен. Могу ли я сделать это с этими? Как?

• матрицы

$\endgroup$

2

$\begingroup$

Предположим, у вас есть две матрицы $A$ и $B$ порядков $a_1\times a_2$ и $b_1\times b_2$ соответственно.

Матричное сложение/вычитание двух матриц будет определено тогда и только тогда, когда $a_1=b_1$ и $a_2=b_2$

Умножение матриц на них определено тогда и только тогда, когда $a_2=b_1$ для $AB$ должно быть определено и $b_2= a_1$ для определения $BA$. $AB$ будет иметь порядок $a_1\times b_2$, а $BA$ будет иметь порядок $b_1\times a_2$

$\endgroup$

2

$\begingroup$

Чтобы добавить две матрицы, они должны иметь одинаковые размеры, поэтому вы не можете добавлять свои матрицы.

Для умножения на матрицы $M$ и $N$ количество столбцов матрицы $M$ должно быть равно количеству строк матрицы $N$. В вашем случае вы можете умножить $A\cdot B$, потому что количество столбцов $A$ равно $2$, а количество строк $B$ равно $2$.

Вы не можете умножить $B\cdot A$, потому что количество столбцов $B$ равно $3$, а количество строк $A$ равно $2$.

$\endgroup$

$\begingroup$

Сложение и умножение матриц не определялись ни с того ни с сего. Матрица $m\times n$ описывает линейное преобразование из векторного пространства размерности $n$ в векторное пространство размерности $m$.

Сумма матриц соответствует преобразованию, которое представляет собой сумму двух заданных преобразований. Добавление линейных преобразований требует, чтобы домен и диапазон были идентичными.

Произведение матриц соответствует преобразованию, которое является композицией двух заданных преобразований.