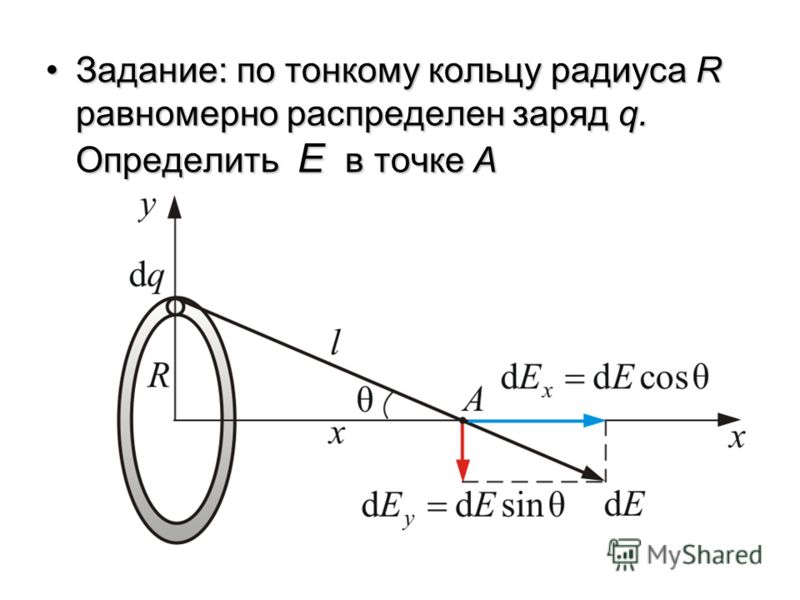
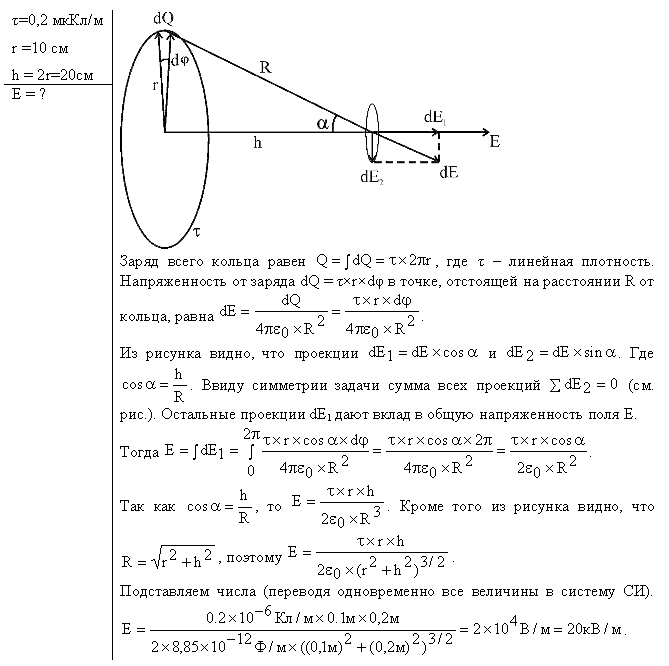
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
Другие ответы
| ||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Физика
| Похожие вопросы |
Решено
Автобус массой 4 т трогается.
Решено
помогите с физикой пожалуйста: Плоско-выпуклая стеклянная линза с радиусом кривизны сферической поверхности R=12,5 см прижата к стеклянной пластинке….
помогите решить задачу,пожалуйста)
Решено
Тіло масою 4кг рухається вздовж…
Контрольная работа
Пользуйтесь нашим приложением
| |||||||||||||||||
| Специальный поиск | |||||||||||||||||
|
Физика Теория вероятностей и мат. статистика Гидравлика Теор. механика Прикладн. механика Электроника Витамины для ума |
Главная Поиск по сайту Формулы Все задачи Помощь Контакты Билеты |
||||||||||||||||
заряд равномерно распределен линейной плотностью Задача 10674 На тонком кольце равномерно распределен заряд с линейной плотностью заряда τ = 20 кКл/см.
Задача 10679 Две длинные прямые параллельные нити находятся на расстоянии d = 10 см друг от друга. На нитях равномерно распределены заряды с линейными плотностями t 1 = –2 нКл/см и t2 = 4 нКл/см. Определить напряженность электрического поля Е в точке, удаленной от первой нити на расстояние r1 = 6 см и от второй на расстояние r2 = 8 см.
Задача 60365 Две длинные прямые параллельные нити находятся на расстоянии 10 см друг от друга. На нитях равномерно распределены заряды с линейными плотностями 0,4 и –0,3 нКл/см.
Задача 60610 На тонком кольце равномерно распределен заряд с линейной плотностью заряда τ = 0,2 нКл/см. Радиус кольца R = 15 см. На срединном перпендикуляре к плоскости кольца находится точечный заряд Q = 10 нКл. Определить силу F, действующую на точечный заряд со стороны заряженного кольца, если он удален от центра кольца на а) a
Задача 11674 На отрезке тонкого прямого проводника длиной l = 10 см равномерно распределен заряд с линейной плотностью τ = 3 мкКл/м. Вычислить напряженность Е, создаваемую этим зарядом в точке, расположенной на оси проводника и удаленной от ближайшего конца отрезка на расстояние, равное длине этого отрезка.
Задача 11690 По тонкому кольцу радиусом R = 10 см равномерно распределен заряд с линейной плотностью τ = 10 нКл/м. Определить потенциал φ в точке, лежащей на оси кольца, на расстоянии а = 5 см от центра.
Задача 11691 На отрезке тонкого прямого проводника равномерно распределен заряд с линейной плотностью τ = 10 нКл/м. Вычислить потенциал φ, создаваемый этим зарядом в точке, расположенной на оси проводника и удаленной от ближайшего конца отрезка на расстояние, равное длине этого отрезка.
Задача 12132 По тонкому кольцу радиусом 20 см равномерно распределен заряд с линейной плотностью 10 нКл/м. Определить работу по перемещению заряда 20 нКл из бесконечности в центр кольца.
Задача 12214 Две длинные прямые параллельные нити находятся на расстоянии d = 5 см друг от друга.
Задача 14614 Кольцо с радиусом 0,2 м равномерно распределенный заряд с линейной плотностью 10 мКл/м. Ось вращения лежит в плоскости кольца и проходит через один из его диаметров. Частота вращения 360 об/мин. Определить магнитный момент кольца.
Задача 14967 На отрезке прямого провода длиной l равномерно распределен заряд с линейной плотностью τ = 1 мкКл/м. Определить работу АBC сил поля по перемещению заряда q = 1 нКл из точки В, отстоящей на расстоянии l от края провода (вдоль прямой, совпадающей с продолжением провода), в точку С, отстоящую на расстоянии 2l от того же края провода (вдоль той же прямой).
Задача 15163 По тонкой нити, изогнутой по дуге окружности, равномерно распределен заряд с линейной плотностью λ. Определить напряженность электрического поля Е, создаваемого таким распределением зарядов в точке, совпадающей с центром кривизны дуги. Длина l нити составляет одну треть длины окружности.
Задача 17354 Две бесконечно длинные параллельные нити находятся на расстоянии a = 5 см друг от друга. На нитях равномерно распределены заряды с линейными плотностями τ1 = –5·10–9 Кл/м и τ2 = +10·10–9 Кл/м. Определить напряженность электрического поля в точке, удаленной от первой нити на расстоянии b = 3 см и от второй — c = 4 см.
Задача 19774 На отрезке прямого провода длиной l = 20 см равномерно распределен заряд с линейной плотностью τ = 10–8 Кл/см.
Задача 19775 На отрезке прямого провода длиной l = 20 см равномерно распределен заряд с линейной плотностью τ = 10–8 Кл/см. Напряженность поля в точке А, расположенной на расстоянии 2l от одного из концов стержня (см. рисунок), равна…
Задача 20868 По тонкому стержню длиной L = 20 см равномерно распределен заряд с линейной плотностью τ = 2·10–8 Кл/м. Стержень равномерно вращается с частотой f = 10 1/с относительно оси, параллельной стержню, и отстоящей от него на расстоянии а = 10 см. Определить магнитный момент кругового тока, вызванного вращением стержня вокруг оси.
Задача 21234 На тонком кольце равномерно распределен заряд с линейной плотностью заряда τ = 20 нКл/см.
| |||||||||||||||||
АМПЕР ЗАКОН
АМПЕР- ЗАКОН АМПЕРА
- 31.1. Введение
- Пример: Задача 31.5
- 31.2. соленоид
- Пример: Задача 31.14
- Пример: Задача 31.15
- 31.3. Движение зарядов в электрическом и магнитном полях
- 31.4. Скрещенные электрические и магнитные поля
- 31.5. Силы на проводе
- Пример: Задача 31.33
- 31.6. Крутящий момент в токовой петле
- 31.1. Введение
Магнитное поле на расстоянии r от очень длинного прямого провода, несущего установившийся ток I, имеет величину, равную
 )
)
и направление, перпендикулярное r и I. Интеграл по путям по окружности вокруг провода (см. рис. 31.1) равно
Здесь мы использовали тот факт, что магнитное поле является тангенциальным в любой точке на круговой траектории интегрирования.
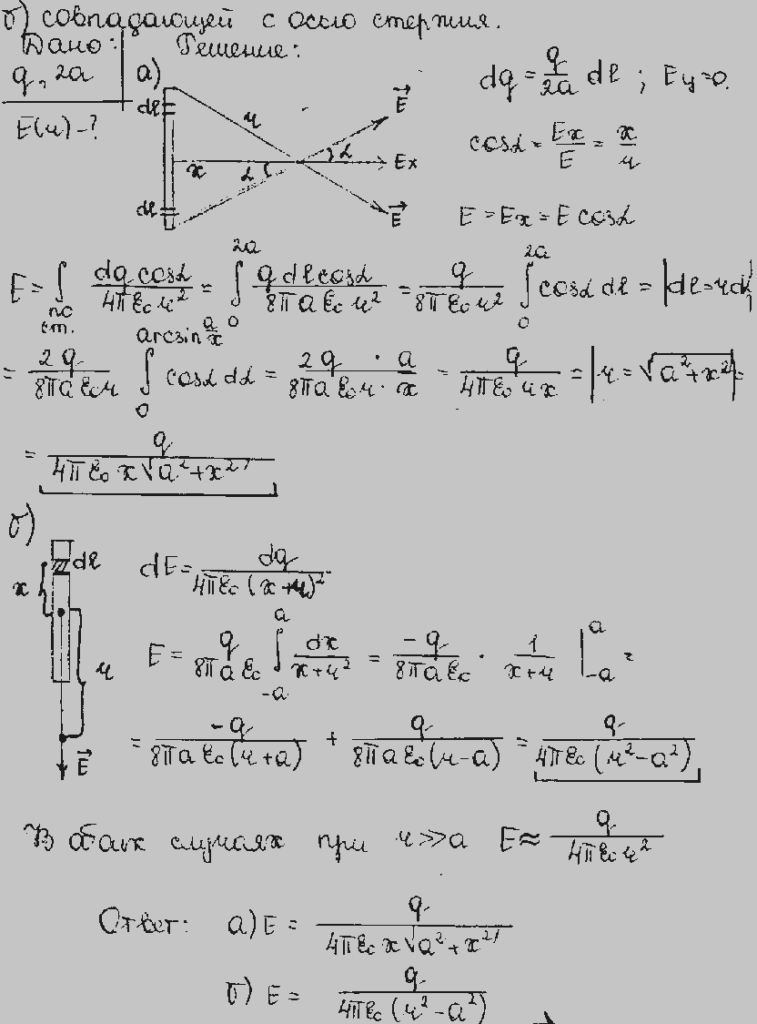
Это выражение Закон Ампера :
» Интеграл от B по любому замкнутому математическому пути равен u 0 умножить ток, перехваченный областью, охватывающей путь »
Пример: Задача 31.5
Шесть параллельных алюминиевых проводов малого, но конечного радиуса лежат в тот же самолет. Провода разделены равным расстоянием d, и они несут равные токи I в том же направлении. Найдите магнитное поле в центре первый провод. Предположим, что токи в каждом проводе распределены равномерно над его поперечным сечением.
Схематическое изображение задачи показано на рис. 31.3. Магнитное поле генерируемое одним проводом, равно
 5)
5)
где r — расстояние от центра провода. Уравнение (31.5) правильно для всех точек за пределами провода, и поэтому может использоваться для определения магнитное поле, создаваемое проводами 2, 3, 4, 5 и 6. Поле на центр провода 1, благодаря току, протекающему по проводу 1, можно определить с помощью по закону Ампера и равна нулю. Полное магнитное поле в центре провод 1 можно найти векторным сложением вкладов каждого из шести провода. Поскольку направление каждого из этих вкладов одинаково, полное магнитное поле в центре провода 1 равно
Соленоид представляет собой устройство, используемое для создания однородного магнитного поля. Может
быть изготовлен из тонкой проводящей проволоки, намотанной на плотную спиральную катушку из многих витков.
Магнитное поле внутри соленоида можно определить суммированием магнитного
поля, генерируемые N отдельными кольцами (где N — число витков
соленоид). Мы ограничим наше обсуждение магнитного поля, создаваемого
соленоида к соленоиду, порожденному идеальным соленоидом бесконечной длины, и
имеет очень плотно намотанные катушки.
Мы ограничим наше обсуждение магнитного поля, создаваемого
соленоида к соленоиду, порожденному идеальным соленоидом бесконечной длины, и
имеет очень плотно намотанные катушки.
Идеальный соленоид обладает поступательной и вращательной симметрией. Однако, поскольку силовые линии магнитного поля должны образовывать замкнутые петли, магнитное поле не может быть направлена вдоль радиального направления (иначе линии поля были бы созданы или разрушен на центральной оси соленоида). Поэтому делаем вывод, что силовые линии в соленоиде должны быть параллельны оси соленоида. Величина магнитного поля можно получить, применяя закон Ампера.
где L — горизонтальная длина пути интегрирования. Текущий закрытый
по пути интегрирования равен N . I 0 где N —
количество витков, заключенных в пути интегрирования, и I 0 является
ток в каждом витке соленоида. Используя закон Ампера, мы заключаем, что
I 0 где N —
количество витков, заключенных в пути интегрирования, и I 0 является
ток в каждом витке соленоида. Используя закон Ампера, мы заключаем, что
или
где n — число витков соленоида на единицу длины. Уравнение (31.9) показывает, что магнитное поле B не зависит от положения внутри соленоид. Мы заключаем, что магнитное поле внутри идеального соленоида равно униформа.
Пример: Задача 31.14
По длинному соленоиду из n витков на единицу длины течет ток I, а по длинному прямому проводу, лежащему вдоль оси этого соленоида, течет ток I’. Найдите чистое магнитное поле внутри соленоида на расстоянии r от оси. Опишите форму силовых линий магнитного поля.
Магнитное поле, создаваемое соленоидом, является однородным, направленным параллельно оси соленоида, и имеет величину, равную
 10)
10)
Магнитное поле длинного прямого провода, по которому течет ток I’, имеет величина равна
и направлен перпендикулярно направлению r и I’. Направление Таким образом, провод B перпендикулярен направлению B соль . Суммарное магнитное поле внутри соленоида равно векторная сумма B проволока и B золь . Его величина равна до
Угол a между направлением магнитного поля и осью z дан по
Пример: Задача 31.15
Коаксиальный кабель состоит из длинного цилиндрического медного провода радиусом
r 1 окружен цилиндрической оболочкой с внутренним радиусом r 2 и внешний радиус r 3 (см. рис. 31.5). Проволока и оболочка несут
равные и противоположные токи I равномерно распределены по их объемам. Находить
формулы для магнитного поля в каждой из областей r < r 1 ,
r 1 < r < r 2 , r 2 < r <
r 3 и r > r 3 .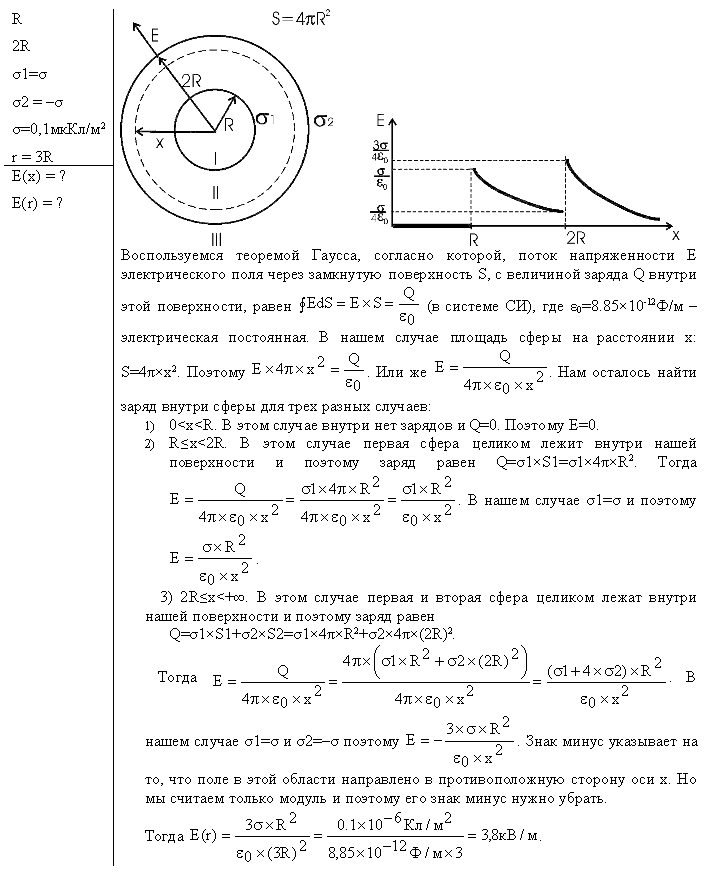
Силовые линии магнитного поля представляют собой окружности с центром на оси симметрии магнитного поля. коаксиальный кабель. Сначала рассмотрим путь интегрирования с r < r 1 . Континуальный интеграл B по этому пути равен
Ток, заключенный в этом пути интегрирования, равен
Применяя закон Фарадея, мы можем связать приложенный ток с путевым интегралом В
Следовательно, магнитное поле B равно
а магнитное поле определяется как
 19)
19)
В третьей области (r 2 < r < r 3 ) интеграл по путям магнитного поля вдоль кругового пути с радиусом r определяется выражением уравнение (31.14). Приложенный ток равен
Таким образом, магнитное поле равно
Ток, ограниченный путем интегрирования радиусом r > r 3 равен нулю (поскольку ток в проводе и в оболочке течет в противоположные направления). Поэтому магнитное поле в этой области также равен нулю.
Магнитная сила, действующая на частицу с зарядом q, движущуюся со скоростью v, равна равно
Эта сила всегда перпендикулярна направлению движения частицы, и поэтому изменит только направление движения, а не величину скорости. Если заряженная частица движется в однородном магнитном поле напряженностью B, перпендикулярное скорости v, то величина магнитной силы определяется как
 23)
23)
и его направление перпендикулярно v. В результате действия этой силы частица будет совершать равномерное круговое движение. Радиус круга определяется требованием равенства напряженности магнитной силы центростремительная сила. Таким образом
Радиус r орбиты равен
где р — импульс заряженной частицы. Расстояние, пройденное на частица за один оборот равна
Время T, необходимое для совершения одного оборота, равно
.
Частота этого движения равна
и называется циклотронная частота . Уравнение (31.28) показывает что циклотронная частота не зависит от энергии частицы, и зависит только от его массы m и заряда q.
Влияние магнитного поля на движение заряженной частицы можно использовать
определить некоторые его свойства. Одним из примеров является измерение
заряд электрона. Электрон, движущийся в однородном магнитном поле, будет
описывает круговое движение с радиусом, определяемым уравнением (31.25). Предположим,
электрон ускоряется потенциалом V 0 . Конечная кинетическая энергия
электрона определяется как
Одним из примеров является измерение
заряд электрона. Электрон, движущийся в однородном магнитном поле, будет
описывает круговое движение с радиусом, определяемым уравнением (31.25). Предположим,
электрон ускоряется потенциалом V 0 . Конечная кинетическая энергия
электрона определяется как
Импульс p электрона определяется его кинетической энергией
Таким образом, радиус кривизны траектории электрона равен
Уравнение (31.31) показывает, что измерение r можно использовать для определения отношение массы к заряду электрона.
Другое применение влияния магнитного поля на движение
заряженная частица — циклотрон. Циклотрон состоит из вакуумированного резонатора.
помещенный между полюсами большого электромагнита. Полость разрезается на две
D-образные детали (называемые ди) с зазором между ними. Осциллирующий максимум
на пластины подается напряжение, генерирующее колеблющееся электрическое поле в
область между двумя деями. Заряженная частица, инжектированная в центр
циклотрон, будет совершать равномерное круговое движение в течение первой половины
один ход. Частота движения частицы зависит от ее массы, ее
заряд и напряженность магнитного поля. Частота генератора
выбирается таким образом, что каждый раз, когда частица пересекает зазор между дуантами, она
будет ускоряться электрическим полем. По мере увеличения энергии иона
его радиус кривизны будет увеличиваться, пока он не достигнет края
циклотрон и экстрагируется. При движении в циклотроне ион будет
пересечь пропасть между деями много раз, и она ускорится до высоких
энергии.
Заряженная частица, инжектированная в центр
циклотрон, будет совершать равномерное круговое движение в течение первой половины
один ход. Частота движения частицы зависит от ее массы, ее
заряд и напряженность магнитного поля. Частота генератора
выбирается таким образом, что каждый раз, когда частица пересекает зазор между дуантами, она
будет ускоряться электрическим полем. По мере увеличения энергии иона
его радиус кривизны будет увеличиваться, пока он не достигнет края
циклотрон и экстрагируется. При движении в циклотроне ион будет
пересечь пропасть между деями много раз, и она ускорится до высоких
энергии.
До сих пор мы предполагали, что направление движения заряженного
частица перпендикулярна направлению магнитного поля. Если это
В этом случае будет происходить равномерное круговое движение. Если направление движения
ион не перпендикулярен магнитному полю, произойдет спиральное движение.
Скорость заряженной частицы можно разложить на две составляющие: одну
параллельно и одно перпендикулярно магнитному полю. Магнитная сила
действующее на частицу, будет определяться составляющей ее скорости
перпендикулярно магнитному полю. Проекция движения
частица в плоскости xy (предполагается, что она перпендикулярна магнитному полю)
будет круговой. Магнитное поле не повлияет на составляющую
движение параллельно полю, и эта составляющая скорости останется
постоянный. Конечным результатом будет движение по спирали.
Магнитная сила
действующее на частицу, будет определяться составляющей ее скорости
перпендикулярно магнитному полю. Проекция движения
частица в плоскости xy (предполагается, что она перпендикулярна магнитному полю)
будет круговой. Магнитное поле не повлияет на составляющую
движение параллельно полю, и эта составляющая скорости останется
постоянный. Конечным результатом будет движение по спирали.
Заряженная частица, движущаяся в области с электрическим и магнитным полем, будет испытать суммарную силу, равную
Эта сила называется силой Лоренца .
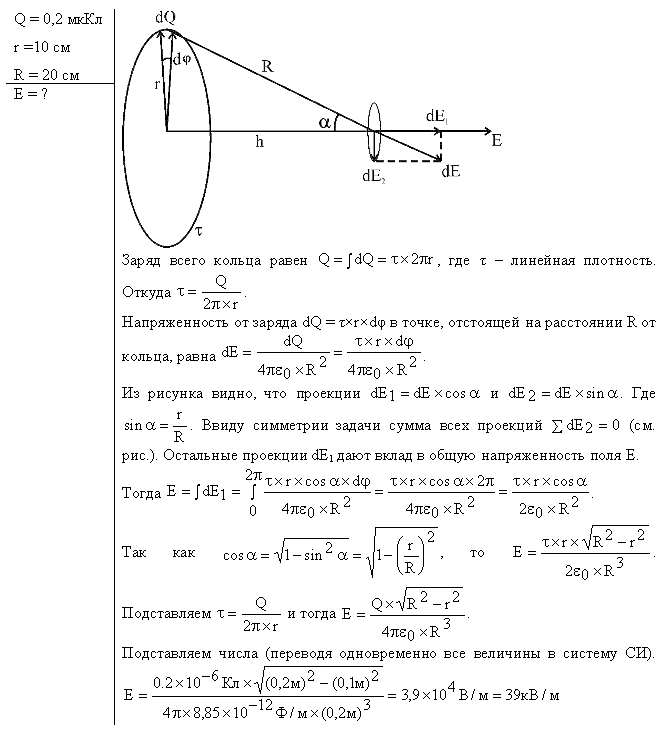 рис. 31.6). Направление
частица, показанная на рис. 31.6, перпендикулярна как электрическому полю, так и
магнитное поле. Электрическая сила, действующая на частицу, направлена
вдоль направления электрического поля и имеет величину, равную
рис. 31.6). Направление
частица, показанная на рис. 31.6, перпендикулярна как электрическому полю, так и
магнитное поле. Электрическая сила, действующая на частицу, направлена
вдоль направления электрического поля и имеет величину, равную
Магнитная сила, действующая на заряженную частицу, направлена перпендикулярно как v, так и B и имеет величину, равную
Суммарная сила, действующая на частицу, представляет собой сумму этих двух составляющих и имеет величина равна
Если заряженная частица имеет скорость, равную
то результирующая сила будет равна нулю, а движение частицы будет
быть равномерным линейным движением. Устройство со скрещенными электрическим и магнитным полями
называется селектором скорости. Если щель расположена в соответствующем
позиции, он будет транспортировать только те частицы, скорость которых определена
величинами электрического и магнитного полей.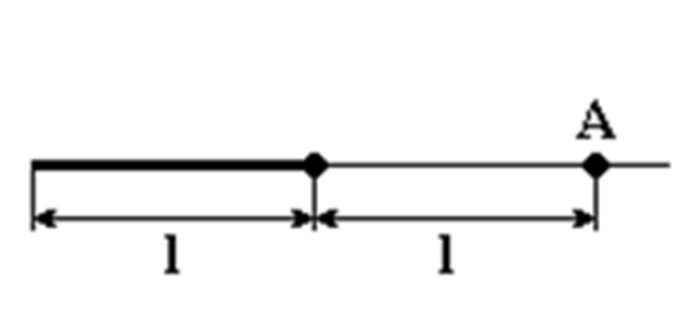
 Когда это происходит, внутренний
электрическое поле, Е в , равно произведению электрона
скорость, v d , и напряженность магнитного поля, B. Как
В результате внутреннего электрического поля будет создана разность потенциалов.
между верхом и низом полосы. Если металлическая полоса имеет ширину w,
тогда разность потенциалов [Delta]V будет равна
Когда это происходит, внутренний
электрическое поле, Е в , равно произведению электрона
скорость, v d , и напряженность магнитного поля, B. Как
В результате внутреннего электрического поля будет создана разность потенциалов.
между верхом и низом полосы. Если металлическая полоса имеет ширину w,
тогда разность потенциалов [Delta]V будет равна
Этот эффект называется эффектом Холла.
Скорость дрейфа электронов зависит от тока I в проводе, его площадь поперечного сечения A и плотность электронов n (см. главу 28):
Объединяя уравнение (31.38) и уравнение (31.37), мы получаем следующее выражение для [Дельта]В
Следовательно, для определения n можно использовать измерение ΔV.
Ток I, протекающий по проводнику, эквивалентен совокупности зарядов
движущийся с некоторой скоростью v d по проводу.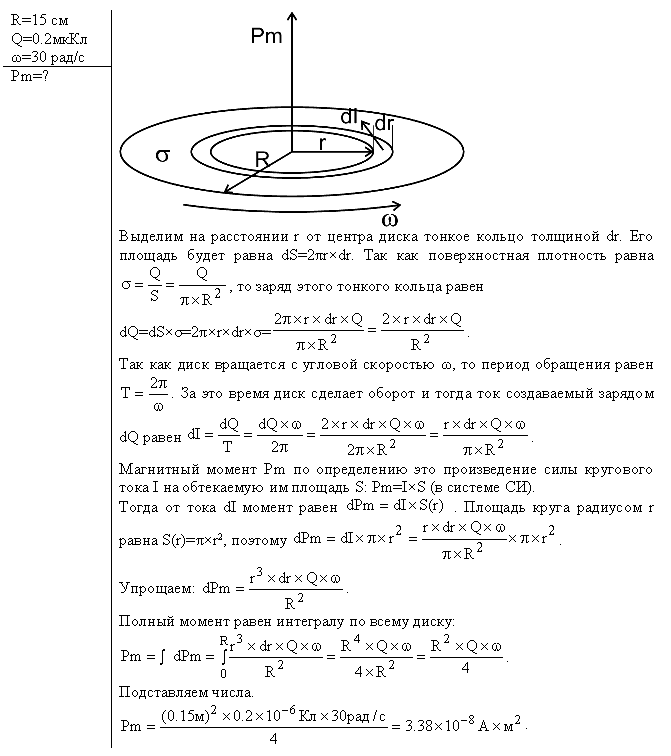 Количество
заряд dq, присутствующий на отрезке dL провода, равен
Количество
заряд dq, присутствующий на отрезке dL провода, равен
Если проволоку поместить в магнитное поле, то на нее будет действовать магнитная сила. каждого из носителей заряда, и в результате на провод. Предположим, что угол между направлением тока и направлением поля равно [тета] (см. рис. 31.8). Магнитная сила, действующая на отрезке dL провода равно
Суммарная сила, действующая на проводник со стороны магнитного поля, может быть найдена по формуле интегрируя уравнение (31.41) по всей проволоке.
Пример: Задача 31.33
Для измерения силы магнитного поля можно использовать весы.
Рассмотрим проволочную петлю, по которой течет точно известный ток, показанный на рис.
31.9, который частично погружен в магнитное поле. Сила, которую
магнитное поле, воздействующее на петлю, можно измерить с помощью весов, и это
позволяет рассчитать силу магнитного поля. Предположим, что
длина короткой стороны петли 10,0 см, сила тока в проводе 0,225
А, а магнитная сила равна 5,35 х 10 -2 Н. В чем сила
магнитное поле?
Предположим, что
длина короткой стороны петли 10,0 см, сила тока в проводе 0,225
А, а магнитная сила равна 5,35 х 10 -2 Н. В чем сила
магнитное поле?
Рассмотрим три сегмента токовой петли, показанные на рис. 31.9. погружены в магнитное поле. Магнитная сила, действующая на сегмент 1 и 3 имеют одинаковую величину, но направлены в противоположные стороны, а потому отменить. Величина магнитной силы, действующей на сегмент 2, может быть рассчитывается по уравнению (31.41) и равен
Эта сила измеряется с помощью весов и равна 5,35 х 10 -2 . Н. Таким образом, напряженность магнитного поля равна
Если петля с током погружена в магнитное поле, результирующая магнитная сила будет
быть равным нулю. Однако крутящий момент на этом контуре в общем случае не будет
равен нулю. Предположим, что прямоугольная петля с током помещена в однородную
магнитное поле (см. рис. 31.10). Угол между нормалью тока
петля и магнитное поле равно [тета]. Магнитные силы, действующие на
верхняя и нижняя части текущего цикла равны
Предположим, что прямоугольная петля с током помещена в однородную
магнитное поле (см. рис. 31.10). Угол между нормалью тока
петля и магнитное поле равно [тета]. Магнитные силы, действующие на
верхняя и нижняя части текущего цикла равны
где L — длина верхней и нижней кромки. Крутящий момент, действующий на токовая петля относительно ее оси равна
где
Используя векторную запись, уравнение (31.45) можно переписать как
где направление магнитного момента определяется с помощью правой
правило.
Работа, которую необходимо совершить против магнитного поля, чтобы повернуть ток петля на угол d[theta] равна — [tau] d[theta]. Изменение в потенциальная энергия контура тока, когда он вращается между [тета] 0 и [тета] 1 равно
Обычный выбор точки отсчета: [тета] 0 = 90 градусов. а также U([theta] 0 ) = 0 Дж. Если этот выбор сделан, мы можем переписать уравнение (31.50) как
В векторном представлении:
Потенциальная энергия токовой петли имеет минимум, когда u и B параллельно и максимально, когда u и B антипараллельны.
Присылайте комментарии, вопросы и/или предложения по электронной почте [email protected] и/или посетите домашнюю страницу Фрэнка Вольфса.
Электрическое поле бесконечно длинного прямого провода
Закон Гаусса — очень важная часть электромагнетизма и физики. Он используется, чтобы связать распределение заряда с результирующим электрическим полем из-за заряда. Этот закон был сформулирован Жозефом Лагранжем в 1773 году, а затем Карлом Гауссом в 1813 году. Оба они сформулировали этот закон в контексте притяжения эллипсоидов. Этот закон также включен в одно из четырех уравнений Максвелла, составляющих основу классической электродинамики. Давайте подробно изучим это понятие.
Он используется, чтобы связать распределение заряда с результирующим электрическим полем из-за заряда. Этот закон был сформулирован Жозефом Лагранжем в 1773 году, а затем Карлом Гауссом в 1813 году. Оба они сформулировали этот закон в контексте притяжения эллипсоидов. Этот закон также включен в одно из четырех уравнений Максвелла, составляющих основу классической электродинамики. Давайте подробно изучим это понятие.
Закон Гаусса
Электрический поток через площадь определяется как произведение электрического поля на площадь поверхности, проецируемую перпендикулярно электрическому полю. В общем, для закона Гаусса предполагаются замкнутые поверхности. Этот закон является важным инструментом, поскольку он позволяет оценить электрический заряд, заключенный внутри замкнутой поверхности. Этот закон можно использовать для упрощения вычислений для геометрий, между которыми есть симметрия.
Электрический флюс
Рассмотрим поверхность dS и жидкость, текущую по поверхности со скоростью v. Скорость потока жидкости через поверхность определяется выражением «vdS». Говорят, что это поток жидкости, протекающей через поверхность. Аналогичным образом определяется поток электрического поля. Он определяется как электрическое поле, протекающее через небольшой участок «dS». Количество силовых линий электрического поля, проходящих через участок, пропорционально
Скорость потока жидкости через поверхность определяется выражением «vdS». Говорят, что это поток жидкости, протекающей через поверхность. Аналогичным образом определяется поток электрического поля. Он определяется как электрическое поле, протекающее через небольшой участок «dS». Количество силовых линий электрического поля, проходящих через участок, пропорционально
Если область наклонена на угол θ, она становится
Поток обозначается ,
Закон Гаусса
Рассмотрим небольшой заряд «q», удерживаемый внутри сферы радиусом r. Эту сферу можно разделить на элементы меньшей площади, как показано на рисунке ниже. Электрическое поле, проходящее через этот элемент, будет иметь вид
.0040
⇒
Это общий результат закона Гаусса.
Полный поток вдоль замкнутой поверхности S, окружающей заряд q is,
Электрическое поле, создаваемое бесконечно длинным прямым проводом
Закон Гаусса можно использовать для вывода уравнений для электрического поля через множество заряженные формы. Рассмотрим бесконечно длинный провод, содержащий заряд. Плата за единицу длины этого провода определяется как . Проволока имеет ось симметрии, показанную на рисунке ниже. Цель состоит в том, чтобы вывести уравнение для расчета электрического поля, создаваемого этим проводом.
Рассмотрим бесконечно длинный провод, содержащий заряд. Плата за единицу длины этого провода определяется как . Проволока имеет ось симметрии, показанную на рисунке ниже. Цель состоит в том, чтобы вывести уравнение для расчета электрического поля, создаваемого этим проводом.
Предположим, что взят радиальный вектор OP, и он вращается вокруг провода. Это означает, что электрическое поле должно иметь одинаковую величину во всех точках Р, Р’ и Р». Направление электрического поля радиально наружу, если заряд положительный, и наоборот.
Чтобы рассчитать электрическое поле, представьте цилиндрическую поверхность Гаусса. Поскольку поле везде радиальное, поток вдоль двух граней цилиндров равен нулю. На цилиндрической части поверхности Е перпендикулярно поверхности в каждой точке, и его величина постоянна, так как зависит только от r. Площадь поверхности изогнутой части равна где l – длина цилиндра.
Поток через поверхность = поток через криволинейную часть цилиндра
= E x
Поверхность содержит заряд, равный
Примеры задач.
Примеры задач
Вопрос 1. По закону Гаусса точечный заряд внутри замкнутой поверхности должен распределяться в
- 9064
- В очереди
- Произвольно.
Ответ:
Согласно закону Гаусса поток, выходящий из закрытой оболочки, зависит только от количества заряда, заключенного внутри оболочки.
Может распространяться произвольно.
Таким образом, ответ (4).
Вопрос 2: Поток, проходящий через шестиугольную призму, равен 2 x 10 3 Н·м 2 /C. Какой заряд находится внутри шестиугольной призмы?
Ответ:
Согласно закону Гаусса, поток и сборы связаны с следующим уравнением:
. Значение в уравнение,
⇒
⇒
⇒ Q = 1,77 × 10 -8 C
ВОПРОС 3: FLUX идет в поверхность Cube -Shaped IS 1 x 10 3 901 3 901 3 901 3 901 3 901 3 901 3 901 3 901 3 901 3 901 3 901 3 901 3901 3 3 3 901 3901 3901 3901 3 3 .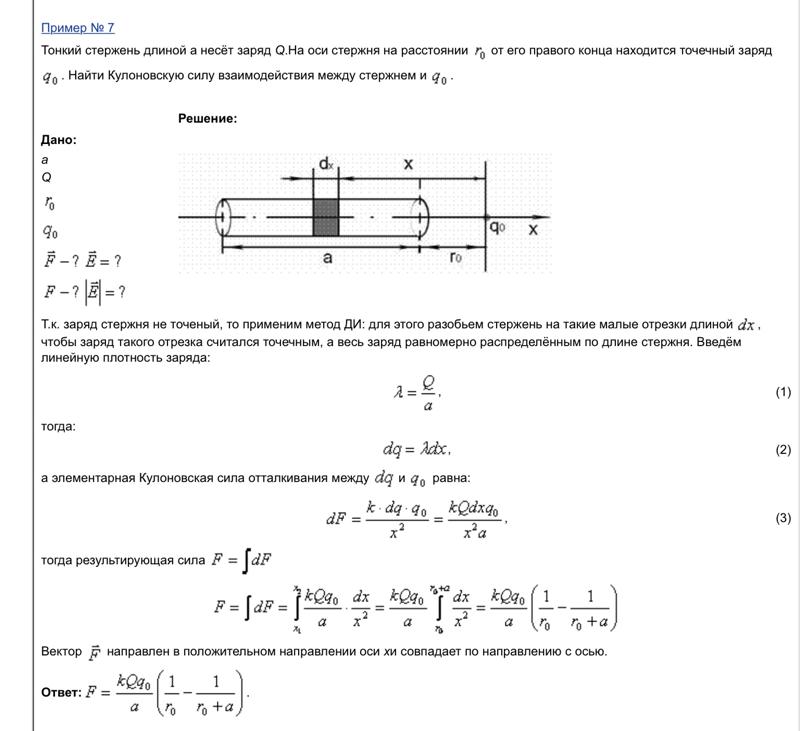 2 /C и поток на выходе 4 x 10 3 Нм 2 /C. Какой заряд находится внутри шестиугольной призмы?
2 /C и поток на выходе 4 x 10 3 Нм 2 /C. Какой заряд находится внутри шестиугольной призмы?
Ответ:
Согласно закону Гаусса, поток и сборы связаны с следующим уравнением:
Даны: ∅ в = 4 x
8 3 . C и ∅ вых = 1 x 10 3 Н·м 2 /C
∅ нетто = ∅ вых – ∅ 3 8 09 3 дюйм
139 N.m 2 /Cplugging this value into the equation,
⇒
⇒
⇒ q = 2.665 × 10 -8 C
Question 4: Find the electric field at 5m из бесконечно длинного провода с линейной плотностью заряда 5 х 10 -3 Кл/м.
Ответ:
Электрическое поле, создаваемое проводником с бесконечным зарядом, определяется выражением
Дано: r = 5m и
Подключение значений в уравнение,
⇒
⇒ E = 18 × 10 × 10 -3
⇒ E = 18 × 6
⇒ E = 18 × 6
⇒ E = 18 × 6
⇒ E = 18 × 6
.

 Для эксперта это ВАЖНО.
Для эксперта это ВАЖНО. 11.14
11.14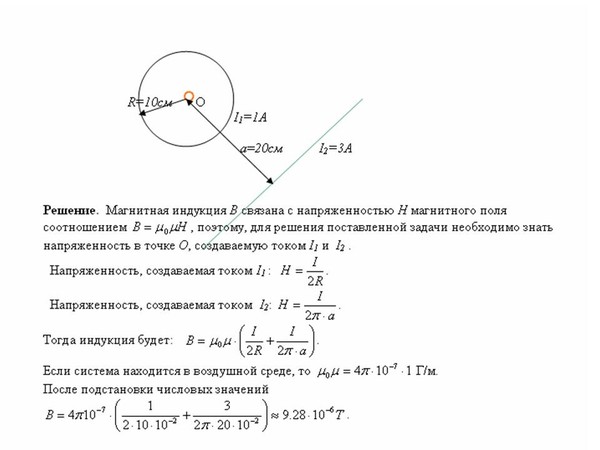 Радиус кольца R = 5 см. На перпендикуляре к плоскости кольца, восстановленном из его середины, находится точечный заряд Q = 40 нКл. Определить силу, действующую на точечный заряд со стороны заряженного кольцо, если он удален от центра кольца на: 1) а1 = 10 см; 2) а2 = 2 м.
Радиус кольца R = 5 см. На перпендикуляре к плоскости кольца, восстановленном из его середины, находится точечный заряд Q = 40 нКл. Определить силу, действующую на точечный заряд со стороны заряженного кольцо, если он удален от центра кольца на: 1) а1 = 10 см; 2) а2 = 2 м.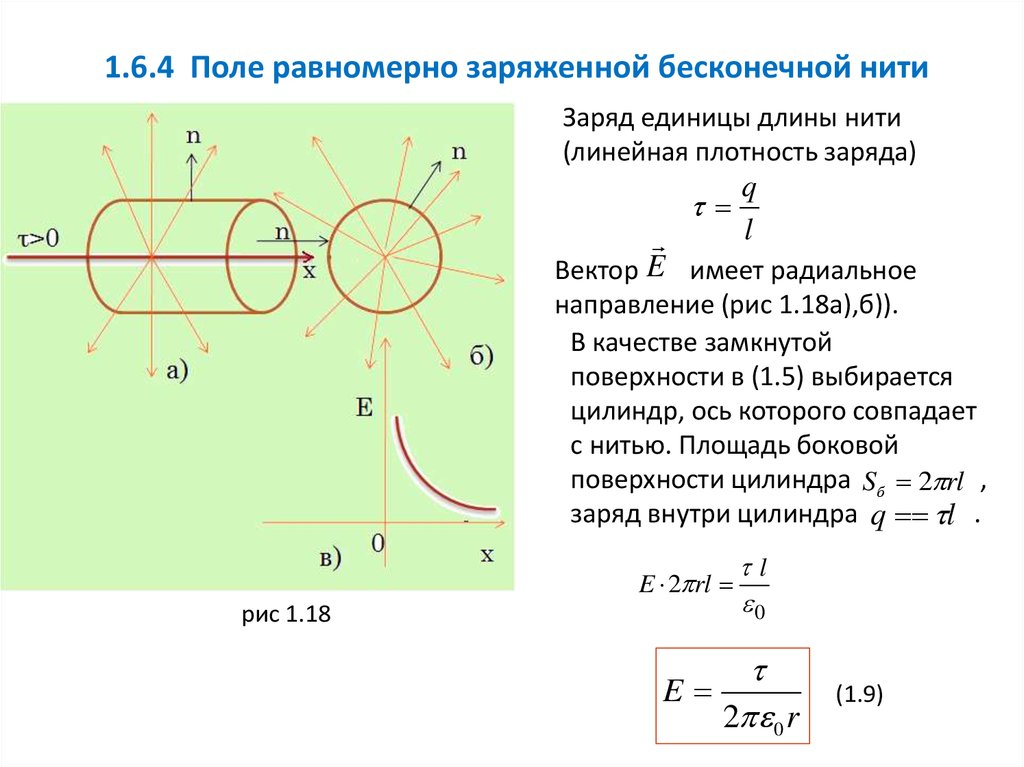 Определить напряженность электрического поля в точке, удаленной от первой нити на расстояние 6 см и от второй – на расстояние 8 см.
Определить напряженность электрического поля в точке, удаленной от первой нити на расстояние 6 см и от второй – на расстояние 8 см.


 Напряженность поля в точке А, расположенной на расстоянии l от одного из концов стержня (см. рисунок), равна…
Напряженность поля в точке А, расположенной на расстоянии l от одного из концов стержня (см. рисунок), равна… Радиус кольца R = 5 см. На перпендикуляре к плоскости кольца, восстановленном из его середины, находится точечный заряд q = 40 нКл. Определить силу, действующую на точечный заряд со стороны заряженного кольца, если он удален от центра кольца на: 1) а1 = 10 см; 2) а2 = 2 м.
Радиус кольца R = 5 см. На перпендикуляре к плоскости кольца, восстановленном из его середины, находится точечный заряд q = 40 нКл. Определить силу, действующую на точечный заряд со стороны заряженного кольца, если он удален от центра кольца на: 1) а1 = 10 см; 2) а2 = 2 м.