Экстремумы функции
Репетиторы ❯ Математика ❯ Экстремумы функции
Автор: Валентин В., онлайн репетитор по математике
●
10.11.2011
●
Раздел: Математика
Обратимся к графику функции у = х3 – 3х2. Рассмотрим окрестность точки х = 0, т.е. некоторый интервал, содержащий эту точку. Логично, что существует такая окрестность точки х = 0, что наибольшее значение функция у = х3 – 3х2 в этой окрестности принимает в точке х = 0. Например, на интервале (-1; 1) наибольшее значение, равное 0, функция принимает в точке х = 0.
Аналогично, точка х = 2 называется точкой минимума функции х3 – 3х2, так как в этой точке значение функции не больше ее значения в иной точке окрестности точки х = 2, например, окрестности (1,5; 2,5).
Таким образом, точкой максимума функции f(х) называется точка х0, если существует окрестность точки х0 – такая, что выполняется неравенство f(х) ≤ f(х0) для всех х из этой окрестности.
Например, точка х0 = 0 – это точка максимума функции f(х) = 1 – х2, так как f(0) = 1 и верно неравенство f(х) ≤ 1 при всех значениях х.
Точкой минимума функции f(х) называется точка х0, если существует такая окрестность точки х0, что выполняется неравенство f(х) ≥ f(х0) для всех х из этой окрестности.
Например, точка х 0 = 2 – это точка минимума функции f(х) = 3 + (х – 2)2, так как f(2) = 3 и f(х) ≥ 3 при всех х.
Точками экстремума называются точки минимума и точки максимума.
Обратимся к функции f(х), которая определена в некоторой окрестности точки х0 и имеет в этой точке производную.
Если х0 – точка экстремума дифференцируемой функции f(х), то f ‘(х0) = 0. Это утверждение называют теоремой Ферма.
Теорема Ферма имеет наглядный геометрический смысл: в точке экстремума касательная параллельна оси абсцисс и поэтому ее угловой коэффициент
f ‘(х0) равен нулю.
Например, функция f(х) = 1 – 3х2 имеет в точке х0 = 0 максимум, ее производная f ‘(х) = -2х, f ‘(0) = 0.
Функция f(х) = (х – 2)2 + 3 имеет минимум в точке х
Отметим, что если f ‘(х0) = 0, то этого недостаточно, чтобы утверждать, что х0 – это обязательно точка экстремума функции f(х).
Например, если f(х) = х3, то f ‘(0) = 0. Однако точкой экстремума точка х = 0 не является, так как на всей числовой оси функция х3 возрастает.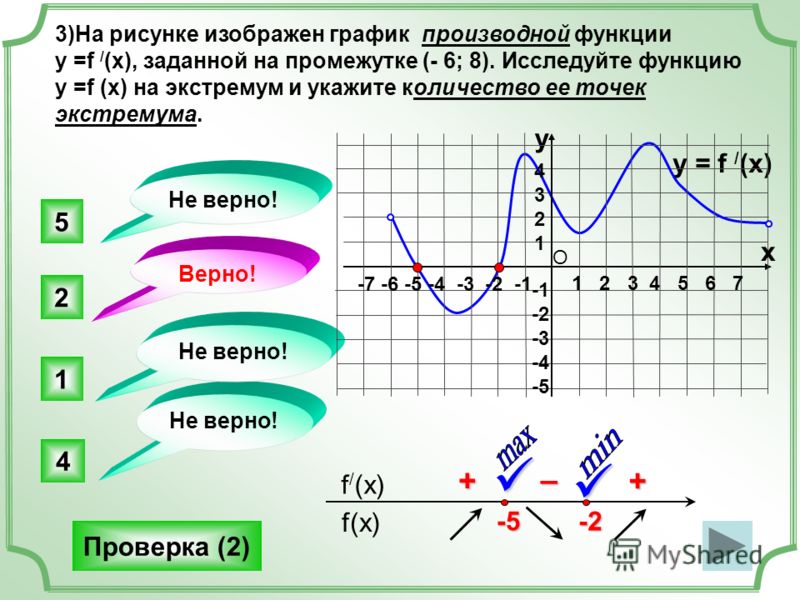
Итак, точки экстремума дифференцируемой функции необходимо искать лишь среди корней уравнения
f ‘(х) = 0, но корень этого уравнения не всегда является точкой экстремума.
Стационарными точками называют точки, в которых производная функции равна нулю.
Таким образом, для того, чтобы точка х0 была точкой экстремума, необходимо, чтобы она была стационарной точкой.
Рассмотрим достаточные условия того, что стационарная точка является точкой экстремума, т.е. условия, при выполнении которых стационарная точка является точкой минимума или максимума функции.
Если производная левее стационарной точки положительна, а правее – отрицательна, т.е. производная меняет знак «+» на знак «–» при переходе через эту точку, то эта стационарная точка – это точка максимума.
Действительно, в данном случае левее стационарной точки функция возрастает, а правее – убывает, т.е. данная точка – это точка максимума.
Если производная меняет знак «–» на знак «+» при переходе через стационарную точку, то эта стационарная точка является точкой минимума.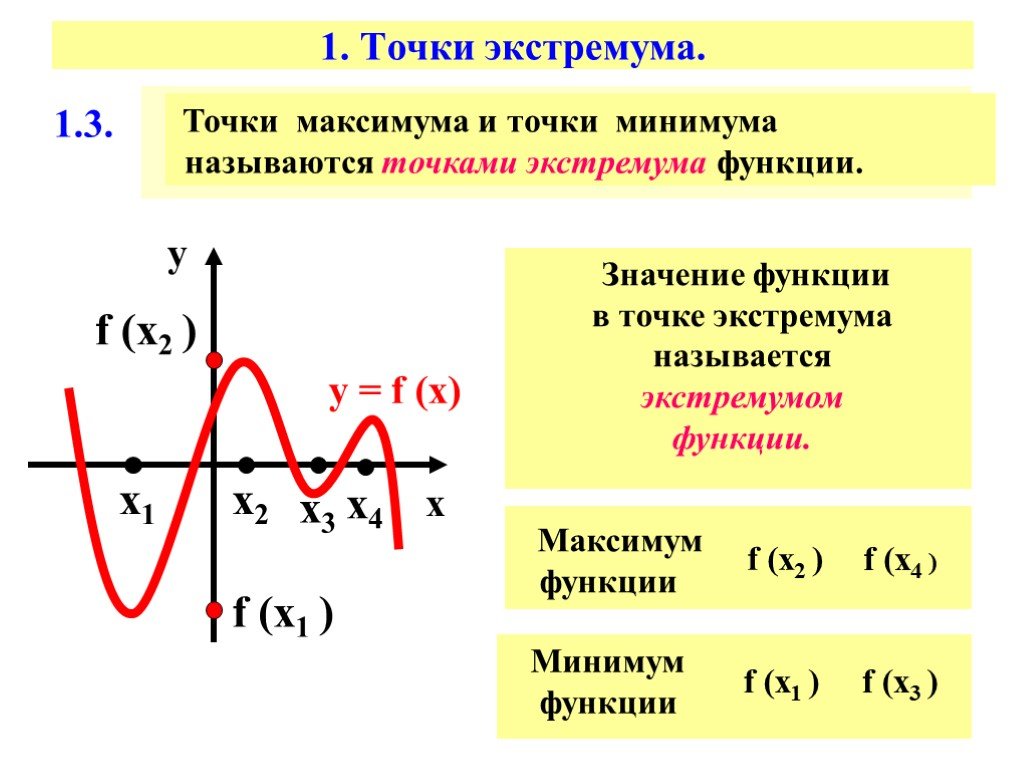
Если производная знак не меняет при переходе через стационарную точку, т.е. слева и справа от стационарной точки производная положительна или отрицательна, то эта точка не является точкой экстремума.
Рассмотрим одну из задач. Найти точки экстремума функции f(х) = х4 – 4х3.
Решение.
1) Найдем производную: f ‘(х) = 4х
2) Найдем стационарные точки: 4х2(х – 3) = 0, х1 = 0, х2 = 3.
3) Методом интервалов устанавливаем, что производная f ‘(х) = 4х2(х – 3) положительна при х > 3, отрицательна при х < 0 и при 0 < х < 3.
4) Так как при переходе через точку х1 = 0 знак производной не меняется, то эта точка не является точкой экстремума.
5) Производная меняет знак «–» на знак «+» при переходе через точку х2 = 3. Поэтому х2 = 3 – точка минимума.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
Задать вопрос
Математика
Курсы по математике 10 класс
Математика
Курсы по математике 9 класс
Математика
Математика 11 класс
Математика
Курсы по геометрии 7 класс
Математика
Курсы по алгебре 7 класс
Математика
Алгебра 8 класс
Математика
Курсы по геометрии 8 класс
Французский язык
Курсы французского языка для начинающих
4.
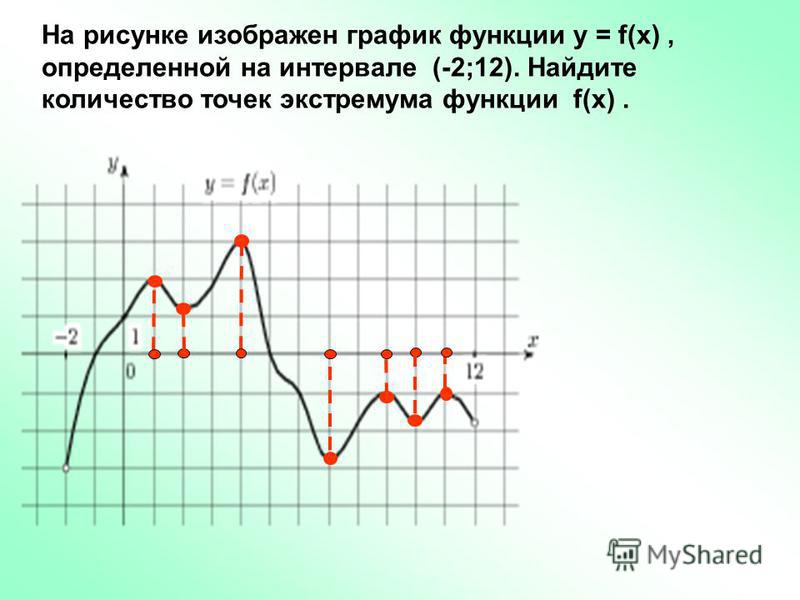 2 Глобальные экстремумы
2 Глобальные экстремумыОпределение 4.2.1. Пусть функция определена на некоторой области . Будем говорить, что в точке функция имеет глобальный максимум (минимум), если для всех точек выполняется неравенство .
По второй теореме Вейерштрасса, непрерывная функция на ограниченном замкнутом множестве всегда достигает минимального и максимального значений, то есть имеет оба глобальных экстремума.
Очевидно, что глобальные экстремумы непрерывных функций могут достигаться либо на границе области , либо в точках локальных экстремумов, лежащих внутри области . Так как локальные экстремумы могут находиться только критических точках, то для нахождения глобальных экстремумов достаточно:
1) найти критические точки функции , лежащие внутри области ;
2) вычислить значения функции в этих точках;
3) найти минимальное и максимальное значения функции на границе области ;
4)
выбрать из значений, найденных в пунктах
2) и 3), наименьшее и наибольшее.
Задача. Найти глобальные экстремумы функции в круге .
Решение.
1. Найдем критические точки функции , лежащие внутри круга .
, .
Полученные частные производные первого порядка существуют всюду на . Найдем стационарные точки, решив систему
Очевидно, что ‑ единственная стационарная точка функции . Она принадлежит кругу .
2. Найдем значение функции в стационарной точке .
.
3. Найдем минимальное и максимальное значения функции на границе круга , то есть на окружности .
Зададим окружность в параметрической форме. Получим:
, где .
Подставив выражения для и в функцию , будем иметь функцию одной переменной .
Из
свойств функции получаем, что минимальное значение
функции на отрезке будет равно и оно будет достигаться при (точка )
и при (точка ),
а максимальное значение будет равно
и оно будет достигаться в точках (точка ), (точка ), (точка
).
4. Выбрав из значений, полученных в пунктах 2 и 3, минимальное и максимальное значения, получим глобальные экстремумы.
1) , минимальное значение функции достигается в точках , ;
2) , максимальное значение функции достигается в точках , .
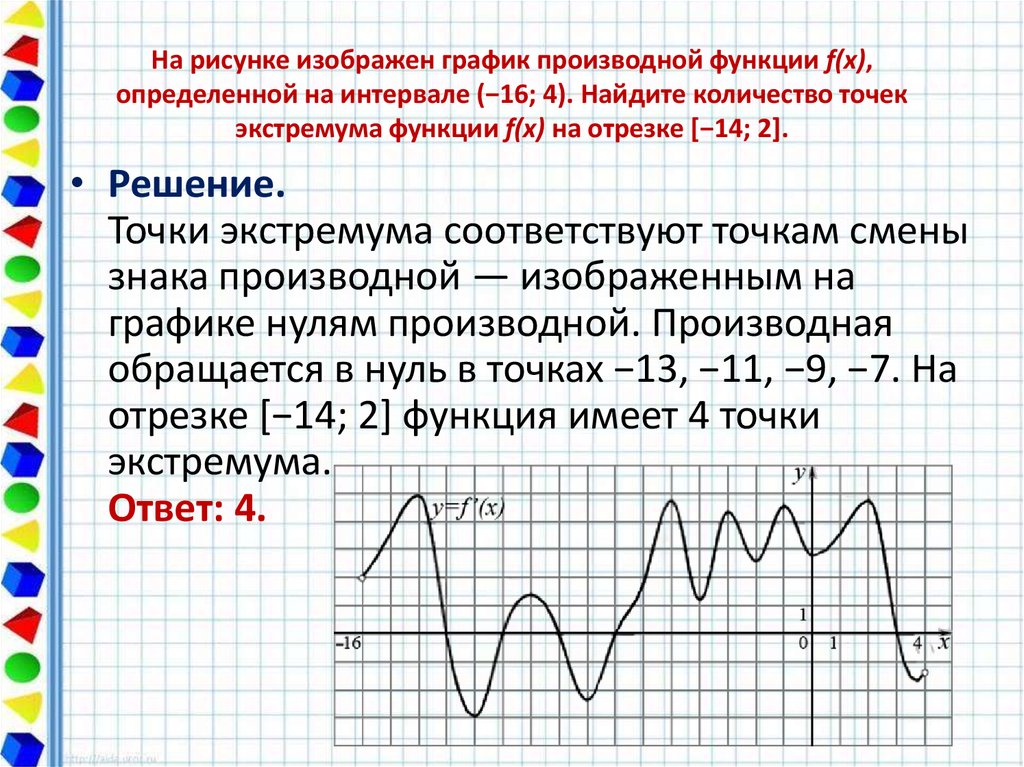
Задача. Найти глобальные экстремумы функции в треугольнике ограниченном прямыми , и .
Решение.
1. Сделаем чертеж.
Рисунок 30
2. Найдем критические точки функции , лежащие внутри треугольника .
,
.
Полученные частные производные первого порядка существуют всюду на . Найдем стационарные точки, решив систему
Очевидно, что ‑ единственная стационарная точка функции . Она принадлежит треугольнику .
3. Найдем значение функции в стационарной точке .
.
4. Найдем минимальное и максимальное значения функции на границе треугольника .
Граница треугольника состоит из трех отрезков: , и .
Отрезок : , .
.
Отсюда следует, что минимальное значение функции при достигается при и равно .
Найдем еще значения функции на концах отрезка . Получим и .
Получили, что минимальное значение функции на отрезке равно , а максимальное значение равно .
Отрезок : , .
.
Отсюда следует, что минимальное значение функции при достигается при и равно .
Найдем еще значения функции на концах отрезка . Получим и .
Получили, что минимальное значение функции на отрезке равно , а максимальное значение равно .
Отрезок : , .
.
Минимум этой функции достигается в точке вершины параболы , и он равен .
Найдем еще значения функции на концах отрезка . Получим и .
Получили, что минимальное значение функции на отрезке равно , а максимальное значение равно .
Таким образом, на границе треугольника минимальное значение функции равно , а максимальное значение равно .
5. Из пунктов 3-4 имеем, что:
Из пунктов 3-4 имеем, что:
1) , минимальное значение функции достигается в точке ;
2) , максимальное значение функции достигается в точке .
Калькуляторкрайних точек | Поиск экстремумов и седловых точек
Знакомство с калькулятором экстремумов
Чтобы найти максимальные и минимальные значения без долгих вычислений, калькулятор экстремумов является лучшим ранговым калькулятором для нахождения экстремальных значений функции. Калькулятор экстремальных значений — это онлайн-инструмент, который используется для нахождения экстремальных значений функции.
Калькулятор точек экстремума — это бесплатный онлайн-решатель производных с шагами и удобным интерфейсом. Он вычисляет достоверные и точные результаты с возможными шагами.
Что вы знаете о калькуляторе седловой точки?
Калькулятор экстремальных точек — это инструмент для нахождения экстремальных значений заданных функций. Калькулятор экстремумов используется для оценки значений прибыли, измерения диаметров или определения количества материалов.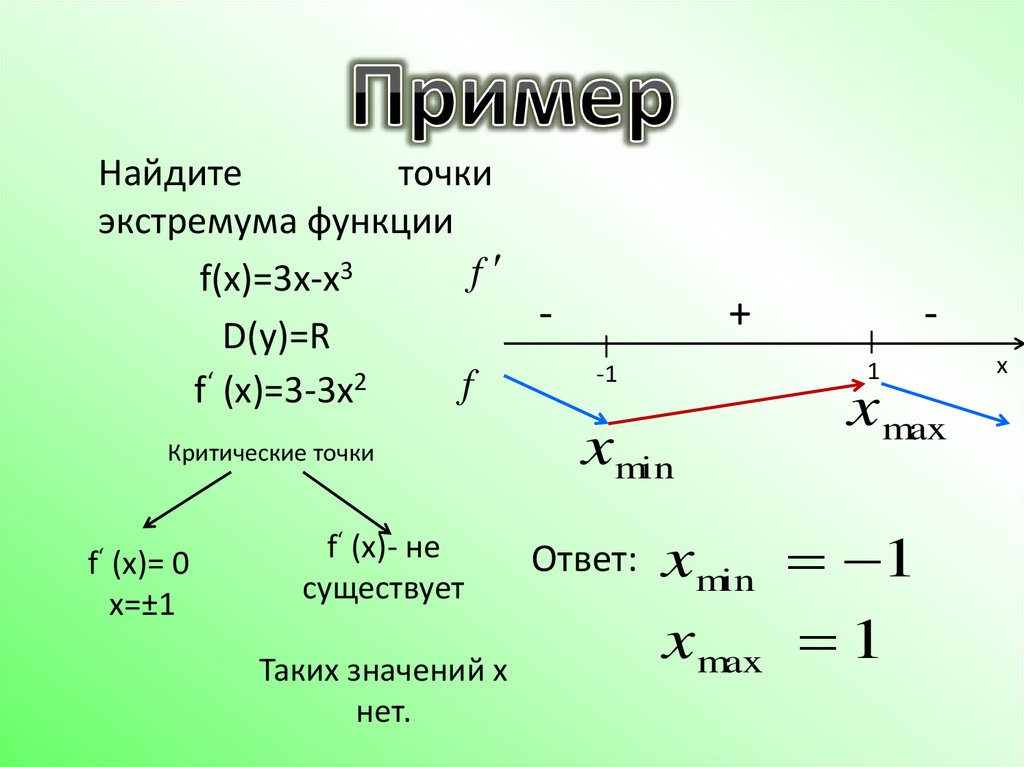
Калькулятор экстремальных точек значительно упрощает работу исследователей и студентов. Пользователю не нужно выполнять долгие лихорадочные вычисления, чтобы найти значения функций.
Формула, используемая калькулятором экстремальных значений
Калькулятор экстремумов предназначен для нахождения минимального и максимального значений заданных функций. Таким образом, нет конкретной формулы для выполнения вычислений, но мы должны выполнить следующие шаги для выполнения вычислений:
- Возьмем производную функции y=f(x).
- Найти, когда наклон равен нулю, т.е. f'(x)=0 .
- Вычислите значение «x».
- Подставьте в основной функции значение «y».
Теперь возникает вопрос, как узнать, является ли точка максимумом или минимумом?
Для этого мы должны выполнить тест второй производной, используя наш калькулятор двойной производной.
- Если тест второй производной будет меньше нуля, то это локальные максимумы.

- Если тест второй производной будет больше нуля, то это локальные минимумы.
- Если проверка второй производной будет равна нулю, то проверка не пройдена.
Как работает калькулятор глобальных экстремумов?
Для нахождения калькулятора экстремумов, как правило, необходимо выполнить следующие шаги для вычисления минимального и максимального значения заданных функций:
- Откройте страницу калькулятора и введите функцию в нужное поле.
- Или вы можете загрузить пример.
- Теперь просто нажмите кнопку «РАССЧИТАТЬ».
Наконец, результаты отображаются на вашем экране. Калькулятор глобальных экстремумов оценит точки максимума и минимума на графике производной (можно рассчитать с помощью графа производной).
После оценки дифференциальной функции обновите страницу для новых расчетов.
Преимущества калькулятора точки экстремума
Калькулятор точки перевала используется для нахождения значений заданных функций. Это лучший из доступных онлайн-инструментов для поиска экстремальных значений заданных дифференциальных функций.
Это лучший из доступных онлайн-инструментов для поиска экстремальных значений заданных дифференциальных функций.
Все, что ему нужно для умной работы с помощью таких эффективных инструментов. Ниже приведен список некоторых преимуществ использования этого калькулятора крайних точек:
- Калькулятор экстремальных точек помогает найти экстремальные значения заданной функции.
- Этот калькулятор производит точные и надежные расчеты без ошибок.
- Пользовательский интерфейс этого онлайн-инструмента очень удобен.
- Этот онлайн-инструмент не содержит ошибок и не взимает плату за подписку со своих пользователей. Этот калькулятор имеет бесплатный неограниченный доступ, то есть пользователь может выполнять расчеты несколько раз.
- Калькулятор седловой точки дает решение с пошаговыми инструкциями.
- Этот калькулятор экстремальных значений выдает результаты за доли секунды.
- Этот калькулятор предоставляет значение экстремального значения заданной функции и его трехмерный график.
 Вы можете понять изменение точек максимума и минимума с помощью этого онлайн-инструмента.
Вы можете понять изменение точек максимума и минимума с помощью этого онлайн-инструмента.
Связанный: Также попробуйте наш калькулятор тройной производной для
Надежно ли использовать калькулятор экстремальных точек?
В исчислении производные отображаются в виде графика для визуального представления функции. Здесь нам часто нужно анализировать максимумы и минимумы функции. Нахождение экстремальных точек отлично подходит для решения реальных задач.
А вот расчеты экстремумов вручную как-то мудрено. Студенты путаются между крайними точками и точкой касания на линии. Поэтому надежно использовать этот инструмент.
С другой стороны, для тех студентов, которые запутались, мы также предлагаем для них калькулятор производной в точке.
глобальных экстремумов — Криста Кинг Математика | Онлайн-помощь по математике
Сообщения с тегами глобальных экстремумов Использование теоремы об экстремальных значениях для нахождения абсолютных максимумов и минимумов Чтобы найти глобальные экстремумы функции, определенной для определенного набора точек, мы выполним 9 определенных шагов. Это позволит нам найти точки абсолютного максимума и абсолютного минимума конкретной области.
Это позволит нам найти точки абсолютного максимума и абсолютного минимума конкретной области.
Читать далее
Learn mathКриста Кинг математика, выучить онлайн, онлайн-курс, онлайн-математика, исчисление iii, исчисление 3, исчисление iii, вычисление 3, теорема об экстремальных значениях, абсолютные максимумы, абсолютные минимумы, глобальные максимумы, глобальные минимумы, абсолютные экстремумы, глобальные экстремумы
Критические точки и тест первой производной Процесс оптимизации заключается в поиске наименьшего и наибольшего значений функции. Если мы воспользуемся калькулятором, чтобы нарисовать график функции, мы обычно сможем определить наименьшее и наибольшее значения. Первая часть исследования оптимизации заключается в поиске критических точек и последующей их классификации как представляющих локальные или глобальные максимумы или минимумы.
Читать далее
Изучение математикиКриста Кинг математика, учиться онлайн, онлайн-курс, онлайн-математика, исчисление 1, исчисление i, вычисление 1, вычисление i, приложения производных, приложения дифференцирования, производные приложения, рисование графиков, рисование кривых, зарисовка кривых, зарисовка графиков, критические точки, поиск критических точек, тест первой производной, локальный максимум, локальные максимумы, локальные экстремумы, локальный экстремум, локальный минимум, локальные минимумы, глобальные экстремумы, глобальные максимумы, глобальный максимум, глобальные минимумы, глобальный минимум, относительный экстремум, относительный экстремум, относительный максимум, относительный максимум, относительный минимум, относительный минимум, абсолютный экстремум, абсолютный экстремум, абсолютный максимум, абсолютный максимум, абсолютный минимум, абсолютный минимум, оптимизация
Нахождение экстремумов (максимумов и минимумов) на замкнутом интервале Экстремумы — это точки функции, в которых существует максимум или минимум.

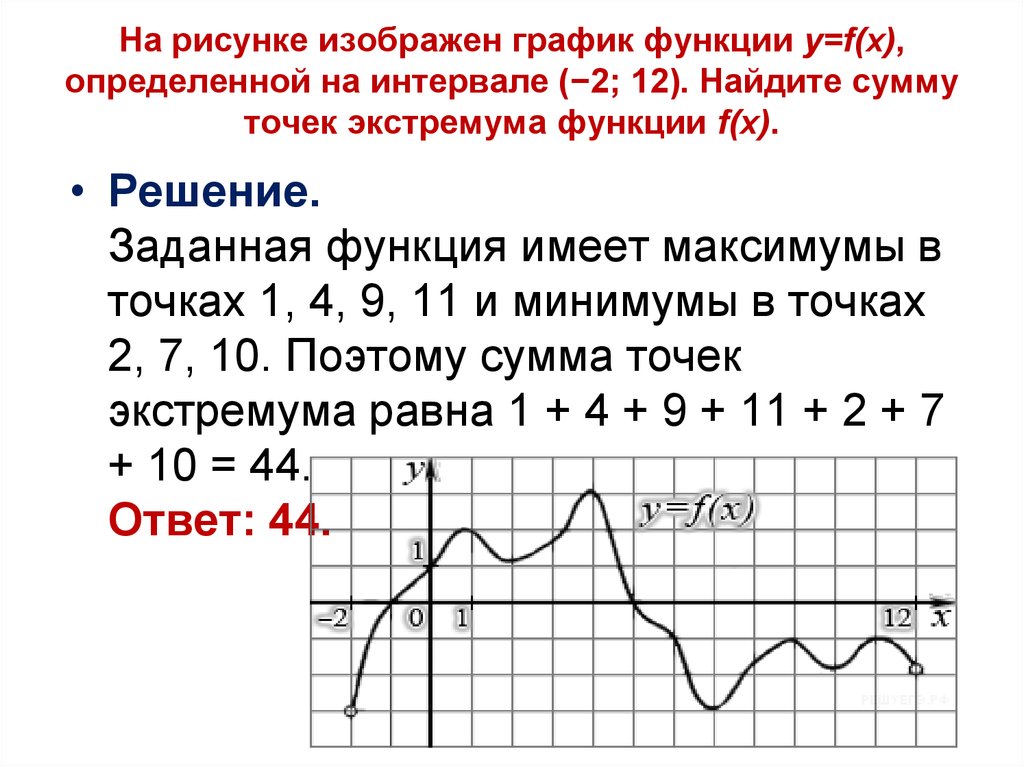
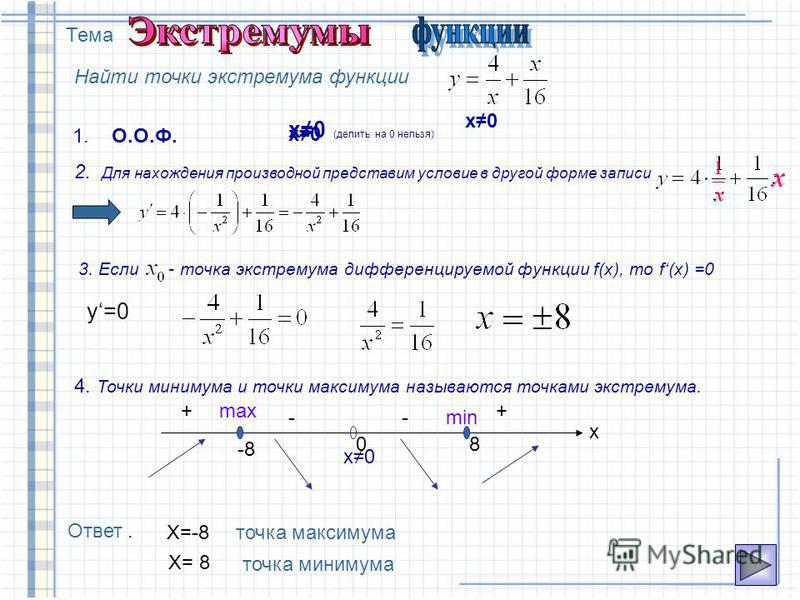 Вы можете понять изменение точек максимума и минимума с помощью этого онлайн-инструмента.
Вы можете понять изменение точек максимума и минимума с помощью этого онлайн-инструмента.