Найдите корни уравнения 4х2-16х=0 .Если корней несколько, запишите их через точку с запятой в порядке возрастания. — Знания.site
Последние вопросы
Алгебра
3 минуты назад
√128 + √18 — √98 \sqrt{128 + \sqrt{18 — \sqrt{98} } } Алгебра
3 минуты назад
Скільки дорівнює коефіцієнт заданої функції y = 4,5x + 11Алгебра
3 минуты назад
Скільки дорівнює коефіцієнт заданої функції y = 110 – 5xАлгебра
13 минут назад
Алгебра 10 клас. Задание на фотографии
Задание на фотографииАлгебра
14 минут назад
СРОЧНО!! Знайдіть значення ь, при якому графік функції y=-⅕x+b +ь проходить через точку M (20; -3)Алгебра
14 минут назад
(3√5-√80+4√20)×(√245)-1степень МОЛЮ ВАС НОГИ РАСЦЕЛУЮАлгебра
18 минут назад
Помогите пожалуйста еще с одним заданием….Алгебра
18 минут назад
Допоможіть мені, будь ласка. Зробити те, що вмієте. Це 9 клас. Я взагалі не готувалася до кр.
Я взагалі не готувалася до кр.Алгебра
33 минут назад
Из цифр 1 3 5 7 9 составить всевозможные комбинации без повторения цифрАлгебра
33 минут назад
Формула Qn = 4n – 3 є формулою n-го члена послідовності: A 1; 7; 16; 19;.. 5 1; 5; 9; 13;.. В 1; 3; 4; 6;.. Г 1; 5; 8; 11;..Алгебра
33 минут назад
В арифметичній прогресії (an) a1 =1,35; d = -2, 4. Обчисліть номер члена цієї прогресії, який дорівнює -25,0533 минут назад
Высоту над землей подброшенного Вертикально вверх камня вычисляют по формуле h(t)=2t² + 5t где h Высота в метрах, 1- время в секундах, прошедшее с момента броска. а) Через сколько секунд мяч будет находиться на высоте 3 м, b) На какой высоте будет мяч через 6 с?
а) Через сколько секунд мяч будет находиться на высоте 3 м, b) На какой высоте будет мяч через 6 с?Алгебра
38 минут назад
Помогите с алгебройАлгебра
53 минут назад
ДАМ 100 БАЛОВ Координати точок перетину графіків функцій у = — 0,5х +2 та у = — 3 + 2х- Алгебра
53 минут назад
чи проходить графік функцій y=-4x+15 через точку А(2;7)В(-6;3)
Все предметы
Выберите язык и регион
English
United States
Polski
Polska
Português
Brasil
English
India
Türkçe
Türkiye
English
Philippines
Español
España
Bahasa Indonesia
Indonesia
Русский
Россия
How much to ban the user?
Дидактические материалы по теме «Квадратные уравнения»
Материалы подготовила учитель математики и физики
Полетайкина В. Н.
Н.
Квадратные уравнения.
Для этой темы характерна большая глубина изложения и богатство устанавливаемых с ее помощью связей в обучении, логическая обоснованность изложения. Поэтому она занимает исключительное положение в линии уравнений и неравенств. К изучению этой темы учащиеся приступают, уже накопив определенный опыт, владея достаточно большим запасом алгебраических и общематематических представлений, понятий, умений. В значительной мере именно на материале этой темы осуществляется синтез материала, относящегося к уравнениям.
Во всех
современных школьных учебниках алгебры и термин, и объем понятия квадратного
уравнения одинаковы. Понятие вводится посредством явного определения, что обязывает
организовать работу по усвоению его формальных признаков. Это тем более,
необходимо, что соответствующие признаки существенно используются при
построении теории квадратных
уравнений, в частности при выводе формулы корней и в теореме Виета.
Вывод формулы корней квадратного уравнения может быть осуществлен несколькими различными способами: сразу для общего или сначала для приведенного квадратного уравнения, сведением к уравнению х2 — а = 0 или к уравнению х2 = а. Но в любом случае приходится использовать выделение полного квадрата в трехчлене ах2+ вх+ с, сводящее уравнение к двучленному. Выделение последовательности шагов, приводящих к решению квадратных уравнений, проводится сначала на конкретных примерах.
Необходимым
этапом при выводе формулы корней квадратного уравнения служит исследование,
выявляющее три возможных случая: отсутствие корней, наличие одного или двух
корней. При этом вводится дискриминант уравнения. В результате исследования формулируется
вывод: «Если дискриминант квадратного уравнения
Учитывая
этот вывод, решение конкретных квадратных уравнений проводится следующим
образом: сначала вычисляется дискриминант, сравнивается с нулем, и если он неотрицателен,
то применяются формулы для нахождения корней.
В ряде учебников, кроме основной формулы для корней квадратного уравнения
ах2 + вх + с = 0, приводятся еще формулы корней уравнения х2+ рх+ q= 0 или х2+ 2рх+ q=0. Иногда использование этих формул упрощает вычисления, при наличии времени полезно их рассмотреть.
При изучении темы «Квадратные уравнения» рассматриваются и неполные квадратные уравнения. Обычно они изучаются перед выводом корней общего квадратного уравнения. Хотя различные виды неполных квадратных уравнений имеют разные алгоритмы решения, при изучении данной темы необходимо показать, что общая формула корней применима и для этих случаев.
Важным моментом в изучении квадратных уравнений является рассмотрение
теоремы Виета, которая утверждает наличие зависимости между корнями и
коэффициентами квадратного уравнения. Сложность освоения теоремы Виета связана
с несколькими обстоятельствами. Прежде всего требуется учитывать различие
прямой и обратной теоремы. В прямой теореме Виета даны квадратное уравнение и
его корни; в обратной — только два числа, а квадратное уравнение появляется в
заключении теоремы. Учащиеся часто совершают ошибку, обосновывая свои
рассуждения неверной ссылкой на прямую или обратную теорему Виета. Например,
при нахождении корней квадратного уравнения подбором ссылаться нужно на
обратную теорему Виета, а не на прямую, как часто делают учащиеся. Для того
чтобы распространить теоремы Виета на случай нулевого дискриминанта, приходится
условиться, что в этом случае квадратное уравнение имеет два равных корня.
Удобство такого соглашения проявляется при разложении квадратного трехчлена на
множители.
В прямой теореме Виета даны квадратное уравнение и
его корни; в обратной — только два числа, а квадратное уравнение появляется в
заключении теоремы. Учащиеся часто совершают ошибку, обосновывая свои
рассуждения неверной ссылкой на прямую или обратную теорему Виета. Например,
при нахождении корней квадратного уравнения подбором ссылаться нужно на
обратную теорему Виета, а не на прямую, как часто делают учащиеся. Для того
чтобы распространить теоремы Виета на случай нулевого дискриминанта, приходится
условиться, что в этом случае квадратное уравнение имеет два равных корня.
Удобство такого соглашения проявляется при разложении квадратного трехчлена на
множители.
Владение теорией квадратных уравнений существенно расширяет возможности решения уравнений методами, изучаемыми в курсе алгебры. Так, прямо сводятся к квадратным сводятся
дробно-рациональные уравнения вида = к и биквадратные уравнения.
Еще один класс составляют алгебраические уравнения, которые разложением
на множители
могут
быть сведены к линейному и квадратному уравнениям.
приемов, имеющихся у учащихся, овладевших сведением различных уравнений к
квадратным, служат необходимой предпосылкой перехода к завершающему этапу освоения
методов решения уравнений. Особенно это сказывается на приложении к алгебраическому
методу решения текстовых задач. Сюжеты их становятся более разнообразными, возрастает
также сложность перевода на язык математики. В целом можно сказать, что освоение темы
«Квадратные уравнения» поднимает учащихся на качественно новую ступень овладения
содержанием школьной математики.
Одним из главных средств обучения математики является
дидактический материал. Он побуждает учащихся к проявлению самостоятельности,
активизирует их мыслительную деятельность в процессе усвоения учебного
материала. Особенно следует отметить достоинство дидактических материалов по
математике, используемых для индивидуальной работы с учащимися. Их применяют в
различных целях: для формирования знаний, умений и навыков; проверки качества
их усвоения; работы по ликвидации пробелов в знаниях.
Разработанные дидактические материалы помогут учащимся овладеть различными приёмами работы с квадратными уравнениями.
Тест №1 Квадратные уравнения и его корни.
- Какое из уравнений является квадратным:
1) 5х2 – 4/х = 0 3) 4х + 3 = 0
2) х2 — 2 х 3 + 7 = 0 4) 1,2 х2 — 3х +1 = 0?
2.В квадратном уравнении 7х + 6 – 2х2 + 1 укажите его коэффициенты:
1) а =7, в = 6, с = -2; 3) а = -2, в =7, с = 6,
2) а=7, в = -2, с = 6, 4)а = -2, в = 6, с = 7.
3) Определите, какое из приведённых уравнений является равносильным уравнению
х2 + (2- х)(1+2х) = 6
1) 3х2 + 5х +2 = 0 3) х2 +3х -2 = 0
2) – х2 +3х +2 = 0, 4) – х2 — 3х + 2 = 0
4) Найдите корни уравнения 6в2 – 54 = 0:
1) 0, 3; 2) -3. 3; 3) не имеет корней; 4) 3;
3; 3) не имеет корней; 4) 3;
5) Какие из чисел -4, -2, -1, 0, 2 являются корнями квадратного уравнения 4 х2 + 8х = 0
1) -2, 0; 2) 0, 2; 3) -4,-1; 4) -4, 0?
6) Решите уравнение 1 – 4у +3 у2 = у2 -4у +9
1) -2, 0; 2) -2, 2; 3) 2; 4) 0.
Тест №2 Формула корней квадратного уравнения.
- Вычислите дискриминант квадратного уравнения 2х2 -5х + 3 = 0:
1) 49; 2) -1; 3) 1; 4) 25.
2. Определите, имеет ли квадратное уравнение х2 +7х +6 = 0 корни, и если имеет, то сколько:
1) имеет один корень; 2) не имеет корней; 3) имеет два корня.
3. Найдите корни уравнения х2 + 10х +9 = 0
1) -1, -9; 2) -1, 9; 3) -9,1; 4)
1,9.
4. Решите квадратное уравнение 4х2 +10х +9 = 0:
1) 3/4,1; 2) -1, 3/4; 3) 3/8, 1; 4) – 3/4,1.
5. Решите уравнение 5у2 = 9у +2:
1) -2, 1/5; 2)-1/5, 2; 3) 4/5, 2; 4) 1/5, 2.
6. Найдите корни уравнения ( х2 +5х) / 2 – 1 = 2:
1) 1, 6; 2) -1, 6 3) -1, -6; 4) -6, 1.
Тест №3 Теорема Виета.
- Найдите сумму корней уравнения х2 +18х -11 = 0
1)18; 2) 11; 3) -18; 4) 1
2. Найдите произведение корней уравнения х2 +27х – 24 = 0
1) 27; 2) -24; 3)1; 4) 24.
3. Найдите сумму корней уравнения 5х2 +10х – 3 = 0:
1) 10; 2) -10; 3) -2; 4) 2.
4. Найдите произведение корней уравнения 3х2 — 16х +9 = 0:
1) 3; 2) 9; 3) -9; 4) 16
5. В уравнении х2 + рх -16 = 0 один из корней равен 8.
Найдите второй корень и коэффициент р:
В уравнении х2 + рх -16 = 0 один из корней равен 8.
Найдите второй корень и коэффициент р:
1) х2 = 2, р = -10; 3) х2 = -2, р=-6;
2) х2 = -2, р=6; 4) х2 = 2, р= 10.
6. один из корней уравнения х2 +7х +q = 0 равен -2. Найдите второй корень и коэффициент q:
1) х2 = -5, q = 10; 3) х2 =5, q = 10
2) х2= 5, q = -10 4) х2= -5, q = -10;
7. Найдите подбором корни уравнения х2 -15х +56 = 0:
1) 4,14; 2) -7, 8; 3) 5, 10; 4) 7,8.
Тест № 4 Дробно – рациональные уравнения
- Какое из уравнений является дробно – рациональным:
1) 3)
2) 4) 2х + 8 = 14(7 – х)?
2. Решите уравнение
Решите уравнение
1) 2 2) – 1 3) 1 4) 3
3. Решите уравнение
1) -2 2) 5 3) 2 4) – 1
4. Найдите корни уравнения
1) 1, 5 2) – 2, 3 3) – 3, 2 4) 2, 3
5. Определите, при каком значении х значение функции у = равно 2:
1) 4 2) 3 3) 8 4) 9
Тест №5 Итоговый
1. Какое из уравнений является квадратным:
1) 3) 5х2 – 20 = 0
2) х3 – 2х + 1 = 0 4) 22х —
2. Укажите в квадратном уравнении 4х – 3х2 + 7 = 0 его коэффициенты:
1) а = 3, в = 4, с = 7 3) а = — 3 в = 4, с = 7
2) а = 4, в = 3, с = 7 4) а = 7, в = 4, с = 3
3. Решите уравнение 3а2 – 27 = 0:
1) 4, 3 2) 3 3) – 3 4) – 3, 3
4. Определите, сколько корней имеет квадратное уравнение 4х2 – 4х + 1 = 0:
Определите, сколько корней имеет квадратное уравнение 4х2 – 4х + 1 = 0:
1) два корня 2) не имеет корней 3) один корень
5. Решите уравнение 2х2 + 3х – 5 = 0
1) 1; 2,5 2) – 1; 2,5 3) – 2,5; 1 4) 1; 5
6. Найдите корни уравнения х(2х + 4) = 6:
1) – 1, 3 2) 1, 3 3) – 2, 3 4) – 3, 1
7. Чему равно произведение корней уравнения 2х2 + 11х – 14 = 0:
1) 14 2) – 14 3) – 7 4) 7
8. Один из корней уравнения х2 + рх + 8 = 0 равен 4. Найдите коэффициент р:
1) 6 2) 5 3) – 6 4) 2
9. Решите уравнение
1) – 1, 1 2) – 2, 3 3) 1, 4) — 1, 1
Ответы:
Тест № 1 | Тест № 2 | Тест №3 | Тест №4 | Тест №5 | |||||
Номер вопроса | Номер ответа | Номер вопроса | Номер ответа | Номер вопроса | Номер ответа | Номер вопроса | Номер ответа | Номер вопроса | Номер ответа |
1 | 4 | 1 | 3 | 1 | 3 | 1 | 3 | 1 | 3 |
2 | 3 | 2 | 3 | 2 | 2 | 2 | 3 | 2 | 3 |
3 | 2 | 3 | 1 | 3 | 3 | 3 | 3 | 3 | 4 |
4 | 2 | 4 | 4 | 4 | 1 | 4 | 4 | 4 | 3 |
5 | 1 | 5 | 2 | 5 | 3 | 5 | 4 | 5 | 4 |
6 | 2 | 6 | 4 | 6 | 1 |
|
| 6 | 3 |
|
|
|
| 7 | 4 |
|
| 7 | 2 |
|
|
|
|
|
|
|
| 8 | 3 |
|
|
|
|
|
|
|
| 9 | 1 |
Тест №6 «Решение задач на составление квадратного уравнения»
№ 1. Решите задачу:
Решите задачу:
Двум рабочим было поручено изготовить по 100 одинаковых
деталей. Один из них изготовлял на 5 деталей в час больше, чем другой. Сколько часов работал рабочий
с
наибольшей производительностью труда, если на всю работу ими было затрачено 9 часов?
Варианты ответов:
1)3 ч; 2) 6,5 ч ; 3) 2,5 ч ; 4) 4 ч
№ 2. Решите задачу:
В колхозе обработали для сева 300 га земли. Если бы колхоз имел на 3 трактора больше, то работу закончили бы на 6 дней раньше. Сколько тракторов было в колхозе, если один трактор обрабатывал за день 15 га земли?
Варианты ответов:
1) 5; 2) 2; 3) 6 4)3.
№ 3. Решите задачу:
Лодка прошла 3 км по течению реки и 2 км против течения за то же время, какое понадобилось бы
ей, чтобы проплыть 6 км в стоячей
воде. Зная, что скорость лодки
в стоячей воде равна 4 км/ч, найти
скорость течения реки.
Варианты ответов:
1) 1,6 км/ч; 2) 0,8 км/ч; 3)2 км/ч; 4)2,4км/ч.
№ 4. Решите задачу:
Катер прошел 10 км по течению реки и 24 км против течения, затратив на весь путь 2 ч. Найти скорость течения реки, если собственная скорость катера 18 км/ч.
Варианты ответов:
1) 2 км/ч; 2) 7 км/ч; 3) 2,5 км/ч; 4) 6,5 км/ч.
№
5. Решите задачу:
Две машинистки, работая вместе, могут выполнить задание за 3 ч. Сколько времени потребуется для выполнения этого задания первой машинистке, если она может выполнить все задание на 8 ч быстрее второй?
Варианты ответов:
1) 4ч; 2) 6 ч; 3) 5ч; 4) 7 ч.
№ 6. Решите задачу:
Два грузовика, работая вместе, перевезли овощи в течение 4 ч. За какое время перевезет ту же массу овощей второй грузовик, если первому нужно для этого на 6 ч больше, чем второму?
Варианты ответов:
1) 4ч; 2) 6
ч; 3) 12 ч; 4) 10 ч.
№ 7. Решите задачу:
За 6 м сатина и 6 м ситца было заплачено 1530 р. Найти цену 1 м ситца, если 5 м сатина стоят столько же, сколько стоят 12 м ситца.
Варианты ответов:
1) 180 р.; 2) 75 р.; 3) 65 р.; 4) 135 р.
№ 8. Решите задачу:.
За 9 кг бананов и 9 кг винограда было заплачено 37 80 р. Найти цену 1 кг бананов, если известно, что 4 кг винограда стоят столько же, сколько стоят 3 кг бананов.
Варианты ответов:
1) 180 р.; 2) 195 р.; 3) 260 р.; 4) 240 р.
Тест №7. Заполните пропуски (многоточия), чтобы получилось верное утверждение или правильная формулировка определения, правила.
1 …………….. уравнением называется уравнение вида ах2 + вх +с =0, где а, в, с-некоторые числа, а≠0, х – неизвестное.
2. Уравнение х2 = с, где с >0, имеет корни х1 = ……….. х2 =………….
3. Уравнение ах2 =0, где а ≠0, называют ……………………квадратным уравнением.
Уравнение ах2 =0, где а ≠0, называют ……………………квадратным уравнением.
4. Уравнение вида ах2 +вх =0, где а ≠0 и в ≠ 0 называют …………………..квадратным уравнением.
5. Если ах2 +вх +с =0 – квадратное уравнение ( а ≠0 ), то в называют ………………..коэффициентом.
6. Корни квадратного уравнения ах2 +вх +с =0 вычисляются по формуле х1,2 =
7. Квадратное уравнение ах2 +вх +с =0 (а ≠0) имеет два различных действительных корня, если
в2 — 4 ас ……….( >, <) 0.
8. Приведённое квадратное уравнение х2 + рх + g = 0 совпадает с уравнением общего вида, в котором а =….., в =….., с =……
9. Если х1 и х2 — корни уравнения х2 + рх + g =0, то справедливы формулы х1 + х2 =……., х1 * х2 = …..,
10 * Если х1 и х2 — корни квадратного уравнения ах2 +вх +с =0, то при всех х справедливо равенство
ах2
+вх +с = а (……. .) (…….)
.) (…….)
Оценочная таблица
№ задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10* |
Балл | 1 | 2 | 1 | 1 | 1 | 2 | 1 | 2 | 2 | 2 |
Тест 8. Установите, истинны или ложны утверждения:
Установите, истинны или ложны утверждения:
- Для уравнения -9х2 + 2х – 4 = 0 приведённым является уравнение
х2 – х + = 0
- Не решая уравнение х2 – 5х + 3 = 0, можно сказать, что корни его имеют одинаковые знаки.
- Числа -11 и 2 являются корнями уравнения х2 + 9х – 22 = 0
- Числа х1= и х2 = — не являются корнями уравнения х2 = —
- Если а = 3, в = 7, с = — 1 – коэффициенты квадратного уравнения, то оно запишется так: 3х2 + 6х + 1 = 0.
- Уравнение 2х2 – 6х + 3 = 0 не имеет действительных корней.
- Уравнение (5 – х)( 3х + 4) = 0 имеет корни х1 = 5 и х2 =
- Уравнение х2 + 6х + к = 0 имеет один корень, если к = 9
10.* Если произведение двух последовательных натуральных
чисел равно 992, то сами числа равны 31 и 32.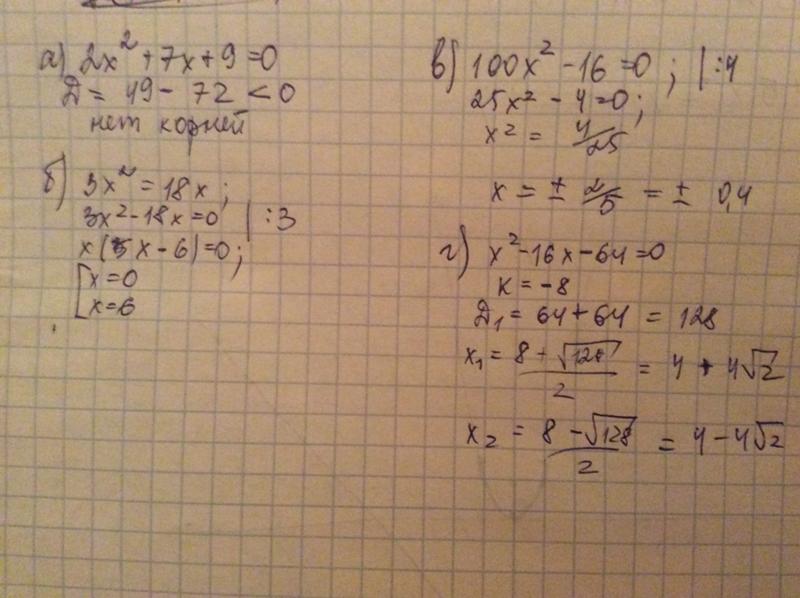
Оценочная таблица
Номер задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10* |
Балл | 1 | 1 | 2 | 2 | 1 | 3 | 3 | 3 | 4 | 5 |
Зачёт по теме «Решение квадратных уравнений»
1. Покажите с
помощью стрелки, сколько корней имеет уравнение: один корень, два корня или
не имеют корней.
Покажите с
помощью стрелки, сколько корней имеет уравнение: один корень, два корня или
не имеют корней.
2. Решите уравнение 7х2 + 13х — 2 = 0.
D = 169 + 56 = 225, х = , х = ,
х1 = -2, х2 = .
3. При каких значениях трёхчлен 3х2 – х – 3 и двучлен х2 + 4х принимают равные значения?
3х2 – х – 3 = х2 + 4х
2х2 – 5х – 3 = 0
D = 25 + 24 = 49, х = , х = ,
х1 = -, х2 = 3.
4. Из данных уравнений выберите те, которые равносильны уравнению х2 + 7х – 8 = 0
А. х2 + 7х = 8 В.
Б. 0,2х2 + 1,4х – 1,6 = 0 Г.
5. При каком значении а один из корней уравнения ах2 – х – 8 = 0 равен 2?
а· 4 – 2 – 8 = 0
4а = 10
а = 2,5
Дополнительно.
6. Не
выполняя построения, найдите координаты точек пересечения параболы у = х2и
прямой у = х + 12.
Не
выполняя построения, найдите координаты точек пересечения параболы у = х2и
прямой у = х + 12.
х2 = х + 12
х2 — х — 12 = 0
D = 1 + 48 = 49, х = ,
х1 = -3, х2 = 4
Если х = — 3, то у = (- 3)2 = 9, если х = 4, то у = 42 = 16.
Графики пересекаются в точках (- 3; 9), (4; 16).
7. При каких значениях р уравнение
(р – 4)х2 + (р2 – 16)х – 9 = 0 является неполным квадратным уравнением?
Р2 — 16 = 0, р = 4 или р = — 4.
При р = 4 уравнение не является квадратным. Искомое значение р = — 4.
8. Найдите значения т, при которых уравнение
х2-тх + т + 3 = 0
имеет единственный корень.
D = т2-4(т + 3),
т2 — 4т — 12 = 0,
= 4 + 12 = 16, m = ,
m1 = — 2, m2 = 6.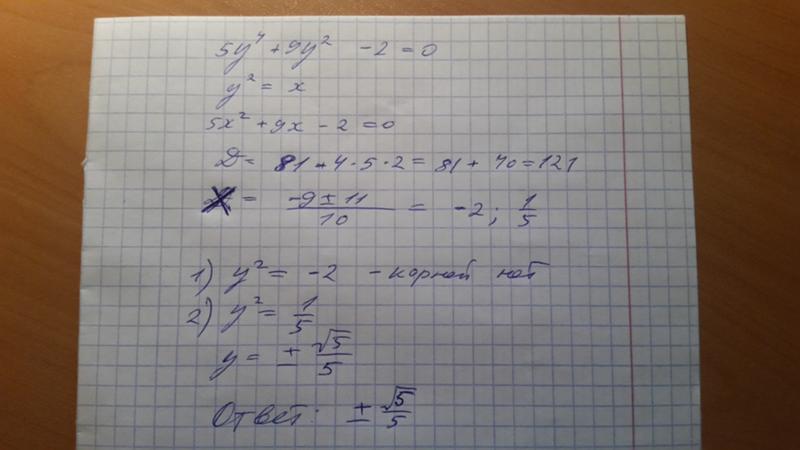

 Задание на фотографии
Задание на фотографии Я взагалі не готувалася до кр.
Я взагалі не готувалася до кр. а) Через сколько секунд мяч будет находиться на высоте 3 м, b) На какой высоте будет мяч через 6 с?
а) Через сколько секунд мяч будет находиться на высоте 3 м, b) На какой высоте будет мяч через 6 с?