Найдите нок чисел 12 и 18: Найдите НОК и НОД чисел: А) 12 и 18; Б) 13 и 39.

Калькулятор онлайн — Нахождение (вычисление) НОД и НОК (с подробным решением)

Наибольшим общим делителем (НОД) для двух целых чисел m и n называется наибольший из их общих делителей.
Пример: для чисел 6 и 9 наибольший общий делитель равен 3.

Наибольший общий делитель существует и однозначно определён, если хотя бы одно из чисел m или n не равно нулю.
В школьной программе обозначается так: НОД(m, n)

Понятие наибольшего общего делителя (НОД) распространяется на любой набор из более чем двух целых чисел. Чаще всего НОД используется для сокращения дроби — если найти НОД числителя и знаменателя, то на это число можно сократить числитель и знаменатель данной дроби.

Наименьшее общее кратное (НОК) двух целых чисел m и n это наименьшее натуральное число, которое делится на m и n без остатка. В школьной программе обозначается так: НОК(m, n)
Пример: НОК(16, 20) = 80
Одно из наиболее частых применений НОК — приведение дробей к общему знаменателю.

С помощью данной математической программы вы можете найти (вычислить) НОД и НОК двух целых чисел.

Программа нахождения НОД и НОК не только выводит ответ задачи, но и отображает процесс вычисления НОД и НОК двух чисел.

Вводить можно только целые положительные числа.

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.

Наибольший общий делитель (НОД). Взаимно простые числа

Определение. Наибольшее натуральное число, на которое делятся без остатка числа а и b, называют наибольшим общим делителем (НОД) этих чисел.

Найдём наибольший общий делитель чисел 24 и 35.
Делителями 24 будут числа 1, 2, 3, 4, 6, 8, 12, 24, а делителями 35 будут числа 1, 5, 7, 35.
Видим, что числа 24 и 35 имеют только один общий делитель — число 1.

Такие числа называют взаимно простыми.

Определение. Натуральные числа называют взаимно простыми, если их наибольший общий делитель (НОД) равен 1.

Наибольший общий делитель (НОД) можно найти, не выписывая всех делителей данных чисел.

Разложим на множители числа 48 и 36, получим:
48 = 2 * 2 * 2 * 2 * 3, 36 = 2 * 2 * 3 * 3.
Из множителей, входящих в разложение первого из этих чисел, вычеркнем те, которые не входят в разложение второго числа (т. е. две двойки).
Остаются множители 2 * 2 * 3. Их произведение равно 12. Это число и является наибольшим общим делителем чисел 48 и 36. Так же находят наибольший общий делитель трёх и более чисел.

Чтобы найти наибольший общий делитель нескольких натуральных чисел, надо:
1) разложить их на простые множители;

2) из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел;
3) найти произ ведение оставшихся множителей.

Если все данные числа делятся на одно из них, то это число и является наибольшим общим делителем данных чисел.
Например, наибольшим общим делителем чисел 15, 45, 75 и 180 будет число 15, так как на него делятся все остальные числа: 45, 75 и 180.

Наименьшее общее кратное (НОК)

Определение. Наименьшим общим кратным (НОК) натуральных чисел а и b называют наименьшее натуральное число, которое кратно и a и b. Наименьшее общее кратное (НОК) чисел 75 и 60 можно найти и не выписывая подряд кратные этих чисел. Для этого разложим 75 и 60 на простые множители: 75 = 3 * 5 * 5, а 60 = 2 * 2 * 3 * 5.
Выпишем множители, входящие в разложение первого из этих чисел, и добавим к ним недостающие множители 2 и 2 из разложения второго числа (т.е. объединяем множители).

Получаем пять множителей 2 * 2 * 3 * 5 * 5, произведение которых равно 300. Это число является наименьшим общим кратным чисел 75 и 60.

Так же находят наименьшее общее кратное для трёх и более чисел.

Чтобы найти наименьшее общее кратное нескольких натуральных чисел, надо:
1) разложить их на простые множители;
2) выписать множители, входящие в разложение одного из чисел;
3) добавить к ним недостающие множители из разложений остальных чисел;
4) найти произведение получившихся множителей.

Заметим, что если одно из данных чисел делится на все остальные числа, то это число и является наименьшим общим кратным данных чисел.

Например, наименьшим общим кратным чисел 12, 15, 20 и 60 будет число 60, так как оно делится на все данные числа.

Пифагор (VI в. до н. э.) и его ученики изучали вопрос о делимости чисел. Число, равное сумме всех его делителей (без самого числа), они называли совершенным числом. Например, числа 6 (6 = 1 + 2 + 3), 28 (28 = 1 + 2 + 4 + 7 + 14) совершенные. Следующие совершенные числа — 496, 8128, 33 550 336. Пифагорейцы знали только первые три совершенных числа. Четвёртое — 8128 — стало известно в I в. н. э. Пятое — 33 550 336 — было найдено в XV в. К 1983 г. было известно уже 27 совершенных чисел. Но до сих пор учёные не знают, есть ли нечётные совершенные числа, есть ли самое большое совершенное число.
Интерес древних математиков к простым числам связан с тем, что любое число либо простое, либо может быть представлено в виде произведения простых чисел, т. е. простые числа — это как бы кирпичики, из которых строятся остальные натуральные числа.

Вы, наверное, обратили внимание, что простые числа в ряду натуральных чисел встречаются неравномерно — в одних частях ряда их больше, в других — меньше. Но чем дальше мы продвигаемся по числовому ряду, тем реже встречаются простые числа. Возникает вопрос: существует ли последнее (самое большое) простое число? Древнегреческий математик Евклид (III в. до н. э.) в своей книге «начала», бывшей на протяжении двух тысяч лет основным учебником математики, доказал, что простых чисел бесконечно много, т. е. за каждым простым числом есть ещё большее простое число.
Для отыскания простых чисел другой греческий математик того же времени Эратосфен придумал такой способ. Он записывал все числа от 1 до какого-то числа, а потом вычёркивал единицу, которая не является ни простым, ни составным числом, затем вычёркивал через одно все числа, идущие после 2 (числа, кратные 2, т. е. 4, 6, 8 и т. д.). Первым оставшимся числом после 2 было 3. Далее вычёркивались через два все числа, идущие после 3 (числа, кратные 3, т. е. 6, 9, 12 и т. д.). в конце концов оставались невычеркнутыми только простые числа.

Калькулятор НОД и НОК с решением онлайн

Найдем наибольший общий делитель НОД (36 ; 24)

Этапы решения

Способ №1

1) Разложим числа на простые множители. Для этого проверим, является ли каждое из чисел простым (если число простое, то его нельзя разложить на простые множители, и оно само является своим разложением)

36 — составное число
24 — составное число

Разложим число 36 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом

36 : 2 = 18 — делится на простое число 2
18 : 2 = 9 — делится на простое число 2
9 : 3 = 3 — делится на простое число 3.
Завершаем деление, так как 3 простое число

Разложим число 24 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом

24 : 2 = 12 — делится на простое число 2
12 : 2 = 6 — делится на простое число 2
6 : 2 = 3 — делится на простое число 2.
Завершаем деление, так как 3 простое число

2) Выделим синим цветом и выпишем общие множители

36 = 2 ⋅ 2 ⋅ 3 ⋅ 3
24 = 2 ⋅ 2 ⋅ 2 ⋅ 3
Общие множители (36 ; 24) : 2, 2, 3

3) Теперь, чтобы найти НОД нужно перемножить общие множители

Ответ: НОД (36 ; 24) = 2 ∙ 2 ∙ 3 = 12

Способ №2

1) Найдем все возможные делители чисел (36 ; 24).

Для этого поочередно разделим число 36 на делители от 1 до 36, число 24 на делители от 1 до 24. Если число делится без остатка, то делитель запишем в список делителей.

Для числа 36 выпишем все случаи, когда оно делится без остатка:
36 : 1 = 36;36 : 2 = 18;36 : 3 = 12;36 : 4 = 9;36 : 6 = 6;36 : 9 = 4;36 : 12 = 3;36 : 18 = 2;36 : 36 = 1;

Для числа 24 выпишем все случаи, когда оно делится без остатка:
24 : 1 = 24;24 : 2 = 12;24 : 3 = 8;24 : 4 = 6;24 : 6 = 4;24 : 8 = 3;24 : 12 = 2;24 : 24 = 1;

2) Выпишем все общие делители чисел (36 ; 24) и выделим зеленым цветом самы большой, это и будет наибольший общий делитель НОД чисел (36 ; 24)

Общие делители чисел (36 ; 24): 1, 2, 3, 4, 6, 12

Ответ: НОД (36 ; 24) = 12

Найдем наименьшее общее кратное НОК (52 ; 49)

Этапы решения

Способ №1

1) Разложим числа на простые множители. Для этого проверим, является ли каждое из чисел простым (если число простое, то его нельзя разложить на простые множители, и оно само является своим разложением)

52 — составное число
49 — составное число

Разложим число 52 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом

52 : 2 = 26 — делится на простое число 2
26 : 2 = 13 — делится на простое число 2.
Завершаем деление, так как 13 простое число

Разложим число 49 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом

49 : 7 = 7 — делится на простое число 7.
Завершаем деление, так как 7 простое число

2) Прежде всего запишем множители самого большого числа, а затем меньшего числа. Найдем недостающие множители, выделим синим цветом в разложении меньшего числа множители, которые не вошли в разложение большего числа.

52 = 2 ∙ 2 ∙ 13
49 = 7 ∙ 7

3) Теперь, чтобы найти НОК нужно перемножить множители большего числа с недостающими множителями, которые выделены синим цветом

НОК (52 ; 49) = 2 ∙ 2 ∙ 13 ∙ 7 ∙ 7 = 2548

Способ №2

1) Найдем все возможные кратные чисел (52 ; 49). Для этого поочередно умножим число 52 на числа от 1 до 49, число 49 на числа от 1 до 52.

Выделим все кратные числа 52 зеленым цветом:

52 ∙ 1 = 52;   52 ∙ 2 = 104;   52 ∙ 3 = 156;   52 ∙ 4 = 208;
52 ∙ 5 = 260;   52 ∙ 6 = 312;   52 ∙ 7 = 364;   52 ∙ 8 = 416;
52 ∙ 9 = 468;   52 ∙ 10 = 520;   52 ∙ 11 = 572;   52 ∙ 12 = 624;
52 ∙ 13 = 676;   52 ∙ 14 = 728;   52 ∙ 15 = 780;   52 ∙ 16 = 832;
52 ∙ 17 = 884;   52 ∙ 18 = 936;   52 ∙ 19 = 988;   52 ∙ 20 = 1040;
52 ∙ 21 = 1092;   52 ∙ 22 = 1144;   52 ∙ 23 = 1196;   52 ∙ 24 = 1248;
52 ∙ 25 = 1300;   52 ∙ 26 = 1352;   52 ∙ 27 = 1404;   52 ∙ 28 = 1456;
52 ∙ 29 = 1508;   52 ∙ 30 = 1560;   52 ∙ 31 = 1612;   52 ∙ 32 = 1664;
52 ∙ 33 = 1716;   52 ∙ 34 = 1768;   52 ∙ 35 = 1820;   52 ∙ 36 = 1872;
52 ∙ 37 = 1924;   52 ∙ 38 = 1976;   52 ∙ 39 = 2028;   52 ∙ 40 = 2080;
52 ∙ 41 = 2132;   52 ∙ 42 = 2184;   52 ∙ 43 = 2236;   52 ∙ 44 = 2288;
52 ∙ 45 = 2340;   52 ∙ 46 = 2392;   52 ∙ 47 = 2444;   52 ∙ 48 = 2496;
52 ∙ 49 = 2548;   

Выделим все кратные числа 49 зеленым цветом:

49 ∙ 1 = 49;   49 ∙ 2 = 98;   49 ∙ 3 = 147;   49 ∙ 4 = 196;
49 ∙ 5 = 245;   49 ∙ 6 = 294;   49 ∙ 7 = 343;   49 ∙ 8 = 392;
49 ∙ 9 = 441;   49 ∙ 10 = 490;   49 ∙ 11 = 539;   49 ∙ 12 = 588;
49 ∙ 13 = 637;   49 ∙ 14 = 686;   49 ∙ 15 = 735;   49 ∙ 16 = 784;
49 ∙ 17 = 833;   49 ∙ 18 = 882;   49 ∙ 19 = 931;   49 ∙ 20 = 980;
49 ∙ 21 = 1029;   49 ∙ 22 = 1078;   49 ∙ 23 = 1127;   49 ∙ 24 = 1176;
49 ∙ 25 = 1225;   49 ∙ 26 = 1274;   49 ∙ 27 = 1323;   49 ∙ 28 = 1372;
49 ∙ 29 = 1421;   49 ∙ 30 = 1470;   49 ∙ 31 = 1519;   49 ∙ 32 = 1568;
49 ∙ 33 = 1617;   49 ∙ 34 = 1666;   49 ∙ 35 = 1715;   49 ∙ 36 = 1764;
49 ∙ 37 = 1813;   49 ∙ 38 = 1862;   49 ∙ 39 = 1911;   49 ∙ 40 = 1960;
49 ∙ 41 = 2009;   49 ∙ 42 = 2058;   49 ∙ 43 = 2107;   49 ∙ 44 = 2156;
49 ∙ 45 = 2205;   49 ∙ 46 = 2254;   49 ∙ 47 = 2303;   49 ∙ 48 = 2352;
49 ∙ 49 = 2401;   49 ∙ 50 = 2450;   49 ∙ 51 = 2499;   49 ∙ 52 = 2548;

2) Выпишем все общие кратные чисел (52 ; 49) и выделим зеленым цветом самое маленькое, это и будет наименьшим общим кратным чисел (52 ; 49).

Общие кратные чисел (52 ; 49): 2548

Ответ: НОК (52 ; 49) = 2548

Наибольший общий делитель, Наименьшее общее кратное

Наибольший общий делитель

Общим делителем нескольких чисел называется число, служащее делителем  для каждого из них. Например, числа 12, 18, 30 имеют общий делитель 3; число 2 — тоже их общий делитель. Среди всех общих делителей всегда имеется наибольший, в нашем примере — число 6. Это число называется наибольшим общим делителем (НОД).

Примеры. Для чисел 16, 20, 28 НОД есть 4; для чисел 5, 30, 60, 90 НОД есть 5.

Пример 1. Найти НОД чисел 252, 441, 1080. Разлагаем на простые множители

252 = 2² · 3²-7;  441 = 3² · 7²; 1080 = 2³ · З² · 5.

Общим для чисел является только простой множитель 3; наименьший из показателей, с которыми он входит в данные числа, есть 2. НОД равен З² = 9.

Пример 2. Найти НОД чисел 234, 1080, 8100.

234 = 2 · З²-13; 1080 = 2³ · З² · 5;   8100 = 2² · З⁴ · 5².     НОД = 2 · 3² = 18.

Может случиться так, что простых множителей, общих для всех данных чисел, не будет вовсе. Тогда наибольший общий делитель есть 1. Например, для чисел 15 = 3 · 5, 10 = 2 · 5, 6 = 2 · 3 НОД = 1.  Два числа, НОД которых равен 1, называются взаимно простыми. Например, 15 и 22 взаимно простые числа.

 

Наименьшее общее кратное

Общим кратным нескольких чисел называется число, служащее кратным  для каждого из них. Например, числа 15, 6, 10 имеют общее кратное 180; число 90 — также общее кратное этих чисел. Среди всех общих кратных всегда есть наименьшее, в данном случае число 30. Это число называется наименьшим общим кратным (НОК). Для небольших чисел НОК находится легко по догадке. Если числа большие, поступаем так: разлагаем данные числа на простые множители; выписываем все простые множители, входящие хотя бы в одно из данных чисел; каждый из
взятых множителей возводим в наибольшую из тех степеней, с которыми он входит в данные числа. Производим умножение.

Пример 1. Найти НОК чисел 252, 441, 1080.

Разлагаем на простые множители: 252 = 2² · З² · 7;  441 = З² · 7²; 1080 = 2³ · З³ · 5. Перемножаем 2³ · З³ · 7² х 5. НОК = 52 920.

Пример 2. Найти НОК чисел 234, 1080, 8100               НОК = 2³ · З⁴ · 5² · 13 = 210 600.

 

Презентация по теме:»Решение задач на нахождение НОД и НОК»

Давайте наш урок начнем с пожелания друг другу добра.

Я желаю тебе добра, ты желаешь мне добра, мы желаем друг другу добра.

Если будет трудно –

я тебе помогу.

Разминка (заполни пропуски)

1. Наибольшее натуральное число, на которое делятся без остатка числа а и в называют ____________________________ этих чисел;

наибольшим общим делителем

2. Чтобы найти наибольший общий делитель нескольких натуральных чисел, надо:

1. разложить данные числа на __________________

простые множители

одновременно

2. выписать все простые множители, которые _____________входят в _______ из полученных разложений

каждое

3. каждое из выписанных простых чисел взять с ______________ из показателей степени, с которыми оно входит в разложения данных чисел

наименьшим

4. записать _____________ полученных степеней.

произведение

3. Разложите на простые множители и найдите наибольший общий делитель чисел 12 и 18

2

12 __ 18 2

6 2 __ __

__ __ 3 __

1 1

12= 2² ∙ 3; 18 = 2 ∙ 3²

9

3

3

3

3

НОД(12;18)= __ ∙ __ = ___

3

2

6

Разминка (продолжи фразу)

4. Наименьшее натуральное число , которое делится без остатка на а и в , называется _________________________ этих чисел;

наименьшим общим кратным

5. Чтобы найти наименьшее общее кратное нескольких натуральных чисел, надо:

1. разложить данные числа на ________ множители

простые

2. выписать все простые числа, которые входят ______________ из полученных разложений

хотя бы в одно

3. каждое из выписанных простых чисел взять с ____________ из показателей степени, с которыми оно входит в разложения данных чисел

наибольшим

степеней

4. записать произведение полученных ____________

6. Найдите наименьшее общее кратное чисел 12 и 18

2

12 2 18 __

__ __ __ 3

3 __ 3 __

1 1

12= 2² ∙ 3; 18 = 2 ∙ 3²

6

2

9

3

3

НОК(12;18)= ____ ∙ ____ = ____

3²

2²

36

Имеется 36 синих и 48 красных листов бумаги. Какое наибольшее число комплектов можно сделать из этих листов, если в каждом комплекте должно быть одинаковое число синих и красных листов бумаги?

Из речного порта одновременно 1 мая 2017 года вышли два теплохода . Продолжительность рейса одного из них – 15 суток, а продолжительность рейса второго – 24 суток.

Через сколько дней теплоходы снова одновременно отправятся в рейс? Сколько рейсов за это время сделает первый теплоход? А сколько второй?

Решение задач на нахождение НОД и НОК

Цели урока:

• Отработка навыков нахождения НОД и НОК чисел.
• Применение полученных знаний для решения задач.
• Развитие интереса к предмету.

Успехов!

Работа в парах

(М)

(О)

(А)

НОК (14;42)

НОД (9;40)

(П)

НОК (17;34)

(Р)

(Т)

НОК (12;40)

(И)

НОК (42;210)

НОД (4;8;12)

(В)

(Ч)

(Л)

НОД (24;48)

(С)

НОК (17;5)

НОК (4;8;16)

НОД (12;46)

НОД (14;21)

(Я)

НОК (72;12)

Работа в парах

24

16

Ч

2

И

7

С

34

Л

А

4

П

120

Р

34

А

85

В

72

210

Я

Т

42

М

16

120

И

Р

1

О

42

М

Числа

правят

миром

Пифагор.

Пифагор – древнегреческий философ, математик и мистик. Пифагор обожествлял числа. Он учил: числа управляют миром. Всемогущество чисел проявляется в том, что всё в мире подчиняется числовым отношениям. Высшее совершенство Пифагор видел в гармонии, гармонии чисел и фигур.

Физ.минутка

Решение задач

Имеется 32 синих и 48 красных листов бумаги. Какое наибольшее число комплектов можно сделать из этих листов, если в каждом комплекте должно быть одинаковое число синих и красных листов бумаги?

32 2

48 2

16 2

24 2

12 2

8 2

4 2

6 2

2 2

3 3

1

1

5

1) 32 = 2

4

2) 48 = 2 ∙ 3

4

3) НОД (32;48) = 2 = 16(к)

Ответ: можно сделать16 комплектов.

Найди ошибку

Из речного порта одновременно 1 мая 2011 года вышли два теплохода. Продолжительность рейса одного из них – 15 суток, а продолжительность рейса второго – 18 суток. Через сколько дней теплоходы снова одновременно отправятся в рейс? Сколько рейсов за это время сделает первый теплоход? А сколько второй?

15 3

18 2

5 5

9 9

1

1

18 2

9 3

3 3

1

1) 15 = 3 ∙ 5

2) 18 = 2 ∙ 3²

3) НОК (15;18) = 5 ∙3² ∙ 2 = 90(дн.) – одновременно отпр. в рейс

4) 90 : 15 = 6(р) – сделает первый теплоход

5) 90 : 18 = 5(р) – сделает второй теплоход

Ответ: через 90 дней снова отправятся в рейс; 6 рейсов сделает первый теплоход и 5 рейсов второй.

Выбери правильное решение задачи

Для участия в эстафете нужно разделить 24 девочки и 36 мальчиков на команды с одинаковым числом участников, состоящие только из мальчиков или только из девочек. Какое наибольшее число человек может быть в каждой команде? Сколько команд получится?

24 2

36 2

24 2

18 2

12 2

12 2

6 2

9 3

6 3

3 3

3 3

2 2

1

1

1

1) 24 = 2³ · 3

2) 36 = 2² ∙ 3²

3) НОД (24;36) = 2² · 3 = 4 ∙ 3 = 12(чел) – в каждой команде

4) 24 : 12 = 2(к) — девочек

3) НОД (24;36) = 2³ · 3² = 6 ∙ 6 = 12(чел) – в каждой команде

5) 36 : 12 = 3(к) — мальчиков

6) 2 + 3 = 5(к) — всего

Ответ: в каждой команде может быть 12 человек; получится 5 команд.

Исправь ошибки и помоги в решении задачи

Ребята получили на новогодней ёлке одинаковые подарки. Во всех подарках вместе было 123 апельсина и 82 яблока. Сколько ребят присутствовало на ёлке? Сколько апельсинов и сколько яблок получил каждый?

82 2

123 3

41 41

41 41

1

1

1) 123 = 3 ∙ 41

2) 82 = 2 ∙ 41

3) НОД (123;82) = 41(чел) – присутствовали на ёлке

4) 123 : 41 = 3(шт) — апельсина

3) НОК (123;82) = 2 ∙ 3 ∙ 41 = 246(чел) – присутствовали на ёлке

5) 82 : 41 = 2(шт) — яблока

Ответ: 41 человек присутствовало на ёлке; каждый получил 3 апельсина и 2 яблока.

Самостоятельная работа

I вариант

II вариант

• НОД(35;63)
• НОК(8;24;40)

• НОД(27;48)
• НОК(14;35;20)

Взаимопроверка

I вариант

• НОД(35;63) = 7
• НОК(8;24;40) = 2³ ∙ 3 ∙ 5 = 120

II вариант

35 5 63 3 8 2 24 2 40 2

• НОД(27;48) = 3
• НОК(14;35;20) = 2² ∙ 5 ∙ 7 = 140

7 7 21 3 4 2 12 2 20 2

27 3 48 2 14 2 35 5 20 2

9 3 24 2 7 7 7 7 10 2

1 7 7 2 2 6 2 10 2

3 3 12 2 1 1 5 5

1 1 3 3 5 5

1 1

1 6 2 1

3 3

1

35 = 5 ∙ 7;

270 = 3³;

63 = 3² · 7;

480 = 2 · 3;

8 = 2³;

24 = 2³∙ 3;

14 = 2 ∙ 7;

40 = 2³∙ 5

35 = 5 · 7;

20 = 2²∙ 5

4

Я умею. ..

Я знаю…

… алгоритм

нахождения

наибольшего

общего делителя

… находить

наибольший

общий делитель

… алгоритм

нахождения

наименьшего

общего кратного

… находить

наименьшее

общее кратное

У меня

получится…

тест

Тест

У

Верно!

Верно!

НОК (45; 30)

НОД (48; 84)

М

Ответы :

Ответы :

6

4

12

90

15

60

НОК (25; 15)

Н

Верно!

Верно!

И

НОД (80; 64)

Ответы :

Ответы :

32

5

375

20

16

75

Верно!

Верно!

НОК (16; 24)

Ц

А

НОД (72; 120)

Ответы :

Ответы :

12

48

16

72

24

72

Домашнее задание

1 группа: Подготовить проект о Пифагоре

2 группа: Если участники демонстрации построятся по 10 человек в ряд, то один человек останется лишним. Если они построятся по 9 человек в ряд, то опять один останется лишним. То же самое произойдёт, если они построятся по 8, 7, 6, 5, 4, 3, 2 человека в ряд. Всего их меньше пяти тысяч, сколько их?

3 группа: Длина комнаты 575см, ширина – 375см. Пол комнаты нужно выложить декоративными плитками в форме квадрата. Каков наибольший возможный размер стороны такого квадрата? Сколько плиток такого размера понадобится?

4 группа: Отец и сын решили измерить шагами расстояние между двумя деревьями, для чего прошли одновременно от одного дерева до другого. Длина шага отца – 70см, сына – 56см. Найдите расстояние между этими деревьями, если известно, что следы совпали ровно 10 раз.

5 группа: На соревнованиях по настольному теннису участвовали равные по количественному составу команды, в которых всего 145 мальчиков и 87 девочек. Во всех командах было одинаковое число мальчиков и девочек. Сколько команд участвовало в соревнованиях? Сколько девочек и сколько мальчиков было в каждой команде?

6 группа: Одно колесо, сделав полный оборот, проходит путь 105 см, другое – 165 см. Найдите наименьшее расстояние, на котором оба колеса сделают по целому количеству оборотов.

Я утверждаю, что

2 * 2 = 5!

И могу это доказать!!!

Где ошибка?

Распределительное свойство

умножения нельзя переносить на деление .

Спасибо!

Наименьшее общее кратное примеры. Наименьшее общее кратное чисел 18 и 45, 6 и 8, 42 и 63, 210 и 350, 20 70 15.

Наименьшее общее кратное (НОК) двух целый чисел a и b есть наименьшее натуральное число, которое делиться и на a и b без остатка. Пример: наименьшее общее чисел 12 и 18 равен 36.

Наименьшее общее кратное чисел a и b

Найдем НОК чисел a и b с помощью разложения на простые множители.

НОК(a, b) = p₁^{max(k1, l1)} * p₂^{max(k2, l2)}*. ..*p₂^{max(kn, ln)}

a = p₁^k1 * p₂^k2*…*p_n^kn;

b = p₁^l1 * p₂^l2*…*p_m^ln;

Наименьшее общее кратное чисел 6 и 8

НОК(6, 8) = 2^{max(1, 3)} * 3^{max(1, 0)}= 24

a = 6 = 2*3;

b = 8 = 2³

Наименьшее общее кратное чисел 18 и 45

НОК(18, 45) = 2^{max(1, 0)} * 3^{max(2, 2)}*5^{max(0, 1)} = 90

a = 18 = 2*3²;

b = 45 = 3²*5

Наименьшее общее кратное чисел 75 и 60

НОК(75, 60) = 2^{max(0, 2)} * 3^{max(1, 1)}*5^{max(2, 1)} = 300

a = 75 = 3*5²;

b = 60 = 2²* 3*5

Наименьшее общее кратное чисел 72 и 99

НОК(72, 99) = 2^{max(3, 0)} * 3^{max(2, 2)}*11^{max(0, 1)}= 792

a = 72 = 2³ * 3²;

b = 99 = 3²*11

Наименьшее общее кратное чисел 396 и 180

НОК(396, 180) = 2^{max(2, 2)} * 3^{max(2, 2)}*5^{max(0, 1)}*11^{max(1, 0)}= 1980

a = 396 = 2² * 3² * 11;

b = 180 = 2² * 3² * 5

Наименьшее общее кратное чисел 210 и 350

НОК(210, 350) = 2^{max(1, 1)}*3^{max(1, 0)} * 5^{max(1, 2)}*7^{max(1, 1)}= 1050

a = 210 = 2*3*5*7;

b = 825 = 2*5²*7

Наименьшее общее кратное чисел 45 и 135

НОК(45, 135) = 3^{max(2, 3)} * 5^{max(1, 1)}= 135

a = 45 = 3²*5;

b = 135 = 3³*5

Наименьшее общее кратное чисел 42 и 63

НОК(42, 63) = 2^{max(1, 0)} * 3^{max(1, 2)}* 7^{max(1, 1)}= 126

a = 42 = 2*3*7;

b = 63 = 3²*7

Наименьшее общее кратное чисел 34, 51 и 68

НОК(34, 51, 68) = 2^{max(1, 0, 2)} * 3^{max(0, 1, 0)}*17^{max(1, 1, 1)}= 204

a = 34 = 2*17;

b = 51 = 3*17;

c = 68 = 2² * 17

Наименьшее общее кратное чисел 168, 231 и 60

НОК(168, 231, 60) = 2^{max(3, 0, 2)} * 3^{max(1, 1, 1)}*5^{max(0, 0, 1)}*7^{max(1, 1, 0)}*11^{max(0, 1, 0)}= 9240

a = 168 = 2³ * 3 * 7;

b = 231 = 3 * 7 * 11;

c = 60 = 2² * 3 * 5

Наименьшее общее кратное чисел 20, 70 и 15

НОК(324, 111, 432) = 2^{max(2, 1, 0)} * 3^{max(0, 1, 0)}*5^{max(1, 1, 1)}*7^{max(0, 1, 0)}= 420

a = 20 = 2² * 5;

b = 70 = 2*5*7;

c = 15 = 3*5

Делители и кратные.

5 класс

1. Делители и кратные

Возьмем два числа:
12
и
18
12 делится на 2 , на 3 , на 4 , на 6 и на 12
18 делится на 2 , на 3 , на 6 , на 9 и на 18
Общие ( одинаковые, равные ) делители
Из чисел
2
,
3
и
6
2 3 6
наибольшим является
Наибольший общий делитель чисел 12 и 18 равен 6
НОД ( 12; 18 ) = 6
Разложим число 12 на простые множители
12 = 2 х 26 х 3
6 составное число , так как делится на 2 , на 3 и на 6
и может быть представлено как 2 х 3
Разложим число 18 на простые множители
18 = 2 х 39 х 3
9 составное число , так как делится на 3 и на 9
и может быть представлено как 3 х 3
Ищем пары одинаковых множителей . Такие пары есть
у чисел 2 и 3
НОД ( 12; 18 ) = 2 х 3 = 6
Алгоритм нахождения НОД нескольких натуральных
чисел
1. Разложить данные натуральные числа на простые
множители
В нашем примере 12 и 18
2. Определить группы одинаковых множителей
В нашем примере
2и3
3. Составить произведение из множителей групп,
любого из данных натуральных чисел
Пусть это будет
12 = 2 х22 хх3 3
4. Найти их произведение
В примере
=6
Решим пример
Найти
НОД (30 , 36 ,48 )
30 = 3 х 10
2 х 5
36= 2 4х 2 х 39 х 3
48= 3 6х 2 х 2 8х 2 х 2
Простые числа:
10 = 2 х 5
4= 2 х 2
9= 3 х 3
6= 2 х 3
8=2 х 2 х 2
3 2 5
НОД (30 , 36 ,48 ) = 3 х 2 = 6
Решим пример
Найти
НОД ( 36 ,48 )
36= 24х 2 х 39х 3
48 = 36х 2х 28х 2 х 2
Простые числа:
4= 2 х 2
9= 3 х 3
6= 2 х 3
8=2 х 2 х 2
3 2
НОД ( 36 ,48 ) = 3 х 2 х 2 = 12
Возьмем два числа:
12
и
18
Числа кратные 12 делятся на 12
12 , 24 , 36 , 48 , 60 , 72 , 84 , 96 , 108 , 120 , ….
Числа кратные 18 делятся на 18
18 , 36 , 54 , 72 , 90 , 108 , 126 , 134 ,152 , ….
Выделим общие кратные для 12 и 18
36
72
Наименьшее общее кратное
108
36
НОК (12 , 18 ) = 36
Разложим 12 и 18 на простые множители
12 = 2 х 2 х 3
12 раскладывается на две
18 = 2 х 3 х 3
18 раскладывается
2
и одну
на две
3
3
и одну
2 х 2 х 3 х 3
12
Н О К ( 12 , 18 ) = 2 х 2 х 3 х 3 = 36
2
Алгоритм нахождения НОК
1. Разложить данные числа на простые множители
В нашем примере 12 и 18
2. Выписать разложение одного из них
В нашем примере
12
3. Добавить недостающие множители из разложений
остальных чисел
В нашем примере добавили 3
4. Найти произведение этих множителей
Решим пример
Найти НОК ( 30 , 36 , 48 )
30 = 5 х 3 х 2
36 = 3 х 3 х 2 х 2
48 = 3 х 2 х 2 х 2 х 2
5 х 3 х 2
3 х 2 х 2 х 2 х 2
3 х 3 х 2 х 2
Разложим данные числа
на простые множители
Возьмем , например ,
число 48
Примерим разложение
числа 36
Примерим разложение
числа 30
х 3
НОК ( 30, 36, 48 ) = 5 х 32 х 24 = 720

Алгоритм Евклида — нахождение наибольшего общего делителя

Алгоритм Евклида – это алгоритм нахождения наибольшего общего делителя (НОД) пары целых чисел.

Наибольший общий делитель (НОД) – это число, которое делит без остатка два числа и делится само без остатка на любой другой делитель данных двух чисел. Проще говоря, это самое большое число, на которое можно без остатка разделить два числа, для которых ищется НОД.

Алгоритм нахождения НОД делением

1. Большее число делим на меньшее.
2. Если делится без остатка, то меньшее число и есть НОД (следует выйти из цикла).
3. Если есть остаток, то большее число заменяем на остаток от деления.
4. Переходим к пункту 1.

Пример:
Найти НОД для 30 и 18.
30 / 18 = 1 (остаток 12)
18 / 12 = 1 (остаток 6)
12 / 6 = 2 (остаток 0)
Конец: НОД – это делитель 6.
НОД (30, 18) = 6

a = 50
b = 130
 
while a != 0 and b != 0:
    if a > b:
        a = a % b
    else:
        b = b % a
 
print(a + b)

В цикле в переменную a или b записывается остаток от деления. Цикл завершается, когда хотя бы одна из переменных равна нулю. Это значит, что другая содержит НОД. Однако какая именно, мы не знаем. Поэтому для НОД находим сумму этих переменных. Поскольку в одной из переменных ноль, он не оказывает влияние на результат.

Алгоритм нахождения НОД вычитанием

1. Из большего числа вычитаем меньшее.
2. Если получается 0, то значит, что числа равны друг другу и являются НОД (следует выйти из цикла).
3. Если результат вычитания не равен 0, то большее число заменяем на результат вычитания.
4. Переходим к пункту 1.

Пример:
Найти НОД для 30 и 18.
30 — 18 = 12
18 — 12 = 6
12 — 6 = 6
6 — 6 = 0
Конец: НОД – это уменьшаемое или вычитаемое.
НОД (30, 18) = 6

a = 50
b = 130
 
while a != b:
    if a > b:
        a = a - b
    else:
        b = b - a
 
print(a)

Функция вычисления НОД

def gcd(a, b):
    while a != b:
        if a > b:
            a = a - b
        else:
            b = b - a        
    print(a)

Блок-схема алгоритма Евклида

Примечание. В модуле math языка программирования Python есть функция gcd(), вычисляющая наибольший общий делитель двух чисел.

>>> import math
>>> math.gcd(30, 18)
6

Геометрическая серия

А геометрическая серия это ряд чьи родственные последовательность геометрический. Это результат добавления термины из геометрическая последовательность .

Пример 1:

Конечная геометрическая последовательность: 1 2 , 1 4 , 1 8 , 1 16 , … , 1 32768

Связанные конечные геометрические ряды: 1 2 + 1 4 + 1 8 + 1 16 + … + 1 32768

Написано в сигма-нотации: ∑ k знак равно 1 15 1 2 k

Пример 2:

Бесконечная геометрическая последовательность: 2 , 6 , 18 , 54 , . ..

Связанные бесконечные геометрические серии: 2 + 6 + 18 + 54 + …

Написано в сигма-нотации: ∑ п знак равно 1 ∞ ( 2 ⋅ 3 п — 1 )

Конечный геометрический ряд

Чтобы найти сумму конечного геометрического ряда, используйте формулу
S п знак равно а 1 ( 1 — р п ) 1 — р , р ≠ 1 ,
где п это количество терминов, а 1 это первый член и р это обычное отношение .

Пример 3:

Найдите сумму первых 8 члены геометрического ряда, если а 1 знак равно 1 а также р знак равно 2 .

S 8 знак равно 1 ( 1 — 2 8 ) 1 — 2 знак равно 255

Пример 4:

Находить S 10 , десятая частичная сумма бесконечного геометрического ряда 24 + 12 + 6 + … .

Сначала найдите р .

р знак равно а 2 а 1 знак равно 12 24 знак равно 1 2

Теперь найдите сумму:

S 10 знак равно 24 ( 1 — ( 1 2 ) 10 ) 1 — 1 2 знак равно 3069 64

Пример 5:

Оценивать.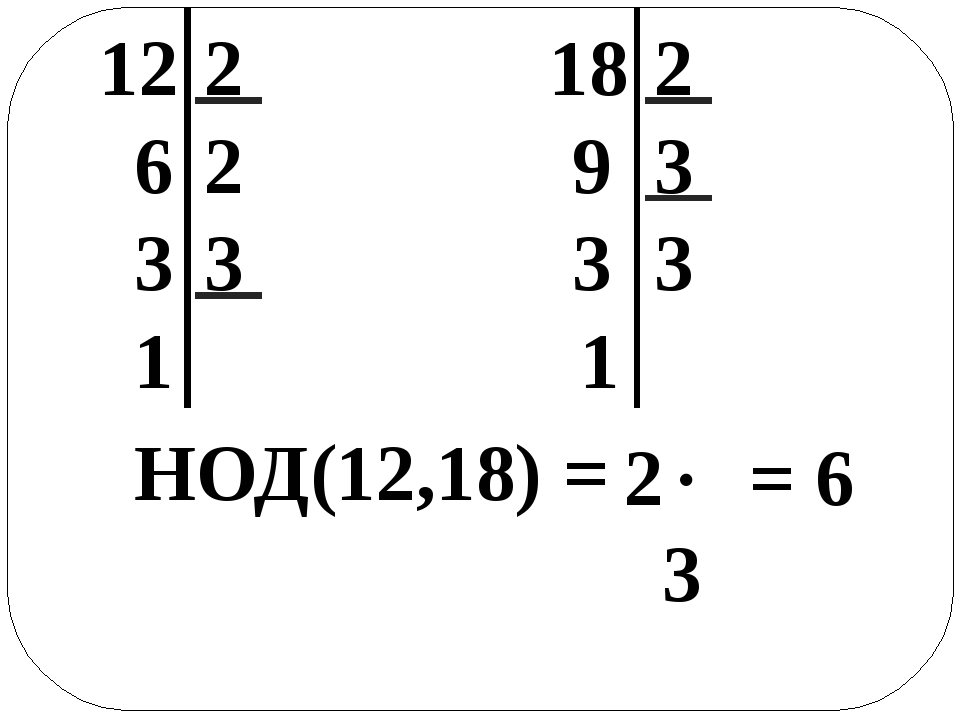

∑ п знак равно 1 10 3 ⋅ ( — 2 ) п — 1

(Вы находите S 10 для сериала 3 — 6 + 12 — 24 + … , обыкновенное отношение которого — 2 .)

S п знак равно а 1 ( 1 — р п ) 1 — р S 10 знак равно 3 [ 1 — ( — 2 ) 10 ] 1 — ( — 2 ) знак равно 3 ( 1 — 1024 ) 3 знак равно — 1023

Бесконечная геометрическая серия

Чтобы найти сумму бесконечного геометрического ряда, имеющего отношения с абсолютная величина меньше единицы, используйте формулу, S знак равно а 1 1 — р ,
где а 1 это первый член и р это обычное отношение.

Пример 6:

Найдите сумму бесконечного геометрического ряда
27 + 18 + 12 + 8 + … .

Первая находка р :

р знак равно а 2 а 1 знак равно 18 27 знак равно 2 3

Затем найдите сумму:

S знак равно а 1 1 — р S знак равно 27 1 — 2 3 знак равно 81 год

Пример 7:

Найдите сумму бесконечного геометрического ряда
8 + 12 + 18 + 27 + . .. если он существует.

Первая находка р :

р знак равно а 2 а 1 знак равно 12 8 знак равно 3 2

С р знак равно 3 2 не меньше единицы, ряды не сходятся.То есть в нем нет суммы.

Найдите сумму, среднее и среднее значение и диапазон 6,12,18,24,30,36,42,4 Tiger Algebra Solver

В этом разделе мы рассмотрим определение и расчет различных статистических показателей. Мы будем использовать следующий набор данных для выполнения указанных расчетов.

Набор данных: (6,12,18,24,30,36,42,4)

Сумма

Сумма. Совокупность группы чисел. Формула выглядит так: Sum =, где символ ∑ представляет собой сложение всех значений данных.

1. 0 + 6 = 6
2. 6 + 12 = 18
3. 18 + 18 = 36
4. 36 + 24 = 60
5. 60 + 30 = 90
6. 90 + 36 = 126
7. 126 + 42 = 168
8. 168 + 4 = 172

Суммируя 8 введенных чисел, мы получаем сумму 172 ( Словами: сто семьдесят два )

Среднее арифметическое (простое среднее)

Определение: совокупность (сумма) всех значений данных, деленная на количество точек данных.

Где µ представляет собой среднее значение генеральной совокупности, а ∑ представляет собой сумму всех значений данных, а N представляет количество значений данных.Если набор данных относится к выборке (части генеральной совокупности), расчет остается тем же, но символы другие. Это важно, потому что это указывает любому, имеем ли мы дело с генеральной совокупностью или выборкой. Набор данных всегда имеет среднее значение и уникален.

Найти среднее значение

Чтобы найти среднее значение, разделите сумму на количество значений.
В нашем случае на предыдущем шаге мы обнаружили, что сумма равна 172, и мы можем подсчитать 8 значений, так что:

Среднее = 172/8 = 21.5

Медиана

Определение: среднее (центральное) значение набора данных после того, как данные были упорядочены от низкого до высокого значения. То есть 50% значений данных ниже среднего значения, а 50% значений данных выше среднего значения. Можно применить простую формулу. Положение (P) медианы: P =. Если n количество точек данных нечетное, медианное значение является одной из точек данных. Если n четно, то медиана — это среднее значение данных непосредственно под и над вычислением позиции.В наборе данных всегда есть медиана, и она уникальна.

Найдите значение медианы

Чтобы найти значение медианы, мы начинаем с сортировки или расположения наших чисел в порядке возрастания или убывания.

4,6,12,18,24,30,36,42

Имея четное (8) количество значений, медиана является промежуточной точкой между двумя средними числами.
В нашем случае два средних числа: 18 и 24

(18 + 24) / 2

Медиана = 21 ( Словами: двадцать один )

Диапазон

Числовая разница между максимальным и минимальным значениями набора данных.
R = максимальное — минимальное значения

Найти диапазон

Используя наш отсортированный список чисел
4,6,12,18,24,30,36,42
, мы вычитаем первое (наименьшее / мин) из последнего ( наибольший / макс.)
Диапазон = 42-4 = 38

Разница

Определение: среднее квадратов разностей от среднего значения набора данных. Это мера разброса набора данных от среднего.

В теории вероятностей и статистике дисперсия измеряет, насколько далеко распределен набор чисел.Нулевое отклонение означает, что все значения идентичны.

Найдите дисперсию

Чтобы вычислить дисперсию, выполните следующие действия:

1. Найдите среднее значение (простое среднее чисел). Мы сделали это выше и нашли, что оно равно 21,5
2. Теперь для каждого числа: вычтите Среднее и возведите результат в квадрат (квадрат разницы).
   • (4-21,5) ² = 306,25
   • (6-21,5) ² = 240,25
   • (12-21,5) ² = 90.25
   • (18-21,5) ² = 12,25
   • (24-21,5) ² = 6,25
   • (30-21,5) ² = 72,25
   • (36-21,5) ² = 210,25
   • (42-21,5) ² = 420,25
3. Найдите среднее значение этих квадратов разностей.
   • 0 + 306,25 = 306,25
   • 306,25 + 240,25 = 546,5
   • 546,5 + 90,25 = 636,75
   • 636,75 + 12,25 = 649
   • 649 + 6,25 = 655,25
   • 655,25 + 7212,5 = 727.25 = 937,75
   • 937,75 + 420,25 = 1358

   Сумма 7 квадратов разностей составляет 1358
   Теперь мы можем рассчитать дисперсию как 1358/7 = 194

Стандартное отклонение

Определение: квадратный корень из дисперсии.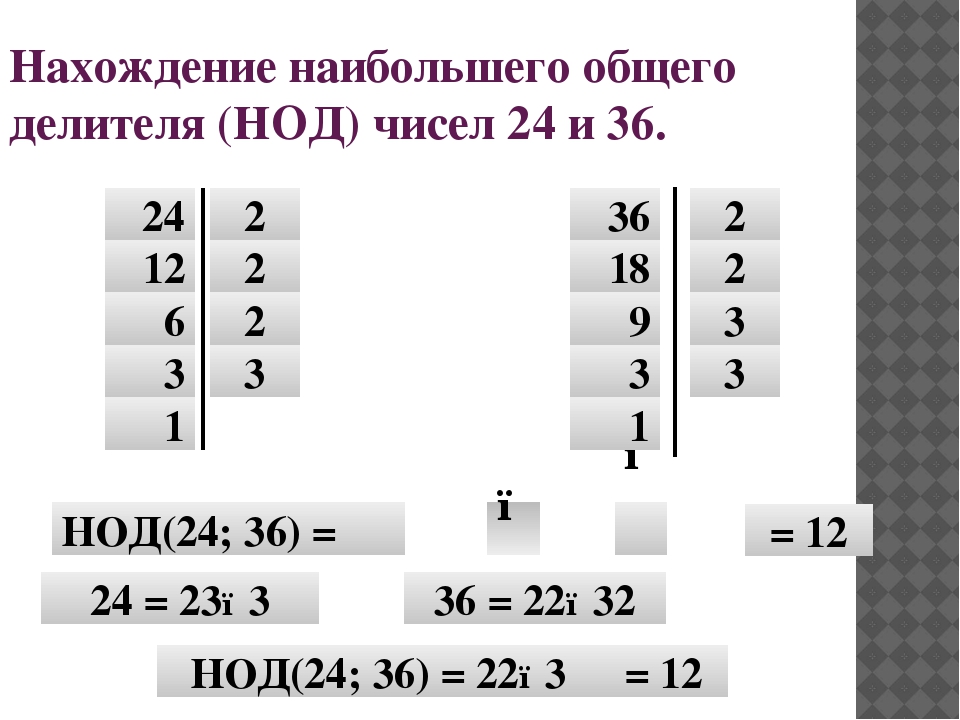 Он измеряет разброс набора данных от среднего. Обратите внимание, что единица измерения стандартного отклонения такая же, как и у данных. То есть, если данные указаны в футах, стандартное отклонение также будет в футах.Это неверно для дисперсии.

В статистике стандартное отклонение (SD, также представленное греческой буквой сигма, σ) — это мера, которая используется для количественной оценки степени вариации или дисперсии набора значений данных.

Стандартное отклонение — это положительный квадратный корень из дисперсии

√ (194) = 13,93

Калькулятор остатка

Этот калькулятор частного и остатка помогает вам разделить любое число на целое и вычислить результат в виде целых чисел.В этой статье мы объясним вам, как использовать этот инструмент и каковы его ограничения. Мы также предоставим вам пример, который лучше проиллюстрирует его назначение.

Дивиденды, делитель, частное и остаток

Когда вы выполняете деление, вы обычно можете записать эту операцию следующим образом:

а / п = д + р / п

где:

• — это начальное число, которое вы хотите разделить, называемое делимым .
• n — это число, на которое вы делите; он называется делителем .
• q — результат деления с округлением до ближайшего целого числа; это называется частным .
• r — это остаток этой математической операции.

При выполнении деления с остатками на нашем калькуляторе важно помнить, что все эти значения должны быть целыми числами. В противном случае результат будет правильным с точки зрения формул, но не будет иметь математического смысла.

Не забудьте проверить наш калькулятор по модулю для практического применения калькулятора с остатками.

Как рассчитать остаток

1. Начните с записи вашей проблемы. Например, вы хотите разделить 346 на 7.
2. Решите, какое из чисел является делимым, а какое — делителем. Делимое — это число, над которым выполняется операция — в данном случае 346. Делитель — это число, которое фактически «выполняет работу», в данном случае 7.
3. Выполните деление — вы можете использовать любой калькулятор, какой захотите. Вы получите результат, который, скорее всего, не является целым числом — в этом примере 49.4285714.
4. Округлите это число в меньшую сторону. В нашем примере вы получите 49.
5. Умножьте число, полученное на предыдущем шаге, на делитель. В нашем случае 49 * 7 = 343 .
6. Вычтите число из предыдущего шага из вашего дивиденда, чтобы получить остаток. 346 - 343 = 3 .
7. Вы всегда можете воспользоваться нашим калькулятором с остатками и сэкономить время 🙂

FAQ

Как вы решаете китайские задачи теоремы об остатках?

1. Убедитесь, что у вас есть неизвестное , равное двум или более различным модулям , например.грамм. x = d mod a, e mod b и f mod c.
2. Убедитесь, что все модули имеют одинаковый наибольший общий делитель .
3. Умножаем каждый по модулю на все, кроме одного, по модулю , пока не будут найдены все комбинации . Для указанных выше модулей это будет: b c, a c, a * b.
4. Разделите каждое число на пропущенный модуль . Если он равен остатку от этого модуля, например (b * c) / a = d, оставьте число как есть.
5. Если остаток не равен остатку по модулю, используйте метод проб и ошибок, чтобы найти положительное целое число, чтобы умножить его на так, чтобы шаг 4 стал истинным.
6. Сложите все числа вместе, как только шаг 4 верен для всех комбинаций.

Какие еще уловки?

Полезно запомнить некоторые оставшиеся ярлыки, чтобы сэкономить ваше время в будущем. Во-первых, если число делится на 10 , то остаток составляет всего последней цифры этого числа . Точно так же, если число делится на 9, складывайте каждую из цифр друг с другом, пока не останется одно число (например, 1164 станет 12, которое, в свою очередь, станет 3), которое является остатком.Наконец, вы можете умножить десятичную дробь частного на делитель, чтобы получить остаток.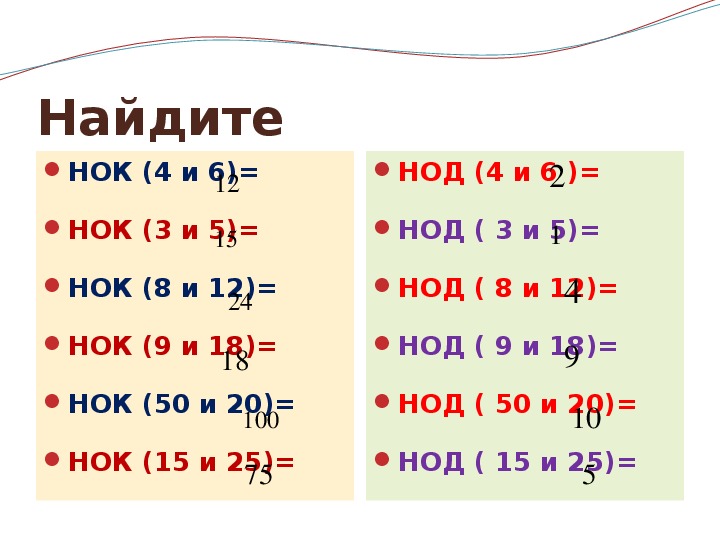

Как интерпретировать остаток?

Изучение того, как вычислить остаток, включает , многие из которых в реальном мире используют , и это то, чему вас учат школа, что вы обязательно будете использовать в своей повседневной жизни. Допустим, вы купили 18 пончиков для своего друга, но появилось только 15 из них, у вас осталось 3 . Или сколько денег у вас осталось после покупки пончиков? Если максимальное количество обезьян в бочке — 150, а в районе 183 обезьяны, сколько обезьян будет в меньшей группе?

Как превратить остаток в десятичную дробь?

1. Настройте деление, добавив десятичный знак, а затем ноль после столбца единицы делимого (если ваш дивиденд уже является десятичным, добавьте дополнительный ноль в конец).
2. Выполните деление как обычно , пока не останется остаток.
3. Вместо того, чтобы писать остаток после частного, переместите остаток выше добавленного вами нуля .
4. Если есть остаток от этого деления, добавьте еще один ноль к делимому и прибавьте к нему остаток.
5. Продолжайте таким же образом до : либо нет остатка, цифра или цифры повторяются бесконечно, либо вы достигнете желаемой степени точности (3 десятичных знака обычно нормально).
6. Результат после десятичной точки — это остаток в виде десятичной дроби.

Что такое частное и остаток?

Частное составляет , количество раз, когда деление завершается полностью , а остаток — это сумма, которая остается , которая не полностью входит в делитель . Например, 127, разделенное на 3, составляет 42 R 1, поэтому 42 — это частное, а 1 — остаток.

Как записать остаток в виде дроби?

После того, как вы нашли остаток от деления, вместо R, за которым следует остаток после частного, просто запишите дробь, где остаток делится на делитель исходного уравнения . Это так просто!

Как писать остатки?

Есть 3 способа записи остатка: с R, как дробная, и как десятичная . Например, 821, разделенное на 4, будет записано как 205 R 1 в первом случае, 205 ¹ / ₄ во втором и 205,25 в третьем.

Какой остаток от деления 26 на 6?

Остаток 2 . Чтобы решить эту проблему, найдите наибольшее кратное 6, которое меньше 26.В данном случае это 24. Затем вычтите 24 из 26, чтобы получить остаток, который равен 2.

Каков остаток от деления 599 на 9?

Остаток 5 . Чтобы вычислить это, сначала разделите 599 на 9, чтобы получить наибольшее кратное 9 перед 599. 5/9 <1, поэтому перенесите 5 в десятки, 59/9 = 6 r 5, поэтому перенесите 5 в цифры. 59/9 = 6 r 5 снова, поэтому наибольшее кратное 66. Умножьте 66 на 9, чтобы получить 594, и вычтите это из 599, чтобы получить 5, остаток.

Как рассчитать остаток от деления 24 на 7?

1. Вычтите 7 из 24 несколько раз , пока результат не станет меньше 7.
2. 24 минус 3 умножить на 7 равно 3.
3. Оставшееся число, 3 , является остатком.
4. Это может быть выражено как ³ / ₇ в дробной форме или как 0,42857 в десятичной форме.

Что такое делитель? — Определение, факты и пример

Что такое делитель?

Делитель — это число, которое делит другое число полностью или с остатком.

Делитель представлен в уравнении деления как:

Дивиденд ÷ Делитель = Частное.

Разделив 20 на 4, мы получим 5. Здесь 4 — это число, которое полностью делит 20 на 5 частей и называется делителем. Его уравнение деления —

.

Аналогично, если мы разделим 20 на 5, мы получим 4. Таким образом, 4 и 5 являются делителями 20.

Делитель и множители

Делитель — это любое число, которое делит другое число. Однако множитель — это делитель, который делит число целиком и не оставляет остатка.

Итак, все множители числа являются его делителями. Но не все делители будут факторами.

В приведенном выше примере 4 и 5 — множители 20.

В то время как, если мы разделим 20 на 3, оно не будет полностью разделить 20. Таким образом, 3 не является множителем 20.

Рассмотрим другой пример,

деление 15 на 5 дает 3. Здесь 5 — делитель. Кроме того, разделив 15 и разделив на 3, мы получим 5. Здесь 3 — делитель.

Множители и делители 15: 1, 3, 5, 15

Нахождение множителей числа

Чтобы найти множители числа, скажем 12, мы выполняем следующие шаги:

1.Начните с 1 и запишите факты умножения так, чтобы произведение было 12, например 1 × 12.

2. Продолжайте тем же способом найти другие факты умножения, пока не дойдете до пары ближайших множителей или делителей, как указано:

1 × 12, 2 × 6, 3 × 4

3. Запишите все числа в факте умножения, поскольку они являются делителями числа 12.

4. Итак, делители числа 12 равны 1,2,3,4,6 и 12.

Различные способы представления делителя

Существуют разные стили выражения уравнения деления.На изображениях ниже показаны различные методы записи делителя:

Особые случаи

1. Число 1 является делителем всех чисел.

Причина : Когда делитель равен 1, то частное совпадает с делимым.

Посмотрите на приведенные примеры,

34 1 = 34

15 1 = 15

2. Само число всегда является одним из делителей числа.

Причина : Когда делитель совпадает с делимым, тогда ответ на такое деление всегда 1.

Посмотрите на приведенные примеры,

34 34 = 1

15 15 = 1

3. Когда делитель меньше делимого, ответ будет не целым, а десятичным числом.

Например,

510 = 0,5

Интересные факты Если мы удвоим делитель, частное будет половиной.

Нахождение GCF и LCM с помощью метода Cake

Сегодняшний урок математики в моем седьмом классе был посвящен нахождению наибольшего общего множителя и наименьшего общего кратного пары чисел.

Я начал со сбора исходной информации о том, что студенты уже знали о GCF и LCM. С небольшой помощью студенты смогли придумать определения для каждого из них и описали метод, который они использовали в прошлом, чтобы найти наибольший общий множитель и наименьшее общее кратное двух чисел.

Раньше ученики учились перечислять все множители двух чисел и находить наибольшее общее из них. Точно так же, чтобы найти наименьшее общее кратное, класс научился перечислять кратные числа, пока они не нашли одно общее.

Мы рассмотрели примеры нахождения GCF и LCM «старой школой», перечислив множители и кратные чисел и найдя те, которые у них общие.

Затем мы обсудили ограничения этого метода нахождения GCF и LCM, в основном тот факт, что если бы я дал им гораздо большие числа, было бы очень много времени, чтобы перечислить все факторы или перечислить кратные, пока они не найдут один общий. Итак … Затем я познакомил класс с «методом торта». (Многие люди называют это методом лестницы или лестницей деления, но я впервые увидел, что это называется методом торта в книге Даники МакКеллар «Математика не отстой», и я подумал, что это мило, так что это то, что я использую , так как напоминает перевернутый торт).

Метод пирога хорош по нескольким причинам… вы можете приготовить один «пирог» и использовать его для поиска как GCF, так и LCM, и это сэкономит вам много времени по сравнению с более традиционным методом.

Для тех, кто раньше не видел этот метод, вы начинаете с написания чисел, для которых вы пытаетесь найти GCF и LCM рядом друг с другом, и рисуете вокруг них «слой торта». Затем вы находите ЛЮБОЙ общий множитель двух чисел и записываете этот множитель слева от них. Затем вы делите числа на их общий множитель и записываете частные под числами. Затем этот процесс повторяется с новыми двумя числами внутри торта. Вы делаете это столько раз, сколько необходимо, пока два числа внизу не станут взаимно простыми. Чтобы найти наибольший общий множитель, вы умножаете все числа слева от торта. Чтобы найти НОК, я говорю студентам нарисовать большую букву «L» вокруг торта и перемножить все числа в букве «L».

Вот пример, который мы сделали в классе, чтобы найти GCF и LCM 24 и 36.

У нас была дискуссия о том, как разные люди могут делать разные «торты», выбирая разные факторы, но что окончательный ответ будет одним и тем же. Мы также обсудили, что чем больше коэффициент, тем меньше будет слоев торта.

В целом урок прошел отлично! Студентам понравился этот «новый» метод поиска GCF и LCM!

Я с нетерпением жду возможности показать им, как метод торта можно использовать и для упрощения дробей. (Сделайте торт для числителя и знаменателя, и два относительно простых числа внизу будут упрощенной дробью. Например, приведенный выше пример пирога можно было использовать для упрощения дроби 24/36 до 2/3.)

Пр. 3.6, 1 — Найдите HCF из (a) 18, 48 (b) 30, 42 (c) 18, 60 (d) 27, 63

Последнее обновление: 3 января 2019 г. , автор: Teachoo

---

Выписка

Пр. 3.6, 1 Найдите HCF из следующих чисел: (a) 18, 48 18 = 2 × 3 × 3 48 = 2 × 2 × 2 × 2 × 3 HCF 18 и 48 = 2 × 3 = 6 Пр. 3.6, 1 Найдите HCF из следующих чисел: (b) 30, 42. Пр. 3.6, 1 Найдите HCF следующих чисел: (b) 30, 42 Пр. 3.6, 1 Найдите HCF из следующих чисел: (c) 18, 60. ЛКФ 18 и 60 лет 18 = 2 × 3 × 3 60 = 2 × 2 × 3 × 5 HCF 18 и 60 = 2 × 3 = 6 Пр. 3.6, 1 Найдите HCF из следующих чисел: (d) 27, 63 HCF из 27 и 63. 27 = 3 × 3 × 3 63 = 3 × 3 × 7 HCF 27 и 63 = 3 × 3 = 9 Пр. 3.6, 1 Найдите HCF из следующих чисел: (e) 36, 84 HCF из 36 и 84. 36 = 2 × 2 × 3 × 3 84 = 2 × 2 × 3 × 7 HCF из 36 и 84 = 2 × 2 × 3 = 12 Пр. 3.6, 1 Найдите HCF из следующих чисел: (f) 34, 102 HCF из 34 и 102. 34 = 2 × 17 102 = 2 × 3 × 17 HCF 34 и 102 = 2 × 17 = 34 Пример 3.6, 1 Найдите HCF из следующих чисел: (g) 70, 105, 175 HCF из 70, 105, 175. 70 = 2 × 5 × 7 105 = 3 × 5 × 7 175 = 5 × 5 × 7 HCF 70, 105, 175 = 5 × 7 = 35 Пример 3.6, 1 Найдите HCF из следующих чисел: (h) 91, 112, 49 HCF из 91, 112, 49. 91 = 7 × 13 112 = 2 × 2 × 2 × 2 × 7 49 = 7 × 7 HCF из 91, 112, 49 = 7 Пр. 3.6, 1 Найдите HCF следующих чисел: (i) 18, 54, 81. 18 = 2 × 3 × 3 54 = 2 × 3 × 3 × 3 81 = 3 × 3 × 3 × 3 HCF из 18, 54, 81 = 3 × 3 = 9 Пр. 3.6, 1 Найдите HCF следующих чисел: (j) 12, 45, 75. 12 = 2 × 2 × 3 45 = 3 × 3 × 5 75 = 3 × 5 × 5 HCF из 12, 45, 75 = 3

Показать больше

Сокращение дробей до наименьших значений

Рассмотрим следующие две дроби:

¹ /2 и ² /4

Эти дроби являются эквивалентными дробями. Они оба представляют одинаковую сумму. Одна половина апельсина равна двум четвертям апельсина. Однако только одна из этих дробей записана в младших членах.

Дробь имеет наименьшее значение, если числитель и знаменатель не имеют общего множителя , кроме 1.

Факторы 2 равны 1 и 2 .
Множители 4 равны 1, 2 и 4.
2 и 4 имеют общий делитель: 2.

Мы можем уменьшить эту дробь, разделив числитель и знаменатель на их общий множитель, 2.

^{2 2} /4 2 = ¹ /2

1 и 2 не имеют общего множителя, кроме 1, поэтому дробь находится в младших членах.

Метод № 1: Общие факторы

(медленный и устойчивый метод)

Давайте попробуем другой пример:

³⁰ /36

Есть ли у 30 и 36 общие факторы, кроме 1?

Множители 30 равны 1, 2, 3, 5, 6 , 10, 15, 30.
Множители 36 равны 1, 2, 3, 4, 6 , 9, 12 , 18, 36.
30 и 36 имеют три общих множителя: 2, 3, и 6.

Давайте посмотрим, что произойдет, если мы разделим числитель и знаменатель на их наименьший общий множитель, 2. (Фактически, мы бы знали, что у них есть 2 в качестве общего множителя без необходимости вычислять все их множители, потому что и 30, и 36 — четные числа.)

^{30 2} /36 2 = ¹⁵ /18

Готово? Есть ли у 15 и 18 общие факторы, кроме 1?

Множители 15 равны 1, 3, 5, 15.
Факторы 18 равны 1, 2, 3, 6, 9, 18.
15 и 18 имеют один общий множитель: 3.

Еще раз, мы делим числитель и знаменатель на их общий делитель, 3 .

^{15 3} /18 3 = ⁵ /6

Готово? Есть ли у 5 и 6 общие факторы, кроме 1?

Факторы 5 равны 1 и 5.
Факторы 6 равны 1, 2, 3 и 6.
5 и 6 не имеют общих множителей, кроме 1.

Этот метод сокращает дробь до наименьшего значения. , но до этой точки может потребоваться несколько шагов.Что бы произошло, если бы вместо деления числителя и знаменателя на их наименьший общий множитель мы начали с их наибольшего общего множителя?

Метод № 2: Наибольший общий множитель

(более эффективный метод)

Попробуем еще раз:

³⁰ /36

Есть ли у 30 и 36 общие множители, кроме 1?

Факторы 30 равны 1, 2, 3, 5, 6 , 10, 15.
Факторы 36 равны 1, 2, 3, 4, 6 , 9, 12, 18 .
30 и 36 имеют три общих множителя: 2, 3, и 6.
Наибольший общий множитель равен 6 .

Разделите числитель и знаменатель на наибольший общий множитель:

^{30 6} /36 6 = ⁵ /6

На этот раз требуется всего один шаг, чтобы получить тот же результат. Чтобы уменьшить дробь до наименьшего значения, разделите числитель и знаменатель на наибольший общий множитель .

Метод № 3: простые множители

(еще более эффективный метод)

Другой способ уменьшить дроби — разбить числитель и знаменатель до их простых множителей и удалить все простые множители, общие для них.Давайте сделаем этот пример еще раз, используя этот метод.

³⁰ /36
Простые множители 30 равны 2 x 3 x 5.
Простые множители 36 равны 2 x 2 x 3 x 3.
^{2 x 3 x 5} /2 x 2 x 3 x 3
Удаляем 2 x 3 , общие для числителя и знаменателя:
⁵ /2 x 3 = ⁵ /6

(Если подумать, это работает точно так же как последний метод.