Найдите объем тела полученного при вращении параболы y x 2: 1)Найдите объем тела,полученного при вращении параболы y=x^2 от точки x=0 до точки x=2 вокруг оси…

2.5. Вычисление работы переменной силы

Пусть тело движется под действием некоторой переменной силы F по прямой, причем направление силы совпадает с направлением движения, а работа А, произведенная силой F при перемещении тела из т.х=а по прямой ОХ в точку х=b той же прямой, может быть выражена (в случае когда F=F(x) есть непрерывная функции на [a; b]) с помощью определенного интеграла следующим образом:

. (1)

Пример 13. Рессора прогибается под нагрузкой 1,5 т на 1 см. Какую работу надо затратить для деформации рессора на 3 см? (Сила деформации пропорциональна величине деформации).

Решение: обозначим через х – величину деформации, т.к. F=kx, где k — коэффициент пропорциональности (коэффициент жесткости).

Известно, что при х=0,01 м F=1,500 (Н),

то , следовательно, .

По формуле (1) работа .

2.6. Вычисление центра тяжести плоской линии

Пусть на плоскости дана дуга АВ материальной линии, уравнение которой y=F(x), где F(x) — непрерывная на отрезке [a; b] функция, имеющая непрерывную производную

Координаты центра тяжести будут:

; , где s – длина дуги;

— дифференциал длины дуги (формула получена ранее).

Статические моменты дуги АВ:

; .

Если дуга АВ расположена симметрично относительно некоторой прямой, то ее центр тяжести непременно лежит на этой прямой.

Пример 14. Найти центр тяжести дуги, составляющей четверть окружности радиуса В.

Выбираем систему координат, как указано на рисунке. Уравнение окружности: , откуда ; ; .

Длина четверти окружности , т.к. дуга АВ симметрична относительно биссектрисы.

Если координаты угла y=x, то х=у, найдем у:

.

Ответ: .

2.7. Центр тяжести плоской фигуры

Рассмотрим плоскую материальную фигуру, ограниченную прямыми х=а, x=b (a<b) и кривыми y= , , где функции и непрерывны на и :

, , где (площадь фигуры).

Если фигура ограничена осью ОХ, прямыми х=а, х=b и кривой y=f(x), где f(x) – неотрицательная непрерывная на отрезках [a; b] ф ункция, то полученные формулы будут проще:

; .

Если фигура располагается симметрично относительно некоторой прямой, то центр тяжести ее лежит на этой прямой.

Пример 15. Найти координаты центра тяжести фигуры, ограниченной кривой и осями координат.

Т.к. данная фигура симметрична относительно биссектрисы I координатам угла, то ее центр тяжести лежит на этой прямой у=х, и следовательно, ;

Ответ:

3. Задания для самостоятельной работы

Задача I.

1. Вычислить (внесение функции под знак дифференциала).

1.1. 1.2.

1.3. 1.4.

1.5. 1.6.

1.7. 1.8.

1.9. 1.10.

1.11. 1.12.

1.13. 1.14.

1. 15. 1.16.

1.17. 1.18.

1.19. 1.20.

1.21. 1.22.

1.23. 1.24.

1.25. 1.26.

1.27. 1.28.

1.29. 1.30.

Задача 2.

Вычислить применением метода интегрирования по частям.

2.1. 2.2.

2.3. 2.4.

2.5. 2.6.

2.7. 2.8.

2.9. 2.10.

2.11. 2.12.

2.13. 2.14.

2.15. 2.16.

2.17. 2.18.

2.19. 2.20.

2.21. 2.22.

2.23. 2.24.

2.25. 2.26.

2.27. 2.28.

2. 29. 2.30.

Задача 3.

Вычислить универсальной подстановкой.

3.1. 3.2.

3.3. 3.4.

3.5. 3.6.

3.7. 3.8.

3.9 3.10.

3.11. 3.12.

3.13. 3.14.

3.15. 3.16.

3.17. 3.18.

3.19. 3.20.

3.21. 3.22.

3.23. 3.24.

3.25. 3.26.

3.27. 3.28.

3.29. 3.30.

Задача 4. (подстановкой)

4.1. 4.2.

4.3. 4.4.

4.5. 4.6.

4.7. 4.8.

4.9. 4.10.

4. 11. 4.12.

4.13. 4.14.

4.15. 4.16.

4.17. 4.18.

4.19. 4.20.

4.21. 4.22.

4.23. 4.24.

4.25. 4.26.

4.27. 4.28.

4.29. 4.30.

Задача 5.

Вычислить площадь плоской фигуры.

1. Вычислить площадь фигуры, ограниченной кривой , прямыми х=-0,5, х=1 и осью абсцисс.

2. Найти площадь фигуры, ограниченной кривой , прямыми , и осью ординат.

3. Найти площадь фигуры, заключенной между окружностью и прямыми 2у-5=0,

4. Найти площадь фигуры, ограниченной эллипсом , прямой и осью ординат.

5. Найти площадь фигуры, ограниченной ветвью гиперболы и прямыми х=1; х=5.

6. Вычислить площадь фигуры, ограниченной кривой и осью абсцисс от до .

7. Найти площадь фигуры, ограниченной кривой , прямыми , х=е и осью абсцисс.

8. Вычислить площадь фигуры, ограниченной параболой , прямыми х=-1, х=3 и осью абсцисс.

9. Найти площадь фигуры, ограниченной параболой , осями координат и прямой х=4.

10. Найти площадь фигуры, заключенной между прямыми у=2х, у=5х, х=2, х=6.

11. Найти площадь части гиперболы , отсекаемой от нее прямой х+у-4=0.

12. Найти площадь фигуры, отсекаемой от параболы прямой 5х-у-8=0.

13. Вычислить площадь фигуры, ограниченной параболой и прямой у=х.

14. Найти площадь фигуры, заключенной между параболами и .

15. Вычислить площадь фигуры, заключенной между параболами и .

16. Вычислить площадь фигуры, заключенной между кривыми и .

17. Найти площадь сегмента, отсекаемого прямой х+у-4=0 от круга, ограниченного окружностью . Проверить результат непосредственным вычислением.

18. Найти площадь фигуры, заключённой между параболой , касательной к ней в точке (3, 5) и осью Оу.

19. Найти площадь фигуры ограниченной линиями

20. Найти площадь фигуры, заключённой между параболой и касательными к ней в точках (0;-3) и (3;0).

21. Найти площадь фигуры ограниченной линиями

22. Вычислить площадь фигуры, заключённой между линиями

23. Найти площадь фигуры ограниченной линиями

24. Вычислить площадь фигуры, заключённой между линиями

25. Найти площадь фигуры, отсекаемой от параболы прямой

26. Вычислить площадь фигуры, заключенной между кривыми

27. Найти площадь фигуры ограниченной линиями

28. Вычислить площадь фигуры, заключённой между линиями

29. Вычислить площадь фигуры, заключенной между кривой и прямыми , где

30. Найти площадь фигуры ограниченной линиями

Задача 6.

Вычислить длину дуги.

6.1. y² = x³ от х=0 до х=5

6.2. y=ln sinx от х= до х=

6.3. 2у= x² -3 между точками пересечения с осью Ox

6.4. x= — t, y=t²+2 от t=1 до t=4

6.5. x=4(t-sint), y=4(1-cost) (длину дуги одной арки циклоиды)

6.6. =5sin

6.7. =sin³ от =0 до

6.8. y=lnx от х= до x=2

6.9. x= , y=2- (между точками пересечения с координатными осями)

6.10. (длину первого витка спирали Архимеда)

6.11. x= cost, y= sint от t=0 до t=ln

6.12. =1-cos

6.13. =2sin

6.14. =2sin³

6.15. x +y =9

6.16. =1+cos

6.17. x= — от y=1, до y=2

6.18. y= от x=-a, до x=a

6.19. x=acos³t; y=asin³t, от t=0 до t=2

6.20. =2acos

6.21. x=8sint+6cost; y=6sint-8cost, от t=0 до t=

6.22. 9y²=x(x-3)² между точками пересечения с осью OX

6. 23. y=ln(1-x²), заключенной между прямыми x= и x=

6.24. y²= (x-1)² , заключенной внутри параболы y²=

6.25. y²=x³, отсеченной прямой x=

6.26. x=e^tsint, y=e^tcost от t=0 до t=

6.27. =acos⁴

6.28. =

6.29. Найдите периметр фигуры, ограниченной линиями x²=(y+1)³ и y=4

6.30. Найдите длину кривой, заданной уравнением y=

Задача 7.

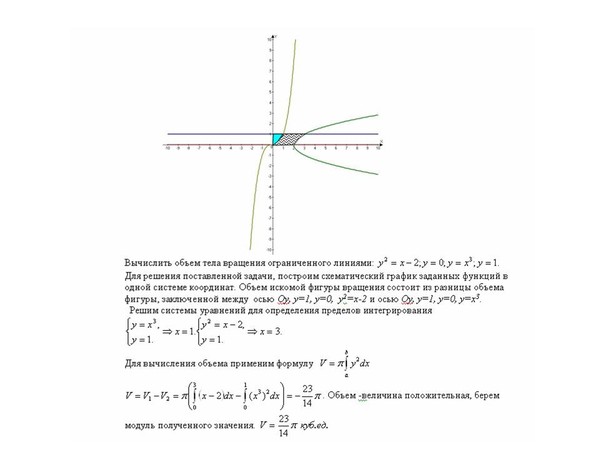
7.1. Вычислить объём тела, образованного вращением вокруг оси фигуры, ограниченной дугой кубической параболы y=x³-4x и осью абсцисс.

7.2. Определить объём тела, полученного в результате вращения вокруг оси ОХ фигуры, которая ограничена дугой окружности х²+y²=16, лежащей в I четверти, и прямыми х=1 и х=3.

7.3. Найти объём тела, образованного вращением эллипса 4x²+9y²=36 вокруг малой оси.

7.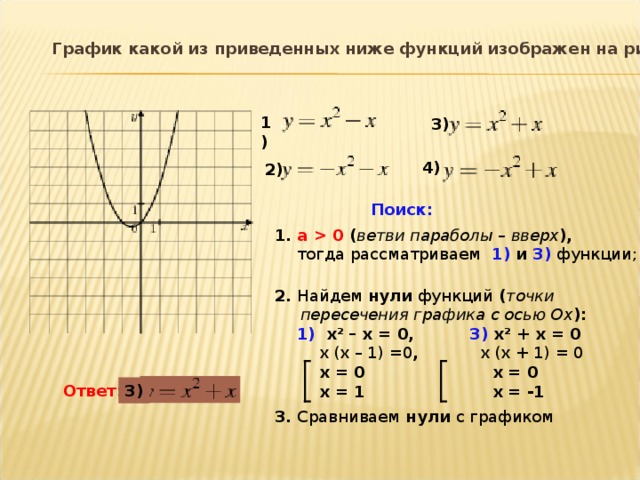 4. Фигура, ограниченная дугой эллипса и двумя прямыми, перпендикулярными к оси абсцисс и проходящими через фокусы эллипса, вращается вокруг оси ОХ. Определить объём тела вращения.

7.5. Найти объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной ветвью гиперболы x²-y²=1 и прямой х=3.

7.6. Найти объем тела, образованного вращением астероиды x=acos³t, y=asin³t вокруг оси ОХ.

7.7. Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной одной аркой циклоиды х=a(t-sint), y=a(1-cost) и отрезком оси абсцисс.

7.8. Найти объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной параболами y=2x² и y=x³.

7.9. Фигура, образованная в результате пересечения параболы y²=4x и прямой y=x, вращается вокруг оси Ох. Найти объём тела вращения.

7.10. Найти объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной параболой y²=2x и прямой 2х+2у-3=0.

7.11. Вычислить объем тела, образованного вращением общей части парабол y=x² и y²=8x: а)вокруг оси Ох; б)вокруг оси Оу.

7.12. Фигура, ограниченная кривыми y=tgx, y=ctgx и прямой x= , вращается вокруг оси OX. Найти объем тела вращения.

7.13. Найти объем тела, полученного в результате вращения вокруг оси OX сегмента, отсекаемого прямой х+у-2=0 от круга, граничная окружность которого x²+y²=4

7.14. Определить объем тела, образованного вращением вокруг оси ОY фигуры, ограниченной кривыми y=log₂x, y=log₄x и прямой y=1.

7.15. Фигура, лежащая в I четверти и ограниченная дугой окружности x²+y²=18, параболой 3y=x² и осью ординат, вращается вокруг оси Ох. Найти объем тела вращения.

7.1б. Фигура, лежащая в I четверти и ограниченная кривыми x²-у² = 3, xy=2 и прямой x=3 вращается вокруг оси Ох. Найти объем тела вращения.

7. 17. Круг радиуса 2 с центром в т. (7,0) вращается вокруг оси ОY. Определить объем полученного тела вращения.

7.18.Найдите объем тела, полученного вращением вокруг оси фигуры, ограниченной кривой y²=

7.19.Найдите объем тела. образованного вращением вокруг оси OY фигуры, ограниченной эллипсом

7.20.Найдите объем тела, образованного вращением вокруг оси OY фигуры, ограниченной кривой и прямыми y= и y=

7.21. Найдите объем, тела, полученного при вращении вокруг оси Оу криволинейной трапеции, ограниченной осью Ох и дугой параболы х=у(4-х).

7.22. Найдите объем тела. подученного от вращения вокруг оси Ох криволинейной трапеции, ограниченной линиями y=xe^x, y=0, x=1.

7.23. Вычислить объем тела, полученного от вращения вокруг оси Оу криволинейной трапеции, ограниченной кривой x²+y2/3=1

7.24. Вычислить объем тела, полученного от вращения фигуры, ограниченной линиями (y-3)²+3x=0, x=-3, вокруг оси абсцисс.

7.25. Вычислить объем тела, образованного вращением фигуры, ограниченной линиями xy=4, x=1, x=4, y=0, вокруг оси Ох.

7.26. Вычислить объем тела, полученного вращением астроиды вокруг оси ординат.

7.27. Вычислить объем тела, образованного вращением вокруг оси Ох одной полуволны синусоиды y=sinx.

7.28. Определить объем тела, отсеченного от круглого цилиндра плоскостью, проходящей через диаметр основания. Радиус основания равен R, высота тела равна Н.

7.29. Вычислить объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной кривой x=2(t-sint), y=2(1-cost) и отрезком [0;4 ] оси Ох.

7.30. Вычислить объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной линиями y=x², 9y=x² и y=1.

Задача 8.

8.1. Параболы y²=4ax от х=0 до х=8

8.2. Прямой у=3х от х=1 до х=3

8.3. Одной полуволны косинусоиды у=cosx.

8.4. Окружности х=acost, y=asint.

8. 5. Астроиды х=acos³t, y=asin³t.

8.6. Цепной линии y= от х=0 до х=2

8.7. Параболы y²=3+x, отсеченной прямой x=3

8.8. Полукубической параболы x= между точками пересечения с осями координат.

8.9. Синусоиды y=sinx от х=0 до х=

8.10. Астроиды

8.11. Круга вокруг оси Ох.

8.12. Цепной линии от х=-а до х=а (а>0).

8.13. Петли кривой х=9t², y=3t-9t³.

8.14. Кардиоиды вокруг полярной оси.

8.15. Кривой вокруг полярной оси.

8.16. Кривой вокруг полярной оси.

8.17. Кривой x²+y(y-2b)=0 вокруг оси Оу.

8.18. Найти поверхность кольца, образованного вращением круга x²+(y-b)²=a² вокруг оси Ох.

8.19. Кривой х²+у²=4х-3 вокруг оси Оу.

8.20. Кривой оси Ох.

8.21. Кривой х²+у²=6х-5 вокруг оси Оу.

8.22. Кривой 8у=х² вокруг оси Оу от т. (0;0) до т.(4;2).

8.23. Кривой вокруг полярной оси.

8.24. Кривой x=cos³t, y=sin³t вокруг оси Оу.

8.25. Кривой х²+у²=6у-5 вокруг Ох.

8.26. Кривой х²+у²=4у-3 вокруг Ох

8.27. Кривой 4х=у² (Ох) от т.(0;0) до т.(3

8.28. Кривой вокруг оси Оу.

8.29. Кривой х=3(t-sint) y=3(1-cost) от т.(0;0) до т.(6 ;0)

8.30. Лемнискаты вокруг полярной оси.

Задача 9.

9.1. Найти силу давления жидкости на вертикальную треугольную пластинку с основанием а и высотой h, погруженную в жидкость так, что вершина пластинки лежит на поверхности.

9.2. Скорость точки меняется по закону. Найти путь, пройденный точкой за первые девять секунд после начала движения.

9.3. Автомобиль, двигающийся со скоростью 48м/с., начинает тормозить и останавливается через 3с. Найти путь, пройденный автомобилем до полной остановки.

9.4. Реактивный самолет в течение 20с увеличил свою скорость от 360 до 720 м/с. Считая его движение равноускоренным, найти с каким ускорением летел самолет и какое расстояние пролетел он за это время.

9.5. С высоты 294м вертикально вниз брошено тело с начальной скоростью 19,6 ^M/с. Через сколько секунд тело упадет на землю? ( Ускорение силы тяжести принять равным 9,8м/с)

9.6. Найти работу, производимую при растяжении пружины на 5см, если известно, что сила, которая требуется для растяжения пружины, пропорциональна ее удлинении и что для удлинения пружины на I см требуется сила 1H.

9.7. Какую работу нужно затратить, чтобы выкачать воду из цилиндрического резервуара, радиус основания которого равен 3м, а высота равна 5m?

9.8. Найти работу, необходимую для выкачивания воды из конической воронки, обращенной вершиной вниз, если высота ее равна Н, а радиус основания r. Как изменится результат, если воронка будет обращена вершиной вверх?

9.9. Вычислить работу, которую надо затратить, чтобы выкачать воду из котла, имеющего форму полушара с радиусом, равным 1м.

9.10. Найти работу, необходимую для выкачивания воды из котла, имеющего форму полуцилиндра с радиусом основания r и высотой H.

9.11. Найти силу давления воды на прямоугольные ворота шлюза, ширина которых 25м, а глубина 18м, если их верхняя грань лежит на свободной поверхности воды. Определить также силу давления на нижнюю половину ворот шлюза.

9.12. Вычислить силу давления жидкости на вертикальный треугольный щит с

основанием а и высотой h, погруженный жидкость так, что основание щита лежит на её свободной поверхности.

9.13. Найти силу давления на плоскость полукруга с радиусом 6см, погруженного в воду вертикально, если его диаметр лежит на свободной поверхности воды.

9.14. Вертикальная пластина имеет форму трапеции, верхнее и нижнее основания которой соответственно равны 80см и 50см, а высота 20м. Вычислить силу давления на всю плотину.

9.15. Определить массу стержня длины 50см, если его линейная плотность меняется по закону , где x – расстояние от одного из концов стержня.

9.16. Цилиндр с высотой 80см и радиусом основания 12см наполнен газом под давлением 1 .Какую работу надо затратить при изометрическом сжатии газа до объема в два раза меньшего?(применяем закон Бойля-Мариотта).

9.17. Найдите статистические моменты дуги параболы y²=2x(y>0), заключенной между прямыми х=0,х=2, относительно осей Ох и Оу.

9.18. Найти статистический момент дуги астероиды лежащей в первом квадрате, относительно оси Оу.

9.19. Найти координаты центра тяжести фигуры, заключенной между кривой и осями координат.

9.20. Найти координаты центра тяжести фигуры, ограниченной правой петлей лемнискаты Бернулли .

9.21. Найти К.Ц.Т. фигуры, ограниченной кардиоидой .

9.22. Найдите центр тяжести фигуры, ограниченной замкнутой кривой y²=ax³-x⁴.

9.23. Найти статический момент (относительно оси Ох) фигуры, ограниченной осью абсцисс и одной аркой циклоиды x=a(t-sint), y=a(1-cost).

9. 24. Найти работу, необходимую для того, чтобы вытащить из воды шар радиусом 3м и удельным весом ,погруженный в воду так, что он касается ее поверхности.

9.25. Найти работу, необходимую для того, чтобы выкачать воду из корыта, имеющего форму полуцилиндра. Радиус цилиндра 2м, длина 6м.

9.26. Найти работу, необходимую для того, чтобы вытащить из воды конус, подвешенный на канате так, что вершина его находится на поверхности воды. Удельный вес конуса , радиус основания 2м, высота 6м.

9.27. Найти работу, необходимую для того, чтобы выкачать воду из полусферического сосуда, диаметр которого равен 20м.

9.28. Найти координаты центра тяжести однородной плоской фигуры,

ограниченной дугой эллипса , расположенной в первой четверти, и осями координат.

9.29. Найти К.Ц.Т. однородной плоской фигуры, ограниченной параболой x²+4у-16=0 и осью Ох.

9.30. Найти К.Ц.Т. однородной плоской фигуры, ограниченной параболами y²=20x, X²=20y.

Задача 10.

Вычислить несобственный интеграл (исследовать его сходимость).

10.1.

10.2.

10.3.

10.4.

10.5.

10.6.

10.7.

10.8.

10.9.

10.10.

10.11.

10.12.

10.13.

10.14.

10.15.

10.16.

10.17.

10.18.

10.19.

10.20.

10.21.

10.22.

10.23.

10.24.

10.25.

10.26.

10.27.

10.28.

10.29.

10.30.

Разберите решение заданий 22-28.

Задание 22. Найти площадь фигуры, ограниченной прямой

у = х и параболой у = 2 – х² .

 

 

Решение. Найдем абсциссы точек пересечения прямой с параболой:

 

	х – 2 + х2 = 0 х1 = –2; х2 = 1

Рис. 3

 

Воспользуемся формулой для вычисления площади фигуры, ограниченной двумя кривыми: .

При а = –2, b = 1, f₂(x) = 2 – x², f₁(x) = x получим:

Ответ: 4,5 кв. ед.

 

Задание 23. Вычислить объем тела, образованного вращением фигуры, ограниченной линиями вокруг оси ОХ.

		Решение.Ограниченная линиями и фигура, при вращении вокруг оси ОХ образует тело, объем которого можно найти как разность объемов V1 и V2, образованных вращением вокруг оси ОХ трапецией А1АВВ1 и А1АОВВ1.

 

Рис.4

;

.

Искомый объем : .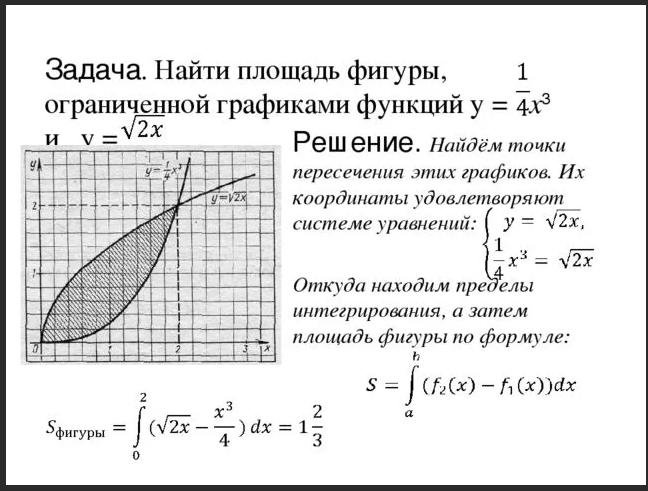

Задание 24.Найти объем тела, образованного вращением фигуры, ограниченной линиями ху=6, х=1, х=4, у=0 вокруг оси Ох и вокруг оси Оу.

Объемы тела вращения, образованного вращением вокруг оси Ох (или Оу) криволинейной трапеции, ограниченной кривой у=f(х) (f(х)³0) и прямыми у=0, х=а, х=в, вычисляют соответственно по формулам

Решение.В результате вращения фигуры, ограниченной линиями ху=6, х=1, х=4, у=0 вокруг оси Ох, получим фигуру, изображенную на рис.6(а), вокруг оси Оу на рис. 6(б).

По формуле (1) находим объем фигуры V_x

По формуле (2) находим объем фигуры V_y :

Рис.2. Графическое пояснение к задаче 5

Задание 25.

Вычислить длину дуги полукубической параболы от начала координат до точки В (4;8).

Решение.Найдем и подставляя в формулу для вычисления дуги кривой , получим

.

Задание 26.

Найти несобственный интеграл:

 

Решение.Пользуясь формулой ,имеем

 

.

Следовательно, несобственный интеграл сходится.

 

Задание 27.

Найти несобственный интеграл:

 

Решение.Согласно равенству

получаем

.

 

Задание 28. Найти несобственный интеграл: .

 

Решение.Подынтегральная функция претерпевает разрыв в точке х=1, лежащей внутри отрезка интегрирования. Используя определение

 

, находим

 

Вопросы для самопроверки

1. Назовите задачи, приводящие к понятию определенного интеграла.

2. Напишите интегральную сумму для функции у=f(х) на отрезке [a;b].

3. Что называется определенным интегралом от функции у=f(х) на отрезке [a;b]?

4. Каков геометрический смысл определенного интеграла?

5. Перечислите основные свойства определенного интеграла.

6. Напишите формулу Ньютона-Лейбница.

7. Напишите формулу интегрирования по частям в определенном интеграле.

8. Как вычислить объем тела, образованного вращением плоской фигуры вокруг оси Ох? Оу?

9. Дайте определение несобственного интеграла с бесконечными пределами интегрирования.

10. Сформулируйте понятие несобственного интеграла от разрывной функции.

Задания для самостоятельного решения

В задачах 1-20 вычислить площадь фигур, ограниченных линиями. Сделать чертеж.

1. у= —; y=-9x 2. y=x²; y=; y=0; x=0; x=3

3. y²=2x+1; y=x-1 4. y= —3x+6; y=-x+1

2. y=x²; y=2x; y=x 6. y=x³-3x; y=x

7. y=x²-2x+3; y=3x-1 8. y²=x³; y=8; x=0

9. xy=8; y=8x³; y=27 10. y²=(4-x)³; x=0

11. y = x² – 6x + 9, 12. y = x², xy =8, x = 6

13. y² + 8x = 16, y² – 24x = 48 14. y = x³, y = 2x, y = x

15. y = x² – 4x + 3, y = -x² + 2x + 3 16. y = -x² + 6x + 5, x = 0, y = 0

17. y = x² – 4x + 3, x = 0, x = 4, y = 4 18. y = 8x – x², y = x² + 18x – 12

19. y = 6x², y = 2x³ 20. y = , y = x, x

 

В задачах 21 — 40 вычислить несобственный интеграл или установить его расходимость.

21.		22.
23.		24.
25.		26.
27.		28.
29.		30.
31.		32.
33.		34.
35.		36.
37.		38.
39.		40.

Кратные интегралы

 

 

Кратные интегралы ограничим рассмотрением двойных интегралов.

Литература: [1] гл.24, §1-3, 6-7; [2] гл.13, §1-4; [3,ч.2] гл.2, §6-7;

[5,ч.2] гл.1, §1-6.

 

Разберите решение заданий 29-33.

Задание 29.Вычислить двойной интеграл по прямоугольной области D, ограниченной прямыми и .

Решение.

Вычисляем интеграл по формуле , где , , , .

.

Внутренний интеграл вычисляем, считая х постоянным:

.

Полученную функцию от х интегрируем по отрезку :

.

 

Обычно вычисление внутреннего интеграла отдельно не делают, а все выкладки записывают в одну строку следующим образом:

 

Задание 30.

Вычислить двойной интеграл по области D, ограниченной параболой и прямыми , и (рис. 3).

 

 

Решение.Область D является простой как относительно оси Ох, так и относительно оси Оу. Однако левая и правая границы области D составлены из двух участков, поэтому для вычисления двойного интеграла по формуле

необходимо разбить область D на три области: (рис.3). Нижняя и верхняя границы области представлены каждая одним уравнением (соответственно и ).

Поэтому вычислим данный интеграл по формуле

: Рис.3

.

 

Задание 31.Вычислить двойной интеграл по области D, ограниченной гиперболой и прямыми и (рис. 4).

 

Решение.Область D является простой как относительно оси Ох, так и

относительно оси Оу. Так как левая и правая границы области D представлены каждая одним уравнением (соответственно и ) в отличие от нижней и верхней границ, каждая из которых составлена из двух участков, то для вычисления интеграла воспользуемся формулой:

Рис.4

.

Задание 32.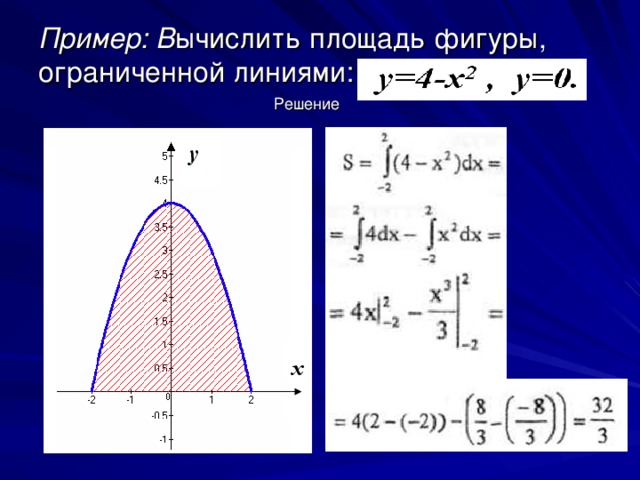 Найти площадь фигуры, ограниченной линиями

 

, .

х = y2 — 2у

х + у = 0

Рис. 5

Решение.Решая систему уравнений , получим точки А(-1;1), О(0;0) пересечения данных линий. Изобразим область интегрирования на рисунке 5. Площадь плоской фигуры D вычисляем по формуле .Перейдем от двойного интеграла к повторному интегралу

.

Задание 33.

Найти координаты центра тяжести пластинки, ограниченной параболой и прямой у=1, если плотность распределения массы в каждой точке равна ординате этой точки (рис. 6).

Решение.

Найдем сначала m массу пластинки. Так как поверхностная плотность , то по формуле получим

.

Вычислим статические моменты пластинки

и относительно координатных осей,

используя формулы ,

 

Рис. 6

;

.

Координаты центра тяжести пластинки и определяем по формулам:

, .

, .

 

 

Предыдущая1234567Следующая

24-03-2020-ДЗ 1 билеты 2020 (ДЗ №1, №2 — Условия) — PDF

Файл «24-03-2020-ДЗ 1 билеты 2020» внутри архива находится в следующих папках: ИИДУ дз 1,2 условия для ИУ-РЛ-БМТ, ИИДУ дз1 условия ИУ-РЛ-БМТ. PDF-файл из архива «ДЗ №1, №2 — Условия», который расположен в категории «». Всё это находится в предмете «математический анализ» из раздела «», которые можно найти в файловом архиве МГТУ им. Н.Э.Баумана. Не смотря на прямую связь этого архива с МГТУ им. Н.Э.Баумана, его также можно найти и в других разделах. .

ДОМАШНЕЕ ЗАДАНИЕ ”ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА”1к, 2 сем. , для факультетов ИУ, РЛ, БМТВариант 1.Задача 1. Вычислить площадь фигуры, ограниченной линиями: y = arctg x, y = arctg(2x − 4),y = 0.(1 балл)Задача 2. Найти объём тела, образованного вращением вокруг оси OX фигуры, ограниченнойx = 2 cos tкривой:для x ≥ 1.(2 балл)y = sin tЗадача 3.

Найти длину дуги кривой ρ = 4(1 − cos ϕ) от точки А(0; 0) до точки пересечения с3прямой ϕ = π.(2 балла)2Z+∞ ln cos 1x dx.Задача 4. Исследовать на сходимость:(1 балл)x21Z1 √x dx√.Задача 5. Исследовать на сходимость:1 − x40(1 балл)Баллы к рейтингу: min −4, max −7.Вариант 2.ϕЗадача 1. Вычислить площадь фигуры, ограниченной линией: ρ = а sin3 , лежащую ниже3полярной оси.(1 балл)Задача 2. Вычислить объем тела, образованноговращением вокруг оси OY фигуры, ограниченx = 7(t − sin t)ной осью OX и одной аркой циклоиды:.(2 балл)y = 7(1 − cos t)Задача 3. Вычислить площадь поверхности, образованной вращением вокруг оси OX кривой:x3y=для −2 ≤ x ≤ 2.(2 балл)3Z+∞ 2sin xdx.(1 балл)Задача 4.

Исследовать на сходимость:x1Задача 5. Исследовать на сходимость:Z10x2 dxp.3(1 − x2 )5(1 балл)Баллы к рейтингу: min −4, max −7.Вариант 3.Задача 1. Найти площадь фигуры, ограниченной кривой: y = ln x, касательной к ней в точкеx = e и осью OX.(1 балл)√ −x2Задача 2. Фигура, ограниченная кривой y = xe , вращается вокруг своей асимптоты. Найтиобъём тела вращения.(2 балл)tx = 5 cos3 4Задача 3. Найти длину дуги всей кривой:.(2 балла)y = 5 sin3 4tZ+∞√ −xЗадача 4. Исследовать на сходимость:xe dx.(1 балл)0Задача 5. Исследовать на сходимость:Z10dx.e −1√x(1 балл)Баллы к рейтингу: min −4, max −7.Вариант 4.Задача 1. Вычислить площадь фигуры, ограниченной линиями: (x − 2)(y + 3) = 6 и x + y = 6.(1 балл)Задача 2.

Определить объем тела, образованного вращением вокруг оси OY фигуры, ограниx2 y 2ченной линиями: 2 − 2 = 1, y = b, y = −b.(2 балл)abЗадача 3. Вычислить площадь поверхности, образованной вращением лемнискаты2ρ = а 2 sin 2ϕ вокруг полярной оси.(2 балл)Z+∞dx√Задача 4. Исследовать на сходимость:.(1 балл)x2 + 3 x4 + 12Задача 5. Исследовать на сходимость:Z1√esin x0xdx.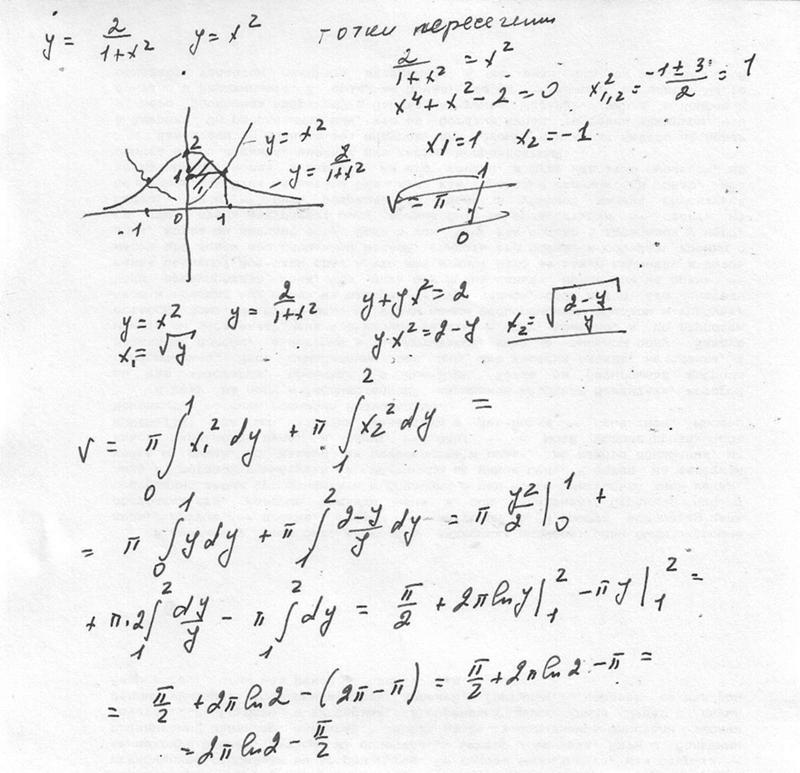 −1(1 балл)Баллы к рейтингу: min −4, max −7.Вариант 5.2Задача 1. Прямая x = −2 делит площадь, заключенную между кривой y = xe−x /2 и ее асимптотой, на две части. Найти ту площадь, для которой x ≥ −2.(1 балл)Задача 2. Найти объем тела, образованного вращением вокруг оси OY фигуры, ограниченнойxлиниями: x = 2, y = arcsin и касательной к этой кривой в начале координат.(2 балл)2Задача 3.

Окружность ρ = 2r sin ϕ вращается вокруг полярной оси. Найти площадь поверхности, которая при этом получается.(2 балл)+∞Zx arctg x√dx.(1 балл)Задача 4. Исследовать на сходимость:31 + x40Задача 5. Исследовать на сходимость:Z1ex0dx.− cos x(1 балл)Баллы к рейтингу: min −4, max −7.Вариант 6.Задача 1.

Вычислить площадь фигуры, расположенной внутри каждой из кривых: ρ = 1,ρ = 2(1 − cos ϕ).(1 балл)x+6Задача 2. Фигура, ограниченная линиями: y =, y = 2 − x, вращается вокруг оси OX.x+3Найти объем тела вращения.(2 балл) Задача33. Вычислить площадь поверхности, образованной вращением астроиды:x = a cos tвокруг оси OY . (2 балл)y = a sin3 tZ+∞ 1 + arctg 1x dx.Задача 4. Исследовать на сходимость:(1 балл)x+21Задача 5.

Исследовать на сходимость:Zπ/20ln(1 + sin x)√dx.x3(1 балл)Баллы к рейтингу: min −4, max −7.Вариант 7.Задача 1. Вычислить площадь фигуры, расположенной внутри окружности ρ = sin ϕ и внеокружности ρ = cos ϕ.(1 балл)Задача 2. Найти объем тела, образованного вращением вокруг оси OY фигуры, ограниченнойлиниями: y = ex + 1, y = e2x − 1, x = 0.(2 балл)64ttЗадача 3. Найти длину дуги кривой x = , y = 2 −между точками ее пересечения с осями64координат.(2 балл)+∞Z2 + arcsin x1√Задача 4. Исследовать на сходимость:dx.(1 балл)1+ x1Задача 5. Исследовать на сходимость:Zπdx.sin8 x0(1 балл)Баллы к рейтингу: min −4, max −7.Вариант 8.Задача 1.

Найти большую из площадей, ограниченных циклоидой:x = 2(t − sin t), осью OXy = 2(1 − cos t)16(x − 3π).(1 балл)πЗадача 2. Найти объем тела, образованного вращением вокруг оси OY фигуры, ограниченнойкривой y = 3×2 − 12x и прямой y = −6.(2 балл)и параболой y 2 = −Задача 3. Вычислить площадь, образованную вращением параболы y 2 =отсекаемой прямой x = H.Z+∞ arctg 1 dx√x.Задача 4. Исследовать на сходимость:x + x2 + 51ZπdxЗадача 5. Исследовать на сходимость:.sin5 x0R2x вокруг оси OX,H(2 балл)(1 балл)(1 балл)Баллы к рейтингу: min −4, max −7.Вариант 9.x = a cos3 t.(1 балл)y = b sin3 tЗадача 2. Фигура, ограниченная линиями: x = 0, y = ex , y = 1 + 2e−x , вращается вокруг осиOX.

Вычислить объем тела вращения.(2 балл)aϕЗадача 3. Найти длину спирали ρ = e , находящейся внутри круга ρ = 1.(2 балла)+∞Zcos 2x√Задача 4. Исследовать на сходимость:dx.(1 балл)x5 + 5x + 2Задача 1. Найти площадь фигуры, ограниченную кривой1Задача 5. Исследовать на сходимость:Z31x5 + 3x + 1pdx.5(x3 − 1)2(1 балл)Баллы к рейтингу: min −4, max −7.Вариант 10.Задача 1.

Найти площадь фигуры, расположенной внутри кривой ρ2 = 4 cos 2ϕ и вне кривойρ = cos 2ϕ.(1 балл)Задача 2. Найти объём тела, образованного вращением вокруг оси OY фигуры, ограниченнойx = 2 cos tкривой:для x ≥ 1.(2 балл)y = sin tЗадача 3. Найти длину всей кривой ρ = 9(1 + cos ϕ).(2 балла)+∞Zsin 3x√Задача 4. Исследовать на сходимость:dx.(1 балл)35x + 2x + 421Задача 5. Исследовать на сходимость:Zπ/21 − cos xdx.x30(1 балл)Баллы к рейтингу: min −4, max −7.Вариант 11.Задача 1. Найти меньшую из площадей, ограниченных линиями: ρ = 1 + cos ϕ, x + 2y = 2.(1 балл)11Задача 2.

Фигура, ограниченная линиями: y = (x − 2)2 , y = (x − 2)2 + 1, вращается вокруг24оси OY . Вычислить объем тела вращения.(2 балл)3x = a cos tЗадача 3. Дана астроида:и точки на ней A(а, 0), В (0, а). Найти на дуге АВy = a sin3 tтакую т. M, чтобы длина дуги AM составляла четверть длины дуги AB.(2 балла)+∞Zx − arctg xЗадача 5. Исследовать на сходимость:dx.(1 балл)3x (x + arctg x)1Задача 6. Исследовать на сходимость:Z10ch x − 1√dx.51 + x4 − 1(1 балл)Баллы к рейтингу: min −4, max −7.Вариант 12.Задача 1. Найти площадь фигуры, ограниченной линиями:x = a cos3 t, x2 = −a(y − a).y = a sin3 t(1 балл)Задача 2. Найти объем тела, образованного вращением вокруг оси OY фигуры, ограниченнойлиниями: y = ex , y = 1 + 2e−x , x = 0. (2 балл)Задача 3.

Вычислить площадь поверхности, образованной вращением кардиоидыρ = a(1 − cos ϕ) вокруг полярной оси.(2 балл)+∞Zx + sin xЗадача 4. Исследовать на сходимость:dx.(1 балл)3x (x − sin x)1Задача 5. Исследовать на сходимость:Ze2ex ln xdx.(x − e)2(1 балл)Баллы к рейтингу: min −4, max −7.Вариант 13.√Задача 1. Найти площадь фигуры, ограниченной кривыми: ρ = 6 cos ϕ, ρ2 = 9 cos 2ϕ, расположенной внутри каждой из них.(1 балл)Задача 2. Вычислить объем тела, образованного вращением вокруг оси OY фигуры, ограниченной параболой y = 2x − x2 и осью OX.(2 балл)Задача 3. Вычислить длину дуги полукубической параболы 5×3 = y 2, заключенной внутриокружности x2 + y 2 = 6.(2 балла)+∞Z 3/xe −1√Задача 4.

Исследовать на сходимость:dx.(1 балл)x2 + 42Задача 5. Исследовать на сходимость:Zπ/4sin x√ dx.x x0(1 балл)Баллы к рейтингу: min −4, max −7.Вариант 14.Задача 1. Найти площадь фигуры, ограниченной параболой y = x2 − 4x + 3, касательной к нейв точке x = 4 и осью OY .(1 балл)x+1Задача 2. Фигура, ограниченная линиями: y =, x = 4, x = 6, y = 1, вращается вокруг осиx−3OY .

Вычислить объем тела вращения.(2 балл)Задача 3. Вычислить площадь поверхности, образованной вращением лемнискаты2ρ = 9 cos 2ϕ вокруг полярной оси.(2 балла)+∞Zxdx√Задача 4. Исследовать на сходимость:.(1 балл)x4 + 12Задача 5. Исследовать на сходимость:Z10dxp.3x(ex − e−x )(1 балл)Баллы к рейтингу: min −4, max −7.Вариант 15.Задача 1. Найти площадь одного лепестка кривой ρ = 4 sin2 ϕ.(1 балл)2Задача 2. Фигура, ограниченная линиями: y = x и y = x + sin x (0 ≤ x ≤ π), вращается вокругоси OY .

Вычислить объем тела вращения.(2 балл)Задача 3. Вычислить площадь поверхности, полученную вращением вокруг оси OX той частиастроиды:x = 8 cos3 t, для которой x 6 −1.(2 балл)y = 8 sin3 tZ+∞ln x dx√Задача 4. Исследовать на сходимость:.(1 балл)3×3 + 11Задача 5. Исследовать на сходимость:Z10.1sin(1/x)√dx.1−x(1 балл)Баллы к рейтингу: min −4, max −7.Вариант 16.1×2,y=и осью1 + x22OX.(1 балл)Задача 2.

Вычислить объемтела, образованного вращением вокруг оси OY фигуры, ограничен√33ной линиями: y = x и y = x.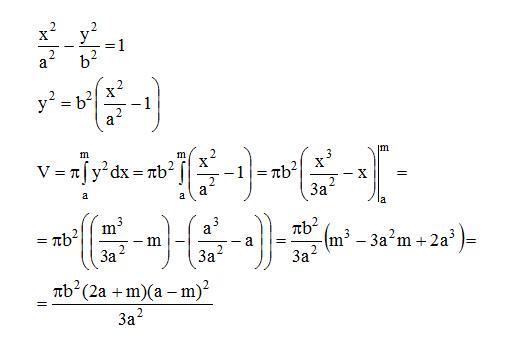 (2 балл)Задача 3. Найти длину всей кривой ρ = a(1 − sin ϕ).(2 балла)Z+∞x13Задача 4. Исследовать на сходимость:dx.(1 балл)(x5 + x3 + 1)3Задача 1. Вычислить площадь фигуры, ограниченной линиями: y =1Задача 5. Исследовать на сходимость:Z30xdx√.31 + x2 − 1(1 балл)Баллы к рейтингу: min −4, max −7.Вариант 17.Задача 1. Вычислить площадь фигуры, ограниченной лемнискатой ρ2 = 2 cos 2ϕ, окружностьюρ = 1, расположенной вне окружности.(1 балл)Задача 2. Вычислить объем тела, образованного вращением вокруг оси OY фигуры, ограниченной линиями: y = ln x, y = 2 − ln x и осью OX.(2 балл)√(3 − x) xЗадача 3.

Вычислить длину дуги линии y =между точками, ординаты которых3равны нулю.(2 балла)+∞Zln cos(1/x)Задача 4. Исследовать на сходимость:dx.(1 балл)x1Задача 5. Исследовать на сходимость:Z32sin 3xdxp.3×5 (x − 2)(1 балл)Баллы к рейтингу: min −4, max −7.Вариант 18.x = 2 cos3 tи прямой x = 14 ,y = sin3 tсодержащей точку A(0, 2).(1 балл)Задача 2. Вычислить объем тела, образованного вращением вокруг оси OX фигуры, ограниченной линиями: y = 0 и y = 1 + sin x (между двумя соседними точками касания этой линии с осьюOX). (2 балл)Задача 3. Вычислить площадь поверхности, образованной вращением меньшей части кривойπ3πρ = 2a sin ϕ, отсекаемой лучами ϕ1 = и ϕ2 =вокруг полярной оси.(2 балл)44Z+∞(2x + 1) sin(1/2x)√Задача 4.

Исследовать на сходимость:dx.(1 балл)5×6 + 3x − 2Задача 1. Вычислить площадь фигуры, ограниченной астроидой:1Задача 5. Исследовать на сходимость:Z21dx.ln x(1 балл)Баллы к рейтингу: min −4, max −7.Вариант 19.√Задача 1. Вычислить площадь фигуры, ограниченной окружностью ρ = 3 sin ϕ и кардиоидойρ = 1 − cos ϕ, расположенной вне кардиоиды.(1 балл)Задача 2. Найти объём тела, образованного вращением вокруг оси OY фигуры, ограниченнойx = 2 cos t(2 балл)кривой:для y ≥ 21 .y = sin tЗадача 3. Вычислить площадь поверхности, образованной вращением вокруг оси OX дугикривой y 2 = 4 + x, отсеченной прямой x = 2.(2 балл)+∞Zdx√Задача 4.

Объем тела вращения: диски и шайбы

Если область на плоскости вращается вокруг линии на той же плоскости, полученный объект называется телом вращения.

Например, сплошной прямоугольный цилиндр можно создать, вращая прямоугольник. Точно так же твердый сферический шар может быть получен путем вращения полудиска.

Линия, вокруг которой мы вращаем фигуру, называется осью вращения.

Дисковый метод

Метод диска используется, когда мы вращаем одну кривую y = f ( x ) вокруг оси x — (или y -).

Предположим, что y = f ( x ) является непрерывной неотрицательной функцией на интервале [ a , b ].

Рис. 1.

Объем твердого тела, образованного вращением области, ограниченной кривой \(y = f\left( x \right)\) и осью \(x-\) между \(x= a\) и \(x = b\) относительно оси \(x-\) определяется как 92}dy} .\]

Метод мойки

Мы можем расширить метод диска, чтобы найти объем полого тела вращения.

В предположении, что функции \(f\left( x \right)\) и \(g\left( x \right)\) непрерывны и неотрицательны на интервале \(\left[ {a,b} \ right]\) и \(g\left( x \right) \le f\left( x \right),\) рассмотрим область, ограниченную двумя кривыми \(y = f\left( x \right)\ ) и \(y = g\left( x \right),\) между \(x = a\) и \(x = b. \) 92}} \right)dx} .\]

В точке \(x\) на оси \(x-\) перпендикулярное поперечное сечение твердого тела имеет форму шайбы с внутренним радиусом \(r = g\left( x \right)\) и внешний радиус \(R = f\left( x \right).\)

Объем твердого тела, образованного вращением вокруг оси \(y-\) области между кривыми \(x = f\left( y \right)\) и \(x = g\left( y \right) ,\) где \(g\left( y \right) \le f\left( y \right)\) и \(c \le y \le d\) определяется формулой

92}\left( t \right)\frac{{dy}}{{dt}}dt} .\]

Объем тела вращения для полярной кривой

Есть много кривых, которые задаются полярным уравнением \(r = r\left( \theta \right).\) Чтобы преобразовать полярные координаты \(\left( {r,\theta } \right)\) в Декартовы координаты \(\left( {x,y} \right),\) используем известные формулы

\[x = r\left( \theta \right)\cos \theta ,\;\; y = r\left( \theta \right)\sin \theta .\]

Итак, мы подошли к параметрической форме кривой, рассмотренной в предыдущем разделе.

Важно иметь в виду, что радиус-вектор \(r\) также зависит от параметра \(\theta.\). Следовательно, производные \(\frac{{dx}}{{dt}}\) и \(\frac{{dy}}{{dt}}\) записываются как

\[\frac{{dx}}{{dt}} = \frac{{d\left( {r\left( \theta \right)\cos \theta } \right)}}{{dt}} = \frac{{d\left( {r\left( \theta \right)} \right)}}{{dt}}\cos \theta — r\left( \theta \right)\sin \theta,\]

\[\frac{{dy}}{{dt}} = \frac{{d\left( {r\left( \theta \right)\sin \theta } \right)}}{{dt}} = \frac{{d\left( {r\left( \theta \right)} \right)}}{{dt}}\sin \theta + r\left( \theta \right)\cos \theta .\]

Решенные проблемы

Щелкните или коснитесь проблемы, чтобы увидеть решение.

Пример 1

Методом круга вычислить объем прямого кругового конуса высотой \(H\) и радиусом основания \(R.\)

Пример 2

Найти объем твердого тела, полученного при вращении функция синуса между \(x = 0\) и \(x = \pi\) относительно оси \(x-\).

Пример 3

Вычислите объем твердого тела, полученного вращением области, ограниченной параболой \(y = {x^2}\) и функцией квадратного корня \(y = \sqrt x\) вокруг \( х-\) ось. 92, y=x вращается вокруг а) оси x и b) оси y. Как начертить область и найти объемы двух тел вращения?

Исчисление

Наука

• Анатомия и физиология
• астрономия
• Астрофизика
• Биология
• Химия
• науки о Земле
• Наука об окружающей среде
• Органическая химия
• Физика

Математика

• Алгебра
• Исчисление
• Геометрия
• Преалгебра
• Предварительный расчет
• Статистика
• Тригонометрия

Гуманитарные науки

• Английская грамматика
• История США
• Всемирная история

.

.. и не только
• Сократическая мета
• Избранные ответы

Темы

Влияние этого вопроса

28252 просмотра по всему миру

Вы можете повторно использовать этот ответ
Лицензия Creative Commons

1.1: Объемы тел вращения — сечения

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

10273

Эта страница является черновиком и находится в активной разработке.

В этом разделе мы используем определенные интегралы для нахождения объемов трехмерных тел. Мы рассматриваем три подхода — срезы, диски и шайбы — для нахождения этих объемов в зависимости от характеристик твердого тела.

Объем и метод срезов

Точно так же, как площадь является числовой мерой двумерной области, объем является числовой мерой трехмерного твердого тела. Большинство из нас вычисляли объемы твердых тел, используя основные геометрические формулы. Объем прямоугольного тела, например, можно вычислить путем умножения длины, ширины и высоты: \(V=lwh.\) Формулы для объемов: 92h\]

• и пирамида

\[V_{pyramid}=\dfrac{1}{3}Ah\]

также были введены. Хотя некоторые из этих формул были получены только с помощью геометрии, все эти формулы можно получить с помощью интегрирования.

Мы также можем рассчитать объем цилиндра. Хотя большинство из нас думает о цилиндре как о круглом основании, таком как банка для супа или металлический стержень, в математике слово «цилиндр» имеет более общее значение. 2h.\)

Рисунок \(\PageIndex{1}\): Каждое поперечное сечение конкретного цилиндра идентично другим.

Если твердое тело не имеет постоянного поперечного сечения (и оно не является одним из других основных тел), у нас может не быть формулы для его объема. В этом случае мы можем использовать определенный интеграл для вычисления объема твердого тела. Мы делаем это, разрезая твердое тело на части, оценивая объем каждого среза, а затем складывая эти оценочные объемы вместе. Все срезы должны быть параллельны друг другу, и когда мы сложим все срезы вместе, мы должны получить цельное тело. Рассмотрим, например, фигуру S, показанную на рисунке, проходящую вдоль ось х.

Рисунок \(\PageIndex{2}\): Твердое тело с переменным поперечным сечением.

Мы хотим разделить \(S\) на срезы, перпендикулярные оси x . Как мы увидим позже в этой главе, могут быть случаи, когда мы хотим разрезать твердое тело в каком-то другом направлении, например, срезами, перпендикулярными оси y. ∗_i)Δx\). Складывая эти приближения вместе, мы видим, что объем всего твердого тела \(S\) может быть приблизительно равен 9a_bA(x)dx.\]

Метод, который мы только что описали, называется методом нарезки. Чтобы применить его, мы используем следующую стратегию.

Стратегия решения задач: поиск объемов методом срезов

1. Изучите твердое тело и определите форму поперечного сечения твердого тела. Часто бывает полезно нарисовать рисунок, если его нет.
2. Определите формулу площади поперечного сечения.
3. Проинтегрируйте формулу площади по соответствующему интервалу, чтобы получить объем.

Напомним, что в этом разделе мы предполагаем, что срезы перпендикулярны оси x . Следовательно, формула площади выражается через x, а пределы интегрирования лежат на оси x 90 284. Однако показанная здесь стратегия решения проблем действительна независимо от того, как мы решили разрезать твердое тело.

Пример \(\PageIndex{1}\): вывод формулы объема пирамиды

Из геометрии мы знаем, что формула объема пирамиды имеет вид \(V=\dfrac{1}{3} А\). 2h\), где a обозначает длину одной стороны основания. Мы собираемся использовать метод нарезки, чтобы вывести эту формулу.

Решение

Мы хотим применить метод разрезания к пирамиде с квадратным основанием. Чтобы настроить интеграл, рассмотрим пирамиду, показанную на рисунке, ориентированную вдоль оси x 90 284.

Рисунок \(\PageIndex{4}\): (a) Пирамида с квадратным основанием ориентирована по оси x. (b) Двухмерный вид пирамиды сбоку.

Сначала мы хотим определить форму поперечного сечения пирамиды. Мы знаем, что основание квадратное, поэтому сечения тоже квадратные (шаг 1). Теперь мы хотим определить формулу площади одного из этих квадратов поперечного сечения. Глядя на рисунок (b) и используя пропорцию, поскольку это подобные треугольники, мы имеем 93. \]

 

Тела вращения

Если область на плоскости вращается вокруг линии на этой плоскости, полученное тело называется телом вращения , как показано на следующем рисунке.

Рисунок \(\PageIndex{5}\): (a) Это область, которая вращается вокруг оси x. (б) Когда область начинает вращаться вокруг оси, она выметает тело вращения. (c) Это твердое тело, которое получается после завершения вращения.

Тела вращения распространены в механических приложениях, таких как детали машин, изготовленные на токарном станке. Оставшуюся часть этого раздела мы посвятим рассмотрению твердых тел этого типа. В следующем примере используется метод срезов для вычисления объема тела вращения. 92−4x+5,x=1\) и \(x=4,\) и вращается вокруг оси x.

Решение

Используя стратегию решения задач, мы сначала нарисуем график квадратичной функции на интервале \([1,4]\), как показано на следующем рисунке.

Рисунок \(\PageIndex{6}\): Область, используемая для создания тела вращения.

Затем поверните область вокруг оси x, как показано на следующем рисунке.

Рисунок по оси абсцисс.

Визуализируйте здесь: https://www.geogebra.org/3d/dvyuyzer

93.\)

Упражнение \(\PageIndex{2}\)

Методом срезов найдите объем тела вращения, образованного вращением области между графиком функции \(f(x)= 1/x\) и оси x на интервале \([1,2]\) вокруг оси x . См. следующий рисунок.

Подсказка

Используйте стратегию решения проблем, представленную ранее. Всегда учитывайте размеры диска. Каков радиус? 92+1\) и по оси x в интервале \([−1,3]\) вокруг оси x . График функции и репрезентативный диск показаны на рисунках (а) и (б). Область вращения и полученное твердое тело показаны на рисунке (c) и (d).

Рисунок \(\PageIndex{8}\): (a) Тонкий прямоугольник для аппроксимации площади под кривой. (b) Репрезентативный диск, образованный вращением прямоугольника вокруг оси x. (c) Область под кривой вращается вокруг оси x, в результате чего (d) тело вращения. 9b A(x)\,dx.\nonumber\]

Единственная разница с методом дисков состоит в том, что мы заранее знаем формулу площади поперечного сечения; это площадь круга. Это дает следующее правило.

Метод дисков

Пусть \(f(x)\) непрерывна и неотрицательна. Определим \(R\) как область, ограниченную сверху графиком \(f(x)\), снизу \(x\) -осью , слева линией \(x=a\) , а справа линией \(x=b\). Тогда объем тела вращения, образованного вращением \(R\) вокруг \(x\) 93. \end{align*}\]

Давайте рассмотрим несколько примеров.

Пример \(\PageIndex{4}\): использование метода диска для нахождения объема тела вращения 1

Использование метода диска для нахождения объема тела вращения, образованного вращением области между графиком из \(f(x)=\sqrt{x}\) и оси x на интервале \([1,4]\) вокруг оси x .

Решение

Графики функции и тела вращения показаны на следующем рисунке. 94_1=\dfrac{15π}{2}\)

Объем равен \((15π)/2\) единиц ³ .

Упражнение \(\PageIndex{3}\)

Используйте метод круга, чтобы найти объем тела вращения, образованного вращением области между графиком \(f(x)=\sqrt{4−x} \) и оси x в интервале \([0,4]\) вокруг оси x .

Подсказка

Используйте процедуру из примера. Всегда рисуйте картинку для себя. Каковы размеры диска? Какова его толщина? Радиус? 93\]

До сих пор в наших примерах все соответствующие области вращались вокруг оси x , но мы можем создать тело вращения, вращая плоскую область вокруг любой горизонтальной или вертикальной линии. В следующем примере мы рассмотрим тело вращения, созданное вращением области вокруг оси y . Механика дискового метода почти такая же, как и в случае, когда ось x является осью вращения, но мы выражаем функцию через \(y\) и интегрируем также по y. Это резюмируется в следующем правиле. 92\,dy.\]

Следующий пример показывает, как это правило работает на практике.

Пример \(\PageIndex{5}\): Использование метода круга для нахождения объема тела вращения 2

Пусть \(R\) будет областью, ограниченной графиком \(g(y)= \sqrt{4−y}\) и 90 284 оси y 90 285 на интервале 90 285 оси y 90 285 \([0,4]\). Используйте метод диска, чтобы найти объем тела вращения, образованного вращением \(R\) вокруг оси y 90 284.

Раствор

На рисунке показаны функция и репрезентативный диск, который можно использовать для оценки объема. Обратите внимание, что поскольку мы вращаем функцию вокруг оси Y , диски расположены горизонтально, а не вертикально.

Рисунок \(\PageIndex{10}\): (a) показан тонкий прямоугольник между кривой функции \(g(y)=\sqrt{4−y}\) и осью y. (b) Прямоугольник образует репрезентативный диск после вращения вокруг оси Y.

Область вращения и полное тело вращения показаны на следующем рисунке. 93\).

Упражнение \(\PageIndex{4}\)

Используйте метод круга, чтобы найти объем тела вращения, образованного вращением области между графиком \(g(y)=y\) и y -ось 90 285 на интервале \([1,4]\) вокруг оси y 90 284.

Подсказка

Используйте процедуру из примера. Вокруг какой оси вращается тело? Нарисуйте диск, который делает срез. Каков его радиус?

94=21\пи\]

Метод шайбы

Некоторые тела вращения имеют полости в середине; они не сплошные на всем пути до оси вращения. Иногда это просто результат формы области вращения относительно оси вращения. В других случаях полости возникают, когда область вращения определяется как область между графиками двух функций. В-третьих, это может произойти, когда ось вращения, отличная от по оси x или по оси y выбрано.

Когда тело вращения имеет полость посередине, срезы, используемые для аппроксимации объема, представляют собой не диски, а шайбы (диски с отверстиями в центре). Например, рассмотрим область, ограниченную сверху графиком функции \(f(x)=\sqrt{x}\), а снизу графиком функции \(g(x)=1\) на интервале \ ([1,4]\). Когда эта область вращается вокруг оси x , в результате получается твердое тело с полостью посередине, а срезы представляют собой шайбы. График функции и репрезентативная шайба показаны на рисунках (а) и (б). Область вращения и полученное твердое тело показаны на рисунке (c) и (d).

Рисунок \(\PageIndex{12}\): (a) Тонкий прямоугольник в области между двумя кривыми.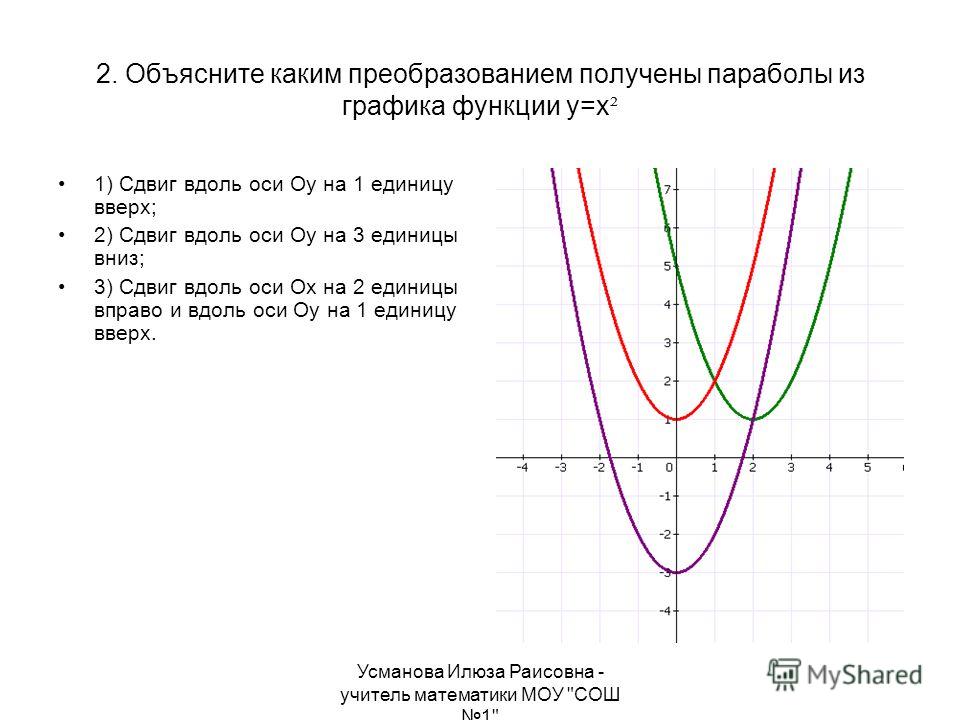 (b) Репрезентативный диск, образованный вращением прямоугольника вокруг оси x. (в) Область между кривыми на данном интервале. (d) Полученное тело вращения.

Рисунок \(\PageIndex{12}\): (e) Динамическая версия этого тела вращения, созданная с помощью CalcPlot3D.

Площадь поперечного сечения равна площади внешнего круга за вычетом площади внутреннего круга. В этом случае 93\).

Обобщение этого процесса дает метод шайбы .

Правило: метод Шайбы

Предположим, что \(f(x)\) и \(g(x)\) — непрерывные неотрицательные функции такие, что \(f(x)≥g(x)\) над \ ([а,б]\). Обозначим через \(R\) область, ограниченную сверху графиком \(f(x)\), снизу графиком \(g(x)\), слева линией \(x=a\ ), а справа линией \(x=b\). Тогда объем тела вращения, образованного вращением \(R\) вокруг оси x 92]dx.\]

Пример \(\PageIndex{6}\): использование метода шайбы

Найдите объем тела вращения, образованного вращением области, ограниченной сверху графиком \(f(x) =x\) и ниже по графику \(g(x)=1/x\) на интервале \([1,4]\) вокруг оси x .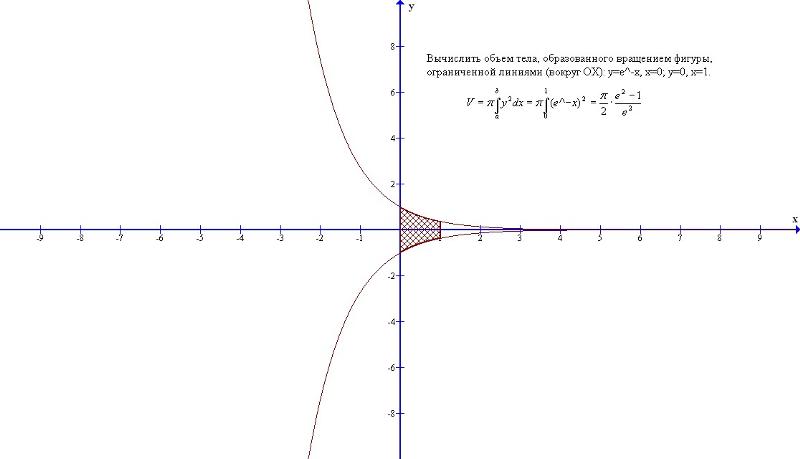

Решение

Графики функций и тела вращения показаны на следующем рисунке.

Рисунок \(\PageIndex{13}\): (a) Область между графиками функций \(f(x)=x\) и \(g(x)=1/x\) на интервале \ ([1,4]\). (b) Вращение области вокруг оси \(x\) порождает тело вращения с полостью посередине. 93. \end{align*}\]

 

Рисунок \(\PageIndex{13}\): (c) Динамическая версия этого тела вращения, сгенерированная с помощью CalcPlot3D.

Упражнение \(\PageIndex{5}\)

Найдите объем тела вращения, образованного вращением области, ограниченной графиками \(f(x)=\sqrt{x}\) и \(g (x)=1/x\) на интервале \([1,3]\) вокруг оси x .

Подсказка

Нарисуйте график функций, чтобы определить, какой график формирует верхнюю границу, а какой — нижнюю границу, затем используйте процедуру из примера.

Ответить

Первым шагом в этом решении является построение графика функций. 2}\Big)\] 93\]

Как и в случае с дисковым методом, мы также можем применить метод шайбы к телам вращения, которые образуются в результате вращения области вокруг оси y . В этом случае действует следующее правило.

Правило: метод шайбы для тел вращения вокруг оси y u(y)\) для \(y∈[c,d]\). Обозначим через \(Q\) область, ограниченную справа графиком \(u(y)\), слева графиком \(v(y)\), снизу линией \(y= c\), а выше строкой \(y=d\). Тогда объем тела вращения, образованного вращением \(Q\) вокруг 92]dy.\]

Другие оси вращения

Вместо того, чтобы рассматривать пример метода шайбы с осью Y в качестве оси вращения, мы теперь рассмотрим пример, в котором ось вращения является линии, отличной от одной из двух координатных осей. Применяется тот же общий метод, но вам, возможно, придется визуализировать, как описать площадь поперечного сечения объема.

Пример \(\PageIndex{7}\):

Найдите объем тела вращения, образованного вращением области, ограниченной сверху \(f(x)=4−x\) и снизу ось x на интервале \([0,4]\) вокруг линии \(y=−2. \)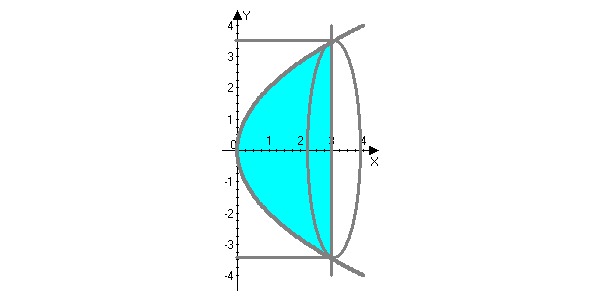

Решение

График области и тело вращения показаны на следующем рисунке .

Рисунок \(\PageIndex{14}\): (a) Область между графиком функции \(f(x)=4−x\) и осью x на интервале \([0,4] \). (b) Вращение области вокруг линии \(y=−2\) порождает тело вращения с цилиндрическим отверстием в его середине.

Мы не можем напрямую применить формулу объема к этой задаче, потому что ось вращения не является одной из осей координат. Однако мы все еще знаем, что площадь поперечного сечения равна площади внешнего круга за вычетом площади внутреннего круга. Глядя на график функции, мы видим, что радиус внешнего круга равен \(f(x)+2,\), что упрощается до 93.\end{align*}\]

Рисунок \(\PageIndex{14}\): (c) Динамическая версия этого тела вращения, сгенерированная с помощью CalcPlot3D.

Упражнение \(\PageIndex{6}\)

Найдите объем тела вращения, образованного вращением области, ограниченной сверху графиком \(f(x)=x+2\) и снизу ось x на интервале \([0,3]\) вокруг линии \(y=−1. \)

Подсказка

Используйте процедуру из примера. Что такое внешняя часть стиральной машины? Что такое внутреннее? Вы построили графики функций на интервале?

Ответить

Как и прежде, первым шагом решения является построение графика функций и определение внешней и внутренней частей нашей стиральной машины.

На графике оранжевая линия представляет \(f(x)=x+2\), фиолетовая линия представляет собой ось x, зеленая представляет собой линию, вокруг которой мы вращаемся, а красная линия представляет собой границы интегрирования. .

Первым шагом в этом решении является определение площади нашей шайбы. Так как наша линия вращения отошла от нашей функции (в этом случае \(y=-1\) находится дальше от \(f(x)=x+2\), чем \(y=0\)) поэтому мы добавим 1 к каждой стороне обоих наших дисков. Наши новые уравнения будут такими: \[f(x)+1=(x+2)+1=x+3\] и \[y=g(x)=0+1=1\] 93\]

 

 

Основные понятия

• Для нахождения объемов твердых тел можно использовать определенные интегралы. Используя метод нарезки, мы можем найти объем, интегрируя площадь поперечного сечения.
• Для тел вращения объемные срезы часто представляют собой диски, а поперечные сечения — круги. Метод кругов предполагает применение метода сечения в частном случае, когда поперечные сечения представляют собой круги, и использование формулы площади круга. 92]dx\)

  Глоссарий

  поперечное сечение

  пересечение плоскости и твердого объекта

  дисковый метод

  частный случай метода срезов, используемый с телами вращения, когда срезы представляют собой диски

  метод нарезки

  метод расчета объема твердого тела, который включает в себя разрезание твердого тела на части, оценку объема каждой части, а затем сложение этих оценок для получения оценки общего объема; по мере того, как количество срезов стремится к бесконечности, эта оценка становится интегралом, который дает точное значение объема.

  No related posts.