Найти корень уравнения примеры: Уравнение. Корень уравнения | Математика

Как найти корень уравнения пример. Что подразумевается под уравнением и его корнем

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.

Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.

Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:

1. Не имеют корней;
2. Имеют ровно один корень;
3. Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .

Дискриминант

Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда дискриминант — это просто число D = b 2 − 4ac .

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

1. Если D
2. Если D = 0, есть ровно один корень;
3. Если D > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:

Задача. Сколько корней имеют квадратные уравнения:

1. x 2 − 8x + 12 = 0;
2. 5x 2 + 3x + 7 = 0;
3. x 2 − 6x + 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 3 2 − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:

a = 1; b = −6; c = 9;
D = (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.

Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:

Основная формула корней квадратного уравнения

Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D

1. x 2 − 2x − 3 = 0;
2. 15 − 2x − x 2 = 0;
3. x 2 + 12x + 36 = 0.

Первое уравнение:
x 2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2) 2 − 4 · 1 · (−3) = 16.

D > 0 ⇒ уравнение имеет два корня. Найдем их:

Второе уравнение:
15 − 2x − x 2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2) 2 − 4 · (−1) · 15 = 64.

D > 0 ⇒ уравнение снова имеет два корня. Найдем их

\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]

Наконец, третье уравнение:
x 2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

1. x 2 + 9x = 0;
2. x 2 − 16 = 0.

Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:

Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.

Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.

Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:

Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c /a ) ≥ 0. Вывод:

1. Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (−c /a ) ≥ 0, корней будет два. Формула дана выше;
2. Если же (−c /a )

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c /a ) ≥ 0. Достаточно выразить величину x 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.

Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

Вынесение общего множителя за скобку

Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:

Задача. Решить квадратные уравнения:

1. x 2 − 7x = 0;
2. 5x 2 + 30 = 0;
3. 4x 2 − 9 = 0.

x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.

5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.

В математике встречаются разнообразные уравнения. Их всегда нужно решать, то есть искать все числа, которые сделают его верным равенством. Пути поиска решений определяются первоначальным видом уравнения. От него же будет зависеть и количество верных значений переменной, которые обозначаются, как корень уравнения. Это число может варьироваться от нуля до бесконечности.

Что подразумевается под уравнением и его корнем?

Из названия понятно, что оно приравнивает две величины, которые могут быть представлены числовыми или буквенными выражениями. Кроме того, они содержат еще неизвестные величины. Самое простое уравнение имеет только одну.

Видов уравнений большое количество, но понятие корня для них всегда одно и то же. Корень уравнения — это такое значение неизвестного числа, при котором уравнение принимает становится верным равенством. Бывают ситуации, когда таких чисел несколько, тогда неизвестная называется переменной.

Поиск всех возможных корней уравнения является его решением. То есть нужно выполнить ряд математических действий, которые его упрощают. А потом приводят к равенству, в котором содержится только неизвестная и какое-либо число.

В алгебре при решении уравнений можно прийти к такой ситуации, что корней не будет совсем. Тогда говорят о том, что оно неразрешимо. А в ответе такого уравнения нужно записать, что решений нет.

Но иногда бывает и противоположное. То есть в процессе многочисленных преобразований появляются посторонние корни. Они не дадут верного равенства при подстановке. Поэтому числа всегда нужно проверять, чтобы избежать ситуации с лишними корнями в ответе. Иначе уравнение не будет считаться решенным.

О линейном уравнении

Оно всегда может быть преобразовано в запись следующего вида: а * х + в = 0. В нем «а» всегда не равно нулю. Чтобы понять сколько корней имеет уравнение, его потребуется решить в общем виде.

Алгоритм преобразований:

• перенести в правую часть равенства слагаемое «в», заменив его знак на противоположный;
• разделить обе части получившегося равенства на коэффициент «а».

Общий вид решения такой:

х = -в/а .

Из него ясно, что ответом будет одно число. То есть всего один корень.

Квадратное уравнение

Его общий вид: а * х 2 + в * х + с = 0 . Здесь коэффициенты являются любыми числами, кроме первого, «а», которое не может быть равным нулю. Ведь тогда оно автоматически превратится в линейное. Ответ на вопрос, сколько корней имеет уравнение, уже не будет столь однозначным, как это было в предыдущем случае.

Все будет зависеть от значения дискриминанта. Он вычисляется по формуле Д = в 2 — 4 а * с . После расчетов «Д» может получиться больше, меньше или равным нулю. В первом случае корней уравнения будет два, во втором ответом будет «корней нет», а третья ситуация даст только одно значение неизвестной.

Формулы, которые используют для нахождения корней квадратного уравнения, и содержащие дискриминант

В общем случае, когда «Д» положительное число, не равное нулю, нужно использовать такую формулу:

х 1,2 = (-в ± √Д) / (2 * а) .

Здесь всегда получится два ответа. Это связано с тем, что в исходной формуле стоит знак «плюс/минус». Он существенно изменяет значение неизвестной.

При равенстве «Д» нулю корень уравнения — это единственное число. Просто потому что квадратный корень из нуля равен нулю. А значит, прибавлять и вычитать нужно будет ноль. От этого число не изменится. Поэтому формулу корня уравнения можно записать без упоминания «Д»:

х = (-в) / (2 * а).

При отрицательном значении дискриминанта извлечь из него квадратный корень не представляется возможным. Поэтому корней у такого уравнения не будет.

Замечание. Это верно для курса школьной программы, в которой не изучаются комплексные числа. Когда они вводятся, то получается, что и в этой ситуации ответов будет два.

Формулы для расчета корней квадратного уравнения, не использующие дискриминант

Речь идет о теореме Виета. Она действительна в случае, когда квадратное уравнение записывается в несколько другом виде:

х 2 + в * х + с = 0.

Тогда формула корней квадратного уравнения сводится к тому, чтобы выполнить решение двух линейных:

х 1 + х 2 = -в
и
х 1 * х 2 = с.

Оно решается за счет того, что из первого выводится выражение для одного из корней. И это значение нужно подставить во второе. Так будет найден второй корень, а потом первый.

К этому варианту всегда можно прийти от общего вида квадратного уравнения.

Достаточно только разделить все коэффициенты на «а».

Как быть, если нужно узнать наименьшее значение корня?

Решать уравнение и находить все возможные числа, которые подойдут для ответа. А потом выбрать самое малое. Это и будет наименьший корень уравнения.

Чаще всего такие вопросы встречаются в заданиях, которые имеют степень большую, чем 2, или содержат тригонометрические функции. Примером, когда нужно найти наименьший корень, может служить такое равенство:

2 х 5 + 2 х 4 — 3 х 3 — 3 х 2 + х + 1 = 0.

Чтобы найти каждое значение, которое можно назвать «корень уравнения», это равенство нужно преобразовать. Первое действие: сгруппировать его члены попарно: первый со вторым и так далее. Потом из каждой пары вынести общий множитель.

В каждой скобке останется (х + 1). Общим множителем в первой из пар будет 2 х 4 , во второй 3 х 2 . Теперь снова нужно выполнить вынесение общего множителя, которым будет являться одинаковая скобка.

После множителя (х + 1) будет стоять (2 х 4 — 3 х 2 + 1). Произведение двух множителей равняется нулю, только если один из них принимает значение, равное нулю.

Первая скобка равна нулю при х = -1. Это будет одним из корней уравнения.

Другие будут получены из уравнения, образованного второй скобкой, приравненной к нулю. Оно биквадратное. Для его решения нужно ввести обозначение: х 2 = у. Тогда уравнение существенно преобразится и примет привычный вид квадратного уравнения.

Его дискриминант равен Д = 1. Он больше нуля, значит корней будет два. Первый корень оказывается равным 1, второй будет 0,5. Но это значения для «у».

Нужно вернуться к введенному обозначению. х 1,2 = ± 1, х 3,4 = ± √0,5. Все корни уравнения: -1; 1; -√0,5; √0,5. Наименьший из них — -1. Это ответ.

В качестве заключения

Напоминание: все уравнения нужно проверять на то, подходит ли корень. Может быть, он посторонний? Стоит выполнить проверку предложенного примера.

Если подставить в изначально данное уравнение вместо «х» единицу, то получается, что 0 = 0. Этот корень верный.

Если х = -1, то получается такой же результат. Корень тоже подходящий.

Аналогично, при значениях «х» равных -√0,5 и √0,5 опять выходит верное равенство. Все корни подходят.

Этот пример не дал посторонних корней. Такое бывает не всегда. Вполне могло оказаться, что самое маленькое значение не подходило бы при проверке. Тогда пришлось бы выбирать из оставшихся.

Вывод: надо помнить о проверке и внимательно подходить к решению.

Сегодня мы будем тренировать навык решения задания 5 ЕГЭ — найдите корень уравнения. Будем искать корень уравнения. Рассмотрим примеры решения такого рода заданий. Но для начала, давайте вспомним — что значит — найти корень уравнения?

Это значит найти такое, зашифрованное под х число, которое мы подставим вместо x и наше уравнение будет верным равенством.

Например, 3x=9 — это уравнение, а 3 . 3=9 — это уже верное равенство. То есть в данном случае, мы вместо x подставили число 3 — получили верное выражение или равенство, это означает, что мы решили уравнение, то есть нашли данное число x=3, которое превращает уравнение в верное равенство.

Вот этим мы и займемся — будем находить корень уравнения.

Задание 1 — найдите корень уравнения 2 1-4x =32

Это показательное уравнение. Оно решается следующим образом — нужно чтобы и слева, и справа от знака «равно» была степень с одинаковым основанием.

Слева у нас основание степени 2, а справа — степени нет вовсе. Но мы знаем, что 32 — это 2 в пятой степени. То есть, 32=2 5

Таким образом, наше уравнение будет выглядеть так: 2 1-4х =2 5

Слева и справа у нас основания степени одинаковы, значит, чтобы у нас было равенство, должны быть равны и показатели степени:

Получаем обыкновенное уравнение. Решаем обычным способом — все неизвестные оставляем слева, а известные переносим вправо, получим:

Делаем проверку: 2 1-4(-1) =32

Мы нашли корень уравнение. Ответ: х=-1.

Самостоятельно найдите корень уравнения в следующих заданиях:

б) 2 1-3х =128

Задание 2 — найдите корень уравнения

Уравнение решаем аналогично — путем приведения левой и правой частей уравнения к одному основанию степени. В нашем случае — к основанию степени 2.

Используем следующее свойство степени:

По этому свойству мы получим для правой части нашего уравнения:

Если равны основания степени, значит, равны и показатели степени:

Ответ: х=9.

Сделаем проверку — подставим найденное значение х в исходное уравнение — если мы получим верное равенство, значит, мы решили уравнение правильно.

Мы нашли корень уравнения правильно.

Задание 3 — найдите корень уравнения

Заметим, что справа у нас стоит 1/8, а 1/8 — это

Тогда наше уравнение запишется в виде:

Если основания степени равны, значит, равны и показатели степени, получим простое уравнение:

Ответ: х=5. Проверку сделайте самостоятельно.

Задание 4 — найдите корень уравнения log 3 (15-х)=log 3 2

Это уравнение решается также как и показательное. Нам нужно, чтобы основания логарифмов слева и справа от знака «равно» были одинаковыми. Сейчас они одинаковы, значит, приравниваем те выражения, которые стоят под знаком логарифмов:

Ответ: х=13

Задание 5 — найдите корень уравнения log 3 (3-x)=3

Число 3 — это log 3 27. Чтобы было понятно внизу нижним индексом под знаком логарифма стоит число которое возводится в степень, в нашем случае 3, под знаком логарифма стоит число, которое получилось при возведении в степень — это 27, а сам логарифм — это показатель степени, в которую нужно возвести 3, чтобы получить 27.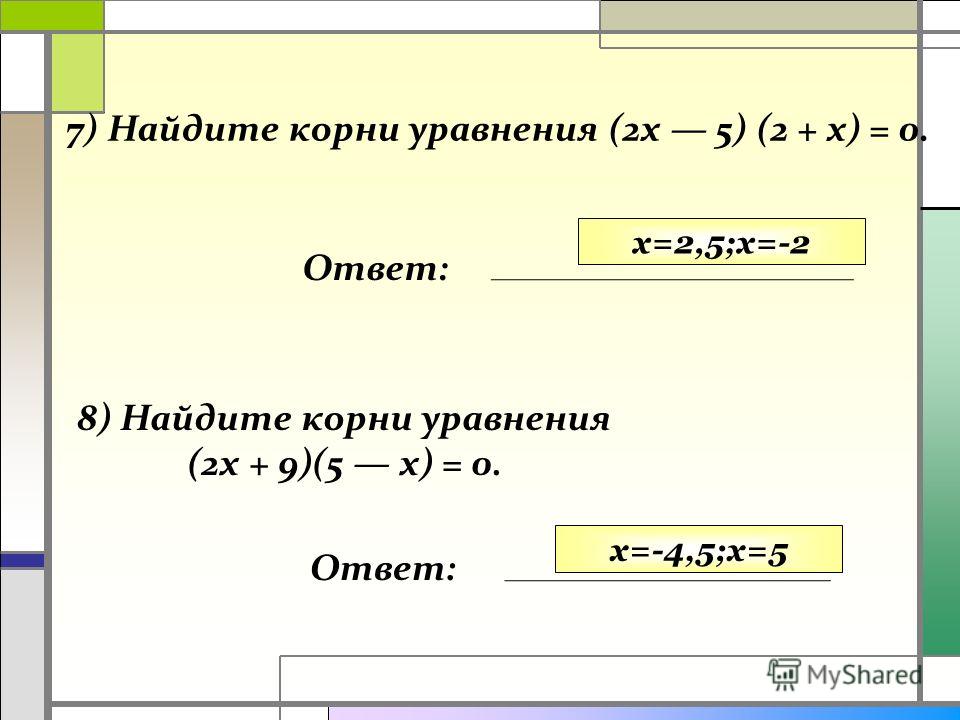

Смотрите на картинке:

Таким образом, любое число можно записать в виде логарифма. В данном случае очень удобно записать число 3 в виде логарифма с основанием 3. Получим:

log 3 (3-x)=log 3 27

Основания логарифмов равны, значит, равны и числа, стоящие под знаком логарифма:

Сделаем проверку:

log 3 (3-(-24))=log 3 27

log 3 (3+24)= log 3 27

log 3 27=log 3 27

Ответ: x=-24.

Найдите корень уравнения. Задание 6.

log 2 (x+3)=log 2 (3x-15)

Проверка: log 2 (9+3)=log 2 (27-15)

log 2 12=log 2 12

Ответ: x=9.

Найдите корень уравнения. Задание 7.

log 2 (14-2x)=2log 2 3

log 2 (14-2x)=log 2 3 2

Проверка: log 2 (14-5)=2log 2 3

log 2 9=2log 2 3

log 2 3 2 =2log 2 3

2log 2 3=2log 2 3

Ответ: x=2,5

Подготовьтесь к ЕГЭ и к ОГЭ -посмотрите предыдущие темы и .

\(2x+1=x+4\) находим ответ: \(x=3\). Если подставить тройку вместо икса, получатся одинаковые значения слева и справа:

\(2x+1=x+4\)
\(2\cdot3+1=3+4\)
\(7=7\)

И никакое другое число, кроме тройки такого равенства нам не даст. {2}+15\cdot(-2)+22=0\)
\(2\cdot4-30+22=0\)
\(0=0\) — сошлось, значит \(-2\) — корень уравнения

Очевидно, что решать уравнения перебором всех возможных значений – безумие, ведь чисел бесконечно много. Потому были разработаны специальные методы нахождения корней. Так, например, для достаточно одних только , для – уже используются формулы и т.д. Каждому типу уравнений – свой метод.

Ответы на часто задаваемые вопросы

Вопрос: Может ли корень уравнения быть равен нулю?
Ответ: Да, конечно. Например, уравнение \(3x=0\) имеет единственный корень — ноль. Можете проверить подстановкой.

Вопрос: Когда в уравнении нет корней?
Ответ: В уравнении может не быть корней, если нет таких значений для икса, которые сделают уравнение верным равенством. Яркий примером тут может быть уравнение \(0\cdot x=5\). 2-5x-6=0\) имеет два корня: \(x_1=-1\) и \(x_2=6\). Меньший из корней: \(-1\). Вот его и надо будет записать в ответ. Если бы спрашивали про больший корень, то надо было бы записать \(6\).

В алгебре существует понятие двух видов равенств — тождества и уравнения. Тождества — это такие равенства, которые выполнимы при любых значениях букв, в них входящих. Уравнения — это тоже равенства, но выполнимы они лишь при некоторых значениях входящих в них букв.

Буквы по условию задачи обычно бывают неравноправными. Это значит, что одни из них могут принимать любые допустимые значения, называемые коэффициентами (или параметрами), другие же — их называют неизвестными — принимают значения, которые необходимо найти в процессе решения. Как правило, неизвестные величины обозначают в уравнениях буквами, последними в (x.y.z и т.д.), либо такими же буквами, но с индексом (х 1 ,х 2 , и т.д.), а известные коэффициенты — первыми буквами того же алфавита.

По количеству неизвестных выделяют уравнения с одним, двумя и несколькими неизвестными. Таким образом, все значения неизвестных, при которых решаемое уравнение превращается в тождество, называются решениями уравнений. Уравнение можно считать решенным в том случае, если найдены все его решения или доказано, что оно таковых не имеет. Задание «решить уравнение» на практике встречается часто и означает, что нужно отыскать корень уравнения.

Определение : корнями уравнения называются те значения неизвестных из области допустимых, при которых решаемое уравнение превращается в тождество.

Алгоритм решения абсолютно всех уравнений одинаков, и смысл его заключается в том, чтобы с помощью математических преобразований данное выражение привести к более простому виду.
Уравнения, которые имеют одинаковые корни, в алгебре называются равносильными.

Простейший пример: 7х-49=0, корень уравнения х=7;
х-7=0, аналогично, корень х=7, следовательно, уравнения равносильные. (В частных случаях равносильные уравнения могут совсем не иметь корней).

Если корень уравнения одновременно является корнем другого, более простого уравнения, полученного из исходного путем преобразований, то последнее называется следствием предыдущего уравнения.

Если их двух уравнений одно является следствием другого, то они считаются равносильными. Еще их называют эквивалентными. Приведенный выше пример это иллюстрирует.

Решение даже самых простых уравнений на практике нередко вызывает сложности. В результате решения можно получить один корень уравнения, два и более, даже бесконечное количество — зависит это от вида уравнений. Есть и такие, у которых нет корней, они называются неразрешимыми.

Примеры:
1) 15х -20=10; х=2. Это единственный корень уравнения.
2) 7х — y=0. Уравнение имеет бесконечное множество корней, так как у каждой переменной может быть бесчисленное количество значений.
3) х 2 = — 16. Число, возведенное во вторую степень, всегда дает положительный результат, поэтому невозможно отыскать корень уравнения. Это и есть одно из неразрешимых уравнений, о которых говорилось выше.

Правильность решения проверяется подстановкой найденных корней вместо букв и решением получившегося примера. Если тождество соблюдается, решение верное. +15\cdot(-2)+22=0\)\(2\cdot4-30+22=0\)\(0=0\) — сошлось, значит \(-2\) — корень уравнения

Очевидно, что решать уравнения перебором всех возможных значений – безумие, ведь чисел бесконечно много. Потому были разработаны специальные методы нахождения корней. Так, например, для Линейных уравнений достаточно одних только Равносильных преобразований , для Квадратных – уже используются формулы Дискриминанта и т. д. Каждому типу уравнений – свой метод.

Ответы на часто задаваемые вопросы

Вопрос: Может ли корень уравнения быть равен нулю?
Ответ: Да, конечно. Например, уравнение \(3x=0\) имеет единственный корень — ноль. Можете проверить подстановкой.

Вопрос: Когда в уравнении нет корней?
Ответ: В уравнении может не быть корней, если нет таких значений для икса, которые сделают уравнение верным равенством. Яркий примером тут может быть уравнение \(0\cdot x=5\). 2-5x-6=0\) имеет два корня: \(x_1=-1\) и \(x_2=6\). Меньший из корней: \(-1\). Вот его и надо будет записать в ответ. Если бы спрашивали про больший корень, то надо было бы записать \(6\).

Так, например, для линейных уравнений достаточно одних только равносильных преобразований, для квадратных уже используются формулы дискриминанта и т.

Cos-cos. ru

27.12.2018 12:59:33

2018-12-27 12:59:33

Источники:

Http://cos-cos. ru/math/95/

Как найти корень уравнения: линейного, квадратного, кубического. » /> » /> .keyword { color: red; }

Как найти корень уравнения в математике

Уравнения в математике так же важны, как глаголы в русском языке. Без умения находить корень уравнения сложно утверждать, что ученик усвоил курс алгебры. К тому же для каждого их вида существуют свои особенные пути решения.

Что это такое?

Уравнение – это два произвольных выражения, содержащих переменные величины, между которыми поставлен знак равенства. Причем количество неизвестных величин может быть произвольным. Минимальное количество – одна.

Решить его – это значит узнать, есть ли корень уравнения. То есть число, которое превращает его в верное равенство. Если его нет, то ответом является утверждение, что «корней нет». Но может быть и противоположное, когда ответом является множество чисел.

Какие виды уравнений существуют?

Линейное. Оно содержит переменную, степень которой равна единице.

Квадратное. Переменная стоит со степенью 2, или преобразования приводят к появлению такой степени. Уравнение высшей степени. Дробно-рациональное. Когда переменная величина оказывается в знаменателе дроби. С модулем. Иррациональное. То есть такое, которое содержит алгебраический корень.

Как решается линейное уравнение?

Оно является основным. К такому виду стремятся привести все остальные. Так как у него найти корень уравнения достаточно просто.

Сначала нужно выполнить возможные преобразования, то есть раскрыть скобки и привести подобные слагаемые. Перенести все одночлены с переменной величиной в левую часть равенства, оставив свободные члены в правой. Привести подобные члены в каждой части решаемого уравнения. В получившемся равенстве в левой его половине будет стоять произведение коэффициента и переменной, а в правой – число. Осталось найти корень уравнения, разделив число справа, на коэффициент перед неизвестной.

Как найти корни квадратного уравнения?

Сначала его нужно привести к стандартному виду, то есть раскрыть все скобки, привести подобные слагаемые и перенести все одночлены в левую часть. В правой части равенства должен остаться только ноль.

Воспользуйтесь формулой для дискриминанта. Возведите в квадрат коэффициент перед неизвестной со степенью «1». Перемножьте свободный одночлен и число перед переменной в квадрате с числом 4. Из полученного квадрата вычтите произведение. Оцените значение дискриминанта. Он отрицательный – решение закончено, так как у него корней нет. Равен нулю – ответом будет одно число. Положительный – два значения у переменной.

Как решить кубическое уравнение?

Сначала найдите корень уравнения x. Он определяется методом подбора из чисел, которые являются делителями свободного члена. Этот способ удобно рассмотреть на конкретном примере. Пусть уравнение имеет вид: х 3 — 3х 2 — 4х + 12 = 0.

Его свободный член равен 12. Тогда делителями, которые требуется проверить, будут положительные и отрицательные числа: 1, 2, 3, 4, 6 и 12. Перебор можно закончить уже на числе 2. Оно дает верное равенство в уравнении. То есть его левая часть оказывается равной нулю. Значит число 2 – это первый корень кубического уравнения.

Теперь необходимо разделить исходное уравнение на разность переменной и первого корня. В конкретном примере это (х — 2). Несложное преобразование приводит числитель к такому разложению на множители: (х — 2)(х + 2)(х — 3). Одинаковые множители числителя и знаменателя сокращаются, а оставшиеся две скобки при раскрытии дают простое квадратное уравнение: х 2 — х — 6 = 0.

Здесь найдите два корня уравнения по принципу, описанному в предыдущем разделе. Ими оказываются числа: 3 и -2.

Итого, у конкретного кубического уравнения получилось три корня: 2, -2 и 3.

Как решаются системы линейных уравнений?

Здесь предложен метод исключения неизвестных. Он заключается в том, чтобы выразить одну неизвестную через другую в одном уравнении и подставить это выражение в другое. Причем решением системы из двух уравнений с двумя неизвестными всегда является пара переменных величин.

Если в них переменные обозначены буквами х1 и х2, то можно из первого равенства вывести, к примеру, х2. Потом оно подставляется во второе. Проводится необходимое преобразование: раскрытие скобок и приведение подобных членов. Получается простое линейное уравнение, корень которого вычислить легко.

Теперь возвратитесь к первому уравнению и найдите корень уравнения x2, используя получившееся равенство. Эти два числа являются ответом.

Простой совет

Для того чтобы быть уверенным в полученном ответе, рекомендуется всегда делать проверку. Ее не обязательно записывать.

Если решается одно уравнение, то каждый из его корней нужно подставить в исходное равенство и получить одинаковые числа в обеих его частях. Все сошлось – решение верное.

При работе с системой корни необходимо подставлять в каждое решение и выполнять все возможные действия. Получается верное равенство? Значит решение правильное.

Уравнения в математике так же важны, как глаголы в русском языке. Без умения находить корень уравнения сложно утверждать, что ученик усвоил курс алгебры. К тому же для каждого их вида существуют свои особенные пути решения.

Уравнение – это два произвольных выражения, содержащих переменные величины, между которыми поставлен знак равенства. Причем количество неизвестных величин может быть произвольным. Минимальное количество – одна.

Решить его – это значит узнать, есть ли корень уравнения. То есть число, которое превращает его в верное равенство. Если его нет, то ответом является утверждение, что «корней нет». Но может быть и противоположное, когда ответом является множество чисел.

Тогда делителями, которые требуется проверить, будут положительные и отрицательные числа 1, 2, 3, 4, 6 и 12.

Www. syl. ru

01.06.2019 5:56:54

2019-06-01 05:56:54

Источники:

Https://www. syl. ru/article/232469/new_kak-nayti-koren-uravneniya-lineynogo-kvadratnogo-kubicheskogo#:~:text=%D0%A2%D0%B0%D0%BA%20%D0%BA%D0%B0%D0%BA%20%D1%83%20%D0%BD%D0%B5%D0%B3%D0%BE%20%D0%BD%D0%B0%D0%B9%D1%82%D0%B8%20%D0%BA%D0%BE%D1%80%D0%B5%D0%BD%D1%8C%20%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D1%8F%20%D0%B4%D0%BE%D1%81%D1%82%D0%B0%D1%82%D0%BE%D1%87%D0%BD%D0%BE,%D0%BB%D0%B5%D0%B2%D1%83%D1%8E%20%D1%87%D0%B0%D1%81%D1%82%D1%8C%20%D1%80%D0%B0%D0%B2%D0%B5%D0%BD%D1%81%D1%82%D0%B2%D0%B0%2C%20%D0%BE%D1%81%D1%82%D0%B0%D0%B2%D0%B8%D0%B2%20%D1%81%D0%B2%D0%BE%D0%B1%D0%BE%D0%B4%D0%BD%D1%8B%D0%B5%20%D1%87%D0%BB%D0%B5%D0%BD%D1%8B%20%D0%B2%20%D0%BF%D1%80%D0%B0%D0%B2%D0%BE%D0%B9.

Решение уравнений с дробями — как решать дробные уравнения » /> » /> . keyword { color: red; }

Как найти корень уравнения в математике

Порой кажется, что на уроках по математике чем дальше, тем сложнее. Но на самом деле все темы, как кирпичики: если разобрался с дробями и уравнениями — решать дробные уравнения будет легко. Об этом и расскажем. Поехали!

О чем эта статья:

5 класс, 6 класс, 7 класс

Понятие дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это рациональное число, представленное в виде A/b, где A — числитель дроби, B — знаменатель. Есть два формата записи:

обыкновенный вид — ½ или a/b, десятичный вид — 0,5.

Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.

Дроби бывают двух видов:

Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5. Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.

Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.

Основные свойства дробей

Дробь не имеет значения, если делитель равен нулю.

Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.

Дроби a/b и c/d называют равными, если a × d = b × c.

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить.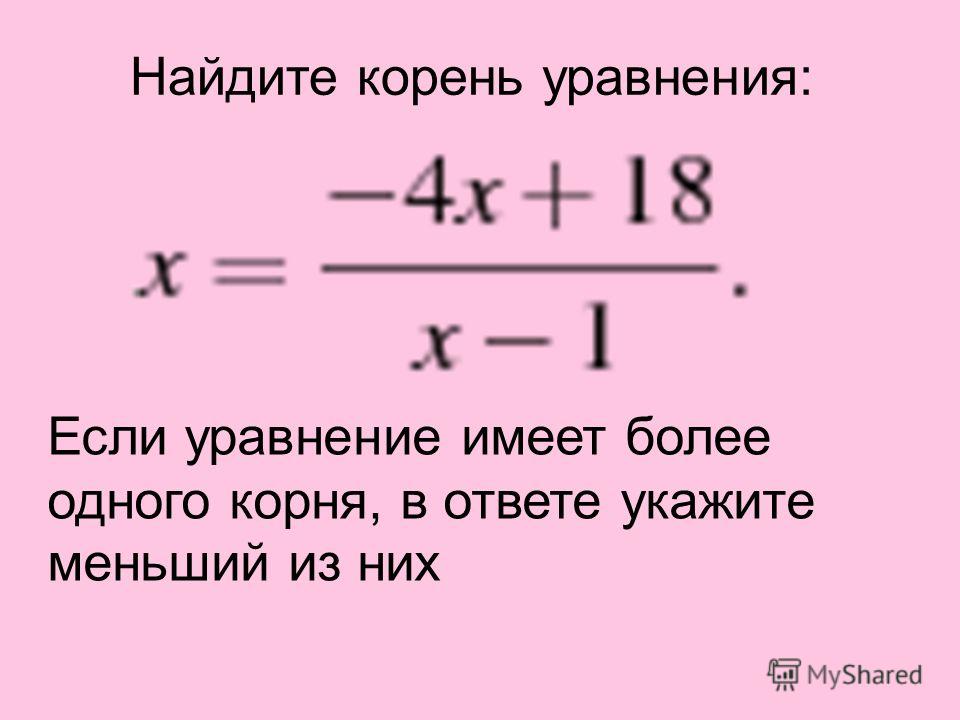 Также, дроби можно сравнивать между собой и возводить в степень.

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:

Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное. Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Решить уравнение значит найти все его корни или убедиться, что корней нет.

Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.

Что поможет в решении:

если А не равно нулю, то у уравнения единственный корень: х = −b : а; если А равно нулю, а B не равно нулю — у уравнения нет корней; если А и B равны нулю, то корень уравнения — любое число.

Понятие дробного уравнения

Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:

Такие уравнения еще называют Дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.

Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:

На алгебре в 8 классе можно встретить такое понятие, как Область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.

Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.

Как решать уравнения с дробями

1. Метод пропорции

Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: Произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.

Итак, у нас есть линейное уравнение с дробями:

В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.

После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.

2. Метод избавления от дробей

Возьмем то же самое уравнение, но попробуем решить его по-другому.

В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:

подобрать число, которое можно разделить на каждый из знаменателей без остатка; умножить на это число каждый член уравнения.

Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!

Вот так просто мы получили тот же ответ, что и в прошлый раз.

Что еще важно учитывать при решении

если значение переменной обращает знаменатель в 0, значит это неверное значение; делить и умножать уравнение на 0 нельзя.

Универсальный алгоритм решения

Определить область допустимых значений.

Найти общий знаменатель.

Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.

Раскрыть скобки, если нужно и привести подобные слагаемые.

Решить полученное уравнение.

Сравнить полученные корни с областью допустимых значений.

Записать ответ, который прошел проверку.

Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.

Примеры решения дробных уравнений

Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.

Пример 1. Решить дробное уравнение: 1/x + 2 = 5.

Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля. Отсчитываем справа налево в числителе дробной части три знака и ставим запятую. Избавимся от знаменателя. Умножим каждый член уравнения на х.

Пример 2. Найти корень уравнения

Область допустимых значений: х ≠ −2. Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2) Избавимся от знаменателя. Умножим каждый член уравнения на х.

Пример 3. Решить дробное уравнение:

Пример 2. Найти корень уравнения

Область допустимых значений: х ≠ −2. Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2) Избавимся от знаменателя. Умножим каждый член уравнения на х.

Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.

Skysmart. ru

29.01.2018 19:22:54

2018-01-29 19:22:54

Источники:

Https://skysmart. ru/articles/mathematic/reshenie-uravnenij-s-drobyami

{{2}}$$$

$$${5}\ne{2}$$$

Поскольку равенство неверно, то $$${2}$$$ не является корнем уравнения.

Обратите внимание, что это уравнение не может иметь корней.

Решить уравнение означает найти все его корни.

В общем, решить уравнение довольно сложно. Часто корни можно найти только приблизительно (с помощью компьютера). Но мы будем рассматривать типы уравнений, которые легко решаются.

Упражнение 1. Определите, являются ли $$${2}$$$ и $$$-{2}$$$ корнями уравнения $$${2}{x}+{4}={ 0}$$$. 9{{2}}+{4}={0}$$$.

Ответ : ни одно из них не является корнем (на самом деле, это уравнение не имеет действительных корней).

• < Определение переменной
• Эквивалентные уравнения >

корней квадратного уравнения в Python с примерами кода

Корни квадратного уравнения в Python с примерами кода

В этом уроке мы попытаемся найти решение корней квадратного уравнения в Python с помощью программирования. Следующий код иллюстрирует это.

 #как найти корни в квадратном уравнении
a=int(input('Введите коэффициент x2 :'))
b=int(input('Введите коэффициент x:'))
c=int(input('Введите константу:'))
если а==0:
  print("а не может быть 0")
еще:
  Д=б**2-4*а*в
  если Д>0:
   print('Корни действительны и различны')
   r1=(-b+D**0,5)/(2*а)
   r2=(-b-D**0,5)/(2*а)
   print("Корни равны",r1,"и",r2)
  Элиф Д==0:
   print('Корни действительны и равны')
   г=-б/(2*а)
   print('Корень есть',r)
  еще:
   print('Корни мнимые')
#выход:
#настоящие и равные
Введите коэффициент x2 :1
Введите коэффициент x:-4
Введите константу :4
Корни вещественные и равные
Корень 2. 0
#не реальный
Введите коэффициент x2 :4
Введите коэффициент x:5
Введите константу :6
Корни воображаемые
#настоящие и не равные
Введите коэффициент x2 :1
Введите коэффициент x:-5
Введите константу :6
Корни настоящие и разные
Корни 3.0 и 2.0
 

Решение той же проблемы, корней квадратного уравнения в Python, также можно найти в другом методе, который будет обсуждаться ниже с некоторыми примерами кода.

 #корень квадратного уравнения
a=int(input('Введите коэффициент x2 :'))
b=int(input('Введите коэффициент x:'))
c=int(input('Введите константу:'))
импортировать математику как m
если а==0:
    print(a,'значение a не может быть равно нулю')
    print("\n прерывание!!!!!!")
еще:
    дельта=b**2- 4*a*c
    если дельта<0:
        root1=((-b + m.sqrt(дельта))/(2*a))
        root2=((-b - m.sqrt(дельта))/(2*a))
        print('корни действительны и различны')
        print('корни есть',root1,'и',root2)
    Элиф дельта == 0:
        root=((-b+ m.sqrt(дельта))/(2*a))
        print('корни действительны и равны')
        print('корень есть',корень,'каждый')
    еще:
        print('корни мнимые')
 

На множестве иллюстративных примеров мы продемонстрировали, как решать задачу «Корни квадратного уравнения в Python».

Как вы используете квадратичную функцию в Python?

Стандартная форма квадратного уравнения в Python записывается как px² + qx + r = 0. Корни квадратного уравнения можно классифицировать как:

• Если b*b < 4*a*c, то корни комплексные.
• Если b*b == 4*a*c, то корни вещественные, и оба корня одинаковы.
• Если b*b > 4*a*c, то корни действительны и различны.

Как найти корни квадратного уравнения?

Формула для нахождения корней квадратного уравнения: x = [-b ± √(b2 - 4ac)]/2a. Сумма корней квадратного уравнения равна α + β = -b/a. Произведение корня квадратного уравнения равно αβ = c/a. Квадратное уравнение, корнями которого являются α, β, равно x2 - (α + β)x + αβ = 0,

.

Можем ли мы решить квадратное уравнение в Python?

Эта программа вычисляет корни квадратного уравнения, когда известны коэффициенты a, b и c. Чтобы понять этот пример, вы должны иметь представление о следующих разделах программирования Python: Типы данных Python.

Как вы решаете уравнения в Python?

Чтобы решить два уравнения для двух переменных x и y, мы будем использовать функцию SymPysolve(). Функцияsolve() принимает два аргумента: набор уравнений (eq1, eq2) и набор переменных для решения (x, y). Объект решения SymPy — это словарь Python.02 октября 2018 г.

Что такое функция ABS в python?

Функция abs() возвращает абсолютное значение указанного числа.

В чем разница между математикой и Cmath в Python?

cmath vs math Модуль math предоставляет математические функции для чисел с плавающей запятой, а модуль cmath предоставляет эквивалентные функции для комплексных чисел. Комплексное число представляет собой комбинацию мнимого и действительного числа.16 июля 2020 г.

Как найти корни параболы?

Как написать программу переменного тока для нахождения корней квадратного уравнения?

Дизайн (Алгоритм)

• Старт.
• Чтение значений a, b, c.
• Вычислить d = b2 4ac.

  No related posts.