1.1.4 Операции над множествами
В результате операций над множествами из одних множеств могут получаться другие множества. Основные из этих операций – объединение, пересечение и дополнение множеств. Кроме того, часто применяются операции разности и симметрической разности множеств.
Объединение множеств. Пусть заданы множества A и В. Объединение этих множеств – множество, состоящее из всех тех и только тех элементов, которые принадлежат или множеству A, или множеству B (т.е. хотя бы одному из них). Объединение двух множеств обозначают как .
Аналогично определяется объединение нескольких множеств. Пусть даны множества . Их объединение — множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из этих множеств. Операция объединения в этом случае обозначается как, или.
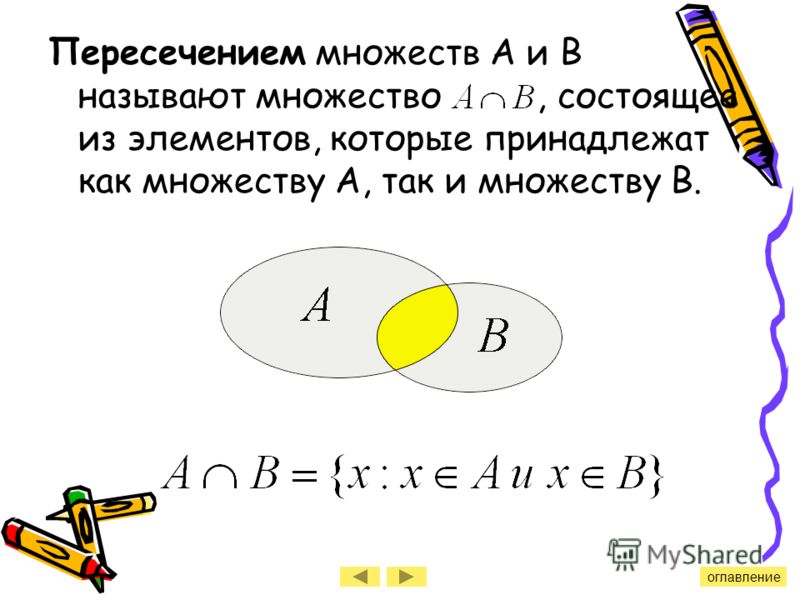
Пересечение множеств. Пусть заданы множества A и В
 Пересечение этих множеств – множество,
состоящее из всех тех и только тех
элементов, которые принадлежат и
множеству A,
и множеству B (т.е. обоим множествам сразу). Пересечение
двух множеств обозначают как
.
Пересечение этих множеств – множество,
состоящее из всех тех и только тех
элементов, которые принадлежат и
множеству A,
и множеству B (т.е. обоим множествам сразу). Пересечение
двух множеств обозначают как
.Аналогично определяется пересечение нескольких множеств. Пусть даны множества . Их пересечение — множество, состоящее из всех тех и только тех элементов, которые принадлежат всем этим множествам сразу. Операция пересечения в этом случае обозначается как, или.
Дополнение множества. Пусть задано множество A. Дополнение этого множества – множество, состоящее из всех тех и только тех элементов, которые не принадлежат множеству A. Дополнение множества обозначают как .
Разность
множеств.
Пусть заданы множества A и В.
Разность этих множеств – множество,
состоящее из всех тех и только тех
элементов, которые принадлежат множеству A,
но не принадлежат множеству B.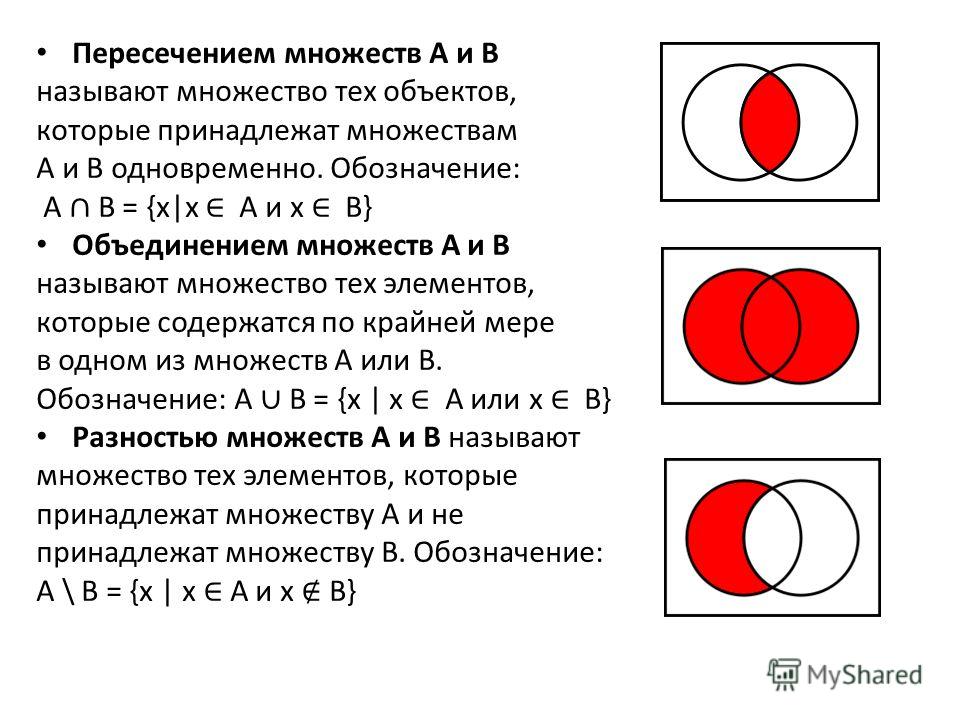 Разность множеств обозначают как S = A \ B.
Разность множеств обозначают как S = A \ B.
Симметрическая разность множеств. Пусть заданы множества A и В. Симметрическая разность этих множеств – множество, состоящее из всех тех и только тех элементов, которые принадлежат или множеству A, или множеству B, но не им обоим сразу. Симметрическую разность множеств обозначают как S = A B.
Следует обратить внимание, что операции пересечения и объединения выполняются с несколькими множествами (двумя или более), а операция дополнения – с одним множеством. Операции разности и симметрической разности выполняются с двумя множествами.
Операции разности и симметрической разности можно выразить через операции пересечения, объединения и дополнения:
, (1.1)
. (1.2)
Эти равенства можно доказать на основе определений операций над множествами.
Пример 1. 1 – Даны
множества: A = {2, 7, 9, 12}, B = {3, 6, 7, 12, 15}. Выполнить над этими множествами
операции, рассмотренные выше.
1 – Даны
множества: A = {2, 7, 9, 12}, B = {3, 6, 7, 12, 15}. Выполнить над этими множествами
операции, рассмотренные выше.
A B = {7, 12}
A B = {2, 3, 6, 7, 9, 12, 15}
A \ B = {2, 9}
B \ A = {3, 6, 15}
A B = {2, 3, 9, 15}.
Чтобы найти дополнения множеств A и B, необходимо уточнить, что в данной задаче имеется в виду под универсальным множеством. Пусть под ним имеется в виду все множество целых чисел (обозначим его как Z). Тогда дополнение множества A можно записать как = { a | a Z, a A}. Аналогично записывается дополнение множества B: = {b | b Z, b B}.
Примечания
1Числа во множествах записаны по
возрастанию только для удобства.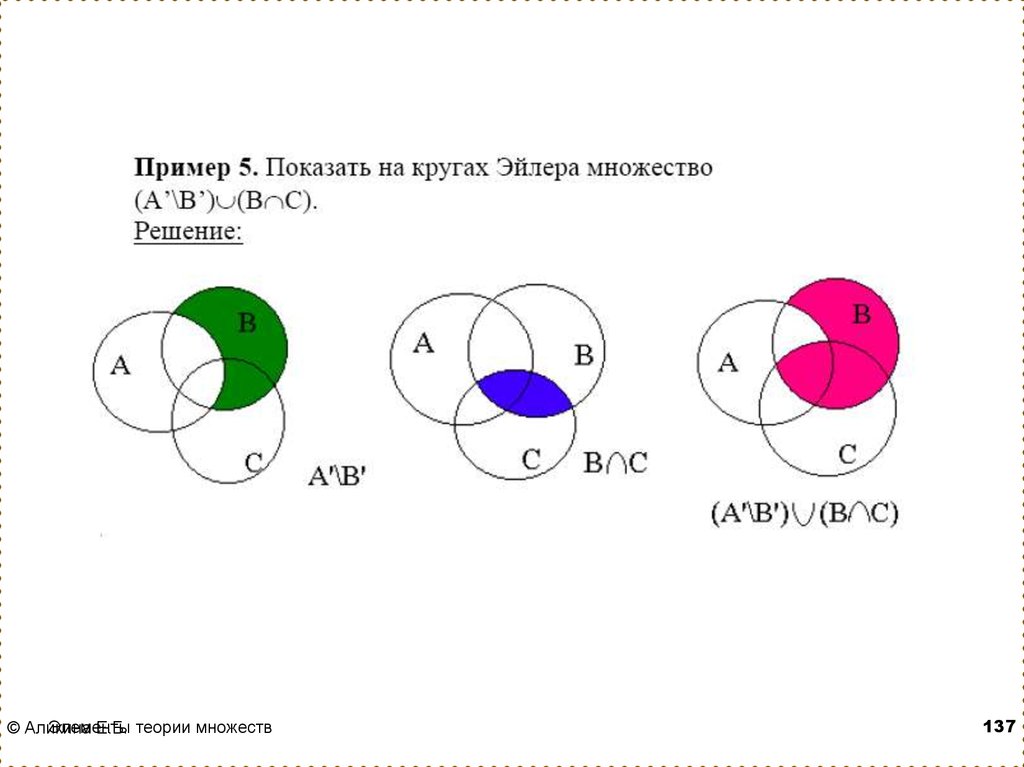 На
самом деле, порядок элементов во
множествах безразличен. Поэтому,
например, пересечение множествAиBможно записать и
как {7, 12}, и как {12, 7}.
На
самом деле, порядок элементов во
множествах безразличен. Поэтому,
например, пересечение множествAиBможно записать и
как {7, 12}, и как {12, 7}.
2Следует обратить внимание, что в операциях пересечения, объединения, а также симметрической разности порядок множеств, с которыми выполняется операция, безразличен:,,AB=BA. Говорят, что эти операции обладают свойством коммутативности. В то же времяA\BB\A.
Пример 1.2 – Даны множества:
X = AB = {x | 5 x 17}
X = AB = {x | x < 20}
X = A \ B = {x | 17 < x < 20}
X = B \ A = {x | x < 5}
X = AC = {x | 10 < x 12}
X = AC = {x | 5 x < 20}
X = A \ C = {x | 5 x 10 или 12 < x < 20}
X = C \ A =
X = = {x | x < 5 или x 20}
X = = {x | x 17}.
НОУ ИНТУИТ | Лекция | Множества
Аннотация: Реализация множеств в Прологе. Операции над множествами: превращение списка во множество, принадлежность элемента множеству, объединение, пересечение, разность, включение, дополнение.
Ключевые слова: множество, встроенные структуры, домен, список, значение, ПО, теоретико-множественные операции, предикат, хвост списка, операции, принадлежность элемента множеству, операция объединения, операция пересечения, операция разности, мощность множества, параметр, аргумент, базис индукции, базис, рекурсия, вычитание, тождество, отношение, операция включения, очередь, подмножество, разность, операция дополнения, Законы де Моргана
В данной лекции мы попробуем реализовать некоторое приближение математического понятия «множество» в Прологе. Заметим, что в Прологе, в отличие от некоторых императивных языков программирования, нет такой встроенной структуры данных, как множество. И, значит, нам придется реализовывать это понятие, опираясь на имеющиеся стандартные домены. В качестве базового домена используем стандартный списковый домен, с которым мы работали на протяжении двух последних лекций.
В качестве базового домена используем стандартный списковый домен, с которым мы работали на протяжении двух последних лекций.
Итак, что мы будем понимать под множеством? Просто список, который не содержит повторных вхождений элементов. Другими словами, в нашем множестве любое значение не может встречаться более одного раза.
На самом деле я не знаю ни одной реализации понятия множества, которая бы достаточно точно соответствовала этому математическому объекту. Наше подобие множества также, по большому счету, лишь отчасти будет приближаться к «настоящему» множеству.
Нам предстоит разработать предикаты, которые реализуют основные теоретико-множественные операции.
Начнем с написания предиката, превращающего произвольный список во множество, в том смысле, в котором мы договорились понимать этот термин. Для этого нужно удалить все повторные вхождения элементов. При этом мы воспользуемся предикатом delete_all, который был создан нами ранее, в седьмой лекции. Предикат будет иметь два аргумента: первый — исходный список (возможно, содержащий повторные вхождения элементов), второй — выходной (то, что остается от первого аргумента после удаления повторных вхождений элементов).
Для этого нужно удалить все повторные вхождения элементов. При этом мы воспользуемся предикатом delete_all, который был создан нами ранее, в седьмой лекции. Предикат будет иметь два аргумента: первый — исходный список (возможно, содержащий повторные вхождения элементов), второй — выходной (то, что остается от первого аргумента после удаления повторных вхождений элементов).
Предикат будет реализован посредством рекурсии. Базисом рекурсии является очевидный факт: в пустом списке никакой элемент не встречается более одного раза. По правде говоря, в пустом списке нет ни одного элемента, который встречался бы в нем хотя бы один раз, то есть в нем вообще нет элементов. Шаг рекурсии позволит выполнить правило: чтобы сделать из непустого списка множество (в нашем понимании этого понятия), нужно удалить из хвоста списка все вхождения первого элемента списка, если таковые вдруг обнаружатся. После выполнения этой операции первый элемент гарантированно будет встречаться в списке ровно один раз. Для того чтобы превратить во множество весь список, остается превратить во множество хвост исходного списка. Для этого нужно только рекурсивно применить к хвосту исходного списка наш предикат, удаляющий повторные вхождения элементов. Полученный в результате из хвоста список с приписанным в качестве головы первым элементом и будет требуемым результатом ( множеством, т.е. списком, образованным элементами исходного списка и не содержащим повторных вхождений элементов).
Для того чтобы превратить во множество весь список, остается превратить во множество хвост исходного списка. Для этого нужно только рекурсивно применить к хвосту исходного списка наш предикат, удаляющий повторные вхождения элементов. Полученный в результате из хвоста список с приписанным в качестве головы первым элементом и будет требуемым результатом ( множеством, т.е. списком, образованным элементами исходного списка и не содержащим повторных вхождений элементов).
Закодируем наши рассуждения.
list_set([],[]). /* пустой список является множеством
в нашем понимании */
list_set ([H|T],[H|T1]) :–
delete_all(H,T,T2),
/* T2 — результат удаления
вхождений первого элемента
исходного списка H из хвоста T */
list_set (T2,T1).
/* T1 — результат удаления
повторных вхождений элементов
из списка T2 */ intuit.ru/2010/edi»>Например, если применить этот предикат к списку [1,2,1,2,3, 2,1], то результатом будет список [1,2,3].Заметим, что в предикате, обратном только что записанному предикату list_set и переводящем множество в список, нет никакой необходимости по той причине, что наше множество уже является списком.
Теперь займемся реализацией теоретико-множественных операций, таких как принадлежность элемента множеству, объединение, пересечение, разность множеств и т.д.
При реализации этих предикатов можно было бы воспользоваться предикатами, предназначенными для работы с обыкновенными списками, но в результате их применения могут получаться списки, содержащие некоторые элементы несколько раз, даже если исходные списки были множествами, в нашем понимании этого слова.
Можно, конечно, после каждого применения теоретико-множественной операции превращать полученный список обратно во множество применением вышеописанного предиката list_set, но это было бы не очень удобно. Вместо этого мы попробуем написать каждую из теоретико-множественных операций так, чтобы в результате ее работы гарантированно получалось множество.
Вместо этого мы попробуем написать каждую из теоретико-множественных операций так, чтобы в результате ее работы гарантированно получалось множество.
Итак, приступим.
В качестве реализации операции принадлежности элемента множеству вполне можно использовать предикат member3, который мы разработали в седьмой лекции, когда только начинали знакомиться со списками. Напомним, что факт принадлежности элемента x множеству A в математике принято обозначать следующим образом: .
Для того чтобы найти мощность множества, вполне подойдет предикат length, рассмотренный нами в седьмой лекции. Напомним, что для конечного множества мощность — это количество элементов во множестве .
Пример. Реализуем операцию объединения двух множеств. На всякий случай напомним, что под объединением двух множеств понимают множество, элементы которого принадлежат или первому, или второму множеству. Обозначается объединение множеств A и B через . В математической записи это выглядит следующим образом: . На рисунке объединение множеств A и B обозначено штриховкой.
Обозначается объединение множеств A и B через . В математической записи это выглядит следующим образом: . На рисунке объединение множеств A и B обозначено штриховкой.
Рис. 9.1. Объединение множеств A и B
У соответствующего этой операции предиката должно быть три параметра: первые два — множества, которые нужно объединить, третий параметр — результат объединения двух первых аргументов. В третий аргумент должны попасть все элементы, которые входили в первое или второе множество. При этом нам нужно проследить, чтобы ни одно значение не входило в итоговое множество несколько раз. Такое могло бы произойти, если бы мы попытались, например, воспользоваться предикатом conc (который мы рассмотрели в седьмой лекции), предназначенным для объединения списков. Если бы какое-то значение встречалось и в первом, и во втором списках, то в результирующий список оно бы попало, по крайней мере, в двойном количестве. Значит, вместо использования предиката conc нужно написать новый предикат, применение которого не приведет к ситуации, в которой итоговый список уже не будет множеством за счет того, что некоторые значения будут встречаться в нем более одного раза.
Значит, вместо использования предиката conc нужно написать новый предикат, применение которого не приведет к ситуации, в которой итоговый список уже не будет множеством за счет того, что некоторые значения будут встречаться в нем более одного раза.
Без рекурсии мы не обойдемся и здесь. Будем вести рекурсию по первому из объединяемых множеств. Базис индукции: объединяем пустое множество с некоторым множеством. Результатом объединения будет второе множество. Шаг рекурсии будет реализован посредством двух правил. Правил получается два, потому что возможны две ситуации: первая — голова первого множества является элементом второго множества, вторая — первый элемент первого множества не входит во второе множество. В первом случае мы не будем добавлять голову первого множества в результирующее множество, она попадет туда из второго множества. Во втором случае ничто не мешает нам добавить первый элемент первого списка. Так как этого значения во втором множестве нет, и в хвосте первого множества оно также не может встречаться (иначе это было бы не множество ), то и в результирующем множестве оно также будет встречаться только один раз.
Давайте запишем эти рассуждения:
union([ ],S2,S2). /* результатом объединения
пустого множества со множеством S2
будет множество S2 */
union([H|T],S2,S):–
member3(H,S2),
/* если голова первого
множества H принадлежит второму
множеству S2, */
!,
union(T,S2,S).
/* то результатом S будет
объединение хвоста первого
множества T и второго
множества S2 */
union([H |T],S2,[H|S]):–
union(T,S2,S).
/* в противном случае результатом
будет множество, образованное
головой первого множества H
и хвостом, полученным объединением
хвоста первого множества T
и второго множества S2 */Если объединить множество [1,2,3,4] со множеством [3,4,5], то в результате получится множество [1,2,3,4,5].
Объединение, пересечение и дополнение | Математика для гуманитарных наук |
Обычно наборы взаимодействуют. Например, вы с новым соседом по комнате решаете устроить домашнюю вечеринку и приглашаете друзей. На этой вечеринке объединяются два набора, хотя может оказаться, что есть друзья, которые были в обоих наборах.
Объединение, пересечение и дополнение
Объединение двух наборов содержит все элементы, содержащиеся в любом наборе (или в обоих наборах).
Союз отмечен A ⋃ B.
Подробнее, x ∊ A ⋃ B , если x ∊ A или x ∊ B (или оба) оба) оба) оба) оба) оба) оба (или оба) оба (или оба) оба) оба) (или оба) оба) (или оба) оба) оба) (или оба) оба) (или оба) оба) (или оба) оба).
Пересечение двух наборов содержит только те элементы, которые есть в обоих наборах.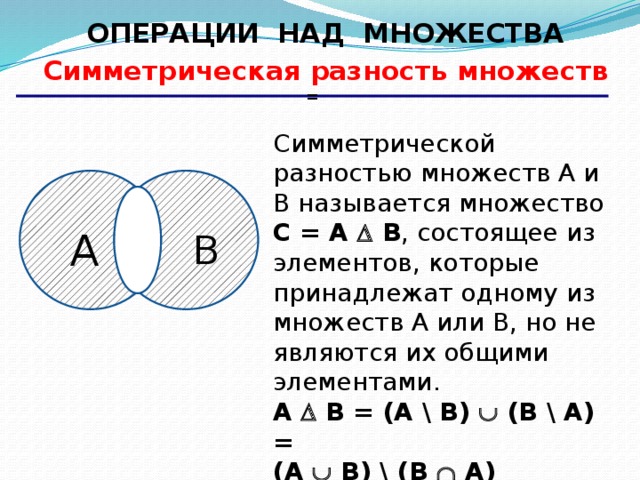
Пересечение обозначается A ⋂ B.
Более формально, x ∊ A ⋂ B , если x ∊ A и x ∊ B
Дополнение набора A содержит все, что является , а не в наборе A .
Дополнение обозначается как A’ , или Ac , или иногда ~ A .
Пример 5
Рассмотрим множества: A = {красный, зеленый, синий} B = {красный, желтый, оранжевый}
C = {красный, оранжевый, желтый, зеленый, синий, фиолетовый}
a) Найти A ⋃ B
Объединение содержит все элементы любого набора: A ⋃ B = {красный, зеленый, синий, желтый, оранжевый}
Обратите внимание, что мы перечисляем только красный цвет однажды.
B) Найти A ⋂ B
В перекрестке содержится все элементы в обоих наборах: A ⋂ B = {RED}
C) Найти AC ⋂ C
C). мы ищем все элементы, которые равны а не в наборе A а также есть в C .
мы ищем все элементы, которые равны а не в наборе A а также есть в C .
Ac ⋂ C = {оранжевый, желтый, фиолетовый}
Попробуйте сейчас 2
Используя наборы из предыдущего примера, найдите A ⋃ C и Bc ⋂ A
. фуксия для щенков и арахисовое масло входят в комплектацию набора. По этой причине дополнения обычно используются только с пересечениями или когда у нас есть универсальный набор.
Универсальный набор
Универсальный набор — это набор, содержащий все интересующие нас элементы. Это должно определяться контекстом.
Дополнение относится к универсальному набору, поэтому Ac содержит все элементы универсального набора, которых нет в A .
Пример 6
а) Если бы мы обсуждали поиск книг, универсальный набор мог бы состоять из всех книг в библиотеке.
b) Если бы мы группировали ваших друзей на Facebook, универсальным набором были бы все ваши друзья на Facebook.
c) Если вы работали с наборами чисел, универсальный набор может состоять из всех целых чисел, всех целых чисел или всех действительных чисел
Пример 7
Предположим, что универсальный набор равен U = все целые числа от 1 до 9. Если A = {1, 2, 4}, то
Ac = {3, 5, 6, 7, 8, 9} .
Как мы видели ранее с выражением Ac ⋂ C , операции над множествами можно группировать вместе. Символы группировки можно использовать так же, как и с арифметикой — для принудительного порядка операций.
Пример 8
Предположим, H = {кошка, собака, кролик, мышь}, F = {собака, корова, утка, свинья, кролик}
W = {утка, кролик, олень, лягушка, мышь}
a ) Найдите ( H ⋂ F ) ⋃ W
Начнем с пересечения: H ⋂ F = {собака, кролик}
H ⋂ F ) ⋃ W = {собака, утка, кролик, олень, лягушка, мышь}
б) Находим H ⋂ ( F ⋃ W )
Начинаем с союза: F ⋃ W = {собака, корова, мышь, лягушка, свинья, олень }
Теперь мы пересекаем этот результат с H : H ⋂ ( F ⋃ W ) = {Dog, Rabbit, мышь}
C) Найти ( H ⋂ F )
C) ⋂ З
Начинаем с пересечения: Н ⋂ Ж = {dog, rabbit}
Now we want to find the elements of W that are not in H ⋂ F
( H ⋂ F ) c ⋂ W = {утка, олень, лягушка, мышь}
Лицензии и атрибуты
Контент по лицензии CC, совместно используемый ранее
- Математика в обществе.
 Автор : Open Textbook Store, Transition Math Project и Open Course Library. Расположен по адресу : http://www.opentextbookstore.com/mathinsociety/. Лицензия : CC BY-SA: Attribution-ShareAlike
Автор : Open Textbook Store, Transition Math Project и Open Course Library. Расположен по адресу : http://www.opentextbookstore.com/mathinsociety/. Лицензия : CC BY-SA: Attribution-ShareAlike
Документ без названия
Документ без названия
С наборами можно выполнять множество операций:
- Мы можем найти UNION из двух наборов. Мы находим UNION двух наборов, беря каждый элемент, который есть в любом наборе, и объединяя все эти элементы в один большой набор. Для обозначения ОБЪЕДИНЕНИЕ A и B мы пишем: A B. Таким образом, объединение A и B представляет собой большее множество, содержащее как A, так и B.
Формально мы можем написать: A B = {x| х А или х В}.
(Помните, мы бы сказали вслух: «множество всех x, таких, что x является элементом A или x является элементом B».
Если элемент находится в объединении A и B, это означает, что он находится в A ИЛИ в B.
Чтобы увидеть, как объединение выглядит на диаграмме Венна, мы нарисуем наши два множества A и B на диаграмме Венна, как показано ниже:0003
Тогда затенение A B красным цветом будет выглядеть так:
Давайте рассмотрим несколько наборов и потренируемся в их объединении.
- Пусть A={1.1, 1.2, 1.3} и B={1.2, 1.4, 1.6}. Если мы возьмем каждый элемент A и каждый элемент B и сложим их все вместе, мы получим A B = {1,1, 1,2, 1,3, 1,4, 1,6}.
- Пусть A={0,1,2,3,4} и пусть B={5,6,7,8,9,10}. Тогда, если мы возьмем каждый элемент A и каждый элемент B и сложим их вместе, мы получим A B = {0,1,2,3,4,5,6,7,8,9,10}.
- Мы можем найти ПЕРЕКРЕСТОК из двух наборов. Мы находим ПЕРЕСЕЧЕНИЕ двух наборов, беря каждый элемент, который находится в обоих наборах одновременно, и объединяя все эти элементы в один меньший набор.
 Чтобы обозначить ПЕРЕСЕЧЕНИЕ точек A и B, мы пишем: A B. Таким образом, пересечение A и B представляет собой меньшее множество, которое содержится как в A, так и в B.
Чтобы обозначить ПЕРЕСЕЧЕНИЕ точек A и B, мы пишем: A B. Таким образом, пересечение A и B представляет собой меньшее множество, которое содержится как в A, так и в B.
Формально мы можем написать: A B = {x| х А и х В}.
(Помните, мы бы сказали вслух: «множество всех x, таких, что x является элементом A, а x является элементом B».
Если элемент находится на пересечении A и B, это означает, что он находится в A И в B.
Чтобы увидеть, как выглядит пересечение на диаграмме Венна, мы нарисуем наши два множества A и B на диаграмме Венна, как показано ниже:
Тогда затенение A B желтым цветом будет выглядеть так:
Давайте посмотрим на несколько наборов и потренируемся на их пересечении.
- Пусть A={1.1, 1.2, 1.3} и B={1.2, 1.4, 1.6}. Если мы возьмем только те элементы, которые одновременно находятся в A и B, и сложим их вместе, мы получим A B={1.
 2}.
2}. - Пусть A={10, 20, 30, 40} и B={10, 15, 20, 25, 30}. Если мы возьмем только те элементы, которые одновременно находятся в A и B, и сложим их все вместе, мы получим A B={10, 20, 30}.
- Пусть A={0,1,2,3,4} и пусть B={5,6,7,8,9,10}. Тогда, если мы возьмем только те элементы, которые одновременно находятся в A и B, и сложим их все вместе, мы получим A B= , потому что в A и B одновременно НЕТ элементов. A и B вообще не перекрываются и не пересекаются, поэтому их пересечение является нулевым множеством или пустым множеством. У нас есть специальное название для таких наборов: .
Когда пересечение двух множеств пусто, мы говорим, что эти два множества являются НЕСОЕДИНЯЕМЫМИ .
Если бы мы нарисовали два непересекающихся множества на диаграмме Венна, они выглядели бы так:
- Мы можем найти ДОПОЛНЕНИЕ набора. Мы находим ДОПОЛНЕНИЕ набора, беря каждый элемент, который находится в универсальном наборе, но не в наборе, который мы рассматриваем, и объединяя все эти элементы в один набор.
 Чтобы обозначить ДОПОЛНЕНИЕ А, мы пишем: А’. Таким образом, дополнение к A — это множество, которое не пересекается с A. Если мы сложим A и A’ вместе, мы получим универсальное множество.
Чтобы обозначить ДОПОЛНЕНИЕ А, мы пишем: А’. Таким образом, дополнение к A — это множество, которое не пересекается с A. Если мы сложим A и A’ вместе, мы получим универсальное множество.
Формально мы можем написать: A’ = {x| х U, но х A}.
(Помните, мы бы сказали вслух: «множество всех x, таких, что x является элементом универсального множества, но x НЕ является элементом A».
Если элемент находится в дополнении к A, это означает, что он , а НЕ в A.
Чтобы увидеть, как дополнение выглядит на диаграмме Венна, мы нарисуем наше множество A на диаграмме Венна, как показано ниже:
Затем заштриховываем A’ синим цветом вот так:
Аналогичным образом, B’ будет выглядеть как область, заштрихованная красным цветом ниже:
Когда вы пытаетесь найти ДОПОЛНЕНИЕ набора, не позволяйте другим наборам отвлекать вас. Заметьте, что когда мы заштриховываем A’, нас волнует только то, где находится множество A на диаграмме Венна; мы пока полностью игнорируем множество B. Точно так же, когда мы закрашиваем B’, мы полностью игнорируем набор A и просто затеняем всю область за пределами овала B.
Заметьте, что когда мы заштриховываем A’, нас волнует только то, где находится множество A на диаграмме Венна; мы пока полностью игнорируем множество B. Точно так же, когда мы закрашиваем B’, мы полностью игнорируем набор A и просто затеняем всю область за пределами овала B.
Давайте посмотрим на несколько наборов и потренируемся дополнять их.
- Пусть U={1,2,3,4,5} и A={1,3,5}. Если мы возьмем каждый элемент U, который НЕ входит в A, и сложим их все вместе, мы получим A’={2,4}.
- Пусть U={3,5, 4,5, 5,5} и пусть A={3,5, 4,5, 5,5}. Если мы возьмем каждый элемент U, который НЕ входит в A, и сложим их все вместе, мы получим A’= .
- Пусть U={1,2,3,…} и пусть A={1,2,3,4,5}. Если мы возьмем каждый элемент U, который НЕ входит в A, и сложим их вместе, мы получим A’={6,7,8,…}.
- Пусть U= Z и пусть A= . Если мы возьмем каждый элемент U, который НЕ входит в A, и сложим их все вместе, мы получим A’=U= Z .
 Поскольку в A ничего нет, дополнением к A является само универсальное множество. (Помните, что набор вместе с его дополнением должен дать вам U.)
Поскольку в A ничего нет, дополнением к A является само универсальное множество. (Помните, что набор вместе с его дополнением должен дать вам U.)
- Мы можем найти РАЗНИЦУ из двух наборов. Мы находим РАЗНИЦУ двух наборов, беря каждый элемент, который есть в первом наборе, но не во втором наборе, и объединяя все эти элементы в один набор. Для обозначения РАЗНИЦА от А и будь пишем: А-Б или Б-А. A-B — это множество всех элементов, которые находятся в A, но НЕ в B, а B-A — это множество всех элементов, которые находятся в B, но НЕ в A. Обратите внимание, что A-B всегда является подмножеством A, а B-A всегда является подмножеством B.
Формально мы можем написать: A-B = {x| х А, но х В}.
(Помните, мы бы сказали вслух: «множество всех таких x, что x является элементом A, но x НЕ является элементом B».
Обратите внимание, что дополнение A, A’ — это то же самое, что и U-A.
Чтобы увидеть, как выглядит разница на диаграмме Венна, мы нарисуем наши множества A и B на диаграмме Венна, как показано ниже:
Теперь закрашиваем А-В красным вот так:
Или мы можем заштриховать B-A синим цветом вот так:
Давайте посмотрим на несколько наборов и потренируемся дополнять их.
- Пусть A={1,2,3,4,5} и B={1,3,5}. Если мы возьмем каждый элемент A, который НЕ входит в B, и сложим их вместе, мы получим A-B={2,4}.
- Пусть A={3,5, 4,5, 5,5} и пусть B={3,5, 4,5, 5,5}. Если мы возьмем каждый элемент A, который НЕ входит в B, и сложим их все вместе, мы получим A-B= .
- Пусть A={1,2,3,…} и пусть B={1,2,3,4,5}. Если мы возьмем каждый элемент A, который НЕ входит в B, и сложим их вместе, мы получим A-B={6,7,8,…}.
- Пусть A= Z и пусть B= . Если мы возьмем каждый элемент из A, который НЕ входит в B, и сложим их все вместе, мы получим A-B=U= Z .


 Автор : Open Textbook Store, Transition Math Project и Open Course Library. Расположен по адресу : http://www.opentextbookstore.com/mathinsociety/. Лицензия : CC BY-SA: Attribution-ShareAlike
Автор : Open Textbook Store, Transition Math Project и Open Course Library. Расположен по адресу : http://www.opentextbookstore.com/mathinsociety/. Лицензия : CC BY-SA: Attribution-ShareAlike 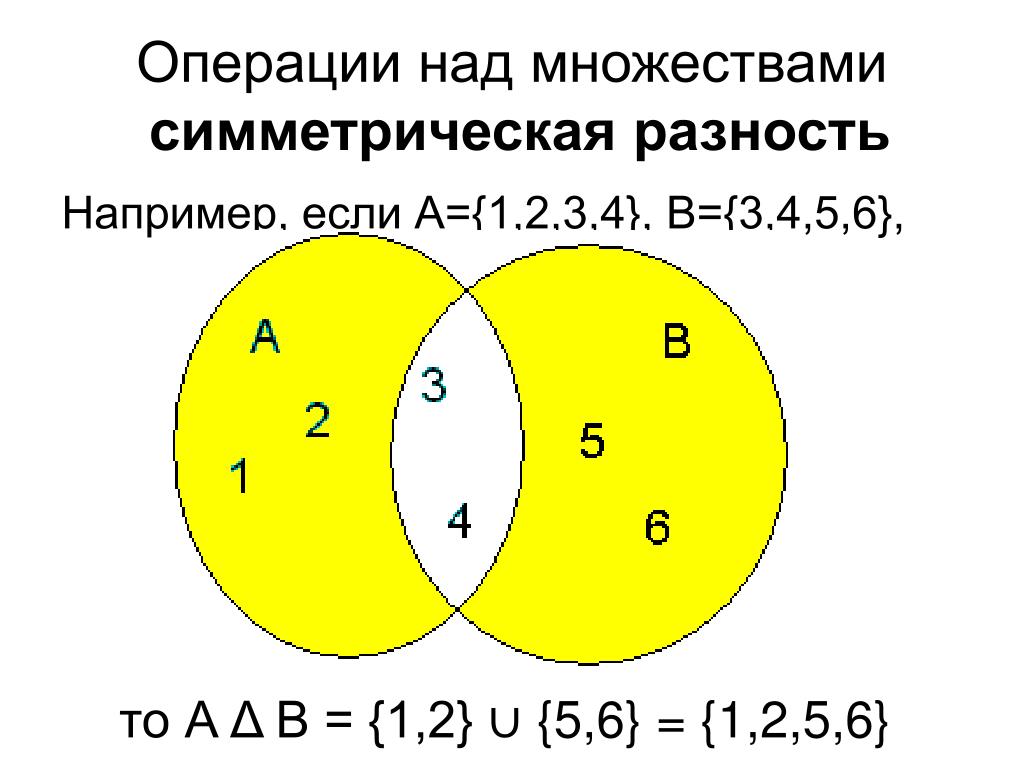 Чтобы обозначить ПЕРЕСЕЧЕНИЕ точек A и B, мы пишем: A B. Таким образом, пересечение A и B представляет собой меньшее множество, которое содержится как в A, так и в B.
Чтобы обозначить ПЕРЕСЕЧЕНИЕ точек A и B, мы пишем: A B. Таким образом, пересечение A и B представляет собой меньшее множество, которое содержится как в A, так и в B.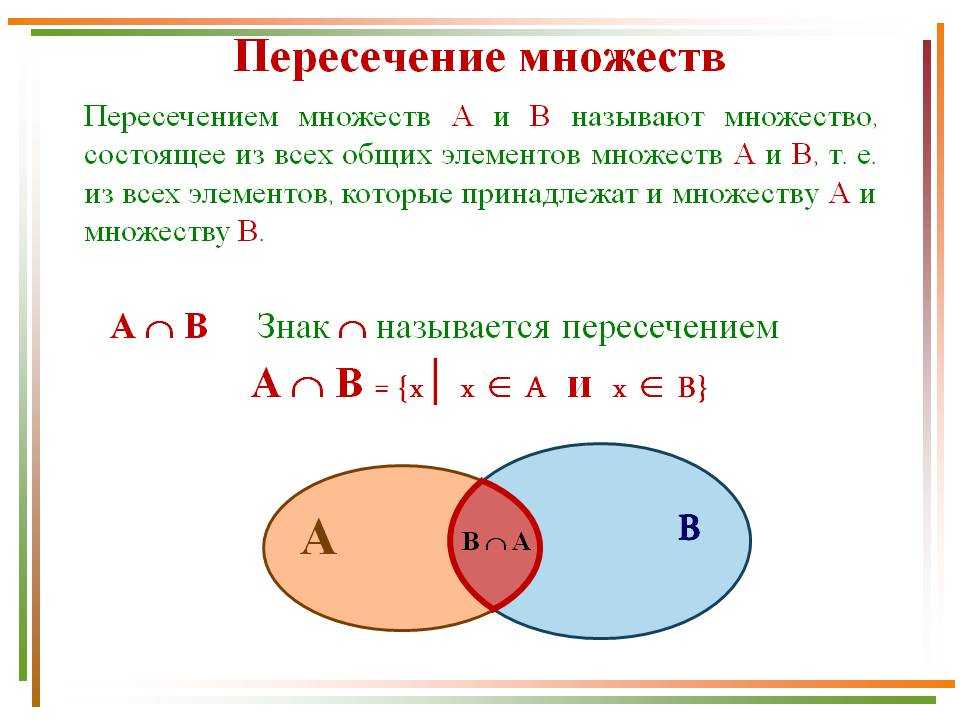 2}.
2}.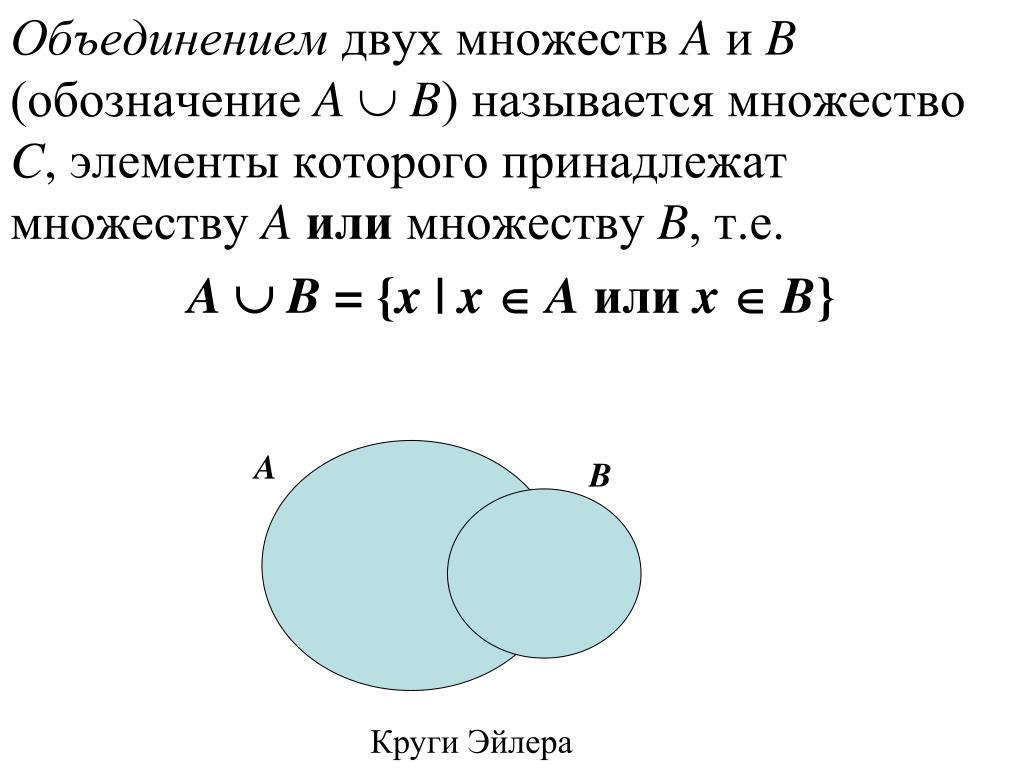 Чтобы обозначить ДОПОЛНЕНИЕ А, мы пишем: А’. Таким образом, дополнение к A — это множество, которое не пересекается с A. Если мы сложим A и A’ вместе, мы получим универсальное множество.
Чтобы обозначить ДОПОЛНЕНИЕ А, мы пишем: А’. Таким образом, дополнение к A — это множество, которое не пересекается с A. Если мы сложим A и A’ вместе, мы получим универсальное множество. Поскольку в A ничего нет, дополнением к A является само универсальное множество. (Помните, что набор вместе с его дополнением должен дать вам U.)
Поскольку в A ничего нет, дополнением к A является само универсальное множество. (Помните, что набор вместе с его дополнением должен дать вам U.)