Найти периметр прямоугольника abcd 3 класс: 3 класс. Рабочая тетрадь №1. Ответы к стр. 18

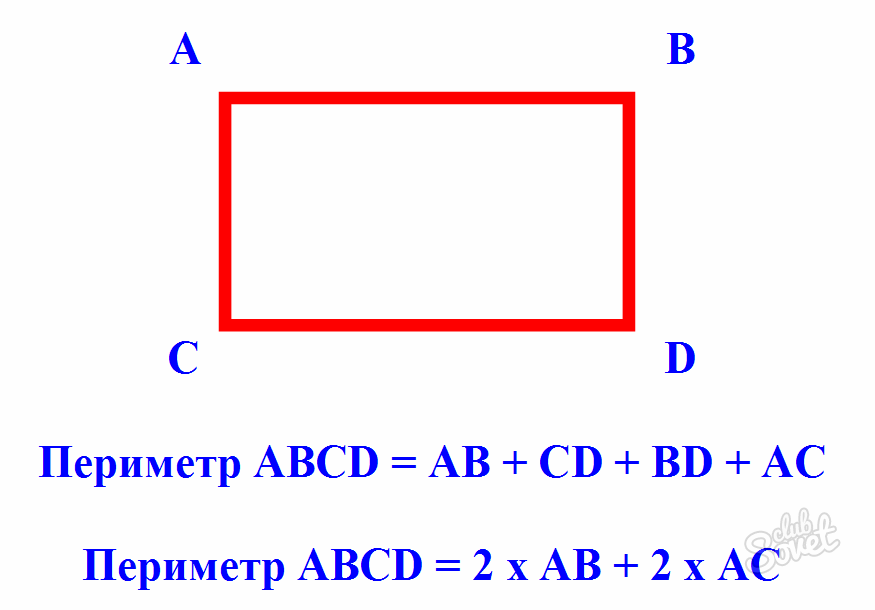
ГДЗ по геометрии 8 класс Атанасян. Гл.V №401. Найдите периметр прямоугольника ABCD… – Рамблер/класс

ГДЗ по геометрии 8 класс Атанасян. Гл.V №401. Найдите периметр прямоугольника ABCD… – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Нужна услуга, не могу разобраться, задача Гл. V №401. 

 Найдите периметр прямоугольника ABCD, если биссектриса угла А делит сторону: а) ВС на отрезки 45,6 см и 7,85 см;
б)  DC на отрезки 2,7 дм и 4,5 дм.
 
 

ответы

Я разобралась. Вот ответ на задачу Гл.V №401


1. BE = 45,6 см, BС = 7,85 см => _PABCD =
= 2(АВ + ВС) = 2(АВ + BE + EС) = 2(45,6 + 45,6 +
+ 7,85) = 198,1 см.
2. BE = 7,85 см, EС = 45,6 => P_ABCD =
= 2(AВ + ВС) = 2(AB + BE + ВС) = 2(7,85 + 7,85 +
+ 45,6) = 122,6 см.
 
б) 

1 . DЕ = 2,7 дм, ЕС = 4,5 => Р_ABCD = 2(АD+
+ DС) = 2(АD + DЕ + ЕС) = 2(2,7 + 2,7 + 4,5) = 19,8 дм.
 2 . DЕ = 4,5 дм, ЕС = 2,7 => Р_АВСD = 2(АD+
+ DС) = 2(АD + DЕ + ЕС) = 2(4,5 + 4,5 + 2,7) = 23,4 дм.

Ответ: а) 198,1 см или 122,6 см; б) 19,8 дм или 23,4 дм.
 

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Экскурсии

Мякишев Г. Я.

Психология

Химия

похожие вопросы 5

Привет! Равносильны ли уравнения? № 55.4 ГДЗ Алгебра 10-11 класс Мордкович.

Равносильны ли уравнения: (Подробнее…)

ГДЗАлгебра10 класс11 классМордкович А.Г.

Найдите координаты № 922 ГДЗ Геометрия 9 класс Атанасян Л.С.

Найдите координаты вектора ͞a + ͞b, если: а)
  (Подробнее…)

ГДЗГеометрия9 классАтанасян Л.С.

ГДЗ по геометрии 8 класс Атанасян. Гл.V №365. Найдите углы А, В и С…

Нужна помощь. Гл.V №365.
Найдите углы А, В и С выпуклого четырёхугольника ABCD, если
(Подробнее…)

ГДЗАтанасян Л.С.8 классГеометрия

Найдите периметр № 941 ГДЗ Геометрия 9 класс Атанасян Л.С.

Найдите периметр треугольника MNP, если М (4; 0), N( 12;-2), P (5;-9).

ГДЗГеометрия9 классАтанасян Л. С.

Найдите № 945 ГДЗ Геометрия 9 класс Атанасян Л.С.

Вершина А параллелограмма ОАСВ лежит на положительной полуоси Ох, вершина В имеет координаты (b; с), а ОА = а. Найдите: а) координаты (Подробнее…)

ГДЗГеометрия9 классАтанасян Л.С.

ГДЗ По Математике 5 Класс. Прямоугольник

Перейти к контенту

ГДЗ по Математике 5 класс Мерзляк А.Г. § 15. Прямоугольник

---

Вопросы к параграфу

1. Какой четырёхугольник называют прямоугольником?

2. Какие стороны прямоугольника называют соседними? Противолежащими?

3. Что называют длиной и шириной прямоугольника?

4. Каким свойством обладают противолежащие стороны прямоугольника?

5. Какую фигуру называют квадратом?

6. Объясните, какие фигуры называют симметричными относительно прямой.

7. Как называют прямую, относительно которой симметрична фигура?

8. Какие вы знаете фигуры, имеющие ось симметрии?

9. Сколько осей симметрии имеет прямоугольник, отличный от квадрата? Квадрат? Равносторонний треугольник

---

Решаем устно

1. Каждая сторона треугольника равна 12 см. Как называют такой треугольник? Чему равен его периметр?

2. Периметр равнобедренного треугольника равен 32 см, а одна из его сторон — 12 см. Найдите длины двух других сторон треугольника. Сколько решений имеет задача?

3. Найдите сторону равностороннего треугольника, если она меньше его периметра на 10 см.

4. Вычислите значение у по формуле у = х • х + 12, если:

---

Упражнения

359. Постройте: 1) прямоугольник, соседние стороны которого равны 4 см и 2 см 2) квадрат со стороной 3 см

360. Постройте прямоугольник, соседние стороны которого равны 25 мм и 35 мм.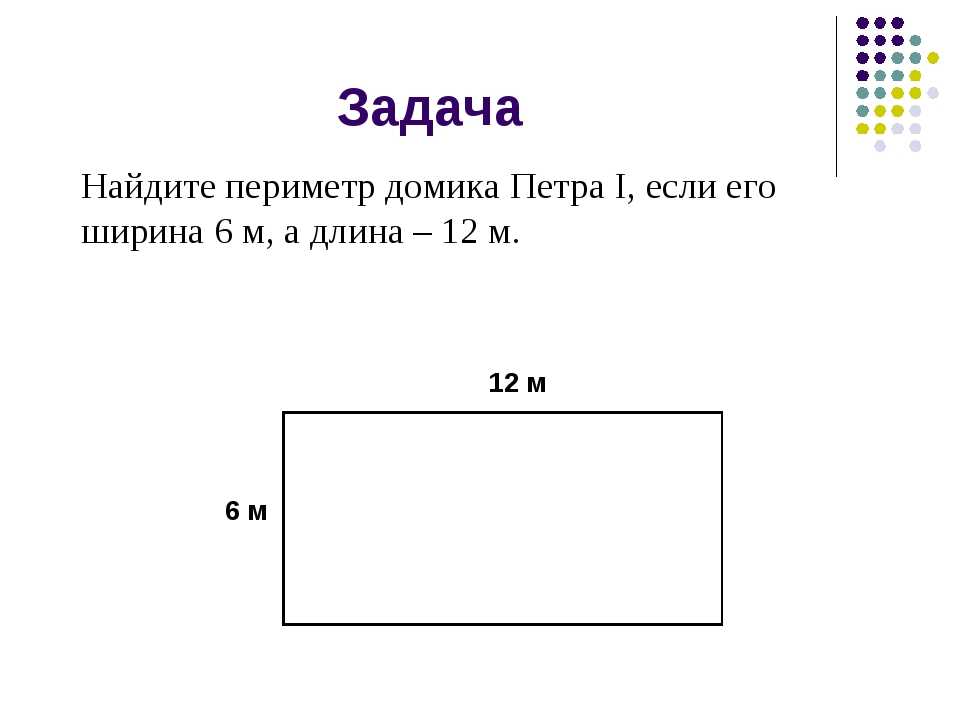

361. Вычислите периметр: 1) прямоугольника, соседние стороны которого равны 42 см и 23 см 2) квадрата со стороной 8 дм

362. Найдите периметр прямоугольника, соседние стороны которого равны 13 мм и 17 мм.

363. Какие из букв, изображённых на рисунке 135, имеют ось симметрии?

364. Сколько осей симметрии имеет многоугольник, изображённый на рисунке 136?

365. 1) Длина одной из сторон прямоугольника равна 14 см, что на 5 см больше длины соседней стороны. Найдите периметр прямоугольника. 2) Периметр прямоугольника равен 34 см, а одна из его сторон — 12 см. Найдите длину соседней стороны прямоугольника.

366. Одна сторона прямоугольника равна 8 см, а соседняя — в 4 раза больше. Найдите периметр прямоугольника.

367. Квадрат со стороной 12 см и прямоугольник, одна из сторон которого равна 8 см, имеют равные периметры. Найдите неизвестную сторону прямоугольника.

368. Прямоугольник, соседние стороны которого равны 42 см и 14 см, и квадрат имеют равные периметры. Найдите длину стороны квадрата.

369. Сколько квадратов изображено на рисунке 137?

370. Из куска проволоки сделали модель пятиугольника (рис. 138). Какие из моделей перечисленных фигур, длины сторон которых выражаются натуральным числом сантиметров, можно сделать из этого куска проволоки: 1) квадрат; 2) пятиугольник, все стороны которого равны; 3) равносторонний треугольник?

371. Прямоугольник ABCD разрезали на квадраты так, как показано на рисунке 139. Сторона наименьшего из квадратов равна 4 см. Найдите длины сторон прямоугольника ABCD.

372. Начертите прямоугольник, соседние стороны которого равны 3 см и 6 см. Разделите его на три равных прямоугольника. Вычислите периметр каждого из полученных прямоугольников. Сколько решений имеет задача?

373. Существует ли среди прямоугольников с периметром 12 см такой, который можно разделить на два равных квадрата? В случае положительного ответа выполните рисунок и вычислите периметр каждого из полученных квадратов.

374. Как надо разрезать квадрат на четыре равные части, чтобы из них можно было сложить два квадрата?

375. Как надо разрезать равнобедренный прямоугольный треугольник на четыре равные части, чтобы из них можно было сложить квадрат?

376. Как надо разрезать прямоугольник со сторонами 8 см и 4 см на четыре части, чтобы из них можно было сложить квадрат?

377. Как надо разрезать квадрат на треугольник и четырёхугольник, чтобы из них можно было сложить треугольник?

378. Как надо разрезать квадрат со стороной 6 см на две части по ломаной, состоящей из трёх звеньев, чтобы из полученных частей можно было сложить прямоугольник?

---

Упражнения для повторения

379. Проведите прямую МК, луч PS и отрезок АВ так, чтобы луч PS пересекал отрезок АВ и прямую МК, а прямая МК не пересекала отрезок АВ.

380. В магазине имеются лимоны, апельсины и мандарины, всего 740 кг. Если бы продали 55 кг лимонов, 36 кг апельсинов и 34 кг мандаринов, то оставшиеся массы лимонов, апельсинов и мандаринов оказались бы равными. Сколько килограммов фруктов каждого вида имеется в магазине?

381. От дома до дачи можно доехать на автобусе, или на электропоезде, или на маршрутном такси. В таблице указано время, которое надо затратить на каждый участок пути. Какое наименьшее время потребуется на дорогу? Каким видом транспорта при этом надо воспользоваться?

382. Найдите сумму корней уравнений: (x — 18) — 73 = 39

---

Задача от мудрой совы

383. Как с помощью пятилитрового бидона и трёхлитровой банки набрать на берегу реки 4 л воды?

---

Этот сайт использует cookie для хранения данных.

Найдите периметр ABCD

Элементарная (к 6) Элементарная математика

Хиди Х.

спросил 14.06.22

Найдите периметр многоугольника, образованного этими точками, соединенными;

A (3,4)

B (3,1)

C (8,1)

D (8,4,4)

D (8,4,4)

D (8,4)

Периметр = ___ единиц

Подписаться І 3

Подробнее

Отчет

3 ответа от опытных наставников

Лучший Новейшие Самый старый

Автор: Лучшие новыеСамые старые

Сьюзен С. ответил 15.06.22

Репетитор

5 (31)

Я люблю математику и люблю ее преподавать.

Смотрите таких репетиторов

Смотрите таких репетиторов

Привет,

Координаты даны, 4 точки на координатном графике.

Шаги:

1. Отметьте 4 точки на графике.

(Пожалуйста, убедитесь, что все точки обозначены координатами и буквенными названиями.)

1. В : Какая фигура у вас есть?

Ответ: Этот 9Многоугольник 0008 — это прямоугольник . Прямоугольник называется прямоугольником ABCD.

Здесь важны характеристики:

Противоположные стороны равны.

Прямоугольник имеет четыре угла по 90 градусов (прямые углы)

3. Найдите длину отрезка AB, просто сложив единицы измерения от точки A до точки B.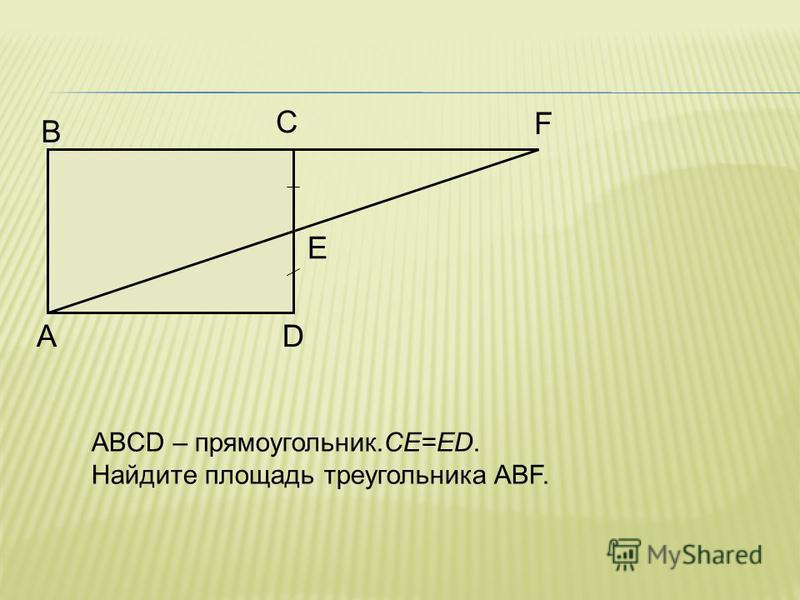 AB=длина AB=3 единицы

4. Теперь найдите длину отрезка AB длина отрезка ВС=5 ед. Просто считайте от точки B до точки C.

Примечание: BC= AD=5. И AB=DC=3

(расстояние от B до C равно расстоянию от A до D, а расстояние от A до B равно расстоянию от D до C).

В: Что вас просят сделать?

A: Найдите периметр многоугольника.

Q : Что такое периметр ?

A: Периметр — это расстояние вокруг прямоугольника.

Вы можете сложить все расстояния вокруг или использовать следующую формулу: Р= 2(л) + 2(ж).

Периметр равен равному удвоенной длине плюс удвоенной ширине .

Голосовать за 1 голос против

Подробнее

Отчет

Уоллен С.

ответил 29.06.22

Репетитор

Новое в Византе

Репетитор средней школы использует математику, чтобы спасти положение.

Смотрите таких репетиторов

Смотрите таких репетиторов

При рассмотрении вопроса нам дали координаты.

1. Постройте свою декартову плоскость на миллиметровой бумаге.
2. Нанесите точки на декартову плоскость, и это будет выглядеть как прямоугольник (многоугольник) после того, как каждая точка будет соединена.
3. Подсчитайте ЕДИНИЦУ между каждой точкой, чтобы узнать, каково расстояние между каждой вершиной.
4. Расстояние между AB будет равно 5 единицам, а расстояние DC будет равно 3 единицам.
5. В прямоугольнике противоположные стороны равны, поэтому AB (5 единиц) = CD (5 единиц) и AC (3 единицы) = AD (3 единицы).
6. Периметр означает расстояние вокруг объекта; Чтобы найти периметр прямоугольника, сложите все длины прямоугольника (AB+BC+CD+DA).

Периметр прямоугольника будет:

5+3+5+3 = 16 единиц

Голосовать за 0 голос против

Подробнее

Отчет

Дерек П. ответил 15.06.22

Репетитор

Новое в Византе

Учитель математики средней школы с 1 годом педагогического стажа

См. таких репетиторов

Смотрите таких репетиторов

Вы можете использовать формулу расстояния, чтобы решить эту проблему. Расстояние = квадратный корень из (x

2 — х ₁ ) + (у ₂ — у ₁ )

От А до В, (3 — 3) ² + (1 — 4) ^{2 2}

2 = + (-3) ² = 0 + 9 = 9. Квадратный корень из 9 = 3

От B до C, (8 — 3) ² + (1 — 1) ² = 5 ² + 0 ² = 25 + 0 = 25. Квадратный корень из 25 = 5

От C к D, (8 — 8) ² + (4 — 1) ² = 0 ² + 3 ² = 0 + 9 = 9. Квадратный корень из 9= 3

От D до A, (3 — 8) ² + (4 — 4) ² = (-5) ² + 0 ² = 25 + 0 = 25. Квадратный корень из 25 = 5.

Теперь сложим все длины сторон вместе: 3 + 5 + 3 + 5 = 16

Периметр = 16

Голосовать за 0 голос против

Подробнее

Отчет

Все еще ищете помощи? Получите правильный ответ, быстро.

Задайте вопрос бесплатно

Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.

ИЛИ

Найдите онлайн-репетитора сейчас

Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.

В прямоугольнике ABCD длины сторон AB, BC, CD, DA равны \\[\\left( {5x + 2y + 2} \\right)\\] см, \\[\\left( { x + y + 4} \\right)\\] см, \\[\\left( {2x + 5y — 7} \\right)\\] см и \\[\\left( {3x + 2y

Подсказка: Здесь нужно найти верные утверждения, воспользуемся свойством прямоугольников составить два линейных уравнения с двумя переменными, затем решим их, чтобы найти значения переменных, и, таким образом, получим длины сторон прямоугольника. Затем мы воспользуемся теоремой Пифагора, чтобы найти длину диагоналей. Мы воспользуемся формулами для периметра и площади прямоугольника, чтобы найти их значение.

Наконец, мы проверим, какое из данных утверждений верны

Полный пошаговый ответ:
Сначала составим два линейных уравнения с двумя переменными, используя предоставленную информацию.
Мы знаем, что противоположные стороны прямоугольника равны.
Таким образом, в прямоугольнике ABCD получаем
\[\begin{array}{l}AB = CD\\BC = DA\end{array}\]
Подставляя \[AB = \left( {5x + 2y + 2 } \right)\] см и \[CD = \left( {2x + 5y — 7} \right)\] см в уравнении \[AB = CD\], получаем
\[ \Rightarrow 5x + 2y + 2 = 2х + 5у — 7\]
Переписывая уравнение, получаем
\[ \Стрелка вправо 5x + 2y + 2 — 2x — 5y + 7 = 0\]
Складывая и вычитая одинаковые члены, получаем
\[ \Стрелка вправо 3x — 3y + 9 = 0\ ]
Разделив обе части на 3, получим
\[ \Стрелка вправо x — y + 3 = 0\]…………………..\[\left( 1 \right)\]
Подставив \[BC = \left( {x + y + 4} \right)\] см и \[DA = \left( {3x + 2y — 11} \right)\] см в уравнении \[BC = DA\], получаем
\[ \Стрелка вправо x + y + 4 = 3x + 2y — 11\]
Переписывая уравнение, получаем
\[ \Стрелка вправо 3x + 2y — 11 — x — y — 4 = 0\]
Складывая и вычитая подобные члены, получаем
\[ \Стрелка вправо 2x + y — 15 = 0\]……………… …. \[\left( 2 \right)\]
Мы можем заметить, что уравнения \[\left( 1 \right)\] и \[\left( 2 \right)\] являются парой линейных уравнений в две переменные.
Мы будем решать уравнения, чтобы найти значения \[x\] и \[y\].
Переписывая уравнение \[\left( 1 \right)\], получаем
\[ \стрелка вправо x = y — 3\]
Подставляя \[x = y — 3\] в уравнение \[\left( 2 \right )\], получаем
\[ \Rightarrow 2\left( {y — 3} \right) + y — 15 = 0\]
Умножив слагаемые по дистрибутивному закону умножения, получим
\[ \Rightarrow 2y — 6 + y — 15 = 0\]
Складывая и вычитая одинаковые члены, получаем
\[ \Стрелка вправо 3y — 21 = 0\]
Прибавляя 21 с обеих сторон, получаем
\[ \Стрелка вправо 3y = 21\]
Разделив обе стороны на 3 получаем
\[ \Rightarrow y = 7\]
Подставляя \[y = 7\] в уравнение \[x = y — 3\], получаем
\[ \Rightarrow x = 7 — 3\ ]
Вычитая члены в выражении, получаем
\[ \Стрелка вправо x = 4\]
Теперь найдем длины сторон прямоугольника.
Подставив \[x = 4\] и \[y = 7\] в уравнение \[AB = \left( {5x + 2y + 2} \right)\] см, получим
\[ \Rightarrow AB = 5\left( 4 \right) + 2\left( 7 \right) + 2\]
Упрощая выражение, получаем
\[\begin{array}{l} \Rightarrow AB = 20 + 14 + 2\\ \Rightarrow AB = 36{\rm{см}}\end{массив}\]
Подставляя \[x = 4\] и \[y = 7\] в уравнение \[BC = \left( {x + y + 4}\вправо)\] см, получаем
\[ \Rightarrow BC = 4 + 7 + 4\]
Упрощая выражение, получаем
\[ \Rightarrow BC = 15{\rm{cm}}\]
Таким образом, получаем
\[ \Rightarrow AB = CD = 36{\rm{см}}\]
\[ \Rightarrow BC = DA = 15{\rm{см}}\]
Мы можем заметить, что одна из пар сторон прямоугольника имеет длину 15 см .
Следовательно, вариант (а) правильный.
Теперь найдем длину диагонали AC по теореме Пифагора.
Мы знаем, что внутренние углы прямоугольника прямые. 92} = 1521\]
Извлекая квадратный корень из обеих сторон, получаем
\[ \Стрелка вправо AC = 39\] см
Диагонали прямоугольника равны.