Найти площадь через диаметр круга: Формулы, как найти площадь круга

alexxlab / / Разное

§ Круг. Площадь круга

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

Скрыть меню

На главную страницу

Войти при помощи

Темы уроков

Начальная школа

  • Геометрия: начальная школа
  • Действия в столбик
  • Деление с остатком
  • Законы арифметики
  • Периметр
  • Порядок действий
  • Разряды и классы. Разрядные слагаемые
  • Счет в пределах 10 и 20

Математика 5 класс

  • Взаимно обратные числа и дроби
  • Десятичные дроби
  • Натуральные числа
  • Нахождение НОД и НОК
  • Обыкновенные дроби
  • Округление чисел
  • Перевод обыкновенной дроби в десятичную
  • Площадь
  • Проценты
  • Свойства сложения, вычитания, умножения и деления
  • Среднее арифметическое
  • Упрощение выражений
  • Уравнения 5 класс
  • Числовые и буквенные выражения

Математика 6 класс

  • Масштаб
  • Модуль числа
  • Окружность. Площадь круга
  • Отношение чисел
  • Отрицательные и положительные числа
  • Периодическая дробь
  • Признаки делимости
  • Пропорции
  • Рациональные числа
  • Система координат
  • Целые числа

Алгебра 7 класс

  • Алгебраические дроби
  • Как применять формулы сокращённого умножения
  • Многочлены
  • Одночлены
  • Системы уравнений
  • Степени
  • Уравнения
  • Формулы сокращённого умножения
  • Функция в математике

Геометрия 7 класс

  • Точка, прямая и отрезок
  • Что такое аксиома и теорема

Алгебра 8 класс

  • Квадратичная функция. Парабола
  • Квадратные неравенства
  • Квадратные уравнения
  • Квадратный корень
  • Неравенства
  • Системы неравенств
  • Стандартный вид числа
  • Теорема Виета

Алгебра 9 класс

  • Возрастание и убывание функции
  • Нули функции
  • Область определения функции
  • Отрицательная степень
  • Среднее
    геометрическое
  • Чётные и нечётные функции

Алгебра 10 класс

  • Иррациональные числа

Алгебра 11 класс

  • Факториал

Если вы хотите, чтобы дело было сделано хорошо, найдите занятого человека; всем остальным некогда.

Элберт Хаббард

на главную

Введите тему

Русский язык Поддержать сайт

Длина окружности. Число Пи Площадь круга Площадь сферы. Объём шара

Прежде чем определится, как рассчитать площадь круга, необходимо хорошо усвоить и понять в чём разница между окружностью и кругом. Что называется окружностью, а что подразумевают под словом круг.

Важно!

Замкнутая кривая (линия), чьи точки лежат на одинаковом расстоянии от одной точки её центра, называется окружностью

.

Окружность разбивает плоскость на две области: внутреннюю и внешнюю.

Важно!

Та часть плоскости, которая лежит внутри окружности (вместе с самой окружностью) называется кругом.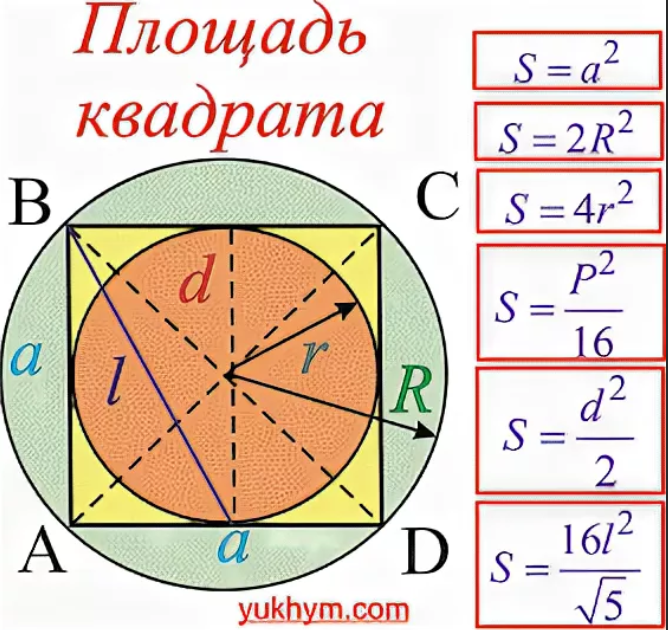

Другими словами, для простоты понимания, следует запомнить:

  • окружность — это замкнутая линия ( граница круга).
  • круг — это внутренняя область окружности.
  • У окружности нельзя посчитать площадь! А у круга найти площадь, зная формулу, достаточно легко.

Как найти площадь круга

Запомните!

Для расчета площади круга используется формула:

  • S = πR2, где R — радиус круга,
  • S = π ()
    2     = π = π , где D — диаметр круга, т.к. R =

Как решать задачи на площадь круга

Теперь, зная, по какой формуле считается площадь круга, решим задачи на площадь круга.

Зубарева 6 класс. Номер 675(г)

Условие задачи:

Найдите площадь круга, радиус которого равен 1,2 см.

Воспользуемся формулой площади круга:
S = πR2 = 3,14 · 1,22 = 3,14 · 1,44 = 4,5216 см2

Обратите внимание, что площадь измеряется в квадратных единицах. Всегда проверяйте свои ответы, правильно ли вы указали единицы измерения.

Зубарева 6 класс. Номер 677(б)

Условие задачи:

Определите радиус круга, площадь которого равна 1,1304 см2.

Выразим из формулы радиус:
S = πR2

R = √ S / π = √ 1,1304 / 3,14 = √ 0,36 = 0,6 см


Длина окружности. Число Пи Площадь круга Площадь сферы. Объём шара

Найти площадь круга онлайн. Площадь круга в задаче B5

Круг – это видимая совокупность множества точек, которые находятся на одинаковом расстоянии от центра. Чтобы найти его площадь, необходимо знать, что такое радиус, диаметр, число π и окружность.

Величины, участвующие в расчете площади круга

Расстояние, ограниченное центральной точкой круга и любой из точек окружности, называется радиусом этой геометрической фигуры. 2. Другими словами диаметр во 2 степени равен стороне квадрата во 2 степени, умноженной на 2.

Вычислив значение длины диаметра круга, можно узнать и его радиус, после чего воспользоваться одной их формул определения площади круга.

Площадь сектора круга

Сектор – это часть круга, ограниченная 2 радиусами и дугой между ними. Чтобы узнать его площадь, нужно измерить угол сектора. После этого необходимо составить дробь, в числителе которой будет значение угла сектора, а в знаменателе – 360. Чтобы высчитать площадь сектора, значение, полученное в результате деления дроби, нужно умножить на площадь круга, вычисленную по одной из вышеперечисленных формул.


Калькулятор круга — это сервис, специально разработанный для расчета геометрических размеров фигур онлайн. Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг. Например: Вы знаете объем шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку рассчитать. Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.

Вычислить радиус

Задача на вычисление значения радиуса – одна из самых распространенных. Причина тому достаточно проста, ведь зная этот параметр, вы без особого труда сможете определить значение любого другого параметра круга или шара. Наш сайт построен именно на такой схеме. Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.

Рассчитать диаметр

Расчет диаметра – самый простой вид расчета из тех, что умеет выполнять наш калькулятор. Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета.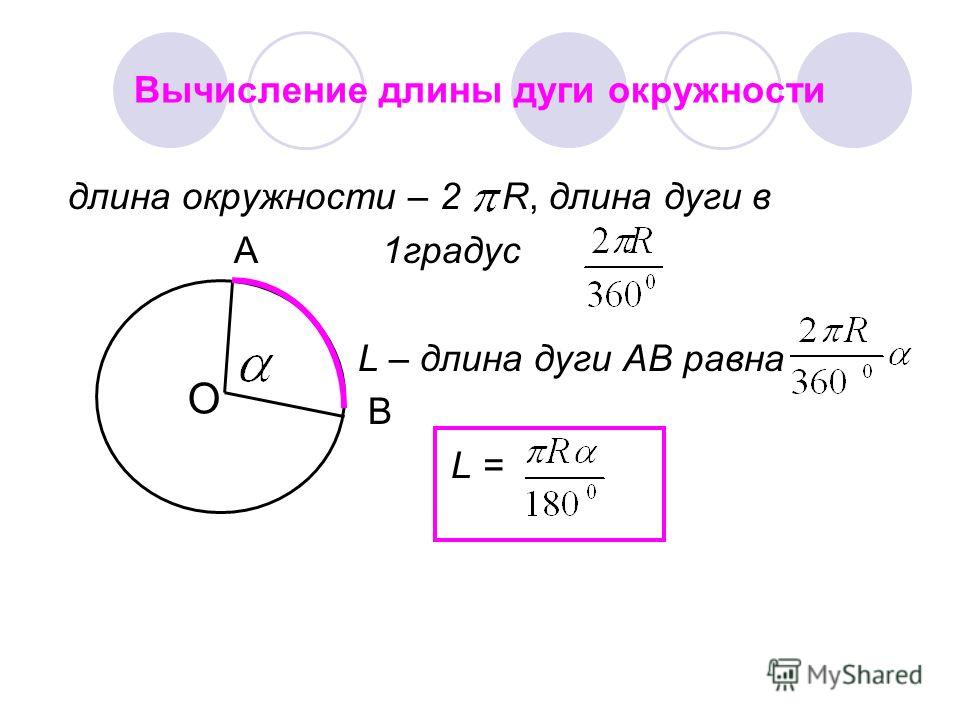 Диаметр равен значению радиуса умноженному на 2. Диаметр – важнейший параметр круга, который чрезвычайно часто используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за доли секунды.

Узнать длину окружности

Вы даже не представляете, как много вокруг нас круглых объектов и какую важную роль они играют в нашей жизни. Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика. Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.

Вычислить площадь круга

Площадь круга – как и все перечисленные перечисленные в этой статье параметры является основой современной цивилизации. Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычисления опять же нетрудная: S=PR 2 . Эта формула и наш онлайн-калькулятор помогут Вам без лишних усилий узнать площадь любого круга. Наш сайт гарантирует высокую точность вычислений и их молниеносное выполнение.

Рассчитать площадь шара

Формула для расчета площади шара ничуть не сложнее формул, описанных в предыдущих пунктах. S=4Pr 2 . Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара. Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.

Вычислить объем шара

Для вычисления объема шара используют формулу V=4/3(Pr 3). Она была использована при создании нашего онлайн сервиса. Сайт сайт дает возможность рассчитать объем шара за считанные секунды, если вы Вам известен любой из следующих параметров: радиус, диаметр, длинна окружности, площадь круга или площадь шара. Так же вы можете применять его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.

В геометрии кругом называется некоторое множество всех точек на плоскости, которые удалены от одной точки, называемой его центром, на расстояние, не большее заданного, называемого его радиусом. При этом внешней границей круга является

окружность , а в том случае, если длина радиуса равна нулю, круг вырождается в точку.

Определение площади круга

При необходимости площадь круга можно вычислить по формуле:

S πr 2D 2

r — радиус круга

D — диаметр круга

S — площадь круга

π — 3. 14

Эта геометрическая фигура очень часто встречается как в технике, так и в архитектуре. Конструкторы машин и механизмов разрабатывают различные детали, сечения многих из которых представляют собой именно круг . К примеру, таковыми являются валы, штоки, тяги, цилиндры, оси, поршни и так далее. При изготовлении этих деталей используются заготовки из различных материалов (металлов, древесины, пластических масс), их сечения также представляют собой именно

круг . Само собой разумеется, что разработчикам нередко приходится вычислять площадь круга через диаметр или радиус, используя для этой цели несложные математические формулы, открытые еще в глубокой древности.

Именно тогда круглые элементы стали активно и широко использоваться в архитектуре. Один из самых ярки тому примеров – цирк, представляющий собой разновидность строений, предназначенных для проведения в них различных зрелищных мероприятий. Их арены имеют форму круга , а впервые они стали строиться еще во времена античности. Само слово «circus » в переводе с латинского языка означает «круг ». Если в древности в цирках шли театральные постановки и проводились бои гладиаторов, то сейчас они служат местом, где практически исключительно проводятся цирковые представления с участием дрессировщиков, акробатов, фокусников, клоунов и т. д. Стандартный диаметр цирковой арены составляет 13 метров, причем это совершенно не случайно: дело в том, что именно он обеспечивает минимально необходимые геометрические параметры манежа, по которому цирковые лошади могут бегать по кругу галопом. Если вычислить

площадь круга через диаметр, то получится, что для цирковой арены эта величина составляет 113,04 квадратных метра.

Архитектурными элементами, которые могут принимать форму круга, являются окна. Конечно, в большинстве случаев они прямоугольные или же квадратные (причем во многом благодаря тому, что это проще как для зодчих, так и для строителей), но в некоторых зданиях можно встретить и круглые окна. Более того, в таких транспортных средствах, как воздушные, морские и речные суда они чаще всего именно такие.

Отнюдь не является редкостью использование круглых элементов для производства мебели, например столов и стульев. Существует даже понятие «круглый стол », которое подразумевает конструктивную дискуссию, в ходе которой происходит всестороннее обсуждение различных важных проблем и вырабатывается пути их решения. Что касается изготовления самих столешниц, имеющих круглую форму, то для их производства применяются специализированные инструменты и оборудование, при условии участия рабочих с довольно высокой квалификацией.

  • Длину диаметра – отрезка, проходящего через центр круга и соединяющего две противоположные точки окружности, либо радиуса – отрезка, одна из крайних точек которого находится в центре круга, а вторая – на дуге окружности. Таким образом, диаметр равен длине радиуса, умноженной на два.
  • Значение числа π. Эта величина представляет собой константу – иррациональную дробь, не имеющую конца.
    При этом она не является периодической. Данное число выражает соотношение длины окружности к ее радиусу. Для вычисления площади круга в заданиях школьного курса используется значение π, приведенное с точностью до сотых – 3,14.

Формулы для нахождения площади круга, его сегмента или сектора

В зависимости от специфики условий геометрической задачи применяются две формулы нахождения площади круга:

Чтобы определить, как найти площадь круга проще всего, нужно тщательно проанализировать условия задания.

Школьный курс геометрии также включает в себя задачи на расчет площади сегментов или секторов, для которых применяются специальные формулы:

  1. Сектор представляет собой часть круга, ограниченную окружностью и углом с вершиной, расположенной в центре. Площадь сектора рассчитывается по формуле: S = (π*r 2 /360)*А;
    • r – радиус;
    • А – величина угла в градусах.
    • r – радиус;
    • р – длина дуги.

    2. Также существует второй вариант S = 0,5*р*r;

  2. Сегмент – представляет собой часть, ограниченную сечением круга (хордой) и окружностью. Его площадь можно найти по формуле S=(π*r 2 /360)*А± S ∆ ;
  • r – радиус;
  • А – величина угла в градусах;
  • S ∆ – площадь треугольника, сторонами которого являются радиусы и хорда круга; при этом одна из его вершин располагается в центре круга, а две других – в точках соприкосновения дуги окружности с хордой. Важный момент – знак “минус” ставится в том случае, если значение А меньше 180 градусов, а знак “плюс” – если больше 180 градусов.

Чтобы упростить решение геометрической задачи, можно вычислить площадь круга он-лайн . Специальная программа быстро и безошибочно сделает расчет за пару секунд. Как рассчитать он-лайн площадь фигур? Для этого необходимо известные ввести исходные данные: радиус, диаметр, величину угла.

Окружности требуют более аккуратного подхода и встречаются в заданиях B5 гораздо реже. Вместе с тем, общая схема решения даже проще, чем в случае с многоугольниками (см. урок «Площади многоугольников на координатной сетке »).

Все, что требуется в таких заданиях — это найти радиус окружности R . Затем можно вычислить площадь круга по формуле S = πR 2 . Из этой формулы также следует, что для решения достаточно найти R 2 .

Чтобы найти указанные величины, достаточно указать на окружности точку, лежащую на пересечении линий сетки. А затем воспользоваться теоремой Пифагора. Рассмотрим конкретные примеры вычисления радиуса:

Задача. Найти радиусы трех окружностей, изображенных на рисунке:

Выполним дополнительные построения в каждой окружности:


В каждом случае точка B выбрана на окружности таким образом, чтобы лежать на пересечении линий сетки. Точка C в окружностях 1 и 3 дополняют фигуру до прямоугольного треугольника. Осталось найти радиусы:

Рассмотрим треугольник ABC в первой окружности. По теореме Пифагора: R 2 = AB 2 = AC 2 + BC 2 = 2 2 + 2 2 = 8.

Для второй окружности все очевидно: R = AB = 2.

Третий случай аналогичен первому. Из треугольника ABC по теореме Пифагора: R 2 = AB 2 = AC 2 + BC 2 = 1 2 + 2 2 = 5.

Теперь мы знаем, как искать радиус окружности (или хотя бы его квадрат). А следовательно, можем найти площадь. Встречаются задачи, где требуется найти площадь сектора, а не всего круга. В таких случаях легко выяснить, какую часть круга составляет этот сектор, и таким образом найти площадь.

Задача. Найти площадь S закрашенного сектора. В ответе укажите S /π .

Очевидно, сектор составляет одну четверть круга. Следовательно, S = 0,25 · S круга.

Остается найти S круга — площадь круга. Для этого выполним дополнительное построение:

Треугольник ABC — прямоугольный. По теореме Пифагора имеем: R 2 = AB 2 = AC 2 + BC 2 = 2 2 + 2 2 = 8.

Теперь находим площади круга и сектора: S круга = πR 2 = 8π ; S = 0,25 · S круга = 2π .

Наконец, искомая величина равна S /π = 2.

Площадь сектора при неизвестном радиусе

Это совершенно новый тип задач, ничего подобного в 2010-2011 годах не было. По условию, нам дан круг определенной площади (именно площади, а не радиуса!). Затем внутри этого круга выделяется сектор, площадь которого и требуется найти.

Хорошая новость состоит в том, что подобные задачи — самые легкие из всех задач на площади, которые бывают в ЕГЭ по математике. К тому же, круг и сектор всегда помещается на координатную сетку. Поэтому, чтобы научиться решать такие задачи, просто взгляните на картинку:

Пусть исходный круг имеет площадь S круга = 80. Тогда его можно разделить на два сектора площадью S = 40 каждый (см. 2 шаг). Аналогично, каждый из этих секторов-«половинок» можно снова разделить пополам — получим четыре сектора площадью S = 20 каждый (см. 3 шаг). Наконец, можно разделить каждый из этих секторов еще на два — получим 8 секторов-«ошметков». Площадь каждого из этих «ошметков» составит S = 10.

Обратите внимание: более мелкого разбиения ни в одной задаче ЕГЭ по математике нет! Таким образом, алгоритм решения задачи B-3 следующий:

  1. Разрезать исходный круг на 8 секторов-«ошметков». Площадь каждого из них составляет ровно 1/8 часть площади всего круга. Например, если по условию круг имеет площадь S круга = 240, то «ошметки» имеют площадь S = 240: 8 = 30;
  2. Выяснить, сколько «ошметков» помещается в исходном секторе, площадь которого требуется найти. Например, если в нашем секторе помещается 3 «ошметка» площадью 30, то площадь искомого сектора равна S = 3 · 30 = 90. Это и будет ответ.

Вот и все! Задача решается практически устно. Если все равно что-то непонятно, купите пиццу и порежьте ее на 8 кусков. Каждый такой кусок будет тем самым сектором-«ошметком», которые можно объединить в более крупные куски.

А теперь разберем примеры из пробного ЕГЭ:

Задача. На клетчатой бумаге нарисован круг, площадь которого равна 40. Найдите площадь заштрихованной фигуры.

Итак, площадь круга равна 40. Разделим его на 8 секторов — каждый площадью S = 40: 5 = 8. Получим:

Очевидно, закрашенный сектор состоит ровно из двух секторов-«ошметков». Следовательно, его площадь равна 2 · 5 = 10. Вот и все решение!

Задача. На клетчатой бумаге нарисован круг, площадь которого равна 64. Найдите площадь заштрихованной фигуры.

Снова разделим весь круг на 8 равных секторов. Очевидно, что площадь одного их них как раз и требуется найти. Следовательно, его площадь равна S = 64: 8 = 8.

Задача. На клетчатой бумаге нарисован круг, площадь которого равна 48. Найдите площадь заштрихованной фигуры.

Опять разделим круг на 8 равных секторов. Площадь каждого из них равна S = 48: 8 = 6. В искомом секторе помещается ровно три сектора-«ошметка» (см. рисунок). Следовательно, площадь искомого сектора равна 3 · 6 = 18.

Площадь круга — предварительная алгебра

Все ресурсы предварительной алгебры

11 Диагностические тесты 177 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 4 5 6 7 8 Следующая →

Pre-Algebra Help » Геометрия » Площадь » Площадь круга

Окружность имеет длину . Какова его площадь?

Возможные ответы:

Правильный ответ:

Пояснение:

Для начала нам нужно найти радиус окружности. Длина окружности задается следующим образом:

,

, где  – радиус.

Тогда окружность с окружностью будет иметь следующий радиус:

Теперь, используя радиус, мы можем найти площадь:

900 площадь круга.

Сообщить об ошибке

Чему равна площадь круга, диаметр которого равен ?

Возможные ответы:

Правильный ответ:

Объяснение:

Если диаметр равен 7, то радиус равен половине 7 или 3,5.

Подставьте это значение радиуса в уравнение площади круга:

Сообщить об ошибке

Прямоугольник на рисунке выше имеет длину 20 и высоту 10. Какова площадь оранжевой области. ?

Возможные ответы:

Недостаточно информации для определения площади.

Правильный ответ:

Пояснение:

Оранжевая область состоит из двух фигур:

Одна из них представляет собой прямоугольник размером 20 на 10, который, следовательно, имеет площадь

.

Другой полукруг диаметром 10 и, следовательно, радиусом 5. Его площадь

.

Добавьте области:

Сообщить об ошибке

Круг имеет диаметр  дюймы. Какова площадь круга? Округлите до ближайшего десятого знака после запятой.

Возможные ответы:

Правильный ответ:

Объяснение:

Формула для нахождения площади круга .

Сначала вы должны найти радиус из диаметра.

В данном случае

Сообщить об ошибке

Какова площадь круга диаметром в дюймах?

Возможные ответы:

Правильный ответ:

Объяснение:

Формула для нахождения площади круга: . В этой формуле представляет собой радиус окружности. Поскольку вопрос дает нам только измерение диаметра круга, мы должны вычислить радиус. Для этого делим диаметр на .

Теперь мы используем for в нашем уравнении.

 

Сообщить об ошибке

Какова площадь круга с диаметром, равным 6?

Возможные ответы:

Правильный ответ:

Объяснение:

Сначала найдите радиус:

Затем найдите площадь:

Сообщить об ошибке

Диаметр круга равен . Укажите площадь круга.

 

 

Возможные ответы:

Правильный ответ:

Пояснение:

Площадь круга можно рассчитать по формуле:

,

где диаметр круга, а примерно .

Сообщить об ошибке

Диаметр круга . Укажите площадь круга в терминах .

Возможные ответы:

Правильный ответ:

Объяснение:

Площадь круга можно рассчитать по формуле:

,

где   — диаметр круга, а — приблизительно .

Сообщить об ошибке

Длина окружности в дюймах. Найдите площадь круга.

Пусть .

Возможные ответы:

Правильный ответ:

Пояснение:

Сначала нам нужно найти радиус окружности. Длина окружности равна , где радиус окружности.

 

Площадь круга – это радиус круга.

Сообщить об ошибке

Найдите площадь круга с радиусом .

Возможные ответы:

Правильный ответ:

Объяснение:

Используйте формулу:

Где  соответствует радиусу окружности.

С момента:

Отчет о ошибке

← Предыдущий 1 2 3 4 5 6 7 8 Next →

Уведомление об авторских правах

Все ресурсы Pre-Algebra

11 Диагностические тесты. 177 практических тестов Вопрос дня Карточки Learn by Concept

Квадрат, вписанный в круг

Главная » Круги » Вписанные фигуры » Квадрат, вписанный в круг

Последнее обновление: от Ido Sarig · Этот веб-сайт получает доход от рекламы и использует файлы cookie · Условия использования · Политика конфиденциальности

Когда квадрат вписан в круг, мы можем вывести формулы для всех его свойств- длина сторон, периметр, площадь и длина диагоналей, используя только радиус круга.

И наоборот, мы можем найти радиус, диаметр, длину окружности и площадь круга, используя только сторону квадрата.

Задача 1

Квадрат вписан в окружность радиуса r. Найдите формулы для длины стороны, длины диагонали, периметра и площади квадрата через r.

Стратегия

Ключевым моментом для решения этой задачи является то, что диагональ квадрата равна диаметру круга. Мы можем показать это, используя аргумент симметрии — квадрат симметричен относительно своей диагонали, поэтому диагональ должна проходить через центр круга.

В качестве альтернативы, мы знаем, что все внутренние углы квадрата прямые, т.е.0°. Поскольку эти углы вписаны в окружность, они измеряют половину центрального угла на той же дуге. Таким образом, центральный угол равен 180°, что означает диаметр.

Вооружившись этим знанием, длина диагонали квадрата равна просто 2r, каждая сторона измеряет r·√2 (теорема Пифагора, примененная к треугольнику 45-45-90), тогда площадь равна 2r 2 , а периметр равно 4·r·√2.

Теперь сделаем обратное, найдем свойства окружности по длине стороны вписанного квадрата.

Задача 2

Квадрат со стороной а вписан в окружность. Найдите формулы для радиуса, диаметра, длины окружности и площади круга через а.

Стратегия

У нас уже есть ключевое понимание сверху — диаметр — это диагональ квадрата. Мы уже видели, как найти длину диагонали квадрата, считая от его стороны: это ·√2. Радиус равен половине диаметра, поэтому r=a·√2/2 или r=a/√2. Длина окружности равна 2·r·π, значит, это a·√2·π. А площадь π·r 2 , значит, это π·a 2 /2.

Теперь, когда мы сделали это, мы можем применить наши знания для решения различных задач «нахождение площади заштрихованной фигуры», связанных с квадратом, вписанным в окружность, например:

Задача 3

A квадрат со стороной а вписан в окружность.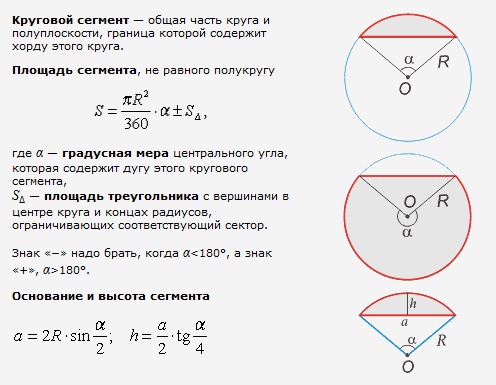 Найдите площадь заштрихованной фигуры.

Стратегия

Стратегия поиска области неправильной формы обычно заключается в том, чтобы посмотреть, можем ли мы выразить эту площадь как разницу между областями, образованными двумя или более правильными фигурами.

Здесь все очень просто — 4 неправильные формы имеют одинаковый размер (из-за симметрии). Сумма их площадей равна разнице между площадью круга и площадью квадрата.

Таким образом, заштрихованная область A заштрихована =(A круг -A квадрат )/4

Если у нас есть сторона квадрата, a, мы получим A заштриховано =(A круг -A квадрат )/4=(π·a 2 /2 -a 2 )/4=(π-2)·a 2 /8.

И если у нас есть радиус, A заштриховано =(A круг -A квадрат )/4= (π·r 2 -2r 2 )/4=(π-2)· r 2 /4

Теперь, когда мы это сделали, мы можем решить аналогичную задачу, где вместо квадрата, вписанного в круг, у нас есть круг, вписанный в квадрат.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *