Найти площадь плоской фигуры ограниченной линиями онлайн: Вычислить площадь фигуры, ограниченной линиями

Вычисление площадей фигур, ограниченных заданными линиями

Вычисление площади фигуры – это, пожалуй, одна из наиболее сложных задач теории площадей. В школьной геометрии учат находить площади основных геометрических фигур таких как, например, треугольник, ромб, прямоугольник, трапеция, круг и т.п. Однако зачастую приходится сталкиваться с вычислением площадей более сложных фигур. Именно при решении таких задач очень удобно использовать интегральное исчисление.

Определение.

Криволинейной трапецией называют некоторую фигуру G, ограниченную линиями y = f(x), у = 0, х = а и х = b, причем функция f(x) непрерывна на отрезке [а; b] и не меняет на нем свой знак (рис. 1). Площадь криволинейной трапеции можно обозначить S(G).

Определенный интеграл ʃ_а^b f(x)dx для функции f(x), являющийся непрерывной и неотрицательной на отрезке [а; b], и есть площадь соответствующей криволинейной трапеции.

То есть, чтобы найти площадь фигуры G, ограниченной линиями y = f(x), у = 0, х = а и х = b, необходимо вычислить определенный интеграл  ʃ

а^b f(x)dx.

Таким образом, S(G) = ʃ_а^b f(x)dx.

В случае, если функция y = f(x) не положительна на [а; b], то площадь криволинейной трапеции может быть найдена по формуле S(G) = -ʃ_а^b f(x)dx.

Пример 1.

Вычислить площадь фигуры, ограниченной линиями у = х³; у = 1; х = 2.

Решение.

Заданные линии образуют фигуру АВС, которая показана штриховкой на рис. 2.

Искомая площадь равна разности между площадями криволинейной трапеции DACE и квадрата DABE.

Используя формулу S = ʃ_а^b f(x)dx = S(b) – S(a), найдем пределы интегрирования. Для этого решим систему двух уравнений:

{у = х³,
{у = 1.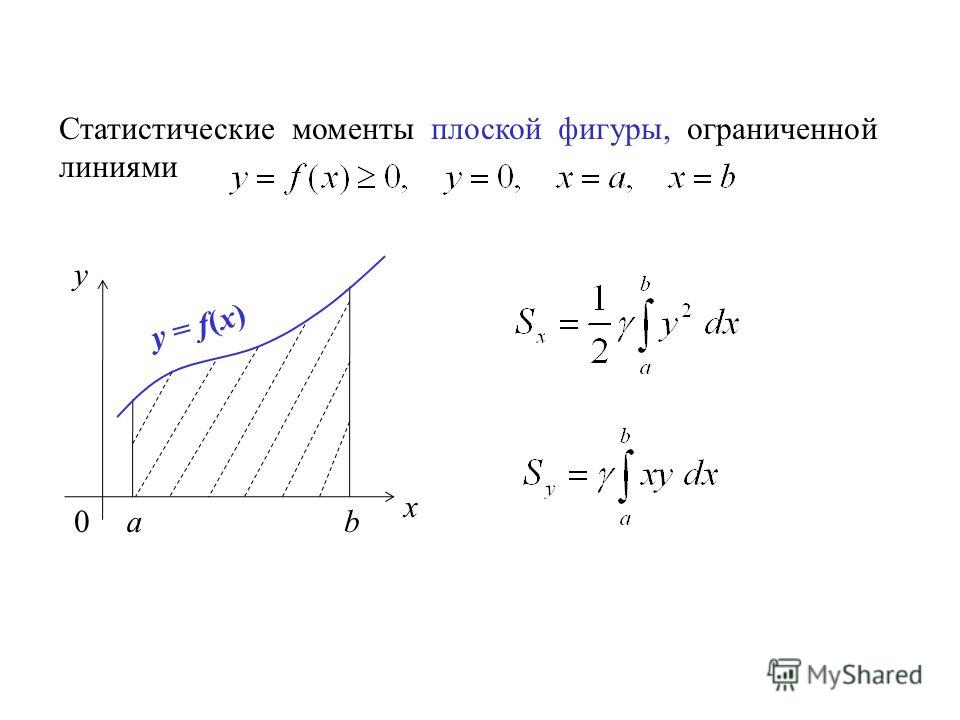

Таким образом, имеем х₁ = 1 – нижний предел и х = 2 – верхний предел.

Итак, S = S_DACE – S_DABE = ʃ₁² x³ dx – 1 = x⁴/4|₁² – 1 = (16 – 1)/4 – 1 = 11/4 (кв. ед.).

Ответ: 11/4 кв. ед.

Пример 2.

Вычислить площадь фигуры, ограниченной линиями у = √х; у = 2; х = 9.

Решение.

Заданные линии образуют фигуру АВС, которая ограничена сверху графиком функции

у = √х, а снизу графиком функции у = 2. Полученная фигура показана штриховкой на рис. 3.

Искомая площадь равна S = ʃ_а^b(√x – 2). Найдем пределы интегрирования: b = 9, для нахождения а, решим систему двух уравнений:

{у = √х,
{у = 2.

Таким образом, имеем, что х = 4 = а – это нижний предел.

Итак, S = ∫₄⁹ (√x – 2)dx = ∫₄⁹ √x dx –∫₄⁹ 2dx = 2/3 x√х|₄⁹ – 2х|₄⁹ = (18 – 16/3) – (18 – 8) = 2 2/3 (кв.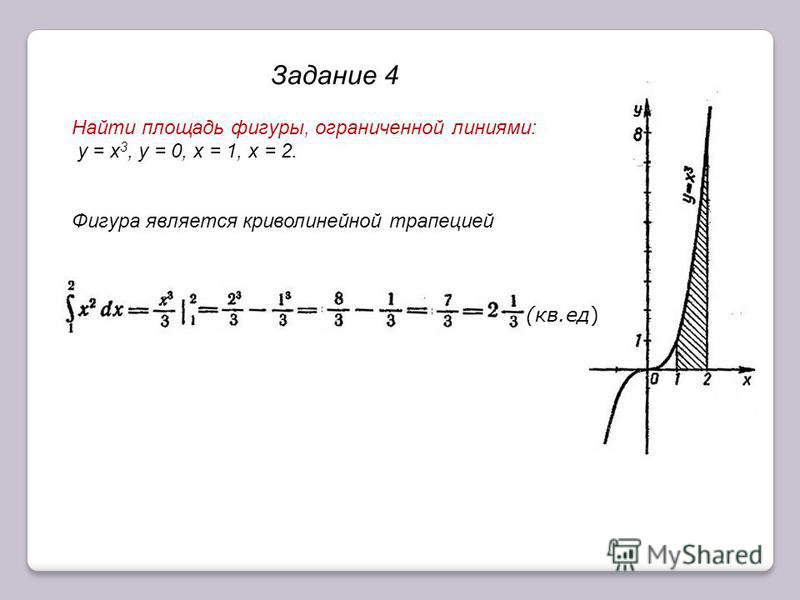 ед.).

Ответ: S = 2 2/3 кв. ед.

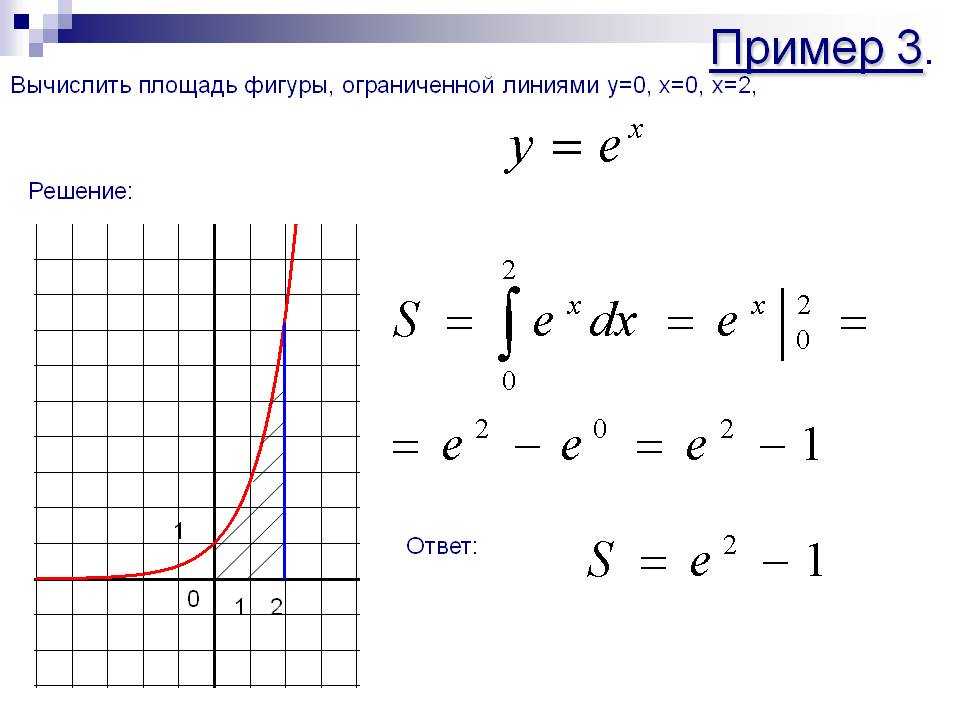
Пример 3.

Вычислить площадь фигуры, ограниченной линиями у = х³ – 4х; у = 0; х ≥ 0.

Решение.

Построим график функции у = х³ – 4х при х ≥ 0. Для этого найдем производную у’:

y’ = 3x² – 4, y’ = 0 при х = ±2/√3 ≈ 1,1 – критические точки.

Если изобразить критические точки на числовой оси и расставить знаки производной, то получим, что функция убывает от нуля до 2/√3 и возрастает от 2/√3 до плюс бесконечности. Тогда х = 2/√3 – точка минимума, минимальное значение функции у_min = -16/(3√3) ≈ -3.

Определим точки пересечения графика с осями координат:

если х = 0, то у = 0, а значит, А(0; 0) – точка пересечения с осью Оу;

если у = 0, то х³ – 4х = 0 или х(х² – 4) = 0, или х(х – 2)(х + 2) = 0, откуда х₁ = 0, х₂ = 2, х₃ = -2 (не подходит, т. к. х ≥ 0).

Точки А(0; 0) и В(2; 0) – точки пересечения графика с осью Ох.

Заданные линии образуют фигуру ОАВ, которая показана штриховкой на рис. 4.

Так как функция у = х³ – 4х принимает на (0; 2) отрицательное значение, то

S = |ʃ₀² (x³ – 4x)dx|.

Имеем: ʃ₀² (x³ – 4х)dx =(x⁴/4 – 4х²/2)|₀²= -4, откуда S = 4 кв. ед.

Ответ: S = 4 кв. ед.

Пример 4.

Найти площадь фигуры, ограниченной параболой у = 2х

2 – 2х + 1, прямыми  х = 0, у = 0 и касательной к данной параболе в точке с абсциссой х₀ = 2.

Решение.

Сначала составим уравнение касательной к параболе у = 2х² – 2х + 1 в точке с абсциссой х₀ = 2.

Так как производная y’ = 4x – 2, то при х₀ = 2 получим k = y’(2) = 6.

Найдем ординату точки касания: у₀ = 2 · 2² – 2 · 2 + 1 = 5.

Следовательно, уравнение касательной имеет вид: у – 5 = 6(х – 2) или у = 6х – 7.

Построим фигуру, ограниченную линиями:

у = 2х² – 2х + 1, у = 0, х = 0, у = 6х – 7.

Г_у =  2х² – 2х + 1 – парабола. Точки пересечения с осями координат: А(0; 1) – с осью Оу; с осью Ох – нет точек пересечения, т.к. уравнение  2х² – 2х + 1 = 0 не имеет решений (D < 0). Найдем вершину параболы:

x_b = -b/2a;

x_b = 2/4 = 1/2;

y_b = 1/2, то есть вершина параболы точка В имеет координаты В(1/2; 1/2).

Итак, фигура, площадь которой требуется определить, показана штриховкой на рис. 5.

Имеем: S_ОAВD = S_OABC – S_ADBC.

Найдем координаты точки D из условия:

6х – 7 = 0, т.е. х = 7/6, значит DC = 2 – 7/6 = 5/6.

Площадь треугольника DBC найдем по формуле S_ADBC = 1/2 · DC · BC. Таким образом,

S_ADBC = 1/2 · 5/6 · 5 = 25/12 кв. ед.

Далее:

S_OABC = ʃ₀²(2x² – 2х + 1)dx = (2x³/3 – 2х²/2 + х)|₀² = 10/3 (кв. ед.).

Окончательно получим: S

О_AВD = S_OABC – S_ADBC = 10/3 – 25/12 = 5/4 = 1 1/4 (кв. ед).

Ответ: S = 1 1/4 кв. ед.

Мы разобрали примеры нахождения площадей фигур, ограниченных заданными линиями. Для успешного решения подобных задач нужно уметь строить на плоскости линии и графики функций, находить точки пересечения линий, применять формулу для нахождения площади, что подразумевает наличие умений и навыков вычисления определенных интегралов.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

4.2. Вычисление площади фигуры, ограниченной линией, заданной параметрически

Пусть кривая задана параметрическими уравнениями то площадь криволинейной трапеции, ограниченной этой кривой, прямымиии отрезком [a,b] оси ОХ, выражается формулой

, (4.

5)

где ,,иопределяются из условий.

Пример 45. Найти площадь фигуры, ограниченной осью ОХ и одной аркой циклоиды

.

Решение. Воспользуемся формулой (4.5). Предварительно найдем :

(кв.ед.)

4.3. Вычисление площади плоской фигуры в полярных координатах

В полярных координатах положение точки на плоскости определяется двумя координатами: полярным радиусоми полярным углом. Связь между декартовыми координатами (x,y) и полярными (, r) осуществляется по формулам

.

Площадь криволинейного сектора,

ограниченного кривой и двумя

полярными радиусами и

(рис.4.7), выражается интегралом

. (4. 6)

Пример 46. Найти площадь фигуры, ограниченной улиткой Паскаля .

Решение. Воспользуемся формулой (4.6). Чтобы найти пределы интегрирования  и , необходимо построить чертеж кривой в полярных координатах. Результаты вычислений занесем в таблицу 1.

Таблица 1


	1				0				1
	3			2,5	2	1,5			1

Так как функция  четная, то график функции строим симметрично относительно горизонтальной оси для значений углов из промежутка.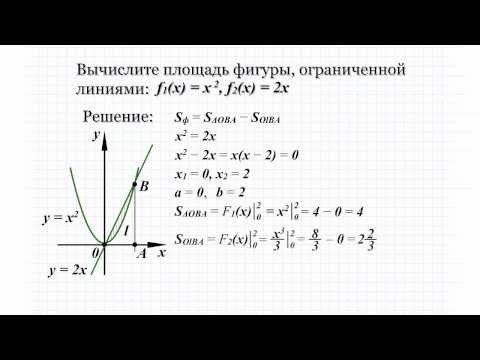

Для построения графика функции припроводим полярную осьr; на лучах, составляющих с осью r углы, значение которых указано в таблице 1, откладываем соответствующее расстояние, затем точки последовательно соединяем. Получаем замкнутую кривую, называемую улиткой Паскаля (рис.4.8).

Площадь искомой фигуры равна

4.4. Вычисление длины дуги плоской кривой

Пусть функция f(x) непрерывно дифференцируема на [a,b], тогда длина дуги кривой на указанном промежутке вычисляется по формуле:

. (4.7)

Если кривая гладкая и задана параметрически, то длина дуги этой кривой при вычисляется по формуле:

. (4.8)

Если гладкая кривая задана в полярных координатах и, то длина ее дуги равна

. (4.9)

Пример 47. Вычислить длину дуги развертки окружности

.

Решение. В нашем случае кривая задана параметрически. Воспользуемся формулой (4.8), предварительно находим производные и.

(ед.длины).

Пример 48. Найти длину дуги кривой ,.

Решение. Кривая задана в полярных координатах. Воспользуемся формулой (4.9). Находим

.

(ед.длины).

4.5. Вычисление объема тел вращения

Предположим, что площадь сечения тела плоскостью, перпендикулярной оси ОХ, может быть выражена функцией от х: при, тогда объем тела, заключенный между перпендикулярными оси ОХ плоскостямии, находится по формуле

. (4.10)

Если криволинейную трапецию (рис.4.10) вращать вокруг оси ОХ, то объем тела вращения будет равен

. (4.11)

Если плоская область, ограниченная кривыми и прямымии, вращается вокруг оси ОХ, то

(4.12)

Аналогично можно записать формулы для вычисления объемов тел вращения вокруг оси ОY:

(4.13)

(4.14)

Если кривые, ограничивающие плоскую область заданы в параметрическом виде, то к формулам (4.10 — 4.14) следует применить соответствующие замены переменной.

Если криволинейный сектор вращать вокруг полярной оси (см.рис.5.7), то

. (4.15)

Пример 49.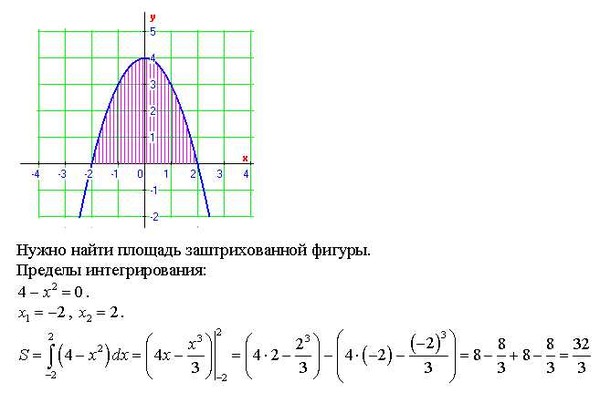 Вычислить объем тела, полученного при вращении дуги кривой ,вокруг оси ОХ.

Решение. Данная кривая называется цепной линией. График ее изображен на рис.4.9. Объем тела вращения (рис.4.10) вычислим по формуле (4.11)

.

Пример 50. Найти объем параболоида вращения, радиус основания которого равен R, а высота  Н.

Решение. Искомый параболоид вращения с указанными параметрами получится, если будем вращать вокруг оси ОY параболу ,(рис.4.11; 4.12), где параметрk легко вычислить исходя из данного условия.

Если , то, поэтому

.

Далее воспользуемся формулой (4.13)

.

Если то

(ед³).

Пример 51. Найти объем тела вращения кривой ,вокруг оси ОХ.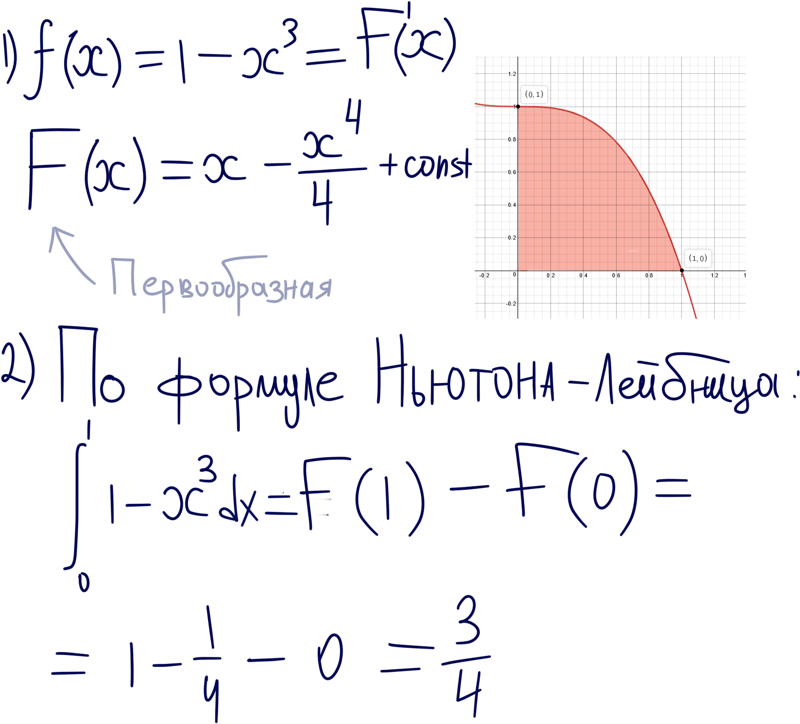 2=4ax$, осью x и ординатой в точке $x=a$, совершает полный оборот вокруг прямой $x=-a$. Найдите объем образовавшегося твердого тела. 9{a} 4ax\mathrm{dx}$$

Как мне ответить на этот вопрос?

Тогда что значит вращать кривую вокруг линии?

• определенные интегралы

$\endgroup$

1

$\begingroup$

Выразите $y$ как функцию $x$ для первого квадранта: $y=2\sqrt{ax}$. Воспользуйтесь ограничением, что $a>0$ (при отрицательных значениях $a$ вы получите тот же объем, потому что тело симметрично относительно оси вращения) и сдвиньте кривую вдоль $x$-оси $a $ единиц вправо: $y=2\sqrt{a(x-a)}$. И затем вы собираетесь использовать интеграцию оболочки с границами $a$ и $2a$: 9{\ гидроразрыва {1} {2}}) \, du. $$

С этого момента интегрирование становится тривиальным.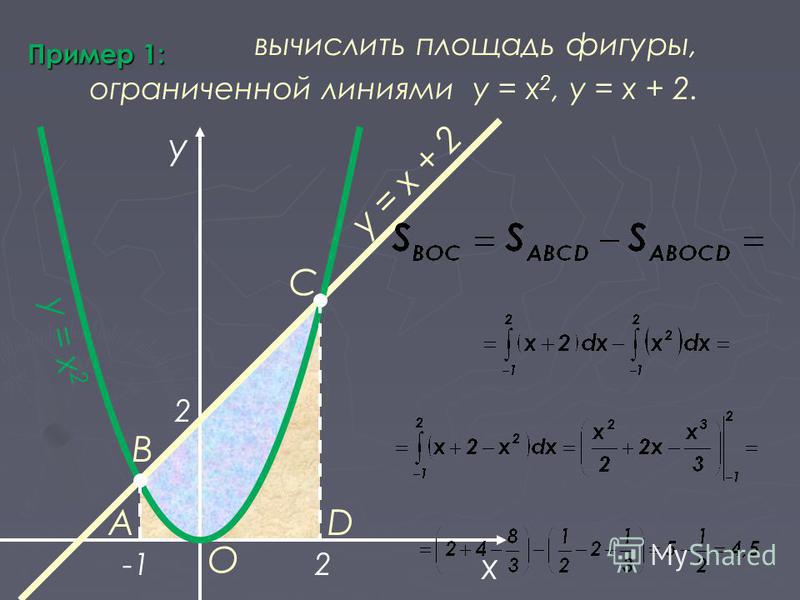

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Исчисление II — площадь с параметрическими уравнениями

Онлайн-заметки Пола
Главная / Исчисление II / Параметрические уравнения и полярные координаты / Площадь с параметрическими уравнениями

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Уведомление для мобильных устройств

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 9.3: Площадь с параметрическими уравнениями

В этом разделе мы найдем формулу для определения площади под параметрической кривой, заданной параметрическими уравнениями,

\[x = f\left( t \right)\hspace{0,25 дюйма}\hspace{0,25 дюйма}y = g\left( t \right)\]

Нам также потребуется дополнительно добавить предположение, что кривая трассируется ровно один раз при увеличении \(t\) от \(\alpha \) до \(\beta \).

Мы сделаем это почти так же, как нашли первую производную в предыдущем разделе. Сначала напомним, как найти площадь под \(y = F\left( x \right)\) на \(a \le x \le b\). 9{{\,b}}{{F\влево( x \вправо)\,dx}}\]

Теперь мы будем думать о параметрическом уравнении \(x = f\left( t \right)\) как о замене интеграла. Мы также будем предполагать, что \(a = f\left(\alpha\right)\) и \(b = f\left(\beta \right)\) для целей этой формулы. На самом деле нет оснований предполагать, что так будет всегда, поэтому мы приведем соответствующую формулу позже, если это будет противоположный случай (\(b = f\left( \alpha \right)\) и \(a = f\влево(\бета\вправо)\)).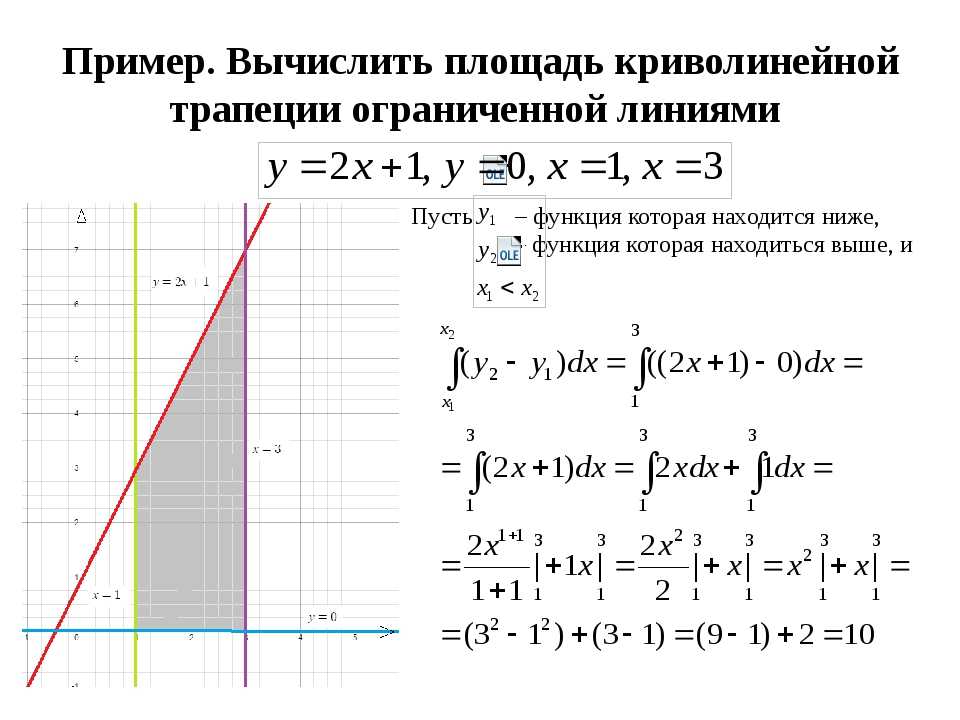 9{{\,\alpha}}{{g\left(t\right)\,f’\left(t\right)dt}}\]

Давайте рассмотрим пример.

Пример 1. Определите площадь под параметрической кривой, заданной следующими параметрическими уравнениями. \[x = 6\left( {\theta — \sin\theta} \right)\hspace{0.5in}y = 6\left({1 — \cos\theta} \right)\hspace{0.5in}0 \ле \тета \ле 2\пи \]

Показать решение

Во-первых, обратите внимание, что мы переключили параметр на \(\theta \) для этой задачи. Это делается для того, чтобы мы не были слишком привязаны к постоянному использованию \(t\) в качестве параметра.

Теперь мы могли бы построить график, чтобы убедиться, что кривая трассируется ровно один раз для заданного диапазона, если бы мы захотели. Мы собираемся рассмотреть эту кривую более подробно после этого примера, поэтому мы не будем рисовать здесь ее график.

В этом примере нет ничего особенного, кроме включения параметрических уравнений в формулу.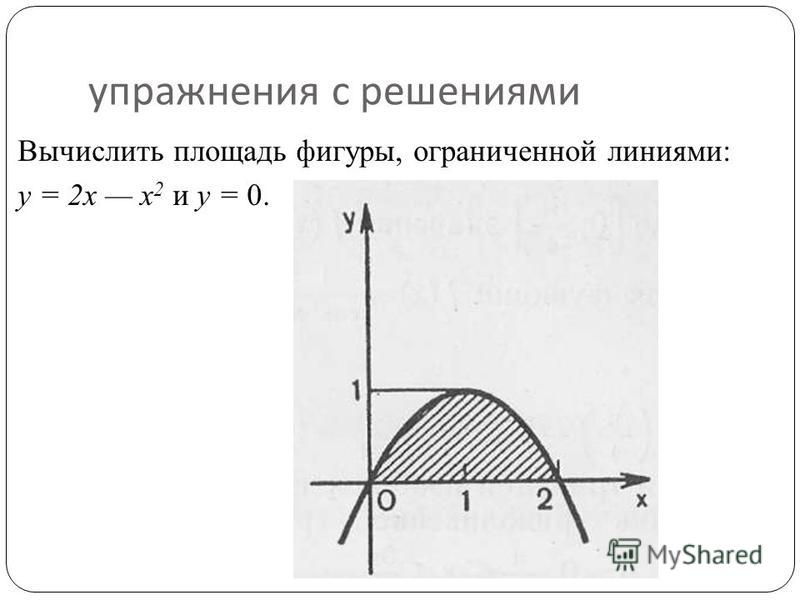 Однако сначала нам понадобится производная параметрического уравнения для \(x\).

\[\frac{{dx}}{{d\theta}} = 6\left( {1 — \cos \theta} \right)\] 9{2\pi}\\ & = 108\pi \end{align*}\]

Параметрическая кривая (без ограничений), которую мы использовали в предыдущем примере, называется циклоидой . В общем виде циклоида имеет вид

. \[x = r\left({\theta -\sin\theta}\right)\hspace{0,25in}\hspace{0,25in}y = r\left({1-\cos\theta}\right)\ ]

Циклоида представляет следующую ситуацию. Рассмотрим колесо радиуса \(r\). Пусть точка, в которой колесо первоначально касается земли, называется \(P\). Затем начните вращать колесо вправо. По мере того, как колесо катится вправо, проследите путь точки \(P\). Путь, который описывает точка \(P\), называется циклоидой и задается приведенными выше уравнениями. В этих уравнениях мы можем думать о \(\theta\) как об угле, на который повернулась точка \(P\).