Помогите решить / разобраться (М)
Сообщения без ответов | Активные темы | Избранное
Правила форума
Посмотреть правила форума
| tremor |
| ||
14/09/16 |
| ||
| |||
| Xaositect |
| |||
06/10/08 |
| |||
| ||||
06.2017, 12:32 | tremor |
| ||
14/09/16 |
| ||
| |||
06.2017, 12:47 | Xaositect |
| |||
06/10/08 |
| |||
| ||||
06.2017, 12:51
| |||
14/09/16 |
| ||
| |||
06.2017, 13:05 | Xaositect |
| |||
06/10/08 |
| |||
| ||||
06.2017, 13:11 | tremor |
| ||
14/09/16 |
| ||
| |||
| |
| |||
06/10/08 |
| |||
| ||||
06.2017, 13:30 | tremor |
| ||
14/09/16 |
| ||
| |||
06.2017, 13:38 | Xaositect |
| ||
06/10/08 | |||
| |||
06.2017, 13:39 | tremor |
| ||
14/09/16 |
| ||
| |||
| Brukvalub |
| |||
01/03/06 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 12 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
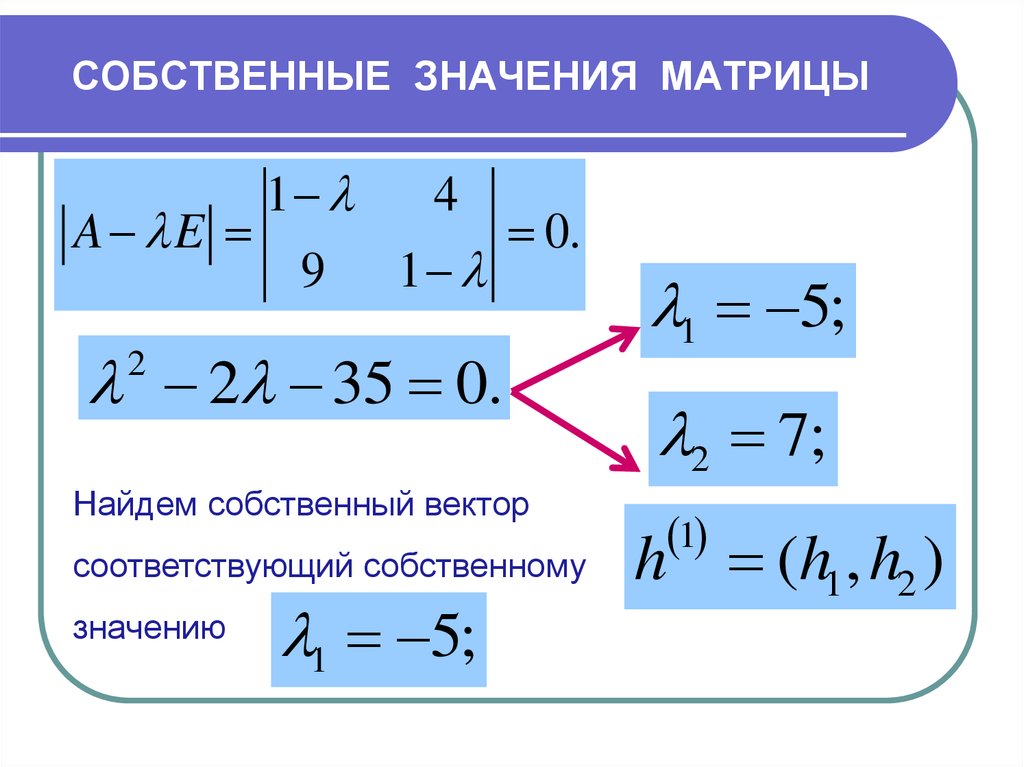
Вычисление сингулярного разложения матриц
%PDF-1.
6
%
1 0 obj
>
endobj
4 0 obj
/Author
/Creator (TeX)
/Keywords
/Producer (MiKTeX pdfTeX-1.40.17)
/ModDate (D:20200419145631+07’00’)
/Title
>>
endobj
2 0 obj
>
stream
2020-04-19T14:56:31+07:002020-04-19T14:55:24+07:002020-04-19T14:56:31+07:00TeXapplication/pdf
Как рассчитать собственные значения | Наука
Обновлено 22 декабря 2020 г.
Кевин Бек
Отзыв: Лана Бандоим, B.S.
Концепция собственных значений неясна, но очень удобна для математиков и ученых-физиков, сталкивающихся с некоторыми интересными проблемами.
Чтобы понять собственное значение, представьте, что у вас есть функция (например, y x 2 + 6 x , или y = log 4 x ), что вы могли бы выполнить некоторый процесс, чтобы результат был таким же, как умножение всей функции на постоянное значение. Такая функция будет квалифицироваться как собственная функция , а константа будет собственным значением.
- «Eigen» по-немецки означает «такой же».
Чтобы лучше понимать собственные значения и собственные функции, а также иметь возможность самостоятельно вычислять собственные значения, вам необходимо иметь общее представление о матрицах. Эти математические приемы используются для определения, скажем, порядка связи NO 9.
0033 2 (двуокись азота) и другие молекулы, поскольку поведение электронов в атомах определяется волновыми функциями, которые квалифицируются как собственные функции.
Что такое матрица?
Матрица представляет собой массив чисел, упорядоченных по строкам и столбцам, которые могут иметь номера от 1 до n . Размеры матриц даны построчно; например, следующая матрица 2 на 3:
\begin{bmatrix} 3 & 0 & 4 \\ 1 & 3 & 5 \\ \end{bmatrix}
Матрицы можно складывать вместе, если они имеют одинаковый размер (то есть имеют одинаковое количество строк и одинаковое количество столбцов). Они также могут быть перемножены вместе с помощью пошагового процесса при тех же условиях. Кроме того, любую матрицу можно умножить на вектор, который представляет собой матрицу 1 на n или n на 1; это включает в себя другие векторы.
Что такое уравнение на собственные значения?
Допустим, у вас есть n -by- n или «квадратная» матрица A , ненулевой n × 1 вектор v и скаляр λ , такие, что выполняется следующее уравнение:
\bold{Av} = λ\ жирный {v}
Любое значение λ , для которого это уравнение имеет решение, называется собственным значением матрицы A .
Не позволяйте своему уму относиться к приведенным выше выражениям как к продукту. A является оператором или линейным преобразованием вектора 92+\hat V(x,y,z)
Это используется для записи формы уравнения волновой функции Шрёдингера в квантовой механике:
\hat Hψ(x,y,z)=Eψ(x ,y,z)
Здесь E представляет собственные значения, удовлетворяющие этому уравнению.
Способы нахождения собственных значений матрицы
Из уравнения Av = λv получаем A v − λ v =0. Это приводит к:
\bold{A v} − λ(\bold{I v})=0
Где I — единичная матрица 2 на 2 со строками [ λ 0] и [0 λ ], что приводит к 1 при умножении на скаляр λ . Этот результат дает:
(\bold{A} — λ\bold{I})\bold{v} = 0
Который, если v отличен от нуля, имеет решение, только если абсолютное значение A − λ I , или | A − λ I |, равен нулю.
Если вы делаете это вручную, это требует решения квадратного уравнения и может быть утомительным.
Чтобы перемножить две матрицы вместе, для каждой точки в матрице произведения вы перемножаете соответствующие точки вместе и добавляете это к произведениям оставшихся элементов строки и столбца в строке и столбце, к которым принадлежит новая точка.
При умножении двух матриц 2 на 2 A и B вместе, если первая строка A равна [1 3] и первый столбец B равен [2 5] число в первом столбце и строке новой матрицы будет [(1 × 2) + (3 × 5)] = 15 и, соответственно, для остальных трех точек.
Расчет собственных значений онлайн
В разделе Ресурсы вы найдете инструмент для расчета матриц, который позволяет находить собственные значения и многое другое для матрицы практически любого мыслимого размера.
Калькулятор собственных значений матрицы
Veerendra
Воспользуйтесь этим простым и понятным калькулятором, который предлагает собственные значения для матрицы. Калькулятор собственных значений берет числа, т. е. матрицу, в полях ввода и генерирует выходные данные за меньшее время, нажав кнопку расчета, расположенную рядом с полем ввода.
Калькулятор собственных значений: Вы пытаетесь получить собственные значения для матрицы? Затем попробуйте этот удобный инструмент калькулятора и сделайте свои математические расчеты быстро и легко. Этот калькулятор дает подробный процесс получения решения вашего вопроса и прямого ответа в течение долей секунд. Мы также предоставляем примеры, которые помогают проверить, правильный результат или нет.
Здесь представлен один из лучших и кратчайших методов вычисления собственных значений матрицы. Ознакомьтесь с простыми шагами Калькулятора собственных значений и получите результат, следуя им.
- Возьмите правильные входные значения и представьте их в виде матрицы.
- Создайте новую матрицу, умножив матрицу идентичности, содержащую v вместо 1, на входную матрицу.
- Найдите определитель полученной матрицы, т.е. произведение диагональных значений матрицы и вычтите результат.
- Описанный выше процесс сформирует характеристический полином.
- Решите уравнение, чтобы получить корни.
- Полученные корни являются собственными значениями для вашей входной матрицы.
Найдите множество других бесплатных математических калькуляторов, которые сэкономят ваше время при выполнении сложных расчетов и помогут найти пошаговые решения всех ваших задач за считанные секунды.
Пример:
Вопрос: Найдите собственные значения матрицы ((-2,-4,2),(-2,1,2),(4,2,5))?
Решение:
Данная матрица A= [(-2,-4,2),(-2,1,2),(4,2,5)]
Чтобы получить характеристическое уравнение матрицы A, make
A-VI=0, где I — матрица идентичности.
Матрица=[(-2,-4,2),(-2,1,2),(4,2,5)]*[(v,0,0),(0,v,0), (0,0,v)]
Matrix=[(-2-v,-4,2),(-2,1-v,2),(4,2,5-v)]
Дет Матрица =0
Det [(-2-v,-4,2),(-2,1-v,2),(4,2,5-v)]= 0
Раскладывая определитель:
(-2-v)x[(1-v)x(5-v)-2×2]+4[(-2)x(5-v)-4×2]+2[(-2)x2 -4(1-v)]=0
После упрощения
-v 3 +4v 2 +27v-90=0
или v 3 -4v 2 -07
Методом проб и ошибок мы получили
v 3 -4v 2 -27v+90=(v-3)(v 2 -v-30)
(v-3)(v 2 -v-30)=( v-3)(v+5)(v-6)
Это означает, что собственные значения равны 3,-5,6
Часто задаваемые вопросы о калькуляторе собственных значений
1. Каждая ли матрица имеет собственные значения?
Каждая матрица имеет собственное значение, но это может быть и комплексное число.
2. Что означает нулевое собственное значение?
Геометрически нулевое собственное значение означает отсутствие информации на оси.