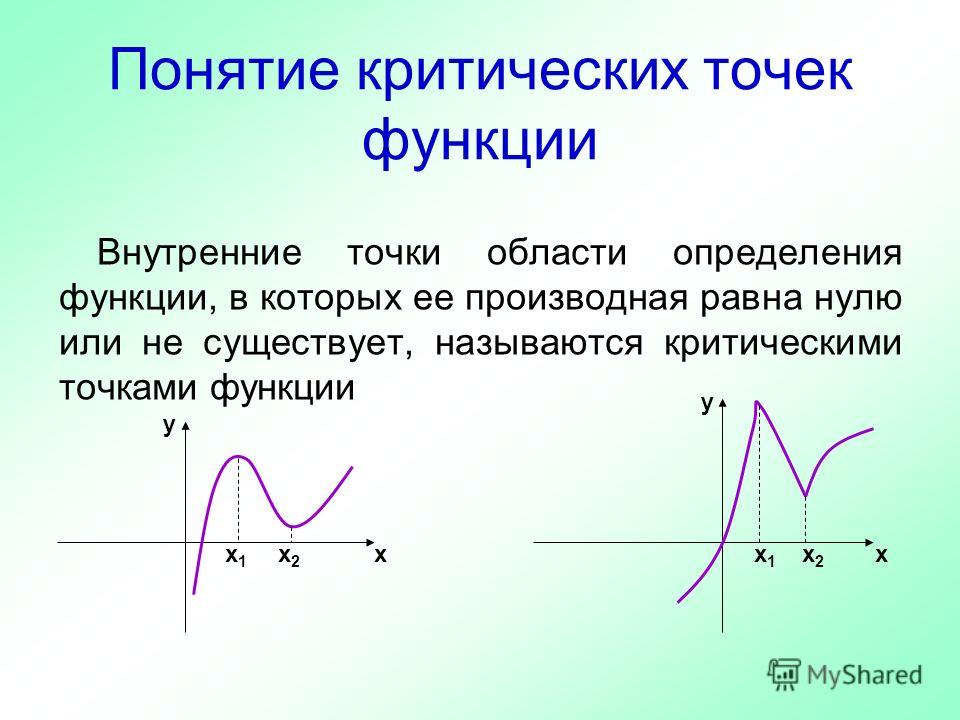
4.2.4. Примеры решения задач по теме «Экстремумы»
Задача 1.
Найти стационарную точку функции
Указание
В стационарной точке
Решение
Следовательно, координаты стационарной точки можно найти как решение системы
Ответ: (1,-2).
Задача 2.
Найти точку минимума функции
Указание
Пусть М0 – стационарная точка,
Тогда М0 является точкой минимума, если D > 0, A > 0.
Решение
Найдем стационарные точки функции:
Итак, стационарные точки функции –
Исследуем их на экстремум.
Нет экстремума.
Ответ:
Задача 3.
Найти экстремум функции
При условии 2Х + 5У + 3 = 0.
Указание
Найдите экстремум функции Лагранжа
Решение
Исследуем на экстремум функцию Лагранжа
Исследуем найденную точку на экстремум:
Следовательно, Точка условного максимума, и значение функции в этой точке равно
Ответ:
Задача 4.
На параболе
Найти точку, ближайшую к прямой Х – У = 2.
Указание
Расстояние от точки М(Х0, У0) до прямой Х – У = 2 определяется по формуле
Следовательно, требуется найти минимум функции
При условии
Решение
Расстояние от точки М(Х0, У0) до прямой Х – У = 2 определяется по формуле
Следовательно, требуется найти минимум функции
При условии
Составим функцию Лагранжа:
Не выполнено условие на знак подмодульного выражения.
Стационарная точка. При этом
Следовательно, найдена точка условного минимума.
Ответ:
Задача 5.
Найти множество значений функции
Указание
Найдите наибольшее и наименьшее значение функции в данной области,
Которые могут достигаться либо на границе, либо в стационарной точке внутри области.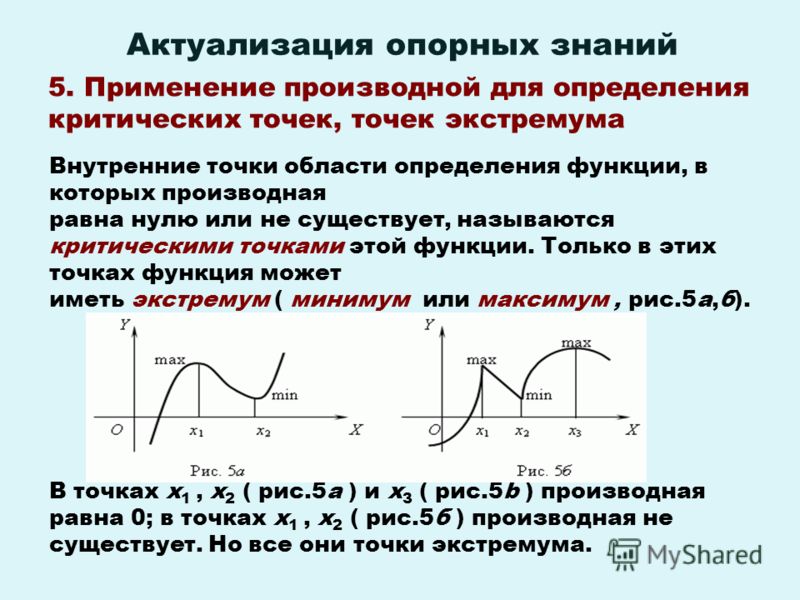
Решение
Найдем стационарные точки функции:
Стационарная точка, Z(0,0) = 0.
Для определения наибольшего и наименьшего значения функции на границе области найдем условный экстремум функции Z = Xy при условии X2 + Y2 = 1.
Составим функцию Лагранжа:
Итак, найдены четыре стационарные точки:
При этом
Следовательно, наименьшее и наибольшее значения достигаются на границе области, а так как функция непрерывна, она принимает внутри области все промежуточные значения между наименьшим и наибольшим, то есть множество ее значений в данной области –
Ответ:
| < Предыдущая | Следующая > |
|---|
| 1 | Trovare la Derivata — d/dx | натуральный логарифм x | |
| 2 | Вычислим интеграл | интеграл натурального логарифма x по x | |
| 3 | Trovare la Derivata — d/dx | e^x | |
| 4 | Вычислим интеграл | интеграл e^(2x) по x | |
| 5 | Trovare la Derivata — d/dx | 1/x | |
| 6 | Trovare la Derivata — d/dx | x^2 | |
| 7 | Trovare la Derivata — d/dx | 1/(x^2) | |
| 8 | Trovare la Derivata — d/dx | sin(x)^2 | |
| 9 | Trovare la Derivata — d/dx | sec(x) | |
| 10 | Вычислим интеграл | интеграл e^x по x | |
| 11 | Вычислим интеграл | интеграл x^2 по x | |
| 12 | Вычислим интеграл | интеграл квадратного корня из x по x | |
| 13 | Trovare la Derivata — d/dx | cos(x)^2 | |
| 14 | Вычислим интеграл | интеграл 1/x по x | |
| 15 | Вычислим интеграл | интеграл sin(x)^2 по x | |
| 16 | Trovare la Derivata — d/dx | x^3 | |
| 17 | Trovare la Derivata — d/dx | sec(x)^2 | |
| 18 | Вычислим интеграл | интеграл cos(x)^2 по x | |
| 19 | Вычислим интеграл | интеграл sec(x)^2 по x | |
| 20 | Trovare la Derivata — d/dx | e^(x^2) | |
| 21 | Вычислим интеграл | интеграл в пределах от 0 до 1 кубический корень из 1+7x по x | |
| 22 | Trovare la Derivata — d/dx | sin(2x) | |
| 23 | Trovare la Derivata — d/dx | tan(x)^2 | |
| 24 | Вычислим интеграл | интеграл 1/(x^2) по x | |
| 25 | Trovare la Derivata — d/dx | 2^x | |
| 26 | График | натуральный логарифм a | |
| 27 | Trovare la Derivata — d/dx | cos(2x) | |
| 28 | Trovare la Derivata — d/dx | xe^x | |
| 29 | Вычислим интеграл | интеграл 2x по x | |
| 30 | Trovare la Derivata — d/dx | ( натуральный логарифм от x)^2 | |
| 31 | Trovare la Derivata — d/dx | натуральный логарифм (x)^2 | |
| 32 | Trovare la Derivata — d/dx | 3x^2 | |
| 33 | Вычислим интеграл | интеграл xe^(2x) по x | |
| 34 | Trovare la Derivata — d/dx | 2e^x | |
| 35 | Trovare la Derivata — d/dx | натуральный логарифм 2x | |
| 36 | Trovare la Derivata — d/dx | -sin(x) | |
| 37 | Trovare la Derivata — d/dx | 4x^2-x+5 | |
| 38 | Trovare la Derivata — d/dx | y=16 корень четвертой степени из 4x^4+4 | |
| 39 | Trovare la Derivata — d/dx | 2x^2 | |
| 40 | Вычислим интеграл | интеграл e^(3x) по x | |
| 41 | Вычислим интеграл | интеграл cos(2x) по x | |
| 42 | Trovare la Derivata — d/dx | 1/( квадратный корень из x) | |
| 43 | Вычислим интеграл | интеграл e^(x^2) по x | |
| 44 | Вычислить | e^infinity | |
| 45 | Trovare la Derivata — d/dx | x/2 | |
| 46 | Trovare la Derivata — d/dx | -cos(x) | |
| 47 | Trovare la Derivata — d/dx | sin(3x) | |
| 48 | Trovare la Derivata — d/dx | 1/(x^3) | |
| 49 | Вычислим интеграл | интеграл tan(x)^2 по x | |
| 50 | Вычислим интеграл | интеграл 1 по x | |
| 51 | Trovare la Derivata — d/dx | x^x | |
| 52 | Trovare la Derivata — d/dx | x натуральный логарифм от x | |
| 53 | Trovare la Derivata — d/dx | x^4 | |
| 54 | Оценить предел | предел (3x-5)/(x-3), если x стремится к 3 | |
| 55 | Вычислим интеграл | интеграл x^2 натуральный логарифм x по x | |
| 56 | Trovare la Derivata — d/dx | f(x) = square root of x | |
| 57 | Trovare la Derivata — d/dx | x^2sin(x) | |
| 58 | Вычислим интеграл | интеграл sin(2x) по x | |
| 59 | Trovare la Derivata — d/dx | 3e^x | |
| 60 | Вычислим интеграл | интеграл xe^x по x | |
| 61 | Trovare la Derivata — d/dx | y=x^2 | |
| 62 | Trovare la Derivata — d/dx | квадратный корень из x^2+1 | |
| 63 | Trovare la Derivata — d/dx | sin(x^2) | |
| 64 | Вычислим интеграл | интеграл e^(-2x) по x | |
| 65 | Вычислим интеграл | интеграл натурального логарифма квадратного корня из x по x | |
| 66 | Trovare la Derivata — d/dx | e^2 | |
| 67 | Trovare la Derivata — d/dx | x^2+1 | |
| 68 | Вычислим интеграл | интеграл sin(x) по x | |
| 69 | Trovare la Derivata — d/dx | arcsin(x) | |
| 70 | Оценить предел | предел (sin(x))/x, если x стремится к 0 | |
| 71 | Вычислим интеграл | интеграл e^(-x) по x | |
| 72 | Trovare la Derivata — d/dx | x^5 | |
| 73 | Trovare la Derivata — d/dx | 2/x | |
| 74 | Trovare la Derivata — d/dx | натуральный логарифм 3x | |
| 75 | Trovare la Derivata — d/dx | x^(1/2) | |
| 76 | Trovare la Derivata — d/d@VAR | f(x) = square root of x | |
| 77 | Trovare la Derivata — d/dx | cos(x^2) | |
| 78 | Trovare la Derivata — d/dx | 1/(x^5) | |
| 79 | Trovare la Derivata — d/dx | кубический корень из x^2 | |
| 80 | Вычислим интеграл | интеграл cos(x) по x | |
| 81 | Вычислим интеграл | интеграл e^(-x^2) по x | |
| 82 | Trovare la Derivata — d/d@VAR | f(x)=x^3 | |
| 83 | Вычислим интеграл | интеграл 4x^2+7 в пределах от 0 до 10 по x | |
| 84 | Вычислим интеграл | интеграл ( натуральный логарифм x)^2 по x | |
| 85 | Trovare la Derivata — d/dx | логарифм x | |
| 86 | Trovare la Derivata — d/dx | arctan(x) | |
| 87 | Trovare la Derivata — d/dx | натуральный логарифм 5x | |
| 88 | Trovare la Derivata — d/dx | 5e^x | |
| 89 | Trovare la Derivata — d/dx | cos(3x) | |
| 90 | Вычислим интеграл | интеграл x^3 по x | |
| 91 | Вычислим интеграл | интеграл x^2e^x по x | |
| 92 | Trovare la Derivata — d/dx | 16 корень четвертой степени из 4x^4+4 | |
| 93 | Trovare la Derivata — d/dx | x/(e^x) | |
| 94 | Оценить предел | предел arctan(e^x), если x стремится к 3 | |
| 95 | Вычислим интеграл | интеграл (e^x-e^(-x))/(e^x+e^(-x)) по x | |
| 96 | Trovare la Derivata — d/dx | 3^x | |
| 97 | Вычислим интеграл | интеграл xe^(x^2) по x | |
| 98 | Trovare la Derivata — d/dx | 2sin(x) | |
| 99 | Вычислить | sec(0)^2 | |
| 100 | Trovare la Derivata — d/dx | натуральный логарифм x^2 |
Как найти и классифицировать стационарные точки – mathsathome.
comПоиск стационарных точек: видеоурок
Что такое стационарные точки?
Стационарные точки — это точки на функции, где ее производная равна нулю. В этих точках касательная к кривой горизонтальна. Стационарные точки названы так потому, что функция не возрастает и не убывает в этих точках. Существует 3 типа стационарных точек: максимумы, минимумы и стационарные перегибы.
- Точка максимума – это точка поворота, в которой кривая вогнута вверх (∩-образная).
- Минимальная точка — это точка поворота, в которой кривая вогнута вниз (∪-образная).
- Стационарная точка перегиба — это точка на кривой, где кривизна изменяется, а касательная в этой точке горизонтальна.
Точки поворота — это точки функции, в которых она поворачивается. То есть график меняется с возрастающего на убывающий или наоборот. Существует два типа точек поворота: точка максимума, в которой функция изменяется с возрастающей на убывающую, и точка минимума, где функция изменяется с убывающей на возрастающую.
Стационарные точки относятся к любой точке, в которой производная равна нулю. Существует три типа стационарных точек: максимумы, минимумы и стационарные перегибы. Точки поворота — это места, где функция меняет производную. Все поворотные точки (максимумы или минимумы) являются типами стационарных точек. Точки перегиба являются стационарными точками, но не поворотными.
Как найти стационарные точки
Чтобы найти стационарные точки:
- Дифференцировать функцию.
- Установите эту производную равной нулю.
- Найдите 𝑥.
- Подставьте координаты 𝑥 обратно в функцию, чтобы найти координаты y.
Например, найдите стационарную точку y = 𝑥 2 – 2𝑥 + 2.
Шаг 1. Дифференцируйте функцию
Производная говорит нам о градиенте.
Шаг 2. Установите эту производную равной нулю
Стационарные точки – это места, где градиент равен нулю.
0 = 2𝑥 – 2
Шаг 3. Находим 𝑥
Прибавляем два к обеим сторонам, чтобы получить 2 = 2𝑥.
Разделив обе стороны на 2, мы получим 𝑥 = 1.
Шаг 4. Подставим координату 𝑥 обратно в функцию, чтобы найти координату y
Когда 𝑥 = 1, функция y = 𝑥 𝑥 + 2 становится:
y = (1) 2 – 2(1) + 2. Оценивая это, мы получаем:
y = 1
Координаты стационарной точки находятся при 𝑥 = 1 , у = 1,
Записывается как (1, 1).
Стационарные точки квадратного уравнения
Квадратное уравнение всегда имеет одну стационарную точку.
Если квадратичный коэффициент имеет положительный коэффициент 𝑥 2 , то он вогнут вверх, и стационарная точка будет точкой минимума. Если коэффициент 𝑥 2 отрицательный, квадратичный вогнут вниз, и стационарная точка будет точкой максимума.
Стационарная точка на квадратике является либо точкой максимума, либо точкой минимума в зависимости от коэффициента 𝑥 2 .
Положительный коэффициент 𝑥 2 всегда дает минимальный балл. Например, квадратичный y = 𝑥 2 — 3𝑥 — 1 имеет коэффициент 𝑥 2 , равный 1, и, поскольку 1 — положительное число, стационарная точка является точкой минимума.
Отрицательный коэффициент 𝑥 2 всегда дает максимальный балл. Например, квадратичный y = -2𝑥 2 + 5𝑥 + 3 имеет коэффициент 𝑥 2 , равный -2, а поскольку -2 является отрицательным числом, стационарная точка является точкой максимума.
Для любого квадратичного числа, записанного в виде y = a𝑥 2 + b𝑥 + c, стационарная точка всегда находится в точке с 𝑥 координатой 𝑥 = -b / 2a .
Например, квадратичный y = 𝑥 2 – 4𝑥 + 3 имеет значения a = 1, b = -4, c = 3.
𝑥 = -b / 2a говорит нам, стационарная точка находится при 𝑥 = 4 / 2 при 𝑥 = 2.
Стационарные точки на квадратичных уравнениях также можно найти, заполнив квадрат.
Чтобы найти стационарную точку квадратного уравнения, сначала заполните квадрат, чтобы записать квадратное выражение в виде y = (x + a) 2 + b. Координаты стационарной точки можно прочитать из этой формы как (-a, b). Например, если y = (x – 2) 2 -1, координаты стационарной точки равны (2, -1).
Чтобы дополнить квадрат квадрата формы a𝑥 2 + b𝑥 + c:
- Разделите b на 2.
- Запишите это значение, добавленное к 𝑥, в скобках.
- Запишите эту скобку в степени 2.
- Возведите в квадрат значение из шага 1 и вычтите его из этой скобки.
- Добавьте к этому c.
Таким образом, для y = 𝑥 2 – 4𝑥 + 3, где a = 1, b = -4 и c = 3:
- b ÷ 2 становится -4 ÷ 2, что равно: -2 .
- Запишем это добавленное к 𝑥 как: (𝑥 – 2)
- Запишем эту скобку в степени 2 как: (𝑥 – 2) 2
- Возведение 9 в квадрат0009 -2 из шага 1, мы получаем 4. Вычитая это, мы получаем: (𝑥 – 2) 2 – 4
- Мы добавляем c к этому. Здесь c = 3, поэтому мы получаем (𝑥 – 2) 2 – 1
Поскольку y = (𝑥 – 2) 2 – 1, точка покоя находится в (2, -1).
Координата 𝑥 стационарной точки — это значение 𝑥, при котором скобка равна нулю. Так как внутри скобки (𝑥 – 2), стационарная точка находится, когда 𝑥 = 2.
Координата y стационарной точки представляет собой постоянный член, следующий за скобкой. Это у = -1.
Стационарные точки кубической функции
Стационарные точки кубической функции находятся путем дифференцирования кубической функции и нахождения значений x, при которых результирующая квадратичная функция равна нулю.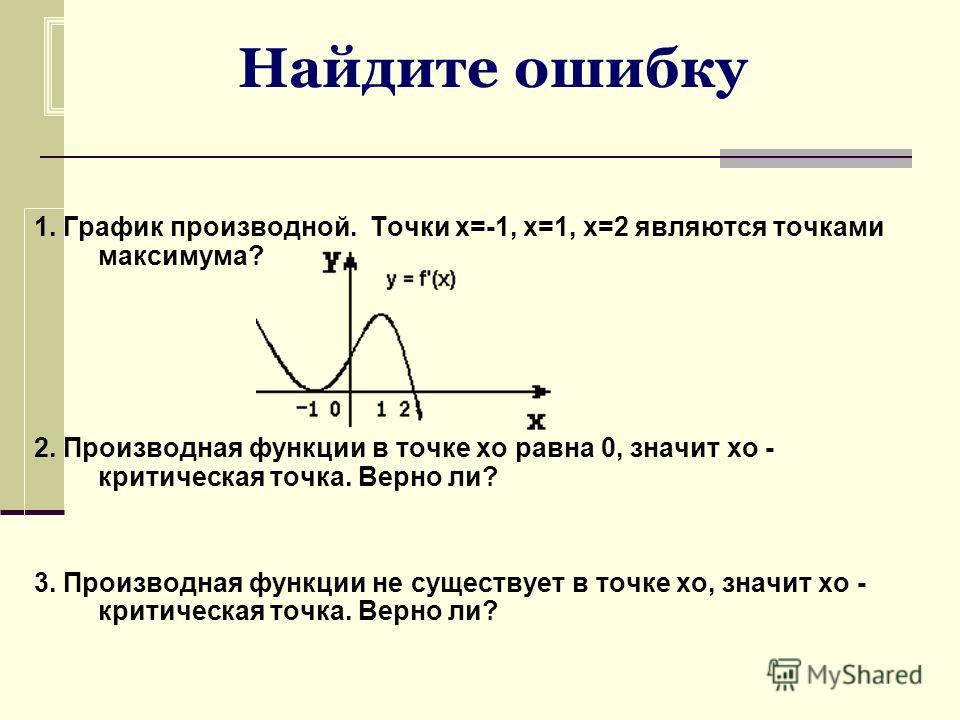
Если кубик имеет положительный коэффициент x 3 , функция сначала будет иметь максимум, а затем минимум. Если коэффициент отрицательный, кубический сначала будет иметь минимум, а затем максимум.
В этом примере мы вычислим стационарные точки y = 𝑥 3 + 6𝑥 2 + 9𝑥 + 4.
Шаг 1. Дифференцируем функцию.
Шаг 2. Установите производную, равную нулю
Шаг 3. Решение для x
Каждый член можно разделить на 3:
. = (𝑥 + 1)(𝑥 + 3)
Чтобы решить, найдите значения 𝑥, при которых каждая скобка равна нулю.
Получаем 𝑥 = -1 и 𝑥 = -3.
Шаг 4. Подставить координаты х в функцию для нахождения координаты у стационарная точка в (-1, 0).
Когда 𝑥 = -3, y = 𝑥 3 + 6𝑥 2 + 9𝑥 + 4 равно 4.
В точках (-3, 4) есть стационарная точка.
Чтобы определить характер стационарных точек кубика, рассмотрим коэффициент 𝑥 3 .
В этом примере коэффициент равен 1. Это положительное число, поэтому стационарные точки располагаются в порядке максимума, а затем минимума. Порядок зависит от их значений координат 𝑥.
Следовательно, (-1, 0) — точка максимума, а (-3, 4) — точка минимума.
Стационарные точки sin(x)
Чтобы найти стационарные точки функции sin(x), продифференцируем ее, чтобы получить cos(x). Затем приравняйте эту производную к нулю и найдите x. Функция cos(x) равна нулю при x = π / 2 и x = 3 π / 2 в интервале 0≤ x ≤ 2 . Поскольку sin(x) периодичен, дальнейшие стационарные точки находятся путем добавления или вычитания из этих значений кратных 2 π.
- sin(x) имеет точку максимума в
- sin(x) имеет точку минимума в
Как определить характер стационарных точек
Характер любой стационарной точки можно определить, подставив координату x стационарной точки во вторую производную функции f”(x).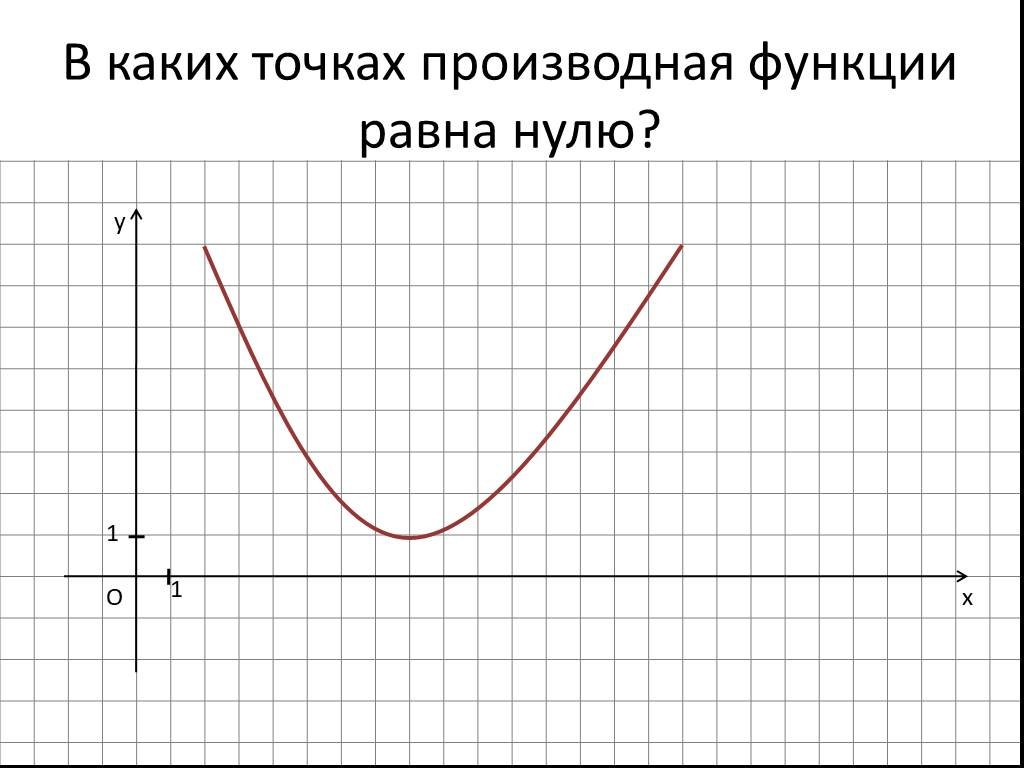
Если это значение f”(x) отрицательно, стационарная точка является максимальной. Если значение f”(x) положительно, стационарная точка является минимумом. Если f”(x) равно нулю, это стационарная точка перегиба.
Существует 3 различных типа стационарных точек.
Вторая производная, которая может быть записана как или описывает кривизну функции.
Положительные значения кривизны приводят к вогнутым функциям. Любая стационарная точка, найденная здесь, является минимумом.
Отрицательные значения кривизны приводят к вогнутым вниз функциям. Любая стационарная точка, найденная здесь, является максимальной.
Кривизна изменяется, когда вторая производная равна нулю. Это означает, что у нас есть точка перегиба.
Например, используйте вторую производную, чтобы определить характер стационарных точек на кривой.
Стационарные точки находятся путем дифференцирования функции, которую нужно получить, и последующего нахождения значений 𝑥, для которых эта производная равна нулю.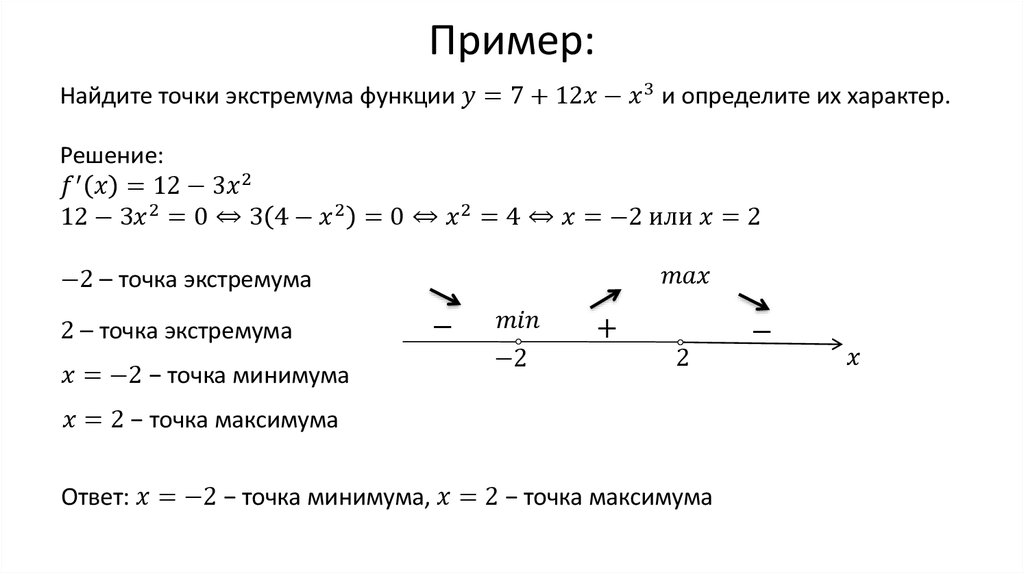
Стационарные точки находятся при 𝑥 = -1 и 𝑥 = -3.
Чтобы классифицировать стационарные точки, мы подставляем 𝑥 координаты стационарных точек во вторую производную.
Чтобы найти вторую производную, продифференцируем .
Вторая производная, .
Подставляя 𝑥 = -1 во вторую производную, получаем 6(-1) + 12 = 6.
6 — положительный результат. Положительное значение второй производной говорит нам о том, что стационарная точка является точкой минимума.
Подставляя 𝑥 = -3 во вторую производную, получаем 6(-3) + 12 = – 6,
-6 — отрицательный результат. Отрицательное значение второй производной говорит нам о том, что стационарная точка является точкой максимума.
Размер второй производной значения не имеет, только ее знак. Имеет значение только то, является ли вторая производная положительной, отрицательной или равной нулю.
Как определить характер стационарных точек с помощью первой производной
Чтобы определить характер стационарной точки с помощью первой производной, оцените знак первой производной по обе стороны от стационарной точки.
Когда производная меняется с положительной на отрицательную, точка является максимальной. Если изменение от отрицательного к положительному, точка является минимальной. Для стационарной точки перегиба изменений нет.
В следующей таблице показано, как изменение первой производной определяет характер стационарной точки.
| First Derivative Sign Diagram | Nature of Stationary Point |
| + / – | Maximum Point |
| – / + | Minimum Point |
| + / + or – / – | Стационарная точка перегиба |
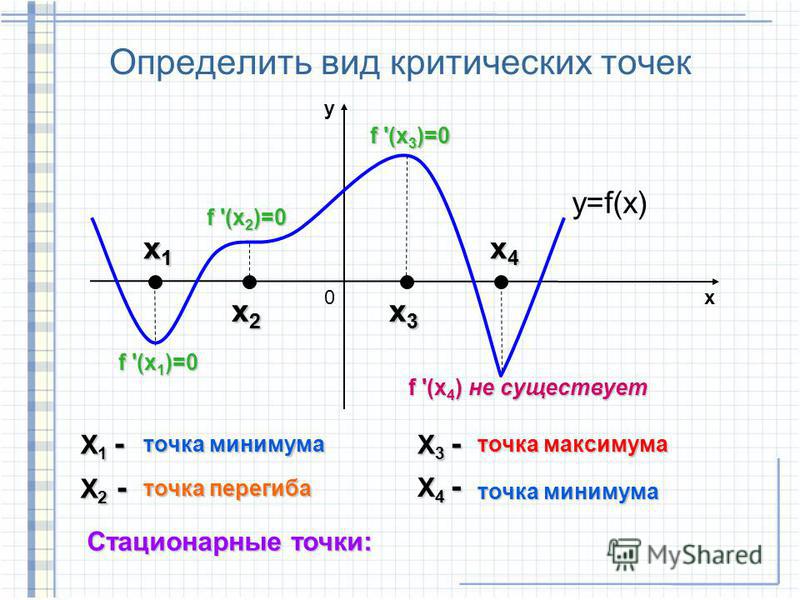
Например, классифицируйте стационарные точки y = 𝑥 3 + 6𝑥 2 + 9𝑥 + 4 с использованием первой производной.
Первая производная находится дифференцированием функции.
Стационарные точки находятся как значения 𝑥, где эта производная равна нулю.
Существуют стационарные точки 𝑥 = -1 и 𝑥 = -3.
Эти значения отмечены на диаграмме знаков, как показано справа на изображении ниже.
Затем значения 𝑥 подставляются в первую производную, чтобы найти знак первой производной в каждой области.
Для значений 𝑥 меньше -3 первая производная положительна. (Например, 𝑥 = -10, первая производная равна 189).
Для значений 𝑥 от -3 до -1 первая производная отрицательна. (Например, 𝑥 = -2, первая производная равна -3).
Для значений 𝑥 больше -1 первая производная положительна. (Например, 𝑥 = 0, первая производная равна 9).
При 𝑥 = -3 знак первой производной меняется с положительного на отрицательный. График меняется с подъема на спад. Схема знаков здесь +/-.
Максимальная точка 𝑥 = -3.
При 𝑥 = -1 знаковая диаграмма первой производной меняется с отрицательной на положительную. График меняется с нисходящего на восходящий. Схема знаков здесь – / +.
Существует точка минимума при 𝑥 = -1.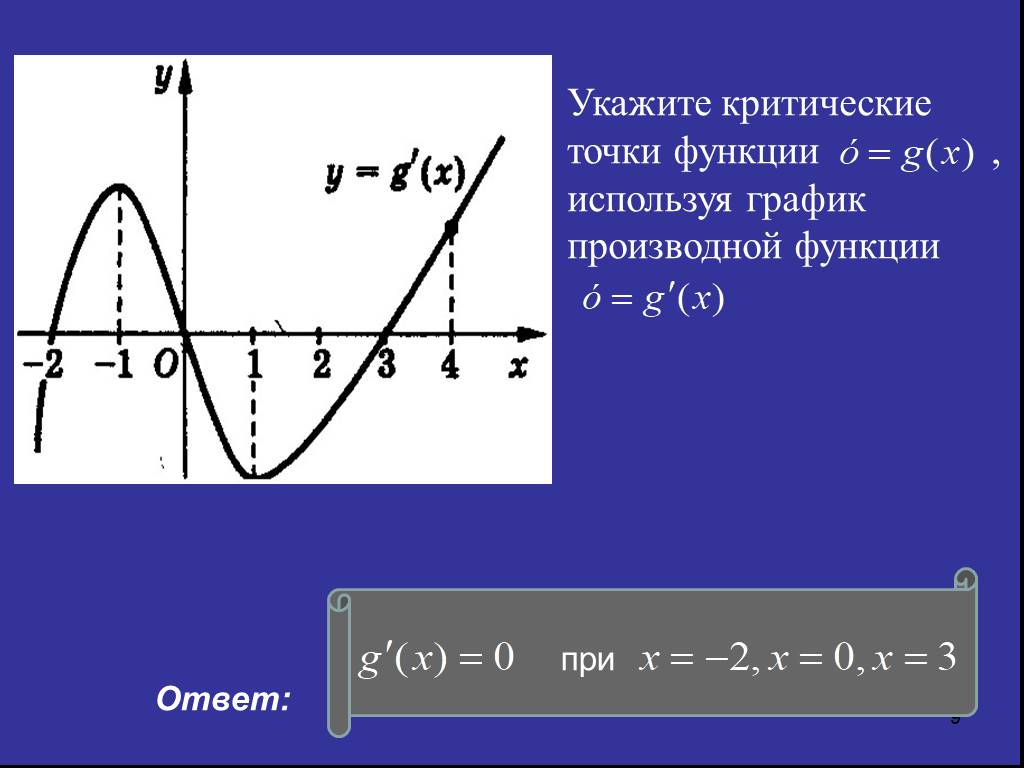
Сколько стационарных точек имеет функция?
Многочлен степени n будет иметь не более n-1 стационарных точек. Если эта функция не имеет повторяющихся корней и стационарных точек перегиба, она будет иметь n-1 точек поворота. Для каждой стационарной точки перегиба, которую содержат эти многочлены, вычтите 3 из ее степени, чтобы найти количество точек поворота, которые она имеет.
В таблице ниже показано максимальное количество стационарных точек, которые может иметь многочлен.
| Degree of Polynomial | Type of Polynomial | Maximum Number of Stationary Points |
| n | 𝑥 n | n-1 |
| 0 | Constant Срок | 0 |
| 1 | Линейный | 0 |
| 2 | Quadratic | 1 |
| 3 | Cubic | 2 |
| 4 | Quartic | 3 |
| 5 | Quintic | 5 |
The table ниже указано количество точек поворота, которые может иметь данный полином.
| Степень многочлена | Тип многочлена | Number of Turning Points |
| 0 | Constant Term | 0 |
| 1 | Linear | 0 |
| 2 | Quadratic | 1 |
| 3 | Cubic | 0 or 2 |
| 4 | Quartic | 1 or 3 |
| 5 | Quintic | 0, 2, 3 or 4 |
Some functions do not have stationary points.
Если производная функции не может быть равна нулю, то на функции нет стационарных точек. y = e x и y = 1 / x являются примерами функций, не имеющих стационарных точек.
Кубическая функция не имеет стационарной точки, если ее производная не равна нулю. Производная кубической функции является квадратичной.
Если эта квадратичная функция имеет отрицательный дискриминант, квадратичная функция не может быть равна нулю, а значит, кубическая не может иметь стационарных точек.
Например, рассмотрим кубический y = 𝑥 3 + 𝑥 2 + 𝑥.
Производная .
Существуют только стационарные точки, в которых эта производная равна нулю. Однако решений нет.
Мы знаем это, поскольку дискриминант квадратичного числа b 2 – 4ac отрицателен.
a = 3, b = 2 и c = 1.
b 2 – 4ac становится 2 2 – 4 × 3 × 1, что равно -8.
Квадратичная с отрицательным дискриминантом не может равняться нулю, поэтому на этой кубике нет стационарных точек.
Счет, математика и статистика — набор для академических навыков
Стационарные точки
ContentsToggle Главное меню 1 Определение 2 Классификация стационарных точек2.1 Тест второй производной2.2 Тест первой производной2.3 Тест первой производной или тест второй производной? 3 Видеопримеры 4 Учебники 5 Проверьте себя 6 Внешние ресурсы
Определение
стационарная точка функции $f(x)$ — это точка, в которой производная от $f(x)$ равна 0.
Эти точки называются «стационарными», поскольку в этих точках функция не возрастает и не убывает. Графически это соответствует точкам на графике $f(x)$, где касательной к кривой является горизонтальная линия.
Стационарные точки функции $y=f(x)$ являются решениями
\[\cfrac{\mathrm{d}y}{\mathrm{d}x}=0.\]
Это повторяет в математической записи определение, данное выше: «точки, где градиент функции равен нулю».
Классификация стационарных точек
Стационарная точка называется точкой поворота , если производная меняет знак (с положительного на отрицательный или наоборот) в этой точке. Есть два типа точки поворота:
- A локальный максимум , наибольшее значение функции в локальном регионе.
- Локальный минимум , наименьшее значение функции в локальной области.
Примечание: все точки поворота являются стационарными, но не все стационарные точки являются точками поворота.
Точка, в которой производная функции равна нулю, но производная не меняет знака, называется точкой перегиба или седловая точка . Их иногда называют восходящих или падающих точек перегиба, в зависимости от того, является ли производная функции положительной или отрицательной по обе стороны от стационарной точки.
Тест второй производной
Тест второй производной используется для определения того, является ли стационарная точка локальным максимумом или минимумом . Стационарная точка $x$ классифицируется в зависимости от того, является ли вторая производная положительной, отрицательной или равной нулю.
$\gt 0$ | Местный минимум |
$\lt 0$ | Локальный максимум |
$= 0$ | Тест не дает результатов |
Если тест не дает результатов, мы должны использовать какой-либо другой метод для определения характера стационарной точки (например, тест первой производной).
Тест первой производной
Тест первой производной определяет характер стационарной точки $x$ путем оценки знака первой производной в точках $x+\epsilon$ и $x-\epsilon$, где $\epsilon\ll1 \in\mathbb{R}$. Это определяет, является ли функция возрастающей или убывающей в этих точках, что указывает на форму графика.
Примечание :
- Если $\dfrac{\mathrm{d}y}{\mathrm{d}x}>0$ в точке $x$, то функция возрастает в точке $x$.
- Если $\dfrac{\mathrm{d}y}{\mathrm{d}x}<0$ в точке $x$, то функция убывает в точке $x$.
В следующей таблице показана классификация стационарной точки на основе теста первой производной.
$>0$ | $0$ | $<0$ | Локальный максимум | |
Форма графика | $\narrow$ | $\rightarrow$ | $\searrow$ | |
$\boldsymbol{\dfrac{\mathrm{d}y}{\mathrm{d}x}}$ | $<0$ | $0$ | $>0$ | Местный минимум |
Форма графика | $\searrow$ | $\rightarrow$ | $\narrow$ | |
$\boldsymbol{\dfrac{\mathrm{d}y}{\mathrm{d}x}}$ | $>0$ | $0$ | $>0$ | Восходящий перегиб |
Форма графика | $\narrow$ | $\rightarrow$ | $\narrow$ | |
$\boldsymbol{\dfrac{\mathrm{d}y}{\mathrm{d}x}}$ | $<0$ | $0$ | $<0$ | Падение перегиба |
Форма графика | $\searrow$ | $\rightarrow$ | $\searrow$ |
Первая производная проверка или вторая производная проверка?
Когда вторую производную легко вычислить, может быть проще и быстрее выполнить проверку второй производной, а не первую производную.
2.\] 92+24\cdot0 \\ &= 0. \end{align}
Здесь проверка второй производной не удалась. Критерий первой производной должен использоваться для определения характера стационарной точки при $x=0.$
Напомним, что критерий первой производной определяет характер стационарной точки путем изучения формы функции в близлежащей области.
Рассмотрим точку $x=-\epsilon$, где $\epsilon$ положительна и сколь угодно мала. Первая производная, оцененная в этот момент, равна:
92 \\ \end{align}Это положительное значение, поэтому функция $f(x)$ также на возрастает на справа от $x=0$.
Функция $f(x)$ возрастает в точках немного левее и немного правее точки $x=0.$ Отсюда следует, что стационарная точка $x=0$ является восходящей точкой перегиба.
- Стационарная точка, найденная при $x=-3$, является локальным минимумом.
- Стационарная точка, найденная при $x=0$, является восходящей точкой перегиба. 93-56x)\sqrt{x}$.
