Найти точки перегиба и интервалы выпуклости и вогнутости функции онлайн: Точки перегиба онлайн

Выпуклость, вогнутость графика функции, точки перегиба

• Признаки выпуклости и вогнутости графика функции
• Признаки существования точки перегиба
• Исследуем характер выпуклости графика вместе
• Исследовать характер выпуклости графика самостоятельно, а затем посмотреть решение
• Продолжаем исследовать характер выпуклости и вогнутости графика функции вместе

Исследование функции на выпуклость и вогнутость может быть как самостоятельной задачей, так и одним из этапов полного исследования функции и построения её графика. Выпуклость и вогнутость функции имеет место только на определённом интервале, с чем и связаны нижеприведённые определения.

В изучении этого урока поможет материал Свойства и графики элементарных функций. График дифференцируемой функции называется выпуклым в интервале ]a, b[, если в этом интервале он расположен ниже любой своей касательной (рис.

1).

График дифференцируемой функции называется вогнутым в этом интервале он расположен выше любой своей касательной  (рис. 2).

---

Теорема (достаточный признак вогнутости или выпуклости графика). Если для функции f(x) во всех точках интервала ]a, b[ вторая производная больше нуля

(),

то кривая y = f(x) вогнута в этом интервале; если же вторая производная меньше нуля

()

во всех точках интервала ]a, b[, то кривая выпукла в этом интервале.

---

Точка графика непрерывной функции, в которой изменяется выпуклость на вогнутость или наоборот, называется точкой перегиба.

Из определения следует, что с одной стороны от точки перегиба кривая расположена под касательной, с другой стороны – над ней, или наоборот.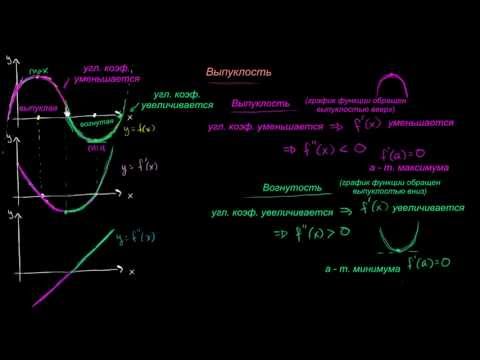

Поэтому точку перегиба на графике принято показывать отрезком касательной, которая в этой точке пересекает кривую (рис. 3).

---

Теорема (достаточный признак существования точки перегиба). Если в точке функция f(x) имеет первую производную , а вторая производная в этой точке равна нулю или не существует, и кроме того, при переходе через точку меняет знак, то точка

является точкой перегиба графика функции y = f(x).

Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.

Как должно быть понятно из определений выше, чтобы исследовать характер выпуклости кривой y = f(x), нужно найти те точки, в которых вторая производная равна нулю () или не существует, а затем, используя достаточный признак, исследовать знаки второй производной слева и справа от каждой возможной точки перегиба (подобно тому, как определялись точки

экстремума по первой производной).

Пример 1. Найти точки перегиба, интервалы выпуклости и вогнутости графика функции .

Решение. Функция определена при (как найти область определения функции). Её производные и . Найдём возможные точки перегиба. Полагая , получим , то есть , полагая , получим .

Однако точки и не входят в область определения заданной функции, поэтому она может иметь только одну точку перегиба при . Исследуем знаки второй производной в окрестности точки . Взяв в интервале точку , получим , а взяв в интервале точку , получим . Следовательно, слева от кривая

выпукла, а справа — вогнута, поэтому при график функции имеет точку перегиба .

График этой функции — на рис. снизу.

Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.

Пример 2.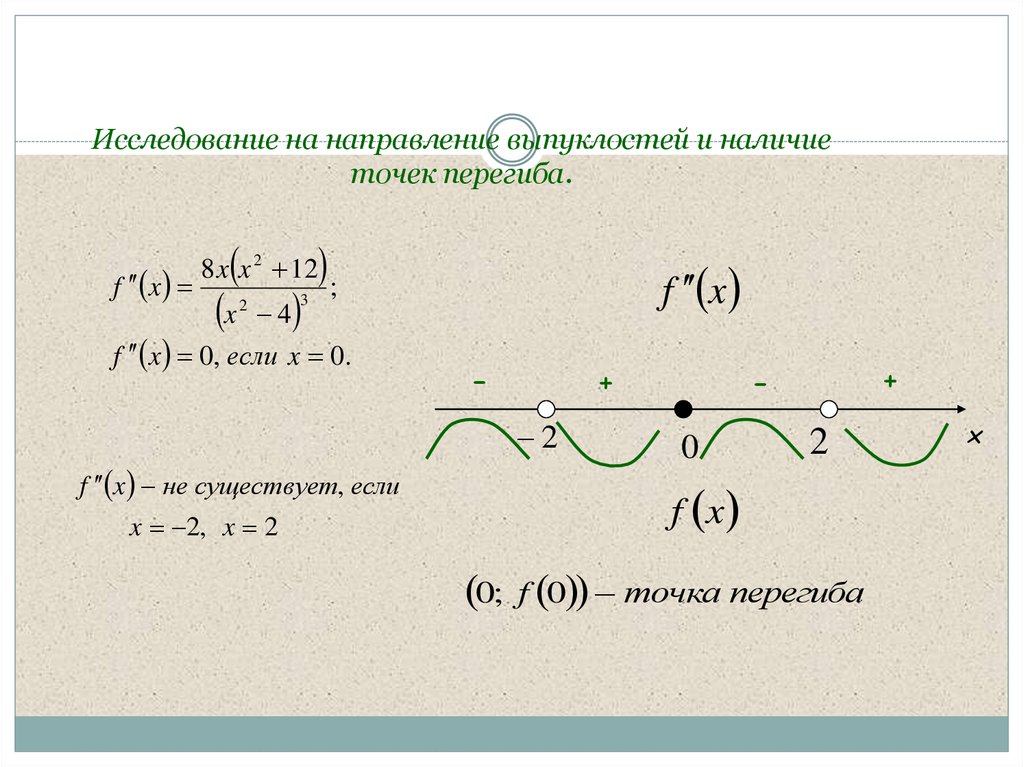 Найти точки перегиба, интервалы выпуклости и вогнутости и построить график функции .

Решение. Функция определена при . Её производные и . Здесь , а при , причём при и при . Следовательно, слева от кривая вогнута, а справа — выпукла, т.е. — точка перегиба графика.

График этой функции — на рис. снизу.

Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных

.

Нет времени вникать в решение? Можно заказать работу!

Пример 3. Исследовать на выпуклость, вогнутость и точки перегиба функцию .

Решение. Находим вторую производную: . Из уравнения получаем одну критическую точку: . Исследовав знак в окрестности точки получаем: слева от точки (выпуклость), а справа — (вогнутость), т. е. точка является точкой перегиба рассматриваемой функции.

График этой функции — на рис. снизу.

Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.

Пример 4. Найти точки перегиба, интервалы выпуклости и вогнутости графика функции .

Посмотреть правильное решение и ответ.

Пример 5. Найти точки перегиба, интервалы выпуклости и вогнутости графика функции .

Посмотреть правильное решение и ответ.

Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.

Пример 6. Найти точки перегиба, интервалы выпуклости и вогнутости графика функции .

Решение. Найдём точки перегиба, решив уравнение :

Таких значений x, при которых вторая производная функции не существовала бы, нет, поэтому найденные — все возможные точки перегиба. Чтобы убедиться в том, что они действительно являются точками перегиба, следует проверить поведение графика функции в этих точках. Для этого найдём значения второй производной слева и справа от точек :

, поэтому график функции в интервале вогнутый,

, поэтому график функции в интервале выпуклый,

, поэтому график функции в интервале вогнутый.

Вывод: точки действительно являются точками перегиба графика данной функции, так как при переходе через них меняется поведение графика. Найдём значения функции в точках перегиба:

Обобщим полученные данные в таблице:

x	(−∞;2)	2	(2;4)	4	(4;+∞)
y»	+	0	−	0	+
y	вогнутый	2	выпуклый	146	вогнутый

График этой функции — на рис. снизу.

Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.

Пример 7. Найти точки перегиба, интервалы выпуклости и вогнутости графика функции .

Решение. Найдём точки перегиба, решив уравнение :

Видим, что не существует таких значений x, при которых вторая производная была бы равна нулю, так как . Таким образом, точки перегиба могут быть только при таких значениях x, в которых вторая производная функции не определена. Определим точки, в которых вторая производная функции не определена:

Определим знаки второй производной функции в интервалах между возможными точками перегиба.

Интервал :

, поэтому график функции в интервале вогнутый.

Интервал :

, поэтому график функции в интервале выпуклый.

Интервал :

, поэтому график функции в интервале вогнутый.

Интервал :

, поэтому график функции в интервале вогнутый.

Найдём значения функции в конечных точках интервалов:

Обобщим полученные данные в таблице:

x	(−∞;−√3)	−√3	(−√3;0)
y»	+	∅	−
y	вогнутый	0	выпуклый

0	(0;√3)	√3	(√3;+∞)
∅	+	∅	−
0	вогнутый	0	выпуклый

График этой функции — на рис. снизу.

Пример 8. Найти точки перегиба, интервалы выпуклости и вогнутости графика функции .

Решение. Область определения данной функции , так как логарифм существует только от положительных чисел. Найдём вторую производную функции:

Приравнивая вторую производную нулю, определим критические точки:

Так как точка x = 0 не принадлежит области определения функции, то

Таким образом, точка x = 1 — единственная критическая точка. Знаки второй производной в интервалах, разграниченных этой точкой:

в интервале — минус,

в интервале — плюс.

Значение функции в точке перегиба:

.

Следовательно, в интервале график данной функции выпуклый, а в интервале — вогнутый. Точка перегиба — (1; −7).

График этой функции — на рис. снизу.

Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.

Пример 9. Найти интервалы выпуклости и вогнутости графика функции .

Решение. Найдём вторую производную функции:

Приравнивая вторую производную нулю, определим точки, в которых вторая производная равна нулю или не существует. Так как 10≠0, то для любого значения x . Вторая производная не существует, если или x = 2. Определим знаки второй производной в интервалах, разграниченных этой точкой:

в интервале — минус,

в интервале — плюс.

Следовательно, в интервале график данной функции выпуклый, а в интервале — вогнутый.

Назад

Листать

Вперёд>>>

К началу страницы

Пройти тест по теме Производная, дифференциал и их применение

Весь блок «Производная»

• Что такое производная
• Найти производную: алгоритмы и примеры решений
• Производные произведения и частного функций
• Производная суммы дробей со степенями и корнями
• Производные простых тригонометрических функций
• Производная сложной функции
• Производная логарифмической функции
• Дифференциал функции
• Дифференциал сложной функции, инвариантность формы дифференциала
• Уравнение касательной и уравнение нормали к графику функции
• Правило Лопиталя
• Частные производные
• Применение производной к исследованию функций
• Экстремумы функции
• Наименьшее и наибольшее значения функции
• Асимптоты
• Возрастание, убывание и монотонность функции
• Выпуклость и вогнутость графика функции, точки перегиба
• Полное исследование функций и построение графиков
• Функции двух и трёх переменных
• Экстремумы функции двух переменных
• Условные экстремумы и функция Лагранжа

Интервалы выпуклости и вогнутости (впуклости) графика функции

Графики функций/ Исследовать

Учитель очень удивится увидев твоё верное решение😉

Введите график функции

Исследуем график функции y=f(x), для этого задайте функцию f(x). 2*arctgh(x)*arcctgh(x)

Что исследует?

Для периодических функций идет исследование графика функции только на промежутке периода

Наш калькулятор позволяет исследовать график функции. Но пока что нет возможности находить область определения функции

Что умеет находить этот калькулятор:

• Область определения функции: Да. Умеет определять только точки, в которых знаменатель функции обращается в нуль, но в остальных случаях:
• Умеет определять точки пересечения графика функции с осями координат: Да
• Экстремумы функции: интервалы (отрезки) возрастания и убывания функции: Да
• Точки перегибов графика функции: перегибы: интервалы выпуклости, вогнутости (впуклости): Да
• Вертикальные асимптоты : Да (это завязано с областью определения функции, на точки, где знаменатель функции обращается в нуль)
• Горизонтальные асимптоты графика функции: Да
• Наклонные асимптоты графика функции: Да
• Четность и нечетность функции: Да
• Минимум и максимум функции: Да

Правила ввода выражений и функций

Выражения могут состоять из функций (обозначения даны в алфавитном порядке):

absolute(x)

Абсолютное значение x
(модуль x или |x|)

arccos(x)

Функция — арккосинус от x

arccosh(x)

Арккосинус гиперболический от x

arcsin(x)

Арксинус от x

arcsinh(x)

Арксинус гиперболический от x

arctg(x)

Функция — арктангенс от x

arctgh(x)

Арктангенс гиперболический от x

exp(x)

Функция — экспонента от x (что и e^x)

log(x) or ln(x)

Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10))

sin(x)

Функция — Синус от x

cos(x)

Функция — Косинус от x

sinh(x)

Функция — Синус гиперболический от x

cosh(x)

Функция — Косинус гиперболический от x

sqrt(x)

Функция — квадратный корень из x

sqr(x) или x^2

Функция — Квадрат x

ctg(x)

Функция — Котангенс от x

arcctg(x)

Функция — Арккотангенс от x

arcctgh(x)

Функция — Гиперболический арккотангенс от x

tg(x)

Функция — Тангенс от x

tgh(x)

Функция — Тангенс гиперболический от x

cbrt(x)

Функция — кубический корень из x

gamma(x)

Гамма-функция

LambertW(x)

Функция Ламберта

x! или factorial(x)

Факториал от x

DiracDelta(x)

Дельта-функция Дирака

Heaviside(x)

Функция Хевисайда

Интегральные функции:

Si(x)

Интегральный синус от x

Ci(x)

Интегральный косинус от x

Shi(x)

Интегральный гиперболический синус от x

Chi(x)

Интегральный гиперболический косинус от x

В выражениях можно применять следующие операции:

Действительные числа

вводить в виде 7. 3

— возведение в степень

x + 7

— сложение

x — 6

— вычитание

15/7

— дробь

Другие функции:

asec(x)

Функция — арксеканс от x

acsc(x)

Функция — арккосеканс от x

sec(x)

Функция — секанс от x

csc(x)

Функция — косеканс от x

floor(x)

Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)

ceiling(x)

Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)

sign(x)

Функция — Знак x

erf(x)

Функция ошибок (или интеграл вероятности)

laplace(x)

Функция Лапласа

asech(x)

Функция — гиперболический арксеканс от x

csch(x)

Функция — гиперболический косеканс от x

sech(x)

Функция — гиперболический секанс от x

acsch(x)

Функция — гиперболический арккосеканс от x

Постоянные:

pi

Число «Пи», которое примерно равно ~3. 14159..

e

Число e — основание натурального логарифма, примерно равно ~2,7183..

i

Комплексная единица

oo

Символ бесконечности — знак для бесконечности

×

Где учитесь?

Для правильного составления решения, укажите:

(не выбрано)9 класс10 класс11 класс1-й курс2-й курс3-й курс4-й курсдругое

Mathway | Популярные задачи

1	Trovare la Derivata — d/dx	натуральный логарифм x
2	Вычислим интеграл	интеграл натурального логарифма x по x
3	Trovare la Derivata — d/dx	e^x
4	Вычислим интеграл	интеграл e^(2x) по x
5	Trovare la Derivata — d/dx	1/x
6	Trovare la Derivata — d/dx	x^2
7	Trovare la Derivata — d/dx	1/(x^2)
8	Trovare la Derivata — d/dx	sin(x)^2
9	Trovare la Derivata — d/dx	sec(x)
10	Вычислим интеграл	интеграл e^x по x
11	Вычислим интеграл	интеграл x^2 по x
12	Вычислим интеграл	интеграл квадратного корня из x по x
13	Trovare la Derivata — d/dx	cos(x)^2
14	Вычислим интеграл	интеграл 1/x по x
15	Вычислим интеграл	интеграл sin(x)^2 по x
16	Trovare la Derivata — d/dx	x^3
17	Trovare la Derivata — d/dx	sec(x)^2
18	Вычислим интеграл	интеграл cos(x)^2 по x
19	Вычислим интеграл	интеграл sec(x)^2 по x
20	Trovare la Derivata — d/dx	e^(x^2)
21	Вычислим интеграл	интеграл в пределах от 0 до 1 кубический корень из 1+7x по x
22	Trovare la Derivata — d/dx	sin(2x)
23	Trovare la Derivata — d/dx	tan(x)^2
24	Вычислим интеграл	интеграл 1/(x^2) по x
25	Trovare la Derivata — d/dx	2^x
26	График	натуральный логарифм a
27	Trovare la Derivata — d/dx	cos(2x)
28	Trovare la Derivata — d/dx	xe^x
29	Вычислим интеграл	интеграл 2x по x
30	Trovare la Derivata — d/dx	( натуральный логарифм от x)^2
31	Trovare la Derivata — d/dx	натуральный логарифм (x)^2
32	Trovare la Derivata — d/dx	3x^2
33	Вычислим интеграл	интеграл xe^(2x) по x
34	Trovare la Derivata — d/dx	2e^x
35	Trovare la Derivata — d/dx	натуральный логарифм 2x
36	Trovare la Derivata — d/dx	-sin(x)
37	Trovare la Derivata — d/dx	4x^2-x+5
38	Trovare la Derivata — d/dx	y=16 корень четвертой степени из 4x^4+4
39	Trovare la Derivata — d/dx	2x^2
40	Вычислим интеграл	интеграл e^(3x) по x
41	Вычислим интеграл	интеграл cos(2x) по x
42	Trovare la Derivata — d/dx	1/( квадратный корень из x)
43	Вычислим интеграл	интеграл e^(x^2) по x
44	Вычислить	e^infinity
45	Trovare la Derivata — d/dx	x/2
46	Trovare la Derivata — d/dx	-cos(x)
47	Trovare la Derivata — d/dx	sin(3x)
48	Trovare la Derivata — d/dx	1/(x^3)
49	Вычислим интеграл	интеграл tan(x)^2 по x
50	Вычислим интеграл	интеграл 1 по x
51	Trovare la Derivata — d/dx	x^x
52	Trovare la Derivata — d/dx	x натуральный логарифм от x
53	Trovare la Derivata — d/dx	x^4
54	Оценить предел	предел (3x-5)/(x-3), если x стремится к 3
55	Вычислим интеграл	интеграл x^2 натуральный логарифм x по x
56	Trovare la Derivata — d/dx	f(x) = square root of x
57	Trovare la Derivata — d/dx	x^2sin(x)
58	Вычислим интеграл	интеграл sin(2x) по x
59	Trovare la Derivata — d/dx	3e^x
60	Вычислим интеграл	интеграл xe^x по x
61	Trovare la Derivata — d/dx	y=x^2
62	Trovare la Derivata — d/dx	квадратный корень из x^2+1
63	Trovare la Derivata — d/dx	sin(x^2)
64	Вычислим интеграл	интеграл e^(-2x) по x
65	Вычислим интеграл	интеграл натурального логарифма квадратного корня из x по x
66	Trovare la Derivata — d/dx	e^2
67	Trovare la Derivata — d/dx	x^2+1
68	Вычислим интеграл	интеграл sin(x) по x
69	Trovare la Derivata — d/dx	arcsin(x)
70	Оценить предел	предел (sin(x))/x, если x стремится к 0
71	Вычислим интеграл	интеграл e^(-x) по x
72	Trovare la Derivata — d/dx	x^5
73	Trovare la Derivata — d/dx	2/x
74	Trovare la Derivata — d/dx	натуральный логарифм 3x
75	Trovare la Derivata — d/dx	x^(1/2)
76	Trovare la Derivata — d/d@VAR	f(x) = square root of x
77	Trovare la Derivata — d/dx	cos(x^2)
78	Trovare la Derivata — d/dx	1/(x^5)
79	Trovare la Derivata — d/dx	кубический корень из x^2
80	Вычислим интеграл	интеграл cos(x) по x
81	Вычислим интеграл	интеграл e^(-x^2) по x
82	Trovare la Derivata — d/d@VAR	f(x)=x^3
83	Вычислим интеграл	интеграл 4x^2+7 в пределах от 0 до 10 по x
84	Вычислим интеграл	интеграл ( натуральный логарифм x)^2 по x
85	Trovare la Derivata — d/dx	логарифм x
86	Trovare la Derivata — d/dx	arctan(x)
87	Trovare la Derivata — d/dx	натуральный логарифм 5x
88	Trovare la Derivata — d/dx	5e^x
89	Trovare la Derivata — d/dx	cos(3x)
90	Вычислим интеграл	интеграл x^3 по x
91	Вычислим интеграл	интеграл x^2e^x по x
92	Trovare la Derivata — d/dx	16 корень четвертой степени из 4x^4+4
93	Trovare la Derivata — d/dx	x/(e^x)
94	Оценить предел	предел arctan(e^x), если x стремится к 3
95	Вычислим интеграл	интеграл (e^x-e^(-x))/(e^x+e^(-x)) по x
96	Trovare la Derivata — d/dx	3^x
97	Вычислим интеграл	интеграл xe^(x^2) по x
98	Trovare la Derivata — d/dx	2sin(x)
99	Вычислить	sec(0)^2
100	Trovare la Derivata — d/dx	натуральный логарифм x^2

Калькулятор точек перегиба и вогнутости, чтобы найти точку перегиба

Используйте этот бесплатный калькулятор точек перегиба, чтобы найти точки перегиба и интервалы вогнутости данного уравнения.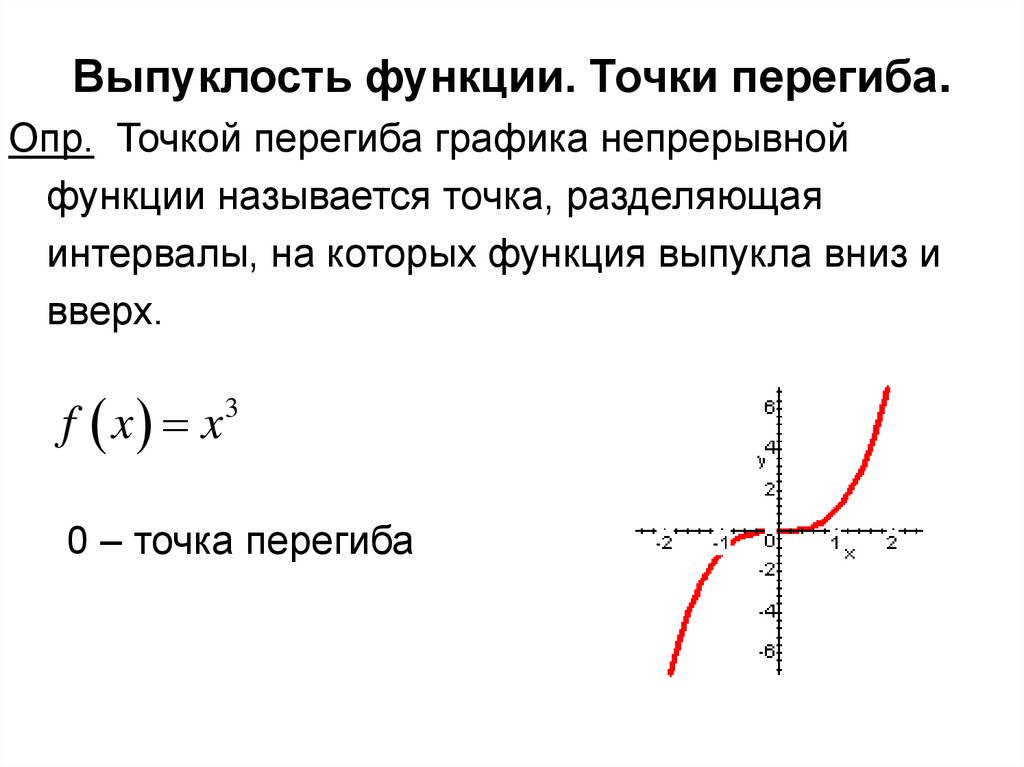 Кроме того, вычисление заменителей является сложной задачей, поэтому с помощью этого калькулятора точки перегиба вы можете найти корни и тип наклона данной функции.

Здесь вы можете изучить, когда вогнутость вверх и вниз и как найти точки перегиба с производными.

Что такое I Точка перегиба?

В исчислении точка перегиба — это точка на кривой, где вогнутость функции меняет свое направление, а кривизна меняет знак. Другими словами, точка на графике, где вторая производная не определена или равна нулю, меняет знак.

Аналогично, вторая производная f’’(x) больше нуля, направление вогнуто вверх, а когда f’’(x) меньше 0, то f(x) вогнуто вниз.

Чтобы найти точку перегиба функции, выполните следующие действия.

Возьмите квадратное уравнение для вычисления первой производной функции f'(x).
Теперь выполните второй вывод f(x), т. е. f”(x), а также найдите третью производную функции.
Третье производное f”'(x) не должно быть равно нулю и сделать f”(x) = 0, чтобы найти значение переменной.
Замените значение x в третьем выводе функции, чтобы узнать минимумы и максимумы функции. 9{«}(x_0) = 0$$

Однако мы можем найти необходимые условия для проверки точек перегиба второй производной f» (x) с помощью калькулятора точек перегиба и получить пошаговые расчеты.

Кроме того, онлайн-калькулятор производных помогает найти производную функции по заданной переменной и показывает полное дифференцирование.

Первое достаточное условие для точки перегиба:

Если функция дифференцируема и непрерывна в точке x_0, имеет вторую производную в некоторой удаленной окрестности точки x_0, и если вторая производная меняет направление наклона при прохождении через точка x_0, тогда x_0 является точкой перегиба функции.

Второе достаточное условие для точки перегиба:

x_0 — это точка перегиба функции f(x), когда вторая производная равна нулю, а третья производная f»’ (x_0) не равна нуль.

$$F” (x_0) = 0$$

$$F”’ (x_0) ≠ 0$$

Как найти вогнутость?

График имеет вогнутость вверх в точке, когда касательная функции изменяется и точка лежит под графиком в соответствии с точками окрестности, и вогнута вниз в той точке, когда прямая лежит над графиком в окрестности точки. Таким образом, калькулятор вогнутости вверх и вниз определяет, когда касательная идет вверх или вниз, тогда мы можем найти точку перегиба, используя эти значения.

Следовательно, график производной y = f’ (x) увеличивается, когда функция y = f(x) вогнута вверх, а когда производная y = f’ (x) уменьшается, функция вогнута вниз и график производная y = f'(x) имеет минимумы или максимумы, когда функция y = f(x) имеет точку перегиба.

Кроме того, онлайн-калькулятор уклона позволяет найти уклон или градиент между двумя точками в декартовой координатной плоскости.

Как Калькулятор точки перегиба работает?

Чтобы найти точки перегиба с помощью калькулятора точек перегиба, вам необходимо выполнить следующие шаги:

Ввод:

• Сначала введите квадратное уравнение для определения точки перегиба, и калькулятор отобразит уравнение который вы введете в данное поле.
• Теперь нажмите кнопку расчета.

Вывод:

При вводе уравнения точки перегиба калькулятор дает следующие результаты:

• Показывает точки перегиба в соответствии с введенными значениями, а также отображает точки при вогнутости вверх и вниз со своими заменителями.
• Кроме того, он сообщает о повышении или понижении касательной и показывает первую, вторую и третью производную функции f(x) с полным вычислением.

Часто задаваемые вопросы:

Как мы получаем максимумы, минимумы и точки перегиба с помощью производных?

Относительными экстремумами могут быть точки, в которых первая производная функции равна нулю:

F’(x_0) = 0

Эти точки будут максимумом, минимумом и точкой перегиба, поэтому они должны удовлетворять второму условию.

Как узнать максимумы, минимумы и точки перегиба?

Как только мы получим точки, для которых первая производная f'(x) функции равна нулю, для каждой точки калькулятор точки перегиба проверяет, что значение второй производной в этой точке больше нуля, тогда эта точка минимальна, и если вторая производная в этой точке равна f»(x)<0, то эта точка максимальна.

Что такое стационарная и нестационарная точка перегиба?

• Когда f’(x) равно нулю, точка перегиба стационарна.
• Точка является нестационарной точкой перегиба, когда f’(x) не равно нулю.

Конечная точка:

Калькулятор точки перегиба специально создан онлайн-калькулятором, чтобы обеспечить лучшее понимание точек перегиба и их производных, типа наклона, вогнутости вниз и вверх с полными расчетами. Несомненно, вы можете получить эти расчеты вручную с помощью графика, но это увеличивает неопределенность, поэтому вам нужно выбрать этот онлайн-калькулятор вогнутости, чтобы получить 100% точные значения.

Ссылка:

Из источника Википедии: Необходимое, но недостаточное условие, Точки перегиба достаточные условия, Категоризация точек перегиба.

Из источника чайников: Функции с разрывами, Графический анализ точек перегиба.

Из источника Академии Хана: Точки перегиба алгебраически, Точки перегиба, Вогнутость вверх, Вогнутость вниз, Точки перегиба.

 

 

 

Интервалы выпуклой вогнутой функции онлайн калькулятор. Выпуклость функции

С помощью онлайн-калькулятора можно найти точки перегиба и интервалы выпуклости графика функции с оформлением решения в Word. Является ли функция двух переменных f(x1,x2) выпуклой, решается с помощью матрицы Гессе.

Правила ввода функций :

Определение: Кривая y=f(x) называется выпуклой вниз на интервале (a; b), если она лежит выше касательной в любой точке этого интервала.

Определение: Кривая y=f(x) называется выпуклой вверх на интервале (a; b), если она лежит ниже касательной в любой точке этого интервала.

Определение: Интервалы, в которых график функции выпукл вверх или вниз, называются интервалами выпуклости графика функции.

Выпуклость вниз или вверх кривой, являющейся графиком функции y=f(x) , характеризуется знаком ее второй производной: если в некотором интервале f»(x) > 0, то кривая выпукла вниз на этом отрезке; если f»(x).

Определение: Точка графика функции y=f(x) , разделяющая интервалы выпуклости противоположных направлений этого графика, называется точкой перегиба.

Только критические точки второго рода могут служить точками перегиба; точки, принадлежащие области определения функции y = f(x), в которых вторая производная f»(x) обращается в нуль или обрывается.

Правило нахождения точек перегиба графика функции y = f(x)

1. Найдите вторую производную f»(x) .
2. Найдите критические точки второго рода функции y=f(x) , т. е. точку, в которой f»(x) обращается в нуль или ломается.
3. Исследуйте знак второй производной f»(x) в интервалах, на которые найденные критические точки разбивают область определения функции f(x) . Если при этом критическая точка x 0 разделяет интервалы выпуклости противоположных направлений, то x 0 является абсциссой точки перегиба графика функции.
4. Вычислить значения функции в точках перегиба.

Пример 1 . Найдите пробелы выпуклости и точки перегиба следующей кривой: f(x) = 6x 2 –x 3 .
Решение: Найдите f'(x) = 12x — 3x 2 , f»(x) = 12 — 6x.
Найдем критические точки по второй производной, решив уравнение 12-6x=0 . х=2 .

f(2) = 6*2 2 — 2 3 = 16
Ответ: Функция выпукла вверх при x∈(2; +∞) ; функция выпукла вниз при x∈(-∞; 2) ; точка перегиба (2;16) .

Пример 2 . Имеет ли функция точки перегиба: f(x)=x 3 -6x 2 +2x-1

Пример 3 . Найдите интервалы, на которых график функции выпуклый и выпуклый: f(x)=x 3 -6x 2 +12x+4

График функции y = f(x) называется выпуклым на интервале (a ;b) , если он расположен ниже любой из его касательных на этом интервале.

График функции y = f(x) называется вогнутым на интервале (a;b) , если он расположен выше любой из его касательных на этом интервале.

На рисунке показана кривая, выпуклая на (a;b) и вогнутой до (b;c) .

Примеры.

Рассмотрим достаточный признак, позволяющий определить, будет ли график функции на данном интервале выпуклым или вогнутым.

Теорема . Пусть y = f(x) дифференцируемо на (a;b) . Если во всех точках отрезка (a;b) вторая производная функции y = f(x) отрицательна, т. е. f «»( x ) f»»( x ) > 0 является вогнутым.

Доказательство . Предположим для определенности, что f «»( x )

Возьмем на графике функции y = f(x) произвольную точку M0 с абсциссой x0 Î ( a ; b ) и проведите через точку M0 касательную. Ее уравнение. Мы должны показать, что график функции на (a;b) лежит ниже этой касательной, т.е. с тем же значением x ордината кривой y = f(x) будет меньше ординаты касательной.

Итак, уравнение кривой y = f(x) . Обозначим ординату касательной, соответствующую оси абсцисс x . Затем . Поэтому разница между ординатами кривой и касательной при одном и том же значении х будет .

Разность f(x) – f(x0) преобразование по теореме Лагранжа, где c между x и x 0 .

Таким образом,

Снова применим теорему Лагранжа к выражению в квадратных скобках: , где c 1 между c 0 и x0 . По теореме f «»( x )

Таким образом, любая точка кривой лежит ниже касательной к кривой для всех значений x и x0 О ( a ; b ), что означает, что кривая выпуклая. Аналогично доказывается вторая часть теоремы.

Примеры .

Точка на графике непрерывной функции, отделяющая ее выпуклую часть от вогнутой, называется точкой перегиба .

Очевидно, что в точке перегиба касательная, если она существует, пересекает кривую, так как с одной стороны от этой точки кривая лежит под касательной, а с другой стороны — над ней.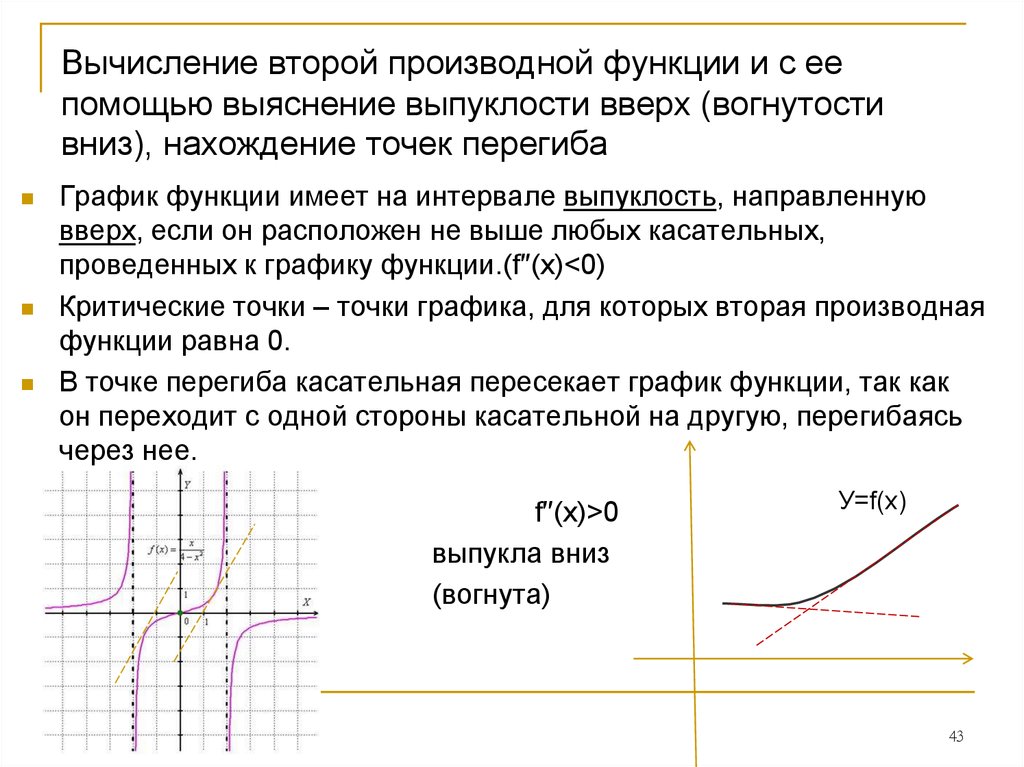

Определим достаточные условия для того, чтобы данная точка кривой была точкой перегиба.

Теорема . Пусть кривая определяется уравнением y = f(x) . Если a f «»( x 0) = 0 или f «»( x 0) не существует и при переходе через значение x = x0 производная f «»( х ) меняет знак, то точка графика функции с абсциссой х = х 0 является точкой перегиба.

Доказательство . пусть будет ф «»( х ) х х0 и ф «»( x ) > 0 при x > x0 . Тогда при x x0 кривая выпуклая, а x > x0 — вогнутая. Отсюда точка А , лежащая на кривой, с абсциссой х 0 есть точка перегиба. Аналогично можно рассмотреть и второй случай, когда f «»( x ) > 0 при x х0 и ф «»( х ) х > х 0 .

Таким образом, точки перегиба следует искать только среди тех точек, где вторая производная равна нулю или не существует.

Примеры. Найдите точки перегиба и определите интервалы выпуклости и вогнутости кривых.

АСИМПТОТЫ ГРАФИКА ФУНКЦИИ

При исследовании функции важно установить форму ее графика с неограниченным удалением точки графика от начала координат.

Особый интерес представляет случай, когда график функции при удалении ее переменной точки в бесконечность неограниченно приближается к некоторой прямой линии.

Прямой вызов асимптота график функции y = f(x) если расстояние от переменной точки M график до этой прямой при удалении точки к нулю бесконечности M M график функции , т. е. точка графика функции при стремлении к бесконечности должна неограниченно приближаться к асимптоте.

Кривая может приближаться к своей асимптоте, оставаясь по одну от нее сторону или по разные стороны, бесконечное число раз пересекая асимптоту и переходя с одной стороны на другую.

Если обозначить через d расстояние от точки М кривой до асимптоты, то ясно, что d стремится к нулю при удалении точки М на бесконечность.

Далее мы будем различать вертикальные и наклонные асимптоты.

ВЕРТИКАЛЬНЫЕ АСИМПТОТЫ

Пусть при x → x0 любая сторона функции y = f(x) неограниченно возрастает по модулю, т.е. или или . Тогда из определения асимптоты следует, что прямая х = х 0 является асимптотой. Обратное также очевидно, если прямая x = x0 является асимптотой, поэтому .

Таким образом, вертикальная асимптота графика функции y = f(x) называется прямой, если f(x) → ∞ при выполнении хотя бы одного из условий x → x0 – 0 или x → x0 + 0, x = x0

Следовательно, чтобы найти вертикальные асимптоты графика функции y = 80 x 9018 найти те значения x = x0 , при которых функция стремится к бесконечности (терпит бесконечный разрыв). Тогда вертикальная асимптота имеет уравнение х = х 0 .

Примеры.

НАКЛОННЫЕ АСИМПТОТЫ

Так как асимптота является прямой линией, то если кривая y = f(x) имеет наклонную асимптоту, то ее уравнение будет б . Наша задача найти коэффициенты k и b .

Теорема . Прямой y = kx + b служит наклонной асимптотой при x → +∞ для графика функции y = f(x) тогда и только тогда, когда . Аналогичное утверждение верно для x → –∞.

Доказательство . Пусть МП — длина отрезка равна расстоянию от точки М до асимптоты. Условием . Обозначим через φ угол наклона асимптоты к оси Ox . Тогда из ΔMNP следует, что . Поскольку φ — постоянный угол (φ ≠ π/2), то , но

Понятие выпуклости функции

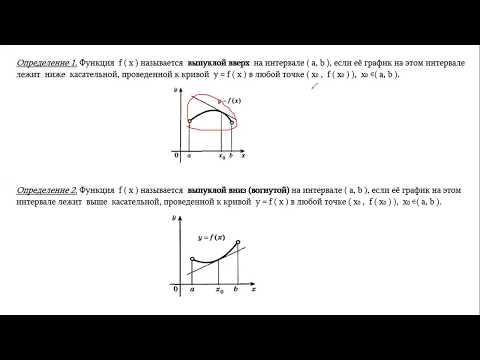
Рассмотрим функцию \(y = f\left(x \right),\), которая предполагается непрерывной на отрезке \(\left[ (a,b) \right ].\) Функция \(y = f\left(x \right),\))\) называется выпуклой вниз (или просто выпуклая ), если для любых точек \((x_1)\) и \((x_2)\) из \(\left[ (a,b) \right]\) x_1),(x_2) \in \left[ (a,b) \right],\) такое, что \((x_1) \ne (x_2),\) то функция \(f\left(x \right) \) называется строго выпуклой вниз

Аналогично определяется выпуклая вверх функция. Функция \(f\left(x \right)\) называется выпуклой вверх (или вогнутое ) если для любых точек \((x_1)\) и \(((x_2)\) отрезка \(\left[ (a,b) \right]\) выполняется неравенство \ Если это неравенство верно строгая для любых \(( x_1),(x_2) \in \left[ (a,b) \right],\) таких, что \((x_1) \ne (x_2),\), то функция \(f\ left(x \right) \) называются строго выпуклыми вверх на отрезке \(\left[ (a,b) \right].\)

Геометрическая интерпретация выпуклости функции

Введенные определения выпуклой функции имеют простую геометрическую интерпретацию.

Для функции выпуклостью вниз (рисунок \(1\)), середина \(B\) любой хорды \((A_1)(A_2)\) лежит на выше

Аналогично, для функции выпуклой вверх (рисунок \(2\)), середина \(B\) любой хорды \((A_1)(A_2)\) лежит на ниже соответствующей точки \((A_0)\) графика функции или совпадает с этой точкой.

Выпуклые функции имеют еще одно визуальное свойство, связанное с расположением касательной к графику функции. Функция \(f\left(x \right)\) выпукла вниз на отрезке \(\left[ (a,b) \right]\) тогда и только тогда, когда его график лежит не ниже касательной, проведенной к нему в любой точке \((x_0)\) отрезка \(\left [ (a ,b) \right]\) (рисунок \(3\)).

Соответственно, функция \(f\left(x \right)\) выпукла вверх на отрезке \(\left[ (a,b) \right]\) тогда и только тогда, когда его график лежит не выше касательной, проведенной к нему в любой точке \((x_0)\) отрезка \(\left [ (a ,b) \right]\) (рисунок \(4\)). Эти свойства являются теоремой и могут быть доказаны с помощью определения выпуклости функции.

Достаточные условия выпуклости

Пусть для функции \(f\left(x \right)\) первая производная \(f»\left(x \right)\) существует на отрезке \(\left[ ( a,b) \right],\) и вторую производную \(f»»\left(x \right)\) − на отрезке \(\left((a,b) \right).\) Тогда выполняются следующие достаточные критерии выпуклости:

функция \(f\left(x \right )\) выпуклая вниз на отрезке \(\left[ (a,b) \right];\)

Если \(f»»\left(x \right) \le 0\) для всех \(x \in \left((a,b) \right),\), то функция \(f\left(x \справа )\) выпуклостью вверх на отрезке \(\left[ (a,b) \right].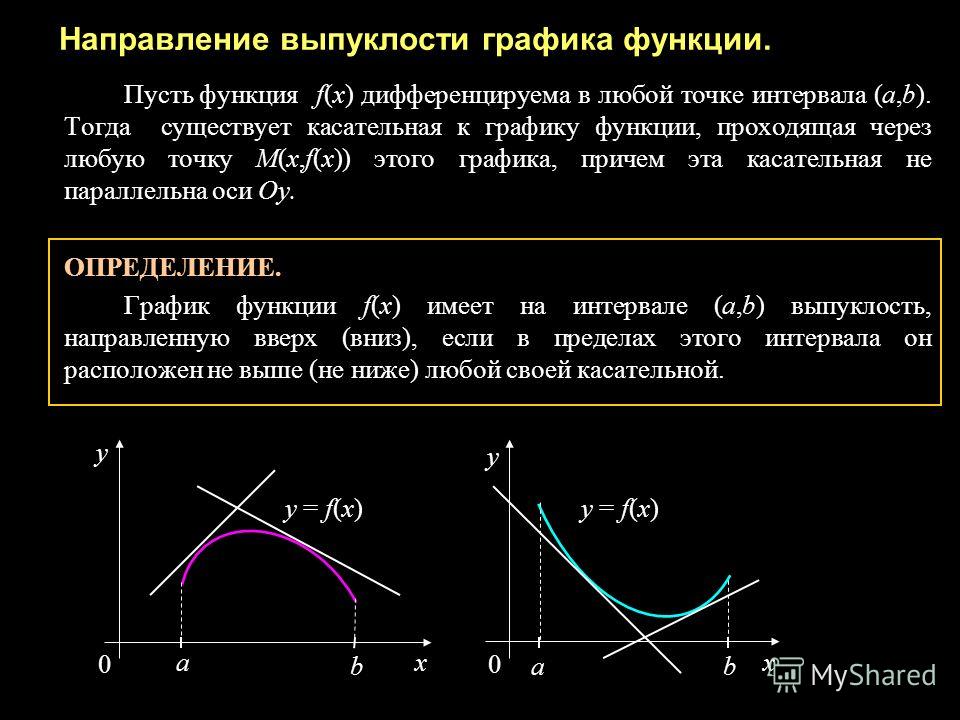 4)\) строго выпукла вниз. Однако в точке \(x = 0\) его вторая производная равна нулю, т. е. строгое неравенство \(f»»\left(x \right) \gt 0\) в этом случае не выполняется.

Свойства выпуклых функций

Перечислим некоторые свойства выпуклых функций, предполагая, что все функции определены и непрерывны на отрезке \(\left[ (a,b) \right].\)

Если функции \ (f\) и \(g\) выпуклы вниз (вверх), то любая из них линейная комбинация \(af + bg,\), где \(a\), \(b\) — положительные действительные числа, также выпуклые вниз (вверх).

Если функция \(u = g\left(x \right)\) выпукла вниз, а функция \(y = f\left(u \right)\) выпукла вниз и неубывающая, то сложная функция \(y = f\left((g\left(x \right)) \right)\) также будет выпуклым вниз.

Если функция \(u = g\left(x \right)\) выпукла вверх, а функция \(y = f\left(u \right)\) выпукла вниз и не возрастает, то комплексная функция \(y = f\left((g\left(x \right)) \right)\) будет выпуклым вниз.

Локальный максимум выпуклая вверх функция, определенная на отрезке \(\left[ (a,b) \right],\) одновременно является ее наибольшим значением на этом сегменте.

Местный минимум выпуклая вниз функция, определенная на отрезке \(\left[ (a,b) \right],\) является одновременно своим наименьшим значением на этом сегменте.

Инструкция

Точки перегиба функции должны принадлежать области ее определения, которую необходимо найти в первую очередь. График функции – это линия, которая может быть непрерывной или иметь изломы, монотонно убывающая или возрастающая, иметь точки минимума или максимума (асимптоты), быть выпуклой или вогнутой. Резкое изменение двух последних состояний называется перегибом.

Необходимым условием существования перегиба функции является равенство секунды нулю. Таким образом, дважды продифференцировав функцию и приравняв полученное выражение нулю, можно найти абсциссы возможных точек перегиба.

Это условие следует из определения свойств выпуклости и вогнутости графика функции, т.е. отрицательных и положительных значений второй производной. В точке перегиба происходит резкое изменение этих свойств, а значит, производная проходит нулевую отметку. Однако равенства нулю еще недостаточно для обозначения точки перегиба.

Есть два достаточных условия, чтобы найденная на предыдущем этапе абсцисса принадлежала точке перегиба: Через эту точку можно провести касательную к функции. Вторая производная имеет разные знаки справа и слева от предполагаемой точки перегиба. Таким образом, его существование в самой точке необязательно, достаточно определить, что он меняет в ней знак. Вторая производная функции равна нулю, а третья нет.

Первое достаточное условие является универсальным и используется чаще других. Рассмотрим наглядный пример: y = (3 x + 3) ∛ (x — 5).

Решение. Найдите область определения. В данном случае ограничений нет, следовательно, это все пространство действительных чисел.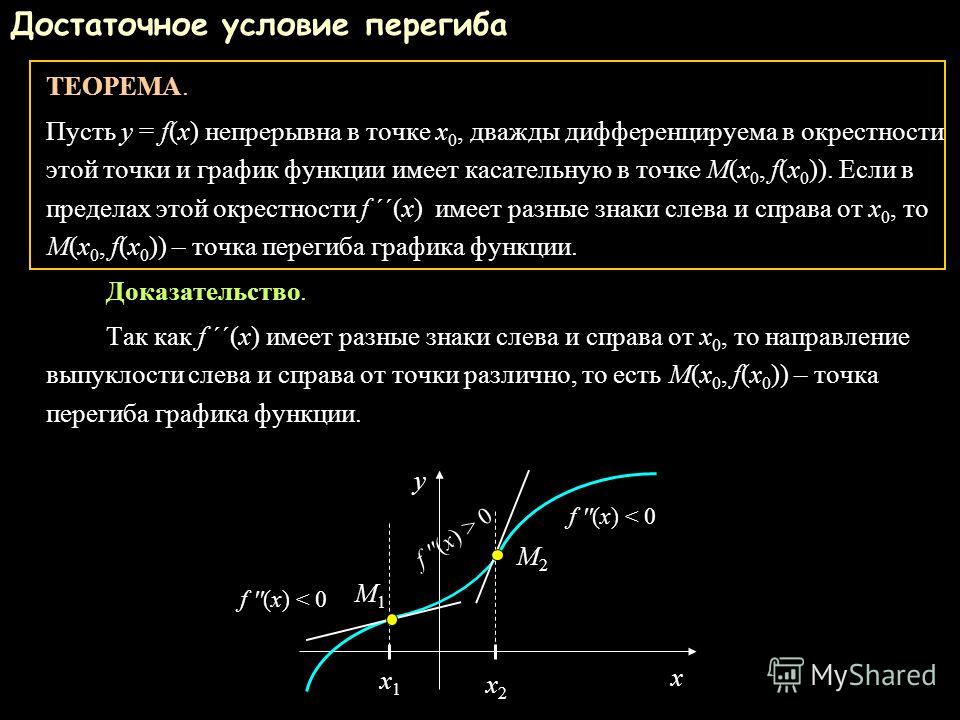 Вычислите первую производную: y’ = 3 ∛ (x — 5) + (3 x + 3) / ∛ (x — 5)².

Обратите внимание на внешний вид дроби. Отсюда следует, что область определения производной ограничена. Точка x = 5 проколота, а значит, через нее может проходить касательная, что отчасти соответствует первому критерию достаточности перегиба. 95.

Опустите знаменатель, т. к. вы уже учли точку x = 5. Решите уравнение 2 x — 22 = 0. Оно имеет единственный корень x = 11. Последний шаг — убедиться, что точки x = 5 и x = 11 — точки перегиба. Проанализируйте поведение второй производной в их окрестности. Очевидно, что в точке x = 5 он меняет знак с «+» на «-», а в точке x = 11, наоборот. Вывод: обе точки являются точками перегиба. Первое достаточное условие выполнено.

Для определения выпуклости (вогнутости) функции на некотором интервале можно использовать следующие теоремы.

Теорема 1. Пусть функция определена и непрерывна на отрезке и имеет конечную производную . Для того чтобы функция была выпуклой (вогнутой) по , необходимо и достаточно, чтобы ее производная убывала (возрастала) на этом интервале.

Теорема 2. Пусть функция определена и непрерывна вместе со своей производной на и имеет непрерывную вторую производную внутри. Для выпуклости (вогнутости) функции в необходимо и достаточно, чтобы внутри

Докажем теорему 2 для случая выпуклости функции .

Нужен. Возьмем произвольную точку. Разложим функцию вблизи точки в ряд Тейлора

Уравнение касательной к кривой в точке, имеющей абсциссу:

Тогда превышение кривой над касательной к ней в точке равно

Таким образом , остаток равен превышению кривой над касательной к ней в точке . В силу непрерывности, если , то и при , принадлежащем достаточно малой окрестности точки , а значит, очевидно, и при любом отличном от значения , принадлежащем указанной окрестности.

Это означает, что график функции лежит выше касательной и кривая выпукла в произвольной точке.

Адекватность. Пусть кривая выпукла на отрезке . Возьмем произвольную точку.

Аналогично предыдущей разложим функцию вблизи точки в ряд Тейлора

Превышение кривой над касательной к ней в точке с абсциссой , определяемое выражением, равно положительна для достаточно малой окрестности точки , положительна и вторая производная.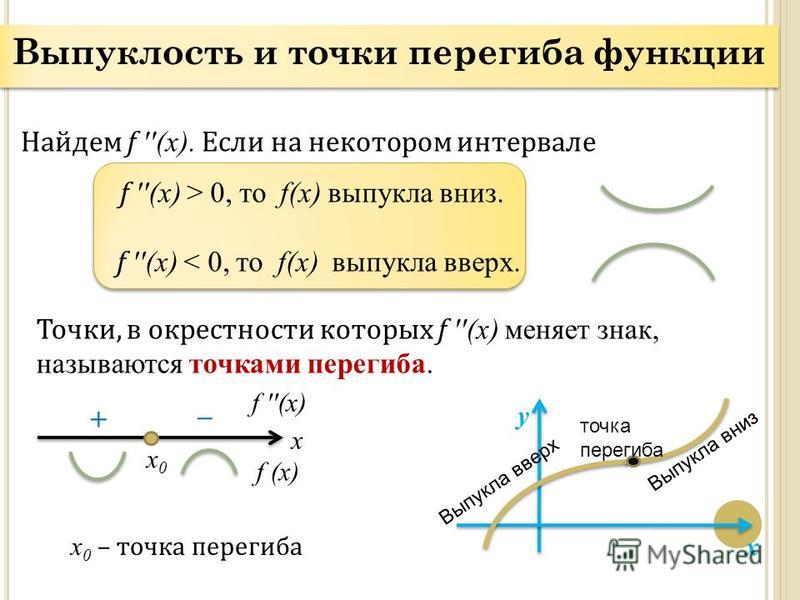 Стремясь, мы получаем это для произвольной точки .

Пример. Исследование функции выпуклости (вогнутости) .

Его производная возрастает на всей вещественной оси, поэтому по теореме 1 функция вогнута на .

Его вторая производная , поэтому по теореме 2 функция вогнута на .

3.4.2.2 Точки перегиба

Определение. Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, в которых функция является выпуклой и вогнутой.

Из этого определения следует, что точками перегиба являются точки экстремума первой производной. Отсюда вытекают следующие утверждения для необходимых и достаточных условий перегиба.

Теорема (необходимое условие перегиба) . Для того чтобы точка была точкой перегиба дважды дифференцируемой функции, необходимо, чтобы ее вторая производная в этой точке была равна нулю ( ) или не существовала.

Теорема (достаточное условие перегиба). Если вторая производная дважды дифференцируемой функции меняет знак при переходе через некоторую точку, то имеется точка перегиба.

Обратите внимание, что вторая производная может не существовать в самой точке.

Геометрическая интерпретация точек перегиба показана на рис. 3.9

В окрестности точки функция выпукла и ее график лежит ниже касательной, проведенной в этой точке. В окрестности точки функция вогнута и ее график лежит выше касательной, проведенной в этой точке. В точке перегиба касательная делит график функции на области выпуклости и вогнутости.

3.4.2.3 Проверка функции на выпуклость и наличие точек перегиба

1. Найти вторую производную.

2. Найдите точки, в которых вторая производная или не существует.

Рис. 3.9.

3. Изучить знак второй производной слева и справа от найденных точек и сделать вывод об интервалах выпуклости или вогнутости и наличии точек перегиба.

Пример. Исследуйте функцию на предмет выпуклости и наличия точек перегиба.

2. Вторая производная равна нулю при .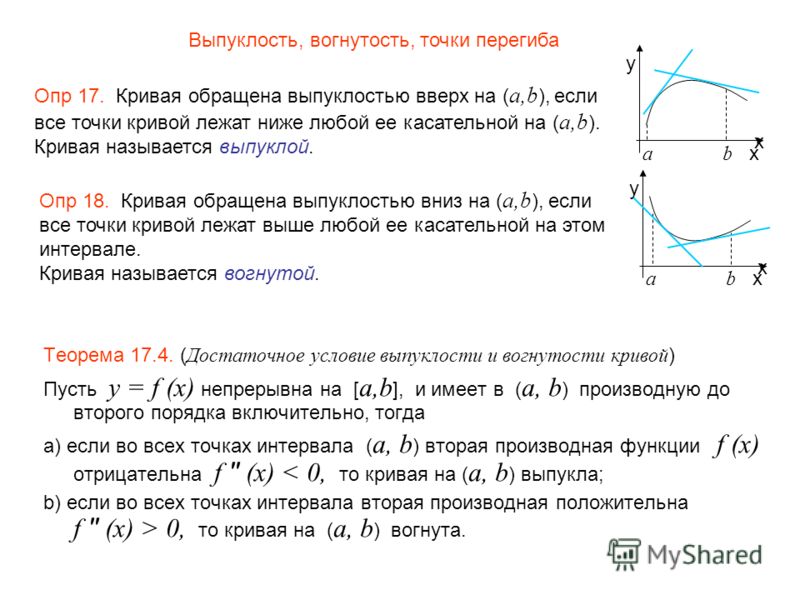

3. Вторая производная меняет знак при , поэтому точка является точкой перегиба.

На отрезке , то на этом отрезке функция выпукла.

На отрезке , то на этом отрезке функция вогнута.

3.4.2.4 Общая схема исследования функций и построения графика

При изучении функции и построении ее графика рекомендуется использовать следующую схему:

1. Найдите область действия функции.
2. Исследуйте функцию чет-нечет. Напомним, что график четной функции симметричен относительно оси y, а график нечетной функции симметричен относительно начала координат.
3. Найдите вертикальные асимптоты.
4. Исследуйте поведение функции на бесконечности, найдите горизонтальные или наклонные асимптоты.
5. Найдите экстремумы и интервалы монотонности функции.
6. Найдите интервалы выпуклости функции и точки перегиба.
7. Найти точки пересечения с осями координат.

Исследование функции проводится одновременно с построением ее графика.

Пример. Исследуйте функцию и постройте ее.

1. Объем функций — .

2. Исследуемая функция четная , поэтому ее график симметричен относительно оси у.

3. Знаменатель функции обращается в нуль при , поэтому график функции имеет вертикальные асимптоты и .

Точки являются точками разрыва второго рода, так как пределы слева и справа в этих точках стремятся к .

4. Поведение функции на бесконечности.

Следовательно, график функции имеет горизонтальную асимптоту.

5. Экстремумы и интервалы монотонности. Нахождение первой производной

При , следовательно, на этих интервалах функция убывает.

При , следовательно, функция возрастает на этих интервалах.

Для , следовательно, точка является критической точкой.

Нахождение второй производной

Так как , то точка является точкой минимума функции .

6. Интервалы выпуклости и точки перегиба.

Функция при , поэтому на этом интервале функция вогнута.

No related posts.