Решение линейных, квадратных и дробно-рациональных неравенств
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Выполнил: учитель математики МБОУ СОШ №23
Шибанова Наталья Николаева
2. I. Алгоритм решения неравенств
I. АЛГОРИТМ РЕШЕНИЯ НЕРАВЕНСТВ№
Этапы алгоритма
Обоснование
1
Приведение неравенства к
стандартному виду.
Можно перейти к следующим
этапам алгоритма.
2
Рассмотрение функции.

Есть возможность перейти к
геометрической модели неравенства
3
Нули функции. (ОДЗ, если
неравенство дробное рациональное)
Делят ось х на промежутки, на
которых функция имеет разные
знаки.
4
Работа с геометрической моделью.
Используя метод коэффициентов,
легко построить схематический
график функции.
Определить промежуток,
удовлетворяющий знаку
неравенства.(для линейных и
квадратных неравенств)
5
Внести промежуток в ответ.
Этого требует задание.
Линейные
Квадратные
неравенства
неравенства
kx + b > 0 (<; ≤ ;≥), где ах2 + bx + c > 0 (<; ≤ ;≥)
k ≠ 0, b – любое число. а ≠ 0, b и c -некоторые
числа.
Неравенства вида
Решить неравенство:
5х > 10
1. 5х-10 > 0
2. у = 5х-10
3. 5х-10 = 0, то х=2
4. k =5, то функция
возрастает:
Решить неравенство:
(х+7)(х-3)(2-4х)/(3x – 18)
≥0
1. (х+7)(х-3)(4х-2)/(3x –
18) ≤ 0
2.
 у = (х+7)(х-3)(4х-2)
у = (х+7)(х-3)(4х-2)/(3x – 18).
3. у=0 , то х=-7; х=0,5;
х=3.
4. ОДЗ: х ≠ 6.
—
2
+
х
Решить неравенство:
х2 > 4
1. х2 — 4 > 0
2. у = х2 – 4.
3. х2 — 4 = 0, то х = -2;
х=2.
4. а = 1, то ветви
параболы вверх:
х
+
—
-2
5.Ответ: (2;+∞).
(х -а)(х -в)…(х -с) 0
(x-d)
(<; ≤ ;≥), где а, в, с, dнекоторые числа.
+
2
+
-7
—
5.Ответ: (-∞;-2) (2;+∞) 5.Ответ:
[-7;0,5]
0,5
+
3
[3;6).
—
6
х
+
Подготовка к решению
квадратных неравенств.
у=ах²+bх+с
а>0
D=0
а>0
D<0
у
а<0
D>0
а>0
D>0
х
0
а<0
D=0
а<0
D<0
Найдите корни квадратного трехчлена:
Ι вариант.
а) х2+х-12
б) х2+6х+9.
ΙΙ вариант.
а) 2х2-7х+5;
б) 4х2-4х+1.
Найдите корни квадратного трехчлена:
а) х2+х-12;
б) х2+6х+9;
ΙΙ вариант.
а) 2х2-7х+5;
б) 4х2-4х+1;
x1=-4; x2=3
x1,2=-3
x1=1; x2=2,5
x1,2=0,5
Решение квадратных
неравенств.

Квадратным называется неравенство, левая часть
которого − квадратный трёхчлен, а правая часть
равна нулю.
ах²+bх+с>0
ах²+bх+с<0
ах²+bх+с≥0
ах²+bх+с≤0
Решением неравенства с одним неизвестным
называется то значение неизвестного, при котором
это неравенство обращается в верное числовое
неравенство.
Решить неравенство − это значит найти все его
решения или установить, что их нет.
v0 sin
h h0
2g
2
2
v0 sin 60
3
2 9,8
h- высота подъема тела над
землей;
v0- начальная скорость;
g- ускорение свободного
падения;
h0- начальная высота
α – угол наклона
h=3м;
α =60º
Являются ли следующие неравенства
квадратными?
2×2 4x 6
a)
0;
2
г )4 y 2 5 y 7 0;
б )4 x 2 x 0;
д)5x 6 x 4 0;
в )2 x 4 0;
е)3 y 5 y 2 7 0.
2
2
Решите неравенство
х²+7х-8 < 0.
Алгоритм решения
квадратных неравенств:
1. Приведите неравенство к виду
ах²+bх+с>0 (≥0) , ах²+bх+с>0 (≤0) .
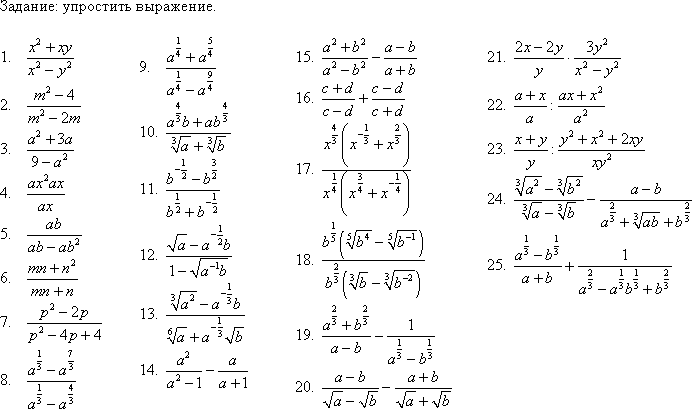
2. Рассмотрим функцию
у=х²+7х-8 .
2. Рассмотрите функцию
у=ах²+bх+с .
3. Определите направления
ветвей.
4. Найдите точки пересечения
параболы с осью абсцисс (для них
у=0; х1 и х2 найдите, решая
уравнение ах²+bх+с=0 ).
5. Схематически постройте
график функции у=ах²+bх+с .
6. Выделите часть параболы для
которой у>0 (≥0) или у<0 (≤0).
7. На оси абсцисс выделите те
значения х, для которых у>0 (≥0)
или у<0 (≤0).
8. Запишите ответ.
3. Графиком функции является
парабола, ветви которой
4. х²+7х-8=0 .
По теореме Виета
х 1+х 2=-7
х 1·х 2=-8
5,6,7.
−8
х 1= -8
х 2=1
//////////////////////
1
.
8. Ответ:
8;1
х
Решите неравенство
х2 – 3х 0
у = х2 – 3х
-7 -6 -5 -4 -3 -2 -1
о
х2 – 3х = 0
х(х-3)=0
х=0 или х-3=0
х=3
1
2
3
4
5
6
7
х
Ответ : ( ;0] [3; )
Решите неравенство
– х2 – 3х > 0
Ответ : ( 3; 0)
у = – х2 – 3х
-7 -6 -5 -4 -3 -2 -1
о
1
2
3
4
5
6
7
х
.

Решите неравенство
– х2 – 3х 0
Ответ :[ 3; 0]
х
Решите неравенство
– х2 + 5х–9,6 > 0
-х2 +5х-9,6 = 0
х²-5х+9,6=0
D=25-38,4=-13,4<0
нет корней,
парабола не
пересекает ось х
Ответ :
Решите неравенство
– х2 +5х–9,6< 0
у = – х2 + 5х –9,6
Ответ : х R.
Решите неравенство
х2 – 6х+ 9 < 0
х2 – 6х+ 9 = 0
(х-3)²=0
х-3=0
х=3
у = х2 – 6х +9
Ответ :
Решите неравенство
х2 –6х + 9 0
3
х
Ответ : х 3
Решите неравенство
х2 –6х + 9 > 0
Ответ
: х 3.
.
Решите неравенство
х2 –6х + 9 0
Ответ : х R.
Решите неравенство
х2 + 4х < 0
1
[-4; 0]
2
(-4; 0)
у
ВЕРНО!
-7 -6 -5 -4 -3 -2 -1
3
; 4 0;
4
( ; 4] [0; )
Сделайте клик на прямоугольнике с цифрой.
7
6
5
4
3
2
1
х
-1 1 2 3 4 5 6 7
-2
-3
-4
-5
-6
-7
у
Решите неравенство
х2 + 4х ≥ 0
1
[-4; 0]
2
(-4; 0)
7
6
5
4
3
2
1
ВЕРНО!
-7 -6 -5 -4 -3 -2 -1
3
( ; 4] [0; )
4
; 4 0;
Сделайте клик на прямоугольнике с цифрой.

х
-1 1 2 3 4 5 6 7
-3
-4
-5
-6
-7
у
Решите неравенство
– х2 + 4х–6 ≥ 0
1
2
3
4
7
6
5
4
3
2
1
x=2
; 2 ( 2; )
-7 -6 -5 -4 -3 -2 -1
нет решений
;
ВЕРНО!
Сделайте клик на прямоугольнике с цифрой.
х
-1 1 2 3 4 5 6 7
-2
-3
-4
-5
-6
-7
у
Решите неравенство
– х2 + 6х–9 < 0
1
x=3
2
х R
7
6
5
4
3
2
1
-7 -6 -5 -4 -3 -2 -1
3
нет решений
4
; 3 (3; )
ВЕРНО!
Сделайте клик на прямоугольнике с цифрой.
х
-1 1 2 3 4 5 6 7
-2
-3
-4
-5
-6
-7
Найдите все значения а, при которых
неравенство х²+(2а+4)х+8а+1 ≤ 0 не имеет
решений?
Решение.
f(x)= х²+(2а+4)х+8а+1
Ветви параболы направлены вверх, т.к. старший
коэффициент равен 1.
D<0
х
D=b²-4ac
D=(2a+4)² -4·1·(8a+1)=4a²+16a+16 -32a-4=
=4a²-16a+12
4a²-16a+12< 0
a²-4a+3< 0
g(a)= a²-4а+3
g(a)= 0
a²-4а+3=0
По теореме Виета
a 1+а 2=4
а 1=1
a 1·а 2=3
а 2=3
1
//////////
3
а
а 1; 3
Ответ: при а 1; 3
неравенство х²+(2а+4)х+8а+1 ≤ 0
не имеет решений.

English Русский Правила
Тема 6. АЛГЕБРАИЧЕСКИЕ НЕРАВЕНСТВА. КВАДРАТНЫЕ НЕРАВЕНСТВА. РАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА ВЫСШИХ СТЕПЕНЕЙ. ДРОБНО-РАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА.Теория. Ключевые методы решения задач. Упражнения. | Материал для подготовки к ЕГЭ (ГИА, алгебра, 9 класс) по теме:
Тема 6. Алгебраические неравенства.
Квадратные неравенства. Рациональные неравенства высших степеней.
Дробно-рациональные неравенства.
Методы решения неравенств зависят в основном от того, к какому классу относятся функции, составляющие неравенство.
I. Квадратные неравенства, то есть неравенства вида
ax2 + bx + c > 0 (
Будем считать, что a>0. Если это не так, то умножив обе части неравенства на -1 и изменив знак неравенства на противоположный, получим желаемое.
Чтобы решить неравенство можно:
1. Квадратный трехчлен разложить на множители, то есть неравенство записать в виде
a (x — x1) (x — x2) > 0 (
2. Корни многочлена нанести на числовую ось. Корни разбивают множество действительных чисел на промежутки, в каждом из которых соответствующая квадратичная функция будет знакопостоянной.
Корни разбивают множество действительных чисел на промежутки, в каждом из которых соответствующая квадратичная функция будет знакопостоянной.
3. Определить знак a (x — x1) (x — x2) в каждом промежутке и записать ответ.
Если квадратный трехчлен не имеет корней, то при D0 квадратный трехчлен при любом x положителен.
Примеры:
- Решить неравенство. x2 + x — 6 > 0.
Решение.
Разложим квадратный трехчлен на множители (x + 3) (x — 2) > 0
Наносим корни трехчлена на числовую ось и определяем знаки на каждом промежутке
+ — +
-3 2 х
Ответ: x (-∞; -3) (2; +∞).
2) (x — 6)2 > 0
Решение:
Это неравенство верно при любом х, кроме х = 6.
Ответ: (-∞; 6) (6; +∞).
3) x² + 4x + 15
Решение:
Здесь D 0. Квадратный трехчлен положителен при всех х.
Ответ: x Ø.
Решить неравенства:
- 1 + х — 2х²
- 3х² — 12х + 12 ≤ 0. Ответ:
- 3х² — 7х + 5 ≤ 0. Ответ:
- 2х² — 12х + 18 > 0. Ответ:
- При каких значениях a неравенство
x² — ax > выполняется для любых х? Ответ:
II. Рациональные неравенства высших степеней, то есть неравенства вида
anxn + an-1xn-1 + … + a1x + a0 > 0 (2.
Многочлен высшей степени следует разложить на множители, то есть неравенство записать в виде
an (x — x1) (x — x2) ·…· (x — xn) > 0 (
Отметить на числовой оси точки, в которых многочлен обращается в нуль.
Определить знаки многочлена на каждом промежутке.
Примеры:
1) Решить неравенство x4 — 6×3 + 11×2 — 6x
Решение:
x4 — 6×3 + 11×2 — 6x = x (x3 — 6×2 + 11x -6) = x (x3 — x2 — 5×2 + 5x +6x — 6) =x (x — 1)( x2 -5x + 6) =
x (x — 1) (x — 2) (x — 3). Итак, x (x — 1) (x — 2) (x — 3)
Итак, x (x — 1) (x — 2) (x — 3)
+ — + — +
0 1 2 3 х
Ответ: (0; 1) (2; 3).
2) Решить неравенство (x -1)5 (x + 2) (x — ½)7 (2x + 1)4
Решение:
Отметим на числовой оси точки, в которых многочлен обращается в нуль. Это х = 1, х = -2, х = ½, х = — ½.
— + + — +
-2 — ½ ½ 1 х
В точке х = — ½ смены знака не происходит, потому что двучлен (2х + 1) возводится в четную степень, то есть выражение (2x + 1)4 не меняет знак при переходе через точку х = — ½.
Ответ: (-∞; -2) (½; 1).
3) Решить неравенство: х2 (х + 2) (х — 3) ≥ 0.
Решение:
Данное неравенство равносильно следующей совокупности
+ — — +
-2 0 3 x
Решением (1) является х (-∞; -2) (3; +∞). Решением (2) являются х = 0, х = -2, х = 3. Объединяя полученные решения, получаем х (-∞; -2 3; +∞).
Решением (2) являются х = 0, х = -2, х = 3. Объединяя полученные решения, получаем х (-∞; -2 3; +∞).
Ответ: х (-∞; -2 3; +∞).
Решить неравенства:
- (5х — 1) (2 — 3х) (х + 3) > 0. Ответ:
- x3 + 5×2 +3x — 9 ≤ 0. Ответ:
- (x — 3) (x — 1)² (3x — 6 — x²)
- (x² -x)² + 3 (x² — x) + 2 ≥ 0. Ответ:
III. Дробно-рациональные неравенства.
При решении таких неравенств можно придерживаться следующей схемы.
1. Перенести все члены неравенства в левую часть.
2. Все члены неравенства в левой части привести к общему знаменателю, то есть неравенство записать в виде
> 0 (
3. Найти значения х, при которых функция y= может менять свой знак. Это корни уравнений
4. Нанести найденные точки на числовую ось. Эти точки разбивают множество действительных чисел на промежутки, в каждом их которых функция будет знакопостоянной.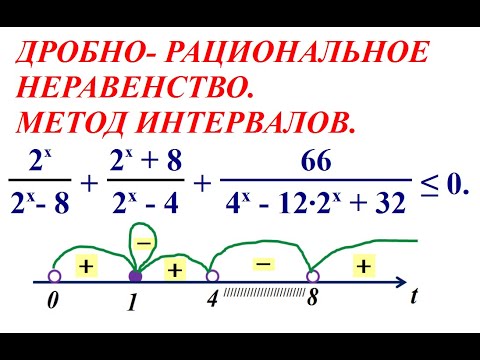
5. Определить знак в каждом промежутке, вычисляя, например, значение данного отношения в произвольной точке каждого промежутка.
6. Записать ответ, обращая особое внимание на граничные точки промежутков. При решении строгого неравенства >0 ( ≥ 0 ( ≤ 0), если точка является корнем знаменателя, то она не включается в ответ (даже если она одновременно является корнем числителя). Если же точка является корнем одного числителя, то она включается в ответ.
Примеры.
1). Решить неравенство .
Решение: > 0, > 0, > 0
Найдем нули числителя и знаменателя. Это х = 3, х = 5, х=1. Наносим найденные точки на числовую ось и определяем знаки в каждом промежутке
— + + —
1 3 5 x
Выбираем любой х(5; +), например х = 10. Тогда
Выбираем х = 4 (3; 5).
Получаем > 0. При х = 2 (1; 3). Получаем > 0.
При х = 2 (1; 3). Получаем > 0.
Наконец, при х = 0 (-; 1). Вычисляем
Ответ: х (1; 3) (3; 5).
2). Найти сумму целых решений неравенства.
Решение. Найдем нули числителя и знаменателя дроби. Это х = -1, х=8, х = 3, х= 5.
Нанесем найденные точки на числовую ось и определим знак дроби в каждом промежутке, вычисляя значение этой дроби в произвольной точке каждого промежутка.
— + + — —
-1 3 5 8 х
Решением исходного неравенства является
х [-1, 3) (3; 5) {8}. Найдем сумму целых решений: -1 +1+0+ 2 + 4 + 8 = =14.
Ответ: 14.
Решить неравенства:
1) . Ответ:
2) >- . Ответ:
3) +
4) > 0. Ответ:
Ответ:
5) — . Ответ:
6) Найти сумму целых решений неравенства . Ответ:
Некоторые интегральные неравенства дробного порядка через предынвексную функцию $ h $-Годунова-Левина
В последние годы изучаются интегральные неравенства из-за их широкого применения в нескольких областях. Целью статьи является исследование некоторых новых дробно-интегральных неравенств, включающих неравенство Эрмита-Адамара и различные формы неравенств типа трапеций, связанных с неравенством Эрмита-Адамара для $ h $-Годуновой-Левина предывексной функции. Кроме того, мы сравниваем полученные нами результаты с имеющимися в литературе работами и представляем следствия.
| [1] | CJ Huang, G. Rahman, K.S. Nisar, A. Ghaffar, F. Qi, Некоторые неравенства типа Эрмита-Адамара для $k$-дробных согласных интегралов,  Math. Анальный. заявл. , 16 (2019), 1–9. Math. Анальный. заявл. , 16 (2019), 1–9. | ||
| [2] | К. С. Нисар, Г. Рахман, К. Мехрез, Неравенства типа Чебышева через обобщенные дробно-согласные интегралы, Дж. Неравный. заявл. , 2019 (2019), 245. https://doi.org/10.1186/s13660-019-2197-1 doi: 10.1186/s13660-019-2197-1 | ||
| [3] | К.С. Ниаср, А. Тасадик, Г. Рахман, А. Хан, Некоторые неравенства с помощью дробно-согласных интегральных операторов, J. Inequal. заявл. , 2019 (2019), 217. https://doi.org/10.1186/s13660-019-2170-z doi: 10.1186/s13660-019-2170-z | ||
| [4] | Ф. Ци, Г. Рахман, С. М. Хуссейн, В. С. Ду, К. С. Нисар, Некоторые неравенства типа Чебышева для согласных $k$-дробных интегральных операторов, Symmetry , 2018 (2018), 614. https://doi .org/10.3390/sym10110614 doi: 10.3390/sym10110614 | ||
| [5] | Г. Рахман, К. С. Нисар, Ф. Ци, Некоторые новые неравенства типа Грусса для согласных дробных интегралов, AIMS Math. , 3 (2018), 575–583. Рахман, К. С. Нисар, Ф. Ци, Некоторые новые неравенства типа Грусса для согласных дробных интегралов, AIMS Math. , 3 (2018), 575–583. | ||
| [6] | Г. Рахман, К. С. Нисар, А. Гаффар, Ф. Ци, Некоторые неравенства типа Грюсса для согласных $k$-дробных интегральных операторов, RACSAM , 114 (2020), 9. https://doi. org/10.1007/s13398-019-00731-3 doi: 10.1007/s13398-019-00731-3 | ||
| [7] | Г. Рахман, З. Уллах, А. Хан, Э. Сет, К. С. Нисар, Некоторые неравенства типа Чебышева с участием дробно-согласных интегральных операторов, Математика , 7 | ||
| [8] | Г. Рахмнан, Т. Абдельджавад, Ф. Джарад, К. С. Нисар, Границы обобщенных пропорциональных дробных интегралов в общем виде через выпуклые функции и их приложения, Математика , 8 (2020), 113. https://doi.org/10.3390/math8010113 doi: 10.3390/math8010113 https://doi.org/10.3390/math8010113 doi: 10.3390/math8010113 | ||
| [9] | XZ Yang, G. Farid, W. Nazeer, YM Chu, CF Dong, Дробные обобщенные неравенства Адамара и Фейера-Адамара для m-выпуклой функции, AIMS Math. , 5 (2020), 6325–6340. | ||
| [10] | М. Вивас-Кортес, М. А. Али, А. Кашури, Х. Будак, А. Влора, Обобщения дробных неравенств Эрмита-Адамара-Мерсера для выпуклых функций, AIMS Math , 6 (2021), 9397–9421 . https://doi.org/10.3934/math.2021546 doi: 10.3934/math.2021546 | ||
| [11] | А. Гессаб, Точные приближения на основе триангуляций Делоне и диаграмм Вороного , Издательско-полиграфический центр НГУ, 2022, 386. | ||
| [12] | L. ER, Uber die fourierreihen, Ⅱ, Math. Натурвисс. Анц. Унгар. акад. Висс , 24 (1906), 369–390. | ||
| [13] | С. Мехмуд, Ф. Зафар, Н. Асмин, Новые неравенства типа Эрмита-Адамара-Фейера для $(\eta_{1}, \eta_{2})$-выпуклых функций с помощью дробного исчисления, ScienceAsia , 46 (2020), 102–108. https://doi.org/10.2306/scienceasia1513-1874.2020.012 doi: 10.2306/scienceasia1513-1874.2020.012 Мехмуд, Ф. Зафар, Н. Асмин, Новые неравенства типа Эрмита-Адамара-Фейера для $(\eta_{1}, \eta_{2})$-выпуклых функций с помощью дробного исчисления, ScienceAsia , 46 (2020), 102–108. https://doi.org/10.2306/scienceasia1513-1874.2020.012 doi: 10.2306/scienceasia1513-1874.2020.012 | ||
| [14] | С. М. Аслани, М. Р. Делавар, С. М. Вэзпур, Неравенства типа Фейера, связанные с обобщенными выпуклыми функциями, Int. Дж. Анал. заявл. , 16 (2018), 38–49. | ||
| [15] | М. Ростамян Делавар, С. Мохаммади Аслани, Де Ла Сен, М. Неравенство Эрмита-Адамара-Фейера, связанное с обобщенными выпуклыми функциями через дробные интегралы, Дж. Матем. , 2018 (2018). https://doi.org/10.1155/2018/5864091 doi: 10.1155/2018/5864091 | ||
| [16] | М. Э. Горджи, М. Р. Делавар, М. Де Ла Сен, О $\phi$-выпуклых функциях. Дж. Матем. Неравенства , 10 (2016), 173–183. https://doi.org/10.7153/jmi-10-15 дои: 10.7153/jmi-10-15 Неравенства , 10 (2016), 173–183. https://doi.org/10.7153/jmi-10-15 дои: 10.7153/jmi-10-15 | ||
| [17] | М. Э. Горджи, М. Р. Делавар, С. С. Драгомир, Некоторые неравенства, связанные с $\eta$-выпуклыми функциями, Препринт Rgmia Res. Респ. сб. , 18 (2015), 1–14. | ||
| [18] | М. Р. Делавар, С. С. Драгомир, О $\eta$-выпуклости. J. Применение неравенств. , 20 (2017), 203–216. https://doi.org/10.7153/mia-20-14 doi: 10.7153/mia-20-14 | ||
| [19] | М. Эшаги, С. С. Драгомир, М. Ростамян Делавар, Неравенство, связанное с $\eta $-выпуклыми функциями (Ⅱ), Int. J. Нелинейный анализ. заявл. , 6 (2015), 27–33. | ||
| [20] | В. Джеякумар, Сильная и слабая сложность в математическом программировании, Мельбурнский университет, факультет математики , 55 (1984), 109–125. | ||
| [21] | А. Бен-Исраэль, Б. Монд, Что такое invexity? Дж. Ост. Мат. соц. , 28 (1986), 1–9. https://doi.org/10.1017/S0334270000005142 doi: 10.1017/S0334270000005142 | ||
| [22] | М. А. Хэнсон, Б. Монд, Проблемы выпуклого трансформируемого программирования и сложность, J. Inform. Оптим. науч. , 8 (1987), 201–207. https://doi.org/10.1080/02522667.1987.10698886 doi: 10.1080/02522667.1987.10698886 | ||
| [23] | М. З. Сарыкая, Э. Сет, Х. Ялдиз, Н. Басак, Неравенства Эрмита-Адамара для дробных интегралов и связанные с ними дробные неравенства, Math. вычисл. Модель. , 57 (2013), 2403–2407. https://doi.org/10.1016/j.mcm.2011.12.048 doi: 10.1016/j.mcm.2011.12.048 | ||
| [24] | С. С. Драгомир, Два отображения в связи с неравенствами Адамара, J. Math. Анальный. заявл. , 167 (1992), 49–56. https://doi.org/10.1016/0022-247X(92) заявл. , 167 (1992), 49–56. https://doi.org/10.1016/0022-247X(92) | ||
| [25] | А. Альмутаири, А. Киличман, Новые уточнения неравенства Адамара о скоординированной выпуклой функции, J. Inequal. заявл. , 2019 (2019), 1–9. | ||
| [26] | С. С. Драгомир, Интегральные неравенства Лебега типа Йенсена для $\lambda $-выпуклых функций, Армянский J. Math. , 10 (2018), 1–19. https://doi.org/10.1186/s13660-019-2143-2 doi: 10.1186/s13660-019-2143-2 | ||
| [27] | С. С. Драгомир, Р. П. Агарвал, Два неравенства для дифференцируемых отображений и приложения к специальным средним действительным числам и формуле трапеций, Appl. Мат. лат. , 11 (1998), 91–95. https://doi.org/10.1016/S0893-9659(98)00086-X doi: 10.1016/S0893-9659(98)00086-X | ||
| [28] | М. Самраиз, Ф. Наваз, С. Икбал, Т. Абдельджавад, Г. Рахман, К. С. Нисар, Некоторые дробно-интегральные неравенства среднего типа через различные выпуклости с приложениями, J. Inequal. заявл. , 2020 (2020), 1–19. https://doi.org/10.1186/s13660-020-02474-x doi: 10.1186/s13660-020-02474-x Самраиз, Ф. Наваз, С. Икбал, Т. Абдельджавад, Г. Рахман, К. С. Нисар, Некоторые дробно-интегральные неравенства среднего типа через различные выпуклости с приложениями, J. Inequal. заявл. , 2020 (2020), 1–19. https://doi.org/10.1186/s13660-020-02474-x doi: 10.1186/s13660-020-02474-x | ||
| [29] | К. Никулеску, Л. Э. Перссон, Выпуклые функции и их приложения , (стр. xvi+-255), Нью-Йорк: Springer. | ||
| [30] | BG Pachpatte, О некоторых интегральных неравенствах, включающих выпуклые функции, RGMIA Res. Респ. Собрать. , 3 (2000). | ||
| [31] | М. Тунц, О некоторых новых неравенствах для выпуклых функций, Turkish J. Math. , 36 (2012), 245–251. | ||
| [32] | О. Альмутаири, А. Киличман, Новые дробные неравенства типа средней точки через s-выпуклость и их применение, J. Inequal. заявл. , 2019 (2019), 1–19. https://doi.org/10.1186/s13660-019-2215-3 doi: 10.1186/s13660-019-2215-3 Inequal. заявл. , 2019 (2019), 1–19. https://doi.org/10.1186/s13660-019-2215-3 doi: 10.1186/s13660-019-2215-3 | ||
| [33] | О. Алабдали, А. Гессаб, Г. Шмайссер, Характеристики равномерной выпуклости для дифференцируемых функций. Заяв. Анальный. Дискретная математика. , 13 (2019), 721–732. https://doi.org/10.2298/AADM1 | 029A doi: 10.2298/AADM1 | 029A |
| [34] | А. Гессаб, О. Нуиссер, Г. Шмайссер, Повышение алгебраической точности линейного оператора и следствия при положительности, Позитивность , 13 (2009), 693–707. https://doi.org/10.1007/s11117-008-2253-4 doi: 10.1007/s11117-008-2253-4 | ||
| [35] | А. Гессаб, Обобщенные барицентрические координаты и приближения выпуклых функций на произвольных выпуклых многогранниках, Comput. Мат. заявл. , 66 (2013), 1120–1136. https://doi.org/10.1016/j.camwa.2013.07.014 doi: 10.1016/j.camwa.2013.07.014 https://doi.org/10.1016/j.camwa.2013.07.014 doi: 10.1016/j.camwa.2013.07.014 | ||
| [36] | JE Peajcariaac, YL Tong, Выпуклые функции, частичные упорядочения и статистические приложения , (1992), Academic Press. https://doi.org/10.1016/S0076-5392(08)62813-1 | ||
| [37] | X. Цян, Г. Фарид, М. Юссуф, К. А. Хан, А. У. Рахман, Новые обобщенные дробные версии неравенств Адамара и Фейера для гармонически выпуклых функций, Дж. Неравный. заявл. , 2020 (2020), 1–13. https://doi.org/10.1186/s13660-020-02457-y doi: 10.1186/s13660-020-02457-y | ||
| [38] | И. Искан, С. Ву, Неравенства типа Эрмита-Адамара для гармонически выпуклых функций через дробные интегралы, Appl. Мат. вычисл. , 238 (2014), 237–244. https://doi.org/10.1016/j.amc.2014.04.020 doi: 10.1016/j.amc.2014.04.020 | ||
| [39] | Д. А. Ион, Некоторые оценки неравенства Эрмита-Адамара через квазивыпуклые функции, Ann. ун-т Крайова-мат. , 34 (2007), 82–87. А. Ион, Некоторые оценки неравенства Эрмита-Адамара через квазивыпуклые функции, Ann. ун-т Крайова-мат. , 34 (2007), 82–87. | ||
| [40] | С. С. Драгомир, К. Пирс, Избранные темы о неравенствах Эрмита-Адамара и приложениях, Архив препринтов по математике , 2003 (2003), 463–817. | ||
| [41] | Х. Чен, У. Н. Катугампола, Неравенства типа Эрмита-Адамара и Эрмита-Адамара-Фейера для обобщенных дробных интегралов, J. Math. Анальный. заявл. , 446 (2017), 1274–1291. https://doi.org/10.1016/j.jmaa.2016.09.018 doi: 10.1016/j.jmaa.2016.090,018 | ||
| [42] | С. С. Драгомир, Интегральные неравенства типа Йенсена для $\lambda$-выпуклых функций, Матем. Вестн. , 68 (2016), 45–57. | ||
| [43] | М. Э. Оздемир, Некоторые неравенства для функций типа s-Годунова-Левина, Мат. науч. , 9 (2015), 27–32. https://doi.org/10.1007/s40096-015-0144-y doi: 10.1007/s40096-015-0144-y науч. , 9 (2015), 27–32. https://doi.org/10.1007/s40096-015-0144-y doi: 10.1007/s40096-015-0144-y | ||
| [44] | С. Варошанек, Об h-выпуклости, J. Math. Анальный. заявл. , 326 (2007 г.), 303–311. | ||
| [45] | О. Альмутаири, А. Киличман, Некоторые интегральные неравенства для h-предвыпуклости Годунова-Левина. Симметрия , 11 (2019), 1500. https://doi.org/10.3390/sym11121500 doi: 10.3390/sym11121500 | ||
| [46] | G. H. Toader, Некоторые обобщения выпуклости , В: Сб. Коллок. прибл. Оптим, Клуж-Напока (Румыния), 1984, 329–338. | ||
| [47] | М. Ростамиан Делавар, С. Мохаммади Аслани, М. Де Ла Сен, Неравенство Эрмита-Адамара-Фейера, связанное с обобщенными выпуклыми функциями через дробные интегралы, J. Math. , 2018 (2018). https://doi.org/10. 1155/2018/5864091 doi: 10.1155/2018/5864091 1155/2018/5864091 doi: 10.1155/2018/5864091 | ||
| [48] | Е. К. Годунова, Неравенства для функций широкого класса, содержащего выпуклые, монотонные и некоторые другие формы функций, Numer. Мат. Мат. физ. , 138 (1985), 166. | ||
| [49] | ED Rainville, Special Functions, Chelsea Publ. Co., Бронкс , 1971, Нью-Йорк. | ||
| [50] | Р. Горенфло, Ф. Майнарди, Дробное исчисление: интегральные и дифференциальные уравнения дробного порядка, препринт arXiv , (2008). архив: 0805.3823. | ||
| [51] | С. С. Драгомир, С. Фицпатрик, Неравенства Адамара для s-выпуклых функций во втором смысле, Demonstr. Мат. , 32 (1999), 687–696. https://doi.org/10.1515/dema-1999-0403 doi: 10.1515/dema-1999-0403 | ||
| [52] | И. Искан, Неравенства Эрмита-Адамара для предынвексных функций через дробные интегралы и связанные дробные неравенства, arXiv Preprint , (2012).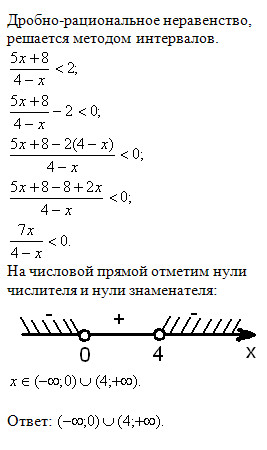 архив: 1204.0272. архив: 1204.0272. | ||
| [53] | М. Муддассар, М. И. Бхатти, М. Икбал, Некоторые новые неравенства типа s-Эрмита-Адамара для дифференцируемых функций и их приложения, Проц. Пакистанская академия наук. , 49 (2012), 9–17. | ||
| [54] | С. С. Драгомир, Р. П. Агарвал, Два неравенства для дифференцируемых отображений и приложения к специальным средним действительным числам и формуле трапеций, Appl. Мат. лат. , 11 (1998), 91–95. https://doi.org/10.1016/S0893-9659(98)00086-X doi: 10.1016/S0893-9659(98)00086-X | ||
| [55] | М. А. Ноор, К. И. Ноор, М. У. Аван, С. Хан, Неравенства Эрмита-Адамара для s-Годуновой-Левина предынвексных функций, J. Adv. Мат. Исследования , 7 (2014), 12–19. |
О BBM-феноменах в дробных неравенствах Пуанкаре–Соболева с весами | Уведомления о международных математических исследованиях
Фильтр поиска панели навигации Уведомления о международных исследованиях в области математикиPure MathematicsBooksJournalsOxford Academic Мобильный телефон Введите поисковый запрос
Закрыть
Фильтр поиска панели навигации Уведомления о международных исследованиях в области математикиPure MathematicsBooksJournalsOxford Academic Введите поисковый запрос
Расширенный поиск
Журнальная статья
Получить доступ
Ритва Хурри-Сюрьянен,
Ритва Хурри-Сюрьянен
Ищите другие работы этого автора на:
Оксфордский академический
Google Scholar
Хавьер К. Мартинес-Пералес,
Мартинес-Пералес,
Хавьер С. Мартинес-Пералес
Ищите другие работы этого автора на:
Оксфордский академический
Google Scholar
Карлос Перес,
Карлос Перес
Ищите другие работы этого автора на:
Оксфордский академический
Google Scholar
Антти В. Вяхакангас
Антти В Вяхакангас
Ищите другие работы этого автора на:
Оксфордский академический
Google Scholar
Уведомления о международных математических исследованиях , rnac246, https://doi.org/10.1093/imrn/rnac246
Опубликовано:
21 сентября 2022 г.
История статьи
получен:
20 апреля 2022 г.
Полученная пересмотр:
13 августа 2022 г.
Принято:
23 августа 2022
Опубликовано:
21 сентябрь 2022
Фильтр поиска панели навигации Уведомления о международных исследованиях в области математикиPure MathematicsBooksJournalsOxford Academic Мобильный телефон Введите поисковый запрос
Закрыть
Фильтр поиска панели навигации Уведомления о международных исследованиях в области математикиPure MathematicsBooksJournalsOxford Academic Введите поисковый запрос
Advanced Search
Abstract
В этой статье мы объединяем и улучшаем некоторые результаты Бургейна, Брезиса и Миронеску, а также взвешенную оценку Пуанкаре–Соболева Фабеса, Кенига и Серапиони. Точнее, мы получаем взвешенные аналоги неравенства типа Пуанкаре–Соболева, а также неравенства типа Харди в дробном случае при некоторых мягких естественных ограничениях. Главной особенностью полученных результатов является тот факт, что мы отслеживаем поведение задействованных констант, когда дробный параметр приближается к |$1$|. Наш основной метод основан на методах гармонического анализа, связанных со свойством самоулучшения обобщенных неравенств Пуанкаре.
Точнее, мы получаем взвешенные аналоги неравенства типа Пуанкаре–Соболева, а также неравенства типа Харди в дробном случае при некоторых мягких естественных ограничениях. Главной особенностью полученных результатов является тот факт, что мы отслеживаем поведение задействованных констант, когда дробный параметр приближается к |$1$|. Наш основной метод основан на методах гармонического анализа, связанных со свойством самоулучшения обобщенных неравенств Пуанкаре.
© Автор(ы), 2022. Опубликовано Oxford University Press. Все права защищены. Для разрешений, пожалуйста, по электронной почте: [email protected].
Раздел выпуска:
Статьи
В настоящее время у вас нет доступа к этой статье.
Скачать все слайды
Войти
Получить помощь с доступом
Получить помощь с доступом
Доступ для учреждений
Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Доступ на основе IP
Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.
Войдите через свое учреждение
Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.
- Нажмите Войти через свое учреждение.
- Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа в систему.
- Находясь на сайте учреждения, используйте учетные данные, предоставленные вашим учреждением.
 Не используйте личную учетную запись Oxford Academic.
Не используйте личную учетную запись Oxford Academic. - После успешного входа вы вернетесь в Oxford Academic.
Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.
Войти с помощью читательского билета
Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Члены общества
Доступ члена общества к журналу достигается одним из следующих способов:
Вход через сайт сообщества
Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
- Щелкните Войти через сайт сообщества.
- При посещении сайта общества используйте учетные данные, предоставленные этим обществом.
 Не используйте личную учетную запись Oxford Academic.
Не используйте личную учетную запись Oxford Academic. - После успешного входа вы вернетесь в Oxford Academic.
Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.
Вход через личный кабинет
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. См. ниже.
Личный кабинет
Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.
Просмотр учетных записей, вошедших в систему
Щелкните значок учетной записи в правом верхнем углу, чтобы:
- Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.

- Просмотр институциональных учетных записей, предоставляющих доступ.
Выполнен вход, но нет доступа к содержимому
Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.
Ведение счетов организаций
Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.
Покупка
Стоимость подписки и заказ этого журнала
Варианты покупки книг и журналов в Oxford Academic
Кратковременный доступ
Чтобы приобрести краткосрочный доступ, пожалуйста, войдите в свой личный аккаунт выше.

 org/10.1093/imrn/rnac246
org/10.1093/imrn/rnac246 Не используйте личную учетную запись Oxford Academic.
Не используйте личную учетную запись Oxford Academic. Не используйте личную учетную запись Oxford Academic.
Не используйте личную учетную запись Oxford Academic.